Первообразная cosx sinx: Mathway | Популярные задачи

3x является первообразной функции f…

Лучший ответ по мнению автора

Михаил Александров 18. 03.19 Лучший ответ по мнению автора

Андрей Андреевич от 70 p. Читать ответы

Eleonora Gabrielyan от 0 p. Читать ответы

Галина Владимировна от 50 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

В треугольнике ABC угол A равен 45 градусов, угол B равен 60 градусов, BC= 6√6. Найдите AC.

Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5√3 см. Напишите решение плиииз

посадили 56 деревьев. 2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные

Через 4 года Вадиму будет 13 лет.Сколько лет будет Вадиму через 10 лет?

Пользуйтесь нашим приложением

Практическое занятие «Вычисление неопределенных интегралов различными методами».

Практическое занятие

Тема: «Математический анализ».

Наименование работы: «Вычисление неопределенных интегралов различными методами».

Цель: Закрепить навыки интегрирования рациональных функций, интегрирования методом замены переменной и интегрирования по частям.

Содержание

Часть 1. Теоретическая

Интегрирование — это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функций находится сама функция.

Дифференцируемая функция F(x), a называется первообразной для функции f(x) на интервале a, если для каждого a.

Так, для функции f(x) = cosx первообразной служит функция F(x) = sinx, поскольку = cosx.

Для заданной функции ее первообразная определяется неоднозначно. Если F(x) – первообразная для f(x) на некотором промежутке, то и функция F(x) + C, где C – любая постоянная, также является первообразной для функции f(x) на этом промежутке. Обратно: каждая функция, являющаяся первообразной для f(x) в данном промежутке, может быть записана в виде F(x) + C.

Совокупность F(x) + Cвсех первообразных функции f(x) на интервале a называют неопределенным интегралом от функции f(x) на этом интервале и пишут = F(x) + C. Здесь – подынтегральное выражение; f(x) – подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.

Пример:

=tgx + C, так как = .

Если функция f(x) имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке a, интегрируема на этом отрезке.

Свойства неопределенного интеграла

1. Дифференциал неопределенного интеграла равен подынтегральному выражению:

d ∫ f(x)dx=f(x) dx.

2.Неопределенный интеграл от дифференциала функции равен этой функции, сложной с произвольной постоянной, т. е.

∫dF(x)=F(x)+C.

3.Постоянный множитель можно выносить за знак неопределенного интеграла:

∫af(x)dx=a∫(x)dx.

4.Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:

∫(f₁(x)±f₂(x))dx=∫f₁(x)dx±∫f₂(x)dx.

Способы интегрирования

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Основные формулы интегрирования (табличные интегралы)

1.∫dx=x+C/

2.∫xⁿdx=(xⁿ⁺¹/n+1)+C (n≠-1).

3.∫x^-1dx=∫dx/x=ln׀x׀+C.

4.∫e^xdx=e^x+C.

5.∫a^xdx=a^x/lna+C.

6.∫sinxdx=-cosx+C.

7.∫cosxdx=sinx+C.

8.∫dx/cos²x = tgx+C.

9.∫dx/sin²x = -ctgx+C.

10.∫dx/√1-x² = arcsinx+C.

11. ∫dx/1+x² = arctgx+C.

Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.

Пример.

Найти∫xdx/√2-3x².

Решение. Проведем подстановку 2-3x²=t; тогда -6xdx=dt, xdx=-(1/6)dt. Далее, получаем∫xdx/√2-3x²=∫-(1/6)dt/√t=-1/6∫t^-1/2dt=-1/6∙t^-1/2+1/(-1/2+1)+C=-1/6∙t^1/2/1/2+C=-1/3√t+C=-1/3√2-3x²+C.

Пример.

Найти ∫(2+cosx)²sinxdx.

Решение. Сначала положим 2+cosx=t; тогда –sinxdx=dt,откуда sinxdx=-dt. Далее, получаем

∫(2+cosx)²sinxdx=∫t²(-dt)=-∫t²dt=-t²⁺¹/(2+1)+C=-1/3t³+C=-1/3(2+cosx)³+C.

Пример.

Найти ∫sin10xdx.

Решение. Положим 10x=t;тогда10dx=dt, откуда dt=(1/10)dt. Далее получаем

∫sin10xdx=∫sint1/10dt=1/10∫sintdt=1/10(-cost)+C=-1/10cost+C=-1/10cos10x+C.

В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы (k≠0, n≠0-постоянные):

1.∫e^kxdx=(1/k)e^kx+C.

2.∫a^kxdx=(1/k)(a^kx/lna+C.

3.∫sinkxdx=(-1/k)coskx+C.

4.∫coskxdx=(1/k)sinkx+C.

5.∫dx/cos²kx=(1/k)tgkx+C.

6.∫dx/sin²kx=(-1/k)ctgkx+C.

7.∫dx/k²+n²x²=(1/nk)arctg (n/k)x+C.

8∫dx/√k²-n²x²=(1/n)arcsin(n/k)x+C.

Так, при вычислении ∫sin10xdx можно использовать формулу ∫sinkxdx=-(1/k)coskx+C, где k=10. Тогда ∫sin10xdx=(-1/10)cos10x+C.

Интегрирование по частям. Общая формула интегрирования по частям имеет вид: где – некоторые функции от х.

Пример.

Вычислить интеграл .

Решение. Обозначим х = , = , находим и . = ,

= = — , найдем = —х + = —х + + С.

Часть 2. Практическая

№	Задание
1	, , ,
2	, , ,
3	, , ,
4	, , ,
5	, , ,
6	, , ,
7	, , ,
8	, , ,
9	, , ,
10	, , ,

Вопросы к практическому занятию

1. Какое действие называется интегрированием?

2.Какая функция называется первообразной для функции f(x)?

3.Дайте определение неопределенного интеграла?

4.Перечислите основные свойства неопределенного интеграла.

5.Каким действием можно проверить интегрирование?

6.Напишите основные формулы интегрирования (табличные интегралы).

Понятие первообразной, приложения первообразной

Понятие первообразной вводится в школе посредством задачи, для решения которой необходимо по известной производной найти (восстановить) саму функцию. Приведём пример такой задачи: «По прямой движется материальная точка, скорость которой в момент времени t задаётся формулой v = gt. Найти закон движения». Используя геометрический смысл производной, для решения задачи следует подобрать функцию, производная которой равна gt. Нетрудно догадаться, что Действительно,

Вводим определение: функцию называют первообразной для функции на заданном промежутке Х, если для любого выполняется равенство .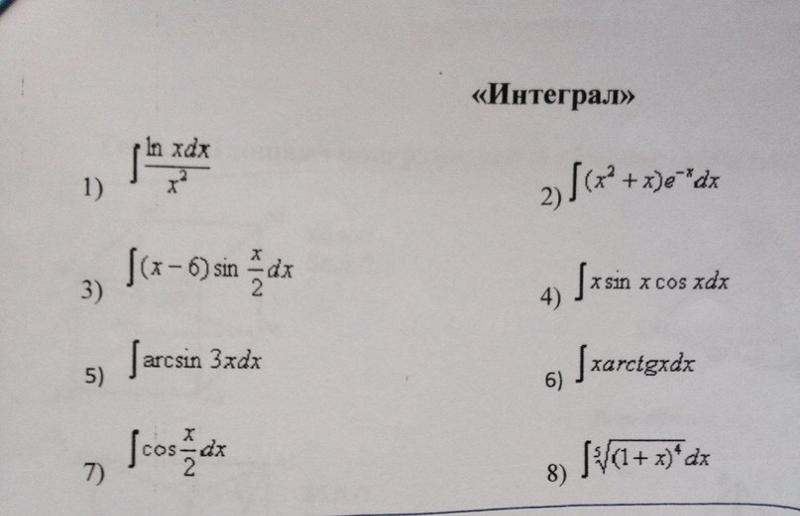

Пример 1. , .

Пример 2. , , .

Контрпример. не является первообразной для функции на промежутке , так как равенство не выполняется при х = 0. Однако на каждом из промежутков и функция является первообразной для функции f.

Для усвоения определения школьникам предлагаются задачи, в которых следует доказать, что некоторая функция F является или не является первообразной для функции f на заданном числовом множестве Х, то есть проверить равенство для всех хÎХ. Формулировка таких заданий может начинаться со слов: «угадайте первообразную функцию».

Когда у учащихся появляется первый опыт работы с понятием первообразной, они изучают теорему об основном свойстве первообразной. Для её доказательства рассматривается лемма (признак постоянства функции): если в каждой точке некоторого промежутка Х, функция

f имеет равную нулю производную, то f – постоянна на этом промежутке.

Дано: функция , Х – числовой промежуток.

при

Доказать:

Что ж это за функция, касательная к графику которой в любой точке параллельна оси Ох? Ясно, что её график – прямая, параллельная оси Ох, то есть функция имеет вид

Приведём доказательство леммы по учебнику Колмогорова.

Доказательство

Зафиксируем некоторое значение х₀ из промежутка Х. Тогда для любого по теореме Лагранжа найдётся такое число с, заключённое между х и х₀, что Так как по условию при , то , следовательно, при всех , то есть функция f сохраняет постоянное значение.

Приведённая лемма имеет богатые алгебраические приложения. Приведём один скромный пример.

Доказать тождество

Пусть . Найдём производную функции f.

, следовательно, . Определим с. Пусть х = 0. , что и требовалось доказать.

Сформулируем основное свойство первообразной.

Теорема.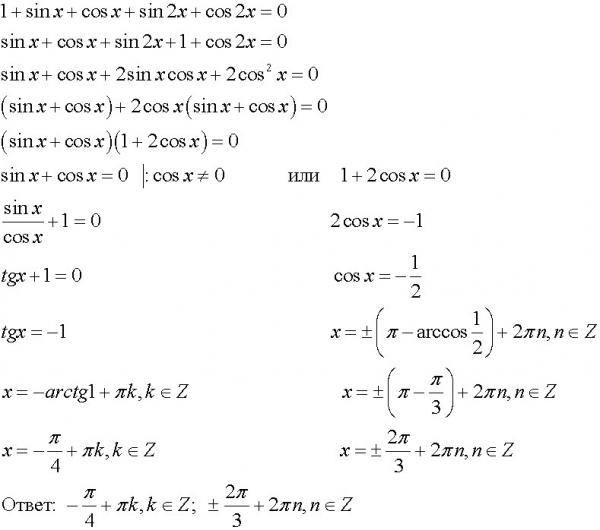 Любая первообразная для функции f на промежутке Х может быть записана в виде F(x) + c, где F(x) – одна из первообразных для функции f, а с – произвольная постоянная.

 

В теореме можно выделить два утверждения:

1) если F(x) – одна из первообразных для функции f , то функция F(x) + c также её первообразная.

Доказательство очевидно. Вывод: первообразная функции f определяется неоднозначно.

2) любая первообразная функции f имеет вид F(x) + c.

Доказательство

(по лемме):

.

Геометрический смысл: графики любых двух первообразных получаются друг из друга параллельным переносом вдоль оси Оу.

Далее совместно с учащимися составляем таблицупервообразных.

Функция у = f(x)			хп, пÎ Z, п ¹ —1		sinx	cosx
Первообразная у = F(x)	C	x+c	+c	+c	— cosx+c	sinx+c	tg x+c	ctg x+c

 

В дальнейшем таблица дополняется первообразными показательной и логарифмической функции.

 

Кроме таблицы первообразных, учащимся сообщаются 3 правила нахождения первообразных.

Правило1.Если F есть первообразная для f, а G — первообразная для g, то F + G есть первообразная для f + g. Правило2.Если F есть первообразная для f, а k -постоянная, то kF – первообразная для kf. Правило3.Если F есть первообразная для f, а k и b -постоянные, причём k¹ 0, то – первообразная для

 

Все 3 правила легко доказываются по определению первообразной. Особое внимание следует уделить записи в правиле 3. Следует обсудить с учащимися её смысл. Так, 1) если , то ; 2) если , то Согласно правилу 3 в здании (1) первообразная функции f равна , а функции равна , а в здании (2)

Первоначально полезно оформлять задания на нахождение первообразной в виде таблицы.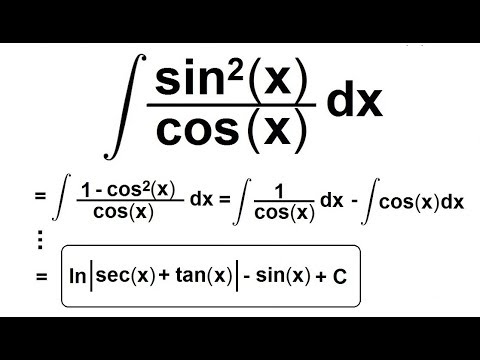 2+3cosx b)… — Учеба и наука

Лучший ответ по мнению автора

Михаил Александров 11. 02.16 Лучший ответ по мнению автора

Андрей Андреевич от 70 p. Читать ответы

Eleonora Gabrielyan от 0 p. Читать ответы

Галина Владимировна от 50 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз

Решено

На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?

Схема района, где живут Маша и Саша, выполнена в масштабе 1:1000. Начертите маршруты, по которым они могут ходить в школу друг к другу в гости и из…

Стоимость автомобиля с гаражом составляет…

Пользуйтесь нашим приложением

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Интегрирование sin x cos x – формула, доказательство

Интегрирование sin x cos x – это процесс определения интеграла sin x cos x относительно x.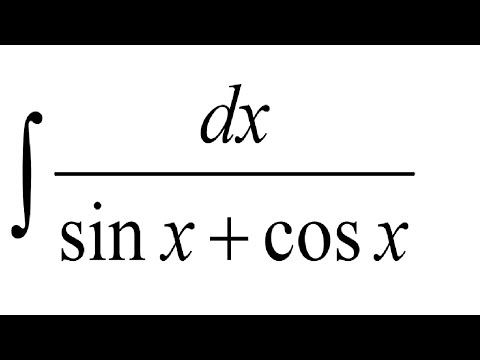 Интегрирование sin x cos x может быть выполнено с использованием различных методов интегрирования. Перед вычислением интеграла от sin x cos x вспомним тригонометрическую формулу, состоящую из sin x cos x, то есть sin 2x = 2 sin x cos x. Интегрирование — это процесс, обратный дифференцированию, поэтому интегрирование sin x cos x также называется антипроизводной sin x cos x.

В этой статье мы изучим интегрирование sin x cos x и выведем его формулу с помощью метода подстановки и формулы sin 2x. Мы также вычислим интегрирование sin x cos x от 0 до π.

1.	Что такое интегрирование Sin x Cos x?
2.	Интеграция формулы Sin x Cos x
3.	Интегрирование Sin x Cos x с использованием формулы 9 Sin 2×0005
4.	Интегрирование Sin x Cos x с использованием метода подстановки
5.	Интегрирование Sin x Cos x От 0 до π
6.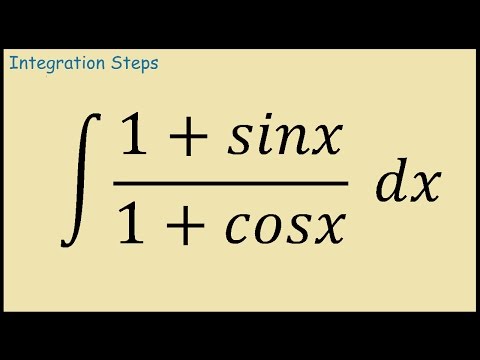	Часто задаваемые вопросы по интеграции Sin x Cos x

Что такое интегрирование Sin x Cos x?

Интегрирование sin x cos x дает площадь под кривой функции f(x) = sin x cos x и дает различные эквивалентные ответы при использовании различных методов интегрирования. Интегрирование sin x cos x дает (-1/4) cos 2x + C как интеграл от sin x cos x с использованием тригонометрической формулы sin 2x. Математически интеграл fo sin x cos x записывается как ∫sin x cos x dx = (-1/4) cos 2x + C, где C — постоянная интегрирования, ∫ обозначает знак интегрирования, а dx показывает, что интегрирование относится к х. Давайте пройдемся по формулам интегрирования sin x cos x.

Интеграция формулы Sin x Cos x

Теперь мы напишем формулы для интегрирования sin x cos x при вычислении с использованием различных формул и методов интегрирования. Интеграл от sin x cos x можно определить, используя формулу sin 2x и метод подстановки. Интегрирование sin x cos x определяется как:

• ∫ sin x cos x dx = (-1/4) cos 2x + C [при оценке по формуле sin 2x]
• ∫ sin x cos x dx = (-1/2) cos ² x + C [при оценке путем подстановки cos x]
• ∫ sin x cos x dx = (1/2) sin ² x + C [при вычислении путем подстановки sin x]

Интегрирование Sin x Cos x с использованием формулы Sin 2x

Мы изучили формулы интегрирования sin x cos x. Далее мы выведем формулу интегрирования sin x cos x, используя формулу sin 2x. Мы будем использовать следующие тригонометрические и интегрированные формулы:

• sin 2x = 2 sin x cos x
• ∫sin (ax) dx = (-1/a) cos (ax) + C

Используя приведенные выше формулы, мы имеем

∫ sin x cos x dx = ∫(2/2) sin x cos x dx [Умножение и деление sin x cos x на 2]

⇒ ∫ sin x cos x dx = (1/2) ∫2 sin x cos x dx

⇒ ∫ sin x cos x dx = (1/2) ∫sin 2x dx [Используя sin 2x = 2 sin x cos x]

⇒ ∫ sin x cos x dx = (1/2) (-1/2) cos 2x + C

⇒ ∫ sin x cos x dx = (-1/4) cos 2x + C

Следовательно, мы получили интеграл от sin x cos x, используя формулу sin 2x.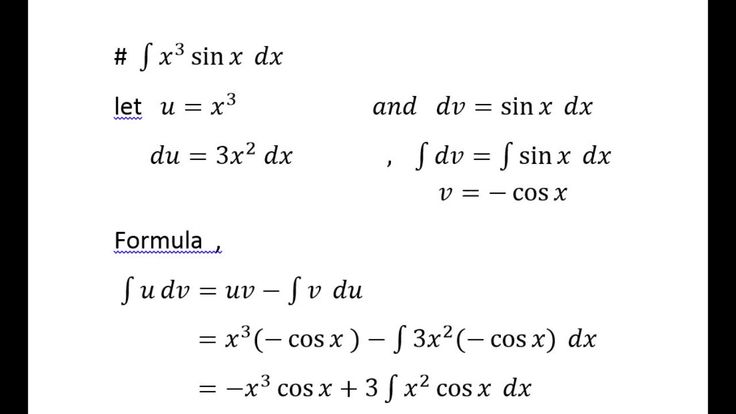

Интегрирование Sin x Cos x с использованием метода подстановки

Теперь мы докажем интегрирование sin x cos x методом подстановки. Мы подставим sin x и cos x отдельно, чтобы определить интеграл от sin x cos x.

Интегрирование Sin x Cos x путем подстановки Sin x

Мы будем использовать следующие формулы для определения интеграла от sin x cos x:

• d(sin x)/dx = cos x
• ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C

Предположим, что sin x = u, тогда мы имеем cos x dx = du. Используя приведенные выше формулы, мы имеем

∫ sin x cos x dx = ∫udu

= u ² /2 + C

⇒ ∫ sin x cos x dx = (1/2) sin ² x + C

Следовательно, мы получили интегрирование sin x cos x, подставив sin x.

Интегрирование Sin x Cos x путем замены Cos x

Мы будем использовать следующие формулы для определения интеграла от sin x cos x:

• d(cos x)/dx = -sin x
• ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1) + C

Предположим, что cos x = v, тогда мы имеем -sin x dx = dv ⇒ sin x dx = -dv.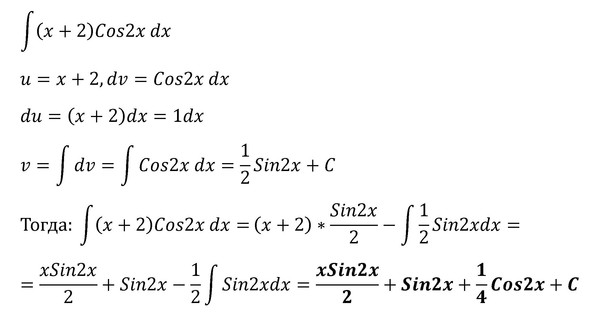 Используя приведенные выше формулы, мы имеем

∫ sin x cos x dx = ∫-vdv

= -v ² /2 + C

⇒ ∫ sin x cos x dx = (-1/2) cos ² x + C

Следовательно, мы получили интегрирование sin x cos x, подставив cos x. 9\pi \\&= \left ( \dfrac{-1}{4}\cos 2\pi + C \right )-\left ( \dfrac{-1}{4}\cos 0 + C \right )\ \&=\left ( \dfrac{-1}{4}+C \right )-\left ( \dfrac{-1}{4}+C \right )\\&=0\end{align}\)

Следовательно, интегрирование sin cos x от 0 до π равно 0.

Важные замечания по интегрированию Sin x Cos x

• ∫ sin x cos x dx = (-1/4) cos 2x + C [При оценке по формуле sin 2x]
• ∫ sin x cos x dx = (-1/2) cos ² x + C [при оценке путем замены cos x]
• ∫ sin x cos x dx = (1/2) sin ² x + C [при вычислении путем подстановки sin x]
• Интегрирование sin cos x от 0 до π равно 0.

Темы, связанные с I Интеграция Sin x Cos x

• Интеграл Tan 2x
• Арктан Интеграл
• Интеграл от Sin, обратный

Часто задаваемые вопросы по интеграции Sin x Cos x

Что такое интегрирование Sin x Cos x в тригонометрии?

Интегрирование sin x cos x дает площадь под кривой функции f(x) = sin x cos x и дает различные эквивалентные ответы при использовании различных методов интегрирования. Интеграл от sinx cosx определяется как ∫ sin x cos x dx = (-1/4) cos 2x + C.

Как найти интеграл от Sin x Cos x?

Мы можем вывести интеграл формулы sin x cos x, используя метод подстановки и формулу sin 2x.

Какие формулы для интегрирования Sin x Cos x?

Интегрирование sin x cos x определяется как:

• ∫ sin x cos x dx = (-1/4) cos 2x + C [при вычислении по формуле sin 2x]
• ∫ sin x cos x dx = (-1/2) cos ² x + C [при оценке путем подстановки cos x]
• ∫ sin x cos x dx = (1/2) sin ² x + C [при вычислении путем подстановки sin x]

Что такое интегрирование Sin x + Cos x?

Интегрирование sin x + cos x равно cos x — sin x + C.

Является ли интегрирование Sin x Cos x тем же самым, что и антипроизводная Sin x Cos x?

Интегрирование есть не что иное, как процесс, обратный дифференцированию, поэтому интеграл функции равен ее первообразной. Следовательно, интегрирование sin x cos x такое же, как антипроизводная sin x cos x.

Интегральный sin, cos, sec2

Интегральный sin, cos, sec2

Дом | Учитель | Родители | Глоссарий | О нас

Отправить эту страницу другу по электронной почте

Ресурсы · · · · · · Поиск    Доказательства: Интеграл sin, cos, sec 2 , csc cot, sec tan, csc 2 (Математика | Исчисление | Интегралы | Стол Из | ResultTrig) Обсуждение кос x dx = sin x + C   sin x dx = -cos x + C   сек 2 x dx = tan x + C   csc x кроватка x dx = -csc x + C   сек x tan x dx = sec x + C   csc 2 х дх = -кот х + С 1. Доказательства Для каждого из них мы просто используем Фундаментальный исчисления, потому что мы знаем их соответствующие производные. cos(x) = sin(x), cos(x) дх = грех(х) + с -грех(х) = cos(x), sin(x) dx = -cos(x) + c 92 (х) dx = -cot(x) + c См. также:  sin(x) = cos(x), cos(x) = -sin(x), tan(x) = sec 2 (x), csc(x) = -csc(x)cot(x), sec(x) = sec(x)tan(x), cot(x) = -csc 2 (x).         Связаться с нами | Реклама и спонсорство | Товарищество | Ссылка на нас © 2000-2005 Math. com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика.     Загадочный интеграл от (sin x)(cos x) — воскресная головоломка — обдумывайте свои решения Если вы покупаете по ссылке в этом посте, я могу получить комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше. Опубликовано 9 августа 2015 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне . Интеграл от (sin x )(cos x ) был задан на уроке математики. Альберт думал о проблеме с точки зрения u-подстановки. Он поставил u = sin x , так что du = cos x dx . Затем он решил задачу следующим образом, чтобы получить ответ (1/2)sin 2 x + C . Бернар также сделал u-подстановку, но он установил u = cos x . Это будет означать, что du = -sin x dx . Затем он решил задачу следующим образом, чтобы получить ответ -(1/2)cos 2 x + С . Шерил придумала совершенно другое решение. Она использовала тождество двойного угла, что sin(2 x ) = 2(sin x )(cos x ). Итак, она отметила, что (1/2)sin(2 x ) = (sin x )(cos x ), поэтому проблема сводилась к интегрированию (1/2)sin(2 x ). Это приводит к ответу -(1/4)cos(2 x ) + C . Все методы кажутся правильными, но трое студентов дали разные ответы. Как это возможно? . . «Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon. . . . . . . М И Н Д . И О У Р . D E C I S I O N S . S U N D A Y . P U Z Z L E . . . . Видео-ответ на сложный интеграл от (sin x)(cos x) Я подготовил видео, которое объясняет эквивалентность ответов на интегралы. Объяснение эквивалентности начинается в 14:00. Непонятный интеграл от (sin x)(cos x) Текст решения ниже. Графическая интуиция Хотя ответы выглядят по-разному, все они являются эквивалентными антипроизводными, поскольку каждый отличается на постоянную величину от других. Вот графики антипроизводных. Как видите, все графики представляют собой вертикальные переносы друг друга — каждая функция отличается от другой на постоянную величину. Антипроизводные, отличающиеся константой, эквивалентны друг другу, поэтому решения на самом деле представляют собой 3 способа записи одной и той же антипроизводной. Тригонометрические доказательства эквивалентности Хотя ответы выглядят по-разному, все они являются эквивалентными антипроизводными, поскольку каждый отличается на постоянную величину от других. Сначала покажем, почему ответы Альберта и Бернара совпадают. Вспомним тождество sin 2 x + cos 2 x = 1. Мы можем переписать это как sin 2 x = 1 – cos 2. Итак, ответ Альберта на (1/2)sin 2 x + C можно записать как (1/2)(1 – cos 2 x ) + C = 1/2 – (1/2)cos 2 09 x 9 + С . Константу 1/2 можно сгруппировать с произвольной константой C , чтобы получить -(1/2)cos 2 x + C . Другими словами, мы определили, что ответы Альберта и Бернара эквивалентны. Что насчет ответа Шерил? Это также эквивалентная антипроизводная. Мы будем использовать формулу двойного угла cos(2 x ) = 2 cos 2 x – 1. Таким образом, ответ Шерил -(1/4)cos(2 x ) + C можно переписать как -(1/4 )[2 cos 2 x – 1] + C = -(1/2) cos 2 x + 1/4 + C . Константу 1/4 можно сгруппировать с произвольной константой C , поэтому ответ будет -(1/2)cos 2 x + C , и поэтому этот ответ также эквивалентен ответам Альберта и Бернара. Интересно, что есть 3 разных подхода к решению этого интеграла, которые дают, казалось бы, разные ответы. В конце концов, ответы равнозначны антипроизводным. Вдохновение для головоломки https://www.youtube.com/watch?v=K5G0s5OzTig МОИ КНИГИ Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите. Рейтинги книг по состоянию на январь 2022 года. 1) Радость теории игр: введение в стратегическое мышление (2) 40 парадоксов логики, теории вероятностей и теории игр (3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения (4) Лучший менталитет Математические трюки (5) Умножение чисел путем рисования линий The Joy of Game Theory показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах) 40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд по 24 отзывам) Лучшие математические трюки в уме учит, как можно выглядеть гением математики, решая задачи в уме (оценка 4,2/5 звезд в 76 обзорах) Умножение чисел путем рисования линий Эта книга является справочником руководство для моего видео, которое имеет более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,3/5 звезд в 30 обзорах) Загадывайте свои головоломки представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр. Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам. Математические головоломки, том 2 — продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам) Math Puzzles Volume 3 — третья книга в серии. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт