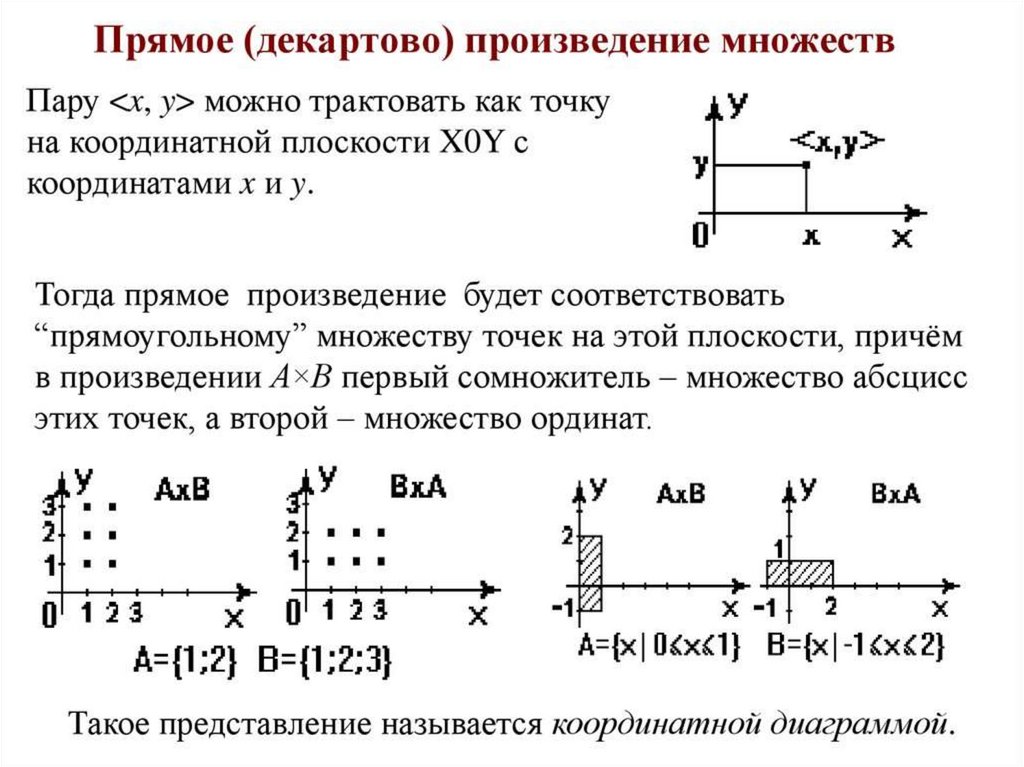
Основные свойства декартова произведения.
1. Если , то . То есть декартово произведение множеств не обладает свойством коммутативности.
Действительно, по определению если то , а . Но так как , то . Отсюда .
2. Декартово произведение множеств не обладает свойством ассоциативности: для любых множеств .
3. Если хотя бы одно из множеств А или В пусто, то и декартово произведение этих множеств есть множество пустое:
Ø= Ø Ø Ø = Ø.
Это свойство следует из понятия декартова произведения и понятия пустого множества.
4. Для любых трех множеств справедливы следующие утверждения:
4.1.
4.
4.3.
Докажем, например, свойство 4.3.
Обозначим множество , а множество . Покажем, что .
Пусть , тогда по определению декартова произведения множеств . По определению разности двух множеств получим: . Так как , то пара . Из того, что следует, что пара . Тогда по определению разности двух множеств пара . В силу доказанного и произвольности выбора элемента во множестве можно сделать вывод о том, что
Докажем, что .
Пусть .
Тогда по определению разности двух
множеств ,
и .
По определению декартова произведения
двух множеств .
Так как ,
то .
Тогда будем иметь ,
откуда следует, что . В силу доказанного и произвольности
выбора элемента во множестве можно
сделать вывод о том, что .
В силу доказанного и произвольности
выбора элемента во множестве можно
сделать вывод о том, что .
Так как и , то , что и требовалось доказать.
Теорема: Число элементов в декартовом произведении двух конечных множеств А и В равно произведению чисел элементов в каждом из них:
.
Раздел II. Элементы комбинаторики
Лекция № 7. АЛГОРИТМЫ И МОДЕЛИ.
Контрольные вопросы:
1. Понятие алгоритма и его свойства.
2. Способы задания алгоритмов.
3. Классификация алгоритмов.
4. Понятия модели и моделирования.
5. Метод математического моделирования. Основные виды математических моделей.
6. Аксиоматический метод и моделирование.
7. Связь с начальным курсом математики.
Литература:
Лекции №№ 8 — 9.
Контрольные вопросы:
Понятие о комбинаторной задаче.

Правила суммы и произведения.
Соединения без повторений и с повторениями.
Бином Ньютона и треугольник Паскаля. Число подмножеств конечного множества.
5. Комбинаторные задачи в начальном курсе математики.
Литература: (1) гл. I, § 2 пп. 8-11; (2) гл. I, § 6, с. 142-149; (3) гл. I, § 2 пп.6-8; (4) гл. V, с. 151-155; (5) гл. IV, §§ 4.1 – 4.7.
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.
Как
раздел математики комбинаторика возникла
в 16 веке. Ее возникновение и развитие
связано с именами ученых Н. Тарталья
(1500-1557гг), Б. Паскаля (1623-1662гг), П. Ферма
(1601-1665гг). Позднее крупный вклад в развитие
комбинаторных методов был сделан Г. Лейбницем (1646-1716гг), я. Бернулли (1654-1705
гг), л. Эйлером (1707-1783гг).
Лейбницем (1646-1716гг), я. Бернулли (1654-1705
гг), л. Эйлером (1707-1783гг).
Решение большинства комбинаторных задач основано на применении двух основных правил: правила суммы и правила произведения.
Задача 1: В вазе лежит 8 слив и 6 абрикосов. Сколькими способами можно выбрать из вазы один плод?
Переведем задачу на язык теории множеств. Имеются 2 множества: . Эти множества не имеют общих элементов: Ø. Требуется узнать, сколько существует способов выбора одного элемента, принадлежащего множеству
Элемент из множества А можно выбрать 8-ю способами, из множества В – 6-ю способами. А так как эти множества не имеют общих элементов, то выбрать один элемент, принадлежащий А или В можно 8+6 =14 способами.
Таким
образом, задача свелась, к нахождению
числа элементов в объединении двух
непересекающихся множеств: .
Правило суммы: если элемент а можно выбрать n способами, а элемент b – m способами, причем ни один из способов выбора элемента а не совпадает со способом выбора элемента b, то выбор элемета «а либо b» можно осуществить (n+m) cпособами.
Задача 2: В столовой имеется 4 вида первых блюд и 6 видов вторых. Сколькими способами можно выбрать обед, состоящий из одного первого и одного второго блюда?
Решение такого вида задач сводится к подсчету числа упорядоченных пар, когда известно число способов выбрать первую компоненту и вторую компоненту.
Пусть . Множество всех упорядоченных пар элементов, состоящих из элементов множеств А и В, образует декартово произведение этих множеств. Известно, что . Тогда наша задача будет иметь решение: (способа).
Правило
произведение: если
элемент а можно
выбрать n способами,
а элемент b – m способами, то пару (а; b)
можно выбрать способами.
Правило
суммы и произведения легко распространяется
на тот случай, когда множеств не два, а
«
Пусть даны множества Ø . Тогда
Замечание: если множества А и В пересекаются, то
Декартово произведение
Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b — второй координатой (компонентой) пары.
В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, 4 = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая- множеству В. Если мы перечислим все такие пары, то получим множество:
{(1;3),(1;5),(2;5),(3;3),(3;5)}.
Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств Аи В.
Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают Ах В. Используя это обозначение, определение декартова произведения можно записать так:
А х В= {(х;у) |х А и у В}.
З а д а ч а 1. Найдите декартово произведение множеств А и В, если:
a)A = {m;p},B={e,f,k};
б)А=В={3,5}.
Решение. а) Действуем согласно определению- образуем все пары, первая компонента которых выбирается из А, а вторая — из В:
А х В= {( m; е), (m; f), (m; k), (p; e), (p;f), (p; к)}.
б) Декартово произведение равных множеств находят, образуя всевозможные пары из элементов данного множества:
А х А={(3;3), (3;5), (5;3), (5;5)}
Операцию нахождения декартова произведения множеств называют декартовым умножением. Выясним, какими свойствами обладает эта операция. Так как декартовы произведения А х В и В х А состоят из различных элементов, то декартово умножение множеств А и В свойством коммутативности не обладает.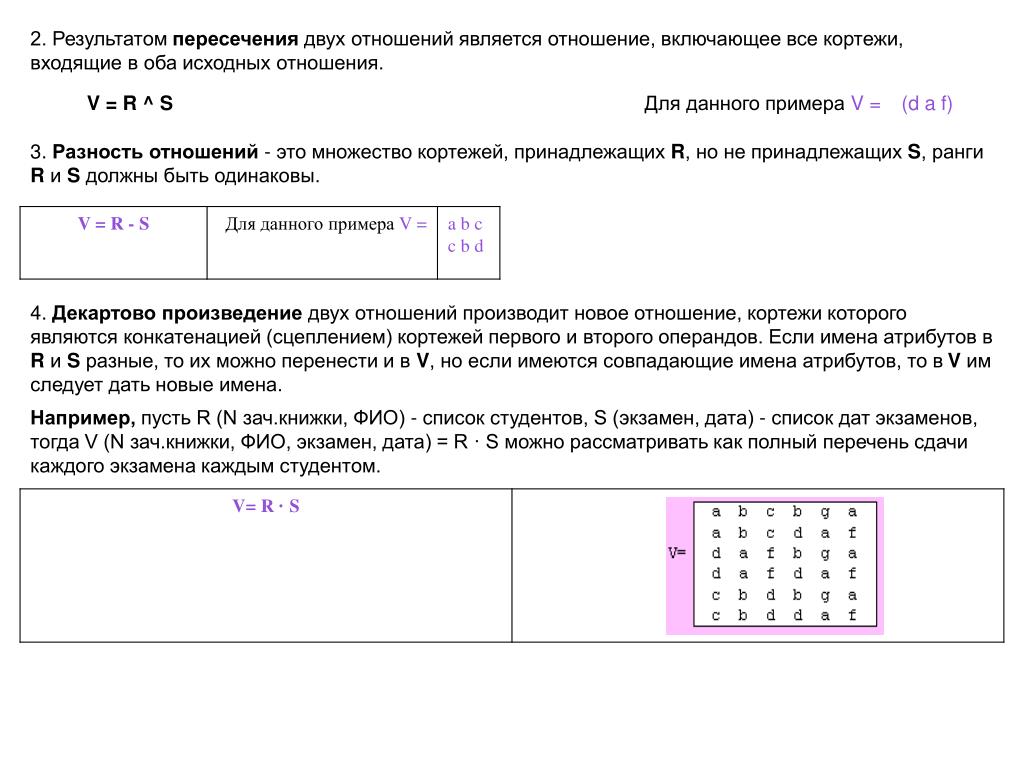
(А В) х С = (А х С) (В х С),
(А \ В) х С = (А х В) \ (В х С).
З а д а ч а 2. Проверьте справедливость свойства дистрибутивности декартова умножения относительно объединения, если:
А = {3; 4; 5}, В ={5; 7}, С ={7; 8}.
Решение. Найдем объединение множеств А и В: А В = {3,4,5,7}. Далее перечислим элементы множества (А В) х С, используя определение декартова произведения: (А В) х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Чтобы найти элементы множества (А х С) (В х С), перечислим сначала элементы множеств А х С и В х С:
А х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)}
В х С={(5;7),(5;8),(7;7),(7;8)}.
Найдем объединение полученных декартовых произведений: (А х С) (В х С) = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Видим, что множества (А В) х С и (А х С) (В х С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (А В) х С = = (А х С) (В х С).
Выясним теперь, как можно наглядно представлять декартово произведение множеств.
Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке 17(а, б).
| В А | ||
| (1,3) | (1,5) | |
| (2,3) | (2,3) | |
| (3,3) | (3,3) |
б) Рис. 17
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение А хВ множеств А = {1, 2, 3} и В = = (3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке 18.
Например, декартово произведение А хВ множеств А = {1, 2, 3} и В = = (3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке 18.
у
5
3
0 1 2 3 х Рис.18
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В — на оси Оу.
Такой способ наглядного представления декартова произведения двух числовых множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.
Задача 3. Изобразить на координатной плоскости декартово произведение Ах В, если:
а) А = {1,2,3},В = [3,5];
б) А = [1,3], В = [3,5];
в) A = R, В = [3,5];
г) А = R, В = R.
Р е ш е н и е, а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А х В будет состоять из бесконечного множества нар, первая компонента которых либо 1, либо 2, либо 3, а вторая-любое действительное число из промежутка [3, 5].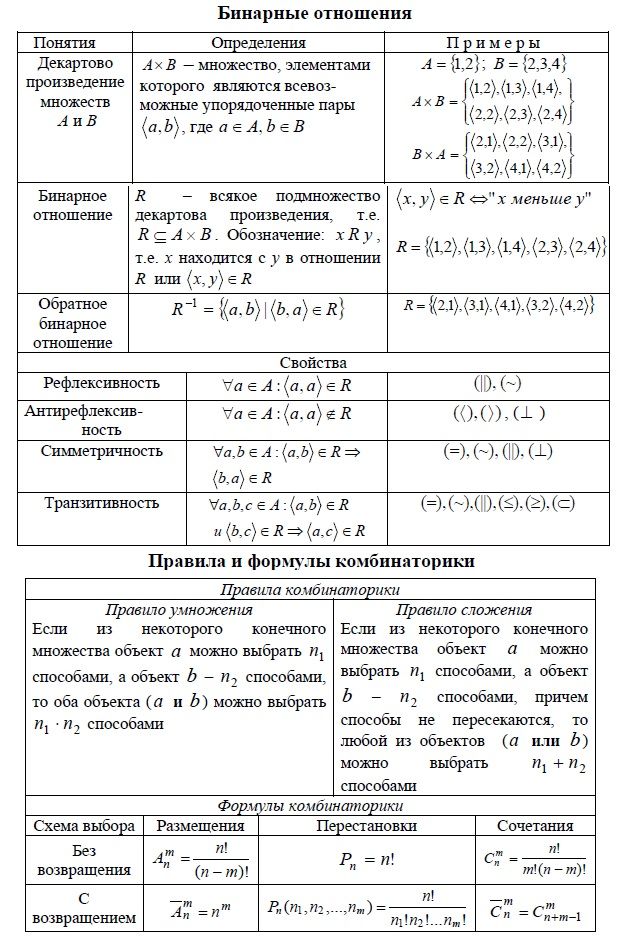 Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 19).
Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 19).
у
5
3
0 1 2 3 х Рис. 19
б) В этом случае бесконечны оба множества А и В. Поэтому первой координатой пары, принадлежащей множеству Ах В, может быть любое число из промежутка [1,3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат (рис. 20).
у
5
3
0 1 2 3 х Рис. 20
Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими внутри квадрата, этот квадрат можно заштриховать.
в) Этот случай отличается от предыдущего тем, что множество А состоит из всех действительных чисел, т. е. абсцисса точек, изображающих элементы множества А х В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3,5]. Множество таких точек образует полосу (рис. 21).
е. абсцисса точек, изображающих элементы множества А х В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3,5]. Множество таких точек образует полосу (рис. 21).
у
5
0 х Рис. 21
г) Декартово произведение R x R состоит из всевозможных действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, декартово произведение R x R содержит столько же элементов, сколько точек находится на координатной плоскости.
В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367- это упорядоченный набор из трех элементов, а запись слова «математика» — это упорядоченный набор из 10 элементов.
Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа — это число элементов, из которых он состоит. Например, (3; 6; 7) — это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) — это кортеж длины 10.
Длина кортежа — это число элементов, из которых он состоит. Например, (3; 6; 7) — это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) — это кортеж длины 10.
Рассматривают в математике и декартово произведение трех, четырех и вообще и множеств.
Определение. Декартовым произведением множеств A1, А2,…, Аn называется множество всех кортежей длины n, первая компонента которых принадлежит множеству A1, вторая — множеству А2,…, n-я — множеству An.
Декартово произведение множеств A1, А2,…, Аnобозначают так: A1 х А2 х… х Аn.
З а д а ч а 4. Даны множества: A1 = {2, b), А2 = {3, 4, 5}, А3 = {6,7}. Найти A1 х А2 х А3.
Ре ш е н и е. Элементами множества A1х А2х А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству A1, вторая — множеству А2, третья — множеству А3.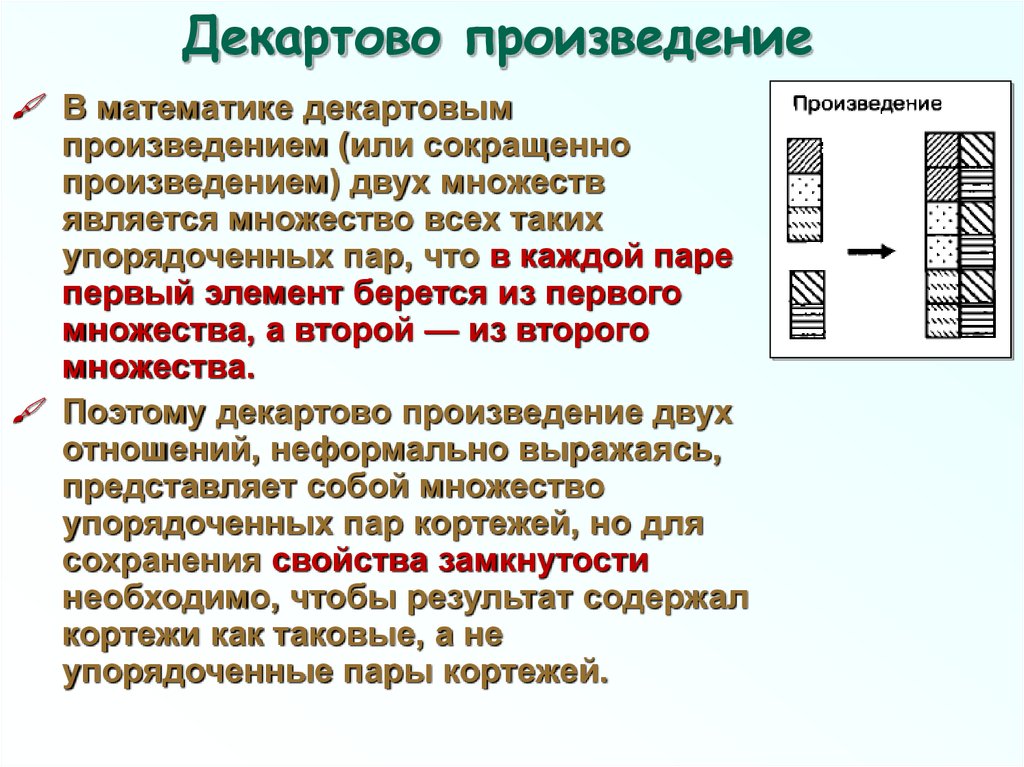
A1х А2х А3 = {(2, 3, 6), (2, 3, 7), (2, 4, 6), (2, 4, 7),
(2, 5, 6), (2, 5,7), (3,3,6), (3,3, 7),
(3,4, 6), (3,4,7), (3,5,6), (3,5,7)}.
Дата добавления: 2017-02-13; просмотров: 16468; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 9 из 74Следующая ⇒ 1) Так как декартовы произведения А´B и В´А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает. 2) Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. 3) Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства: (AÈB) ´ С = (A ´ С) È (B ´ С), (A \ B) ´ С = (A ´ С) \ (B ´ С). Пример Проверьте справедливость свойства дистрибутивности декартова произведения относительно объединения, если: А = {3; 4; 5}, В = {5; 7}, С = {7; 8}. Решение. Найдем объединение множеств А и В: AÈB = {3; 4; 5;7}. Далее перечислим элементы множества (AÈB) ´ С, используя определение декартова произведения: (AÈB) ´ С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}. Чтобы найти элементы множества (A ´ С) È (B ´ С), перечислим сначала элементы множеств А ´ С и В ´ С: А ´ С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)} В ´ С = {(5; 7), (5; 8), (7; 7), (7; 8)}. Найдем объединение полученных декартовых произведений: (A ´ С) È (B ´ С) = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}. Видим, что множества (AÈB) ´ С и (A ´ С) È (B ´ С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (AÈB) ´ С = (A ´ С) È (B ´ С). Выясним теперь, как можнонаглядно представить декартово произведение множеств. · Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи таблицы или графа. Пример
Декартово произведение множеств А = {1; 2; 3} и В = {3; 5} можно представить так, как показано на рисунке 1 и 2
Рис. · Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Способ наглядного представления декартова произведения двух числовых множеств удобно использовать в случае, когда хотя бы одно из них бесконечное. Пример Изобразите на координатной плоскости декартово произведение A ´ В, если: а) А = {1; 2; 3} и В = [3; 5]; б) А = [1; 3], В = [3; 5]; в) А = R, В = [3; 5]; г) А = R, В = R. Решение а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа о т 3 до 5, включая и сами эти числа, то декартово произведение A ´ В будет состоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо 3, а вторая – любое действительное число из промежутка [3; 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками. у
1 2 3 х б) В этом случае бесконечны оба множества А и В. Поэтому первой координатой может быть любое число из промежутка [1; 3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат. Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими внутри квадрата, этот квадрат можно заштриховать. у 3 1 2 х в) Этот случай отличается от предыдущих тем, что множество А состоит из всех действительных чисел, т.е. абсцисса точек, изображающих элементы множества A ´ В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3; 5]. Множество таких точек образует полосу. y
х г) Декартово произведение R´R состоит из всевозможных действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, декартово произведение R´R содержит столько же элементов, сколько точек находится на координатной плоскости. Кортеж. Длина кортежа В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367 – это упорядоченный набор из трех элементов, а запись слова «математика» – это упорядоченный набор из 10 элементов. Упорядоченные наборы часто называют кортежамии различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10. Рассматривают в математике и декартово произведение трех, четырех и вообще n множеств. Определение. Декартовым произведением множеств А1, А2, …, Аn называется множество всех кортежей длины n, первая компонента которых принадлежит множеству А1, вторая – множеству А2, …, n – я – множеству Аn. Декартово произведение множеств А1, А2, …, Аnобозначают так: А1´ А2´ …´ Аn. Пример Даны множества: А1= {2, 3}, А2= {3, 4, 5}, А3 = {6, 7}. Найти А1´ А2 ´А3. Решение Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3. А1´ А2 ´А3 ={(2,3,6), (2,3,7), (2,4,6), (2,4,7), (2,5,6), (2,5,7), (3,3,6), (3,3,7),(3,4,6), (3,4,7), (3,4,7),(3,5,6), (3,5,7)}.
⇐ Предыдущая45678910111213Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Декартово произведение множеств, его свойства. Понятие кортежа. Примеры заданий из начального курса математики, связанных с образованием декартова произведения множеств.
Декартово произведение множеств.
В начальных классах ученики решают задачу: используя цифры 1,2,3 образовать всевозможные двузначные числа.
Путем перебора дети получают
11 12 13
21 22 23
31 32 33
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (a;b) образованные из элементов a и b.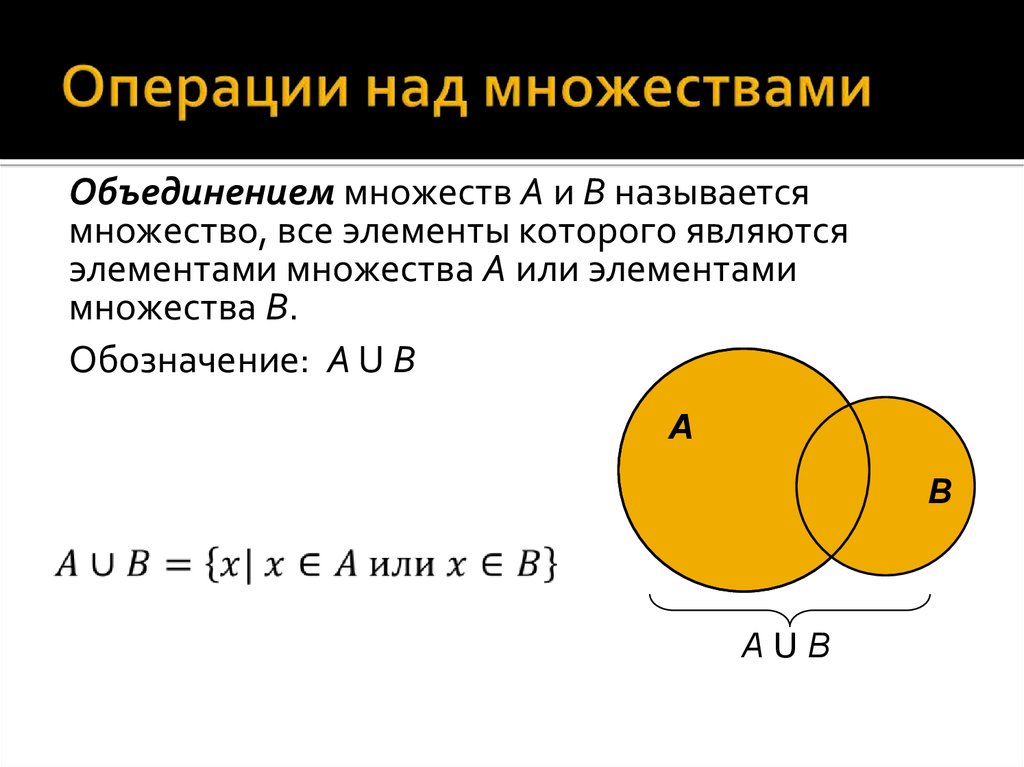 Это (1;2), (1;3), (1;4) и тд. Первый элемент аназывают первой координатой пары, элемент b – второй.
Это (1;2), (1;3), (1;4) и тд. Первый элемент аназывают первой координатой пары, элемент b – второй.
Значит в нашей задаче мы оперировали множеством A={1,2,3} и образовали всевозможные пары.
Рассмотрим другой пример. Пусть А={1,2,3}, B={4,5}. Образуем всевозможные пары (a;b) так, что a A, b B. Получим некоторое новое множество { (1;5), (1;4), (2;4), (2;5), (3;4), (3;5)}, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств A и B.
Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А В. Таким образом А В ={(х;у) |х А, у В}
Операцию нахождения декартового произведения множеств А и В называют декартовым умножениемэтих множеств.
Рассмотрим следующий пример. Известно, что А В= {(2;3),(2;5), (2;6), (3;3), (3;5), (3;6)}.Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, вторая множеству В, то данные множества имеют следующий вид А={2,3}, В={3,5,6}.
Так как первая компонента пары декартового произведения принадлежит множеству А, вторая множеству В, то данные множества имеют следующий вид А={2,3}, В={3,5,6}.
Перечислим элементы принадлежащие множеству А В, если А={a,b,c,d}, В=А. Декартово произведение А В={(a,a), (a,b), (a,c), (a,d), (b,a), (b,b), (b,c), (b,d), (c,a), (c,b), (c,c), (c,d), (d,a), (d,b), (d,c), (d,d)}
Количество пар в декартовом произведении А В будет равно произведению числа элементов множества А и числа элементов множества В: n(A B)=n(A) n(B).
В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и тд. элементов.
Такие упорядоченные наборы называют кортежами.Так, набор (1,5,6) есть кортеж длины 3, т.к в нем три элемента. Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А1, А2….Аn называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А1, вторая А2, n-ая множеству А: А1 А2 …. Аn.
Аn.
Пусть даны множества А1 ={2,3} ; А2={3,4,5}; А3={7,8}. Декартово произведение А1 А2 А3 ={(2,3,7), (2,3,8), (2,4,7), (2,4,8),(2,5,7),(2,5,8),(3,3,7),(3,4,7),(3,3,8),(3,4,8),(3,5,7),(3,5,8)}
Примеры из начального курса математики.
Например: построй четырехугольник ABCD по координатам его вершин. Если возможно, проведи его оси симметрии. А(0;1), В(2;5), С(6;5) и D(8;1).
Для изображения декартового произведения нечисловых множеств используется таблица. Например: «Фабрика верхнего трикотажа изготавливает мужские пуловеры, женские костюмы, кофты, платья следующих расцветок: бордовая, синяя, голубая,зеленая, коричневая, серая. Составьте таблицу, иллюстрирующую каких цветов могут быть данные изделия».
5.Особенности математический понятий. Объем и содержание понятий. Отношение между понятиями. Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.
Термин понятие соединяет в себе целый класс объектов или отношений произвольной природы, обладающий определенным характеристическим свойством или целым набором таких свойств.
Например понятие четырехугольник обозначает класс всевозможных многоугольников, обладающих свойствами: иметь четыре стороны; иметь четыре вершины; иметь; иметь четыре угла. Понятия условимся обозначать строчными буквами латинского алфавита: a b c
Понятия, изучаемые в начальном курсе математики, представляют в виде четырех групп:
Понятия, связанные с числами и операциями над ними: число, сложение, слагаемое, меньше и др.
Выражение, равенство, уравнение
Геометрические понятия: прямая, отрезок, треугольник
Понятия, связанные с величинами и их измерениями.
Особенности математических понятий: 1)математические объекты, о которых необходимо составить понятия, в реальности не существуют, а существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык
2)в математике рассматриваются не только понятия, появившиеся при изучении реальных предметов, но и понятия, возникшие на основе первых ( например, понятие переменной является абстракцией конкретных переменных величин, т. е. абстракцией от абстракции).
е. абстракцией от абстракции).
Объем и содержание понятия.
Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.
Существенное свойство- свойство, без которого объект не может существовать.
Несущественное свойство- свойство, отсутствие которого не влияет на существование объекта.
Совокупность всех существенных свойств объекта называют содержанием понятия.
Когда говорят о математическом объекте, имеют в виду всю совокупность объектов, обозначаемых одним термином.
Совокупность всех объектов, обозначенное одним термином, составляет объем понятия.
Например, содержание понятия «квадрат»- это совокупность всех существенных свойств, которыми обладают квадраты, а в объем этого понятия входят квадраты различных размеров.
Итак, любое понятие характеризуется:
-термином( название)
-объемом( совокупность всех объектов, называемых этим термином)
-содержанием( совокупность всех существенных свойств объектов, входящих в объем понятия).
Между объектом понятия и его содержанием существует связь: чем «больше» объем понятия, тем « меньше» его содержание, и наоборот. Объем понятия « треугольник» « больше», чем объем понятия « прямоугольный треугольник», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «треугольник» « меньше», чем содержание понятия «прямоугольный треугольник», так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.
Отношения между понятиями.
Определив объем понятия, можно рассмотреть, какие отношения могут существовать между различными их типами.
Отношение эквивалентности существует тогда и только тогда, когда объемы сравниваемых понятий полностью совпадают. Это означает, что отличительные и существенные признаки, присущие сравниваемым понятиям, принадлежат всем элементам множеств, составляющих их объемы. Так, понятия эквивалентности характеризует отношение между классами равносторонних и равноугольных треугольников, равноугольных ромбов и квадратов, понятий, все они принадлежат к одному классу элементов, т. е. имеют тот же самый объем. Обратите внимание на то, что все перечисленные понятия оказываются эквивалентными только по объему, содержание же их различию. Так, признаки « иметь равные стороны» или « обладать равными углами» отличаются друг от друга по смыслу.
е. имеют тот же самый объем. Обратите внимание на то, что все перечисленные понятия оказываются эквивалентными только по объему, содержание же их различию. Так, признаки « иметь равные стороны» или « обладать равными углами» отличаются друг от друга по смыслу.
Отношение перекрещивания (частичного совпадения) объемов понятий существует тогда и только тогда, когда часть объема одного понятия входит в объем другого, и в свою очередь часть объема второго понятия входит в объем первого. Таковы отношения между объемами понятий «студенты» и «спортсмены», «студенты» и «филателисты», ибо ясно, что не все студенты являются спортсменами или филателистами. Обычно для наглядного изображения отношений между объемами понятий употребляются диаграммы Эйлера, в которых объем понятий представляются кругом. Поскольку у эквивалентных понятий объемы совпадают, то отношение между ними изображается одним кругом. В случае частичного совпадения объемов отношение изображается пересечением двух кругов. Если обозначить объем одного понятия через A , другого через В, то графически отношения эквивалентности (Рис.1) и перекрещивания (Рис.2) можно представить соответствующими диаграммами.
Если обозначить объем одного понятия через A , другого через В, то графически отношения эквивалентности (Рис.1) и перекрещивания (Рис.2) можно представить соответствующими диаграммами.
Отношение субординации (подчинение объемов) понятий существует тогда и только тогда, когда объем одного понятия полностью входит в объем второго. Понятие меньше объема составляет часть, или, точнее, вид понятия с большим объемом, который по отношению к нему называют родом. На диаграмме Эйлера (рис.3) это отношение изображается включением меньшего круга в больший.
Все перечисленные выше отношения имеют место между совместными понятиями, объемы которых либо совпадают, либо перекрещиваются, либо составляют часть другого.
Несравнимые («неположенные») понятия – это понятия, объемы которых либо полностью исключают друг друга, либо находятся в отношении противоречия друг другу . Так объемы понятий «треугольник» и «растение» не содержит ни одного общего элемента, их пересечение – пусто. То же самое можно сказать о понятиях которые употребляются в хорошо известном утверждении, характеризующем несравнимость: «в огороде бузина, а в Киеве дядька». Особый интерес представляют понятия, объемы которых находится в отношении контрарности (противности) друг другу, как, например, «белый» и «черный», «холодный» и «горячий» «длинный» «короткий» и т.д, которые представляют собой свойства, расположенный на границе соответствующих множеств, свойств. Между «белым» и «черным» «холодным» и «горячим» и т.д располагаются промежуточные свойства. В силу этого объемы контрарных понятий занимают крайние положения на круговых диаграммах (рис.4).
То же самое можно сказать о понятиях которые употребляются в хорошо известном утверждении, характеризующем несравнимость: «в огороде бузина, а в Киеве дядька». Особый интерес представляют понятия, объемы которых находится в отношении контрарности (противности) друг другу, как, например, «белый» и «черный», «холодный» и «горячий» «длинный» «короткий» и т.д, которые представляют собой свойства, расположенный на границе соответствующих множеств, свойств. Между «белым» и «черным» «холодным» и «горячим» и т.д располагаются промежуточные свойства. В силу этого объемы контрарных понятий занимают крайние положения на круговых диаграммах (рис.4).
Отношение контрадикторности (противоречивость) между объемами понятий существует тогда , когда они, с одной стороны, отрицают друг друга, а с другой стороны исчерпывают объем целого понятия (рис.5).
В языке противоречий выражается отрицательной частицей перед словом, выражающем свойство. Примерами могут служить свойства, выражающие такие понятий, как белый и не белый, холодный не холодный, черный и не черный и т. д. На диаграмме (рис.5) объемы таких понятий составляют две половины круга, хотя гораздо лучше представить объем положительного понятия кругом, а отрицательного – прямоугольником, в который входит этот круг, поскольку противоположное (отрицательное) понятие содержит обычно больше число элементов (рис.6).
д. На диаграмме (рис.5) объемы таких понятий составляют две половины круга, хотя гораздо лучше представить объем положительного понятия кругом, а отрицательного – прямоугольником, в который входит этот круг, поскольку противоположное (отрицательное) понятие содержит обычно больше число элементов (рис.6).
Поскольку объемы понятий образуют классы (или множества) предметов, элементы которых обладают признаками, сформулированными в их содержании, то над этими классами (или множествами) можно производит определенные логические операции. Они тождественны операциям, которые изучаются в теории множеств.
Объединением классов (или множеств) называют класс, который содержит в своём составе те элементы, входящие в каждый отдельный класс. Если обозначить отдельные классы через , то объединенные множества можно представить как дизъюнкцию (или логическое сложение) всех перечисленных классов (или множеств):
Например, объединение плоских фигур будет состоять из класса треугольников, классы четырехугольников, окружностей и других фигур, класс деревьев – из классов хвойных, лиственных и др. деревьев.
деревьев.
Пересечение (или умножение) классов называется новый класс, который содержит в своём составе те и только те элементы, которые входят в каждый из отдельных классов. Иначе говоря, он содержит элементы, общие всем отдельным классам. Поэтому сама операция пересечения классов иногда называется взятием их общей части. Обозначив отдельные классы через , их пересечение можно представить в виде , где знак л обозначает операцию пересечения, умножения или конъюнкции классов.
Остенсивные и контекстуальные определения понятий, их отличие от определений через род и видовое отличие.
Контекстуальное (от лат. Contextus-«соединение», «связь») определение характеризуется тем, что она позволяет выяснить суть, значение слова, смысла которого мы не знаем, через контекст, т.е. через относительно законченный отрывок информации, которое сопровождает данное слово, относится к нему и содержит его признаки.
Остенсивное определение устанавливает значение термина, прибегая к демонстрации предмета, обозначаемого этим термином. Такие определения применяются при раскрытии сущности предмета чувственного мира, другими словами, предметов, которые доступны, для непосредственного восприятия.
Такие определения применяются при раскрытии сущности предмета чувственного мира, другими словами, предметов, которые доступны, для непосредственного восприятия.
Декартово произведение. Разбиение множеств на классы
КАРТА – СХЕМА УЧЕБНОГО ЗАНЯТИЯ
продолжительность — 90 минут
Тема занятия: Декартово произведение и разбиение множеств на классы
Цели занятия:
· расширить знания студентов с темы действия с множествами, рассмотреть Декартово произведение, разбиение множеств на классы;
· способствовать развитию памяти, внимания, логического мышления;
· создать условия для применения полученных знаний при выполнении расчетных заданий.
Необходимое аппаратное и программное обеспечение:
· компьютер;
· экран;
·
проектор.
Дидактическое обеспечение:
1. Карточки с заданиями самостоятельной работы
2. Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
3. Информационные источники:
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
Тип и вид учебного занятия:
· лекция.
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Этапы урока | Содержание и виды деятельности преподавателя | Примечания |
1. | Приветствие, выявление отсутствующих, информирование о теме и целях занятия. |
|
2. Актуализация ЗУН | Устный опрос. — Что такое множество? Что означает задать множество? — Способы задания множеств — Что такое подмножество? -какие действия выполняем над множествами? — Что такое пересечение? Объединение? — Какие свойства пересечения, объединения? Самостоятельная работа (с взаимопроверкой) 1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите: а) А∩В; б) А∩С; в) С∩В.
2. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите: а) АUВ; б) АUС; в) СUВ.
3. Даны множества:
А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}. Найдите а)(А∩В)∩С; б) )(АВ)С; в) (А В)∩С |
|
3. Изучение нового материала |
Теоретические сведения. — Декартово произведение. — разбиение множеств на классы
|
|
4. Первичное закрепление | Практическое выполнение заданий |
|
5. Информация о домашнем задании | Самостоятельная работа | Методические рекомендации для самостоятельной работы |
6. Подведение итогов урока | Подведение итогов работы группы, отдельных студентов. Корректирование
пробелов знаний. Рефлексия |
|
Декартово произведение
В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.
Путем перебора дети получают:
11 12 13
21 22 23
31 32 33
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В
том случае, когда важен порядок следования элементов множества, в математике
говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные
пары (а; b), образованные из элементов а и b. Это (1;
2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой
координатой пары, элемент b – второй.
Значит, в нашей задаче мы оперировали множеством А={1, 2, 3} и образовывали всевозможные пары.
Рассмотрим другой пример. Пусть А={1, 2, 3}, B={4, 5}. Образуем всевозможные пары (а;b) так, что аА, bВ. Получим некоторое новое множество {(1; 5), (1; 4), (2; 4), (2; 5), (3; 4), (3; 5)}, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.
Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают АВ. Таким образом АВ = {(x;y) | xA, yB}.
Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
Рассмотрим
следующий пример. Известно, что АВ={(2,
3), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6)}. Установим,
из каких элементов состоят множества А и В. Так как первая
компонента пары декартового произведения принадлежит множеству А, а
вторая – множеству В, то данные множества имеют следующий
вид: А={2, 3}, B={3, 5, 6}.
Установим,
из каких элементов состоят множества А и В. Так как первая
компонента пары декартового произведения принадлежит множеству А, а
вторая – множеству В, то данные множества имеют следующий
вид: А={2, 3}, B={3, 5, 6}.
Перечислим
элементы, принадлежащие множеству АВ, если
А={a, b, c, d}, B=A. Декартово произведение АВ={(a,
a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a),
(d, b) ,(d, c), (d, d)}.
Количество пар в декартовом прoизведении АВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АВ)=n(A)n(B).
В
математике рассматривают не только упорядоченные пары, но и наборы из трех,
четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем
три элемента.
Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.
Пусть
даны множества А={2,
3}; А={3,
4, 5}; A={7,
8}. Декартово произведение ААА={
(2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7),
(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)}.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие
распределения объектов по классам на основании сходств внутри класса и их
отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х, Х,…, Х, если:
1) подмножества Х, Х,…, Х попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на
три класса: остроугольные, прямоугольные и тупоугольные. Действительно,
выделенные подмножества попарно не пересекаются, а их объединение совпадает с
множеством Х; b) Из множества треугольников Х выделили подмножества
равнобедренных, равносторонних и разносторонних треугольников. Так как
множества равнобедренных и равносторонних треугольников пересекаются, значит,
не выполнено первое условие классификации, и разбиения множества Х на
классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство,
то это множество разбивается на два класса. Первый – это класс объектов,
обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным
свойством не обладают. Такую классификацию называют дихотомической.
Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
Таким образом, выделение двух свойств привело к разбиению
множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Примеры
Приведем несколько примеров разбиения:
1. Множество четырехугольников разбито
на два класса:
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их
объединения совпадают с множеством .
2. Множество четырехугольников разбито
на три класса:
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат –
частные случаи параллелограмма, то данные подмножества пересекаются, значит, не
выполнено первое условие классификации, и разбиение множества не получено.
3. Дано множество прямых в
пространстве, которое разбито на классы по их взаимному расположению:
параллельные, пересекающиеся, скрещивающиеся. Данные подмножества попарно
не пересекаются, а их объединения совпадают с множеством .
Данные подмножества попарно
не пересекаются, а их объединения совпадают с множеством .
4. Дано множество , которое можно разделить на два класса: и , где – множество натуральных четных чисел, а – множество натуральных нечетных чисел.
5. Множество разбито на три класса: , и . множество чисел, которые делятся на , – множество чисел, которые делятся на , множество чисел, которые делятся на . Но существуют числа, которые могут делится одновременно и на , и . Отсюда следует, что подмножества пересекаются, и разбиение не получено.
Практические задания
Пример 1. Даны множества: А1= {2, 3}, А2= {3, 4, 5}, А3 = {6, 7}. Найти А1´ А2 ´А3.
Решение. Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3.
А1´ А2 ´А3 ={(2, 3, 6), (2,3,7), (2,4,6), (2,4,7), (2,5,6), (2,5,7), (3,3,6),
(3,3,7),(3,4,6), (3,4,7), (3,4,7),(3,5,6), (3,5,7)}.
Пример 2. Пусть на множестве Х={3, 5, 7} задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение X´X. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше».
Решение.
Декартово произведение X ´ Х может быть записано в виде множества из упорядоченных пар:
X ´ Х= {(3;3),(3;5),(3;7),(5;3),(5;5),(5;7),(7;3),(7;5),(7;7)}.
Из этого множества выбираются элементы, которые удовлетворяют отношению «меньше». В результате получится новое множество из упорядоченных пар:
W={(3;5),(3;7),(5;7)}.
В новом множестве все пары являются элементами декартова произведения X´X. Отношение «меньше» на множестве Х является подмножеством декартова произведения X´X. Бинарное отношение на множестве Х есть подмножество декартова произведения WÌ X´X.
2) Декартово произведение двух множеств X ´ Y.
Пример 3.
Пусть заданы два
множества: X= {2, 6, 1}, Y= {7, 4,
8}.
Записать декартово произведение X ´ Y .
Решение.
Декартово произведение двух множеств равно:
X ´ Y={(2, 7), (2, 4), (2, 8), (6, 7), (6, 4), (6, 8), (1, 7), (1, 4), (1, 8)}.
Аналогично можно найти декартово произведение трёх множеств: X ´ Y´ Z.
Декартово произведение множеств
Математика Декартово произведение множеств
просмотров — 746
Понятие разбиения множества на классы с помощью одного, двух, трех свойств
Понятия множества и операций над множествами позволяют уточнить наше представление о классификации – действии распределения объектов по классам.
Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса – четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.
Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы Х₁, Х₂, …, Хn,…, если:
1) подмножества Х₁, Х₂, …, Хn,… попарно не пересекаются;
2) объединение подмножеств Х₁, Х₂, …, Хn, … совпадает с множеством Х.
В случае если не выполнено хотя бы одно из условий, классификацию считают неправильной. К примеру, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмножества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, к примеру, множество натуральных чисел. Его элементы обладают различными свойствами. Положим,. что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, ᴛ.ᴇ. получаем еще одно подмножество множества натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.
Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.
N N
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый — ϶ᴛᴏ класс объектов, обладающий этим свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. К примеру, «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А – подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого. Проанализируем получившийся рисунок (справа). Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей – на рисунке они пронумерованы. Каждая область изображает неĸᴏᴛᴏᴩᴏᴇ подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратных 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IY – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.
Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей – на рисунке они пронумерованы. Каждая область изображает неĸᴏᴛᴏᴩᴏᴇ подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратных 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IY – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. К примеру, при помощи двух таких свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса: I – класс чисел, кратных 6; II – класс чисел, кратных 3; но не кратных 6; III — класс чисел, не кратных 3.
Используя две цифры, к примеру, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55.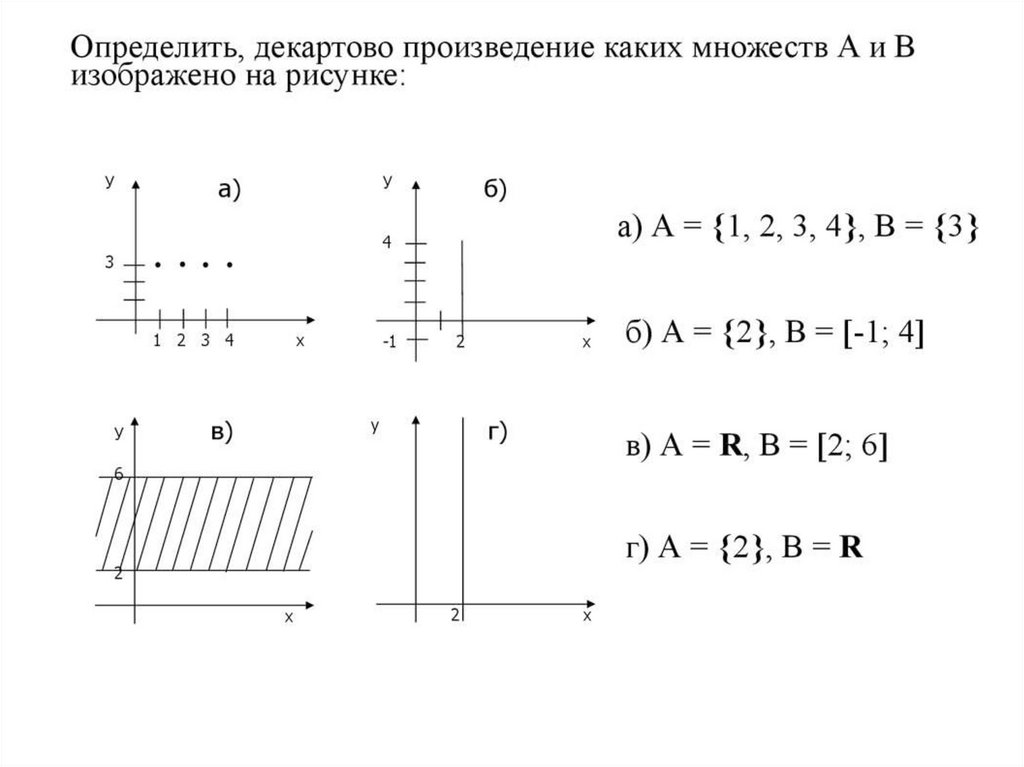 Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b – второй координатой (компонентой) пары.
Пары (а; b) и (с; d) равны в том и только в том случае, когда а = с и b = d.
В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, к примеру, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая компонента – множеству В. В случае если мы перечислим все такие пары, то получим множества:
{(1; 3), (1; 5) (2; 3), (2; 5), (3; 3), (3; 5)}.
Видим, что, имея два множества А.и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.
Определение. Декартовым произведением множеств А и В принято называть множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:
А х В = {х; у) / х ∈ А и у∈ В}.
Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А х В и В х А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.
Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, ᴛ. ᴇ. для любых множеств А, В и С выполняются равенства:
ᴇ. для любых множеств А, В и С выполняются равенства:
(А∪В) х С = (А х С) ∪ (В х С),
(А / В) х С = (А х С) / (В х С).
Доказывать эти свойства мы не будем, но проверить их можно на конкретных примерах.
Выясним теперь, как можно наглядно представить декартово произведение множеств.
В случае если множества А и В конечны и содержат небольшое количество элементов, то его можно изобразить при помощи графа или таблицы. К примеру, декартово произведение множеств
А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке.
А В
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изобразить на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. К примеру, декартово произведение выше названных множеств на координатной плоскости будет выглядеть так:
1 2 3
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В – на оси Оу.
Такой способ наглядного изображения декартова произведения множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.
В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. К примеру, запись числа 367 — ϶ᴛᴏ упорядоченный набор из трех элементов, а запись слова «математика» — это упорядоченный набор из 10 элементов.
Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа — ϶ᴛᴏ число элементов, из которых он состоит. К примеру, (3; 6; 7) — ϶ᴛᴏ кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) — ϶ᴛᴏ кортеж длины 10.
Рассматривают в математике и декартово произведение трех, четырех и вообще n множеств.
Определение. Декартовым произведением множеств А₁, А₂, …, Аn принято называть множество всех кортежей длины n, первая компонента которых принадлежит множеству А₁, вторая – множеству А₂, …, n-я — множеству Аn.
Декартово произведение множеств А₁, А₂, …, Аn обозначают так:
А₁ х А₂ х …х Аn.
Операции над множествами Основными операциями над множествами являются объединение, пересечение и разность. Определение 1. Объединением двух множеств называется новое множество Определение 2. Пересечением двух множеств называется новое множество Определение… [читать подробенее]
Пример 3. Пример 2. Среди студентов группы присутствуют следующие три студента-прогульщика: Иванов (И), Петров (П) и Сидоров (С). Хотя все они часто прогуливают занятия, И умудряется учиться на отлично, П является хорошистом, а С – троечником. Преподаватель, желая… [читать подробенее]
Понятие разбиения множества на классы с помощью одного, двух, трех свойств
Понятия множества и операций над множествами позволяют уточнить наше представление о классификации – действии распределения объектов по классам. Классификацию мы выполняем достаточно часто…. [читать подробенее]
Классификацию мы выполняем достаточно часто…. [читать подробенее]
Разбиение множества на классы Пусть задано некоторое множество, например, множество треугольников. В этом множестве выделим свойство (например, быть прямоугольным). Тогда множество треугольников разбивается на два класса: прямоугольные и непрямоугольные. … [читать подробенее]
Пример 3. Пример 2. Среди студентов группы присутствуют следующие три студента-прогульщика: Иванов (И), Петров (П) и Сидоров (С). Хотя все они часто прогуливают занятия, И умудряется учиться на отлично, П является хорошистом, а С – троечником. Преподаватель, желая… [читать подробенее]
Понятие разбиения множества на классы с помощью одного, двух, трех свойств
Понятия множества и операций над множествами позволяют уточнить наше представление о классификации – действии распределения объектов по классам. Классификацию мы выполняем достаточно часто…. [читать подробенее]
Классификацию мы выполняем достаточно часто…. [читать подробенее]
Разбиение множества на классы Пусть задано некоторое множество, например, множество треугольников. В этом множестве выделим свойство (например, быть прямоугольным). Тогда множество треугольников разбивается на два класса: прямоугольные и непрямоугольные. … [читать подробенее]
Тема 3. ОТНОШЕНИЯ НА МНОЖЕСТВАХ Бином Ньютона Объединение комбинаторных конфигураций Комбинаторные числа не всегда определяются непосредственно по известным комбинаторным конфигурациям. Часто используются различные способы сведения одних… [читать подробенее]
Декартово произведение множеств A и B – это множество упорядоченных пар, первый элемент которых принадлежит A, а второй – принадлежит B.
Пример. Свойства декартова произведения:
1) — некоммутативность
2) =- ассоциативность
Свойство ассоциативности позволяет… [читать подробенее]
Свойства декартова произведения:
1) — некоммутативность
2) =- ассоциативность
Свойство ассоциативности позволяет… [читать подробенее]
Бинарные отношения Декартовым произведением двух множеств X и Y называется множество всех упорядоченных пар ( x,y )таких, что , а . Пример 1. Пусть . Тогда , . Очевидно, что , т.е. для операции декартова произведения множеств закон коммутативности не выполняется. … [читать подробенее]
Определение, как найти с примерами
Если X и Y обозначают любые два непустых множества. Тогда множество всех упорядоченных пар (x, y), таких что x ∈ X и y ∈ Y, называется декартовым произведением двух множеств; X и Y. Произведение обозначается как X × Y. В математике совокупность элементов или группы вещей обозначает множество.
В этой статье о декартовом произведении множеств вы узнаете об определении декартова произведения, о том, как найти декартово произведение пустых множеств, двух множеств и трех множеств, а также о теоремах, свойствах и решенных примерах по декартовому произведению. наборов на основе базовой теории множеств с часто задаваемыми вопросами.
наборов на основе базовой теории множеств с часто задаваемыми вопросами.
Термин «произведение» в декартовом произведении множеств указывает на умножение членов. Например, 12, умноженное на 2, дает 24. Теперь, что означает декартово произведение? Декартово произведение — это произведение компонентов, скажем, x и y, в упорядоченном порядке.
Упорядоченная пара в декартовом произведении множеств указывает на фиксированное представление значения. То есть, если A и B — два непустых множества, то декартово произведение множеств A и B — это множество всех упорядоченных пар элементов/компонентов из A и B. С точки зрения математики, сформулированное как:
A × B = {(a, b) : a ∈ A, b ∈ B}
Здесь первый элемент из A, а второй элемент из B, что делает их упорядоченной парой.
Узнайте о дополнении набора здесь!
Решите декартовы произведения быстрее после просмотра этого видео
«0» разрешить = «акселерометр; Автовоспроизведение; буфер обмена-запись; зашифрованные носители; гироскоп; картинка в картинке» allowfullscreen?rel=0>
Как найти декартово произведение? В математике существуют различные типы множеств, а именно: пустое множество, конечное множество, одноэлементное множество, эквивалентное множество, подмножества, степенное множество, универсальное множество, надмножество и бесконечное множество. Все эти типы множеств имеют свой вес в математике. При работе с декартовыми произведениями важно понимать, что декартово произведение двух или даже трех множеств само по себе является множеством. Результирующий набор состоит из набора компонентов в указанном порядке.
Все эти типы множеств имеют свой вес в математике. При работе с декартовыми произведениями важно понимать, что декартово произведение двух или даже трех множеств само по себе является множеством. Результирующий набор состоит из набора компонентов в указанном порядке.
Теперь, когда мы знаем определение и математическое представление, давайте научимся находить декартово произведение для счетных множеств, пустых множеств и нескольких множеств.
Декартово произведение множествДекартово произведение счетных множеств означает, что множество и результирующие множества счетны. Если оба данных множества счетны, то результирующее множество также будет счетно. Давайте поймем то же самое с помощью двух и трех наборов в следующих заголовках.
Декартово произведение двух множествНачнем с рассмотрения двух непустых множеств X = {a, b, c} и Y = {7, 14, 21}. Декартово произведение получается с помощью следующих шагов:
Шаг 1: Для начала берется первый элемент X и умножается на первый элемент Y, чтобы получить первую упорядоченную пару как {a, 7}.
Шаг 2: Описанный выше метод повторяется для всех компонентов до тех пор, пока не будут выбраны все вероятные комбинации.
Шаг 3: Полный набор декартовых произведений двух множеств:
X x Y = {(a,7), (a,14), (a,21), (b,7), ( б, 14), (б, 21), (в, 7), (в, 14), (в, 21)}.
Формула для того же:
X × Y = {(x, y) : x ∈ X, y ∈ Y}
Здесь (x, y) обозначают упорядоченные пары. Декартово произведение двух счетных множеств счетно.
Узнайте больше о последовательностях и сериях здесь.
Декартово произведение трех множествВ предыдущем заголовке мы увидели, как получить декартово произведение 2 наборов. Точная процедура применяется для получения декартова произведения трех наборов. Если нам даны три конечных множества P, Q и R, то декартово произведение P, Q и R обозначается P x Q x R и в терминах обозначений определяется как:
(P x Q X R) = {(p , q, r) p∈P, q ∈ Q и r ∈ R}
Декартово произведение пустого множества пустой набор будет равен нулю. Декартово произведение любого непустого множества на пустое (обозначаемое -∅) дает пустое множество.
Декартово произведение любого непустого множества на пустое (обозначаемое -∅) дает пустое множество.
ИЛИ
Можно сказать, что если в заданных множествах любое из множеств является нулевым множеством, то декартово произведение также будет пустым множеством/пустым множеством.
т. е. для двух множеств, если P = ∅ или Q = ∅, то P x Q = ∅
ИЛИ
A × ∅ = {(a,c)| a ∈ A, c∈ ∅}.
Декартово произведение нескольких множествДо сих пор мы читали о декартовом произведении двух, трех и пустых множеств. Хотя мы можем определить декартово произведение и для более чем двух/трех множеств. Пусть \(C_1,C_2\dots,C_n\) — n непустых множеств. Декартово произведение \(C_1\times C_2\times\dots\times C_n\) представляется как множество всех вероятно упорядоченных n−кортежей (\(c_1,c_2\dots,c_n\)), где \(c_i∈C_i \) и i=1, 2, ……n.
Декартово произведение нескольких входных наборов — это больший набор, содержащий все упорядоченные комбинации всех элементов входного набора.
Обозначение множества обычно дается фигурными скобками, {} и каждый элемент в множестве отделяется запятыми, как показано; {a, e, i, o, u}, где a, e, i, o и u представляют элементы множеств. Элементы декартова произведения являются упорядоченными парами. Здесь под упорядоченной парой можно понимать набор из двух сущностей вместе с порядком, связанным с ними. На данный момент мы знаем, как найти декартово произведение множества; будь то счетное, пустое или много множеств. Давайте теперь изучим важные теоремы, связанные с этой темой.
Если у нас есть три множества A, B и C. Тогда:
- A×(B∩C)=(A×B)∩(A×C)
- A×(B∪C)=(A×B)∪(A×C)
- A×( B−C)=(A×B)−(A×C)
- Если P⊆A , то P×B⊆A×B .
- Если A⊆B и C⊆D, то A×C⊆B×D
Декартово произведение множеств и отношений понимается также как векторное произведение или произведение наборы. В предыдущем заголовке мы прочитали теоремы, теперь давайте приступим к свойствам:
В предыдущем заголовке мы прочитали теоремы, теперь давайте приступим к свойствам:
- Декартово произведение множеств некоммутативно, то есть если нам даны два множества, скажем, P и Q, то:
- P × Q ≠ Q × P
- И, P × Q = Q × P, тогда и только тогда если P = Q.
- Декартово произведение множеств неассоциативно, т. е. если нам даны три множества, скажем, P, Q и R, то:
- (P × Q) × R ≠ P × (Q × R)
- Распределительное свойство для пересечения множеств, если нам даны три множества, скажем, P, Q и R, тогда:
- P × (Q ∩ R) = (P × Q) ∩ (P × R)
- Распределительное свойство объединения множеств, если нам даны три множества, скажем P, Q и R, равны:
- P × (Q∪R) = (P × Q) ∪ (P × R)
- распределительное свойство разности между множествами:
- P × (Q-R) = (P ×Q)-(P ×R)
- Свойство пустого множества; если какое-либо из множеств в декартовом произведении пусто, то результатом также будет пустое множество.

- P × Q = ∅, если либо P = ∅, либо Q = ∅
Прочтите эту статью о скалярном произведении.
Мощность декартова произведенияМощность набора определяет общее количество компонентов, присутствующих в наборе. Кроме того, кардинальное число набора равно количеству всех присутствующих элементов. Мощность декартова произведения двух множеств эквивалентна произведению мощностей данных множеств. Отсюда следует, что если у нас есть два множества, а именно A и B, то:
n(A × B) = n(B × A) = n(A) × n(B).
Таким же образом \(n(C_1\times C_2\times\dots\times C_n)=n(C_1)\times n(C_2)\times\dots\times n(C_n)\).
Решенные примеры на декартово произведение множеств Отношения и функции обычно представляют собой различные операции с множествами, выполняемые над данным множеством. Отношение в математике определяется как ассоциация между компонентами двух или более наборов с условием, что наборы должны быть непустыми. Зная все о декартовом произведении множеств через определение, как найти их для разных множеств с последующими теоремами и свойствами. Давайте попрактикуемся в некоторых решенных примерах, касающихся того же самого:
Зная все о декартовом произведении множеств через определение, как найти их для разных множеств с последующими теоремами и свойствами. Давайте попрактикуемся в некоторых решенных примерах, касающихся того же самого:
Решено Пример 1: Если A = {1, 2, 3} и B = {r}, то определить A × B и B × A. Равны ли эти два произведения?
Решение:
Даны A = {1, 2, 3} и B = {r}
Теперь A × B={(1, r), (2, r), (3, r) }
и B × A={(r, 1), (r, 2), (r, 3)}
Согласно свойству коммутативности P × Q ≠ Q × P
Следовательно, A × B ≠ B × A
Кроме того, упорядоченная пара в обоих исходах различна, поэтому A × B ≠ B × A.
Решенный пример 2: Если существуют два множества, такие что C = {3,4} и n(C) = 2, D = {1,4,8} и n(D) = 3. Получите мощность C × D.
Решение:
Дано: C = {3,4}, n(C) = 2, D = {1,4,8} и n(D) = 3
Теперь, n(C × D) = n(C) × n(D) = 2 × 3 = 6.
Таким образом, мощность результирующего набора C × D эквивалентна произведению мощностей всех входных наборов.
Решено Пример 3: Даны A = {2, 4, 8} и B = {3, 6}. Найдите А х В. 9{2}\)= {а, Ь, с} х {а, Ь, с} = {(а, а), (а, Ь), (а, с), (Ь, а), (Ь, b), (b, c), (c, a), (c, b), (c, c)}
Решено Пример 5: Найдите декартово произведение B×P(B), если B={2 , 4}.
Решение:
P(B)=P{{2, 4}}={∅, {2}, {4}, {2, 4} }
Теперь B×P(B)= {2, 4}×{∅, {2}, {4}, {2, 4} }={{2, ∅}, {2, {2}}, {2, {4}}, {2, {2, 4}}, {4, ∅}, {4, {2}}, {4, {4}}, {4, {2, 4} }
Подводя итоги темы, можно констатировать, что:
- Две упорядоченные пары идентичны тогда и только тогда, когда равны соответствующие первый и второй элементы данной упорядоченной пары.
- Если в P имеется x элементов, а в Q y элементов, то в P × Q будет xy элементов. так как если n(P) = x и n(Q) = y, то n(P × Q) = xy.

- Если X и Y — два непустых множества и либо X, либо Y — бесконечное множество, то X × Y — тоже.
- P × P × P = {(a, b, c): a, b, c ∈ P}. Здесь (a, b, c) называется упорядоченной тройкой.
Мы надеемся, что приведенная выше статья о декартовом произведении множеств поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Декартово произведение множеств Часто задаваемые вопросыQ.1 Что такое определение множеств в математике?
Ответ 1 В математике множества представлены как наборы четко определенных объектов/вещей. Например; набор гласных образует группу, поскольку гласные четко определены, поэтому эта группа образует набор.
Q.2 Что такое декартово произведение двух множеств?
Ответ 2 Декартово произведение двух наборов, скажем, P и Q, т. е. P×Q — это набор всех потенциально упорядоченных пар с первым компонентом из P и вторым элементом из Q. Математически выражается как P× Q={(p,q):p∈P и q∈Q}.
е. P×Q — это набор всех потенциально упорядоченных пар с первым компонентом из P и вторым элементом из Q. Математически выражается как P× Q={(p,q):p∈P и q∈Q}.
Q.3 Что вы подразумеваете под декартовым произведением множества?
Отв.3 Набор, составленный из заданных наборов (двух или трех) и включающий все пары элементов таким образом, что первый компонент пары из 1-го набора, за которым следует второй из второй набор и так далее.
Q.4 Чему равно декартово произведение 3 наборов?
Ответ 4 Декартово произведение трех множеств говорит; X, Y и Z могут быть составлены как X × Y × Z = {(a,b,c): a ∈ X, b ∈ Y, c ∈ Z}.
Q.5 Что такое отношение в множествах?
Ответ 5 В математике отношение описывает отношения между наборами значений упорядоченных пар. Набор компонентов в первом наборе называется доменом, связанным с набором компонентов в другом наборе, который обозначается как диапазон.
Q.6 Что такое декартова форма?
Ответ 6 Декартова форма функции или отношения состоит из координат (x, y) или (x, y, z).
Q.7 Что такое набор AxB?
Ответ 7 AxB обозначает декартово произведение двух наборов A и B, которые содержат упорядоченные пары из A и B. Примечание. Приведенные ниже ссылки должны быть связаны со статьей после ее публикации. пустой набор операций над наборами объединение наборов
Скачать публикацию в формате PDF| Свойства арифметической прогрессии: определение и формулы |
| Latus Rectum: определение, уравнение, важные свойства, с подробными изображениями |
| Иррациональные числа: изучите определения, символы, списки, свойства на примерах! |
| Типы, реакции, структура, формула и свойства ароматических соединений |
| Постулаты, важность, ограничения теории валентных связей |
5.
 09: Декартовы произведения — Математика
09: Декартовы произведения — Математика- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7063
- Тед Сандстром
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
- 0
ПРЕДПРОСМОТР \(\PageIndex{1}\): уравнение с двумя переменными
В разделе 2.3 мы ввели понятие множества истинности открытого предложения с одной переменной . Это было определено как набор всех элементов в универсальном наборе, которые можно заменить переменной, чтобы сделать открытое предложение истинным утверждением.
В предыдущих курсах математики у нас также был опыт с открытыми предложениями с двумя переменными. Например, если мы предположим, что x и y представляют собой действительные числа, то уравнение
Например, если мы предположим, что x и y представляют собой действительные числа, то уравнение
\(2x + 3y = 12\)
— открытое предложение с двумя переменными. Элементом множества истинности этого открытого предложения (также называемого решением уравнения) является упорядоченная пара (\(а\), \(b\)) действительных чисел, так что при замене \(а\) на \(x\) и \(b\) заменяются на \(y\), открытое предложение становится истинным высказыванием (в данном случае истинным уравнением). Например, мы видим, что упорядоченная пара (6, 0) находится в наборе истинности для этого открытого предложения, поскольку
\(2 \cdot 6 + 3 = 12\)
является истинным утверждением. С другой стороны, упорядоченная пара (4, 1) не находится в истинном множестве для этого открытого предложения, поскольку
\(2 \cdot 4 + 3 \cdot 1 = 12\)
является ложным утверждением.
Важное примечание: Порядок двух чисел в заказанной паре очень важен. Мы используем соглашение, согласно которому первое число должно быть заменено на \(x\), а второе число должно быть заменено на \(y\). При таком соглашении (3, 2) является решением уравнения \(2x + 3y = 12\), но (2, 3) не является решением этого уравнения.
При таком соглашении (3, 2) является решением уравнения \(2x + 3y = 12\), но (2, 3) не является решением этого уравнения.
- Перечислите шесть различных элементов множества истинности (часто называемого множеством решений) открытого предложения с двумя переменными \(2x + 3y = 12\).
- Из предыдущих курсов математики мы знаем, что график уравнения \(2x + 3y = 12\) представляет собой прямую линию. Начертите график уравнения \(2x + 3y = 12\) в координатной плоскости \(xy\). Что показывает график уравнения \(2x + 3y = 12\)?
- Напишите описание набора решений \(S\) уравнения \(2x + 3y = 12\), используя нотацию конструктора наборов.
ПРЕДПРОСМОТР \(\PageIndex{1}\): Декартово произведение двух множеств
В ходе предварительного просмотра \(\PageIndex{1}\) мы работали с упорядоченными парами без предоставления формального определения упорядоченной пары. Вместо этого мы полагались на вашу предыдущую работу с упорядоченными парами, в основном с графическими уравнениями с двумя переменными. Ниже приводится формальное определение упорядоченной пары.
Ниже приводится формальное определение упорядоченной пары.
Определение: упорядоченная пара
Пусть \(A\) и \(B\) — множества. Упорядоченная пара (с первым элементом из \(A\) и вторым элементом из \(B\)) представляет собой одну пару объектов, обозначаемую (\(a\), \(b\)), с \ (a \in A\) и \(b \in B\) и подразумеваемый порядок. Это означает, что для того, чтобы две упорядоченные пары были равны, они должны содержать одни и те же объекты в одном и том же порядке. То есть, если \(a, c \in A\) и \(b, d \in B\), то
(\(a\), \(b\)) = (\(c\), \(d\)) тогда и только тогда, когда \(a = c\) и \(b = d\).
Объекты в упорядоченной паре называются координатами упорядоченной пары. В упорядоченной паре (\(a\), \(b\)), \(a\) — первая координата , а \(b\) — вторая координата .
Теперь мы введем новую операцию над множествами, которая позволяет объединять элементы из двух заданных множеств в упорядоченные пары. Основная идея заключается в том, что мы создадим набор упорядоченных пар. 2\) вместо \(A \times A\). то есть 92 = A \times A = \{(a, b)\ |\ a \in A \text{ и } b \in A\}\).
2\) вместо \(A \times A\). то есть 92 = A \times A = \{(a, b)\ |\ a \in A \text{ и } b \in A\}\).
Пусть \(A\ = \) {1, 2, 3} и \(B\ = \) {\(a\), \(b\)}.
- Является ли упорядоченная пара (3, \(a\)) декартовым произведением \(A \times B\)? Объяснять.
- Является ли упорядоченная пара (3, \(a\)) декартовым произведением \(A \times A\)? Объяснять.
- Является ли упорядоченная пара (3, 1) декартовым произведением \(A \times A\)? Объяснять.
- Использование метода списка для указания всех элементов \(A \times B\). (Помните, что элементы \(A \times B\) будут упорядоченными парами. 92\).
- Для любых множеств \(C\) и \(D\) подробно объясните, что значит сказать, что упорядоченная пара (\(x\), \(y\)) не входит в декартово произведение \(C \ раз D\).
Декартово произведение
При работе с декартовым произведением важно помнить, что декартово произведение двух множеств само по себе является множеством. Как набор, он состоит из набора элементов. В этом случае элементы декартова произведения являются упорядоченными парами. Мы должны думать об упорядоченной паре как об одном объекте, который состоит из двух других объектов в определенном порядке. Например,
Как набор, он состоит из набора элементов. В этом случае элементы декартова произведения являются упорядоченными парами. Мы должны думать об упорядоченной паре как об одном объекте, который состоит из двух других объектов в определенном порядке. Например,
- Если \(a \ne 1\), то упорядоченная пара (1, \(a\)) не равна упорядоченной паре (\(a\), 1). То есть (1, \(а\)) \(\пе\) (\(а\), 1).
- Если \(A\ = \) {1, 2, 3} и \(B\ =\) {\(a\), \(b\)}, то упорядоченная пара (3, \(a\) ) является элементом множества \(A \times B\). То есть (3, \(a\)) \(\in A \times B\).
- Если \(A\ = \) {1, 2, 3} и \(B\ =\) {\(a\), \(b\)}, то упорядоченная пара (5, \(a\) ) не является элементом множества \(A \times B\), так как \(5 \notin A\). То есть \((5, а) \не в А \раз В\).
В разделе 5.3 мы изучили некоторые свойства объединения множеств, пересечения множеств и дополнений множеств, которые мы назвали алгеброй множеств. Теперь мы начнем нечто подобное для декартовых произведений. Мы начнем с изучения некоторых конкретных примеров в Progress Check 5.23 и чуть позже в Progress Check 5.24.
Мы начнем с изучения некоторых конкретных примеров в Progress Check 5.23 и чуть позже в Progress Check 5.24.
проверка прогресса 5.23 (отношения между декартовыми произведениями)
Пусть \(A =\) {1, 2, 3}, \(T =\) {a, b} и \(C =\) {a, в}. Затем мы можем сформировать новые множества из всех изученных нами операций над множествами. Например, \(B \cap C =\) {\(a\)}, поэтому
\(A \times (B \cap C) = \{(1, a), (2, a), (3, a)\}.\)
- Используйте метод реестра, чтобы перечислить все элементов (упорядоченные пары) в каждом из следующих множеств:
(а) \(А \крат В\)
(б) \(Т \крат В\)
(в) \(А \крат С\)
( г) \(A \times (B \cap C)\)
(e) \((A \times B) \cap (A \times C)\)
(f) \(A \times (B \cup В)\)
(г) \((А \раз В) \чашка (А \раз С)\)
(з) \(А \раз (В — С)\)
(i) \((А \раз В) — (А \раз С)\)
(к) \(В \раз А\) - Перечислите все взаимосвязи между наборами в Части (1), которые вы заметили.
- Ответить
Добавьте сюда текст.
 2\). Этот самолет называется 92\ |\ 1 \le x \le 3 \text{ и } 2 \le y \le 5\}.\)
2\). Этот самолет называется 92\ |\ 1 \le x \le 3 \text{ и } 2 \le y \le 5\}.\)График множества \(A \times B\) можно построить в декартовой плоскости, как показано на рисунке 5.6.
Это показывает, что график декартова произведения двух интервалов конечной длины в \(\mathbb{R}\) соответствует внутренней части прямоугольника и, возможно, некоторой или всей его границе. Сплошная линия границы на рис. 5.6 указывает, что граница включена. В этом случае декартово произведение содержало всю границу прямоугольника. Когда граф не содержит части границы, мы обычно рисуем эту часть границы пунктирной линией.
Примечание. Предупреждение об обозначениях. Стандартное обозначение открытого интервала в \(\mathbb{R}\) совпадает с обозначением упорядоченной пары, которая является элементом \(\mathbb{R} \times \mathbb{R}\). Нам нужно использовать контекст, в котором используется обозначение, чтобы определить, какая интерпретация предназначена. Например,
- Если мы напишем (\(sqrt 2\), 7) \(\in \mathbb{R} \times \mathbb{R}\), то мы используем (\(sqrt 2\), 7) для представления упорядоченной пары действительных чисел.

- Если мы напишем (1, 2) \(\times\) {4}, то мы интерпретируем (1, 2) как открытый интервал. Мы могли бы написать
(1, 2) \(\раз\) {4} = {(\(х\), 4) | 1 < \(х\) < 2}.
Следующая проверка выполнения исследует некоторые из тех же идей, что и в разделе Проверка выполнения 5.23, за исключением того, что для наборов используются интервалы действительных чисел.
Проверка выполнения 5.24: Декартово произведение интервалов
Мы будем использовать следующие интервалы, которые являются подмножествами \(\mathbb{R}\).
\(A =\) [0, 2] \(T =\) (1, 2) \(B =\) [2, 4) \(C =\) (3, 5]
- Ничья график каждого из следующих подмножеств декартовой плоскости и запишите каждое подмножество, используя нотацию построителя множеств:
(a) \(A \times B\)
(b) \(T \times B\)
(c) \ (A \times C\)
(d) \(A \times (B \cap C)\)
(e) \((A \times B) \cap (A \times C)\)
(f) \(A \times (B \cup C)\)
(g) \((A \times B) \cup (A \times C)\)
(h) \(A \times (B — C)\ )
(i) \((A \times B) — (A \times C)\)
(к) \(В \х А\) - Перечислите все взаимосвязи между наборами в Части (1), которые вы заметили.

- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Одной из целей незавершенных проверок 5.23 и 5.24 было показать правдоподобие многих результатов, содержащихся в следующей теореме.
Теорема 5.25
Пусть \(А\), \(В\). и \(С\) — множества. Затем
- \(A \times (B \cap C) = (A \times B) \cap (A \times C)\)
- \(A \times (B \times C) = (A \times B) \cup (A \times C)\)
- \((A \cap B) \times C = (A \times C) \cap (B \times C)\)
- \((A \чашка B) \times C = (A \times C) \cup (B \times C)\)
- \(А \умножить на (В — С) = (А \умножить на В) — (А \умножить на С)\)
- \((A — B) \times C = (A \times C) — (B \times C)\)
- Если \(T \subseteq A\), то \(T \times B \subseteq A \times B\).
- Если \(T \subseteq B\), то \(A \times Y \subseteq A \times B\).
Мы не будем доказывать все эти результаты; скорее, мы докажем часть (2) теоремы 5.
 25, а остальное оставим для упражнений. При построении этих доказательств нам нужно помнить, что декартовы произведения — это множества, поэтому мы следуем многим из тех же принципов для доказательства отношений множеств, которые были введены в разделах 5.2 и 5.3.
25, а остальное оставим для упражнений. При построении этих доказательств нам нужно помнить, что декартовы произведения — это множества, поэтому мы следуем многим из тех же принципов для доказательства отношений множеств, которые были введены в разделах 5.2 и 5.3.Следует также помнить, что элементы декартова произведения представляют собой упорядоченные пары. Поэтому, когда мы начинаем доказательство такого результата, как часть (2) теоремы 5.25, основная цель — доказать равенство двух множеств. Мы сделаем это, доказав, что каждое из них является подмножеством другого. Итак, если мы хотим доказать, что \(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\), мы можем начать с выбора произвольного элемента \(A \times C)\ раз (В \чашка С)\). Затем цель состоит в том, чтобы показать, что этот элемент должен быть в \((A \times B) \cup (A \times C)\). Когда мы начинаем с выбора произвольного элемента \(A \times (B \cup C)\), мы можем дать этому элементу имя. Например, мы могли бы начать с того, что
\[u \text{ быть элементом } A \times (B \cup C).
 \]
\]Затем мы можем использовать определение «упорядоченной пары», чтобы заключить, что
\[\text{существует } x \in A \text{ и существует выход } y \in B \cup C \text{ такой, что } u = (x, y).\]
Чтобы доказать, что \(A \times (B \ cup C) \subseteq (A \times B) \cup (A \times C)\), мы должны теперь показать, что упорядоченная пара \(u\) из (5.4.1) находится в \(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\). Для этого мы можем воспользоваться определением объединения множеств и доказать, что
\[u \in (A \times B) \text{ или } u \in (A \times C).\]
Поскольку \(u = (x, y)\), мы можем доказать (5.4 .3) доказав, что
\[(x \in A \text{ и } y \in B) \text{ или } (x \in A \text{ и } y \in C).\]
Если мы посмотрим на предложения в (5.4.2) и (5.4.4), может показаться, что мы очень близки к доказательству того, что \(A \times (B \cup C) \subseteq (A \times B) \ чашка (А \раз С)\). Ниже приводится доказательство части (2) теоремы 5.
 25.
25.Теорема 5.25 (часть (2)).
Пусть \(А\), \(В\). и \(С\) — множества. Тогда
\(A \times (B \cup C) = (A \times B) \cup (A \times C)\)
- Доказательство
Пусть \(А\), \(В\). и \(С\) — множества. Мы докажем, что \(A \times (B \cup C)\) равно \((A \times B) \cup (A \times C)\), доказав, что каждое множество является подмножеством другого множества .
Чтобы доказать, что \(A \times (B \cup C) \subseteq (A \times B) \cup (A \times C)\), пусть \(u \in A \times (B \cup C) \). Тогда существует \(x \in A\) и существует \(y \in B \cup C\) такие, что \(u = (x, y)\). Поскольку \(y \in B \cup C\), мы знаем, что \(y \in B\) или \(y \in C\).
В случае, когда \(y \in B\), мы имеем \(u = (x, y)\), где \(x \in A\) и \(y \in B\). Итак, в этом случае \(u \in A \times B\), и, следовательно, \(u \in (A \times B) \cup (A \times C)\). Аналогично, в случае, когда \(y \in C\), мы имеем \(u = (x, y)\), где \(x \in A\) и \(y \in C\).
 Итак, в этом случае \(u \in A \times C\) и, следовательно, \(u \in (A \times B) \cup (A \times C)\).
Итак, в этом случае \(u \in A \times C\) и, следовательно, \(u \in (A \times B) \cup (A \times C)\).В обоих случаях \(u \in (A \times B) \cup (A \times C)\). Отсюда можно заключить, что если \(u\) является элементом \(A \times (B \times C)\), то \(u \in (A \times B) \cup (A \times C) \), и это доказывает, что
\[A \times (B \times C) \subseteq (A \times B) \cup (A \times C).\]
Теперь мы должны доказать, что \((A \times B) \cup (A \times C) \subseteq A \times (B \cup C)\). Итак, пусть \(v \in (A \times B) \cup (A \times C)\). Тогда \(v \in (A \times B)\) или \(v \in (A \times C)\).
В случае, когда \(v \in (A \times B)\), мы знаем, что существуют \(s \in A\) и существует \(t \in B\) такие, что \(v = ( с, т)\). Но поскольку \(t \in C\), мы можем заключить, что \(t \in B \cup C\) и, следовательно, \(v \in A \times (B \cup C)\).
В обоих случаях \(v \in A \times (B \cup C)\). Отсюда можно заключить, что если \(v \in (A \times B) \cup (A \times C)\), то \(v \in A \times (B \cup C)\), а это доказывает что
\[(A \times B) \cup (A \times C) \subseteq A \times (B \cup C).
 \]
\]Соотношения в (5.4.5) и (5.4.6) доказывают, что \(A \times (B \times C) = (A \times B) \cup (A \times C)\).
Последнее примечание.
Определение упорядоченной пары в Preview Activity \(\PageIndex{2}\) может показаться слишком длинным, но в некоторых областях математики требуется еще более формальное и точное определение «упорядоченной пары». Это определение исследуется в упражнении (10). 92\)
(e) \(A \times (B \cap C)\)
(f) \((A \times B) \cap (A \times C)\)
(g) \(A \ раз \emptyset\)
(h) \(B \times \{2\}\)- Нарисуйте график каждого из следующих декартовых произведений на декартовой плоскости.
(а) [0, 2] \(\раз\) [1, 3]
(б) (0, 2) \(\раз\) (1, 3]
(в) [2, 3] \ (\times\) {1}
(d) {1} \(\times\) [2, 3]
(e) \(\mathbb{R}\) \(\times\) (2, 4)
(е) (2, 4) \(\times\) \(\mathbb{R}\)
(g) \(\mathbb{R}\) \(\times\) {-1}
(h) {-1} \(\times\) [1, +\(\infty\))- Докажите теорему 5.
 25, часть (1): \(A \times (B \cap C) = (A \times B) \cap (A \times C)\).
25, часть (1): \(A \times (B \cap C) = (A \times B) \cap (A \times C)\).- Докажите теорему 5.25, часть (4): \((A \чашка B) \times C = (A \times C) \cup (B \times C)\).
- Докажите теорему 5.25, часть (5): \(A \times (B — C) = (A \times B) — (A \times C)\).
- Докажите теорему 5.25, часть (7): если \(T \subseteq A\), то \(T \times B \subseteq A \times B\).
- Пусть \(A =\) {1}, \(B =\) {2} и \(C =\) {3}.
(a) Объясните, почему \(A \times B \ne B \times A\).
(b) Объясните, почему \(A \times B) \times C \ne A \times (B \times C)\).- Пусть \(A\) и \(B\) — непустые множества. Докажите, что \(A \times B = B \times A\) тогда и только тогда, когда \(A = B\).
- Верно или ложно следующее утверждение? Обоснуйте свой вывод.
Пусть \(A\), \(B\) и \(C\) множества с \(A \ne \emptyset\). Если \(A \times B = A \times C\), то \(B = C\). Объясните, где требуется предположение, что \(A \ne \emptyset\).
Разведка и деятельность
- (Теоретико-множественное определение упорядоченной пары) В элементарной математике достаточно понятия упорядоченной пары, введенного в начале этого раздела.
 Однако, если нас интересует формальное развитие декартова произведения двух множеств, нам нужно более точное определение упорядоченной пары. Ниже приведен один из способов сделать это с точки зрения наборов. Это определение приписывают Казимежу Куратовскому (189 г.6 – 1980). Куратовский был известным польским математиком, основная работа которого была связана с топологией и теорией множеств. Он был назначен директором Польской академии наук и проработал на этой должности 19 лет.
Однако, если нас интересует формальное развитие декартова произведения двух множеств, нам нужно более точное определение упорядоченной пары. Ниже приведен один из способов сделать это с точки зрения наборов. Это определение приписывают Казимежу Куратовскому (189 г.6 – 1980). Куратовский был известным польским математиком, основная работа которого была связана с топологией и теорией множеств. Он был назначен директором Польской академии наук и проработал на этой должности 19 лет.Пусть \(х\) — элемент множества \(А\), а \(у\) — элемент множества \(В\). Упорядоченная пара (\(x\), \(y\)) определяется как множество \(\{\{x\}, \{x, y\}\}\). То есть
\[(x, y) = \{\{x\}, \{x, y\}\}.\]
(a) Объясните, как это определение позволяет нам различать упорядоченные пары (3 , 5) и (5, 3).(b) Пусть множества \(A\) и \(B\) и \(a, c \in A\) и \(b, d \in B\). Используйте это определение упорядоченной пары и концепцию равенства множеств, чтобы доказать, что \((a, b) = (c, d)\) тогда и только тогда, когда \(a = c\) и \(b = d\) .

Упорядоченную тройку можно рассматривать как одну тройку объектов, обозначаемую (\(a\), \(b\), \(c\)), с подразумеваемым порядком. Это означает, что для того, чтобы две упорядоченные тройки были равны, они должны содержать точно такие же объекты в одном и том же порядке. То есть \((a, b, c) = (p, q, r)\) тогда и только тогда, когда \(a = p\), \(b = q\) и \(c = r\).
(c) Пусть \(A\), \(B\) и \(C\) — множества, и пусть \(x \in A\), \(y \in B\) и \(z \в С\). Напишите теоретико-множественное определение упорядоченной тройки \((x, y, z)\), аналогичное теоретико-множественному определению «упорядоченной пары».
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Эта страница под названием 5.4: Декартовы продукты распространяется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстрем
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу Содержание
- нет
- Теги
- Декартова плоскость
- Декартовы произведения
- источник@https://scholarworks.
 gvsu.edu/books/7
gvsu.edu/books/7
Объяснение урока: Декартовы произведения | Нагва
В этом объяснении мы узнаем, как выполнять декартово произведение и использовать операции, применяемые к множествам.
Напомним, что набор — это набор чисел, таких как 𝐴={1,2}. Мы обозначаем множества с помощью фигурных скобок, а числа между ними — это элементы, которые могут идти в любом порядке. Напомним, что мы также можем выполнять операции над несколькими множествами, например находить их объединение, пересечение или различие. Если мы допустим 𝐵={2,3,4}, то мы имеем 𝐴∪𝐵={1,2,3,4},𝐴∩𝐵={2},𝐴−𝐵={1}.
Символ ∪ обозначает объединение и представляет собой набор всех элементов, принадлежащих любому набору, который в данном случае равен 1, 2, 3 и 4 (цифра 2 повторяется, но мы не должны включать ее дважды) . Символ ∩ обозначает пересечение , и это означает набор элементов, общих для обоих наборов, который равен всего 2, поскольку он является единственным элементом в обоих наборах.
 Наконец, — обозначает вычитание одного набора из другого, что означает удаление любых элементов из первого набора, присутствующих во втором наборе. Здесь это просто означает убрать 2 из {1,2}, оставив только 1.
Наконец, — обозначает вычитание одного набора из другого, что означает удаление любых элементов из первого набора, присутствующих во втором наборе. Здесь это просто означает убрать 2 из {1,2}, оставив только 1.Теперь рассмотрим четвертую операцию, декартово произведение , которое мы определяем следующим образом.
Определение: Декартово произведение
Декартово произведение 𝐴×𝐵 двух множеств 𝐴 и 𝐵 — это множество всех упорядоченных пар (𝑥,𝑦), таких что 𝑥∈𝐴 и 𝑦∈𝐵.
Чтобы продемонстрировать, как это работает, возьмем декартовы произведения наших наборов примеров, 𝐴={1,2} и 𝐵={2,3,4}. Чтобы получить упорядоченную пару с помощью этих наборов, мы берем один элемент из 𝐴 и один элемент из 𝐵 и помещаем их в пару в скобках. Взяв первый элемент из каждого набора, мы имеем (1,2). Мы хотим взять все возможные комбинации пар между двумя наборами, которые мы иллюстрируем на следующей стрелочной диаграмме.
Следовательно, декартово произведение равно 𝐴×𝐵={(1,2),(1,3),(1,4),(2,2),(2,3),(2,4)}.

Обратите внимание, что это дает нам 6 различных элементов, что означает, что размер множества 𝑛(𝐴×𝐵) равен 6. Стоит отметить, что мы также можем взять противоположное произведение, 𝐵×𝐴: 𝐵×𝐴={(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)}.
Важно понимать, что два набора 𝐴×𝐵 и 𝐵×𝐴 не совпадают, поскольку порядок пар имеет значение. Например, (1,2)≠(2,1). В этой ситуации единственная пара, общая для обоих наборов, это (2,2). В общем случае отметим, что 𝐴×𝐵≠𝐵×𝐴, а значит, декартовы произведения равны некоммутативный .
Также можно взять произведение множества с самим собой, которое мы обозначаем 𝐴=𝐴×𝐴. В этом случае у нас было бы 𝐴={(1,1),(1,2),(2,1),(2,2)}.
Отметим, что 𝐴 является одним из двух исключений, где декартово произведение коммутативно (т.е. 𝐴×𝐵=𝐵×𝐴), так как если 𝐴=𝐵, то явно порядок не имеет значения. Другой случай, когда либо 𝐴, либо 𝐵 — это пустое множество (множество, в котором нет чисел), обозначаемое ∅, поскольку 𝐴×∅=∅ и ∅×𝐵=∅. В этом смысле это в основном то же самое, что и умножение на 0,9.
 0003
0003Учитывая размер множества 𝐴×𝐵, как в приведенном выше случае, так и вообще, мы можем видеть, что 𝑛(𝐴×𝐵)=𝑛(𝐴)𝑛(𝐵).
То есть количество элементов в 𝐴×𝐵 равно (количество элементов в 𝐴) × (количество элементов в 𝐵), поскольку это общее количество упорядоченных пар, которые мы можем составить между двумя наборами . Обратите внимание, что если мы изменим порядок, мы получим 𝑛(𝐵×𝐴)=𝑛(𝐵)𝑛(𝐴)=𝑛(𝐴)𝑛(𝐵)=𝑛(𝐴×𝐵).
Итак, мы видим, что 𝑛(𝐴×𝐵)=𝑛(𝐵×𝐴), что означает, что 𝐴×𝐵 и 𝐵×𝐴 всегда имеют одинаковое количество элементов.
Чтобы попрактиковаться в декартовом произведении двух множеств, давайте рассмотрим пример, аналогичный приведенному выше, где нам дано декартово произведение в виде стрелочной диаграммы.
Пример 1. Нахождение декартовых произведений с помощью стрелочных диаграмм
Используйте приведенную ниже стрелочную диаграмму, чтобы найти 𝑋×𝑌.
Ответ
Напомним, что декартово произведение 𝑋×𝑌 двух множеств 𝑋 и 𝑌 — это множество всех упорядоченных пар (𝑥,𝑦), таких что 𝑥∈𝑋 и 𝑦∈𝑌.

Чтобы составить эти пары, возьмем каждый элемент 𝑥, принадлежащий 𝑋, проследим стрелки, ведущие от него к каждому элементу 𝑦 в 𝑌, и для каждой такой стрелки построим пару вида (𝑥,𝑦).
Для начала мы видим, что 4 соединяется оранжевыми стрелками с 9, 3 и 8, в результате чего получаются упорядоченные пары (4,9),(4,3),(4,8).
Затем 0 соединяется синими стрелками с 9, 3 и 8. Это дает нам упорядоченные пары (0,9),(0,3),(0,8).
Объединив эти элементы в один набор, мы имеем 𝑋×𝑌={(4,9),(4,3),(4,8),(0,9),(0,3),(0,8)}.
Как мы только что видели, использовать стрелочную диаграмму для нахождения декартова произведения довольно просто. Однако в некоторых случаях нам нужно найти декартово произведение множеств, заданных в системе обозначений. Возможно, нам также придется комбинировать декартово произведение с другими операциями над множествами. Следующий пример поможет нам проверить эти навыки.
Пример 2. Нахождение декартова произведения множества и пересечения множеств
Если 𝑋={8,4,6}, 𝑌={6,7} и 𝑍={7}, найти 𝑋×(𝑌 ∩𝑍).

Ответ
Здесь у нас есть вопрос, касающийся трех разных наборов. Рассматривая 𝑋×(𝑌∩𝑍), мы видим, что, поскольку 𝑌∩𝑍 стоит в скобках, из-за порядка операций мы должны сначала вычислить его. После этого мы можем взять декартово произведение результата, чтобы получить решение.
Теперь 𝑌∩𝑍 — это пересечение {6,7} и {7}. Пересечение этих наборов представляет собой набор элементов, которые находятся как в {6,7}, так и в {7}. Так как 7 есть в обоих наборах, а 6 нет, мы имеем {6,7}∩{7}={7}.
Другими словами, 𝑌∩𝑍={7}.
Теперь мы должны вычислить 𝑋×(𝑌∩𝑍), или {8,4,6}×{7}. Поскольку это декартово произведение, это означает, что мы создаем набор, содержащий каждую упорядоченную пару двух наборов. Это приводит к набору, содержащему три пары следующим образом: {8,4,6}×{7}={(8,7),(4,7),(6,7)}.
Таким образом, у нас есть решение 𝑋×(𝑌∩𝑍)={(8,7),(4,7),(6,7)}.
Иногда нам даются наборы в системе обозначений, но в других случаях мы должны выяснить, какие наборы представлены с помощью диаграмм.
 Рассмотрим пример, использующий диаграммы Венна для представления множеств.
Рассмотрим пример, использующий диаграммы Венна для представления множеств.Пример 3. Нахождение декартова произведения разности и объединения множеств по их диаграмме Венна
Определите (𝑍−𝑌)×(𝑋∪𝑌), используя приведенную ниже диаграмму Венна.
Ответ
Когда вы сталкиваетесь с вопросом, связанным с диаграммой, лучше всего начать с записи того, что представляют собой наборы. Мы видим, что 𝑋={4},𝑌={7,9},𝑍={3,7,8}.
Теперь, чтобы найти (𝑍−𝑌)×(𝑋∪𝑌), мы должны сначала выяснить, что такое 𝑍−𝑌 и 𝑋∪𝑌.
𝑍−𝑌 — это множество элементов в 𝑍 после того, как мы удалили все элементы, которые также есть в 𝑌. Вот, то есть {3,7,8}−{7,9}={3,8}.
Мы получили {3,8}, вычитая 7 из {3,7,8}, так как это единственный элемент, присутствующий в обоих наборах. Мы видим, что на диаграмме это соответствует голубому участку 𝑍, который не пересекается с 𝑌.
Далее мы должны найти 𝑋∪𝑌, представляющее собой объединенный набор точек, которые находятся либо в 𝑋, либо в 𝑌.
 Это
{4}∪{7,9}={4,7,9},
где мы просто объединили два набора вместе. Наконец, мы должны вычислить (𝑍−𝑌)×(𝑋∪𝑌), то есть {3,8}×{4,7,9}. Поскольку это декартово произведение, мы должны составить множество, содержащее все возможные упорядоченные пары между двумя множествами. Это дает нам
{3,8}×{4,7,9}={(3,4),(3,7),(3,9),(8,4),(8,7),(8,9)}.
Это
{4}∪{7,9}={4,7,9},
где мы просто объединили два набора вместе. Наконец, мы должны вычислить (𝑍−𝑌)×(𝑋∪𝑌), то есть {3,8}×{4,7,9}. Поскольку это декартово произведение, мы должны составить множество, содержащее все возможные упорядоченные пары между двумя множествами. Это дает нам
{3,8}×{4,7,9}={(3,4),(3,7),(3,9),(8,4),(8,7),(8,9)}.В итоге решение (𝑍−𝑌)×(𝑋∪𝑌)={(3,4),(3,7),(3,9),(8,4),(8,7) ,(8,9)}.
Теперь мы увидели, как строить декартовы произведения между множествами различными способами. Иногда у нас могут быть вопросы, где у нас есть обратная задача; учитывая множество, являющееся декартовым произведением, можем ли мы восстановить исходные множества? Как мы увидим в следующем примере, это довольно просто сделать из-за природы декартова произведения.
Пример 4. Нахождение множества по заданному его декартовому произведению на другое множество
Если 𝑋×𝑌={(8,0),(8,6),(1,0),(1,6),(3, 0),(3,6)}, найти 𝑋.
Ответ
Напомним, что для декартова произведения 𝑋×𝑌 его элементы имеют вид (𝑥,𝑦), где 𝑥∈𝑋 и 𝑦∈𝑌.
 Заметим, что в первую компоненту входят только элементы из 𝑋, а во вторую — только элементы из 𝑌. Рассмотрим только первые компоненты каждого элемента 𝑋×𝑌, так как это элементы, соответствующие 𝑋. Это дает нам
8,8,1,1,3,3.
Заметим, что в первую компоненту входят только элементы из 𝑋, а во вторую — только элементы из 𝑌. Рассмотрим только первые компоненты каждого элемента 𝑋×𝑌, так как это элементы, соответствующие 𝑋. Это дает нам
8,8,1,1,3,3.Теперь мы знаем, что 𝑋×𝑌 содержит все возможные комбинации упорядоченных пар между элементами 𝑋 и 𝑌. Это означает, что приведенный выше набор чисел должен содержать каждый элемент 𝑋 в некоторой комбинации. Удаление повторяющихся чисел дает нам набор 𝑋 целиком, 𝑋={8,1,3}.
Найдя решение, мы могли бы остановиться на этом, но давайте проверим его правильность, также найдя 𝑌 и вычислив их декартово произведение. Рассмотрение вторых компонент каждого элемента 𝑋×𝑌 так же, как и раньше, дает нам 𝑌={0,6}.
Далее, взяв 𝑋×𝑌, получим 𝑋×𝑌={(8,0),(8,6),(1,0),(1,6),(3,0),(3,6)}.
Это действительно тот самый набор, который нам дали изначально. Следовательно, мы можем сделать вывод, что 𝑋={8,1,3}.
Давайте продолжим развивать наше понимание того, как работают декартовы произведения, рассмотрев другой пример, где мы должны тщательно рассмотреть, как взаимодействуют наборы.

Пример 5. Определение того, какое декартово произведение двух заданных множеств будет содержать заданный элемент
Если 𝑋={0,−1} и 𝑌={8,−4,−3,−2}, то какое из следующих отношений будет (−1,−4) элементом?
- 𝑋
- 𝑋×𝑌
- 𝑌×𝑋
- 𝑌
Ответ
−1 для проверкиОдин из возможных подходов к этому вопросу: принадлежит.
Начнем с 𝑋. Напомним, что 𝑋=𝑋×𝑋, то есть множество всех упорядоченных пар 𝑋 с самим собой. Поскольку 𝑋={0,−1}, 𝑋={0,−1}×{0,−1} задается выражением 𝑋={(0,0),(0,−1),(−1,0),(−1,−1)}.
Мы видим, что (−1,−4) не является элементом этого множества. Двигаясь дальше, давайте посчитаем 𝑋×𝑌. Поскольку 𝑋×𝑌={0,−1}×{8,−4,−3,−2}, мы должны взять каждую упорядоченную пару между двумя наборами, что в сумме составляет 2×4=8 пар. Это дает нам 𝑋×𝑌={(0,8),(0,−4),(0,−3),(0,−2),(−1,8),(−1,−4),(−1 ,−3),(−1,−2)}.
Здесь мы обнаруживаем, что (−1,−4) является шестым элементом в нашем списке, поэтому на этом этапе мы можем заключить, что ответ равен B.
 Однако для полноты картины продолжим вычисление других множеств . Для 𝑌×𝑋 мы должны найти {8,−4,−3,−2}×{0,−1}, что на самом деле является просто элементами 𝑋×𝑌, но с переставленным порядком пар. В частности, у нас есть
𝑌×𝑋={(8,0),(−4,0),(−3,0),(−2,0),(8,−1),(−4,−1),(−3 ,−1),(−2,−1)}.
Однако для полноты картины продолжим вычисление других множеств . Для 𝑌×𝑋 мы должны найти {8,−4,−3,−2}×{0,−1}, что на самом деле является просто элементами 𝑋×𝑌, но с переставленным порядком пар. В частности, у нас есть
𝑌×𝑋={(8,0),(−4,0),(−3,0),(−2,0),(8,−1),(−4,−1),(−3 ,−1),(−2,−1)}.Обратите внимание, что это дает нам (−4,−1), что почти равно (−1,−4). Однако, поскольку порядок пары имеет значение, они не совпадают. Наконец, имеем 𝑌={8,−4,−3,−2}×{8,−4,−3,−2}. Поскольку этот набор имеет 16 элементов, вероятно, лучше всего представлять его в таблице:
8 -4 -3 –2 8960 696969696969696969696969696969696969696969693939. 9696969696969696969696969696 -2 –2 -3 –2 -3 –2 . (8,−4) (8,−3) (8,−2) −4 (-4,8) (-4,-4) (-4,-3) (-4,-2) -3 (-3,8) (-3,-4) (-3,-3) (-3,-2) -2 (-2,8) (-2,-4) (−2,−3) (−2,−2) Здесь 𝑌 — множество всех элементов таблицы.
 Как и ожидалось, мы не видим (−1,−4) среди элементов.
Как и ожидалось, мы не видим (−1,−4) среди элементов.Следовательно, как мы выяснили ранее, решение B: 𝑋×𝑌.
Дальнейшие комментарии : Хотя мы вычислили все наборы для полноты, важно отметить, что мы могли бы найти решение этой проблемы намного проще, если бы использовали наши знания о позициях, которые занимают элементы 𝑋 и 𝑌 в каждой паре. Рассматривая (−1,−4), мы видим, что −1 — это только элемент 𝑋, а −4 — только элемент 𝑌. Единственным декартовым произведением, которое ставит элемент 𝑋 в первую позицию, а элемент 𝑌 во вторую позицию, является 𝑋×𝑌.
Теперь мы видели, как работает декартово произведение, на множестве примеров, но, возможно, наиболее важным применением декартова произведения являются декартовы координаты. Декартовы координаты — это еще один термин для системы координат 𝑥−𝑦, используемой для построения графиков и точек.
Как видно из диаграммы, декартовы координаты представляют собой упорядоченные пары, первая компонента которых относится к оси 𝑥, а вторая — к оси 𝑦.
 Три точки, нанесенные на диаграмму,
(1,2)∶1𝑥2𝑦,(3,−1)∶3𝑥−1𝑦,(0,0)∶0𝑥0𝑦.на оси и на оси на оси и на оси на оси и на оси
Три точки, нанесенные на диаграмму,
(1,2)∶1𝑥2𝑦,(3,−1)∶3𝑥−1𝑦,(0,0)∶0𝑥0𝑦.на оси и на оси на оси и на оси на оси и на осиФактически эта система координат может быть определена в терминах декартова произведения. Если ℝ, набор действительных чисел, представляет ось 𝑥, а ℝ также представляет ось 𝑦, то их произведение, ℝ × ℝ или ℝ, представляет собой двумерную плоскость, с помощью которой мы можем представлять точки вида (𝑥,𝑦) и функции вида 𝑦=𝑓(𝑥). Заметим, что ℝ на самом деле является бесконечным множеством, что немного отличает его от конечных множеств, которые мы рассматривали до сих пор, хотя концепция остается той же.
Следующий пример точно продемонстрирует, как декартова диаграмма соотносится с декартовым произведением.
Пример 6. Нахождение декартова произведения по декартовой диаграмме
Используя приведенную ниже декартову диаграмму, определите отношение 𝑋×𝑌.
Ответ
Важно понимать, какой именно вопрос задает нам здесь вопрос.
 Нас просят найти множество 𝑋×𝑌 такое, что когда его элементы нанесены на декартову диаграмму, оно дает показанные точки. Чтобы сделать это, мы должны найти, что это за точки, а затем как они представлены в виде декартова произведения.
Нас просят найти множество 𝑋×𝑌 такое, что когда его элементы нанесены на декартову диаграмму, оно дает показанные точки. Чтобы сделать это, мы должны найти, что это за точки, а затем как они представлены в виде декартова произведения.Чтобы найти значения точек на диаграмме, нам просто нужно найти их 𝑥- и 𝑦-значения, посмотрев, как они совпадают с 𝑥- и 𝑦-осями.
- Для нижнего левого значения у нас есть значение 1 для 𝑥 и значение 1 для 𝑦, что дает нам точку (1,1).
- Для верхнего левого значения 𝑥=1 и 𝑦=2, что дает нам (1,2).
- Для нижнего правого значения 𝑥=6 и 𝑦=1, что дает нам (6,1).
- Наконец, для верхнего правого значения 𝑥=6 и 𝑦=2, что дает нам (6,2).
Теперь нам нужно представить эти точки как множество 𝑋×𝑌. Во-первых, отметим, что множества 𝑋 и 𝑌 в этом произведении представляют 𝑥- и 𝑦-оси соответственно. Таким образом, если бы мы захотели выразить 𝑋 и 𝑌 по отдельности, у нас было бы 𝑋={1,6},𝑌={1,2}.
Их произведение 𝑋×𝑌 представляет собой набор этих точек в виде упорядоченных пар.
 Поэтому наш ответ
𝑋×𝑌={(1,1),(1,2),(6,1),(6,2)}.
Поэтому наш ответ
𝑋×𝑌={(1,1),(1,2),(6,1),(6,2)}.Давайте закончим резюмированием основных свойств декартовых произведений, которые мы изучили.
Ключевые моменты
- Декартово произведение 𝐴×𝐵 двух множеств 𝐴 и 𝐵 — это множество всех упорядоченных пар (𝑥,𝑦), таких что 𝑥∈𝐴 и 𝑦∈𝐵.
- Операция взятия декартова произведения некоммутативна (поэтому в большинстве случаев 𝐴×𝐵≠𝐵×𝐴).
- Декартово произведение можно комбинировать с другими операциями над множествами, такими как ∪, ∩ и −. Порядок работы важно учитывать.
- Декартовы произведения могут быть представлены с помощью стрелочных диаграмм и декартовых диаграмм. Плоскость 𝑥−𝑦 является формой декартова произведения.
Декартово произведение — Примечания Озанера
Определение
Декартово произведение $\times$ — это операция над двумя множествами, назовем их $A$ и $B$, которая возвращает множество всех упорядоченных пар, первый элемент которых принадлежит $A$, а второй — $B$.
\[A\times B=\{(a,b)\mid a\in A \land b\in B\}\] Формально мы можем думать об этом как о сокращении для следующего:
Формально мы можем думать об этом как о сокращении для следующего:Существование в ZFC
Используя определение упорядоченных пар Куратовского, мы можем показать, что декартово произведение двух множеств может быть построено из аксиом ZFC. В частности, это подмножество следующего легко конструируемого множества:
\[A\times B \subseteq \mathcal{P}\left(\mathcal{P}\left(A\cup B\right)\right)\] Доказательство Во-первых, обратите внимание, что $A\cup B$ гарантируется аксиомой объединения, а его набор степеней гарантируется аксиомой множества степеней. Далее обратите внимание, что среди многих других элементов набор степеней $A\cup B$ содержит: $$\{a\},\{a,b\}\in\mathcal{P}\left(A\cup B\right)$$ где $a$ и $b$ — элементы в $A$ и $B$ соответственно. Теперь, если мы снова возьмем набор мощности, мы увидим, что результат содержит, среди прочего, элементы: $$\{\{a\},\{a,b\}\}\in\mathcal{P}\left(\mathcal{P}\left(A\cup B\right)\right)$$ для всех $a$ и $b$ в $A$ и $B$. Теперь вызовите аксиому подмножества, чтобы выбрать только те элементы, которые соответствуют описанию, и все готово!
Теперь вызовите аксиому подмножества, чтобы выбрать только те элементы, которые соответствуют описанию, и все готово!$n$-арное декартово произведение
Легко понять, как можно обобщить это понятие на $n$ множеств. Например, соединив декартово произведение дважды, мы получим набор из $3$-кортежей:
\[\begin{align*}(S_1\times S_2)\times S_3&=\{(\left(s_1,s_2),s_3\right)\mid\forall i\in[1..3],\ s_i\ в S_i)\}\\ &=\{\left(s_1,s_2,s_3\right)\mid\forall i\in[1..3],\ s_i\in S_i)\} \конец{выравнивание*}\]Повторив это $n$ раз, мы получим следующее для любых $n$ наборов:
\[S_1\times S_2\times \cdots \times S_n=\{\left(s_1,\cdots,s_n\right)\mid\forall i\in[1..n],\ s_i\in S_i)\} \] 9{n-k+1}_{i=1}S_i\справа)\times S_{n-k+2}\times \cdots \times S_n\]Индексированные и бесконечные продукты
Можно расширить понятие декартова произведения, чтобы учесть произведение любого индексированного семейства множеств:
\[\prod_{i\in I}S_i=\{f:I\to\bigcup_{i\in I}S_i\mid \forall i,f(i)\in S_i\}\]Другими словами, это декартово произведение возвращает каждую функцию, которая принимает элемент $i\in I$ и отображает его в элемент $f(i)\in S_i$.
\[\underbrace{\text{двоичный},\text{тройной},\cdots,n\text{-арный}}_{\text{конечный}},\cdots;\underbrace{\aleph_0\text{-арный },\aleph_1\text{-ary},\cdots}_{\text{infinitary}}\] Обратите внимание, что это позволяет использовать наборы индексов с бесконечным числом элементов, что приводит к бесконечность Декартовы произведения:
Обратите внимание, что это позволяет использовать наборы индексов с бесконечным числом элементов, что приводит к бесконечность Декартовы произведения:Обратите внимание, что это обобщает первое определение, потому что $n$ можно рассматривать как множество с $n$ элементами в соответствии с его построением как натуральное число (т. е. $n=[0..n-1]$), и поэтому мы можем принять его за наш набор индексов $I$. В результате эти два определения изоморфны для конечных продуктов.
Полезная стенография
Обратите внимание, что обычный конечный продукт создает набор кортежей, а этот индексированный продукт создает набор функций. Это различие важно, потому что определение функции зависит от конечного продукта.
Таким образом, индексированное произведение является скорее удобным сокращением для обозначения множества всех функций от некоторого $I$ до некоторого множества доменов $S_i$, чем заменой конечного произведения.
 1S_i=\prod_{i\in\{1\}}S_i=S_1$$
1S_i=\prod_{i\in\{1\}}S_i=S_1$$Мы определяем унарный продукт таким образом, чтобы сделать нашу нотацию продукта более удобной (например, рекурсивное определение продукта имеет базовый случай 1 множества). Это также соответствует нашему соглашению о том, что $1$-кортежи просто являются элементами набора, как упоминалось в посте о $n$-кортежах.
Нулевой продукт Другим частным случаем является произведение 0 наборов, то есть произведение с набором индексов $I=\emptyset$. Это называется пустым или нульарным декартовым произведением . Пустой набор индексов означает, что в продукте может быть только одна функция (пустая функция): $$\prod_\emptyset=\{f_\emptyset:\emptyset\to\emptyset\}=\{(\emptyset,\emptyset)\}$$ Напомним, что мы определяем функцию как упорядоченную пару декартова произведения и подмножества этого произведения. В этом случае оба являются $\emptyset$. 9\emptyset=\{f_\emptyset\}$ для любого набора $S$.Свойства
Обратите внимание, что следующие свойства относятся к стандартному двоичному декартовому произведению, а не к его индексированному варианту.

Позиционные свойства
Лево-ассоциативный Столкнувшись с $n$-арным декартовым произведением без скобок, оно обычно оценивается слева направо. Другими словами, декартово произведение ассоциативно слева: $$A\раз B \раз C=(A \раз B)\раз C$$ Это соглашение интуитивно согласуется с определением $n$-арных декартовых произведений и $n$-кортежей, то есть $((a,b),c)=(a,b,c)$. Некоммутативный Декартово произведение является некоммутативным оператором: $$A\раз B \не= B \раз A$$ Это должно быть очевидно, поскольку упорядоченные кортежи $(a,b)\not=(b,a)$, где $a\in A$ и $b\in B$, определяются равенством кортежей. Неассоциативный Декартово произведение является неассоциативным оператором: $$\left(A\times B\right) \times C \not= A\times \left(B \times C\right)$$ Подобно его некоммутативности, мы можем проиллюстрировать это, заметив, что $((a,b),c)\not= (a,(b,c))$, где $a\in A$, $b\in B $ и $c\in C$.Распределительные свойства
\[\начать{выравнивать*} A\times\left(B\times C\right)&=\left(A\times B\right)\cup \left(A\times C\right)\\ A\times\left(B\cap C\right)&=\left(A\times B\right)\cap \left(A\times C\right)\\ \left(A\times B\right)\cap \left(C\times D\right)&=\left(A\cap B\right)\times \left(C\cap D\right)\\ A\times\left(B\setminus C\right)&=\left(A\times B\right)\setminus \left(A\times C\right)\\ B\subseteq C&\leftrightarrow\left(A\times B\right)\subseteq \left(A\times C\right)\\ \left(A\times B\right)\subseteq \left(C\times D\right)&\leftrightarrow\left(A\subseteq B\right)\land \left(C\subseteq D\right)\\ \конец{выравнивание*}\] 9С\справа)\]Декартова факторизация
Декартово произведение аналогично знакомому нам целочисленному произведению следующим образом: декартово произведение можно «разложить» на наборы его компонентов.
 Более того, существует уникальная первичная факторизация любого декартова произведения, которая восстанавливает исходные множества.
Более того, существует уникальная первичная факторизация любого декартова произведения, которая восстанавливает исходные множества.Конечный продукт
Чтобы найти $i$-й декартовский множитель (CF) $n$-арного декартова произведения $P$, нам просто нужно найти объединение $i$-го индекса всех кортежей в $P$: 9n_i(p)$ — функция извлечения кортежей.
Индексированный продукт
В более общем случае, когда наше декартово произведение $P$ принадлежит индексированному семейству $\{S_i\} _{i\in I}$, мы можем найти $i$-й множитель следующим образом:
\[\operatorname{CF}_i(P)=\bigcup_{p\in P}\{p(i)\}=S_i\]Обратите внимание, что мы можем восстановить набор индексов $I$ из произведения $P$, просто выбрав любой из его элементов (функцию, т.е. упорядоченную пару) и извлекая его первый элемент. Это будет декартово произведение его домена $I$ и кодомена. Затем мы можем, наконец, извлечь $I$ из этого бинарного произведения, как описано в конечном случае.
 Это все, что нужно сказать: 9п\]
Это все, что нужно сказать: 9п\]Обратите внимание, что из-за одновременности арности факторизация конечного произведения зависит от того, какой арностью мы его считаем. Мы можем решить эту проблему, если укажем, что уникальная простая факторизация конечного произведения требует, чтобы оно считалось максимально возможной арностью.
Для индексированного декартова произведения $\prod_{i\in I}S_i=P$ мы можем сказать:
\[\operatorname{CPF}(P)=(\operatorname{CF}_i(P))_{i\in I}=(S_i)_{i\in I}\]Факторизация пустого множества
По аналогии с числом ноль пустое множество $\emptyset$ не имеет единственной простой факторизации. Это связано с тем, что если один из факторов декартова произведения окажется пустым множеством, то и результат будет пустым, и поэтому невозможно восстановить из него исходные факторы. Другими словами, любое семейство множеств может служить факторизацией $\emptyset$, если одно из них является самим $\emptyset$.
Примеры и использование
Отношения
$n$-арное отношение определяется как упорядоченная пара, первый элемент которой является $n$-арным декартовым произведением, а второй — подмножеством этого произведения.
\[\ начать {собирать} \le\,\,\equiv\,(\mathbb R\times\mathbb R,G)\\ G\subseteq\mathbb R\times\mathbb R \конец{собрать}\] Например, $\le$ — бинарное отношение на множестве $\mathbb R$:
Например, $\le$ — бинарное отношение на множестве $\mathbb R$:Это позволяет нам формализовать такие утверждения, как $4\le7$, как принадлежность множества $(4,7)\in G$.
Кардинальное умножение
Декартовы произведения используются для определения произведения двух количественных чисел:
\[\влево|X\умножить на Y\вправо|=\влево|X\вправо|\влево|Y\вправо|\]И вообще для любого пронумерованного семейства количественных чисел:
\[\left|\prod_{i\in I}X_i\right|=\prod_{i\in I}\left|X_i\right|\] 9n=\{(x_1,x_2,\cdots,x_n)\mid (\forall i\in [1..n])\, x_i\in\mathbb{R}\}\]Точки в $3$-пространстве необходимы для описания положения объектов и частиц в пространстве и, таким образом, положили начало изучению движения, причин этого движения и, в конечном счете, всей остальной физики.
Более того, $2$-пространство и реже $3$-пространство используются для построения графиков и выводов из данных, а также для визуализации функций на интервале чисел.
 \mathbb \omega$, также известное как множество всех реальных последовательностей.
\mathbb \omega$, также известное как множество всех реальных последовательностей.Теги: математика, теория множеств
Обновлено:
Декартово произведение множеств и его свойства
Декартово произведение множеств и его свойства | ВажныйГк Ученый 20 июля 2022 г. Комментариев нет
Декартово произведение множеств:
Если A и B два непустых множества, то декартово произведение множества A на множество B обозначается A x B и определяется как множество упорядоченных пар (x, y) такие, что x ∈ A и y ∈ B, т. е.
A x B = {(x, y) : x ∈ A и y ∈ B} Свойства декартова произведения множеств:
- n (A x B) = n (A) . n (B)
- A x B является пустым множеством, если либо A, либо B пусты.

- A x B ≠ B x A (т. е. декартово произведение некоммутативно).
- A x B = B x A, если A = B.
(1) Если A = {1, 2} и B = {a, b, c}. Найдите А х В? Решение: А = {1, 2}
B = {a, b, c}Теперь A x B = {(1, a) (1, b) (1, c) (2, a) (2, b ) (2, c)}
(2) Если A = {1, 4}, B = {2, 3}, C = {-1, 2}. Убедитесь, что A x (B ∪ C) = (A x B) ∪ (A x C). Решение: B ∪ C = {2, 3} ∪ {-1, 2} = {-1, 2, 3}
Кроме того, A x (B ∪ C) = {(1, -1) (1, 2) (1, 3) (4, -1) (4, 2) (4, 3)} ……….(i)
Теперь A x B = {(1, 2) (1, 3) (4, 2) (4, 3)}
и А х С = {(1, -1) (1, 2) (4, -1) (4, 2)}(А х В) ∪ (А х С) = {(1, 2) (1, 3) (4, 2) (4, 3) (1, -1) (4, -1)} …… ….(ii)
Из (i) и (ii)-
A x (B ∪ C) = (A x B) ∪ (A x C)(3) Если (P, 5) и (2q, 1) принадлежат множеству {(x, y) : x + y = 3}.  Найдите P и q?
Найдите P и q? Решение: {(x, y) : x + y = 3} и (P, 5) (2q, 1) ∈ множество.
∴ P + 5 = 3 и 2q + 1 = 3
⇒ P = -2 и q = 1(4) Если x ∈ A = {2, 4, 6} и y ∈ B = {3, 4, 5, 7, 8}. Найдите множество R всех упорядоченных пар (x, y) таких, что x < y и x является множителем y? Решение: R 1 = {(x, y) : x < y}
= {(2, 3) (2, 4) (2, 5) (2, 7) (2, 8) (4, 5) (4, 7) (4, 8) (6, 7) (6, 8)}R 2 = {(x, y) : x является коэффициентом y}
= { (2, 4) (2, 8) (4, 4) (4, 8)}Теперь R = R 1 ∩ R 2 = {(2,4) (2, 8) (4, 8)}
(5) Для любых трех множеств A, B и C. Докажите, что- (i) A x (B ∪ C) = (A x B) ∪ (A x C).
Решение: Пусть (x, y) ∈ A x (B ∪ C)
⇒ x ∈ A и y ∈ (B ∪ C)
⇒ x ∈ A и {y ∈ B или y ∈ C}
⇒ {x ∈ A и y ∈ B} или {x ∈ A и y ∈ C}
⇒ (x, y) ∈ (A x B) или (x, y) ∈ (A x C)
⇒ (x, y) ∈ (A x B) ∪ (A x C)∴ A x (B ∪ C) ⊆ (A x B) ∪ (A x C) ……….
 (i)
(i)
Аналогично, (A x B ) ∪ (A x C) ⊆ A x (B ∪ C) ……….(ii)Из (i) и (ii)-
A x (B ∪ C) = (A x B) ∪ (A x C)(ii) A x (B ∩ C) = (A x B) ∩ (А х С).
Решение: Пусть (x, y) ∈ A x (B ∩ C)
⇒ x ∈ A или y ∈ (B ∩ C)
⇒ x ∈ A или {y ∈ B и y ∈ C}
⇒ {x ∈ A или y ∈ B} и {x ∈ A или y ∈ C}
⇒ (x, y) ∈ (A x B) и (x, y) ∈ (A x C)
⇒ (x, y) ∈ (A x B) ∩ (A x C)∴ A x (B ∩ C) ⊆ (A x B) ∩ (A x C) ……….(i)
Аналогично, (A x B ) ∩ (A x C) ⊆ A x (B ∩ C) ……….(ii)Из (i) и (ii)-
A x (B ∩ C) = (A x B) ∩ (A x C)(iii) A x (B – C) = (A x B) – (А х С).
Решение: Пусть (x, y) ∈ A x (B – C)
⇒ x ∈ A и y ∈ (B – C)
⇒ x ∈ A и {y ∈ B и y ∉ C}
⇒ {x ∈ A и y ∈ B} и {x ∈ A и y ∉ C}
⇒ (x, y) ∈ (A x B) и (x, y) ∉ (A x C)
⇒ (x, y) ∈ (A x B) – (A x C)∴ A x (B – C) ⊆ (A x B) – (A x C) ……….(i)
Аналогично, (A x B ) – (А х С) ⊆ А х (В – С) ………. (ii) 9(6) Если A и B любые два непустых множества, то A x B = B x A ⇔ A = B?
(ii) 9(6) Если A и B любые два непустых множества, то A x B = B x A ⇔ A = B? Решение: Предположим, что A x B = B x A, тогда мы должны доказать, что A = B.
Пусть x ∈ A
⇒ (x, a) ∈ A x B
⇒ (x, a) ∈ B x A [∵ A x B = B x A]
⇒ x ∈ B∴ A ⊆ B
Аналогично, B ⊆ A
∴ A = BОбратно, предположим, что A = B, тогда мы должны доказать, что А х В = В х А
Теперь, A x B = A x A [∵ B = A] ……….(i)
Кроме того, B x A = A x A [∵ B = A] ……….(ii)Из (i) и (ii)-
A x B = B x A(7) Если подмножество A B и подмножество C D, то докажите, что A x C является подмножеством B x D или А х С ⊆ В х D? Решение: Пусть (x, y) ∈ A x C
⇒ x ∈ A и y ∈ C
⇒ x ∈ B и y ∈ D [∵ A ⊆ B и C ⊆ D]
⇒ (x, y ) ∈ (B x D)∴ A x C ⊆ B x D
(8) Для любых трех множеств A, B и C.  Докажите, что A x (B’ ∪ C’)’ = (A x B) ∩ (A x C).
Докажите, что A x (B’ ∪ C’)’ = (A x B) ∩ (A x C). Решение: A x (B’ ∪ C’)’
= A x [(B’)’ ∩ (C’)’] [с использованием закона Де Моргана]
= A x (B ∩ C)
= (А х В) ∩ (А х С)Обнаружен блокировщик рекламы
Работа нашего веб-сайта стала возможной благодаря показу онлайн-рекламы нашим посетителям. Пожалуйста, поддержите нас, отключив блокировщик рекламы.
Обновить
Декартово произведение | Определение, примеры, свойства, элементы и схема
ОпределениеДекартово произведение — это произведение любых двух множеств в упорядоченной форме. Это означает, что результирующее множество декартова произведения двух множеств содержит все возможные и упорядоченные пары, такие что первый элемент пары принадлежит первому множеству, а второй элемент принадлежит второму множеству.
Напомним, что мы понимаем под упорядоченной парой.

Упорядоченная пара состоит из двух объектов или элементов в заданном фиксированном порядке. Давайте разберемся на примере. Предположим, у нас есть A и b как два множества. Тогда под упорядоченной парой элементов понимается пара ( a , b ) в том порядке, где a ∈ A и b ∈ B. Здесь важно отметить, что упорядоченная пара не является множеством, состоящим из двух элементов. Порядок двух элементов в упорядоченной паре важен, и эти два элемента не обязательно должны быть разными. Теперь давайте узнаем о декартовом произведении множеств.
Как найти декартово произведениеПусть A и B — два непустых множества. Множество всех упорядоченных пар ( a , b ), таких что a A и b B, называется декартовым произведением множеств A и B и обозначается A x B. Таким образом,
A x B = { ( a , б ) : a ∈ A и b ∈ B }
Разберем это на примере.
Предположим, у нас есть два набора, A = {2, 4, 6} и B = {1, 2}, тогда каково будет значение A x B?
У нас будет,
A x B = {2, 4, 6} x {1, 2} = {(2, 1), (2, 2), (4, 1), (4, 2) , ( 6 , 1 ), ( 6 , 2 )
Каково будет значение B X A?
B x A = { 1 , 2 } x ( 2 , 4 , 6 } = { ( 1 , 2 ) , ( 1 , 4 ) , ( 1 , 6 ) , ( 2 , 2 ) , ( 2 , 4 ) , ( 2 , 6 ) }
Из приведенного выше примера видно, что для записи A x B мы берем элемент из множества a и формируем все упорядоченные пары с этим элементом в качестве первого элемента и элементами B в качестве вторых элементов.
 Затем мы выбираем другой элемент из A и, соответственно каждому элементу из B, формируем упорядоченные пары с этим элементом в качестве первого элемента и элементами B в качестве второго элемента. Этот процесс продолжается до тех пор, пока не будут исчерпаны все элементы A.
Затем мы выбираем другой элемент из A и, соответственно каждому элементу из B, формируем упорядоченные пары с этим элементом в качестве первого элемента и элементами B в качестве второго элемента. Этот процесс продолжается до тех пор, пока не будут исчерпаны все элементы A. Рассмотрим другой пример.
Пример Если A = {a, b} и B = {1, 2, 3}, найти A x B, B x A, A x A, B x B и ( A x B ) ∩ ( B x A )
Решение Нам даны наборы A = {a, b} и B = {1, 2, 3}. Нам нужно найти A x B, B x A, A x A, B x B и ( A x B ) ∩ ( B x A ).
Найдем их по одному.
Имеем A = {a, b} и B = {1, 2, 3}, следовательно,
A x B = {a, b} x {1, 2, 3} = {(a, 1 ), (а, 2), (а, 3), (б, 1), (б, 2), (б, 3)}
Следовательно, A x B = {(а, 1), (а, 2), (а, 3), (б, 1), (б, 2), (б, 3)}. . . . . . . . . . (1)
В Икс А знак равно {1, 2, 3} Икс {а, б} = {(1, а), (1, б), (2, а), (2, б), ( 3, а), (3, б)}
Следовательно, В х А = {(1, а), (1, б), (2, а), (2, б), (3, а) , ( 3 , б ) } .
 . . . . . . . (2)
. . . . . . . (2) А х А = {а, б} х {а, б} = {(а, а), (а, б), (б, а), (б, б)}
Следовательно, А Икс А знак равно { ( а , а ) , ( а , б ) , ( б , а ) , ( б , б ) } . . . . . . . . . . . . . . . . . . . (3)
B x B = {1, 2, 3} x {1, 2, 3} = {(1, 1), (1, 2), (1, 3), (2, 1) , (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Следовательно, B x B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 4 )
Теперь, чтобы найти значение ( A x B ) ∩ ( B x A ), из (1) и (2) мы имеем,
A x B = { ( a , 1 ), ( a , 2 ) , ( а , 3 ) , ( б , 1 ) , ( б , 2 ) , ( б , 3 ) } и
B x A = { ( 1 , а ), ( 1 , б ), ( 2 , а ) , ( 2 , b ), ( 3 , a ), ( 3 , b ) }
Как видно выше, A x B и B x A не имеют общих элементов. Следовательно, ( A x B ) ∩ ( B x A ) = ∅
Свойства декартова произведенияНиже приведены свойства декартова произведения –
- Декартово произведение не удовлетворяет коммутативному закону, т.
 е. оно не коммутативно. Это означает, что если мы изменим порядок наборов, результат также изменится. Например, если A и B — два множества, то декартово произведение A и B, A × B ≠ B × A.
е. оно не коммутативно. Это означает, что если мы изменим порядок наборов, результат также изменится. Например, если A и B — два множества, то декартово произведение A и B, A × B ≠ B × A. - Декартово произведение не удовлетворяет ассоциативному закону, т. е. не является ассоциативным. Это означает, что если мы перегруппируем множества в декартовом произведении, то это изменит результат. Например, если A, B и C — три множества, то (A × B) × C ≠ A × (B × C)
- Свойство распределения декартова произведения по пересечению множеств определяется как A × (B ∩ C) = (A × B) ∩ (A × C)
- Свойство распределения декартова произведения по объединению множеств определяется как A × ( B ∪ C ) = ( A × B ) ∪ ( A × C )
- Результатом декартова произведения множеств является множество всех упорядоченных пар.
Пусть A, B и C — три множества. Тогда A x B X C представляет собой набор всех упорядоченных троек, имеющих первый элемент из A, второй элемент из B и третий элемент из C.
 Это можно сформулировать как –
Это можно сформулировать как – A x B x C = {( a , b ,c ) : a ∈ A , b ∈ B , c C }
Давайте разберемся на примере.
Предположим, у нас есть три набора, A = {1, 2}, B = {3, 4} и C = {4, 5, 6}, тогда
A x B = {1, 2} x {3, 4 } = { ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 )
Теперь,
A x B x C = ( A x B ) x C = { ( 1 , 3 ), ( 1 , 4 ), ( 2 , 3 ), ( 2 , 4 ) x { 4 , 5 , 6 } Это означает, что
A x B x C = { ( 1 , 3 , 4 ) , ( 1, 3, 5), (1, 3, 6), (1, 4, 4), (1, 4, 5) (1, 4, 6), (2, 3, 4) (2, 3, 5), (2, 3, 6), (2, 4, 4) (2, 4, 5), (2, 4, 6) }
Здесь важно отметить, что A x B x C = (A x B) x C = A x (B x C)
Количество элементов в декартовом произведении множествМожем ли мы определить число элементов, которые должны присутствовать в декартовом произведении двух множеств? Если A и B — два конечных множества, то n (A x B) = n (A) x n (B). Это означает, что если множество A состоит из m элементов, а множество B состоит из n элементов, то число элементов A x B будет равно m n.
Графическое представление декартова произведения множеств
Пусть A и B — два непустых множества. Чтобы представить A x B графически, мы проводим две взаимно перпендикулярные линии, одну горизонтальную и одну вертикальную. На горизонтальной линии мы изображаем элементы множества A, а на вертикальной линии мы изображаем элементы множества B. Если a A и b B, мы проводим вертикальную линию через a и горизонтальную линию через B. Эти две линии пересекутся в точка, которая будет обозначать упорядоченную пару ( a , b ). Таким образом, мы отмечаем точки, соответствующие каждой упорядоченной паре в A x B. Давайте разберемся с этим на примере.
Предположим, у нас есть два множества, A = (a, b, c} и B = {1, 2}
Тогда A x B = {(a, 1), (a, 2), (b, 1 ) , ( b , 2 ), ( c , 1 ), ( c , 2 ) }
Графическое представление приведенного выше декартова произведения будет –
Схематическое представление декартова произведения двух множеств представим A x B стрелочной диаграммой, сначала нарисуем диаграммы Венна, изображающие множества A и B одно напротив другого, а затем нарисуем отрезки, начинающиеся от каждого элемента A и заканчивающиеся каждым элементом множества B.
Давайте разберемся на примере.
Предположим, у нас есть два множества: A = {3, 4, 5} и B = {6, 8, 10}
Теперь A x B = {(3, 6), (3, 8), ( 3, 10), (4, 6), (4, 8), (4, 10), (5, 6), (5, 8), (5, 10)
Мы видим, что n (A) = 3 , n ( B ) = 3 и n ( A x B ) = 3 x 3 = 9
Приведенное выше декартово произведение может быть представлено с помощью стрелочной диаграммы, как показано ниже –
Ключевые факты и резюме- Декартово произведение — произведение любых двух множеств в упорядоченной форме.
- Упорядоченная пара состоит из двух объектов или элементов в заданном фиксированном порядке.
- Пусть A и B — два непустых множества. Множество всех упорядоченных пар (a, b), таких что a A и b B, называется декартовым произведением множеств A и B и обозначается A x B. Таким образом, A x B = {(a, b): a ∈ A и b ∈ B }
- Пусть A, B и C — три множества. Тогда A x B X C представляет собой множество всех упорядоченных троек, имеющих первый элемент из A, второй элемент из B и третий элемент из C.

- Декартово произведение не удовлетворяет коммутативному закону, т. е. не является коммутативным. Это означает, что если мы изменим порядок наборов, результат также изменится. Например, если A и B — два множества, то декартово произведение A и B, A × B ≠ B × A.
- Декартово произведение не удовлетворяет ассоциативному закону, т. е. не является ассоциативным. Это означает, что если мы перегруппируем множества в декартовом произведении, то это изменит результат. Например, если A, B и C — три множества, то (A × B) × C ≠ A × (B × C)
- Свойство распределения декартова произведения по пересечению множеств определяется как A × (B ∩ C) = (A × B) ∩ (A × C)
- Свойство распределения декартова произведения по объединению множеств задается как A × ( B ∪ C ) = ( A × B ) ∪ ( A × C )
- Результатом декартова произведения множеств является множество всех упорядоченных пар.
- Если A и B — два конечных множества, то n (A x B) = n (A) x n (B). Это означает, что если множество A состоит из m элементов, а множество B состоит из n элементов, то число элементов A x B будет равно m n.

- Если мы напишем (\(sqrt 2\), 7) \(\in \mathbb{R} \times \mathbb{R}\), то мы используем (\(sqrt 2\), 7) для представления упорядоченной пары действительных чисел.



 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 1
1

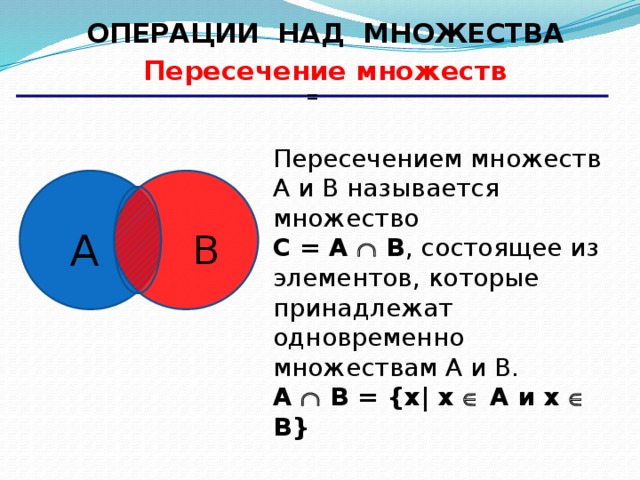
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.008 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.008 с.)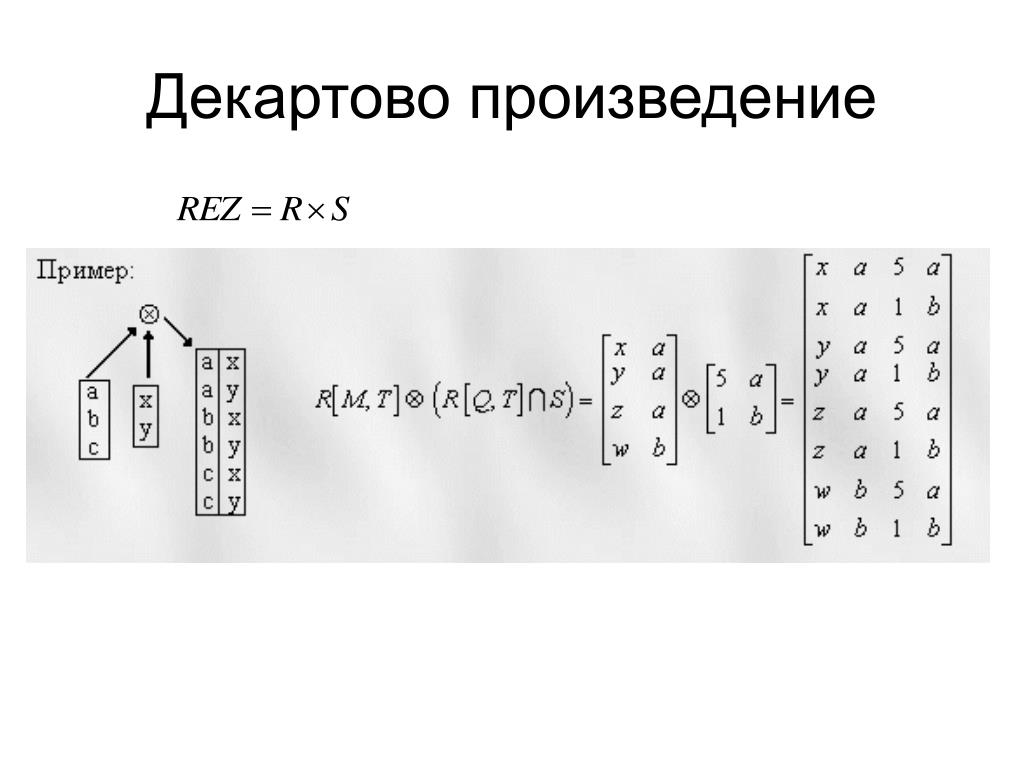 Организационный этап
Организационный этап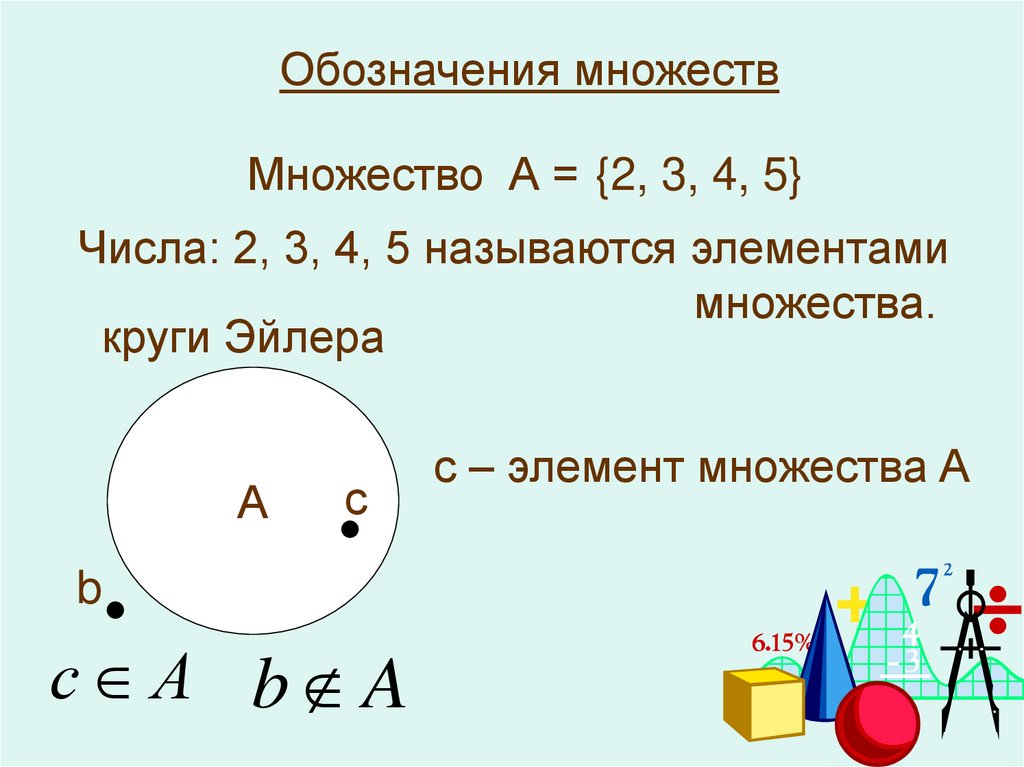



 2\). Этот самолет называется 92\ |\ 1 \le x \le 3 \text{ и } 2 \le y \le 5\}.\)
2\). Этот самолет называется 92\ |\ 1 \le x \le 3 \text{ и } 2 \le y \le 5\}.\)

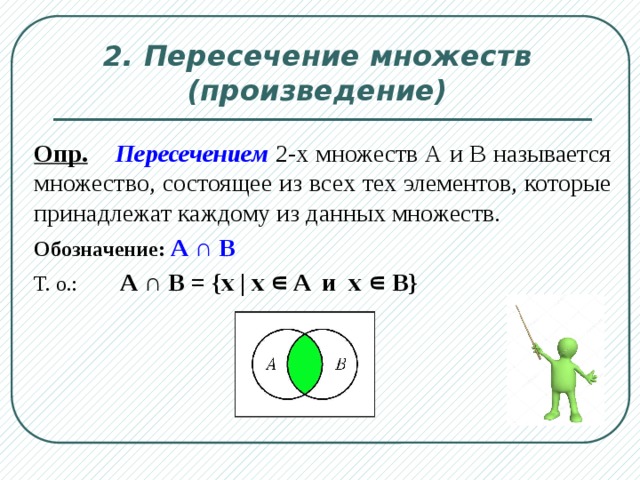 25, а остальное оставим для упражнений. При построении этих доказательств нам нужно помнить, что декартовы произведения — это множества, поэтому мы следуем многим из тех же принципов для доказательства отношений множеств, которые были введены в разделах 5.2 и 5.3.
25, а остальное оставим для упражнений. При построении этих доказательств нам нужно помнить, что декартовы произведения — это множества, поэтому мы следуем многим из тех же принципов для доказательства отношений множеств, которые были введены в разделах 5.2 и 5.3. \]
\]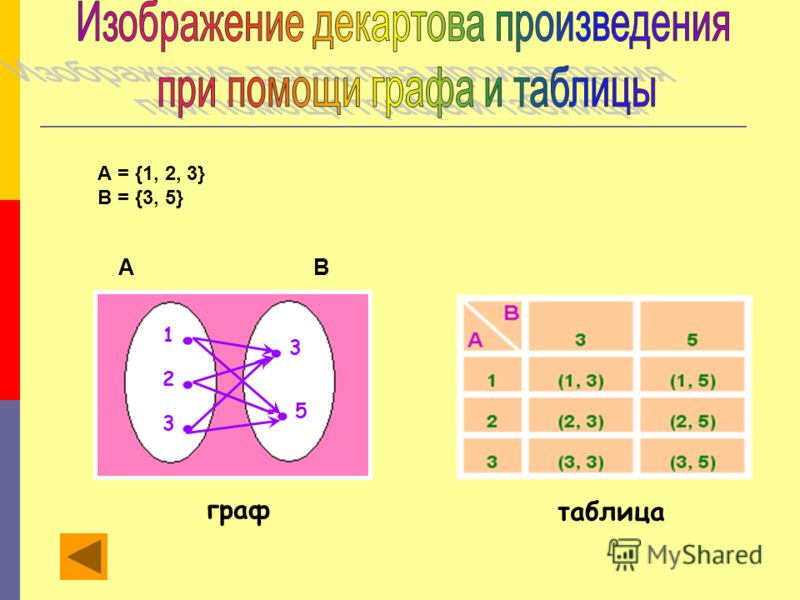 25.
25. Итак, в этом случае \(u \in A \times C\) и, следовательно, \(u \in (A \times B) \cup (A \times C)\).
Итак, в этом случае \(u \in A \times C\) и, следовательно, \(u \in (A \times B) \cup (A \times C)\). \]
\] 25, часть (1): \(A \times (B \cap C) = (A \times B) \cap (A \times C)\).
25, часть (1): \(A \times (B \cap C) = (A \times B) \cap (A \times C)\). Однако, если нас интересует формальное развитие декартова произведения двух множеств, нам нужно более точное определение упорядоченной пары. Ниже приведен один из способов сделать это с точки зрения наборов. Это определение приписывают Казимежу Куратовскому (189 г.6 – 1980). Куратовский был известным польским математиком, основная работа которого была связана с топологией и теорией множеств. Он был назначен директором Польской академии наук и проработал на этой должности 19 лет.
Однако, если нас интересует формальное развитие декартова произведения двух множеств, нам нужно более точное определение упорядоченной пары. Ниже приведен один из способов сделать это с точки зрения наборов. Это определение приписывают Казимежу Куратовскому (189 г.6 – 1980). Куратовский был известным польским математиком, основная работа которого была связана с топологией и теорией множеств. Он был назначен директором Польской академии наук и проработал на этой должности 19 лет.

 gvsu.edu/books/7
gvsu.edu/books/7 Наконец, — обозначает вычитание одного набора из другого, что означает удаление любых элементов из первого набора, присутствующих во втором наборе. Здесь это просто означает убрать 2 из {1,2}, оставив только 1.
Наконец, — обозначает вычитание одного набора из другого, что означает удаление любых элементов из первого набора, присутствующих во втором наборе. Здесь это просто означает убрать 2 из {1,2}, оставив только 1.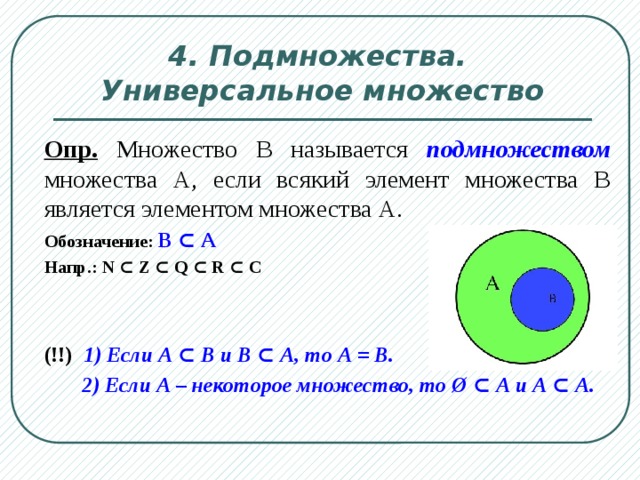
 0003
0003

 Рассмотрим пример, использующий диаграммы Венна для представления множеств.
Рассмотрим пример, использующий диаграммы Венна для представления множеств. Это
{4}∪{7,9}={4,7,9},
где мы просто объединили два набора вместе. Наконец, мы должны вычислить (𝑍−𝑌)×(𝑋∪𝑌), то есть {3,8}×{4,7,9}. Поскольку это декартово произведение, мы должны составить множество, содержащее все возможные упорядоченные пары между двумя множествами. Это дает нам
{3,8}×{4,7,9}={(3,4),(3,7),(3,9),(8,4),(8,7),(8,9)}.
Это
{4}∪{7,9}={4,7,9},
где мы просто объединили два набора вместе. Наконец, мы должны вычислить (𝑍−𝑌)×(𝑋∪𝑌), то есть {3,8}×{4,7,9}. Поскольку это декартово произведение, мы должны составить множество, содержащее все возможные упорядоченные пары между двумя множествами. Это дает нам
{3,8}×{4,7,9}={(3,4),(3,7),(3,9),(8,4),(8,7),(8,9)}. Заметим, что в первую компоненту входят только элементы из 𝑋, а во вторую — только элементы из 𝑌. Рассмотрим только первые компоненты каждого элемента 𝑋×𝑌, так как это элементы, соответствующие 𝑋. Это дает нам
8,8,1,1,3,3.
Заметим, что в первую компоненту входят только элементы из 𝑋, а во вторую — только элементы из 𝑌. Рассмотрим только первые компоненты каждого элемента 𝑋×𝑌, так как это элементы, соответствующие 𝑋. Это дает нам
8,8,1,1,3,3.
 Однако для полноты картины продолжим вычисление других множеств . Для 𝑌×𝑋 мы должны найти {8,−4,−3,−2}×{0,−1}, что на самом деле является просто элементами 𝑋×𝑌, но с переставленным порядком пар. В частности, у нас есть
𝑌×𝑋={(8,0),(−4,0),(−3,0),(−2,0),(8,−1),(−4,−1),(−3 ,−1),(−2,−1)}.
Однако для полноты картины продолжим вычисление других множеств . Для 𝑌×𝑋 мы должны найти {8,−4,−3,−2}×{0,−1}, что на самом деле является просто элементами 𝑋×𝑌, но с переставленным порядком пар. В частности, у нас есть
𝑌×𝑋={(8,0),(−4,0),(−3,0),(−2,0),(8,−1),(−4,−1),(−3 ,−1),(−2,−1)}. Как и ожидалось, мы не видим (−1,−4) среди элементов.
Как и ожидалось, мы не видим (−1,−4) среди элементов. Три точки, нанесенные на диаграмму,
(1,2)∶1𝑥2𝑦,(3,−1)∶3𝑥−1𝑦,(0,0)∶0𝑥0𝑦.на оси и на оси на оси и на оси на оси и на оси
Три точки, нанесенные на диаграмму,
(1,2)∶1𝑥2𝑦,(3,−1)∶3𝑥−1𝑦,(0,0)∶0𝑥0𝑦.на оси и на оси на оси и на оси на оси и на оси Нас просят найти множество 𝑋×𝑌 такое, что когда его элементы нанесены на декартову диаграмму, оно дает показанные точки. Чтобы сделать это, мы должны найти, что это за точки, а затем как они представлены в виде декартова произведения.
Нас просят найти множество 𝑋×𝑌 такое, что когда его элементы нанесены на декартову диаграмму, оно дает показанные точки. Чтобы сделать это, мы должны найти, что это за точки, а затем как они представлены в виде декартова произведения. Поэтому наш ответ
𝑋×𝑌={(1,1),(1,2),(6,1),(6,2)}.
Поэтому наш ответ
𝑋×𝑌={(1,1),(1,2),(6,1),(6,2)}. Формально мы можем думать об этом как о сокращении для следующего:
Формально мы можем думать об этом как о сокращении для следующего: Теперь вызовите аксиому подмножества, чтобы выбрать только те элементы, которые соответствуют описанию, и все готово!
Теперь вызовите аксиому подмножества, чтобы выбрать только те элементы, которые соответствуют описанию, и все готово! Обратите внимание, что это позволяет использовать наборы индексов с бесконечным числом элементов, что приводит к бесконечность Декартовы произведения:
Обратите внимание, что это позволяет использовать наборы индексов с бесконечным числом элементов, что приводит к бесконечность Декартовы произведения: 1S_i=\prod_{i\in\{1\}}S_i=S_1$$
1S_i=\prod_{i\in\{1\}}S_i=S_1$$
 Более того, существует уникальная первичная факторизация любого декартова произведения, которая восстанавливает исходные множества.
Более того, существует уникальная первичная факторизация любого декартова произведения, которая восстанавливает исходные множества. Это все, что нужно сказать: 9п\]
Это все, что нужно сказать: 9п\] Например, $\le$ — бинарное отношение на множестве $\mathbb R$:
Например, $\le$ — бинарное отношение на множестве $\mathbb R$: \mathbb \omega$, также известное как множество всех реальных последовательностей.
\mathbb \omega$, также известное как множество всех реальных последовательностей.
 Найдите P и q?
Найдите P и q?  (i)
(i)  (ii) 9(6) Если A и B любые два непустых множества, то A x B = B x A ⇔ A = B?
(ii) 9(6) Если A и B любые два непустых множества, то A x B = B x A ⇔ A = B?  Докажите, что A x (B’ ∪ C’)’ = (A x B) ∩ (A x C).
Докажите, что A x (B’ ∪ C’)’ = (A x B) ∩ (A x C). 
 Затем мы выбираем другой элемент из A и, соответственно каждому элементу из B, формируем упорядоченные пары с этим элементом в качестве первого элемента и элементами B в качестве второго элемента. Этот процесс продолжается до тех пор, пока не будут исчерпаны все элементы A.
Затем мы выбираем другой элемент из A и, соответственно каждому элементу из B, формируем упорядоченные пары с этим элементом в качестве первого элемента и элементами B в качестве второго элемента. Этот процесс продолжается до тех пор, пока не будут исчерпаны все элементы A.  . . . . . . . (2)
. . . . . . . (2)  е. оно не коммутативно. Это означает, что если мы изменим порядок наборов, результат также изменится. Например, если A и B — два множества, то декартово произведение A и B, A × B ≠ B × A.
е. оно не коммутативно. Это означает, что если мы изменим порядок наборов, результат также изменится. Например, если A и B — два множества, то декартово произведение A и B, A × B ≠ B × A. Это можно сформулировать как –
Это можно сформулировать как –