Первообразная и неопределенный интеграл.
Функция $F(x)$ называется первообразной функции $f(x),$ заданной на некотором множестве $X,$ если $F'(x)=f(x)$ для всх $x\in X.$ Если $F(x -)$ первообразная функции $f(x),$ то $\Phi(x)$ является первообразной той же функции в том и только в том случае, когда $\Phi(x)=F(x)+C,$ где $C$ — некоторая постоянная. Совокупность всех первообразных функции $f(x)$ называется неопределенным интегралом от этой функции и обозначается символом $$\int f(x)\,dx.$$ Таким образом, по определению $$\int f(x)\,dx=F(x)+C,$$ где $F(x)$ одна из первообразных функции $f(x)$ а постоянная $C$ принимает действительные значения.
Свойства неопределенного интеграла.
1. $\left(\int f(x)\,dx\right)’=f(x).$
2. $\int f'(x)dx=f(x)+C.$
3. $\int af(x)dx=a\int f(x) dx.\,\,\,\,\,\,a\neq 0.$
4. $\int (f_1(x)+f_2(x))dx=\int f_1(x)\,dx+\int f_2(x)\, dx.$
Таблица основных неопределенных интегралов.
2-7}|+c.$
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
12.
1 АнтипроизводнаяПоэтому мы иногда говорим, что первообразная функции есть функция плюс произвольная константа. Таким образом первообразная от \(\cos x\) равна \((\sin x) + c\).
Более распространенное название первообразной — неопределенный интеграл. Это то же самое понятие, просто другое название для него.
В качестве символа используется волнистая линия. Таким образом, предложение «первообразная \(\cos x\) равна \((\sin x) + c\)» обычно формулируется как: неопределенный интеграл от \(\cos x\) равен \((\sin x) + c\), и это обычно записывается как
\[\int \cos х \; дх = (\ грех х) + с\]
На самом деле это плохая запись.
Переменная \(x\), которая появляется справа, является переменной и представляет
аргумент синусоидальной функции. Символы слева просто говорят, что функция, первообразной которой мы являемся
ищет функцию косинуса. Вы избежите путаницы, если выразите это совершенно другим языком.
символ (скажем, \(y\)) слева, чтобы обозначить это. Правильный способ написать это тогда
\[\int \cos у \; dy = (\sin x) + c\]
Зачем использовать эту своеобразную и уродливую нотацию?
Мы делаем это из уважения к традициям. Это обозначение, которое люди использовали на протяжении веков. Мы увидим, почему они сделал это в следующем разделе.
Первый вопрос, к которому мы обращаемся, таков: если вы дадите мне функцию, скажем, \(g\), и попросите меня найти ее неопределенный интеграл, как мне это сделать?
Основной ответ на этот вопрос таков: для этого не существует никаких новых уловок.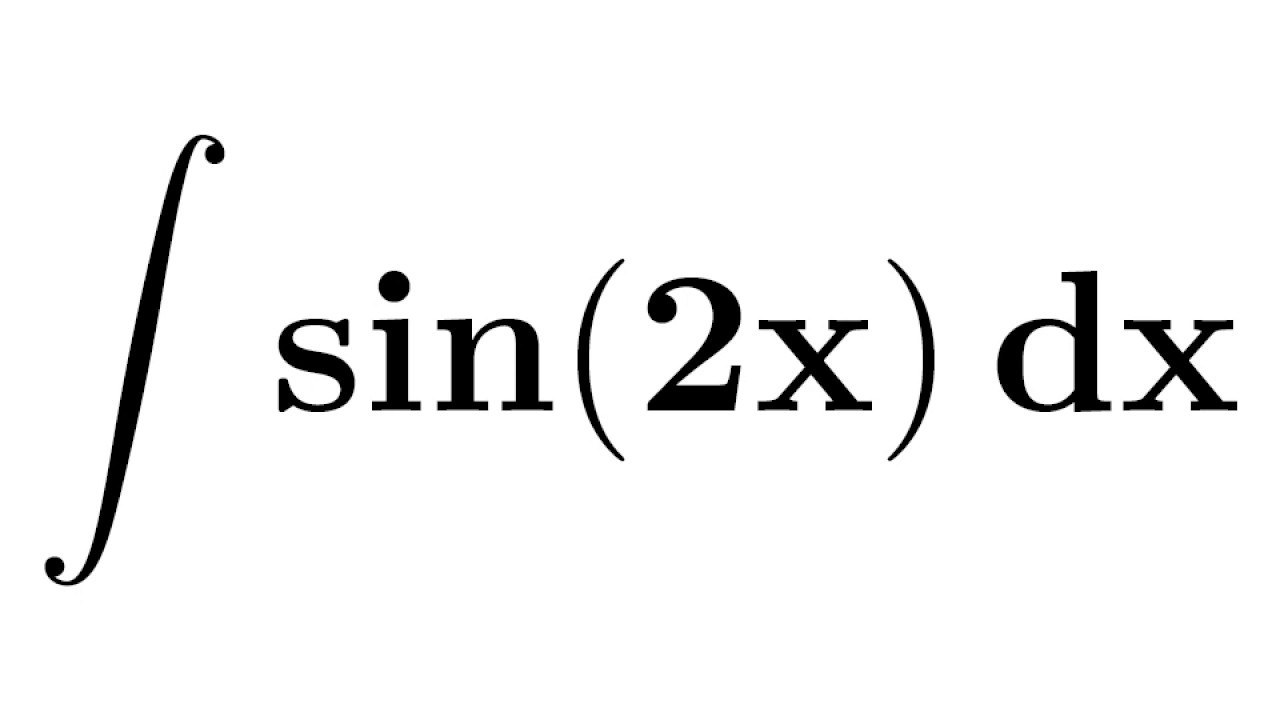
Вы можете работать в обратном направлении от
правила для дифференцирования и получить некоторые правила для интегрирования, и это, по сути, все, что вы можете сделать. Но затем
позволяет интегрировать (находить первообразные) множество полезных функций.
Первообразная суммы нескольких слагаемых есть сумма их первообразных. Это следует из факта что производная суммы есть сумма производных членов. И аналогично, умножая функцию на константу умножает свою первообразную на ту же константу. 9{k+1}}{k+1} +c\).
Что это за штука \(+c\)?
Это напоминание о том, что производная константы равна \(0\), поэтому антипроизводная как обратная операция к
производная полностью не определена. Вы можете добавить любую константу к антипроизводной и получить другую.
Некоторые считают, что это придумали педанты, чтобы мучить студентов, наказывая их за периодическое игнорирование.