Пи в степени е: «Что больше «e» в степени «пи» или «пи» в степени «e»? И почему?» — Яндекс Кью

Число Пи и другие мировые числа.: moris_levran — LiveJournal

Мир вокруг нас заполнен числами. Эти числа отображают удивительную связь между различными природными явлениями, помогают проникать в саму суть мира. Ещё Пифагор высказал мысль «Всё есть число». Галилей говорил «Математика есть язык природы», а нобелевский лауреат, физик Юджин Вигнер выдвинул знаменитый тезис о «непостижимой эффективности математики». Но что означают эти числа? Объективную реальность, существующую в природе, независимо от сознания, или это только продукт мышления человека. Какова связь чисел с миром, в котором мы живём, со всей Вселенной. Между фундаментальными числами существует связь, кроме этого, существует глубинная связь между этими числами и свойствами мира, в котором мы живём.
• Число Архимеда π =3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…
Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр. То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это 25/8 (Вавилон) и 256/81 (Египет).Архимед, возможно, первым предложил математический способ вычисления π. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку
3 + 10/71 < π < 3 + 1/7
Число π имеет важнейшее значение в современной науке. Это число появилось из за евклидовости пространства – однородного и симметричного. Поэтому фронт взрывной волны имеет сферическую форму, а круги от брошенного камня на воде имеет круговую формы. 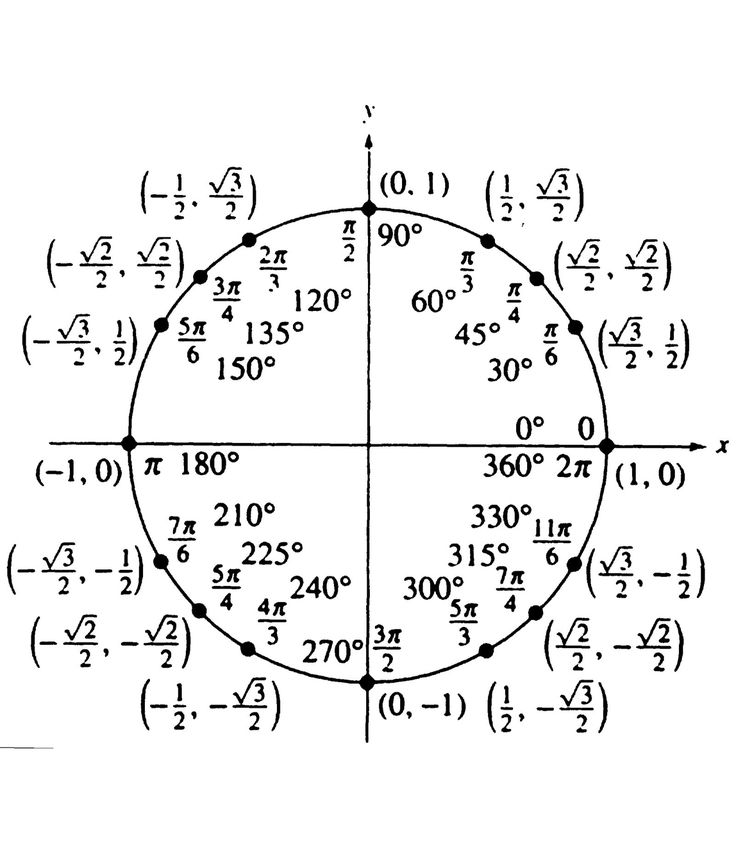А интенсивность света, рентгеновского излучения снижается пропорционально квадрату расстояния от источника излучения. Число π отражает изотропность свойств пустого пространства нашей Вселенной, их одинаковость по любому направлению. С изотропностью пространства связан закон сохранения вращательного момента.
Но в областях с неевклидовым пространством, число π не играет существенную роль, так как симметрия была бы там другой. В областях огромных гравитационных полей, вблизи сингулярностей, в частности, у чёрных дыр появляется свойство кривизны пространства. В нём исчезает и точная формулировка законов сохранения, как они были приняты в классической физике.
Число пи. Музыкальный клип.

• Число Непера e=2,718 281 828 459 045 235 360 287 471 352 662 497 757…
e называют числом Эйлера или числом Непера. e в степени ix = cos(x) = i sin (x), в частности e в степени iπ + 1 = 0 Число е связано со свойствами времени, которое и в настоящее время остаётся странным и загадочным.

Закон радиоактивного распада N=N0 * e в степени -λt, прирост нейтронов в цепной реакции N=N0 * e в степени (k-1)t/T . Множество не природных процессов, связанных со временем, подчиняется законам, с участием числа e. Незатухающая волна во времени е в степени iπt = cos πt + isin πt. Трансляция по оси t изменит фазу, но не изменит амплитуду и частоту волн, т.е. не изменит энергию гармоничной незатухающей волны. Стоячая волна (неизменная в пространстве) е в степени iх = cos х + isin х Трансляция по оси x не изменит синусоиды и косинусоиды, если пространство однородно вдоль оси x. Изменится лишь их фаза.

Однородность пространства приводит к закону сохранения импульса. Число е как основание функции комплексного переменного отражает два основных закона сохранения: энергии — через однородность времени, импульса — через однородность пространства.
• Константа Фейгенбаума δ=4,66920016…
Число, характеризующее хаос. Число δ задаёт форму фракталов, связанных с хаосом. Множество хаотических процессов описывается с помощью этого числа.
• Мнимая единица. i= √-1 i в степени 2 = -1
С помощью мнимой единицы можно решать нерешаемые уравнения. Теория поля, теория волновых процессов, квантовая физика вот сфера применения комплексных чисел. Число е связывает воедино главные константы и действия математики. e в степени πi + 1=0
• Золотое сечение Ø=0,61803398874989484…
В нашем мире одно число характеризует и гармонию живого мира и неживого мира материальных сущностей. Ему подчиняются и Солнечные циклы и пропорции в растительном и животном мире, и пропорции человеческого тела, и самые гениальные творения художников и скульпторов, а, возможно и самого Творца. Это золотое сечение. С ней связаны в геометрии правильный пятиугольник пентаграмма, логарифмическая спираль, в архитектуре – пропорции Парфенона Пирамиды Хеопса, других шедевров архитектуры и живописи. Циклы солнечной активности, закономерности течения истории, строение растений, моллюсков, кровеносной системы, основные мозговые ритмы – всё подчиняется «божественной» пропорции Математически выражается через ряд Фибоначчи. В пределе при делении последующего числа на предыдущее должно получатся число всё более и более приближающееся к 0,61803398874989484…….
В этом короткометражном фильме представляются некоторые из многих проявлений этой золотой пропорции.

• Гугол 10 в степени 100 = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Число всех элементарных частиц во Вселенной 10 в степени 80. Гугол больше этого числа.
• Гуголплекс. 10 в степени 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
т. е. десять в степени гугол. Согласно Р. Пенроузу, вероятность того, что начальная сингулярность Вселенной была слабее, чем сейчас равна 1/10 в степени 1000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 или 1/10 в степени 10 в степени 123
Эту величину можно оценить по формуле С. Хоукинга для энтропии чёрных дыр. Если эту формулу можно применить ко всей Вселенной. Эта точность должна будет отображена в ещё не созданной теории всего, объединяющей общую теорию относительности и квантовую теорию.
• Число Грэхема G
3↑3 это 33=27 3↑↑3 это 3 в степени 3 возведённой в степень 3, т.е. 327, или 7625597484987
3↑↑↑3 это 3↑7625597484987 или три в степени три в степени ………всего 7625597484987 раз. Это больше всех атомов Вселенной (3168) А в формуле Грэхема растет не сам результат, а число стрелочек на каждой стадии подсчёта. Итак….
G= 3↑…..↑3
…….. 64 раза
……..
3↑↑↑↑3

Это, наверное, и есть сама бесконечность! Во всяком случае, такому числу ничего не соответствует – Вселенная слишком мала для такого числа.
• Постоянная Больцмана. k=1,38*10 в степени -23 Дж/К
Входит во многие уравнения термодинамики, молекулярной физики. Больцман вывел знаменитое уравнение S=k lnW связывающее энтропию с термодинамической вероятностью состояния. Эта формула высечена на могильном памятнике Больцману. На открытии памятника Вальтер Тирринг, директор Института теоретической физики в Вене произнёс знаменитую фразу «Эта формула сохранит свою силу даже тогда, когда все памятники будут погребены под мусором тысячелетий».
• Масса протона μ=1836,152
Это соотношение двух базовых элементарных частиц протона и электрона.
• Космологическая константа Λ=1*10 в степени -23 г/м3.
Плотность тёмной энергии, ответственной за ускоренное расширение Вселенной. На неё приходится 74% всей массы Вселенной. Впервые ввёл в уравнения А. Эйнштейн. В дальнейшем своё открытие он считал своим «главным промахом». Λ описывает плотность «тёмной энергии», которая находясь в каждом кубическом сантиметре пространства, «расталкивает» это пространство изнутри. Грубо говоря это микроскопический Большой взрыв, происходящий каждую секунду и повсевместно.
• Постоянная Хаббла H = 77км/с/МПс
Мера скорости, с которой расширяется Вселенная. 1/Н даёт 13,8 миллиард лет, возраст Вселенной. Скорость света, делённая на Н даёт 13,8 миллиард световых лет – хаббловская сфера. За её пределами скорость разбегания галактик больше скорости света. Однако противоречия с СТО нет – это скорость в разбегающейся Вселенной – стоит выбрать другую систему координат, и противоречие снимается само собой. За хаббловской сферой видимая Вселенная не заканчивается.
• Планковская масса mp= 21,76 мкг
Условная граница между макро и микромиром. Между теорией гравитации и квантовой механикой. Столько должна весить чёрная дыра, размеры которой совпадают с длиной волны, отвечающей ей как микрообъекту.
• Пла́нковское вре́мя tP =5,39121(40)*10 в степени -44 с
Физический смысл этой величины — время, за которое частица, двигаясь со скоростью света, преодолеет планковскую длину. Спустя одно планковское время после Большого взрыва, согласно современной теоретической физике, гравитационные силы отделяются от остальных сил.
• Планковская длина lp=1,6 × 10 в степени -35 м
Фундаментальная единица длины
• Постоянная тонкой структуры. α = 1/137,035 999 679 (94)
является фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия. Впервые она была описана в 1916 г. немецким физиком Арнольдом Зоммерфельдом в качестве меры релятивистских поправок при описании атомных спектральных линий в рамках модели атома Бора. Постоянная тонкой структуры (ПТС) — это безразмерная величина, и её численное значение не зависит от выбранной системы единиц. Постоянная тонкой структуры является отношением двух энергий:
1. энергии, необходимой, чтобы преодолеть электростатическое отталкивание между двумя электронами, сблизив их с бесконечности до некоторого расстояния s, и
2. энергии фотона с длиной волны 2πs.
В формулу постоянной тонкой структуры кроме величины скорости света c входят константа Планка, мера «квантовости » мира и заряд электрона.
• Большое космологическое число Do=4,16650385(15)∙10 в степени 42
С этим числом связанны большие чисела:
1.отношение плотностей фотонов и барионов nγ/nB≈D в степени 1/4
2.отношение времени жизни типичной звезды к планковскому времени tH/tpl≈D в степени 3/2
3.отношение характерного ядерного времени к планковскому времени tN/tpl≈D в степени 1/2
4. количество заряженных частиц во Вселенной Nq≈10 в степени 80=D в степени 2
5.отношение действия Метагалактики к элементарному действию 2MU c2tH/h ≈ 10 в степени 120 = D в степени 3
6.отношение квадрата гравитационного заряда Вселенной к hc GMh3/hc ≈ 10 в степени 120=D в степени 3.
Такие совпадения между различающихся на 127 порядков чисел, отличающихся принадлежностью к микромиру и мегамиру, не могут быть случайными, а указывают на глубинную связь их в рамках единой физической теории, которую, начиная с Эйнштейна, ищет не одно поколения физиков.
Есть множество других констант, ОТО и Стандартная Модель даёт их 26.
• масса кварка up
• масса кварка down
• масса кварка charm
• масса кварка strange
• масса кварка top
• масса кварка bottom
• 4 числа для матрицы Кобаяши-Масакава
• масса электрона
• масса электронного нейтрино
• масса мюона
• масса мюонного нейтрино
• масса тау лептона
• масса тау нейтрино
• 4 числа для матрицы Маки-Накагава-Саката
• масса бозона Хиггса
• ожидаемая величина поля Хиггса
• константа взаимодействия U(1)
• константа взаимодействия SU(2)
• константа сильного взаимодействия
• космологическая константа
Учёные стоят на пороге открытия новой физики. Величайшее открытие, которое предстоит в теоретической физике, поможет воедино связать все мировые константы и числа в рамках единой теории. Теория всего свяжет воедино ОТО со Стандартной теорией. Природа проста и гармонична на самом элементарном уровне, все современные теории говорят о существовании единой теории всего. И новые эксперименты на новых ускорителях, новые эксперименты по обнаружению гравитационных волн, попытки обнаружить тёмную материю это далеко не полный перечень попыток найти подход к обнаружению этого «Священного Грааля» физики.

Дополнения. О числе Грэхема. http://sly2m.livejournal.com/620353.html

Самые известные трансцендентные числа (перевод)

Оригинальная статья доступна здесь, автор — Клифф Пиковер

Я влюблен в таинственные трансцендентные числа. Знаете ли вы, что существует «больше» трансцендентных чисел, чем более знакомых алгебраических? Несмотря на это, людям известно лишь несколько классов трансцендентных чисел, и очень трудно доказать, что конкретное число трансцендентно. В 1844 году математический гений Джозеф Лиувилль (1809-1882) первым доказал существование трансцендентных чисел. (Точнее, он был первым, кто доказал, что определенное число было трансцендентным.) Эрмит доказал, что число* e* было трансцендентным в 1873 году. Линдеман доказал, что число pi было трансцендентным в 1882 году.

Для получения дополнительной информации см. Мою книгу «Чудеса чисел», из которой это выдержка.

Математическая константа pi представляет собой отношение длины окружности к ее диаметру. Это самое известное соотношение в математике как на Земле, так и, вероятно, для любой развитой цивилизации во вселенной. Число пи, как и другие фундаментальные константы математики, такие как е = 2,718 …, является трансцендентным числом. Цифры пи и е никогда не заканчиваются, и никто не обнаружил упорядоченную структуру в их расположении. Люди знают значение пи более чем триллионом цифр.

Трансцендентные числа не могут быть выражены как корень любого алгебраического уравнения с рациональными коэффициентами. Это означает, что pi не может точно удовлетворить уравнения типа: pi 2 = 10 или 9pi 4 — 240pi 2 + 1492 = 0. Это уравнения, включающие простые целые числа со степенями числа пи. Числа pi и e могут быть выражены как бесконечная непрерывная дробь или как предел бесконечного ряда. Замечательная фракция 355/113 выражает число Пи с точностью до шести знаков после запятой.

В 1882 году немецкий математик Ф. Линдеманн доказал, что пи трансцендентен, и, наконец, положил конец 2500 годам спекуляций. Фактически он доказал, что пи превосходит силу алгебры, чтобы показать ее во всей ее полноте. Это не может быть выражено ни в какой конечной серии арифметических или алгебраических операций. Используя шрифт фиксированного размера, его нельзя написать на клочке бумаги размером с вселенную.

Я также рассказываю обо всех загадках пи в моей книге «Ключи к бесконечности».

Многие из вас, наверное, слышали о пи и е. Но есть ли другие известные трансцендентные числа? Проведя краткий опрос читателей, я составил список из пятнадцати самых известных трансцендентных чисел. 2 = 1 — 1/9 + 1/25 — 1/49 + … (не доказано, что она трансцендентна, но обычно считается математиками.)

Номер Лиувилля 0.110001000000000000000001000 … который имеет единицу в 1-м, 2-м, 6-м, 24-м и т. Д. Местах и нулях в других местах.

«Постоянная» Чейтина, вероятность того, что случайный алгоритм останавливается. (Ноам Элкис из Гарварда отмечает, что это число не только трансцендентно, но и неисчислимо).

Число Chapernowne, 0.12345678910111213141516171819202122232425 … Построено путем объединения цифр положительных целых чисел. (Можете ли вы увидеть шаблон?)

Специальные значения дзета-функции, такие как дзета (3). (Обычно можно ожидать, что трансцендентные функции дадут трансцендентные результаты в рациональных точках.)

Ln (2).

Число Гильберта, 2 (кв. 2) . (Это называется числом Гильберта, потому что доказательство того, является ли оно трансцендентным, было одной из знаменитых проблем Гильберта. Фактически, согласно теореме Гельфонда-Шнайдера, любое число формы a bтрансцендентно, где a и b алгебраичны ( a ne 0, a ne 1) и b не является рациональным числом. Многие тригонометрические или гиперболические функции ненулевых алгебраических чисел являются трансцендентными.)

e pi

pi e (Не доказано, что он трансцендентен, но, как полагают, математики.)

Номер Морзе-Тью, 0.01101001 …

i i = 0.207879576 … (Здесь i — воображаемое число sqrt (-1). Разве это не настоящая красота? Сколько людей на самом деле думали о том, чтобы приравнять i к степени i? Если a является алгебраическим, а b алгебраическим, но иррационально, тогда a b трансцендентно. Поскольку i является алгебраическим, но иррациональным, применяется теорема. Отметим также: i i равно e (- pi / 2) и нескольким другим значениям. Рассмотрим i i = e (i log i) = e (i раза i pi / 2) . Так как log многозначен, существуют другие возможные значения для i i .
Вот как вы можете вычислить значение i i = 0.

(- Пи / 2) = .207879576 …

Числа Фейгенбаума, например 4.669 …. (Они связаны со свойствами динамических систем с удвоением периода. Соотношение последовательных различий между параметрами бифуркации удвоения периода приближается к числу 4.669 …, и оно было обнаружено во многих физических системах до того, как они входят в хаотический режим. Не было доказано, что число трансцендентно, но считается, что это так)

Давным-давно Кейт Бриггс из математического факультета Мельбурнского университета в Австралии вычислил то, что он считал мировым рекордом по количеству цифр для числа Фейгенбаума:

669201609102990671853203820466201617258185577475768632745651 343004134330211314737138689744023948013817165984855189815134 408627142027932522312442988890890859944935463236713411532481 714219947455644365823793202009561058330575458617652222070385 410646749494284981453391726200568755665952339875603825637225

Бриггс выполнил вычисления с использованием специального программного обеспечения, разработанного Дэвидом Бэйли из НАСА Эймс, работающего на IBM RISC System / 6000. Вычисление потребовало нескольких часов работы.

Сегодня мы знаем гораздо больше цифр для постоянной Фейгенбаума. На этой странице приведено более 10 000 цифр.

Муравьи и Трансцендентные Числа

Представьте себе расу говорящих муравьев. Муравьи могут сжимать бесконечные цифры числа Пи интересным способом. Например, представим, что муравьи могут говорить, манипулируя своими грубыми челюстями. Первый муравей в длинном параде муравьев выкрикивает первую цифру «3». Следующий выкрикивает цифру на своей спине — «1». Следующий выкрикивает «4» и так далее. Далее представьте, что каждый муравей произносит свою цифру только за половину времени предыдущего муравья. Каждый муравей говорит по очереди. В любой момент времени произносится только последняя цифра. Если для произнесения первой цифры числа Пи требуется 30 секунд (из-за громоздких челюстей и маленького мозга муравья), то может ли вся муравьиная колония произнести все цифры числа Пи за минуту? (Опять же, это потому, что бесконечная сумма 1/2 минуты + 1/4 минуты + 1/8 минуты + . .. равна 1 минуте). Поразительно, но в конце минуты найдется быстро говорящий муравей, который действительно произнесет «последнюю» цифру числа пи! Бог-геометр, услышав эту последнюю цифру, может воскликнуть: «Это невозможно, потому что у пи нет последней цифры!».

(См. ниже письмо от Брайана Б. о говорящих муравьях).

Вот несколько интересных страниц о трансцендентных числах:

1 2 3

Вот книга о трансцендентных числах.

Номер дотти

Число Дотти — уникальный действительный корень cosx = x (а именно, уникальная действительная фиксированная точка функции косинуса), которая равна 0,739085…

Дотти замечала, что всякий раз, когда она вводила число в свой калькулятор и нажимала кнопку косинуса несколько раз, результат всегда сходится к этому значению. Вот это да! Число известно, и появилось в многочисленных элементарных работах по алгебре уже к концу 1880-х годов. Число Дотти является трансцендентным как следствие теоремы Линдемана-Вейерштрасса.

Этот текст о Дотти добавлен в MathWorld.

Комментарии коллег

Комментарии RM Mentock:

Существует множество часто используемых чисел (хотя они не часто признаются таковыми даже математиками), которые также являются трансцендентными. Это легко показать с помощью теоремы Гельфонда-Шнайдера, упомянутой в десятом пункте списка. Если a — алгебраическое, c — алгебраическое, а b = логарифм (основание a) от c не является рациональным, то b должно быть трансцендентным. Иначе из теоремы следовало бы, что c должно быть трансцендентным — а это противоречие. Тогда, при a=10 и c=2, логарифм двойки по основанию 10 является трансцендентным, как и любой логарифм по основанию 10 любого рационального числа, кроме рациональных чисел, равных десяти. То же самое относится и к любому другому рациональному логарифму по основанию. Таким образом, существует множество трансцендентных чисел, которые широко используются. Или они были таковыми сорок лет назад, до появления карманных калькуляторов!

Хочу также отметить, что любое число может быть использовано для получения трансцендентного с помощью алгоритма Лиувилля (см. пункт номер пять). Если число конечное, преобразуйте его в не конечное, вычитая единицу из последней цифры и добавляя в конец бесконечную строку из 9. Затем просто поместите каждую из его цифр туда, куда Лиувилль поместил единицу, даже если цифра равна нулю. В результате получится трансцендентное число.

Брайан Б. комментирует «говорящих муравьев» выше:

На своей странице трансцендентных чисел (https://sprott.physics.wisc.edu/Pickover/trans.html) вы говорите: «Поразительно, но в конце минуты появится быстро говорящий муравей, который действительно произнесет «последнюю» цифру числа пи!». Это неверно. В бесконечной череде муравьев не существует последнего муравья, так же как не существует последней цифры числа Пи. В этом можно легко убедиться, если заставить всех муравьев объявить свою цифру в одно и то же время. На произнесение всех цифр уйдет ноль секунд, но все равно не будет ни последней цифры, ни последнего муравья. Или совсем забудьте о муравьях и просто попросите каждого муравья объявить свою цифру в один и тот же момент. Но последней цифры все равно нет, как нет конца у натуральных чисел. Надеюсь, вы исправите эту ошибку. Я думаю, что было бы лучше просто удалить весь раздел «Муравьи». Спасибо.

е$.

Я ничего не смог придумать, и мне просто любопытно, как вы могли бы справиться с этим, имея в виду, что это взято из учебника алгебры колледжа, менее чем на полпути, так что я не думаю, что автор имел в виду какую-то суперпродвинутую тактику.

• неравенство
• экспоненциальная функция
• возведение в степень
• пи

$\endgroup$

5

9e$ тогда и только тогда, когда $\pi > e\ln\pi$. Взяв снова натуральный логарифм, мы увидим, что это верно тогда и только тогда, когда $\ln\pi > 1 + \ln\ln\pi$.

Чтобы показать это, рассмотрим функцию $f(x) = \ln x — 1 — \ln\ln x$. Тогда $f'(x) = \frac1x — \frac{1}{x\ln x}$. Эта производная непрерывна при $x>0$ и имеет один нуль при $x = e$.

е$. 9{\pi i}$ и убедимся, что оно равно сумме разложений Тейлора (Маклорена) $\cos {\pi}$ и $i \sin {\pi}$. Обе суммы составляют $-1$! Или, если вам лень, вы можете просмотреть Википедию

ОБА $e$ и $i$ очаровательны, потому что они «всплывают» почти везде в математике, физике и многих других областях. Дополнительные способы представления $e$ см. в этом списке.

$\endgroup$

5

$\begingroup$ 9{я \ тета} $. Тогда $f»(\theta)=-f(\theta)$. Дифференциальные уравнения говорят нам, что любое такое решение является линейной комбинацией $\sin(\theta)$ и $\cos(\theta)$ [причина: Вронскианск говорит нам, что $f, \sin(x), \cos( x)$ линейно зависимы, а $\sin(x), \cos(x)$ линейно независимы].

Таким образом, $f(\theta)=A \cos(\theta)+ B \sin(\theta)$ для некоторых $A,B$. Установка $\theta=0$ дает $A=1$, а вывод и установка $\theta=0$ дает $B=i$.