Площадь грани куба формула: Как найти площадь грани куба 🚩 сторона грани куба ответ 🚩 Математика

Содержание

Объем куба площадь полной и боковой поверхности. Как найти площадь и объем куба. Как найти площадь куба

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Куб — одна из простейших трехмерных фигур. Каждому знакомы кубики льда, квадратные коробки или кристаллы соли – все они являются такими фигурами. Площадь поверхности куба — это общая площадь всех сторон на его поверхности. Все шесть его граней соразмерны, поэтому, зная длину одной из них, можно рассчитать боковую площадь и площадь поверхности любой фигуры.

Как найти площадь куба — что собой представляет фигура?

Куб — это трехмерная фигура, которая имеет одинаковые размеры.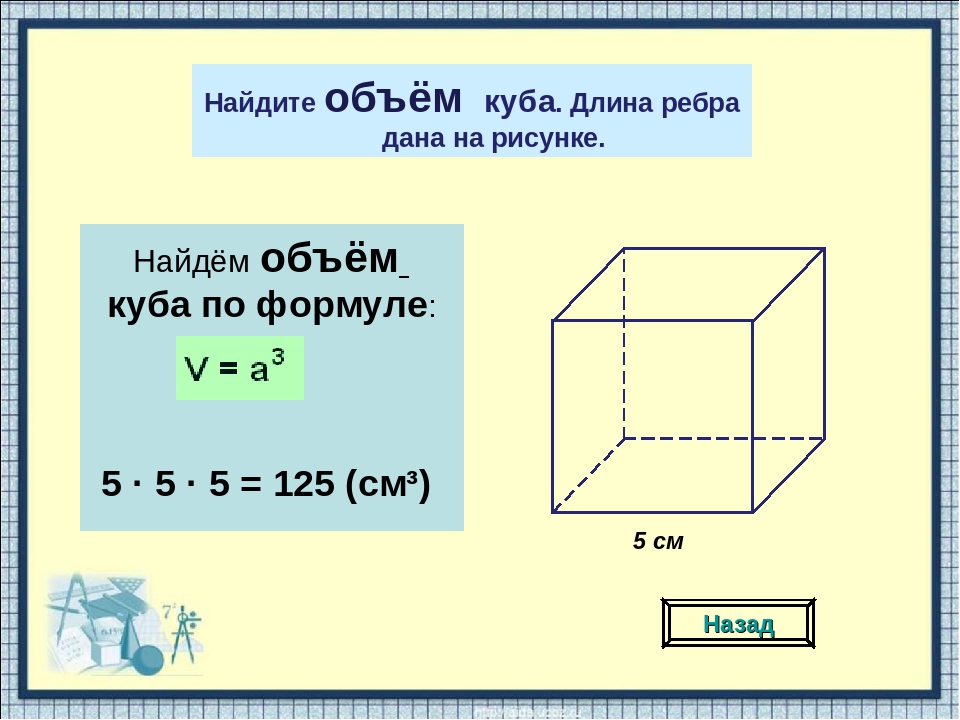 Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.

Как найти площадь куба — грани фигуры

Из иллюстрации видно, что куб имеет переднюю и заднюю грань, две боковые и верхнюю с нижней стороны. Площадь любого куба будут составлять шесть конгруэнтных квадратов. Фактически, если развернуть его, можно четко увидеть шесть квадратов, которые составляют общую поверхность фигуры.

Как найти площадь куба

Площадь куба состоит из площади шести граней. Поскольку все они равны, достаточно знать площадь одной из них и умножить значение на 6. Площадь фигуры также находят по простой формуле: S = 6 x а², где «а» — одна из сторон куба.

Как найти площадь куба — установите площадь стороны

Предположим, что высота куба составляет 2 см. Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
Чтобы найти площадь одного из квадратов, вспомните базовые знания геометрии, где S = а², где а — длина одной из сторон. В нашем случае, а = 2 см, так что S = (2 см)² = 2 см х 2 см = 4 см².
Площадь одного из квадратов поверхности составляет 4 см². Не забудьте указать свое значение в квадратных единицах.

Как найти площадь куба — пример

Поскольку вся поверхность фигуры состоит из шести соразмерных квадратов, нужно умножить площадь одной стороны на 6, следуя формуле S = 6 x а². В нашем случае S = 6 х 4 см² = 24 см². Площадь трехмерной фигуры составляет 24 см².

Находим площадь куба, если сторона выражена в дробях

Если вам сложно работать с дробью, конвертируйте ее в десятичную.
Например, высота куба 2 ½ см.

S = 6 х (2½ см) ²
S = 6 х (2,5 см) ²
S = 6 х 6,25 см ²
S = 37,5 см ²
Площадь поверхности куба — 37,5 см ².

Зная площадь куба, находим его сторону

Если площадь поверхности куба известна, можно определить длину его сторон.

Площадь куба составляет 86,64 см². Необходимо определить длину грани.
Решение. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень.
Сделав необходимые вычисления, получаем длину 3,8 см.

Как найти площадь куба — онлайн измерение площади

Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.

Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.

Геометрия является одной из основных математических наук, базовый курс которой изучается даже в школе. На самом деле польза от знаний различных фигур и законов пригодится в жизни каждому. Очень часто встречаются геометрические задачи на нахождение площади . Если с плоскими фигурами особых проблем у учащихся не возникает, то вот объемные могут вызвать определенные трудности. Вычислить площадь поверхности куба бывает не так просто, как кажется на первый взгляд. Но при должном внимании решается даже самая сложная задача.

Необходимо:

Знания основных формул;
— условия задачи.

Инструкция:

В первую очередь надо определиться, какая формула площади куба применима в конкретном случае . Для этого нужно посмотреть на заданные параметры фигуры . Какие данные известны: длина ребра , объем , диагональ , площадь грани . В зависимости от этого выбирается формула.

Если по условиям задачи известна длина ребра куба , то достаточно применить простейшую формулу для нахождения площади. Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2 . Где х — длина ребра куба .
Допустим, что ребро куба не задано, но известен. Так как объем данной фигуры вычисляется возведением в третью степень длины его ребра , то последнюю можно получить достаточно легко. Для этого из числа, обозначающего объем, необходимо извлечь корень третей степени. Например, для числа 27 корнем третей степени будет число 3 . Ну а что делать дальше, мы уже разбирали. Таким образом, формула площади куба при известном объеме также существует, где вместо
х стоит корень третей степени из объема.
Бывает, что известна только длина диагонали . Если вспомнить теорему Пифагора , то можно легко вычислить длину ребра. Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2 .
Подводя итог, стоит отметить, что для правильных вычислений нужно узнать длину ребра. Условия в задачах встречаются самые разные, поэтому следует научится выполнять сразу несколько действий. Если известны другие характеристики геометрической фигуры, то с помощью дополнительных формул и теорем можно вычислить ребро куба. И уже на основании полученного результата посчитать результат.

Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками — квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.

Инструкция

Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.

Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:

S = a?, где а — сторона квадрата (ребро куба).

Пример: Длина ребра куба 11 см, требуется найти ее площадь.

Решение: зная длину грани, можно найти ее площадь:

S = 11? = 121 см?

Ответ: площадь грани куба с ребром 11 см равна 121 см?

Обратите внимание

Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб — это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр — это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т.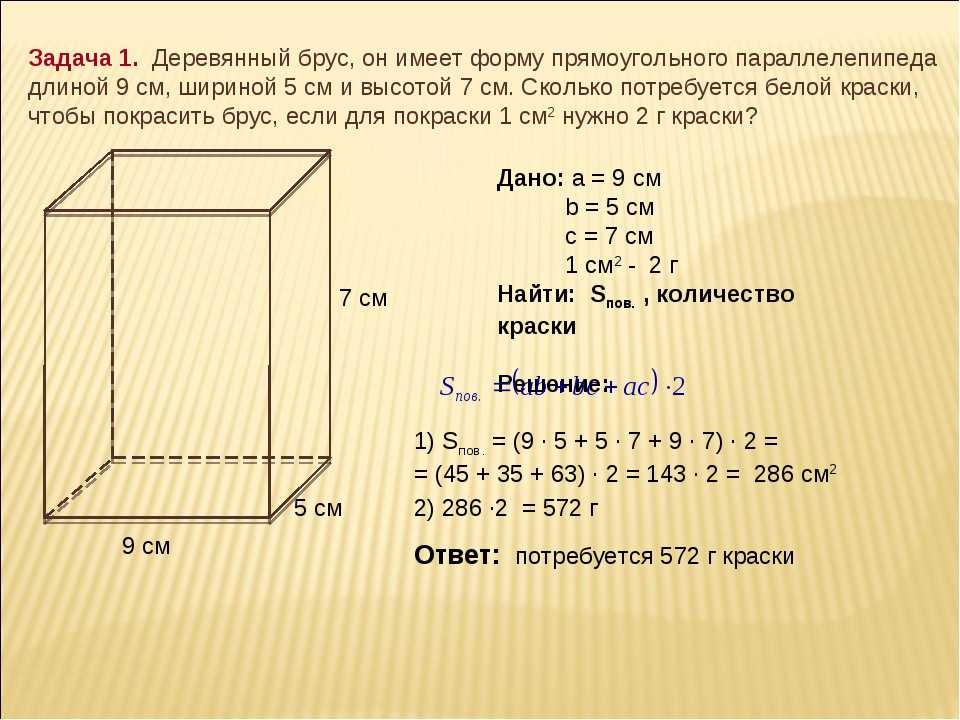 п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы — баррель (1м? = 6.29 баррелей)

Полезный совет

Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a?;
Объем: V = 6*a?;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((?3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*?3

Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются. И неважно, что нужно найти — объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.

Что такое площадь?

Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.

Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.

Какая фигура называется кубом?

Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.

Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.

Эта фигура настолько гармонична, что часто используется в быту.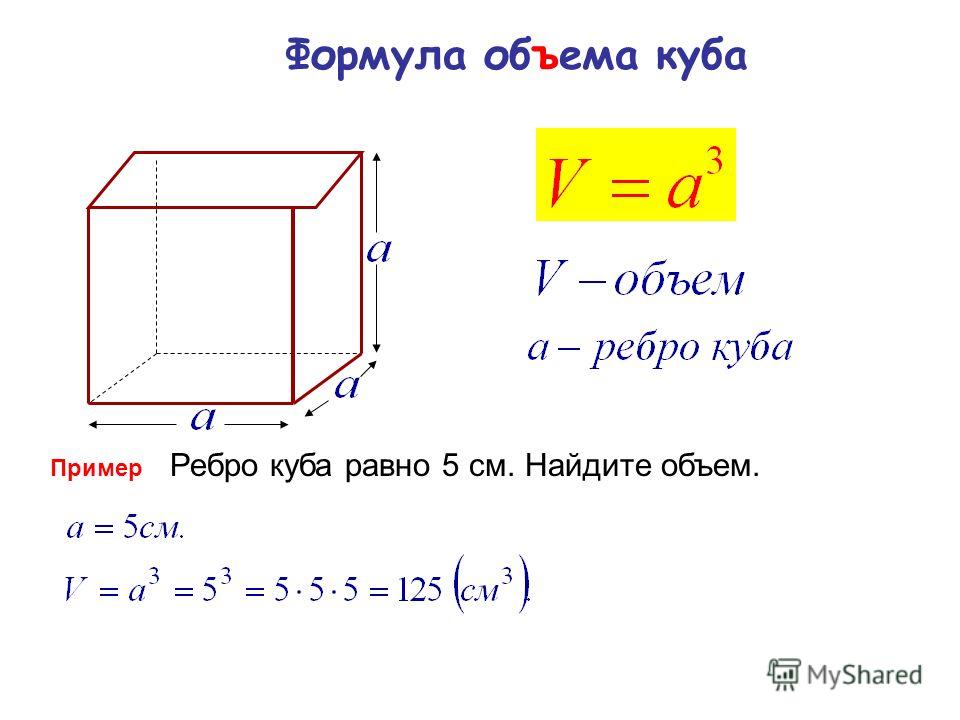 Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.

Как связан куб с другими фигурами и телами?

Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Метод 1: вычисление площади куба по его ребру

Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».

Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S 1 .

Для удобства лучше задать номера всем формулам. Эта будет первой.

Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a 2 . Ее номер 2.

Метод 2: как вычислить площадь, если известен объем тела

Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:

Нумерация продолжается, и здесь уже цифра 3.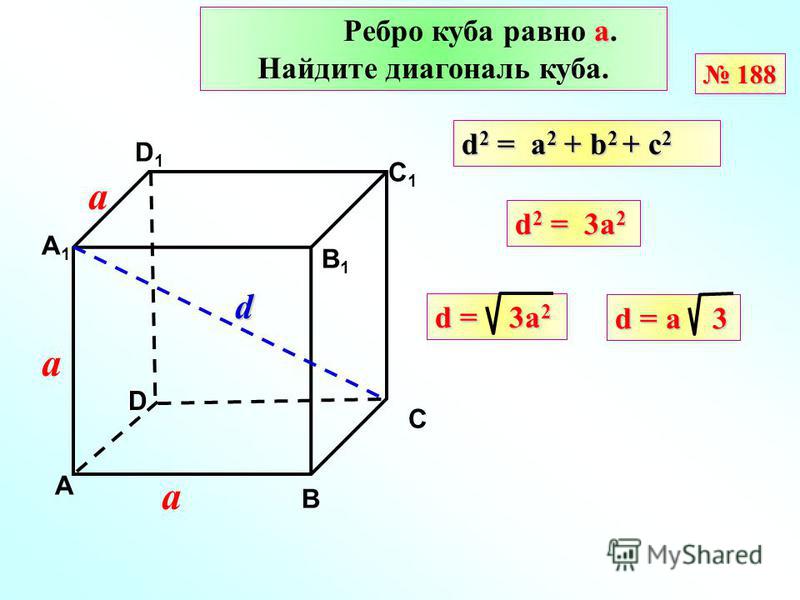

Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:

Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.

Метод 3: расчет площади по диагонали куба

Это формула №5.

Из нее легко вывести выражение для ребра куба:

Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:

Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.

Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба

Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:

Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.

Обозначив радиус вписанной окружности латинской буквой r, можно получить такую формулу для площади всей поверхности гексаэдра:

Это формула №9.

Несколько слов о боковой поверхности гексаэдра

Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:

Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.

Примеры задач

Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.

1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:

а = √ (200/6) = √ (100/3) = 10 √3 (см).

Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.

2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.

Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.

х² = а² + а², где х — диагональ квадрата.

d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.

Ответ: диагональ куба равна 10 см.

Условие второй. По известной площади поверхности, которая равна 54 см 2 , вычислить объем куба.

Пользуясь формулой под вторым номером, нужно узнать значение ребра куба. То, как это делается, подробно описано в первом способе решения предыдущей задачи. Проведя все вычисления, получим, что а = 3 см.

Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 3 3 = 27 см 3 .

Ответ: объем куба равен 27 см 3 .

Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.

Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).

Зная это, нужно записать формулу для площади поверхности куба два раза. Первая — для начального значения ребра — совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9).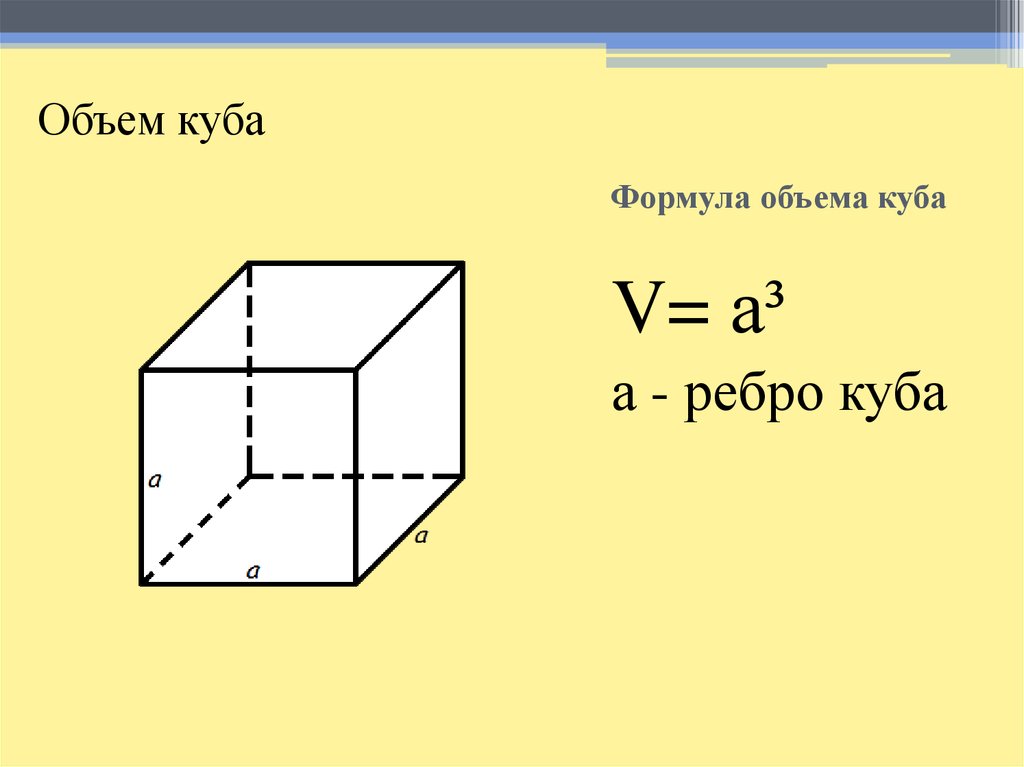 Так как в задаче идет речь о разности площадей, то нужно вычесть из большей площади меньшую:

6 * (а + 9) 2 — 6 * а 2 = 594.

Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9) 2 — а 2 . Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 — а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).

Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить. Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.

Это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности.

Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.

Выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) — это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а — сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть.

В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а — ребро куба (сторона квадрата).

Чему равна площадь поверхности куба.

Измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.

Пример : а = 2 см.

Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2

Вы вычислили значение площади одной из граней куба.

Пример : а = 2 см

a 2 = 2 х 2 = 4 см 2

Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.

Вот мы и пришли к конечному действию по вычислению площади поверхности куба .

Пример : а 2 = 4 см 2

SA = 6 х а 2 = 6 х 4 = 24 см 2

Куб обладает множеством интересных математических свойств и известен людям с давних времен. Представители некоторых древнегреческих школ считали, что элементарные частицы (атомы), из которых состоит наш мир, имеют форму куба, а мистики и эзотерики даже обожествляли эту фигуру. И сегодня представители паранауки приписывают кубу удивительные энергетические свойства.

Куб — это идеальная фигура, одно из пяти Платоновых тел. Платоново тело — это

правильная многогранная фигура, удовлетворяющая трем условиям:

1. Все ее ребра и грани равны.

2. Углы между гранями равны (у куба углы между гранями равны и составляют 90 градусов).

3. Все вершины фигуры касаются поверхности описанной вокруг нее сферы.

Точное количество этих фигур назвал древнегреческий математик Теэтет Афинский, а ученик Платона Евклид в 13-ой книге Начал дал им подробное математическое описание.

Древние греки, склонные с помощью количественных величин описывать строение нашего мира, придавали Платоновым телам глубокий сакральный смысл. Они считали, что каждая из фигур символизирует вселенские начала: тетраэдр — огонь, куб — землю, октаэдр — воздух, икосаэдр — воду, додекаэдр — эфир. Сфера же, описанная вокруг них, символизировала совершенство, божественное начало.

Итак, куб, называемый также гексаэдром (от греч. «hex» — 6), — это трехмерная правильная Его также называют или прямоугольным параллелепипедом.

У куба шесть граней, двенадцать ребер и восемь вершин. В эту фигуру можно вписать другие тетраэдр (четырехгранник с гранями в виде треугольников), октаэдр (восьмигранник) и икосаэдр (двадцатигранник).

Называется отрезок, соединяющий две симметричные относительно центра вершины. Зная длину ребра куба a, можно найти длину диагонали v: v = a 3.

В куб, как говорилось выше, можно вписать сферу, при этом радиус вписанной сферы (обозначим r) будет равен половине длины ребра: r =(1/2)а.

Если же сферу описать вокруг куба, то радиус описанной сферы (обозначим его R) будет равен: R= (3/2)a.

Довольно распространенный в школьных задачах вопрос: как вычислить площадь

поверхности куба? Очень просто, достаточно наглядно представить себе куб. Поверхность куба состоит из шести граней в форме квадратов. Следовательно, для того, чтобы найти площадь поверхности куба, сначала нужно найти площадь одной из граней и умножить на их количество: S п = 6а 2.

Аналогично тому, как мы нашли площадь поверхности куба, рассчитаем площадь его боковых граней: S б =4а 2.

Из этой формулы понятно, что две противолежащие грани куба — это основания, а остальные четыре — боковые поверхности.

Отыскать куба можно и другим способом. Учитывая тот факт, что куб — это прямоугольный параллелепипед, можно воспользоваться понятием трех пространственных измерений. Это значит, что куб, являясь трехмерной фигурой, имеет 3 параметра: длину (а), ширину(b) и высоту (c).

Используя эти параметры, вычислим площадь полной поверхности куба: S п = 2(ab+ас+bc).

Объем куба — это произведение трех составляющих — высоты, длины и ширины:
V= abc либо трех смежных ребер: V=а 3.