Контрольная работа №1
16
Задание 1.1.
Даны координаты вершин пирамиды , , , .
1). длину ребра ;
2). угол между ребрами и ;
3). угол между ребром и гранью ;
4). площадь грани ;
5). объём пирамиды;
6). уравнение прямой ;
7). уравнение плоскости ;
8). уравнение высоты, опущенной из вершины на грань .
Решение.
1). Используем формулу для нахождения длины ребра через координаты его конечных точек:
.
2). Запишем координаты векторов и :
;
.
Тогда, получим:
.
3). Угол между ребром и гранью – это угол между вектором и нормальным вектором плоскости .
Находим нормальный вектор плоскости как векторное произведение векторов и :
.
Далее, используем соответствующую формулу для вычисления искомого угла:
.
Следовательно,
.
4). Площадь грани вычисляется как половина длины векторного произведения векторов и , на которых она построена, т.е. половина длины нормального вектора плоскости . Тогда, получим:
Векторное произведение:
i(5 • 2-0 • (-3)) — j(0 • 2-(-3) • (-3)) + k(0 • 0-(-3) • 5) = 10i + 9j + 15k
.
5). Используем формулу для нахождения объёма пирамиды через координаты векторов ; ; , на которых она построена:
.
6). Запишем симметричные уравнения прямой через координаты точки и направляющего вектора :
;
.
7). Запишем уравнение плоскости по известному нормальному вектору и точке плоскости :
;
;
;
.
8). Направляющим вектором искомой высоты есть нормальный вектор плоскости : (поскольку высота перпендикулярна к этой плоскости).
Запишем симметричные уравнения высоты через координаты точки и направляющего вектора :
;..
Задание 1.2.
Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки относятся как 2:1.
Решение.
Пусть – произвольная точка данной линии.
Находим расстояние от точки линии к началу координат по соответствующей формуле расстояния между двумя точками:
.
Находим расстояние от точки на линии к точке :
.
По условию, найденные расстояния относятся как 2:1. Следовательно,
; ;
.
Преобразуем полученное уравнение указанной линии:
;
;
;
;
;
.
Выделяем полные квадраты:
;
;
;
;
;
.
Следовательно, – каноническое уравнение окружности с центром в точке и радиусом .
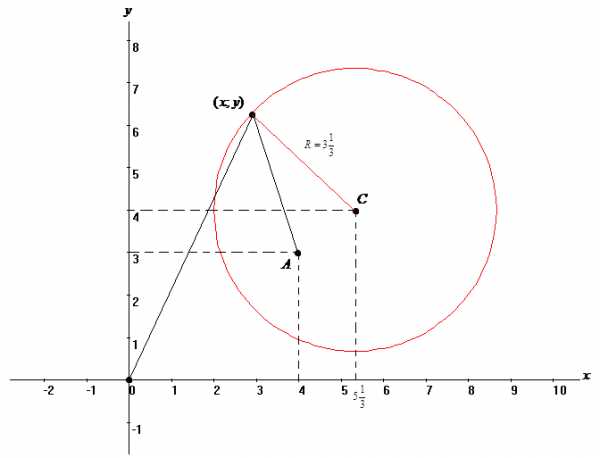
Задание 1.3.
Дана система линейных уравнений. Доказать её совместность и решить методом Гаусса.
.
Решение.
Теорема Кронекера-Капелли: для того, чтобы линейная система уравнений являлась совместной необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы.
Запишем расширенную матрицу системы:
.
Сводим расширенную матрицу системы к трапециевидной форме, используя эквивалентные преобразования.
Поменяем местами первую и третью строки расширенной матрицы:
.
Разделим первую строку на 2.
.
Умножим первую строку на (-2) и прибавим ко второй. Полученные результаты запишем во вторую строку новой расширенной матрицы.
.
Умножим первую строку на (-3) и прибавим к третьей. Полученные результаты запишем в третью строку новой расширенной матрицы.
.
Прибавим вторую строку к третьей. Полученные результаты запишем в третью строку новой расширенной матрицы.
.
Требуемая форма расширенной матрицы получена. Количество ненулевых строк основной и расширенной матрицы одинаковы, поэтому ранг основной матрицы равен рангу расширенной. Это означает, что система линейных уравнений является совместной
.Из последней расширенной матрицы находим решение системы (обратный ход):
1). из третьей строки получим:
; ;
2). из второй строки получим:
; ; ;
3). из первой строки получим
; ; .
Таким образом ,,.
Выполним проверку полученного решения. Подставляя найденные значения x1,x2,x3.
Приходим к тождеству.
Задание 1.4.
Привести к каноническому виду уравнения линий второго порядка. Сделать чертежи.
а). ;
б). ;
в). .
Решение.
а). .
Разделим обе части уравнения на 2:
; ; .
Следовательно, имеем каноническое уравнение эллипса с центром в начале координат, с фокусами на оси ординат (поскольку ), малой полуосью и большой полуосью .
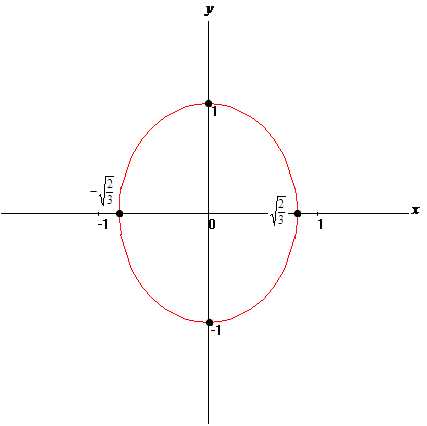
б). .
Разделим обе части уравнения на 3:
; ; .
Следовательно, имеем каноническое уравнение гиперболы с фокусами на оси абсцисс, действительной полуосью и мнимой полуосью .
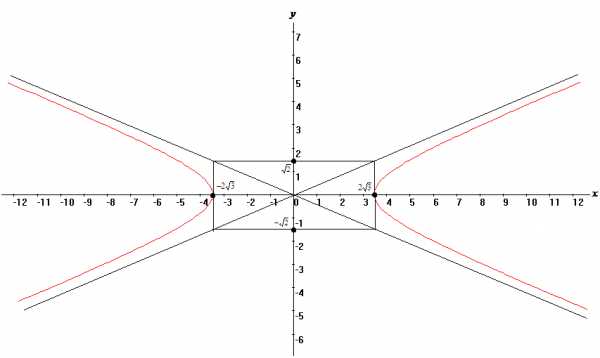
в). .
Выделяем полный квадрат по переменной :
; ;
.
Тогда, получим:
; ; .
Следовательно, получили каноническое уравнение параболы с вершиной в точке , с фокусом на отрицательной полупрямой (парабола опущена ветками вниз)
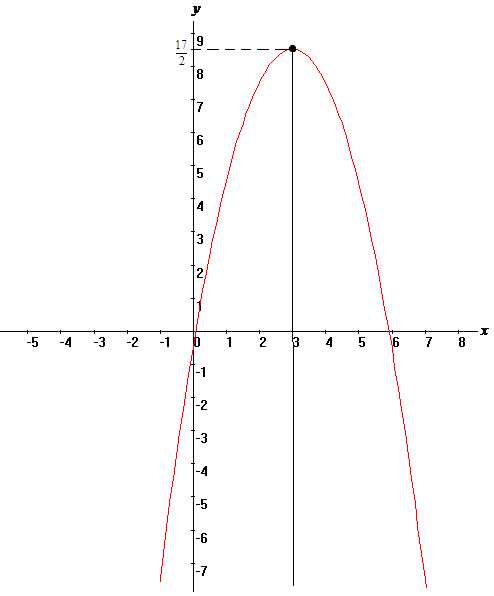
studfiles.net
Тетраэдр (треугольная пирамида) в пространстве
Задача 1.
Тетраэдр в пространстве задано вершинами
Необходимо найти:
1) уравнение грани ;
2) уравнение высоты пирамиды, которая проходит через вершину ;
3) длину этой высоты;
4) угол между ребром и гранью в градусах;
5) площадь грани;
6) Объем пирамиды.
Решение.
1) Уравнение грани
Запишем уравнение плоскости в виде.
.
Поскольку все три точки принадлежат этой плоскости, то, подставляя их по очереди получим систему уравнений
Решая ее получим.
.
Подставляя в исходное уравнение получим
, Или .
2) Уравнение высоты пирамиды, проходящей через вершину
Запишем уравнение высоты пирамиды, проходящей через вершину
.
3) Высота с вершины
Найдем высоту, для этого найдем
Высоту найдем учитывая уравнение грани , по формуле
4)Угол между ребром и гранью в градусах
Найдем угол между ребром и гранью () . Запишем уравнение прямой, проходящей через точки
, или .
Найдем синус угла по формуле
.
Подставим значения
Найдем значение угла
5) Площадь грани
Площадь гранинайдем по формуле
6) Объем пирамиды
Найдем объем пирамиды пирамиды по формуле
, где
Математический калькулятор YukhymCalc решает эту задачу и немало типичных для студенческой практики математических задач. Фрагмент работы калькулятора приведены ниже.
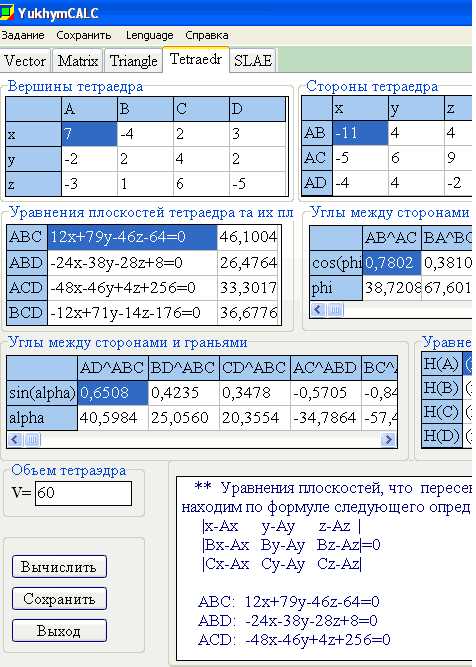
——————————
Посмотреть материалы:
yukhym.com
Нахождение элементов в пирамиде. Контрольные онлайн
Нахождение элементов в пирамиде
Даны вершины пирамиды
и точка .
Найти:
а) длину ребра ;
б) косинус угла между рёбрами и ;
в) площадь грани ABC;
г) объём пирамиды;
д) уравнение прямой, на которой лежит ребро;
е) уравнение прямой, на которой лежит высота пирамиды, опущенная из вершины ;
Выяснить, лежат ли точки и по одну сторону плоскости грани
или по разные? Решение
а) Длину найдём по формуле расстояния между двумя точками
б) Угол между рёбрами и будет равен углу между векторами и
Введём в рассмотрение векторы и и найдём их координаты:
в) Площадь грани ABС (площадь треугольника АВС)
Введём в рассмотрение векторы и и найдём их координаты:
,
Найдём
Далее и
г) Объём пирамиды
, ,
Найдём =
д) Прямая, на которой лежит ребро , проходит через точки и . Запишем уравнение этой прямой, воспользовавшись уравнением прямой, проходящей через две точки и :
Для решаемой задачи или
е) Прямая, на которой лежит высота пирамиды , проходит через точку перпендикулярно плоскости BCD. Следовательно, нормальный вектор плоскости BCD будет являться направляющим вектором для прямой.
Уравнение плоскости BCD найдём, используя уравнение плоскости, проходящей через три заданные точки :
Для решаемой задачи это точки , , и, следовательно, уравнение
, , .
Вектор является нормальным вектором плоскости , следовательно, этот вектор является направляющим вектором для прямой, проходящей через точку перпендикулярно плоскости . Уравнение этой прямой
Найдём уравнение плоскости грани как уравнение плоскости, проходящей через точку и имеющей нормальный вектор :
.
Для решаемой задачи , а найден в п. в) решаемой задачи. Следовательно, уравнение плоскости грани : или .
Для всех точек , лежащих на плоскости, будет выполняться равенство , для точек, лежащих по одну сторону плоскости, будет выполняться неравенство , для точек, лежащих по другую сторону плоскости, — неравенство .
Для точки выполняется неравенство .
Для точки выполняется неравенство .
www.matem96.ru
Площадь поверхности пирамиды | Мозган калькулятор онлайн
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Апофема – опущенный перпендикуляр из вершины на ребро основания.
Боковая поверхность через периметр и апофему
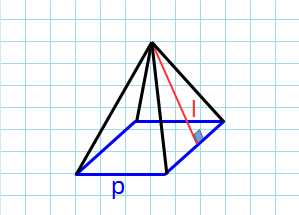
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p — периметр основания пирамиды; l — апофема пирамиды.Боковая поверхность через высоту и сторону основания
Формула площади боковой поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.Полная поверхность через высоту и сторону основания
Формула площади полной поверхности правильной пирамиды через высоту и сторону основания:
a — сторона основания; h — высота пирамиды; n — число сторон в основании.Полная площадь тетраэдра
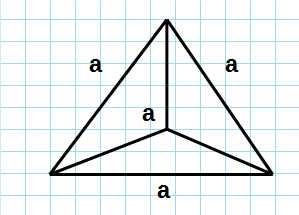
Формула полной площадь тетраэдра:
a — сторона основания.www.mozgan.ru
