Несколько способов решения одной геометрической задачи
Для успешного изучения геометрии учащиеся старших классов должны не только знать основные формулы и теоремы, но и владеть различными методами решения геометрических задач. В успешном усвоении различных методов решения может помочь рассмотрение различных способов решения одной и той же задачи.
Рассмотрим несколько основных способов, которые чаще всего применяются при решении геометрических задач: координатный, векторный, аналитический (то есть сводящийся к решению уравнений и систем уравнений), тригонометрический (то есть основанный на формулах тригонометрии) и чисто геометрический.
1. Способ координат
Этот способ считается самым универсальным для решения геометрических задач.
Рассмотрим его и другие возможные способы на примере одной задачи.
Задача.
В произвольном треугольнике АВС биссектриса ВЕ перпендикулярна медиане АD, причем ВЕ = AD = 4. Найти стороны треугольника АВС.
Решение.
Рассмотрим треугольник АВС (рис. 1).
Точка О – точка пересечения биссектрисы ВЕ и медианы АD.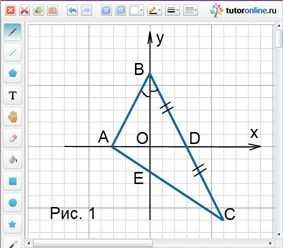
Прямоугольные треугольники АВО и DВО равны по катету и острому углу. Поэтому АО = ОD = 2 и АВ = ВD, так что
ВС = 2АВ.
Пусть точка О – начало прямоугольной системы координат. Ось абсцисс совпадает с направлением вектора ОD. Будем считать, что |OD|/2 есть единичный отрезок координатной плоскости.
В введенной системе координат точки А, D, В имеют следующие координаты:
А(-2; 0), В(0; b), и D(2; 0).
Чтобы вычислить длины сторон треугольника АВС надо определить, чему равно число b.
Его можно выразить через координаты точек С и Е. Зная, что D – середина ВС, получаем, что С(4; -b). Найдем вторую координату точки Е(0; у), пользуясь тем, что она принадлежит прямой АС.
Уравнение прямой АС имеет вид: (х + 2)/6 = у/(-b).
Координаты точки E(0; у) этому уравнению удовлетворяют, поэтому, подставив в него 0 вместо х, получим,
что y = -⅓·b.Следовательно, ВЕ = 4/3 · b. По условию задачи BE = 4, значит, b = 3.
Итак, имеем A(-2; 0), В(0; 3), С(4; -3). Теперь, зная координаты вершин треугольника АВС, найдем его стороны:
АВ = √13, ВС = 2√13, АС = 3√5.
2. Векторный способ
Введем обозначения: ВА = а, ВС = с.
Теперь через а и с выразим векторы ВЕ и АD.
По свойству биссектрисы треугольника из того, что ВС = 2BD, следует, что
СЕ = 2АЕ. По формуле деления отрезка в данном отношении имеем:
ВЕ = (c + 2a)/3.
По правилу вычитания векторов АD = 1/2 · c – a. У векторов ВЕ и АD длины известны.
Пусть |a|= a, тогда |c|= 2a. Вычислив скалярные квадраты векторов ВЕ и AD, получим уравнения:
2a2 + ac = 36; 2a2 – ac = 16.
Отсюда a2 = 13 и ac = 10.
Значит, АВ= √13, ВС=2√13.
Найдем сторону АС по теореме косинусов: AC2 = 5a2 – 2ac. Подставив вместо a2 и ас найденные выше значения, получим АС = 3√5.
3. Аналитический способ
Медиану AD и биссектрису ВЕ треугольника АВС выразим через длины а, b и с сторон треугольника АВС по формулам: AD2 = (b2 + c2)/2 – a2/4 и BE2 = ac – a₁c₁, где а1 = СЕ и с1= АЕ.
Пусть АВ = х, АЕ = у, тогда ВС = 2х и СЕ = 2у. Получим систему уравнений:
{(х2 + 9у2)/2 – х2 = 16
{х2 – у2 = 8.
Отсюда x2 = 13, у2 = 5.
Значит, АВ = √13, ВС = 2√13 и АС=3√5.
4. Тригонометрический способ
Обозначим АВ = х, а угол АВС = 2α. По теореме косинусов из треугольников АВЕ и ВСЕ можно выразить АЕ и СЕ:
АЕ2 = х2 + 16 – 8х · cos α и CE 2 = 4x2 + 16 – 16x · cos α.
Пользуясь тем, что СЕ = 2АЕ или CE2 = 4AE2, имеем: x · cos α = 3.
Но x · cos α = ВО, а значит, ВО = 3 и ОЕ = 1.
Далее, пользуясь теоремой Пифагора, остается только вычислить стороны треугольника АВС.
5. С помощью площадей
Так как АО = ОD = 2, ВЕ = 4 и АD перпендикулярно ВЕ, то площадь каждого из  треугольников ВАЕ и ВDE равна 4 (рис. 2). Площадь треугольника СDE также равна 4, так как медиана ED делит треугольник ВСЕ на два равновеликих треугольника. Значит, площадь треугольника АВС равна 12.
треугольников ВАЕ и ВDE равна 4 (рис. 2). Площадь треугольника СDE также равна 4, так как медиана ED делит треугольник ВСЕ на два равновеликих треугольника. Значит, площадь треугольника АВС равна 12.
Так как AD – медиана треугольника АВС, то площадь треугольника ABD равна 6.
По формуле площади треугольника
SABD = АО · ВО = 6.
Но АО = 2, а значит,
ВО = 3.
Стороны треугольника АВС можно найти по теореме Пифагора.
6. С помощью осевой симметрии
Точки А и D симметричны относительно биссектрисы ВЕ. Построим еще точку, симметричную точке С относительно прямой ВЕ. Для этого продолжим отрезок DE до пересечения с прямой АВ и обозначим через F точку пересечения прямых АВ и DЕ.
Получим равнобедренный треугольник ВСF. Из равенства треугольников ВЕF и ВЕС следует, что ВF = ВС.
Продолжим еще биссектрису ВЕ до пересечения с СF в точке Н.
Тогда ВН – биссектриса треугольника ВСF, а следовательно, и его медиана.
Таким образом, Е – точка пересечения медиан треугольника ВСF, и поэтому ЕН = 0,5; ВЕ = 2, а ВН = 6.
Средняя линия АD треугольника ВСF делит медиану ВН пополам, поэтому ВО = 3. Далее поступаем так же, как и при решении задачи другими способами.
Как видим, вспомогательные построения привели к простому, чисто геометрическому способу решения задачи.
7. По теореме о средней линии треугольника
Проведем среднюю линию DK треугольника ВСЕ (рис. 3).
Так как DK || ВЕ и АО = ОD, то ОЕ – средняя линия треугольника АDK. Следовательно,
ОЕ = 1/2 · DK и DK = 1/2 · ВЕ, т.е. ОЕ = 1/4 · ВЕ.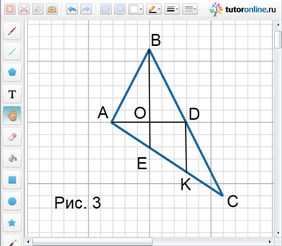
Так как ВЕ = 4, то ОЕ = 1 и ВО = 3.
Из решения видно, что отношение ВО/ОЕ не зависит от длин отрезков ВЕ и АD. Найти это отношение можно используя лишь тот факт, что АD – медиана треугольника АВС и
АО = ОВ, причем без всяких вспомогательных построений.
8. По теореме Менелая
Секущая ВЕ пересекает стороны треугольника АСD в точках Е и О.
По теореме Менелая из треугольника АСD имеем:
AE/EC · CB/BD · DO/OA = 1, а так как СВ/ВD = 2 и DО = ОА, то АЕ = ЕС.
Применив теорему Менелая к треугольнику ВСЕ и секущей АD, получим:
BO/OE · EA/AC · CD/DB = 1.
Но ЕА/АС = 1/3 и СD = DВ.
Следовательно, ВО/ОЕ = 3.
На примере одной задачи мы рассмотрели несколько способов ее решения. Кроме приведенных решений можно отыскать и другие, более сложные, чем геометрические способы. Решение этой задачи можно выполнить с помощью теоремы косинусов, формулы Герона для площади треугольника, составления и решения системы из трех уравнений. Однако, можно найти наиболее простое и красивое решение с помощью дополнительных построений.
Остались вопросы? Не знаете, как решать задачи по геометрии?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Геометрия. Урок 7. Практические задачи по геометрии
Содержание страницы:
Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника соответственно пропорциональны сторонам другого треугольника.
Подобие треугольников обозначается значком «∼». Запишем подобие двух треугольников:
△ABC∼△A1B1C1Соответственные стороны двух подобных треугольников – это стороны, которые лежат напротив равных углов.

Пары равных углов:
∠A и ∠A1
∠B и ∠B1
∠C и ∠C1
Пары соответственных сторон:
BC и B1C1
AC и A1C1
AB и A1B1
Представьте себе, что на смартфоне или планшете вы открыли изображение треугольника. Вы захотели получше его рассмотреть и увеличили изображение. Сам треугольник увеличился, но его пропорции сохранились (он не сплюснулся, не вытянулся, просто стал больше). Вот такие два треугольника: исходный и увеличенный будут подобными. Масштаб увеличенной картинки изменился в k. Это число k будет являться коэффициентом подобия этих треугольников.
Коэффициент подобия k это число, равное отношению соответственных сторон подобных треугольников.

k=A1B1AB=A1C1AC=B1C1BC
- Если стороны большего треугольника относить к сторонам меньшего треугольника, то коэффициент подобия k>1.
- Если стороны меньшего треугольника относить к сторонам большего треугольника, то коэффициент подобия k<1.
Отношение периметров подобных треугольников равно коэффициенту подобия.
P△A1B1C1P△ABC=k
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S△A1B1C1S△ABC=k2
Первый признак подобия треугольников (по двум углам)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

∠A=∠A1∠B=∠B1|⇒△ABC∼△A1B1C1
Второй признак подобия треугольников (по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

∠A=∠A1A1B1AB=A1C1AC=k|⇒△ABC∼△A1B1C1
Третий признак подобия треугольников (по трём сторонам)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

A1B1AB=A1C1AC=B1C1BC=k⇒△ABC∼△A1B1C1
В задании 17 ОГЭ встречаются задачи, в которых необходимо найти угол между часовой и минутной стрелкой. Давайте разберёмся, как их решать.
Часовой циферблат – это окружность.
Градусная мера всей окружности равна 360°.
Стрелки – стороны центральных углов.
На окружности 60 маленьких делений и 12 больших.
Каждое маленькое деление отсекает от окружности дугу, градусная мера которой равна 360°60=6°.
Каждое большое деление отсекает от окружности дугу, градусная мера которой равна 360°12=30°.
Можно рассуждать, что одна большая дуга содержит пять маленьких, то есть её градусная мера равна 6°⋅5=30°.

В задании 17 ОГЭ встречаются задачи, в которых дано колесо со спицами и требуется определить либо угол между соседними спицами (если дано количество спиц), либо количество спиц (если дан угол между соседними спицами). Будем разбираться, как такие задачи решать.
Пусть у нас есть колесо, в котором n спиц. Тогда эти спицы образуют n равных центральных углов α.

Формула, которая связывает количество спиц и угол между двумя соседними:
α⋅n=360°
В задаче данного типа дана лестница, состоящая из n ступенек. Каждая ступенька характеризуется своей высотой (вертикальный отрезок) и длиной (горизонтальный отрезок). Сама лестница характеризуется своей длиной (отрезок AC), высотой (отрезок BC) и отрезком AB.

Высота всей лестницы – количество ступенек, умноженное на высоту одной ступеньки. Длина всей лестницы – количество ступенек, умноженное на длину одной ступеньки. Для нахождения длины лестницы необходимо применить теорему Пифагора.
Теоретический и практический материал по нахождению площадей треугольников и четырехугольников можно найти в уроках 3 и 4 модуля геометрия.
Перейти по ссылкам:
epmat.ru
Геометрические задачи ЕГЭ с решениями
Автор Сергей Валерьевич
Суббота, Сентябрь 3, 2016
В данной статье разобраны решения геометрических задач, встречающихся в вариантах профильного ЕГЭ по математике. Всего таких задач 5: 3 из первой части и 2 из второй. По крайней мере, такой расклад был на момент написания статьи. Представленные материалы будут полезны тем, кто только начал подготовку к предстоящему экзамену. Здесь вы найдёте геометрические задачи ЕГЭ с решениями, снабжёнными подробными и понятными комментариями от профессионального репетитора по математике. Представлен также видеоразбор решений каждого задания.
Задачи представлены под номерами, под которыми они числятся в вариантах профильного ЕГЭ по математике.
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.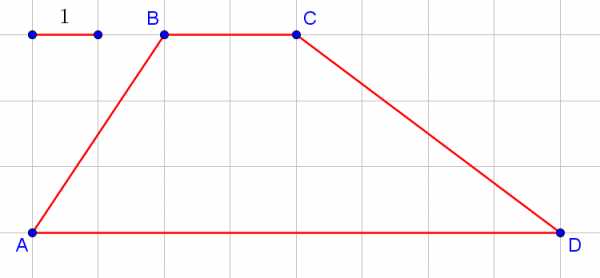 |
Даже если вы забыли формулу площадь трапеции на экзамене, не спешите отчаиваться. Вы всегда может решить задачу проще, чем вас научили в школе. В данном случае можно просто посчитать площадь по клеточкам:

Искомая площадь равна половине площади синего прямоугольника, плюс площади зелёного прямоугольника, плюс половина площади красного прямоугольника. Итого, получаем .
Задача 6. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции. |
По-хорошему, рисунок здесь не нужен. Поскольку в трапецию вписана окружность, то суммы противоположных сторон равны. Следовательно, сумма оснований равна 8, а полусумма и, соответственно, средняя линия трапеции равны 4.
| Задача 8. Площадь полной поверхности конуса равна 35. Сечение конуса плоскостью, проведенной параллельно основанию конуса, делит его высоту в отношении 3:2, если считать от вершины. Вычислите площадь полной поверхности полученного отсечённого конуса.
|
Все линейные размеры малого конуса в раз отличаются от линейных размеров большого конуса. Следовательно, квадратичные размеры (площадь поверхности) малого конуса в раз отличаются от квадратичных размеров большого конуса. То есть искомая площадь полной поверхности отсечённого конуса равна .
yourtutor.info
Техника поиска решений репетитором задач по геометрии
Если Вы регулярно просматриваете решения задач по математике в тех или иных источниках, то, безусловно, обращали внимание на их декларационный характер. То есть последовательность шагов просто сообщается и не разъясняется, почему она именно такая и, самое главное, как до нее догадаться обычному школьнику. При индивидуальном подходе к обучению ситуация, как правило, не улучшается. Приглашенный репетитор по математике попросту повторяет Вашему ребенку то, что написано в книжках. При таком формате работы ценность репетитора неуклонно снижается, ибо на ОГЭ/ЕГЭ обязательно подвернется какая-нибудь незнакомая задача. Кроме того при желании можно и самостоятельно прочесть кучу решений, добиваясь в итоге (с той или иной скоростью) определенного уровня знаний. Конечно, большинство школьников и этого сделать не могут. Им нужен руководитель и проверяющий в одном лице, а также привычные «инфраструктурные условия», в которых привычно вести учебную деятельность: четкое расписание и план освоения предмета, ведение тетрадей, вопросы и ответы и т.д. Но если уж говорить о репетиторе по математике как о максимальном средстве борьбы за знания и развитие, то стоит остановиться на методах обучения поиску решений.
Такое обучение под силу только профессионалу с большой буквы. Мыслительную механику чрезвычайно сложно описывать словами. Одна размытая ориентировка и ученик запутается. Глубокий анализ порой неоднозначно воспринимается и упирается в законы мироздания, но все же попытаемся разобраться в принципах на примере нескольких геометрических задач. Предположим, что ученик знает теорию и не испытывает проблем с реализацией простейших логических операций.
Пример, на котором репетитору легко показать технику поиска

Два равнобедренных треугольника ABC и DBC склеены общим основанием BC. Докажите перпендикулярность прямых BC и AD.
Прежде всего, репетитору важно научить ребенка правильно «брать старт» в решении, а для этого требуется понять, какие факторы влияют на отрезок AD и как вообще можно придти к перпендикулярности. Допустим, что ответ получен: надо придти к углу 90 градусов. Как? Перебираем в голове все известные в 7 классе приемы, теоремы и определения, связанные прямыми углами. Их не так много: 1) определение высоты 2) непосредственный поиск угла через вычисления или через уравнение. Напрягаем мозги. Вычисления нереальны – нет никаких значений в градусах. Для уравнений желательно иметь равные углы, которые можно было бы обозначить одной буквой «икс», либо иметь несколько связующих условий. А у нас только есть вертикальные и смежные углы. Значит надо либо доказывать, что смежные углы AОC и DОC равны, либо брать теорему о высоте, а ей нужен равнобедренный треугольник с медианой, либо биссектрисой. Это в свою очередь потребует объяснить то, что равны отрезки, или равны углы. То есть в любой случае надо получить какие-нибудь равные элементы рисунка. Откуда их взять? Нужно помнить о том, что в 7 классе 80% задач решается через равные треугольники. Вот и возникает с подачи репетитора по математике главный вопрос для старта: «Какие треугольники рассмотреть?»
На старт, внимание, марш
Как правило, ученики видят по рисунку равенство ABО и ACО и зависают над ними. В чем принципиальная ошибка? В разрезании верхнего треугольника на интересующие нас части участвует линия AD, положение которой зависит от точки D. Если в рассмотренных треугольниках не будет вершины D – мы получим произвольное разрезание на части, которое не гарантирует нам их равенство, поэтому доказательство зайдет в тупик. Аналогичная история и с нижней парой треугольников. Здесь уже тупиком будет выброс точки A. Получается, что в паре искомых треугольников должны участвовать обе точки A и D, а значит AD — сторона хотя бы одного из треугольников.
У нас имеется только два треугольника со стороной AD, подозрительно похожих на равные: ABD и ACD. Вот мы и вышли на старт. Любой хорошист укажет репетитору по математике на третий признак в обосновании их равенства.
Далее собираем урожай с нашего поиска – любые соответствующие элементы в треугольниках равны. Какие взять? Помним о том, что нам нужны либо отрезки, либо углы. И то, и другое есть. Например, BO=CO или угол BAD равен углу CAD. В первом случае мы имеем медиану AO, во втором – биссектрису AO. А тогда AO – высота.
«Ясновидение» по математике
Как Вы видите, никакого ясновидения со стороны репетитора. Все действия подкрепляются целесообразностью шагов и логически продиктованы ситуацией. Умению «вскрывать» математику можно и нужно учить, с раннего возраста на систематических занятиях, начиная с подобных простых примеров. В последние годы я резко снизил на своих занятиях процент деклараций решений. Все чаще открываю ученику сам процесс размышлений, озвучивая свои мысли. Говорю: «Если был я не был репетитором и учился математике на твоем месте, то размышлял бы следующим образом …». И начинаю подробно описывать все этапы поиска, вместе с возможными тупиковыми ходами и даже ошибками, то есть ровно так, я должен размышлять обычный человек. Постепенно ученик проникается идеями и каким-то волшебным образом начинает чувствовать математику интуитивно. В каждом человеке живет некое разумное начало, надо только до него достучаться и заставить работать во благо получения знаний. Что я и делаю на своих уроках в Строгино.
С уважением, Колпаков А.Н. Репетитор. Москва.
Метки: Методики для репетиторов, Примеры объяснений, Репетиторам по математике
ankolpakov.ru
Как решать задачи по геометрии: практические советы и рекомендации
Как решать задачи по геометрии? Многие учащиеся задаются этим вопросом на протяжении многих лет. Иногда даже сам предмет вызывает страх и отвращение из-за непонимания отдельных тем. Потом бывает очень сложно преодолеть неприязнь к геометрии и снова с заинтересованностью посещать уроки.
В чем причина
Во многом все зависит от того, как преподаватель объясняет свой предмет. Если учитель сможет заинтересовать учеников, дальше дело пойдет по накатанной, и каждый урок будет захватывающим. Дети даже будут оставаться на переменке, чтобы успеть решить как можно больше задач.
Если вам плохо объясняли этот предмет или есть еще какие-то причины, по которым у вас совершенно не получается вникнуть в тему, эта статья поможет разобраться.

Как научиться решать задачи по геометрии?
Для начала нужно понять, что за один день вы вряд ли далеко продвинетесь в своих знаниях, так что настраивайтесь на длительный процесс обучения.
Также нужно определиться с целью. Если вам нужно просто решить задачу по геометрии, чтобы не получить плохую оценку за контрольную работу, достаточно лишь выучить определенную тему и потренироваться в практических аспектах.
Что делать?
Возьмите учебник и пролистайте последние несколько параграфов, которые вы изучили. Постарайтесь вникнуть в информацию, поймите, что от этого зависит то, как будут оценены ваши знания. Теперь можете взять листочек и изучить несколько задач, обязательно смотрите в текст учебника и пытайтесь понять алгоритм решения.
Если что-то не получается, обратитесь к решебнику, который выпущен специально под ваш учебник. Только не списывайте абсолютно все, старайтесь понять, как решать задачи по геометрии.
Вспомните, о чем говорил преподаватель на занятиях, возможно, какая-то информация окажется полезной.
Не стоит пренебрегать и человеческим фактором. Хорошо знающие предмет школьники или студенты не откажут вам в помощи. Некоторые из них могут объяснить гораздо доходчивее преподавателей.
А тем, кто решил не просто разобраться в отдельных темах, а научиться решать задачи и как орешки их щелкать, нужно основательно потрудиться.

Во-первых, главное – это мотивировать себя на дальнейшие занятия. Бывает так, что вопрос о том, как научиться решать задачи по геометрии, встает лишь один раз, а потом начинается просто списывание примеров из интернета. Так делать крайне нежелательно.
Развивайте усидчивость. Посмотреть в решебник намного проще, разумеется, но подумайте, какое наслаждение вы испытаете, когда самостоятельно решите сложную задачку. Поэтому лучше лишние полчаса посидеть за учебником, чем стараться списать побыстрее чье-то решение.
Может быть, геометрия вам понадобится для будущей профессии. Тогда тем более не стоит откладывать дело в долгий ящик, нужно приниматься за задачи прямо сейчас.

Во-вторых, практика, и только она, поможет вам стать на шаг ближе к своей цели!
Заведите привычку узнавать что-то новое каждый день. Просто старайтесь с утра решать одну задачу, а потом проверяйте по ключам ее правильность. Позже заметите, что с каждым днем процесс идет все быстрее и качественнее.
Самое главное здесь – не сдаваться и не обращать внимания на мелкие трудности. Если вы включите в распорядок дня этот совет, то вопрос о том, как решать задачи по геометрии, отпадет сам собой.
В-третьих, обращайтесь за помощью к знакомым.
Не бойтесь в школе лишний раз поднять руку и выйти к доске, чтобы решить сложный пример, который никто не отважился постичь. Даже если что-то пойдет не так, и вам не удастся сделать задание, ничего страшного в этом нет. Преподаватель объяснит решение примера и даже похвалит вас за смелость. Также это неплохой способ показать свои знания одноклассникам.
Ребята могут помочь с выполнением заданий, когда узнают, что вы настроены серьезно в изучении предмета.

Не вешаем нос!
Не отчаивайтесь, если никто не откликнулся на вашу просьбу. Всегда можно обратиться за помощью к репетитору, который точно объяснит, как решить задачу по геометрии. Даже при ограничении в денежных средствах хорошим выходом станут занятия по скайпу, которые ничем не хуже уроков, проходящих при личной встрече.
Вот и все советы. Будем надеяться, что вы все-таки поняли, как решать задачи по геометрии. В любом случае старайтесь применять эти методы на практике, и вы осуществите задуманное!
fb.ru
Примеры по геометрии 7 класс. | Геометрия
Примеры по геометрии 7 класс. | Геометрия — просто!Добрый день!
Сегодня мы с вами разберём несколько примеров по геометрии 7 класса, которые даются в ОГЭ-2015.
Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре.
Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.
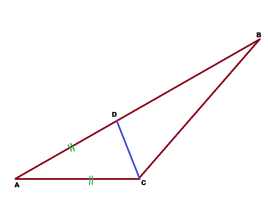
 Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
 Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.
 Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних углов, не смежных с ним, т.е. сумме углов В и ВАК.
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54°.
 Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний угол в треугольнике равен
180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
 Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Решение: Угол ВОМ смежный углу СОМ и равен 180-119 = 61°.
Угол СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним.
Отсюда, угол ОВМ равен 90-61 = 29°.
А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°.
Значит, угол А равен 90 — 29 = 61°.
Ответ: угол А равен 61°.
На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.
Вам так же будет интересно:
Оставить комментарий
geometriyaprosto.ru
Задачи по геометрии
Дата: января 10, 2019 Автор: baluНа прямой AG отмечен отрезок AB длиной 2a. Из точек А и B перпендикулярно прямой AG по разные её стороны проведены отрезки AC и BD, причем AC=BD=b.
Из точки C и точки D проведены отрезки СM и DM так, что CM пересекает AB, обозначим точку их пересечения через K, DM пересекает прямую AG вне отрезка AB, обозначим точку их пересечения через E, причем угол MKB равен углу MEB. Найти геометрическое место точек M (составить уравнение кривой).
На сколько частей делит пространство лента Мёбиуса бесконечной ширины?
Дата: декабря 5, 2017 Автор: baluС помощью циркуля и линейки построить окружность, касающуюся двух данных окружностей, причем одной из них в данной точке.
Дата: апреля 21, 2017 Автор: baluГород имеет форму круга радиуса R. По всей площади города магазины торговой сети расположены равномерно. Расстояние от центра города до распределительного центра сети равно r. Найти среднее расстояние от распределительного центра до магазина сети.
Дата: апреля 15, 2017 Автор: baluКвадрат ABCD и правильный пятиугольник BEFGC имеют общую сторону BC. Вершины квадрата A и D лежат вне пятиугольника. Найти угол между отрезками AG и FD.
http://blog.kknop.com/2017/03/blog-post.html
Дата: марта 5, 2017 Автор: baluМетеорит падает на сферическую Землю радиусом R под углом ѳ к отвесу со скоростью V и упруго (без потери энергии) отскакивает. В каком случае (при каком соотношении параметров) метеорит, попрыгав. вернётся в точку падения? (Допустим, g не меняется с высотой).
Е.Скляревский
Дата: февраля 26, 2017 Автор: baluПроведем прямую AQ. С центром в точке O на ней построим окружность диаметром 3 так, что |AO|=1,5 (красная окружность). Отметим на прямой точку K так, что |AK|=1. Проведем через точку K под произвольным углом прямую, пересекающую окружность в точках G и E. Очевидно, в любом случае |GK|*|GE|=2. Построим с центром на прямой AQ окружность диаметром 17, касающуюся первой окружности в точке A (фиолетовая окружность). Пусть прямая GE пересекает вторую окружность в точках B и C. Очевидно, в любом случае |BK|*|CK|=16. Вращая прямую GE вокруг точки K можно найти такое ее положение, что |KE|=2^(1/3), а |GK|=2^(2/3), т.е. |GK|=|EK|^2. Вращая прямую BC вокруг точки K можно найти такое ее положение, что |KC|=2*2^(1/3), а |GE|=4*2^(2/3). С помощью гомотетии с коэффициентом 2 и центром в точке K построим синюю окружность. Точка C пересечения синей и фиолетовой окружности будет обладать замечательным свойством |KE|=|CK|=2^(1/3). Проверим наше построение с помощью окружности, полученной с помощью гомотетии с центром в точке K и коэффициентом 4 (зеленая окружность). На её пересечении с фиолетовой окружностью находится точка B такая, что |BK|=4*|GK|=4*2^(2/3), т.е. |BK|=|CK|^2. Легко убедиться, что точки B, K и E лежат на одной прямой.
Однако, почему не ликуют древние греки? Ведь мы построили отрезок, равный кубическому корню из 2, решив таким образом задачу об удвоении куба! Возможно, в наше построение вкралась ошибка? Найдите её.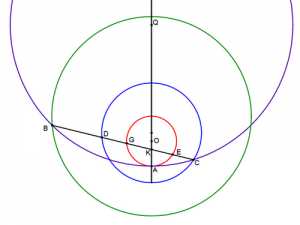
Дана окружность с отмеченной на ней точкой А и точка В вне окружности. Найти параболу (построив ее директрису) с фокусом в точке В, касающуюся окружности в точке А.
Дата: ноября 9, 2016 Автор: baluВ просторном зале, стоя на полу, вы видите на полу отражение светильника, подвешенного под потолком. Пусть ваш рост h, высота потолка H, расстояние между вами и точкой на полу под светильником S. Вы двигаетесь в направлении светильника со скоростью V. С какой скоростью вы догоняете отражение светильника? С какой скоростью отражение светильника движется к точке под светильником?
Дата: июня 30, 2016 Автор: baluНа плоскости построены два отрезка длинами a и b. С помощью циркуля и двух прямых углов (например, в виде школьных угольников) построить отрезки длинами c и d — два средних пропорциональных отрезка к данным a и b, т.е. чтобы выполнялось соотношение a:c = c:d = d:b.
Дата: июня 26, 2016 Автор: baluИз точки, где плоскость, наклоненная под углом α к горизонту, сопрягается с горизонтальной плоскостью, выстрелили шариком под углом β к горизонту. Каким должен быть угол β, чтобы шарик, отскочив от наклонной плоскости, вернулся в точку выстрела?
Е. Скляревский
Дата: июня 23, 2016 Автор: baluДве окружности равного радиуса с центрами в точках О и О1 имеют общую хорду АВ. Из точки О проведен в произвольном направлении отрезок, пересекающий хорду AB, затем пересекающий окружность O в точке С и окружность О1 в точке D. Пусть М – середина отрезка CD. Доказать (или опровергнуть), что геометрическим местом точек M является дуга окружности.
Дана окружность и в ней центральный острый угол альфа. Построить угол, равный третьей части альфа, используя циркуль и линейку, на которой можно делать засечки, так, чтобы все построения не выходили за пределы окружности.
Дата: января 2, 2016 Автор: baluВ горизонтальной плите имеются два параллельных желоба полукруглого сечения радиуса R. Центры полукружий находятся в плоскости поверхности плиты на расстоянии L
Дата: января 2, 2016 Автор: baluНа наклонной плоскости два ткача придерживают два совершенно одинаковых рулона ткани. Одновременно отпускают. Один рулон скатывается со склона как цельный цилиндр, а второй во время спуска разматывается. Скольжение отсутствует. Какой рулон скатится быстрее?
geom.uz


 Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.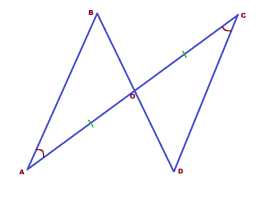 Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны. Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС. Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С. Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.