Решение линейных уравнений с модулем
Уравнение — это равенство, содержащее букву, значение которой надо найти.Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
Рассмотрим уравнение вида |kx + b| = c, где x — неизвестная величина, k ≠ 0.Если c<0, то уравнение не имеет решений, так как модуль числа не может принимать отрицательные значения.
Если c = 0, то уравнение принимает вид kx + b = 0. Оно имеет единственный корень x = −b/k.
Если же c>0, то выражение под знаком модуля может принимать значения c и −c. Значит, возможны два случая:kx + b = c, то есть x = (c−b) / k.
kx + b = −c, то есть x=( −c−b) / k
Рассмотрим теперь уравнение вида |ax+b| = |cx+d|, где a, b, c, d – некоторые числа.
Решите уравнение: |2x−5| = |3x+6|.
РЕШЕНИЕ
Согласно определению модуля, указанное равенство возможно в следующих случаях:
2x−5 = 3x+6, то есть x=−11;
2x−5 = −(3x+6), то есть x=−0,2.
Ответ. {−11;−0,2}.
Алгоритм решения уравнений с модулями:1. Найти в уравнении все выражения, содержащиеся под знаком модуля.
2. Найти, при каких значениях переменной они обращаются в нуль.
3. Разбить найденными значениями числовую прямую на непересекающиеся промежутки.
4. Определить для каждого числового промежутка, чему равно значение каждого модуля: самому выражению, содержащемуся под знаком модуля, или противоположному ему.
5. Для каждого числового промежутка записать и решить исходное уравнение без знаков модуля.
6. Оставить только те решения, которые соответствуют числовому промежутку, и записать их в ответе.
ПРИМЕР 2
Решите уравнение: |x−3| − |2x+4| = 5.
Точки −2 и 3 разбивают ось на три непересекающихся промежутка: (−∞;−2) (−∞;−2), [−2;3) [−2;3), [3;∞)[3;∞). Решим уравнение на каждом из них:
Решение уравнения
−(x−3) + (2x+4) = 5
x+7=5
x =−2
Учет промежутка
x∈∅
Второй Промежуток x∈[−2;3)Решение уравнения
−(x−3) − (2x+4) = 5
−3x−1 = 5
x = −2
Учет промежутка
x = −2
Третий Промежуток x∈[3;∞)
Решение уравнения
(x−3) − (2x+4) = 5
−x−7 = 5
x = −12
Учет промежутка
x∈∅
Ответ: x = −2
ПРИМЕР 3
Решите уравнение |x−1| = 3.Решение задачи
Если |x−1| = 3, то x−1 = ±3. То есть либо x = 3+1 = 4, либо x = −3+1 = −2.
ПРИМЕР 4
Найдите количество целых решений уравнения 5x+|5x| = 0 на отрезке [−2015;2015].Решение задачи
Заметим, то так как модуль — величина неотрицательная, а из уравнения получаем, что 5x ≤ 0 или x ≤ 0. Поэтому |5x| =−5x и уравнение примет вид 5x−5x = 0. Следовательно, x≤0 — это множество решений уравнения. Тогда количество целых решений на отрезке [−2015;2015] равно 2016.
ПРИМЕР 5
Решите уравнение |||x|−2|−2|=2. В ответе укажите произведение всех решений.Решение задачи
Будем последовательно раскрывать каждый из модулей и разбирать каждый случай отдельно.
По условию |||x|−2|−2|=2, поэтому ||x|−2|−2=−2 или ||x|−2|−2=2.
Случай 1:
||x|−2|−2=−2.
Из первого равенства: ||x|−2|=0, тогда |x|−2=0 или |x|=2. Следовательно, x=−2 или x=2.
Случай 2:
||x|−2|−2=2.
Из второго равенства: ||x|−2|=4. Значит, случай разбивается на два: |x|−2=4 или |x|−2=−4.
Случай 2(а):
|x|−2=4.
Из первого равенства: |x|=6. Следовательно, x=−6 или x=6.
Случай 2(б):
|x|−2=−4.
Из второго равенства: |x|=−2. Но модуль есть величина неотрицательная, поэтому в этом случае решений нет.
В итоге мы получили 4 различных решения — −2,2,−6,6. Их произведение равно 144.
spishy-u-antoshki.ru
РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ
Решение уравнений
с модулем.
МБОУ СОШ №46
учитель математики
Дряева Минат Георгиевна.
Г. Владикавказ
2014г.
Слайд 1 . Основные этапы урока:
1⁰. Мотивация учения.
2⁰. Ознакомление учащихся с целями и задачами.
3⁰. Повторение теоретических знаний по данной теме.
4⁰. Устная работа с элементами исследования.
5⁰. Совместная работа учителя и учащихся.
6⁰. Минута отдыха.
7⁰. Нестандартные приемы решения уравнений с модулем.
8⁰. Разноуровневая самостоятельная работа.
9⁰. Постановка домашнего задания.
10⁰. Подведение итогов урока.
Слайд 2 . Во всем дойти до самой сути.
Цель: Обобщение и систематизация, расширение и углубление знаний.
Задачи: 1. Проанализировать различные способы решения уравнений с модулем.
2. Сформировать навык решения различных типов уравнений с модулем.
3. Заинтересовать учащихся в изучении данной темы.
Тип урока: Урок совершенствования знаний (с элементами исследования).
Оборудование: Компьютер, мультимедийный проектор, интерактивная доска,
опорные конспекты, оценочные листы.
Ход урока:
1⁰. Мотивация учения.
Подарите улыбки друг другу ,
Веселыми будьте всегда,
И этим добьётесь удачи,
Успехов во всем и всегда.
А успех нам сегодня так необходим. Прочтите эпиграф , так как он тесно связан с темой нашего урока.
Тема «Решение уравнений с модулем» выбрана мною не случайно. Она является одной из самых сложных тем. В школьной программе ей, на мой взгляд, уделяется недостаточно внимания, не разобраны в системе методы и приемы решения задач с модулем. У многих модуль вызывает страх. Есть замечательные задания с модулем, у которых своя специфика. Попробуем разобрать некоторые из них.
2⁰. Ознакомление учащихся с целями и задачами.
Сегодня мы с вами повторим основные типы уравнений с модулем и проанализируем различные способы их решения.
Слайд 3 . 3⁰. Сначала повторим и систематизируем теоретические знания по данной теме.
Учитель: Дайте определение модуля или абсолютной величины.
Учащиеся :|x|= .
Учитель: Назовите основные свойства модуля.
Учащиеся: |a|0,
|a|²= a²
|a*b|=|a|*|b|,
|a/b|=|a|/|b|, b≠0
Слайд 4. 4⁰. Устная работа с элементами исследования.
Постановка проблемы:
Для каждого из уравнений указать стрелками соответствующий тип уравнения.
Уравнения
Тип уравнения
Способ решения
|3x-5|=2
|4-3x|=-1
|9-5x|=|7x-5|
|11-3x|=3-2x
2x²+3|x-1|+2=0
|3-x|+|x-5|=1
² = 16
|f(x)| = a, a- const
Если а>0, то
Если а=0, то f(x) = 0
Если а < 0, то корней нет.
|f(x)| = g(x)
|f(x)| = |g(x)|
|f1(x)|+ |f₂(x) | +…+|fn(x)|=g(x)
Метод интервалов.
Ответы учащихся:
— Уравнение 1 можно решить, используя определение модуля.
— Уравнение 2 не имеет решений т.к. модуль – величина неотрицательная.
С помощью рассуждений сделаем выводы:
Если |f(x)| = |g(x)| f²(x) – g² (x) = (f (x) – g(x)) (f(x) + g(x)) = 0
Таким образом, указали способ решения уравнения 3 .
Если |f(x)| = g(x), то g(x)
По определению модуля
Таким образом, указали способ решения уравнения 4.
— Как же можно решить уравнение 5?
— Рассмотрим два случая т.е. воспользуемся определением модуля.
x-10 и x-1<0.
— Уравнение 7 разве имеет отношение к теме «Модуль»?
— Да, т.к. по свойству корней ² = |x|, и получим уравнение, содержащее модуль.
— А как решить уравнение 6?
— Методом интервалов.
5⁰. Совместная работа учителя и учащихся
Осторожно! Простая задача!
Учиться плавать можно по-разному. Например, сразу броситься в глубокое место, или начать с «лягушатника». Так обстоит дело и в решении сложных задач. Мы пойдем по второму пути, не забывая при этом, что захлебнуться можно и в ванной.
(решение уравнений у доски и в тетрадях).
Пример 1⁰.
|x-3| = 11
Пример 2⁰.
|2x-5| = x-1
Ответ: 2;4
Пример 3⁰.
|x+3| = |2x-1|
Ответ: -2/3;4
Слайд 6. Пример 4⁰.
|x²-1|+|x²-4|=3.
Воспользуемся методом интервалов. Для этого удобно пользоваться алгоритмом.
(см. опорный конспект).
x²-1=0, x= ±1,
x²-4=0, x= ±2.
Слайд 7.
Ответ: Ø.
Ответ: -2x<-1
Ответ: x=-1
Ответ: 1x<2
Ответ: x=2
Решив совокупность данных систем, получим:
Ответ: [-2;-1] U {-1} U [1;2) U {2} или [-2;-1] U [1;2]
Этот метод является универсальным методом решения уравнений всех видов, но иногда оказывается не самым рациональным.
Мы проанализировали различные типы уравнений, решаемые с помощью равносильных преобразований.
Слайд 8. Более наглядную картину дает графическое исследование данного уравнения.
Для построения графика функции y=|x²-1|+|x²-4| воспользуемся схемой знаков на рисунке.
y=|x²-1|+|x²-4|=
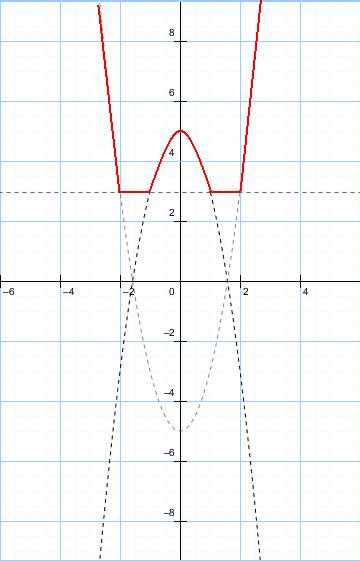
2) Проведем прямую y=3.
По графику очевидно, что графики левой и правой части совпадают (пересекаются) на множестве
и
Ответ: [-2;-1] U [1;2]
Мы еще вернемся к данному уравнению.
Слайд 9. 6⁰. Минута отдыха.
— Примем царственную позу. Спина прямая.
— Три раза вдохнем.
— Помассажируем кончики пальцев каждой руки.
— Поставим указательный палец на точку между бровями и массажируем три раза. — Роняем руки.
— Трясем кистями.
— Стряхиваем воду с пальцев.
— Поднимаем и опускаем плечи.
— Твердые и мягкие руки.
— Мельница.
Продолжаем урок.
7⁰. Рассмотрим нестандартные приемы решения уравнений с модулями.
«Умный гору обойдет».
Зачастую по закону зловредности короткое решение более замаскировано, чем длинное. В тех случаях, когда выбранный путь решения сопряжен с большими техническими сложностями, бывает полезно еще раз проанализировать условие задачи, попытаться найти ее конкретные особенности, позволяющие обнаружить нетрадиционную идею.
Слайд 10. Когда модуль можно не раскрывать.
Решение некоторых уравнений может значительно сократить знание ряда свойств модуля:
1. |a|+|b| = a+b a≥0, b≥0;
2. |a| + |b| = |a+b| ab≥0;
3. |a| + |b| = |a-b| ab≤0;
4. |a| — |b| = |a-b| b (a-b) ≥0;
5. |a| — |b| = |a+b| b(a+b) ≤0
(доказательство рассмотрим на факультативных занятиях).
Вернемся к примеру 4:
|x²-1|+|x²-4|=3.
-Посмотрите внимательно. Что вы заметили?
Кто-нибудь из учеников обязательно заметит, что
(x²-1) – (x²-4) = 3 т.е. выполняется условие |a|+|b| = |a-b|.
Применив свойство 3, получим неравенство
(x²-1) (x²-4)≤0.
Решим его методом интервалов.
x²-1=0, x₁=1, x₂=-1
x²-4=0, x₃=2, x₄=-2.
x є [-2;-1] U [1;2].
Ответ: [-2;-1] U [1;2].
Данное уравнение решили тремя способами. Какой способ
— Самый трудный?
— Самый простой?
Пример 5.
|x-2|+|2-3x|=2|x|
Заметим, что |x-2|+|2-3x| = |(x-2)+(2-3x)|=|-2x|=2|x|, т.е. выполняется условие
|a|+|b|=|a+b|.
Используя свойство 2, будем иметь неравенство:
(x-2)(2-3x)≥0,
(x-2)(x-2/3)≤0.
x є [2/3;2]
Ответ: [2/3;2].
Слайд 11. Пример 6.
|x²+6|-|x²-x+6|=|x|
Имеем: |x²+6|-|x²-x+6|=|(x²+6)-(x²-x+6)|=|x|, т.е выполняется условие
|a|-|b|=|a-b|.
Использую свойство 4, получим неравенство x (x²-x+6)≥0
Решив его, получим x≥0.
Ответ: [0;+∞)
8⁰. Разноуровневая самостоятельная работа.
Учащимся выдаются опорные конспекты, рабочие листы и оценочные листы.
(Индивидуальная консультация учителя по мере возникновения затруднений).
Слайд 12. Самостоятельная работа.
1 – ый уровень.
Цель: закрепить умение решать простейшие уравнения, содержащие модули, вида: |f(x)|=a, a –const
Вариант-1
Решите уравнения:
|x|=5 (1 балл)
x= ±5,
Ответ: x₁=-5, x₂=5.
|x+3|=-2 (1 балл)
Нет корней, т.к. модуль – величина неотрицательная.
Ответ: нет корней.
|x²-4|= 0 (1 балл)
x²-4=0
x=±2
Ответ: x₁=-2; x₂=2.
Вариант-2
Решите уравнение:
|x|=8 (1 балл)
x=±8
Ответ: x₁=-8; x₂=8.2 .|x+7|=-3 (1 балл)
Нет корней, т.к. модуль – величина неотрицательная.
Ответ: нет корней.
3. |x²-9|=0 (1 балл)
x²-9=0,
x=±3
Ответ: x₁=-3; x₂=3.
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
2 – ой уровень
Цель: закрепить навыки решения уравнений вида:
|f(x)|= g(x) и |f(x)|=|g(x)|.
Вариант – 1
|2x-3|=6-x (2 балла)
Ответ: x₁=-3, x₂=3
|x-2|=|2x-1| (2 балла)
Ответ: x₁=-1, x₂=1.
Вариант – 2
Решение уравнений.
|3x-4|=2x-6 (2 балла)
Ответ: нет корней.
|2x-3|=|x-3| (2 балла)
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
Ответ: x₁=0, x₂=2
3 – ий уровень
Цель: сформировать навык решения уравнений с использованием свойств модуля.
Вариант -1
Решите уравнение:
|2x+5|+|x-3|= 3x+2 (3 балла)
Заметим, что
(2x+5)+(x-3)=3x+2, т.е. выполняется условие
|a|+|b|=a+b
По свойству 1, имеем:
x≥3
Ответ: x≥3
2 .Используя свойства, освободитесь от знака модуля .
|x²+x-2|+|x-3|=x²+1 ( 3 балла)
Заметим, что
(x²+x-2)-(x-3)=x²+1, т.е. выполняется условие
|a|+|b|=|a-b|.
Используя свойство 3, получим неравенство
(x²+x-2)(x-3)≤0
Ответ: (x²+x-2)(x-3)≤0.
Вариант – 2
1. Решите уравнение
|x-2|+|x+2|=2|x| (3 балла)
т.к. |x-2|+|x+2|=|(x-2)+(x+2)| = 2|x|, то выполняется условие |a|+|b|= |a+b|.
Используя свойство 2, получим неравенство (x-2)(x+2)≥0
xє (-∞;-2]U [2;+∞)
Ответ: (-∞;-2]U [2;+∞)
2. Используя свойства, освободитесь от знака модуля
|4x²-1|-|x²-4|=|5x²-5| ( 3 балла)
Заметим, что |4x²-1|-|x²-4|=|4x²-1+x²-4| = |5x²-5| т.е. выполняется условие
| a|-|b|=|a+b|.
Используя свойство 5, получим неравенство:
(x²-4)(5x²-5)≤0. Ответ: (x²-4)(5x²-5)≤0.
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
Молодцы! Вы прошли 3 уровня усвоения материала. Посчитайте количество набранных баллов.
Если вы набрали от 11 до 13 баллов, то получаете оценку «5».
Если вы набрали от 7 до 10 баллов, то получаете оценку «4».
Если вы набрали от 5 до 6 баллов, то получаете оценку «3».
Сдайте оценочные листы учителю.
Слайд 13. 9⁰. Домашнее задание:
Трем группам (по 2-3 учащихся в каждой) подготовить презентации по темам:
1) Использование понятия расстояния при решении уравнений с модулем.
2) «Вложенные модули»
3) «Красивейшие уравнения».
Остальным — решить уравнения:
1. |x-5|=1
2. |x²-3x|=2x-4
3. |x-2|=|2x-1|
4. |2x-1|+|x|= -5
5. |x-4|+|x-5|=|2x-9|
6. |x²-9|+|x²-4x+3|=0
7. |x-1|+|x-2|=x+3
Слайд 14. 10⁰. Подведение итогов урока:
— Какие типы уравнений мы повторили на уроке?
— какие методы решения уравнений с модулем вы можете выделить?
— какой способ самый эффективный?
— решение каких уравнений вам показалось сложным?
— чему надо уделить особое внимание?
Слайд 15. Используемая литература:
И.И. Гайдуков. «Абсолютная величина»
Изд. «Просвещение», 1968 г.
2) Г.И.Ковалева. «Тренировочные тематические задания повышенной сложности».
Изд. «Учитель», 2009 г.
3) С.В.Кравцев. «Методы решения задач по алгебре».
Изд. «Экзамен», 2005 г.
4) П.И. Горнштейн, А.Г. Мерзляк. «Экзамен по математике и его подводные рифы».
Изд. «Илекса», 2004 г.
Пояснительная записка.
Данный урок проводится в 11-ом классе в 4-ой четверти при повторении. Урок рассчитан на класс, в котором есть учащиеся с математическими способностями.
infourok.ru
Решение уравнений с модулем в курсе алгебры 7-8 классов
Методические рекомендации по теме: «Решение уравнений с модулем в курсе математики 7-8 класса»
Автор: Давыдова Наталья Александровна,
учитель математики МОУ «Лицей №4»
города Саратова.
Введение.
Практически каждый учитель знает, какие проблемы вызывают у учащихся задания, содержащие модуль. Это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах.
Выбор темы обусловлен тем, что, во-первых, задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах и на экзаменах, во-вторых, это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсе высшей математики. Так в математическом анализе понятие абсолютной величины числа используется при определении основных понятий: предела, ограниченности функции и других. В теории приближенных вычислений употребляется понятие абсолютной погрешности. В механике, в геометрии изучается понятие вектора, одной из характеристик которого служит его длина (модуль вектора).
Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе — 4 часа).
Исходя из всего вышесказанного, учителю необходимо находить разнообразные методические приемы, использовать различные подходы и методы в обучении решению задач с модулем. Разнообразие методов будет способствовать сознательному усвоению математических знаний, вовлечению учащихся в творческую деятельность, а также решению ряда методических задач, встающих перед учителем в процессе обучения, в частности, реализации внутрипредметных связей (алгебра-геометрия), расширению области использования графиков, повышению графической культуры учеников.
Указанные обстоятельства обусловили выбор темы творческой работы. Цель работы: показать необходимость более глубокого рассмотрения темы «Решение уравнений с модулем» в школьной программе; разработать методические рекомендации по использованию различных методов при решении задач с модулем.
§1. Основные способы, используемые при решении уравнений, содержащих модуль.
Напомним основные понятия, используемые в данной теме. Уравнением с одной переменной называют равенство, содержащее переменную. Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство. Решить уравнение – значит, найти все его корни или доказать, что корней нет. Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.
При решении уравнений, содержащих знак абсолютной величины, мы будем о
educontest.net
Проект «Решение уравнений с модулем»
«Решение уравнений с модулем»
Математика
Учебный проект
Тема проекта «Решение уравнений с модулем»
Участники проекта: обучающиеся 11 класса Тюхтин Евгений и Яковлева Светлана
Руководитель проекта: учитель математики Олейникова Г.М.
Содержание:
Автор проекта
Портфолио проекта
Предмет
Участники проекта
Краткая аннотация проекта
Вопросы, направляющие проект
Публикация учителя
Пример продукта проектной деятельности
Критерии оценки проекта
10.Материалы по сопровождению и поддержке проектной деятельности.
Краткая аннотация проекта
Проект может быть использован при изучении темы «Решение уравнений с модулем» в 10-11 классах. Применяться при подготовке к единому государственному экзамену.
Данная работа позволяет увидеть различные способы решения уравнений с модулем: по определению, возведение в квадрат, с помощью числовой прямой.
Данный проект позволит обучающимся расширить объем знаний по данной теме, развивать специальные и общеучебные умения.
Цель проекта:
Развивать коммуникативные способности обучающихся, навыки исследовательской работы.
Учить обобщать и систематизировать, применять на практике.
Что участие в проекте даст его участникам
После завершения проекта обучающиеся смогут
— знать определение модуля, решать уравнения с модулем по определению;
— решать уравнения с модулем способом возведения в квадрат обеих частей уравнения;
— уметь решать уравнения с модулем, использую числовую ось, определяя знак модуля на промежутках;
— уметь раскрывать знак модуля;
— научаться работать по алгоритму;
— приобретут навыки, умения ориентироваться в информационной среде.
Этапы проекта:
Планирование проекта.
Поиск информации.
Оформление материалов исследования.
Защита проекта.
Рефлексия.
Ход проекта.
Подготовительный этап:
Обсуждение темы проекта
Подбор литературы.
Основной этап:
Подбор материала
Последовательность подачи материала
Обсуждение форм представления работы
Заключительный этап:
Презентация работы.
Подведение итогов, оценивание.
Вопросы, направляющие проект
Основополагающий вопрос
Способы решения уравнений с модулем?
Проблемные вопросы
Можно ли решить уравнение с модулем используя определение модуля?
Можно ли решить уравнение с модулем используя другие способы решения?
Можно ли составить алгоритмы решения уравнения с модулем?
Учебные вопросы
Публикации учителя
Буклет
Публикации обучающихся
Презентация обучающихся:
«Решение уравнений с модулем по определению модуля»
«Решение уравнений с модулем способом возведения в квадрат»
«Решение уравнений с модулем с использованием числовой оси»
Наглядность
Карточки с заданиями
Алгоритм решения
Критерии оценки проекта
Самостоятельность работы над проектом
Актуальность и значимость темы
Полнота раскрытия темы
Оригинальность решения проблемы
Презентация содержания проекта
Использование средств наглядности, технические средства
Ответы и вопросы
Оформление проекта
Материалы по сопровождению и поддержке проектной деятельности:
С.М. Никольский «Алгебра и начала математического анализа» изд. Просвещение 2009 г
Р.Б. Райхмист «Задачник по математике» изд. «Московский лицей» Москва 2003 г.
Е.Е. Калугина «Уравнения, содержащие знак модуля» изд. «Илекса» Москва 2010 г.
infourok.ru
Конспект урока по математике «Различные способы решения уравнений с модулями»
МБОУ «СОШ № 20 им. В. Митты с углубленным изучением отдельных предметов»
Урок математики для 8 класса
(углубленное изучение математики)
по теме « Различные способы решения
уравнений с модулями».
.
Учитель математики: Судеркина Маргарита Владимировна
МБОУ «СОШ № 20 им. В. Митты с углубленным изучением отдельных предметов»
г.Новочебоксарск Чувашской Республики.
План урока:
Вступительное слово учителя.
Повторение ранее изученного.
1.Фронтальный опрос.
2. Математический диктант с последовательной проверкой.
3.Индивидуальная работа с последовательной проверкой.
Физкультминутка.
Изучение новой темы.
Закрепление изученного. Работа по вариантам.
Решение уравнений, сводящихся к уравнениям с модулями. ГИА 2010.
Подведение итогов.
Домашняя работа.
Цели и задачи:
Отработать навыки решений уравнений с модулем;
Рассмотреть некоторые новые методы решения уравнений с модулем;
Развивать внимательность, логическое мышление, самостоятельность и творческий подход к решению уравнений с модулем.
«Знание – самое превосходное из владений.
Все стремятся к нему,
само же оно не приходит».
Ал — Бируни
Задания, содержащие модуль-это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах.
Задачи, связанные с абсолютными величинами, часто встречаются и на математических олимпиадах. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсе высшей математики.
II. Повторение изученного.
Блиц-опрос.
Определение уравнения с одной переменной?
Что такое корень уравнения?
Что значит решить уравнение?
Какие уравнения называются уравнениями с модулем?
Математический диктант с последующей проверкой. Выставление оценок.
начала координат до точки, выраженное
в единичных отрезках.
положителен.
всегда отрицателен.
иногда положителен, иногда
отрицателен.
положителен
Модуль О всегда равен О.
Модуль О всегда положителен.
Модуль любого числа всегда равен
числу, противоположному данному
всегда равен числу, противопо-
ложному данному отрицательному
числу.
Если |х|= 17, то х = 17.
Если | -х | =27, то х = 27.
Если |с | = -12, то с = 12.
Индивидуальная работа. Работа у доски.
Решить уравнения:
Ответ: 5,5; -4,5.
Рассмотрим два случая.
1) Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то уравнение примет вид :
|2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо
2х-1= -10. Откуда х1=5,5;х2= -4,5
2)Если значение выражения под знаком модуля отрицательно, то по определению имеем уравнение
|2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.
Найдем точки перемены знака модуля из условий:
х – 1 = 0 и х + 2 = 0
х = 1 х = — 2
Рассмотрим данное уравнение
на промежутках
(- ∞;-2], [-2;1] , [1;+∞)
На промежутке (- ∞; -2 ]
│ х – 1 │ = – х + 1 ; │ х + 2 │ = – х – 2
значит, уравнение имеет вид:
( – х + 1 ) – 2∙ (– х – 2) = 0
– х + 1 +2х + 4 = 0
х + 5 = 0
х = – 5
— 5 принадлежит (- ∞; -2 ]
На промежутке [-2;1]
│ х – 1 │ = – х + 1; │ х + 2 │ = х + 2
значит, уравнение имеет вид:
( – х + 1 ) – 2∙ ( х + 2) = 0
– х + 1– 2х – 4 = 0
– 3х – 3 = 0
3х = – 3
х = — 1
— 1 принадлежит промежутку [-2;1]
На промежутке [1;+∞)
│ х – 1 │ = х – 1; │ х + 2 │ = х + 2
значит, уравнение имеет вид:
( х – 1 ) – 2∙ ( х + 2) = 0
х – 1 – 2х – 4 = 0
– х – 5 = 0
х = – 5
— 5 не принадлежит [1;+∞)
Ответ: -5;-1.
Построим график функции у = │x — 1│- 2 │x + 2│
Найдем точки перемены знака модуля из условий:
х – 1 = 0 и х + 2 = 0
х = 1 х = — 2
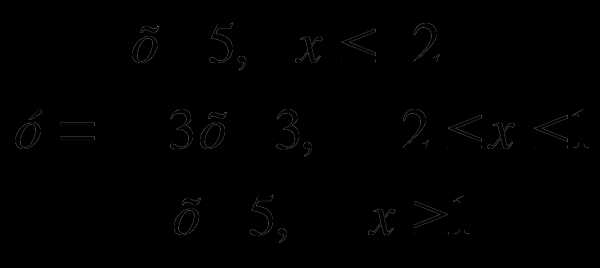
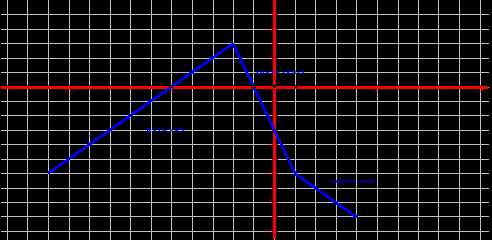
Ответ: -5;-1
III. Физкультминутка.
IV. Изучение новой темы.
1.Основные способы решения уравнений с модулями:
Метод последовательного раскрытия модуля.
Раскрытие модуля на интервалах.
«Сравнение модулей»
«Сравнение квадратов»
Графический способ.
2. Опорная информация. Свойства модуля, на котором основаны способы «Сравнение модулей»,
«Сравнение квадратов»:
|а|2=а2
Если |а|=|в|, то а=в или а=-в;
Если а2=в2 , то а=в или а=-в;
Если |а|=|в|, то а2=в2
|cx|=c|x|, c-неотриц.
3.Решение уравнения │x — 1│- 2 │x + 2│= 0
«Сравнение модулей»,
│x — 1│= 2 │x + 2│
│x — 1│= │2x + 4│
Модули равны у чисел равных или противоположных
х – 1 = 2х + 4 или х – 1 = – 2х – 4
– х = 5 3х = – 3
х = – 5 х = — 1
Ответ:-5,-1
«Сравнение квадратов»
│x — 1│= 2 │x + 2│
Учитывая, что если |а|=|в|, то а2=в2
Получим:
(x — 1) 2 = (2 (x + 2)) 2
используем формулы квадратов суммы и разности двучлена
х2– 2х + 1 = 4 ∙ (х2 + 4х + 4)
х2– 2х + 1 = 4х2 + 16х + 16
3х2 + 18х + 15=0
х2 + 6х + 5=0
по теореме, обратной теореме Виета, найдем корни
х = – 5 х = — 1 Ответ: -5,-1
V. Закрепление изученного.
Решите уравнения:
Вариант1
Сравнение модулей
|х2-8х+5|=|х2-5|
Решение:
Учитывая соотношение( если |а|=|в|, то а=в или а=-в), получим:
х2-8х+5=х2-5 или х2-8х+5=-х2+5
х=1,25 х=0 или х=4.
Ответ: 1,25; 0; 4.
Вариант2
Сравнение квадратов
|х+3|=|х-5|.
Решение:
В силу соотношения (если |а|=|в|, то а2=в2) получаем:
(х+3)2=(х-5)2;
х2+6х+9= х2-10х+25;
х=1.
Ответ:1.
VI. Решение уравнений, сводящихся к уравнениям с модулями.
1.
Р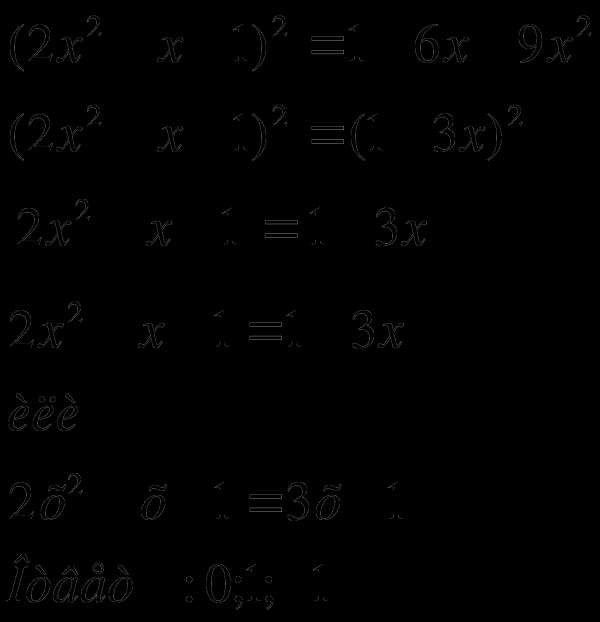
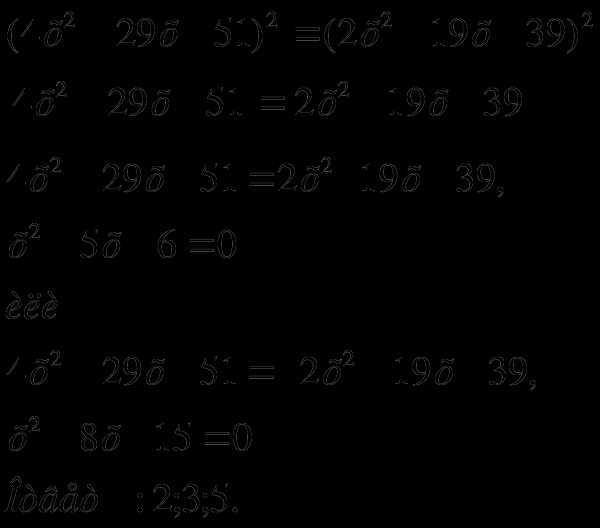 ешение:
ешение:
2. Решите уравнение.
Решение:
VI. Подведение итогов
.
infourok.ru
«Решение уравнений с модулем».

Алгебраическое и графическое решение уравнений, содержащих модули
2017 г.
 0; lаl= о, если а = 0; -а, если а «
0; lаl= о, если а = 0; -а, если а «
Определение.
Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна –а, если а меньше нуля:
а, если а0;
lаl= о, если а = 0;
-а, если а

Способы решения уравнений, содержащих модуль.

Решим аналитически и графически уравнение:
lх-2l=3

Аналитическое решение
1-й способ
 0 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 . Таким образом, получаем, либо х-2=3, либо х-2=-3. Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1. «
0 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 . Таким образом, получаем, либо х-2=3, либо х-2=-3. Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1. «
Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т.е. х-20 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 .
Таким образом, получаем, либо х-2=3, либо
х-2=-3.
Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1.

2-й способ
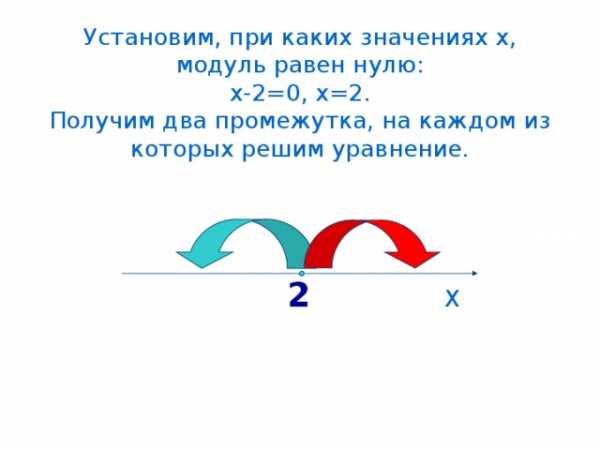
Установим, при каких значениях х, модуль равен нулю: х-2=0, х=2. Получим два промежутка, на каждом из которых решим уравнение. 2 Х

Получим две смешанные системы: х2, -(х-2)=3 х-2=3 Решим каждую систему: х2 х=-1 х=5 Ответ: х 1 =-1, х 2 =5.

Графическое решение.
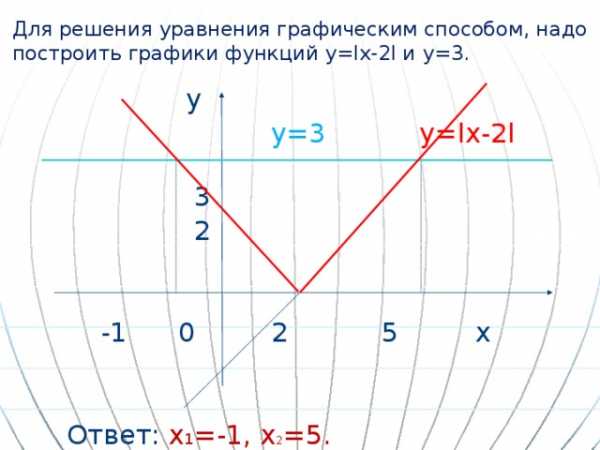
Для решения уравнения графическим способом, надо построить графики функций у=lх-2l и у=3.
у
у=3 у=lх-2l
3
2
-1 0 2 5 х
Ответ: х 1 =-1, х 2 =5.

Решим аналитически и графически уравнение
1+lхl=0,5

Аналитическое решение:
1+lхl=0,5,
lхl=0,5-1,
lхl=-0,5
Ответ: решений нет.

Графическое решение:
Преобразуем уравнение 1+ lхl=0,5.
Получим lхl=-0,5
Графиком функции у= lхl являются лучи – биссектрисы 1-го и 2-го координатных углов.
Графиком функции у=-0,5 является прямая, параллельная оси ох и проходящая через точку -0,5 на оси оу.
Ответ: решений нет.

Решение при помощи зависимостей между числами а и b, их модулями и квадратами этих чисел.
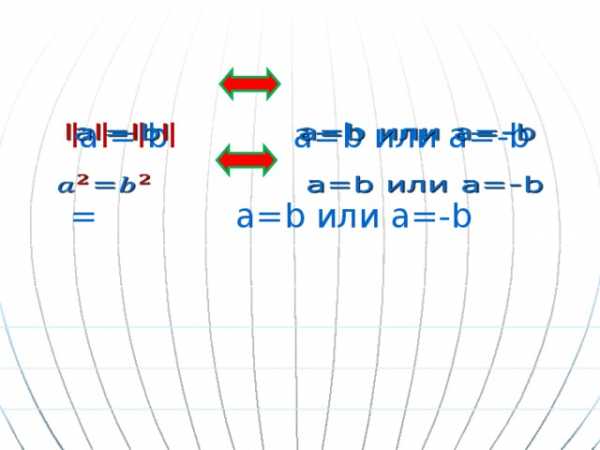
l a l = l b l a=b или a=-b = a=b или a=-b

Решим уравнение l x+1 l = l 2x-5 l двумя различными способами.
1-й способ
Учитывая первое соотношение получим:
Х+1=2х-5 х+1=-2х+5
х-2х=-5-1 х+2х=5-1
-х=-6 3х=4
х=6 х=1
Таким образом корни уравнения: х 1 =6, х 2 = 1

2-й способ В силу второго соотношения имеем = Решив это уравнение, получим: х 1 = 1 , х 2 =6 Ответ: х 1 = 1 , х 2 =6

Графики простейших функций, содержащих знак абсолютной величины
Алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n+1 прямолинейного отрезка.
Тогда график может быть построен по n+2 точками, n из которых представляют собой корни внутримодульных выражений, ещё одна произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя – с абсциссой, большей большего из этих корней.
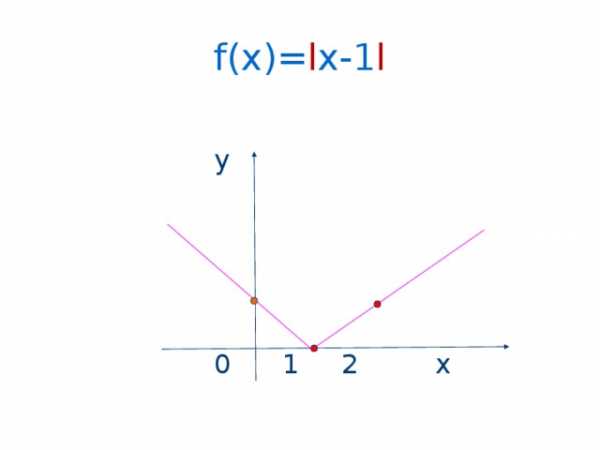
f(x)= l x-1 l
у
0 1 2 х
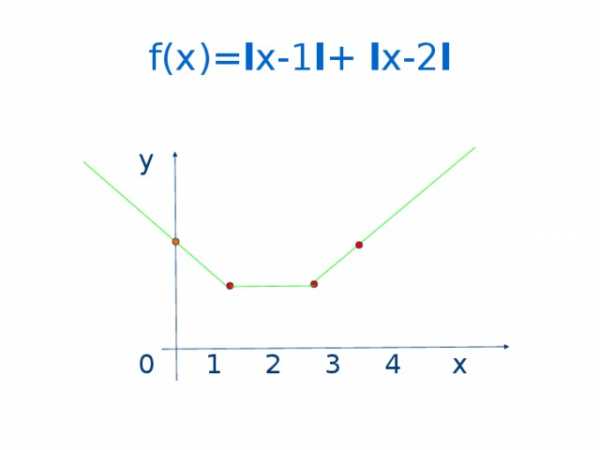
f(x)= l x-1 l + l x-2 l
у
0 1 2 3 4 х
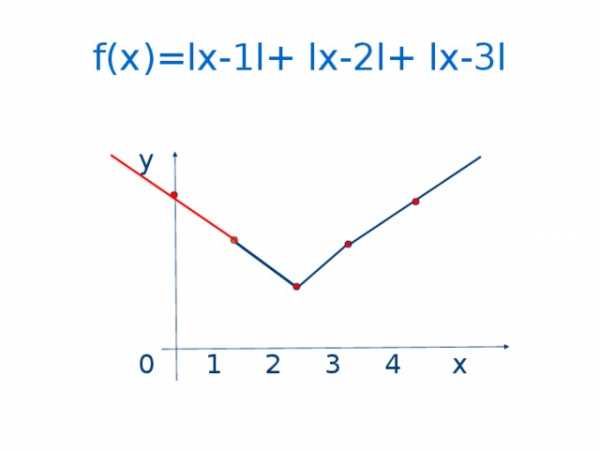
f(x)=lx-1l+ lx-2l+ lx-3l
у
0 1 2 3 4 х
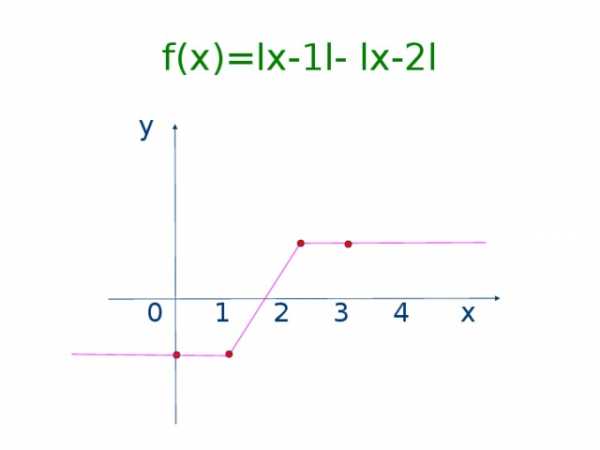
f(x)=lx-1l- lx-2l
у
0 1 2 3 4 х

конец
videouroki.net
