Площадь квадрата формула 3 класс правило: Как найти площадь квадрата, формула

Площадь прямоугольника / Площадь / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Площадь
5. Площадь прямоугольника

 Теорема

Площадь прямоугольника равна произведению его смежных сторон.

Доказательство

Дано: прямоугольник, , — стороны, — площадь.

Доказать: .

Доказательство:

Достроим прямоугольник до квадрата со стороной .

Площадь квадрата равна квадрату его стороны, значит, площадь полученного квадрата равна .

При этом полученный квадрат составлен из данного прямоугольника с площадью , равного ему прямоугольника с площадью (равные многоугольники имеют равные площади) и двух квадратов с площадями и (т.к. площадь квадрата равна квадрату его стороны). По свойству 2⁰площадей, которое говорит о том, что если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, получаем:

или , откуда .

Теорема доказана.

Советуем посмотреть:

Понятие площади многоугольника

Площадь квадрата

Площадь параллелограмма

Площадь треугольника

Площадь трапеции

Теорема Пифагора

Теорема, обратная теореме Пифагора

Формула Герона

Площадь

Правило встречается в следующих упражнениях:

7 класс

Задание 452, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 453, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 454, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 455, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 456, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 457, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 467, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 951, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1236, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Что такое Площадей правило | значение термина

Физика — конспекты, новости, репетиторы » Техническая энциклопедия

Опубликовано 03. 03.2020

Площадей правило это
в аэродинамике: волновое сопротивление тонкого тела при нулевой подъёмной силе в транс- или сверхзвуковом потоке идеального газа определяется распределением S(x) площади поперечного сечения тела вдоль его оси и имеет то же значение, что и сопротивление тела вращения (эквивалентного тела), имеющего аналогичное распределение Sэкв(x) площади поперечного сечения. Волновое сопротивление тонкого тела можно вычислить, применяя импульсов теорему к некоторой (контрольной) поверхности, расположенной на достаточно большом расстоянии от него.
На таких расстояниях поле течения, согласно правилу эквивалентности (см. Тонкого тела теория), не зависит от формы поперечного сечения тела, является осесимметричным и соответствует полю течения около эквивалентного тела вращения. Это и приводит в результате к П. п.

П. п. справедливо и для комбинации тонкого тела (фюзеляжа) с тонким крылом малого удлинения. При трансзвуковом обтекании это следует из принципа эквивалентности, который выполняется для конфигурации рассматриваемого типа, и Sэкв равна полной площади её поперечного сечения.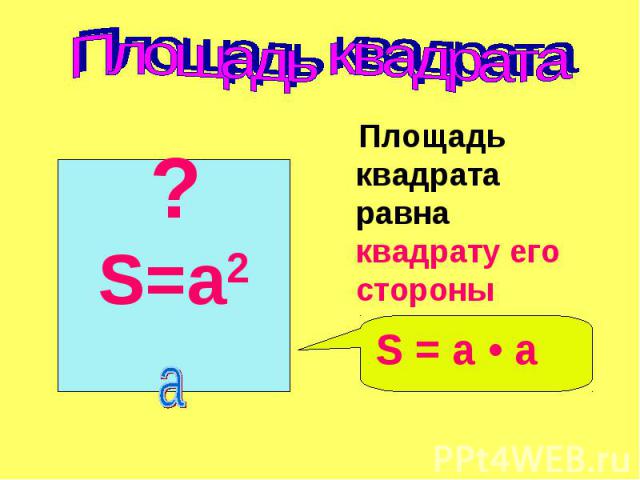 При сверхзвуковых скоростях Sэкв вычисляется несколько иначе. Например, в случае осесимметричного фюзеляжа она определяется суммой

Sэкв = Sф + Sкр,

где Sф — площадь поперечного сечения фюзеляжа, Sкр — площадь проекции на поперечную плоскость сечения крыла плоскостью, составляющей угол Маха (см. Маха конус) с направлением набегающего потока.

Тела вращения, обладающие минимальным волновым сопротивлением при различных условиях имеют достаточно плавные обводы (см. Осесимметричное течение). Тогда из П. п. следует, что волновое сопротивление можно уменьшить путём обеспечения по возможности более гладкого и близкого к оптимальному распределения площадей поперечного сечения. Например, для комбинации «крыло — фюзеляж» с этой целью в месте расположения крыла у фюзеляжа должно быть предусмотрено сужение, компенсирующее увеличение полной площади сечения за счёт крыла.

Экспериментальные данные подтверждают П. п. и оно успешно применяется при разработке компоновок летательных аппаратов для уменьшения их волнового сопротивления.

Источник: Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев. 1994.

№ 5.6. Периметр и площадь квадрата (дополнение)

3 класс. Математика. Площадь. Единицы измерения площади

Математика без Ху{2ae0ca1c6d1a3e9536eb80ee8693f50fcb1c31316243117074825f53da4b6b5d}!ни. Определенные интегралы, часть 3. Площадь фигуры.

СПЛИН — Романс [Клип]

Криволинейная трапеция и ее площадь. 11 класс.

Как находить площадь любой фигуры? Геометрия | Математика

5 класс, 19 урок, Единицы измерения площадей

Как сделать стильный и современный ремонт без дизайнера в 2022 году. Ремонт в новостройке цена.

Что такое площадь. Как найти площадь прямоугольника?

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | Математика

Электромеханические переходные процессы, правило площадей

5 класс, 18 урок, Площадь. Формула площади прямоугольника

Математика 3 класс (Урок№21 — Площадь. Способы сравнения фигур по площади. Единица площади — кв.см.)

Площадь. Единицы площади | Математика 3 класс #15 | Инфоурок

№ 9. Квадратные метры, сантиметры и т.д. (4 класс)

Длина окружности. Площадь круга. 6 класс.

Елена Ханга, Парфенюк, Кискин, Тарлецкий (Исторический Квиз-Стендап)

Математика 4 класс (Урок№13 — Единицы площади — квадратный километр, квадратный миллиметр.)

Математика 3 класс (Урок№22 — Площадь прямоугольника.)

КАК найти площадь трапеции? Геометрия 8 класс | Математика

Поделиться или сохранить к себе:

Нахождение объема и площади поверхности пирамиды (видео и практика)

Привет и добро пожаловать на это видео о пирамидах! В этом видео мы рассмотрим различные типы пирамид и способы расчета их объема и площади поверхности. Давайте узнаем о пирамидах!

Нельзя говорить о пирамидах, не упомянув самые известные пирамиды в мире, расположенные в Египте и построенные как усыпальницы египетских царей. Хотя пирамиды не совсем распространены, их форма настолько поразительна, что кажется, что они используются для того, чтобы сделать заявление, возможно, именно поэтому египетские цари использовали их в качестве своих гробниц. Лувр в Париже, который является крупнейшим художественным музеем в мире, также имеет форму пирамиды. Как видно из изображений египетских пирамид, 9Пирамида 0005 представляет собой трехмерную фигуру с треугольными сторонами, которые встречаются по краям и наверху, образуя вершину , и имеет многоугольник в качестве основания.

Многоугольное основание определяет тип пирамиды. Здесь вы видите пирамиду с треугольником в основании — треугольную пирамиду, пирамиду с прямоугольником в основании — прямоугольную пирамиду, а пирамиду с пятиугольником в основании — пятиугольную пирамиду. У нас также есть шестиугольные пирамиды и семиугольные пирамиды, и так далее.

Давайте на минутку вспомним, что означают объем и площадь поверхности трехмерной фигуры.

объем трехмерной фигуры является мерой того, сколько она может вместить, и измеряется в кубических единицах.

Площадь поверхности трехмерной фигуры является мерой общей площади, которую покрывает поверхность фигуры, и измеряется в квадратных единицах.

Прежде чем мы сможем вычислить объем и площадь поверхности пирамиды, мы должны знать разницу между высотой и наклонной высотой. высота пирамиды — длина перпендикуляра от вершины до основания, а наклонная высота — длина от вершины до середины нижнего края одной из треугольных граней.

Вот формулы объема и площади поверхности любой пирамиды.

\(V=\frac{1}{3}Bh\)
\(SA=B+\frac{1}{2}ps\)

 

Для расчета объема и площади поверхности любой пирамиды нам нужно B, который представляет площадь основания, и p, который представляет периметр основания. Важно отметить, что, поскольку основанием пирамиды может быть любой многоугольник, мы будем использовать наши предварительные знания о нахождении площади и периметра различных многоугольников для вычисления объема и площади поверхности пирамиды.

\(V=\frac{1}{3}Bh\)
\(SA=B+\frac{1}{2}ps\)

 

\(B\) = площадь основания
\( h\) = высота пирамиды
\(p\) = периметр основания
\(s\) = наклонная высота

Рассмотрим пример. {3}\) 9{3}\)

 

Тогда, если мы подставим это в калькулятор, мы получим, что это примерно равно 91,67 кубических сантиметров.

Но когда нам это понадобится в реальной жизни? Что ж, я рад, что вы спросили! Взгляните на следующий пример и попробуйте сами.

Крыша деревянного коттеджа имеет форму пирамиды с квадратным основанием. Длина сторон квадратного основания 22 фута, а высота треугольной грани 14 футов. Питер хочет покрасить крышу своего деревянного коттеджа и должен определить, сколько краски ему нужно купить. Предположим, что 1 пинта краски покрывает 400 квадратных футов. Сколько краски нужно купить Петру?

Крыша коттеджа не включает основание пирамиды. Следовательно, нам нужно только найти площадь 4-х треугольных граней. Это так называемая боковая зона. Таким образом, площадь боковой поверхности равна площади поверхности минус площадь основания. Итак, все, что нам нужно, это:

\(LA=\frac{1}{2}ps\)

 

Периметр нашего квадрата в 4 раза больше длины стороны.

\(LA=\frac{1}{2}(4\times 22)(14)\)

 

Что мы можем вставить в калькулятор, чтобы получить: 9{2}\)

 

Таким образом, нам потребуется 616 квадратных футов для покрытия.

Если 1 пинта краски покрывает 400 квадратных футов, нам нужно разделить 616 на 400, чтобы вычислить, сколько краски нам нужно. Итак:

\(616\div 400=1.54\)

 

Итак, Петру нужно будет купить 2 пинты краски, чтобы покрыть крышу коттеджа, потому что 1 пинту не хватит, и вы не сможете получить 0,54 пинты. Таким образом, 2 литра краски покроют всю крышу.

Надеюсь, это видео о нахождении объема и площади поверхности пирамиды было полезным! Спасибо за просмотр и удачной учебы!

Часто задаваемые вопросы

Q

Как найти объем пирамиды?

A

Чтобы найти объем пирамиды, мы умножаем площадь ее основания на высоту пирамиды и делим на \(3\). Выразим это произведение формулой \(V=\frac{1}{3}\times B\times h\), где \(B\) — площадь основания пирамиды, а \(h\) это его высота. 2\). 92)\times h\), где \(h\) — высота пирамиды.

Q

Как найти общую площадь поверхности пирамиды?

A

Чтобы найти общую площадь поверхности пирамиды, нам нужно сложить площади каждой стороны, включая основание. Для треугольных пирамид будет три боковых панели; для квадратных и прямоугольных пирамид их будет четыре; и так далее.

Q

Какова формула площади поверхности треугольной пирамиды?

A

Чтобы найти общую площадь поверхности, нам нужно сложить площади основания и трех других сторон. \(SA=B+\frac{1}{2}(P\times l)\), где \(B\) — площадь основания пирамиды, \(P\) — периметр основания, \(l\) — наклонная высота пирамиды. Мы можем найти \(B\), используя формулу \(\frac{1}{2}bh\) для площади треугольника. \(P\) можно легко определить, сложив длины сторон базового треугольника. Наклонную высоту \(l\) можно найти по теореме Пифагора, где \(l\) — длина гипотенузы.

Q

Какова общая площадь поверхности квадратной пирамиды?

A

Чтобы найти общую площадь поверхности квадратной пирамиды, мы суммируем площадь основания с площадью четырех сторон. Поскольку четыре боковые панели идентичны, нам просто нужно найти эту площадь один раз и умножить ее на четыре.

\(SA=A_{основание}+(4\times A_{сторона})\)
 
Пример. Найдите общую площадь поверхности квадратной пирамиды, длина сторон основания которой равна \(8\text{см}\) , а высота равна \(3\text{см}\). Начнем с вычисления площади поверхности основания. 92\).

Практические вопросы

Вопрос №1:

 
Вычислите площадь поверхности следующей квадратной пирамиды.

95 cm ²

100 cm ²

105 cm ²

110 cm ²

Show Answer

Answer:

The formula \(SA=B+\frac {1}{2}pl\) можно использовать для вычисления площади поверхности квадратной пирамиды.
\(B\) представляет собой площадь основания.
\(p\) представляет собой периметр основания.
\(l\) представляет наклонную высоту.
Когда в формулу подставляются соответствующие значения, \(SA=B+\frac{1}{2}pl\) становится \(SA=25+\frac{1}{2}(20)(8)\) что упрощается до 105 см ² . Площадь поверхности квадратной пирамиды равна 105 см ² .

Скрыть ответ

Вопрос №2:

 
Вычислите площадь поверхности следующей равносторонней треугольной пирамиды.

357 в ²

350 в ²

257 в ²

332 в ²

Покажите ответ

Ответ:

. к формуле квадратной пирамиды. Единственная разница возникает при определении площади базовой формы. Формула \(SA=B+\frac{1}{2}pl\) по-прежнему будет применяться, но B будет рассчитываться путем умножения \(\frac{1}{2}bh\). Это можно подставить в формулу для 92\).

Скрыть ответ

Вопрос №3:

 
Вычислите объем пирамиды.

2 670 в ³

3 670 в ³

4,670 в ³

5 670 в ³

Show

9030 8

95 9000 3

95 9000 3

95 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3

039. 1}{3}Bh\) можно использовать для вычисления объема пирамиды.
B представляет площадь базовой формы.
h представляет собой высоту пирамиды (не высоту наклона). Когда в формулу подставляются соответствующие значения, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(2{,}130)(27)\) что упрощается до \(V=5{,}670\). Объем пирамиды равен 5670 ³ .

Скрыть ответ

Вопрос № 4:

 
У Лео есть треугольная стеклянная пирамида, которую он надеется заполнить небольшим количеством пляжного песка. Во время своего отпуска во Флориде он собирает 6,5 см ^.3 песка. Треугольник в основании стеклянной пирамиды имеет площадь 5 см ² , а высота пирамиды 6 см. Если он соберет 6,5 см ³ песка, будет ли пирамида достаточно большой, чтобы вместить весь песок?

Да, пирамида достаточно большая

Нет, пирамида слишком маленькая.

Показать Ответ

Ответ:

Объем пирамиды с треугольным основанием можно рассчитать по формуле \(V=\frac{1}{3}Bh\), где B — площадь основания треугольника, а h — высота пирамиды. Когда B и h подключены, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(5)(6)\), что упрощает до \(V=10\). Объем пирамиды составляет 10 см ³ , что достаточно для 6,5 см ³ песка.

Скрыть ответ

Вопрос № 5:

 
Некоторые из первых эскизов парашютов Леонардо да Винчи имели форму пирамид с квадратным основанием. Для конструкции парашюта с прямоугольным основанием, длиной сторон шести футов и восьми футов и высотой семь футов, сколько воздуха будет захвачено пирамидой после ее полного развертывания?

112 ft ³

109 ft ³

115 ft ³

118 ft ³

Show Answer

Answer:

The formula \(V=\frac{ 1}{3}Bh\) можно использовать для вычисления объема пирамиды. B представляет площадь основания фигуры, а h представляет высоту пирамиды. Когда в формулу подставляются соответствующие значения, \(V=\frac{1}{3}Bh\) становится \(V=\frac{1}{3}(48)(7)\), что упрощается до \ (V=112\). Объем полностью развернутого парашюта составит 112 футов 9 дюймов.0329 3 .

Скрыть ответ

Площадь треугольника | Формула, правила, виды треугольников

Слово треугольник составлено из двух слов – « три », что означает три и «угол». Следовательно, треугольник можно определить как замкнутую фигуру, имеющую три вершины, три стороны и три угла. На следующем рисунке показан треугольник ABC:

Треугольник — это многоугольник, состоящий из трех ребер и трех вершин. Вершины соединяются вместе, образуя три стороны треугольника. Площадь, занимаемая этими тремя сторонами, называется площадью треугольника.

Формула для нахождения площади треугольника

Общая формула

Обычно площадь треугольника определяется как 1/2 x b x h

Площадь треугольника = 1/2 x b x h

, где b =

основание треугольника (или любую сторону треугольника), и  

H = высота треугольника от этого основания (или стороны)

На следующем рисунке показаны основание и высота треугольника

Приведенная выше формула применимо независимо от того, является ли треугольник разносторонним (у него разные стороны), равнобедренным треугольником (у которого две стороны равны) или равносторонним треугольником (у которого все стороны равны).

Давайте лучше разберемся с этим на примере. Предположим, у нас есть треугольник, одна сторона которого равна 6 см, а высота (высота) этого основания равна 8 см, как показано на следующем рисунке: b = 6 см и h = 8 см

Следовательно, площадь = 1/2 x 6 x 8 = 24 см сначала нужно понять, что мы подразумеваем под прямоугольным треугольником?

Треугольник называется прямоугольным, если один из углов треугольника прямой, то есть 90 ^o . Предположим, у нас есть треугольник ABC, где △ABC = 90 ^o . Тогда такой треугольник называется прямоугольным треугольником, который будет иметь форму, подобную рисунку ниже.

На изображении выше видно, что прямоугольный треугольник имеет определенную высоту в виде стороны AB, а сторона BC является его основанием. Следовательно, площадь прямоугольного треугольника можно рассчитать только по общей формуле, которая определяется как 9.0003

Площадь треугольника = 1/2 x b x h

, где b = основание треугольника, а h = высота треугольника от этого основания (или стороны)

До изучения площади равностороннего треугольника , мы должны сначала понять, что мы подразумеваем под равносторонним треугольником?

Треугольник называется равносторонним, если все его стороны равны. Кроме того, если в треугольнике все три стороны равны, то и три угла равны.

Площадь равностороннего треугольника можно рассчитать по приведенной выше общей формуле. Но можем ли мы вычислить площадь равностороннего треугольника, если нам известны все три стороны, но нет высоты? Давайте узнаем 9{2}}{4}} =\frac{\sqrt{3a}}{2}$ единиц

Следовательно, площадь ∆ABC = 1/2 x (основание x высота)

Площадь ∆ABC = 1/ 2 x BC x AD

Площадь ∆ABC = $(\frac{1}{2} \times a \times \frac{\sqrt{3a}}{2})$ кв. единиц

 =[ $\ frac{\sqrt{3}}{4}$ x (сторона) ² ] кв. единиц

Эта площадь равностороннего треугольника =[ $\frac{\sqrt{3}}{4}$ x ( сторона) ² ] кв. ед.

Прежде чем узнать о площади равнобедренного треугольника, мы должны сначала понять, что мы подразумеваем под равнобедренным треугольником?

Треугольник называется равнобедренным, если две его стороны равны. Если две стороны равны, то равны и углы, лежащие против этих сторон.

Например, в следующем треугольнике AB = AC. Следовательно, треугольник ∆ABC равнобедренный.

∠B = ∠C

Площадь равнобедренного треугольника можно рассчитать по общей формуле, как указано выше. Но можем ли мы вычислить площадь равнобедренного треугольника, если нам известны две равные стороны и основание? Давайте узнаем. 9{2}}$

Пример 1    

Площадь прямоугольного треугольника составляет 50 м2. Если одна из сторон равна 20 м, найдите высоту другой стороны.

Решение: В области прямоугольного треугольника, если одна сторона является основанием, то другая сторона является его высотой или высотой.

Нам дано, что одна из сторон равна 20 м. Пусть это будет основание (b) треугольника.

Мы знаем, что площадь треугольника = 1/2 x b x h

Площадь треугольника равна 50 м 9{2}}$

=  $\frac{1}{2} \times 6 \times \sqrt{25-\frac{1}{4}\times 36}$

=  $\frac{1}{ 2} \times 6 \times \sqrt{25-9}$

=  $\frac{1}{2}\times6\times\sqrt{16}$

= $\frac{1}{2}\ умножить на 6\раз\ 4$

= 12 см ²

Следовательно, площадь данного равнобедренного треугольника = 12 см ²

9019 в форме

8 треугольник с гипотенузой 100 м и стороной 60 м. найти площадь поля.

Решение : Чтобы найти площадь поля, нам нужно знать третью сторону треугольника. Нам дано, что гипотенуза поля 100 м с одной стороны равна 60 м. Это означает, что поле представляет собой прямоугольный треугольник. Теперь мы знаем, что в прямоугольном треугольнике один из углов треугольника равен 90 ^o , а стороны, образующие прямой угол, называются основанием и перпендикуляром, а третья сторона называется гипотенузой.

Следовательно, по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Следовательно,

Основание ² + Перпендикуляр ² = Гипотенуза ²

Теперь пусть заданная сторона будет основанием треугольника.

Это означает, что База (b) = 60 м. We have,

60 ² + Perpendicular ² = 100 ²

⇒ 3600 + Perpendicular ² = 10000

⇒ Perpendicular ² = 10000 – 3600 = 6400

⇒ Perpendicular ² = (80) ²

Следовательно, перпендикуляр = 80 м.

Теперь, когда мы знаем основание и перпендикуляр, площадь треугольника определяется как –

Площадь треугольника = 1/2 x b x h

Площадь треугольника = 1/2 x 60 x 80 м ²

 Площадь треугольника = 2400 м ²

Следовательно, площадь данного треугольника равна 2400 м ²

Пример 4     Основание треугольника вдвое меньше 5 единиц

высота. Если площадь 75 квадратных единиц, то каковы длина основания и высота?

Решение : Пусть высота треугольника равна «h». Нам известно, что основание треугольника на 5 единиц меньше, чем удвоенная высота. Это означает, что основание (b) треугольника будет:

b = 2h – 5

Теперь нам также известно, что площадь равна 75 квадратных единиц. Мы знаем, что площадь треугольника определяется по формуле:

Площадь треугольника = 1/2 x b x h

Это означает, что 1/2 x b x h = 75

Следовательно, b x h = 75 x 2 = 150

Подставляя полученные значения b и h в приведенную выше формулу, получаем:

(2h – 5) x h = 150

⇒ 2h ² – 5h = 150

⇒ 2h ^{03 –}

150 = 0

⇒ 2h ² – 20h + 15h – 150 = 0 (Решение квадратного уравнения)

⇒ (2h ² – 20h) + (15h – 150) = 0 ⇒ 1 ⇒ 9 ) + 15(h – 10) = 0

⇒ (2h + 15)(h – 10) = 0

⇒h = -15/2 или 10 единиц

Мы знаем, что высота треугольника не может быть отрицательной. . Поэтому значение -15/2 нельзя учитывать. Это оставляет нам единственное значение, равное 10. Следовательно, мы можем сказать, что h = 10

Теперь, когда мы знаем значение h, мы можем узнать значение b.

Следовательно,

b = 2h – 5

b = 2 x 10 – 5 = 15 единиц

Следовательно, высота треугольника равна 10 единицам, а основание треугольника равно 15 единицам.

Примечание. Здесь мы можем проверить, что полученное значение основания равно 15, что на 5 единиц меньше удвоенной высоты треугольника. Также, если мы подставим значения основания и высоты в формулу вычисления площади треугольника, мы получим площадь в 75 квадратных единиц, что показывает, что наше решение верное.

Пример 5    

Серене необходимо заказать штору для окна треугольной формы с основанием 6 футов и высотой 4 фута. Чему равна площадь тени?

Решение : Нам известно, что основание окна треугольной формы, для которого Серене нужно заказать штору, = 6 футов. для = 4 фута.

Требуется вычислить площадь этого оттенка. Так как жалюзи предназначены для окна треугольной формы, воспользуемся формулой расчета площади треугольника.

Имеем,

Площадь треугольника = 1/2 x b x h

Следовательно,

Площадь треугольника = 1/2 x 4 x 6

Площадь треугольника = 12 футов ²

900 , площадь тени = 12 футов ²

Пример 6    

Площадь треугольника равна площади квадрата, каждая сторона которого равна 60 метрам. Найдите сторону треугольника, высота которой равна 90 м.

Решение : Нам известно, что площадь треугольника равна площади квадрата, каждая сторона которого равна 60 метрам. Теперь мы знаем, что площадь квадрата определяется как:

Площадь квадрата = Сторона x Сторона

Следовательно,

Теперь, когда сторона квадрата равна 60 метрам, следовательно,

Площадь квадрата квадрат = 60 x 60 м ²

Площадь квадрата = 3600 м ²

Согласно вопросу, это также площадь треугольника. Следовательно,

Площадь треугольника = 3600 м ²

Теперь мы знаем, что

Площадь треугольника = 1/2 x b x h = 3600 м ²

Нам известно, что высота треугольника равна 90 метров. Следовательно, нам нужно найти основание треугольника.

Теперь, 1/2 x B x 90 = 3600 M ²

⇒ B x 90 = 3600 x 2 = 7200 M ²

⇒ B = 7200/90 = 80 M

Отсюда, базовая базовая треугольник = 80 м

Пример 7    

Найдите площадь равностороннего треугольника, каждая сторона которого равна 4 см.

Решение : Мы знаем, что площадь равностороннего треугольника равна:

Эта площадь равностороннего треугольника = [ $\frac{\sqrt{3}}{4}\times$ (сторона) ² ] квадратных единиц

Теперь сторона равностороннего треугольника равна 4 см. Подставив значение стороны в приведенную выше формулу, мы получим

 Площадь треугольника =  [ $\frac{\sqrt{3}}{4}\times$ 4 ² ]

=  $\sqrt{3}\times4=4\sqrt{3}$ см ²

Следовательно, площадь равностороннего треугольника со стороной 4 см = $4\sqrt{3} $  см ²

Пример 8    

Основание равнобедренного треугольника равно 12 см, а его периметр равен 32 см. найти площадь треугольника.

Решение : Нам дано, что

Основание равнобедренного треугольника = 12 см

Периметр треугольника = 32 см

Мы знаем, что периметр треугольника = Сумма всех его сторон

Поскольку периметр равен 32 см, а одна из сторон равна 12 см, поэтому пусть длина каждой из двух равных сторон равна «b ».

Следовательно, мы можем сказать, что

2b + 12 = 32

⇒ 2b = 32 – 12

⇒ 2b = 20

⇒ теперь b = 10 см

Следовательно, мы имеем равные стороны по 10 см каждый.

Итак, теперь имеем

Основание треугольника = 12 см 9{2}}$  

=  $\frac{1}{2}\times 12\times\sqrt{100-\frac{1}{4}\times144}$

=  $\frac{1}{2 }\times 12\times\sqrt{100-36}$

= $6\times\sqrt{64}$

= 6 x 8

 = 48 см ²

Следовательно, площадь данного равнобедренный треугольник = 48 см ²

Пример 9    

Найдите площадь в квадратных сантиметрах треугольника, основание которого равно 1,5 м, а высота = 0,8 м.