Онлайн-калькулятор расчета площади четырехугольника: по сторонам и тд
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
- Расчет площади
- 1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 3. Через полупериметр и радиус вписанной окружности
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
3. Через полупериметр и радиус вписанной окружности
Формула расчета
S = p ⋅ r
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Все формулы площади треугольника — найти онлайн с помощью калькулятора
{S = \dfrac{1}{2} \cdot a \cdot h}
Найти площадь
треугольникапрямоугольного треугольникаравнобедренного треугольникаравностороннего треугольника
Известные данные
через основание и высотучерез две стороны и угол между нимичерез сторону и два прилежащих углачерез радиус описанной окружности и 3 сторонычерез радиус вписанной окружности и 3 стороныпо формуле Герона
Сторона a
ммсмдммкмдюймы (in)футы (ft)
Высота h
ммсмдммкмдюймы (in)футы (ft)
Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
дюймы (in²)кв. футы (ft²)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
a — сторона треугольника
α и β — прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = \dfrac{a \cdot b \cdot c}{4 \cdot R}}
a, b и c — стороны треугольника
R — радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r \cdot \dfrac{a + b + c}{2}}
a, b и c — стороны треугольника
r — радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = \sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)}} {p= \dfrac{a+b+c}{2}}
a, b и c — стороны треугольника
p — полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).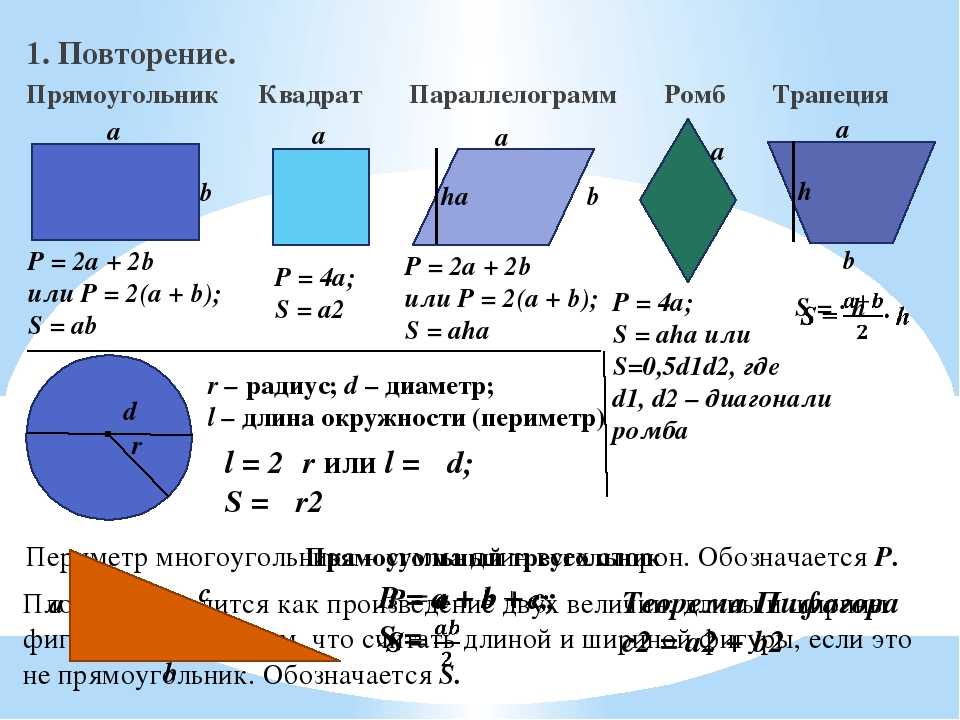 2 \cdot \tg{(\alpha)}}
2 \cdot \tg{(\alpha)}}
a — катет прямоугольного треугольника
α — прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r \cdot (r+c)}
r — радиус вписанной окружности
c — гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 \cdot c_2}
с1 и с2 — отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) \cdot (p-b)} {p= \dfrac{a+b+c}{2}}a, b и c — стороны треугольника
p — полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = \dfrac{1}{2} \cdot a \cdot \sqrt{c^2 — a^2}}
a — катет прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.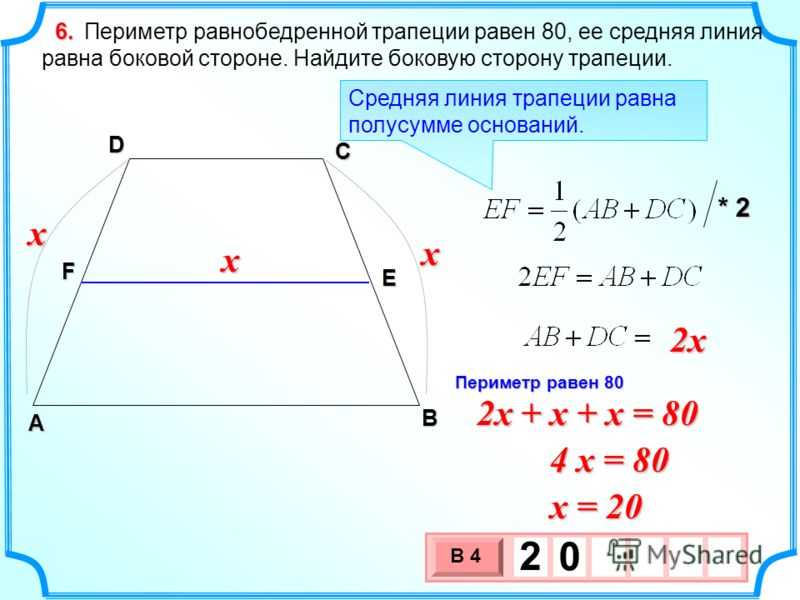 2
2
Проверка .
Площадь равнобедренного треугольника – формула, определение, примеры
Площадь равнобедренного треугольника – это пространство, заключенное между сторонами треугольника. Помимо общей формулы площади равнобедренного треугольника, которая равна половине произведения основания и высоты треугольника, для вычисления площади треугольников используются разные формулы в зависимости от их классификации по сторонам. Эти различные типы в зависимости от сторон приведены ниже:
- Равносторонний треугольник — треугольник, у которого все стороны равны.
- Равнобедренный треугольник — треугольник, у которого любые две стороны/углы равны.
- Разносторонний треугольник — треугольник, все стороны которого не равны.
Давайте подробно разберем площадь равнобедренного треугольника в следующем разделе.
| 1. | Какова площадь равнобедренного треугольника? |
2. | Формулы площади равнобедренного треугольника |
| 3. | Площадь равнобедренного треугольника с использованием сторон |
| 4. | Площадь равнобедренного треугольника по формуле Герона |
| 5. | Площадь равнобедренного треугольника с использованием тригонометрии (SAS и ASA) |
| 6. | Площадь равнобедренного прямоугольного треугольника |
| 7. | Часто задаваемые вопросы о площади равнобедренного треугольника |
Какова площадь равнобедренного треугольника?
Площадь равнобедренного треугольника — это полное пространство или область, занимаемая между сторонами равнобедренного треугольника в двумерном пространстве. Равнобедренный треугольник определяется как треугольник, у которого две равные стороны, что также означает два равных угла. Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются катетами , а угол между ними называется углом при вершине или углом при вершине.

- Сторона, противоположная углу при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр из угла при вершине делит пополам основание и угол при вершине.
Площадь равнобедренного треугольника выражается в квадратных единицах. Следовательно, некоторые единицы измерения, которые можно использовать для представления площади равнобедренного треугольника, это м 2 , см 2 , дюймов 2 , ярдов 2 и т. д.
Формулы площади равнобедренного треугольника
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2D. Площадь равнобедренного треугольника можно рассчитать разными способами на основе известных элементов равнобедренного треугольника. Общая основная формула, которую можно использовать для расчета площади равнобедренного треугольника с использованием высоты, задается как (1/2) × основание × высота 9.0003
В следующей таблице приведены различные формулы, которые можно использовать для расчета площади равнобедренного треугольника для другого набора известных параметров.
| Известные параметры данного равнобедренного треугольника | Формула для расчета площади (в квадратных единицах) |
| А = ½ × ширина × высота |
| A = ½[√(a 2 − b 2 ⁄4) × b] |
| А = ½ × b × a × sin(α) |
| А = [а 2 × sin (β/2) × sin (α)] |
| A = ½ × a 2 |
где,
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
- β = угол, противоположный основанию
Площадь равнобедренного треугольника с использованием сторон
Если известны длины равных сторон и основания равнобедренного треугольника, то можно вычислить высоту или высоту треугольника.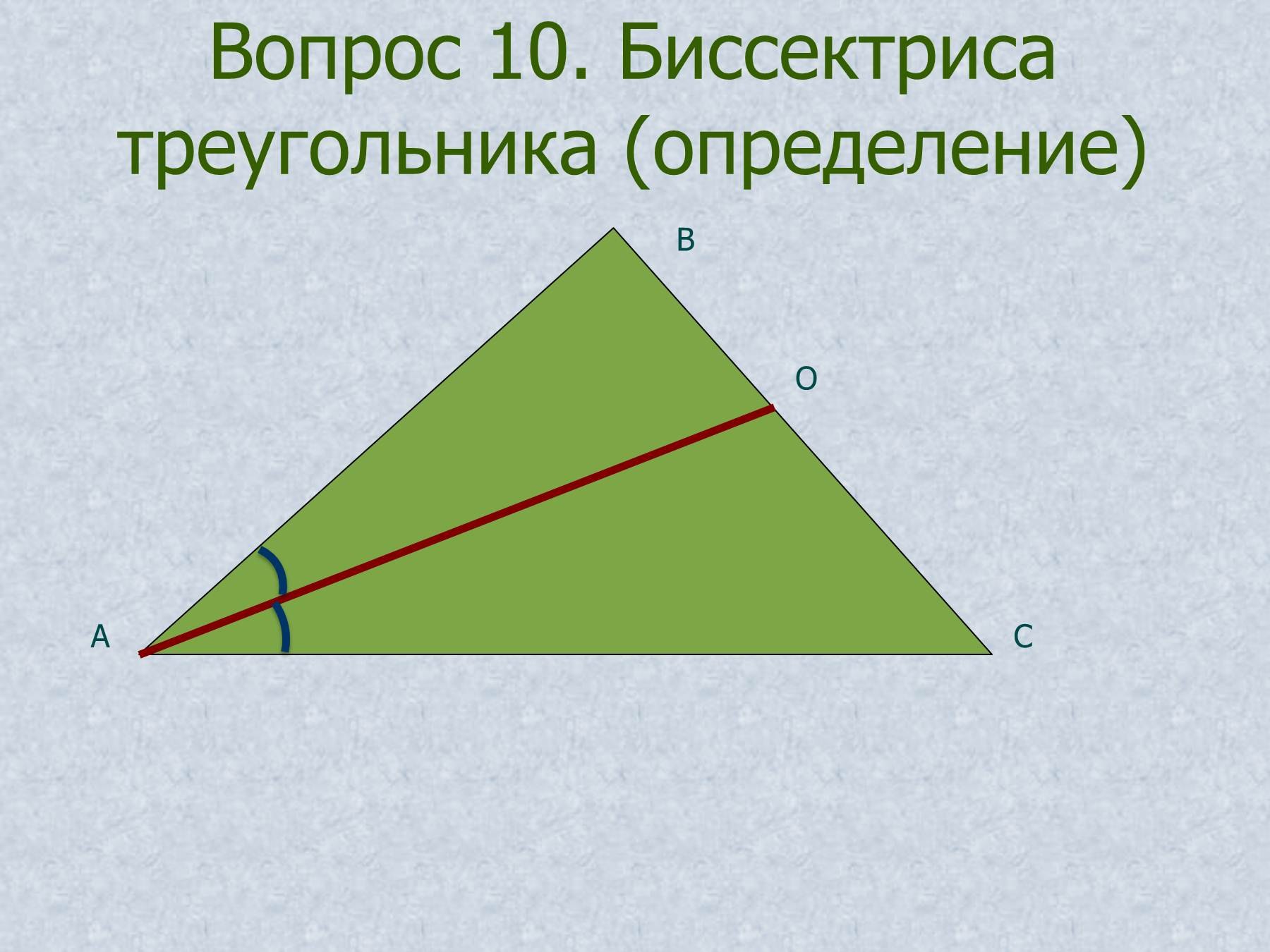 Формула для вычисления площади равнобедренного треугольника с использованием сторон задается следующим образом:
Формула для вычисления площади равнобедренного треугольника с использованием сторон задается следующим образом:
Площадь равнобедренного треугольника с использованием только сторон = ½[√(a 2 — b 2 /4) × b]
где,
- b = основание равнобедренного треугольника
- h = высота равнобедренного треугольника
- a = длина двух равных сторон
Вывод:
Из рисунка выше мы знаем:
BD = DC = ½ BC = ½ b (перпендикуляр от угла при вершине делит основание пополам)
AB = AC = a (равные стороны равнобедренного треугольника)
Применяя теорему Пифагора для ΔABD, получаем:
а 2 = (б/2) 2 + (АД) 2
AD = √(a 2 − b 2 /4)
Высота равнобедренного треугольника = √(a 2 − b 2 /4)
Кроме того, мы знаем, что общая площадь треугольника определяется как:
Площадь = ½ × b × h
Заменяющее значение высоты:
Площадь равнобедренного треугольника с использованием только сторон = ½[√(a 2 − b 2 /4) × b]
Площадь равнобедренного треугольника по формуле Герона
Формула площади равнобедренного треугольника может быть легко получена с помощью формулы Герона, как описано в следующих шагах. Формула Герона используется для нахождения площади треугольника, когда даны измерения его трех сторон.
Формула Герона используется для нахождения площади треугольника, когда даны измерения его трех сторон.
Вывод:
Формула Герона для нахождения площади A треугольника, стороны которого равны a, b и c:
A = √s(s-a)(s-b)(s-c)
где,
- a, b и c — стороны треугольника.
- с — полупериметр треугольника.
Мы знаем, что периметр треугольника со сторонами a, b и c равен a + b + c. Здесь s — половина периметра треугольника, поэтому его называют полупериметром.
Таким образом, полупериметр равен:
s = (a + b + c)/2
Теперь для равнобедренного треугольника
s = ½(a + a + b)
⇒ s = ½ (2a + b)
или, s = a + (b/2)
Кроме того,
Площадь = √[s(s-a)(s-b)(s-c)]
или, Площадь = √[s (s−a) 2 (s−b)]
⇒ Площадь = (s−a) × √[s (s−b)]
Подстановка значения «s»
⇒ Площадь = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]
⇒ Площадь = b/2 × √[(a + б/2) × (а — б/2)]
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4) квадратных единиц
где,
- b = основание равнобедренного треугольника
- а = длина двух равных сторон
Площадь равнобедренного треугольника с использованием тригонометрии (SAS и ASA)
Формула для нахождения площади равнобедренного треугольника по длине двух сторон и углу между ними или по двум углам и длине между ними может быть рассчитана с использованием основных понятий тригонометрии.
Используя 2 стороны и угол между ними:
Площадь = ½ × b × a × sin(α) квадратных единиц
где,
- b = основание равнобедренного треугольника
- а = длина двух равных сторон
- α = угол между неравными сторонами
Используя 2 угла и длину между ними:
Площадь = [a 2 × sin(β/2) × sin(α)] квадратных единиц
где,
- a = длина двух равных сторон
- α, β = углы равнобедренного треугольника
Площадь равнобедренного прямоугольного треугольника
Прямоугольный равнобедренный треугольник определяется как равнобедренный треугольник, один из углов которого равен 90°. Формула для расчета площади равнобедренного прямоугольного треугольника может быть выражена следующим образом:
Площадь = ½ × a 2
, где a — длина равных сторон.
Вывод:
Обозначим равные стороны прямоугольного равнобедренного треугольника как «а», как показано на рисунке ниже:
Длина гипотенузы BC может быть рассчитана с помощью теоремы Пифагора,
BC 2 = a 2 + a 2
BC = 90½02 a Площадь база × высота
Площадь = ½ × a × a = a 2 /2 квадратных единиц
Примеры площади равнобедренного треугольника
Пример 1: Найдите площадь равнобедренного треугольника, если длина основания 10 см, а высота 17 см?
Решение:
Основание треугольника (b) = 10 см
Высота треугольника (h) = 17 см
Площадь равнобедренного треугольника = (1/2) × b × h
= ( 1/2) × 10 × 17
= 5 × 17
= 85 см 2
Ответ: Площадь данного равнобедренного треугольника равна 85 см 2 .

Пример 2: Найдите длину основания равнобедренного треугольника, площадь которого 243 см 2 , а высота треугольника 9 см.
Решение:
Площадь треугольника, A = 243 см 2
Высота треугольника (h) = 9 см
Основание треугольника = b =?
Площадь равнобедренного треугольника = (1/2) × b × h
243 = (1/2) × b × 9
243 = (b × 9)/2
b = (243 × 2)/ 9
b = 54 см
Ответ: Высота данного равнобедренного треугольника равна 54 см.
Пример 3: Найдите длины равных сторон равнобедренного треугольника с основанием 24 см и площадью 60 см 2 .
Решение:
Мы знаем, что
Основание равнобедренного треугольника = 24 см
Площадь равнобедренного треугольника = 60 см 2 − b 2 /4)
Следовательно,
60 = (24/2)√(a 2 − 24 2 /4)
60 = 12√(a 2 − 144)
5 = √(a 2 −144) получаем
3 обе стороны 3
25 = a 2 −144
a 2 = 169
⇒a = 13 см
Ответ: Длина равных сторон данного равнобедренного треугольника равна 13 см.

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по площади равнобедренного треугольника
перейти на слайдперейти на слайд
Часто задаваемые вопросы о площади равнобедренного треугольника
Что означает площадь равнобедренного треугольника?
Площадь фигуры — это область, ограниченная фигурой. Таким образом, площадь равнобедренного треугольника означает все пространство, заключенное в равнобедренном треугольнике.
Что такое равнобедренный треугольник?
Равнобедренный треугольник определяется как треугольник, у которого две равные стороны, что также означает два равных угла. Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются катетами , а угол между ними называется углом при вершине или углом при вершине.

- Сторона, противоположная углу при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр из угла при вершине делит пополам основание и угол при вершине.
Какая формула площади равнобедренного треугольника?
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2D. Площадь равнобедренного треугольника можно рассчитать разными способами на основе известных элементов равнобедренного треугольника.
- При использовании основания и высоты: площадь = ½ × ширина × высота
- Используя все три стороны: Площадь = ½[√(a 2 − б 2 ⁄4) × б]
- Используя длину двух сторон и угол между ними: Площадь = ½ × b × a × sin(α)
- Используя два угла и расстояние между ними: A = [a 2 ×sin(β/2)×sin(α)]
- Формула площади равнобедренного прямоугольного треугольника: Площадь = ½ × a 2
где
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольника
α = мера равных углов равнобедренного треугольника
β = мера угла, противоположного основанию
Как найти высоту, используя площадь равнобедренного треугольника?
Высоту или высоту равнобедренного треугольника можно вычислить, применив теорему Пифагора для любых двух сторон. Формула для расчета высоты равнобедренного треугольника дается как,
Формула для расчета высоты равнобедренного треугольника дается как,
Высота равнобедренного треугольника = √(a 2 − b 2 /4) единиц
, где
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольника
Что такое периметр и площадь равнобедренного треугольника?
Периметр равнобедренного треугольника определяется как длина границы равнобедренного треугольника. Формула для периметра равнобедренного треугольника дается как P = 2a + b единиц. В то время как площадь — это общая область, покрытая равнобедренным треугольником, определяемая как ½ [√ (a 2 — b 2 ⁄4) × b]
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Как найти площадь равнобедренного треугольника без высоты?
Выражение для вычисления площади равнобедренного треугольника без высоты можно вычислить по формуле Герона. Формула для расчета площади равнобедренного треугольника без высоты дается как,
Формула для расчета площади равнобедренного треугольника без высоты дается как,
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Как найти площадь равнобедренного треугольника по двум сторонам и углу?
Площадь треугольника равна половине произведения данных двух сторон и синуса прилежащего к ним угла.
Формула площади треугольника с двумя сторонами и прилежащим углом (SAS) используется для нахождения общей формулы для расчета площади равнобедренного треугольника для SAS как,
Площадь = ½ × b × a × sin(α)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
Как найти площадь равнобедренного треугольника с тремя сторонами?
Площадь равнобедренного треугольника с тремя сторонами можно рассчитать по формуле Герона, то есть Площадь = \(\sqrt {s(s — a)(s — b)(s — c)} \). В равнобедренном треугольнике сторона с = стороне а. Общая формула для расчета площади равнобедренного треугольника имеет следующий вид:
В равнобедренном треугольнике сторона с = стороне а. Общая формула для расчета площади равнобедренного треугольника имеет следующий вид:
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Площадь равнобедренного треугольника – формула, определение, примеры, часто задаваемые вопросы
Площадь равнобедренного треугольника – это пространство, ограниченное сторонами треугольника. Общая формула нахождения площади равнобедренного треугольника определяется как половина произведения основания и высоты треугольника. Помимо этого, для нахождения площади треугольников используются различные формулы. Треугольники классифицируются в зависимости от их сторон, различные типы треугольников в зависимости от сторон приведены ниже:
Что такое равнобедренный треугольник?Равносторонний треугольник: Треугольник, у которого все три стороны равны.
Равнобедренный треугольник: Треугольник, у которого две стороны равны.
Разносторонний треугольник: Треугольник, все стороны которого не равны.
Равнобедренный треугольник — это треугольник с двумя равными сторонами. Два угла, противолежащие двум равным сторонам, также равны. Предположим, что в треугольнике △ABC, если стороны AB и AC равны, ABC является равнобедренным треугольником с ∠B = ∠C. Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен».
Какова площадь равнобедренного треугольника?
Полное пространство внутри границы равнобедренного треугольника называется его площадью. В равнобедренном треугольнике площадь легко вычислить, если известны высота и основание треугольника. Произведение половины на основание и высоту равнобедренного треугольника дает площадь равнобедренного треугольника.
Площадь равнобедренного треугольника определяется по следующей формуле:
Формулы площади равнобедренного треугольникаПлощадь = ½ × основание × высота равнобедренного треугольника (Р) = 2a + b
Высота равнобедренного треугольника (h) = √(a 2 − b 2 /4), где a, b — стороны равнобедренного треугольника.
Для нахождения площади равнобедренного треугольника используются различные формулы. Некоторые из наиболее часто используемых формул для площади равнобедренного треугольника перечислены ниже:
- Если даны основание и высота A = ½ × b × h
- Если даны все три стороны A = ½[√( a 2 − b 2 ⁄4) × b]
- Если даны длины двух сторон и угол между ними A = ½ × b × c × sin(α)
- Если два угла а длина между ними равна A =
- Для равнобедренного прямоугольного треугольника A = ½ × a 2
треугольника, то высоту треугольника можно вычислить по следующей формуле:
Высота равнобедренного треугольника = √(a 2 − b 2 /4)
Площадь равнобедренного треугольника Треугольник (если даны все стороны) = ½[√(a 2 − b 2 /4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон
Как найти площадь треугольника Равнобедренный треугольник?
Чтобы найти площадь равнобедренного треугольника, выполните следующие действия:
Шаг 1: Отметьте длину (l) и ширину (b) данного треугольника.
Шаг 2: Умножьте значения, полученные на шаге 1, и разделите их на 2.
Шаг 3: Полученный результат представляет собой требуемую площадь, она измеряется в м 2
Вычисление площади равнобедренного треугольника высота треугольника или высота могут быть вычислены. Формула для вычисления площади равнобедренного треугольника со сторонами выглядит следующим образом:Площадь равнобедренного треугольника = ½[√(a 2 − b 2 /4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон
Площадь прямоугольного равнобедренного треугольника(стороны равной длины)
BD = DC = ½ BC = ½ b (Перпендикуляр от угла при вершине ∠A делит основание BC пополам)
Используя теорему Пифагора об ΔABD,
a 2 = (b/2) 2 + (AD) 2
AD =
Высота равнобедренного треугольника =
Известно, что общая формула площади треугольника: Площадь = ½ × b × h
Подставляя значение высоты, получаем
Площадь равнобедренного треугольника = ½ [√(a 2 − b 2 /4) × b]
Площадь равнобедренного прямоугольного треугольника находится по формуле 9 000 3
90 Формула равнобедренного положения Прямоугольный треугольник Площадь = ½ × a 2
Вывод:
Площадь равнобедренного треугольника (площадь) = ½ × основание × высота 080 / 2
Периметр равнобедренного прямоугольного треугольника P = (2+√2)a
Вывод:
Периметр равнобедренного прямоугольного треугольника равен сумме всех сторон равнобедренного прямоугольного треугольника.
Пусть две равные стороны равны и . По теореме Пифагора неравная сторона равна a√2.
Периметр равнобедренного прямоугольного треугольника = a+a+a√2 = a(2+√2)
Тригонометрия
Когда дана длина двух сторон и угол между ними,
A = ½ × b × c × sin(α)
где,
b, c — стороны данного треугольника
α — угол между ними
стороны между ними даны,
A =
где,
c — стороны данного треугольника
α, β — связанный с ними угол 906 513
Примеры на площади Равнобедренный треугольникПример 1: Найдите площадь равнобедренного треугольника, сторона которого равна 13 см, а основание равно 24 см.

Решение:
Имеем a = 13 и b = 24.
Площадь равнобедренного треугольника определяется как
A =
=
0003
= 60 см 2
Пример 2: Найдите площадь равнобедренного треугольника с равна стороне 10 см и основанию 12 см.
Решение:
Имеем a = 10 и b = 12.
Площадь равнобедренного треугольника определяется выражением
A =
=
0/8 003
= 48 см 2
Пример 3. Найдите площадь равнобедренного треугольника, сторона которого равна 5 см, а основание равно 6 см.
Решение:
Имеем a = 5 и b = 6.
Площадь равнобедренного треугольника определяется выражением
= 12 см 2
Пример 4.
Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см.
Решение:
Имеем a = 15 и b = 24,
Площадь равнобедренного треугольника определяется как треугольник с равна стороне 17 см и основание 30 см.
Решение:
Имеем a = 17 и b = 30.0002 = 1/2 × 8 × 30
= 120 см 2
.
Решение:
Имеем a = 20 и b = 24.
Площадь равнобедренного треугольника определяется выражением 0003
= 192 см 2
Пример 7: Найдите площадь равнобедренного треугольника с равна стороне 25 см и основанию 30 см.
Решение:
Часто задаваемые вопросы о площади равнобедренного треугольникаИмеем a = 25 и b = 30.
Площадь равнобедренного треугольника определяется выражением 0003
= 300 см 2
Вопрос 1: Какова площадь равнобедренного треугольника?
Ответ:
Площадь фигуры – это пространство, ограниченное границами фигуры. Итак, площадь равнобедренного треугольника можно определить как пространство, занимаемое равнобедренным треугольником.
Вопрос 2: Что вы подразумеваете под равнобедренным треугольником?
Ответ:
Равнобедренный треугольник можно определить как треугольник, который имеет две равные стороны, а также противоположные углы также равны в равнобедренном треугольнике. Некоторые из свойств равнобедренного треугольника:
- Две равные стороны равнобедренного треугольника равны, и угол между ними называется углом при вершине или углом при вершине.
- Сторона, противоположная углу при вершине, называется основанием, и в равнобедренном треугольнике углы при основании также равны.
Вопрос 3: Напишите формулу для нахождения площади равнобедренного треугольника.
Ответ:
Для вычисления площади равнобедренного треугольника используется следующая формула:
A = ½ × b × h
где
b — основание треугольника,
h — высота треугольника.Вопрос 4 : Напишите формулу для нахождения периметра равнобедренного треугольника.
Ответ:
Для вычисления периметра равнобедренного треугольника используется следующая формула:
P = 2a + b
где0205 а, b — стороны равнобедренного треугольника.
Вопрос 5: Напишите формулу площади равнобедренного прямоугольного треугольника.


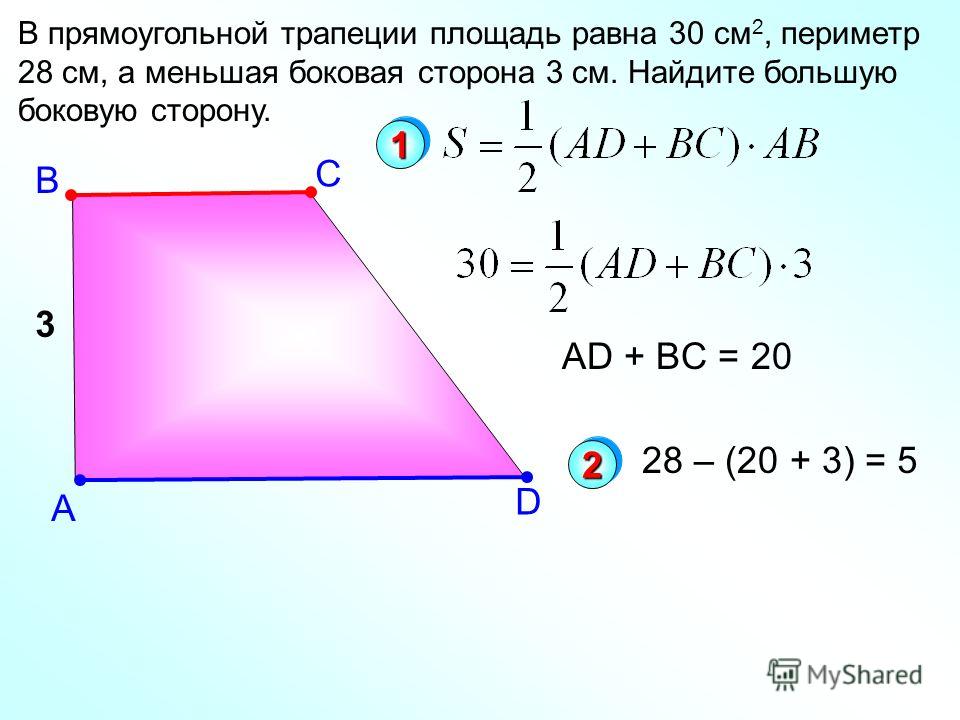





 Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см.
Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см. 

