| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
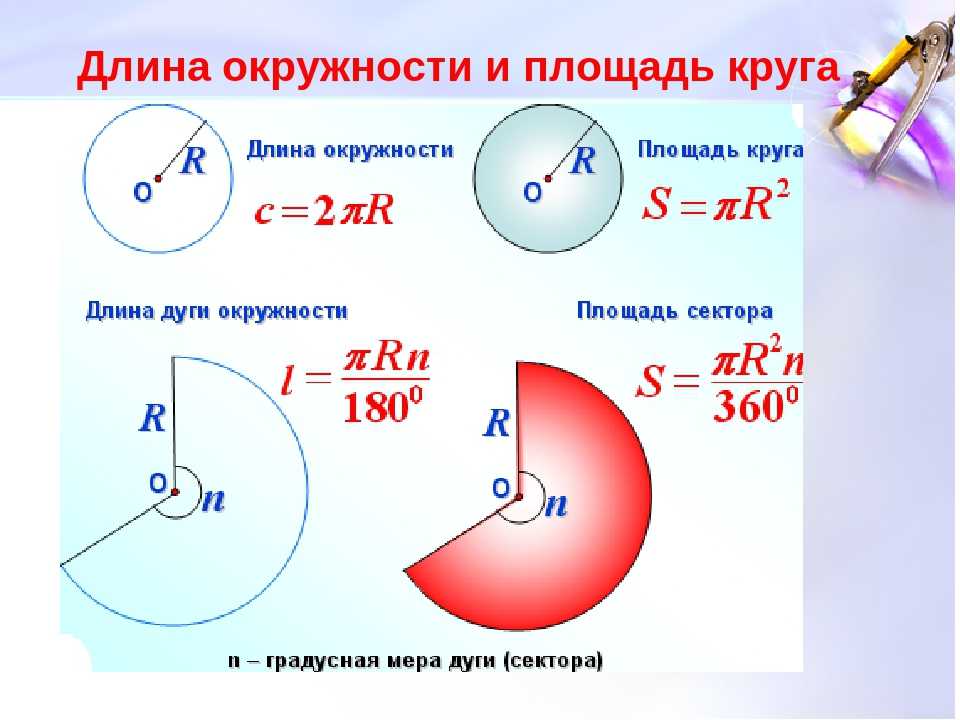
Длина окружности и площадь круга
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
ТЕМА
ДЛИНА ОКРУЖНОСТИ
И ПЛОЩАДЬ КРУГА
Для изучения темы: «Длина окружности и
площадь круга» нам потребуется ответить на
ряд вопросов
1. Что называется окружностью?
2. Что называется кругом?
3. Что такое диаметр и радиус окружности?
4. Как связаны между собой диаметр и радиус
окружности?
5. Что такое прямая и обратная
пропорциональные зависимости?
2
ДЛИНА ОКРУЖНОСТИ
Возьмём круглый стакан, поставим на лист бумаги и
обведём его карандашом. На бумаге получится
окружность. Если «опоясать» стакан ниткой, а потом
распрямить её, то длина нитки будет приближённо
равна длине нарисованной окружности (рис.
39).
3
ДЛИНА ОКРУЖНОСТИ
Длина окружности прямо
пропорциональна длине её диаметра!
То есть, отношение длины окружности к длине её диаметра
является одним и тем же числом для всех окружностей. Это
число обозначают греческой буквой
π
Обозначим длину окружности буквой
буквой
(читается: «пи»).
C,
а длину диаметра
d, получим отношение:
C:d=π
Выразим отсюда
C и получим:
С=π·d
Так как диаметр окружности вдвое больше её радиуса
(d = 2r), то длина окружности с радиусом
C = 2πr
r равна:
4
ПРИМЕР
Чему равна длина окружности, если её радиус равен 2,45 м?
Значение числа π возьмите равным
22
7
.
Нам известны две формулы нахождения длины окружности,
но так как нам известен радиус окружности r = 2,45 м, то
воспользуемся второй формулой:
C = 2πr
Подставим известные нам значения в формулу и найдём
длину окружности:
C = 2 · 22 · 2,45
7
5
ПЛОЩАДЬ КРУГА
A
E
D
F
B
r
O
M
K
C
На рисунке изображены круг и
два квадрата ABCD и EFKM.
Радиус
круга равен r, поэтому длина стороны
квадрата ABCD равна 2r, а его площадь
4r2.
Площадь
треугольника
EOF
вдвое меньше площади квадрата AEOF,
поэтому площадь EFKM вдвое меньше
площади квадрата ABCD и равна 2r2.
Площадь круга S большое площади
квадрата EFKM, но меньше площади
квадрата ABCD:
2r2 < S < 4r2
Примерно площадь круга равна 3r2.
Можно доказать, что
S = π · r2.
6
ПРИМЕР
Чему равна площадь круга, если её радиус равен 0,7 м?
Значение числа π возьмите равным
22
7
.
Воспользуемся формулой нахождения
учитывая что радиус круга: r = 0,7 м.
площади
круга,
S = πr2
Подставим известные нам значения в формулу и найдём
площадь круга:
S=
22
7
·
(0,7)2
=
22
7
· 0,49 = 1,54 м2
Ответ: площадь круга равна 1,54 м2
7
ЧИТАЕМ ПРАВИЛЬНО
Формулы длины окружности и площади круга
читаются так:
C = πd – «цэ» равно «пи дэ»;
C = 2πr – «цэ» равно двум «пи эр»;
S = πr2 – «эс» равно «пи эр» квадрат.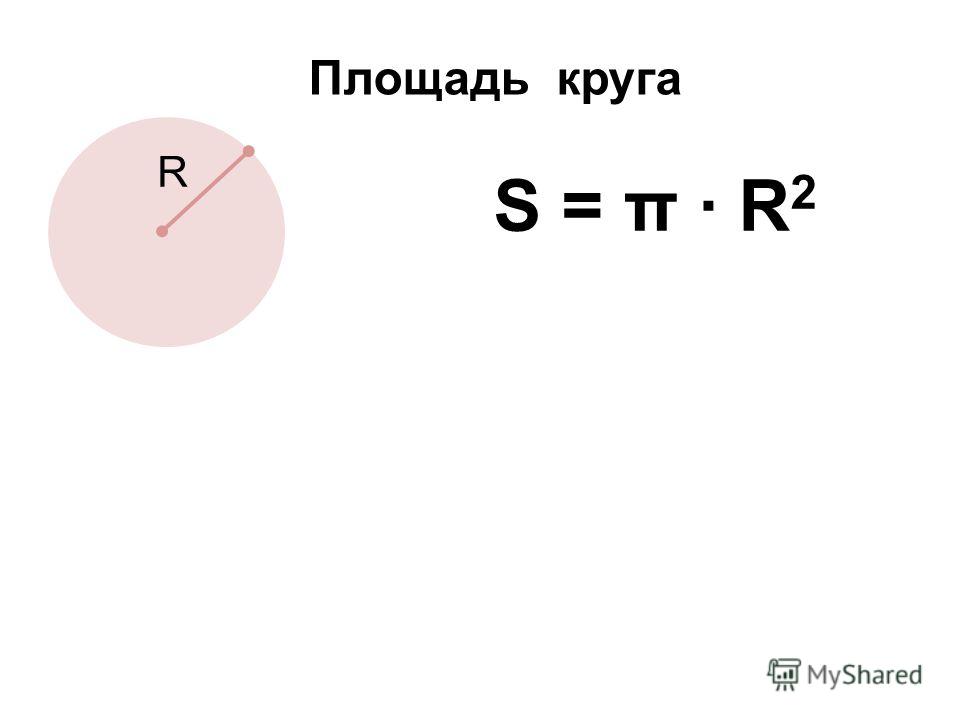
Выражение π ≈ 3,14 читают:
«Пи
приближённо
равно
четырнадцати сотым».
трём
целым
8
Страница 141, № 864(1)
Решите задачу, составив пропорцию:
1) В 2,5 кг баранины содержится 0,4 кг белков.
Сколько килограммов белков содержится в 3,2 кг баранины?
Решение задачи под цифрой (1):
Вес баранины
Содержание белка
2,5 кг
0,4 кг
3,2 кг
? (обозначим за x)
С увеличением веса баранины, содержание белка увеличивается,
значит стрелки направлены вверх, значит мы имеем прямую
пропорциональную зависимость.
Составим пропорцию:
2,5
3,2
=
0,4
x
9
Страница 141, № 864(1)
Продолжение решение задачи под цифрой (1):
Воспользуемся основным свойством пропорций (в верной
пропорции произведение крайних членов равно произведению
средних) и получим:
2,5 · x = 3,2 · 0,4
(выражаем x: чтобы найти неизвестный множитель, нужно
произведение разделить на известный множитель)
x = 3,2 · 0,4 : 2,5
(умножаем числитель и знаменатель дроби до 100, чтобы
избавиться от десятичных дробей и приводим новую дробь к
знаменателю 1000)
x = 0,512
Ответ: в 3,2 кг баранины содержится 0,512 кг белка.
10
ВОПРОСЫ ДЛЯ РАЗМЫШЛЕНИЙ
1. Где в реальной жизни может пригодится знание
о нахождении длины окружности?
2. Где в реальной жизни может пригодится знание
о нахождении площади круга?
3. В каких профессиях могут пригодится
полученные знания?
11
ДОМАШНЕЕ ЗАДАНИЕ
Страница 137 – 139. § 24
№ 848
№ 851
(№ 848 и № 851 решаются по формулам на слайде №5)
№ 864(2)
( № 864(2) решать по примеру № 864(1) )
№ 870
12
English Русский Правила
Вычисление площади и окружности — SAT Mathematics
Все ресурсы SAT по математике
137 Практические тесты Вопрос дня Карточки Learn by Concept
SAT Mathematics Help » Круги » Расчет площади и окружности
Пиццерия измеряет пиццу по ее диаметру при указании размеров в меню. В чем разница в квадратных дюймах площади поверхности между 10-дюймовой пиццей и 8-дюймовой пиццей из этой пиццерии (предположим, что каждая пицца имеет пренебрежимо малую высоту/толщину)?
Возможные ответы:
Правильный ответ:
Объяснение:
Чрезвычайно важным соображением в этой задаче является то, что размеры указаны в терминах длины диаметра, но формула площади требует, чтобы вы работали с радиусом.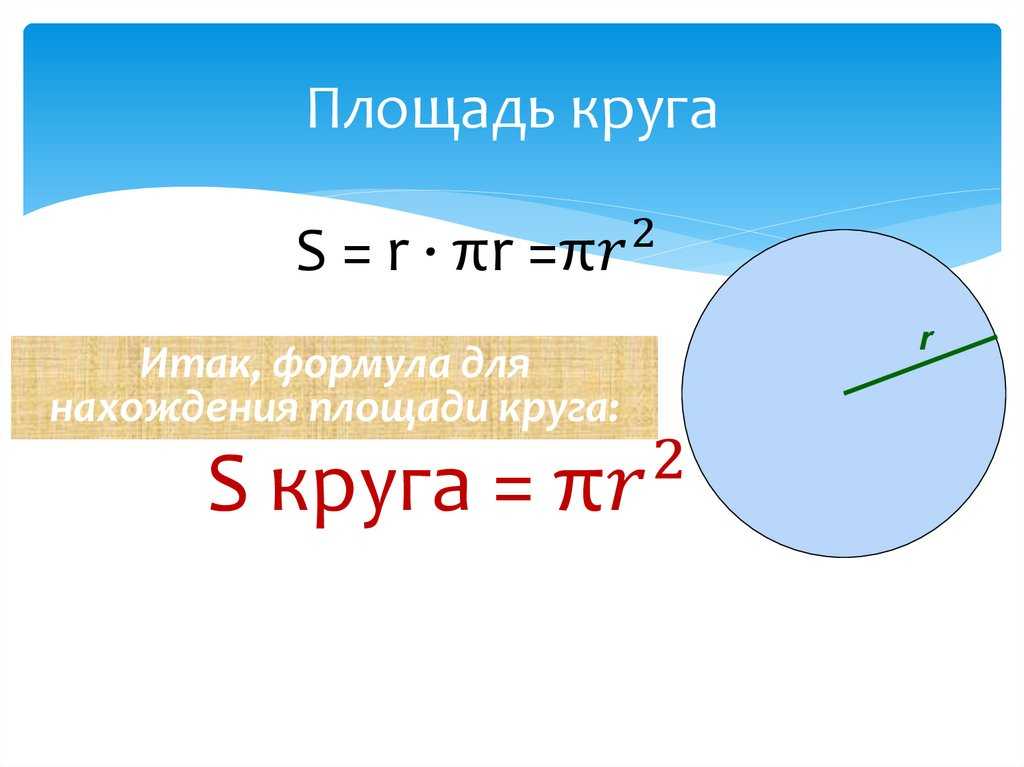
Поэтому, когда вы вычисляете площадь каждой пиццы, очень важно сначала разделить диаметр на 2, чтобы вы работали с радиусом в формуле .
10-дюймовая пицца → радиус 5 → квадратные дюймы
8-дюймовая пицца → радиус 4 → квадратные дюймы
Следовательно, разница в площади поверхности равна квадратным дюймам.
Сообщить об ошибке
В приведенном выше круге с центром в точке O угол AOB составляет 40 градусов. Если отрезок BD имеет длину 18 дюймов, то какова мера малой дуги BC в дюймах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы рассчитать длину дуги, вам нужны две части информации:
1) Длина окружности (рассчитывается как или , где – радиус, а – диаметр)
2) Мера центрального угла которая соединяет две конечные точки дуги.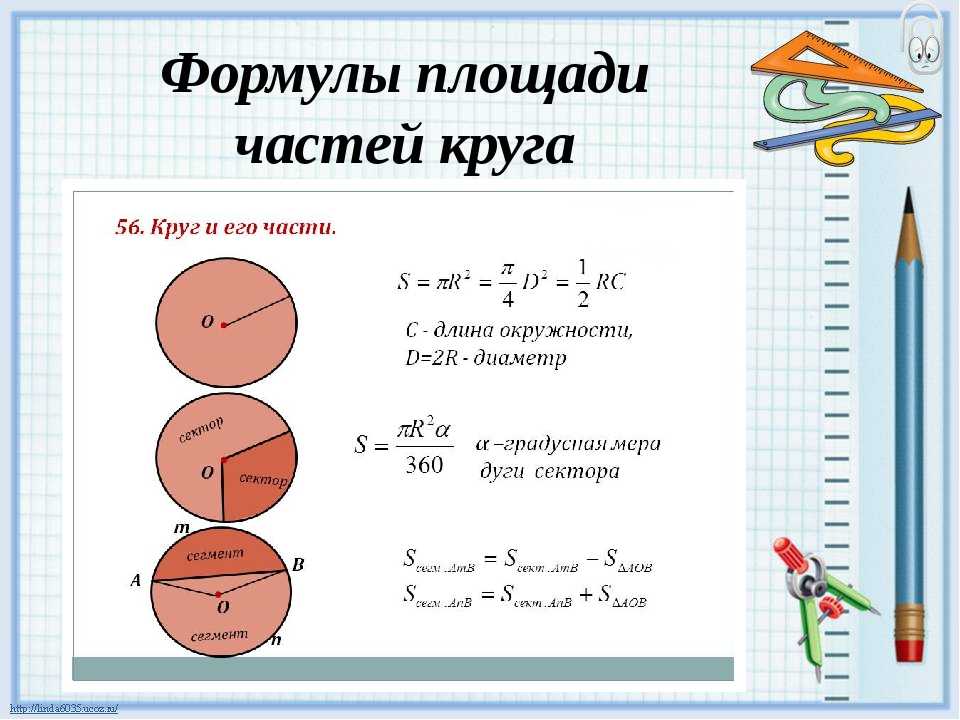
Тогда длина дуги равна пропорции длины окружности, представленной этим углом: умножьте на длину окружности, и вы получите длину дуги.
Здесь диаметр (через отрезок BD) равен 18, поэтому вы знаете, что длина окружности . И вы знаете, что угол AOB равен 40 градусам, поэтому вы можете заключить, что угол BOC равен 140 градусам, поскольку углы AOB и BOC должны дополнять прямую AC, а прямые равны 180 градусам.
Следовательно, ваш расчет равен , что упрощается до .
Сообщить об ошибке
Велосипедная шина имеет диаметр 70 сантиметров. Приблизительно сколько оборотов сделает шина, если велосипед проедет 1 км? (1 километр = 1000 метров = 100000 сантиметров)
Возможные ответы:
1500
900
150
450
Правильный ответ: 909014 4
Объяснение: Расстояние вокруг внешней стороны круга, конечно же, является окружностью. Здесь вы знаете, что диаметр колеса равен 70 сантиметрам, а это значит, что длина окружности, рассчитанная как , равна . Обратите внимание, что вопрос требует «приблизительно» количества оборотов, и что варианты ответов разбросаны довольно далеко друг от друга. Это означает, что вы можете использовать оценку 3,14 или для и сказать, что за один оборот колесо перемещается примерно на 220 сантиметров. Поскольку колесо должно покрывать 100 000 сантиметров, вам следует разделить 100 000 сантиметров на 220, чтобы увидеть, что ответ примерно равен 450. Сообщить об ошибке Если круг выше имеет центр A и площадь , каков периметр сектора ABCD? Возможные ответы: Правильный ответ: Объяснение: Эта задача проверяет несколько основных свойств окружностей: Площадь = Окружность = Длина дуги = Здесь вам дана площадь, но чтобы определить периметр этого сектора, вам нужно найти радиус (для отрезков AB и AD) и длину дуги BCD. Что касается длины дуги, обратите внимание, что центральный угол равен 45°, а . Значит, дуга BD будет равна одной восьмой длины окружности. Окружность равна , поэтому вы можете найти дугу, вычислив . Сложив две стороны плюс дугу, вы получите ответ Сообщить об ошибке На рисунке выше AC – это диаметр круга с центром O. Если площадь круга , какова длина малой дуги до н.э.? Возможные ответы: Правильный ответ: Объяснение: Чтобы вычислить длину дуги, например длину малой дуги BC здесь, ваша задача состоит в том, чтобы найти долю, которую представляет эта дуга от общей длины окружности. Здесь, поскольку вы знаете, что площадь равна , вы можете использовать формулу , чтобы определить, что радиус измеряется 9. Затем вы можете подставить этот радиус в формулу длины окружности, , чтобы определить, что длина окружности равна Начиная с этой точки, вам нужно найти величину угла BOC. Поскольку угол AOC равен 180 градусам (вы знаете, что это прямая линия, поскольку определяется как диаметр), а угол AOB = 110, это означает, что BOC равен 70 градусам. Таким образом, малая дуга BC будет равна общей окружности, установив расчет: . Сообщить об ошибке Газовая труба имеет внешний диаметр 24 дюйма. Стальная стенка трубы имеет толщину 1 дюйм. Какова площадь поперечного сечения стальной стенки трубы? Возможные ответы: Правильный ответ: Объяснение: Поперечное сечение можно найти, вычислив площадь большего круга диаметром 24 (включая трубу, выделенную серым цветом) и вычитая площадь меньшего круга диаметром 22 (все, что находится внутри трубы белого цвета). Радиус большего круга равен 12, а радиуса меньшего круга равен 11, что означает, что ваши площади можно рассчитать как: Внешний/больший круг: Внутренний/меньший круг: Затем вычтите площади, и вы останется только площадь серого кольца: Сообщить об ошибке На определенной круглой мишени диаметр круглого яблочка составляет 4 дюйма, а диаметр всей доски составляет 20 дюймов. Если дротик попадает в доску в случайном месте, какова вероятность того, что он попадет в цель? Возможные ответы: Правильный ответ: Объяснение: Хотя в этой задаче речь идет о вероятности, по сути, это проблема области круга. Вероятность попадания в яблочко — это просто площадь яблочка, деленная на общую площадь мишени. Поскольку ваша задача – найти радиус каждого круга. Яблочко: Диаметр = 4, значит Радиус = 2. Площадь = Мишень: Диаметр = 20, значит Радиус = 10. Площадь = Таким образом, вероятность попадания в яблочко равна , что уменьшается до . Сообщить об ошибке Какова площадь круга с длиной окружности ? Возможные ответы: Правильный ответ: Объяснение: Это задание проверяет вашу способность работать с двумя наиболее важными формулами окружности (обе даны вам в буклете SAT). Длина окружности равна , а площадь круга равна . Поскольку длина окружности известна как , вы можете составить уравнение для решения радиуса: Затем вы можете подставить 6 в качестве радиуса в формулу площади: Сообщить об ошибке Площадь полукруга выше равна . Возможные ответы: Правильный ответ: Объяснение: В этой задаче немного изменена формула площади круга . Вам дана площадь половины круга как , поэтому, чтобы применить формулу площади, вы должны удвоить , чтобы учесть недостающую половину круга, чтобы вы могли использовать классическую формулу площади. Поскольку площадь всего круга будет 64pi, вы можете использовать формулу площади для определения радиуса: Итак, радиус равен 8, что означает, что вы готовы применить формулу для длины окружности. Но опять же, вы имеете дело только с половиной окружности, поскольку в задаче требуется длина дуги полукруга, поэтому, хотя формула для длины окружности верна, вы можете разрезать ее пополам, чтобы найти расстояние половины окружности. Сообщить об ошибке Площадь круга . Какова его окружность? Возможные ответы: Правильный ответ: Объяснение: Это задание проверяет вашу способность работать с двумя наиболее важными формулами окружности (обе даны вам в буклете SAT). Длина окружности равна , а площадь круга . Поскольку вам дана площадь круга как , вы можете составить уравнение для решения радиуса: Теперь вы можете подключить этот радиус 12 в формулу окружности: Отчет о ошибке Практические тесты 137 Практические тесты
Вопрос дня
Карточки
Learn by Concept Поиск Геометрия круга, отрезок, хорда, плоскость, радиус, диаметр, число пи, длина окружности и площадь окружности. Цели обучения для всех уроков по окружности и площади окружностей 2-го блока. отрезок, плоскость. Учащийся сможет: Ученик сможет: Учащийся сможет: Учащийся сможет:
Обычный способ проверить окружность в словесной задаче — использовать длину окружности колеса как расстояние по прямой: за каждый оборот колеса транспортное средство будет проходить длину окружности.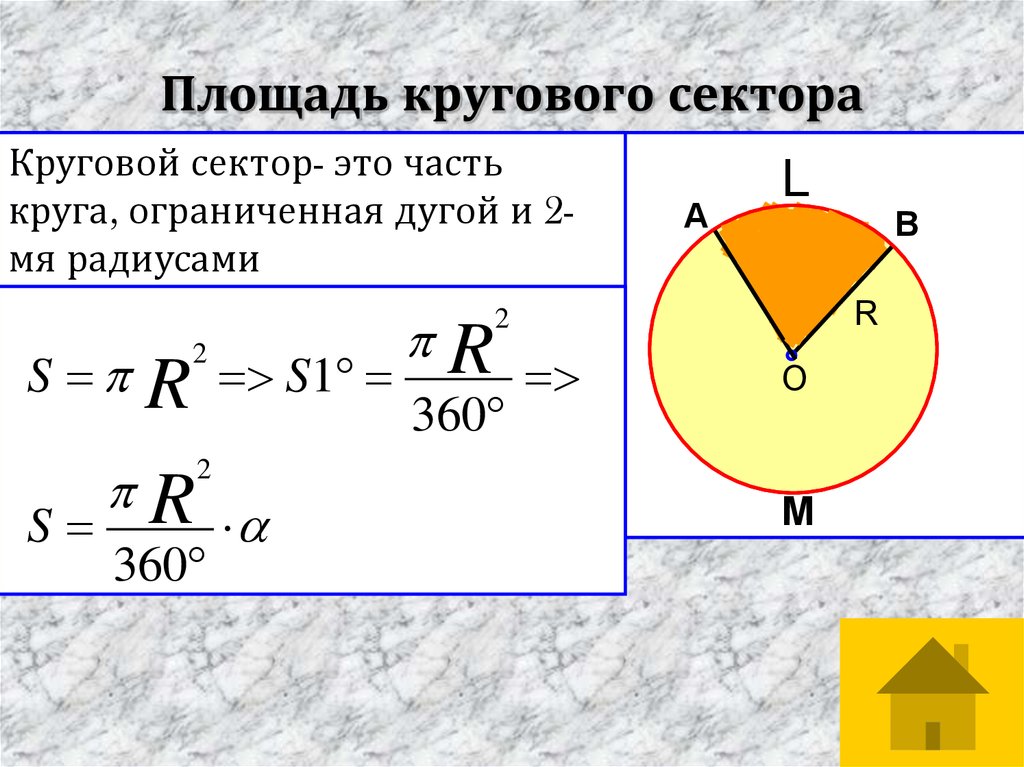
С площадью это означает, что радиус равен 12. Поскольку вам нужны два радиуса (AB и AD), чтобы сформировать «ноги» сектора, это означает, что сумма прямых сторон равна 24 (хороший намек на то, что ваш правильный ответ должен включать число 24).
Итак, вам нужно найти 1) длину окружности и 2) меру центрального угла этой дуги.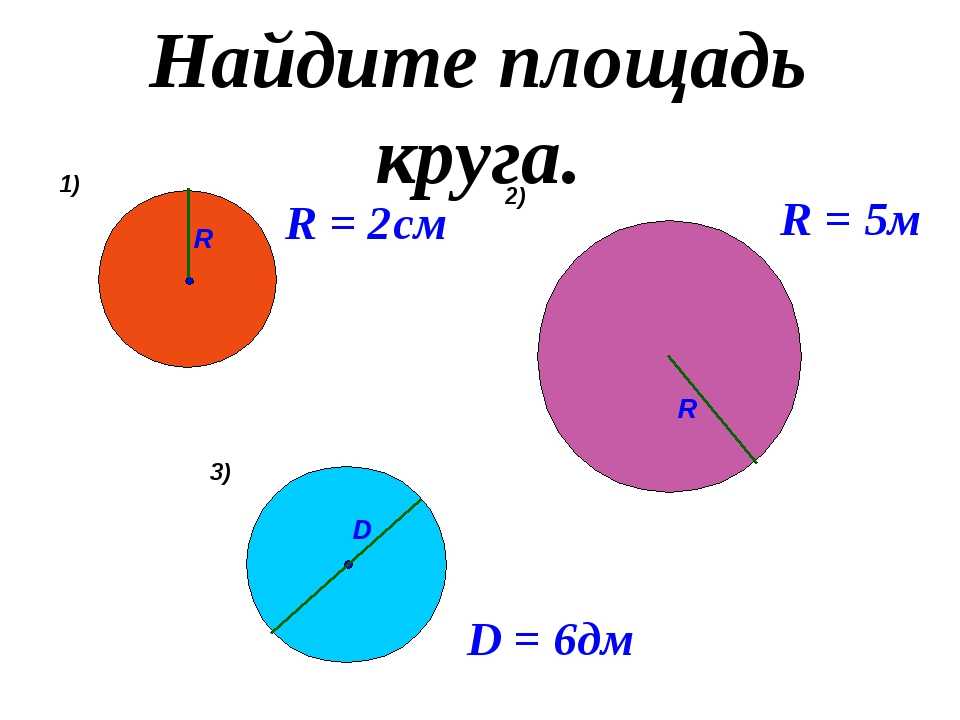
). Для этого используйте формулу площади: .
Вы указали диаметры, поэтому, чтобы найти радиус, просто разделите диаметр на 2.
Какова длина дуги, соединяющей точки А и В?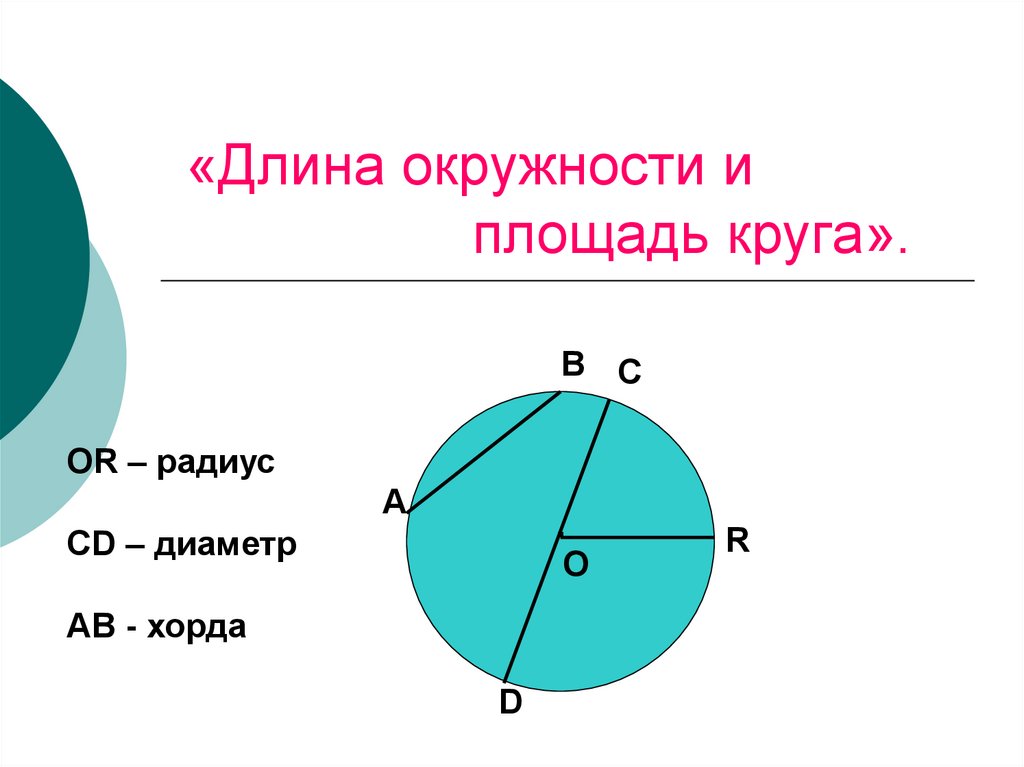
Это значит, что вам нужно рассчитать. С радиусом 8 это означает, что ваш ответ . Все SAT Mathematics
Окружность и площадь кругов
Форма поиска
Темы обучения:
Длина окружности 
Площадь кругов 
Практические упражнения
Контрольные упражнения 