Площадь параболы формула: Недопустимое название — Циклопедия

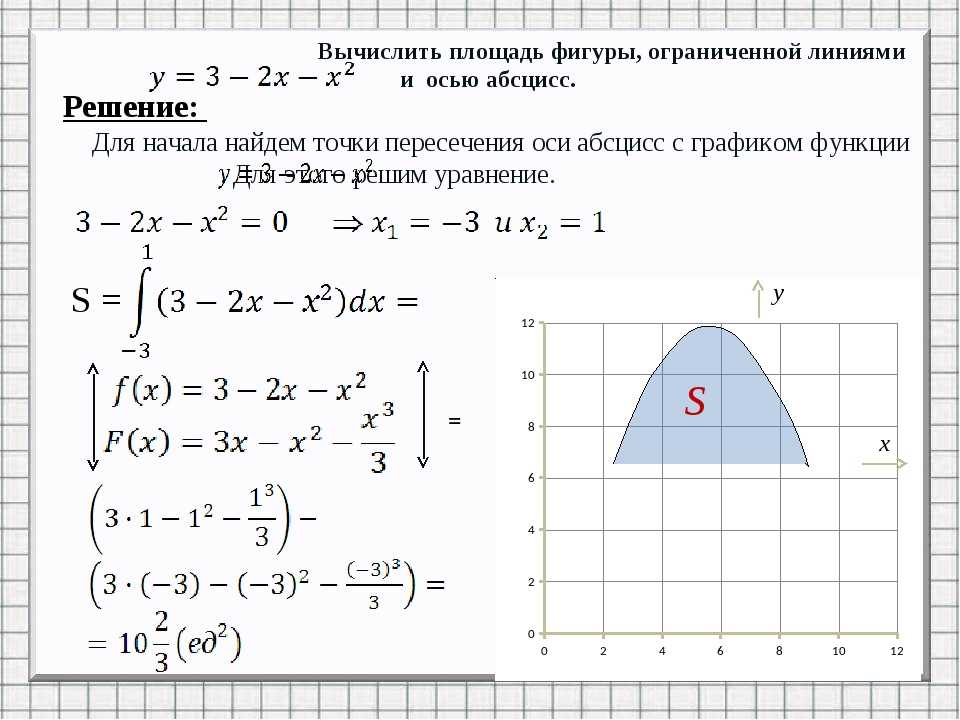
Простая физика — EASY-PHYSIC

Мы продолжаем использовать формулу  Ньютона-Лейбница, и научимся определять площади различных фигур, ограниченных теми или иными кривыми. Задачи в этой статье сложнее, чем в предыдущей.

Задача 1. Найти площадь фигуры, ограниченной заданными линиями: параболой и касательными к ней, проведенными из точки (0;1).

Так как касательная и график имеют только одну общую точку, то определить ее можно, приравняв выражения и . У полученного квадратного уравнения дискриминант должен быть равен 0:

Так как касательные проходят через точку (0;1), то :

Таким образом, уравнение первой касательной , а второй — . Строим!

К задаче 1

Определим пределы интегрирования:

Аналогично слева:

Эту фигуру нам придется разбить на две. Можно так:

Первый способ разбиения

Тогда будем вычислять площадь зеленого и бежевого участка отдельно и складывать их. А можно поступить так: вычислить площадь под параболой, а потом вычесть из нее площади  двух желтых  трапеций.

Второй способ разбиения

Покажем, что результат будет одинаков в обоих случаях. Вычисляем первым способом:

Вычисляем вторым способом. Для этого определим ординату точки касания:. То есть у трапеции основания 1 и 19, а высота . Тогда:

Ответ: .

 

Задача 2. Найти площадь фигуры, ограниченной заданными линиями:

гиперболой , прямой и касательной к кривой в точке с абсциссой .

Гипербола и касательная имеют одну общую точку. Уравнение прямой . Прямая эта по условию пройдет через точку с абсциссой 2. Определим ординату этой точки через уравнение гиперболы:

Таким образом, подставив координаты точки касания в уравнение прямой, получим:

Так как гипербола и касательная имеют одну общую точку, то приравняем:

Домножив на , имеем уравнение:

Дискриминант этого уравнения  равен 0: одна точка контакта, один корень. 2-2-(ln 1+frac{1}{8}-1)=ln 2+frac{1}{2}-2-frac{1}{8}+1=ln 2-frac{5}{8}

Ответ: .

Задача 3. В какой точке графика функции надо провести  касательную, чтобы она отсекала от фигуры, образованной графиком этой функции и прямыми трапецию наибольшей площади?

Найдем уравнение касательной к графику.

Тогда уравнение касательной

К задаче 3

Прямая отсечет трапецию . Определим длины оснований этой трапеции и . Так как прямая пересечет ось , то координаты точки пересечения будут:

Абсцисса второй точки, которая нам нужна – точки , , поэтому

Таким образом, определены основания трапеции. Первое, малое: , второе, большое, , а высота . Определяем площадь:

Определим ее минимум. Для этого возьмем производную и приравняем к нулю:

Определим ординату искомой точки:

Ответ: нужно провести касательную через точку с координатами .

Определенный интеграл и его приложения, страница 3

Математика \ Высшая математика

Таким образом, формула трапеций даёт результат значительно точнее, чем формулы прямоугольников.

3.  Способ парабол (Симпсона).

Пусть требуется вычислить

Разбив на 2n равных частей и сохранив введённые выше обозначения, имеем

Это так называемая формула парабол (формула Симпсона).

Абсолютная погрешность R_2n:

где М – наибольшее значение  

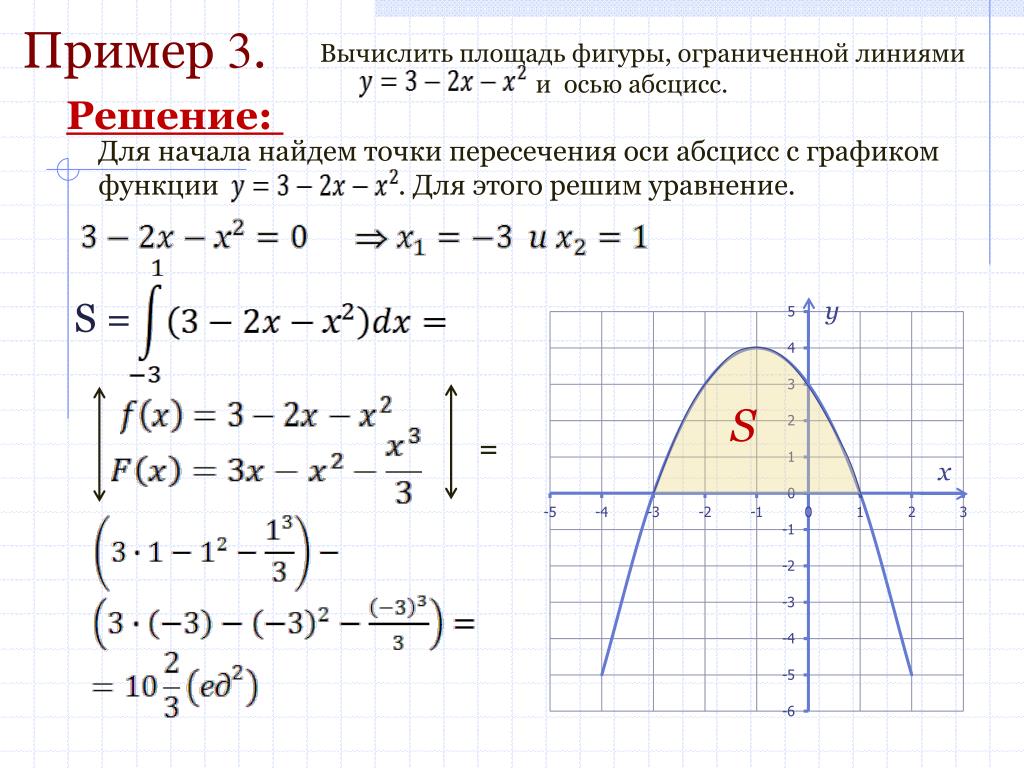
Пример 3.

Вычислить приближённо

Решение.

Найдём сначала точное значение этого интеграла по формуле Ньютона – Лейбница

Вычислим теперь приближённое значение его по формулам (1) и (3). Пусть n=10.

	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	1,00000	0,99010	0,96154	0,91743	0,86207	0,80000	0,73529	0,67114	0,60976	0,55249	0,50000

По второй формуле прямоугольников получим  Верен только один десятичный знак.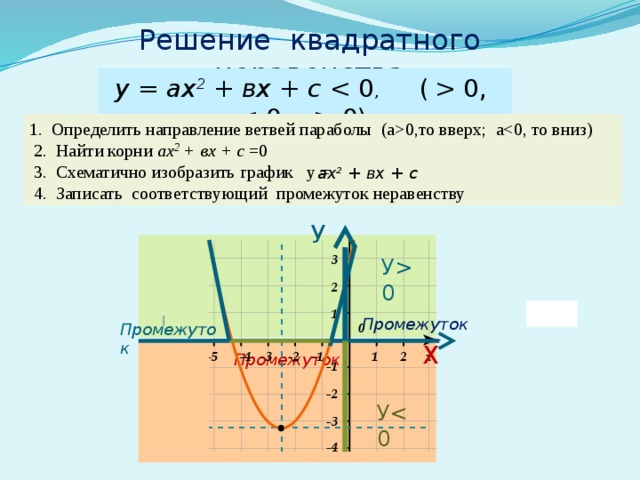

По формуле трапеций (3) получим  верны уже два десятичных знака.

Теперь вычислим этот интеграл по формуле Симпсона, для чего разделим сегмент  всего на 4 части, тогда

	0
	1,0	0,94118	0,8	0,64	0,5

Согласно формуле (5) получаем:

 где все пять десятичных знаков верны.

Задание 2.

Вычислить точное значение определённого интеграла I по формуле Ньютона – Лейбница. Вычислить этот же интеграл приближёнными способами: в способах прямоугольников и трапеций задать n=10, в способе парабол n=4. Найти относительные погрешности приближённых вычислений δ₁, δ₂ и δ₃.

Примечание.

δ=где — абсолютная погрешность,

x — точное значение.

3. Приложение определённого интеграла к задачам геометрии

3.1 Вычисление площадей плоских фигур

1. Площадь в прямоугольных координатах

При постановке задачи определённого интегрирования было показано, что определённый интеграл в случае, когда , с геометрической точки зрения определяет площадь криволинейной трапеции , т.е. фигуры , ограниченной прямыми  и кривой , где  — неотрицательная, непрерывная на  функция.

                                                      (1)

Площадь всякой плоской фигуры можно рассматривать как сумму или разность площадей некоторых криволинейных трапеций.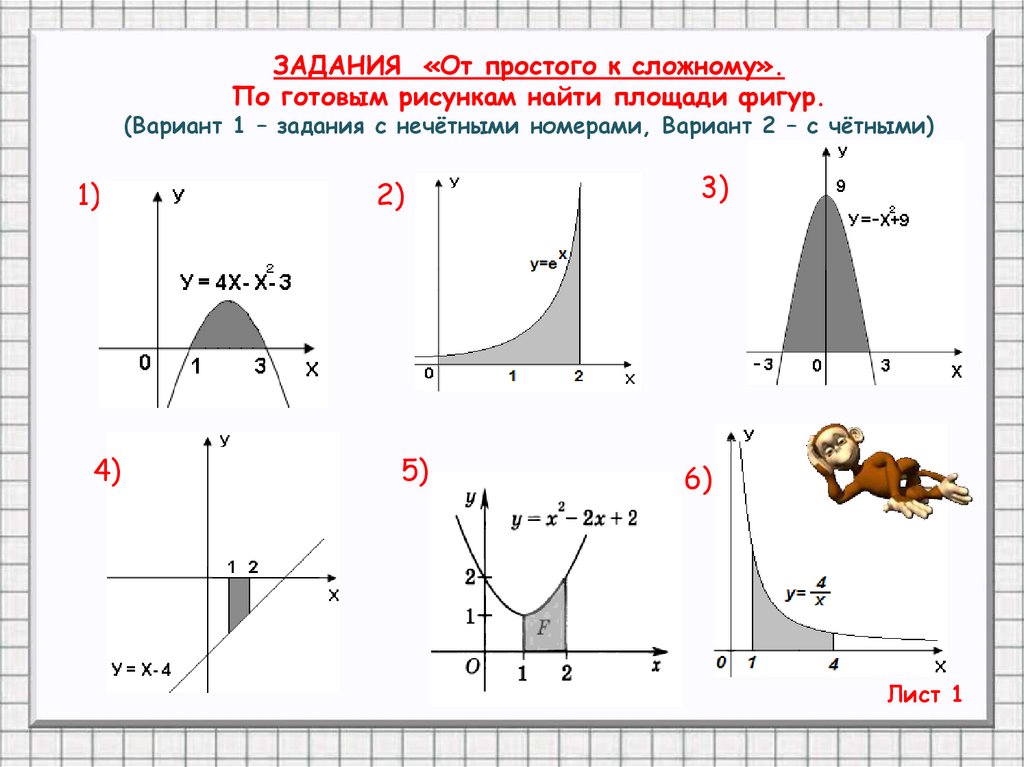 Это означает, что с помощью определённых интегралов можно вычислить площади любых плоских фигур.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями

Решение.

Вначале построим фигуру, ограниченную данными линиями, предварительно приведя уравнение параболы к каноническому виду.

Это парабола с вершиной в точке О′(2;-4), ветви направлены вверх, параметр .

Искомая площадь  поэтому

Фигуру, ограниченную прямыми   и кривой , где   также называют криволинейной трапецией .  Площадь её вычисляется по формуле

                                  (2)

Пример 2.

Вычислить площадь фигуры, ограниченной осью Оу и параболой

Решение.

Найдём сначала ординаты точек пересечения параболы с осью Оу:

Находим площадь по формуле (2)

Площадь фигуры, ограниченной двумя кривыми  и  и двумя вертикальными прямыми  причём  при  очевидно, легко вычислить как разность площадей криволинейных трапеций  и  т.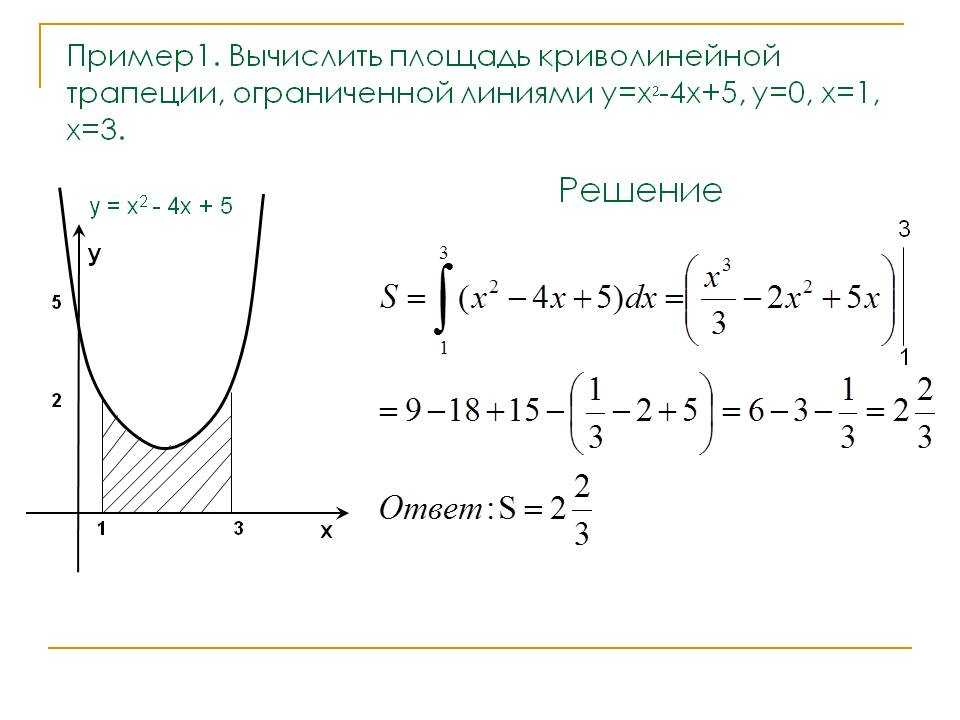 е.

                          (3)

Пример 3.

Вычислить площадь фигуры, ограниченной линиями

Решение.

Приведём уравнения парабол к каноническому виду:

 – парабола, вершина в т. О (0;0), ветви направлены влево, параметр   

 – парабола, вершина в т. О′ (1;0), ветви направлены влево, параметр

Найдём точки пересечения, приравняв уравнения парабол:  

Из рисунка видно, что для вычисления площади данной фигуры удобнее интегрировать по оси Оу:

Когда плоская фигура ограничена дугами нескольких кривых, её разбивают на части прямыми, параллельными оси Ох ( или оси Оу) так, чтобы к вычислению площади каждой полученной части можно было применить используемые ранее формулы. Площадь всей фигуры вычисляется как алгебраическая сумма площадей частей, на которые оказалась разбитой данная фигура.

Пример 4.

Вычислить площадь фигуры, ограниченной линиями ,

Решение.

Решая системы:

Скачать файл

Выбери свой ВУЗ

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Площадь параболического сегмента

Математические слова: Площадь параболического сегмента

индекс: нажмите на букву индекс: предметные области
	Площадь параболического сегмента формула приведена ниже.       См. также Парабола
	эта страница обновлена 19 июля 17 Математические слова: термины и формулы от алгебры I до исчисления написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом Авторские права © Брюс Симмонс, 2000 г. 92)$ я прав? и тогда я должен продифференцировать и приравнять дифференцирование к нулю после этого. У меня вопрос, верна ли моя формула для площади? или его нужно умножить на 2? если да то почему? исчисление оптимизация максимумы-минимумы $\endgroup$ 1 $\begingroup$ Всегда рисуй. Если предположить, что длина стороны прямоугольника по горизонтали $2x$, то картина будет следующей: 92= ​​0$, т.е. когда $x=\frac{7}{\sqrt{3}}$. Таким образом, максимальная площадь равна $$f\left ( \frac 7 {\sqrt{3}}\right) = \frac{14}{\sqrt{3}}\left( 49-\frac {49}3 \right)=\frac{1372}{3\sqrt 3}$$ $\endgroup$ 2 $\begingroup$ Обратите внимание, чтобы быть прямоугольником, его верхние вершины должны быть $(x, 49-x²)$ и $(-x,49-x²)$, потому что точка $A$ и точка $B$ в парабола образует горизонтальную прямую только в том случае, если $B$ является вертикальным отражением $A$. Его нижние вершины должны быть $(x,0)$ и $(-x, 0)$, потому что они являются перпендикулярной проекцией верхних вершин на ось $x$. Итак, длина основания равна $x-(-x)=2x$, поэтому нужно умножить на два. Имея это в виду, просто примените тот же алгоритм, что и раньше: умножьте $2x$ и $y$, продифференцируйте их, а затем приравняйте к 0,9. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт