Площадь параллелограмма онлайн калькулятор: Онлайн калькулятор. Площадь параллелограмма

Онлайн-калькулятор расчета площади параллелограмма: через стороны, диагонали

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

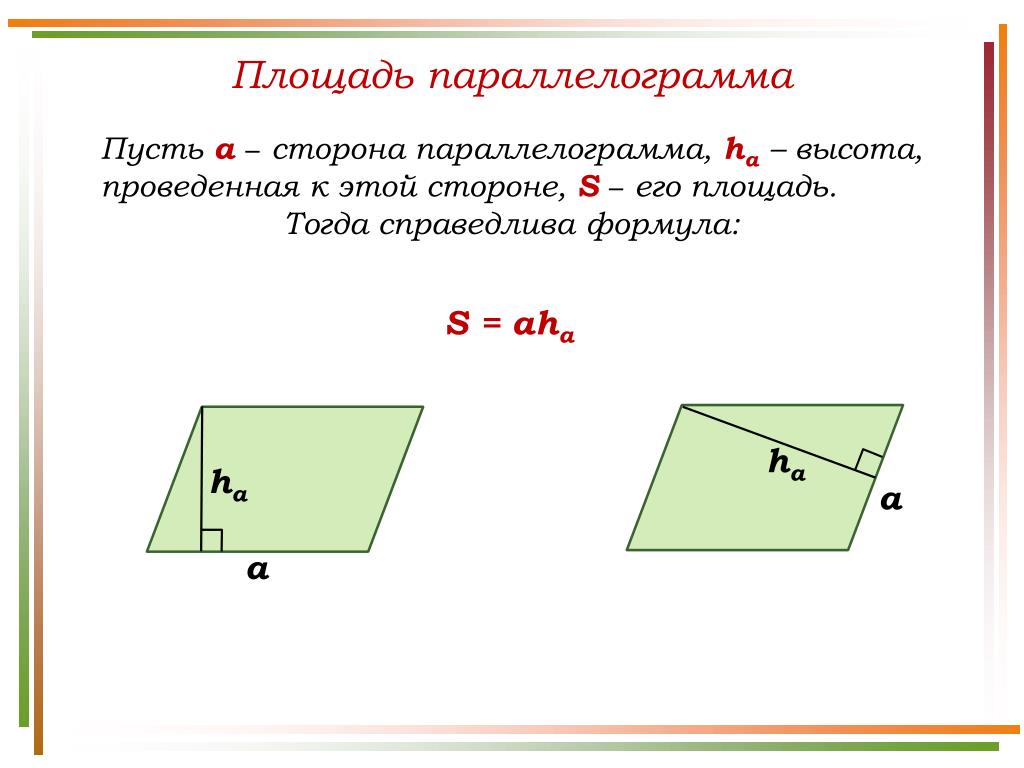
В публикации представлены онлайн-калькуляторы и формулы для расчета площади параллелограмма по разным исходным данным: через сторону и высоту, проведенную к ней; через стороны (или диагонали) и угол между ними.

• Расчет площади
  • 1. Через сторону и высоту
  • 2. Через стороны и угол между ними
  • 3. Через диагонали и угол между ними

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через сторону и высоту

Формула расчета

S = a ⋅ h

2.

Через стороны и угол между ними

Формула расчета

S = a ⋅ b ⋅ sin α

3. Через диагонали и угол между ними

Формула расчета

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Вычислить площадь параллелограмма онлайн

Площадь двухмерной фигуры – характеристика объекта, которая показывает её размер в одной плоскости.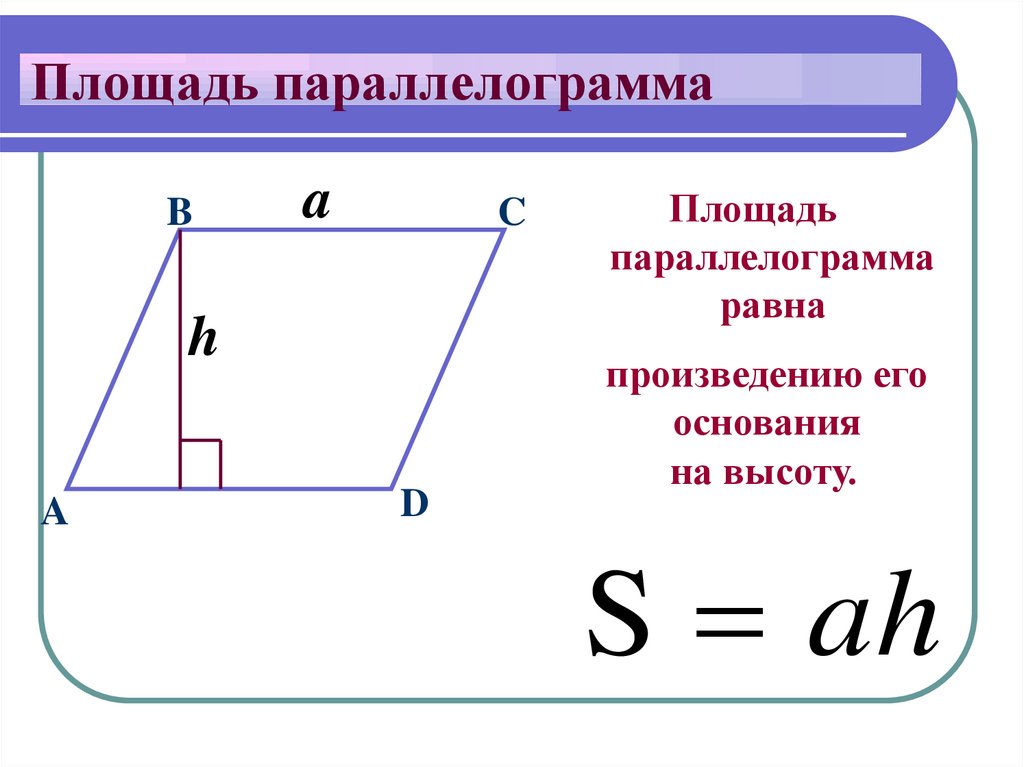

Эта величина указывается при помощи квадратных единиц.

Параллелограмм – геометрический объект, у которого противоположные края равны и параллельны. Примером может послужить прямоугольник, ромб или квадрат.

• Через сторону и высоту
• Через диагонали и острый угол
• Через 2 стороны и угол между ними

Чтобы не спутать с прямоугольником нужно знать его признаки:

1. Диагонали делятся пополам точкой пересечения.
2. Прилежащие углы при складывании дают 180°.
3. Равенство противоположных граней.

Площадь параллелограмма, это атрибут данного объекта, который необходимо определить при помощи теорем.

Через сторону и высоту

Это самая первая формула темы, которая изучается. Для неё должны быть известны высота вместе с длиной грани.

S = a · h

Площадь равна произведению длины стороны и высоты.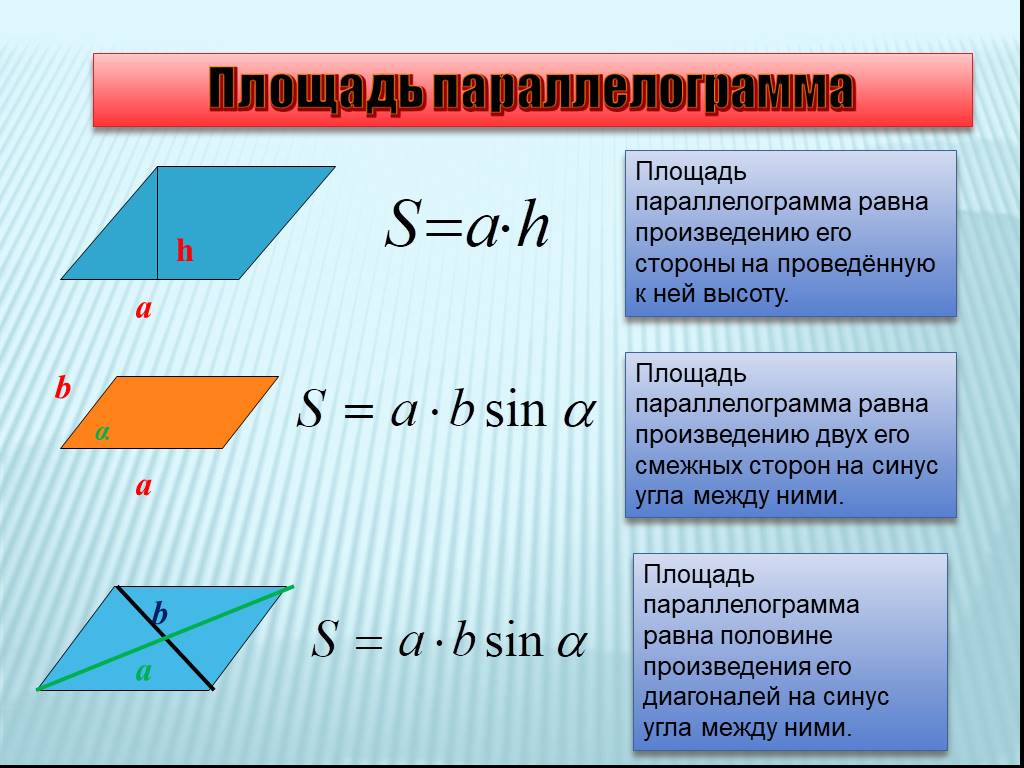

Где: a — сторона, h — высота.

Сторона (a):

ммсмдмм

Высота (h):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Пример задания:
Дан четырёхугольник с основанием AD. Его стороны при наложении одинаковы. Основание — 15 см, высота — 12 см. Чему равен занятый участок данной фигурой?

Для начала нарисуем чертёж.

Исходя из формулы ответ будет равняться произведению 15 и 12.

S = 15 см * 12 см = 180 см2 – это будет ответ.

Через диагонали и острый угол

Она может пригодиться девятиклассникам в экзамене, так как недавно её добавили в задание.

S = d1 * d2 * sin α

Где: D, d — диагонали, sin α — острый угол между диагоналями.

Диагональ (D):

ммсмдмм

Диагональ (d):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Площадь будет найдена, если перемножить диагонали на синус угла при их пересечении.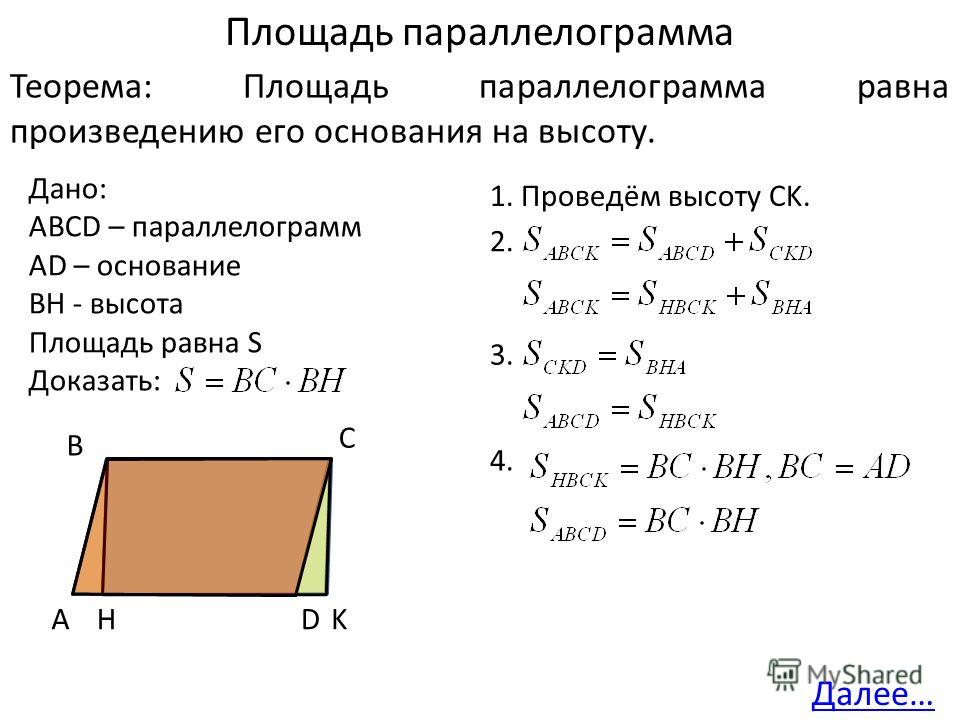

Через 2 стороны и угол между ними

Этот способ пригодится школьникам, сдающим экзамены по математике. Эта формула изучается в 9 классе, может встретиться в ОГЭ.

S = a · b · sin α

Площадь можно найти, умножив 2 стороны на синус угла, который складывается из этих отрезков.

Где: a, b — стороны, sin α — угол между сторон.

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Задача:
Диагонали четырёхугольника — 7 и 11. Уголок между ними равняется 45º. Узнайте величину пространства, занятой этой фигурой.
Решение:

S = 8 * 10 * sin 45º = 80 *√2/2 = 40 √2- ответ задачи.

Перейдём к примеру:

Одна из граней параллелограмма — 12, другая — 5, уголок — 45°. Определите размер участка, занятый четырёхугольником, делённый на √2.
Решение:

Зная формулу, задача будет довольно лёгкая.
S = 12 * 5 * sin 45° = 60 *√2 / 2 = 30
S/√2=30√2/√2= 30

Итак, в статье были разобраны 3 формулы по нахождению площади параллелограмма. Все они пригодятся на экзамене для 9 — 11 класса. Чтобы не тратить на лёгкие задание много времени нужно выучить эти теоремы, тогда любой тест будет простой.

Калькулятор площади параллелограмма

Автор: Hanna Pamuła, PhD

Отредактировано Bogna Szyk и Steven Wooding

Последнее обновление: 2 февраля 2023 г.

Содержание:

• Формулы площади параллелограмма 010
• Как пользоваться калькулятором площади параллелограмма?
• Часто задаваемые вопросы

Если у вас возникли проблемы с геометрией параллелограмма, проверьте этот калькулятор площади параллелограмма (а также его брат-близнец, калькулятор периметра параллелограмма).

Хотите ли вы вычислить площадь по основанию и высоте, сторонам и углу или диагоналям параллелограмма и углу между ними, вы находитесь в правильном месте. Не спрашивайте, как найти площадь параллелограмма; просто попробуйте калькулятор!

Ниже вы можете узнать, как работает инструмент — формулы площади параллелограмма и четкое объяснение — все, что вам нужно, чтобы понять тему.

Формулы площади параллелограмма

Параллелограмм — это простой четырехугольник с двумя парами параллельных сторон. Каждый прямоугольник является параллелограммом, так же как каждый ромб и квадрат. Помните, это не работает наоборот!

Какие формулы использует калькулятор площади параллелограмма?

• Площадь с учетом основания и высоты

  площадь = основание × высота

  Вы что-то заметили? Формула площади параллелограмма почти такая же, как и для прямоугольника! Почему это так? Взгляните на рисунок: параллелограмм можно разделить на трапецию и прямоугольный треугольник и превратить в прямоугольник.

  Узнайте больше о площади прямоугольника с помощью нашего калькулятора площади прямоугольника.

• Площадь с учетом сторон и угла между ними

  площадь = a × b × sin(угол)

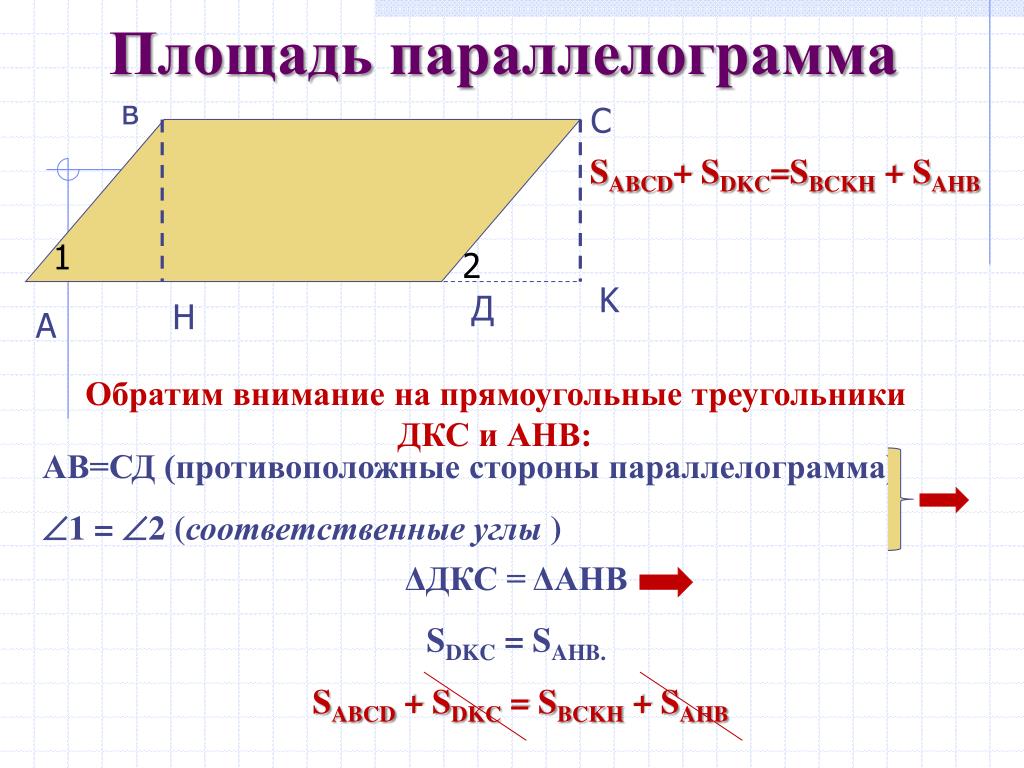
Это звонит в колокольчик? Эта формула пришла из тригонометрии и используется, например, в нашем калькуляторе площади треугольника — параллелограмм можно рассматривать как два конгруэнтных треугольника. Смежные углы в параллелограмме являются дополнительными, поэтому вы можете выбрать любой угол, который вы хотите, потому что sin(угол) = sin(180° - угол) .

• Площадь диагоналей параллелограмма и угла между ними

  площадь = ½ × e × f × sin(угол)

  Формула тоже взята из тригонометрии. Хотите знать, откуда оно?

  Разделите параллелограмм на два треугольника и предположите, что наша диагональ e является «базой» для обоих новых треугольников.

  Какова высота этого треугольника? Используйте функцию синуса. Это

  (f/2) × sin(угол) !

  Площадь треугольника равна нашему «основанию» e умножить на высоту: e × (f/2) × sin(угол)

  Параллелограмм состоит из двух таких треугольников, поэтому его площадь равна e × f × sin(angle) .

Как пользоваться этим калькулятором площади параллелограмма?

Вы все еще не уверены, что наш калькулятор площади параллелограмма работает? Мы покажем вам шаг за шагом:

1. Посмотрите на свое упражнение. Что дано, что неизвестно? Выберите нужную часть калькулятора для ваших нужд . Предположим, что мы хотим вычислить площадь, зная диагонали параллелограмма и угол между диагоналями.

2. Введите указанные значения в правые поля . Примите 5 дюймов, 13 дюймов и 30° для первой диагонали, второй диагонали и угла между ними соответственно.

3. Калькулятор отображает площадь параллелограмма значением . В нашем случае это 32,5 дюйма².

Ознакомьтесь с нашими калькуляторами площади для других форм, таких как калькулятор площади ромба, калькулятор площади круга и калькулятор площади трапеции.

Часто задаваемые вопросы

Как найти площадь параллелограмма, зная его смежные стороны?

Чтобы определить площадь по смежным сторонам параллелограмма, необходимо также знать угол между сторонами .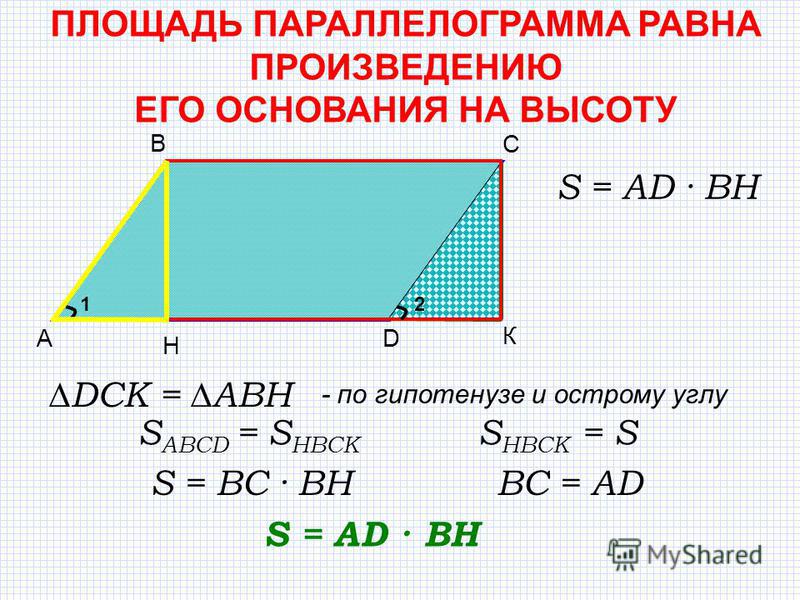 Тогда можно применить формулу: площадь = a × b × sin(α) , где a и b — стороны, а α — угол между ними.

Как найти площадь параллелограмма по диагоналям?

Площадь параллелограмма можно определить по его диагоналям, при условии, что вы также знаете угол между диагоналями .

Если e и f длины диагоналей и φ угол между ними, то площадь можно вычислить следующим образом: площадь = ½ × e × f × sin(φ) .

Как найти площадь параллелограмма без высоты?

Можно найти площадь параллелограмма без высоты! Например, достаточно знать одну из следующих вещей:

1. Длина смежных сторон и угол между ними — используйте тригонометрию.
2. Длину диагоналей и угол между ними по формуле – использовать тригонометрию.
3. Длина диагоналей и одной стороны – по формуле Герона.

Какова площадь параллелограмма с перпендикулярными диагоналями длиной 10 и 15?

Ответ: 75 . Мы используем формулу, которая говорит, что площадь равна ½ , умноженных на произведение длин диагоналей на синус угла между ними. Поскольку наши диагонали перпендикулярны, угол между ними равен 90° и sin 90° = 1 . Следовательно, вычисление, которое нам нужно выполнить, равно ½ × 10 × 15 = 75 .

Ханна Памула, доктор философии

Основание (b)

Высота (h)

Посмотреть 23 похожих калькулятора 2d геометрии 📏

ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20

Калькулятор параллелограмма — Найдите площадь параллелограмма 9000 1

Онлайн-калькулятор параллелограмма помогает вам рассчитать каждый параметр параллелограмма в зависимости от предоставленного набора входных данных. Но перед этим вам нужно пройти через этот контекст, который был специально устроен, чтобы помочь вам, людям, исследовать эту геометрическую фигуру.

Дай почитать!

Что такое параллелограмм в геометрии?

«Четырехугольник, противоположные стороны которого параллельны друг другу, называется параллелограммом»

 

2 и b — длины сторон (где b считается базовым)

p и q — длины большей и меньшей диагоналей соответственно

h представляет собой высоту параллелограмма

P и K периметр и площадь соответственно

A, B, C и D — четыре вершины с соответствующими углами ∠A, ​​∠B, ∠C, и ∠D

Параллелограмм Важные формулы:

Здесь мы обсудим все формулы, которые используются для определения различных технических констант, связанных с параллелограммом. К ним относятся: 9\text{o} \hspace{0.25in} \left(\frac{π}{2} < ∠B < π\right) $$

Площадь:

Если заданы углы A и B в радианах, то можно вычислить площадь параллелограмма с помощью следующей формулы:

$$ K = b * h $$
Или;
$$ K = a*b sin\left(A\right) $$
Или;
$$ K = a*b sin\left(B\right) $$

Вы также можете использовать калькулятор площади параллелограмма, чтобы найти площадь, если вам трудно вычислить вручную.

Высота:

Высоту параллелограмма можно найти по следующим формулам:

$$ h = a sin\left(A\right) = a sin\left(B\right) $$

Вы можете также используйте простой в использовании калькулятор высоты параллелограмма, чтобы точно определить высоту.

Диагонали:

В параллелограмме есть две диагонали, которые можно пронумеровать следующим образом:

Длинная диагональ:

Это диагональ, образованная соединением вершин A и C. 9{2}\right) $$

Периметр параллелограмма:

Для нахождения периметра параллелограмма можно использовать следующее уравнение:

$$ P = 2a + 2b $$

Все эти основные ограничения могут можно мгновенно определить с помощью калькулятора свободного периметра параллелограмма.

Дальнейшие случаи(преобразования):

До сих пор мы обсуждали только основные формулы параллелограмма. Теперь мы обсудим различные случаи, основанные на основных формулах, упомянутых выше. 9\text{o} – ∠A $$
$$ ∠C = ∠A $$
$$ ∠D = ∠B $$

Учитывая P и a для вычисления b:

$$ b = \frac {\left(P – 2a\right)}{2} $$

Учитывая P и b для вычисления a:

$$ a = \frac{\left(P – 2b\right)}{2} $$

При заданных K и b для расчета h:

$$ h = \frac{K}{b} $$

При заданных K и h для расчета b:

$$ b = \frac {K}{h} $$

Учитывая b и h для вычисления K: 9{2}\right)}{\left(2ab\right)}\right) $$

Для остальных членов используйте уже рассмотренные выше формулы.

При данных a, b и h для вычисления ∠A, ∠B, p, q, P и K:

$$ ∠A = arcsin\left(\frac{h}{a}\right) $$

Здесь для оставшихся параметров используйте уже упомянутые ранее формулы.

При наличии a, b и K для вычисления ∠A, ∠B, p, q, h и P:

$$ ∠A = arcsin\left(\frac{K}{ab}\right) $$

Для остальных членов вы можете использовать уже обсуждавшиеся формулы. 9{2}\right)}{2} $$

А для всех оставшихся терминов можно использовать выражения, которые уже были разработаны выше в контексте.

Здесь вычислитель площади параллелограмма находит все эти пределы с точными выводами и отображает в виде четко определенной таблицы.

Как решить параллелограмм?

Нахождение всех координат параллелограмма может показаться сложной задачей. Но если вы понимаете самые основные уравнения, вы также сможете выполнять преобразования. Давайте решим несколько примеров, чтобы вы лучше поняли суть. 9{2} $$

Наш бесплатный калькулятор площади параллелограмма показывает те же результаты, но с большей точностью и за более короткий промежуток времени.

Пример № 04:

Расчет параллелограмма: Найдите a, если c периметр параллелограмма равен 6,2 см, а сторона b равна 2 см.

Решение:

Мы знаем, что:

$$ a = \frac{\left(P – 2b\right)}{2} $$
$$ a = \frac{\left(6.2 – 2) *2\справа)}{2} $$
$$ a = \frac{\left(6.2 – 2*2\right)}{2} $$
$$ a = \frac{2.2}{2} $$
$$ a = 1,1 см $$

Как работает калькулятор параллелограмма?

Наш бесплатный решатель параллелограммов — лучший метод тщательной проверки параллелограмма. Если вы балуетесь сложностью при вычислениях и не находите способа решить проблему, то эта область параллелограмма с калькулятором вершин — правильный выбор для вас. Давайте подскажем, что вам нужно сделать:

Введите:

• Просто нажмите «Расчет с» и появится выпадающий список
• Выберите параметр, с помощью которого вы хотите найти различные связанные параметры
• Введите значение выбранных параметров
• Нажмите кнопку расчета

Выход:

Свободная диагональ калькулятора параллелограмма вычисляет:

• Стороны параллелограмма
• Углы параллелограмма
• Диагонали параллелограмма 9\text{o}\), что неверно в случае параллелограмма.

  No related posts.