Как найти Объем Параллелепипеда?
Поможем понять и полюбить математику
Начать учиться
315.4K
В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила.
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Реши домашку по математике на 5.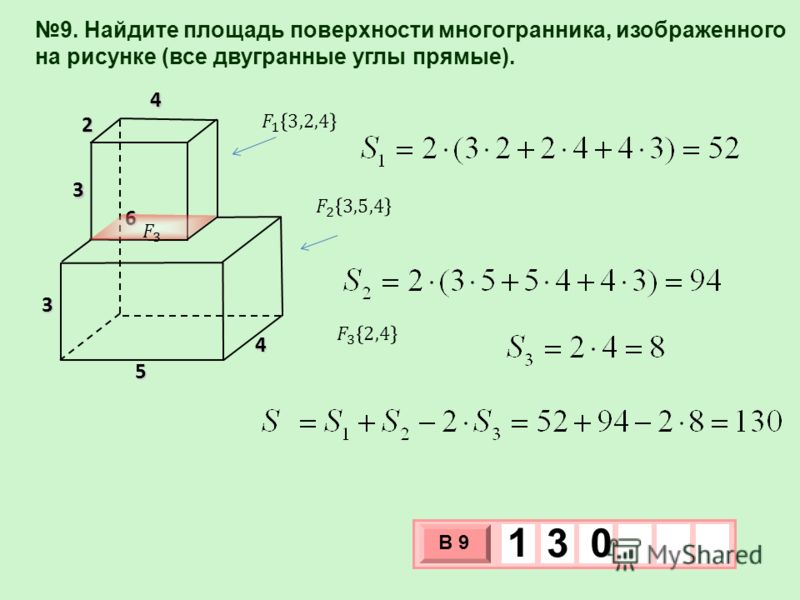
Подробные решения помогут разобраться в самой сложной теме.
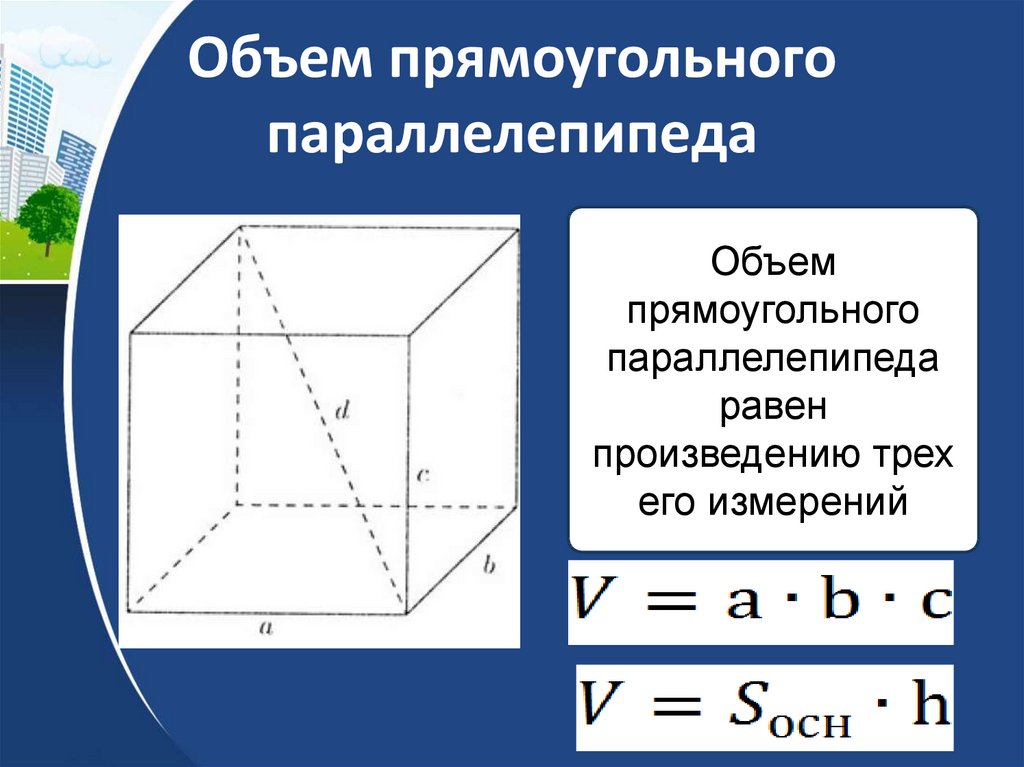
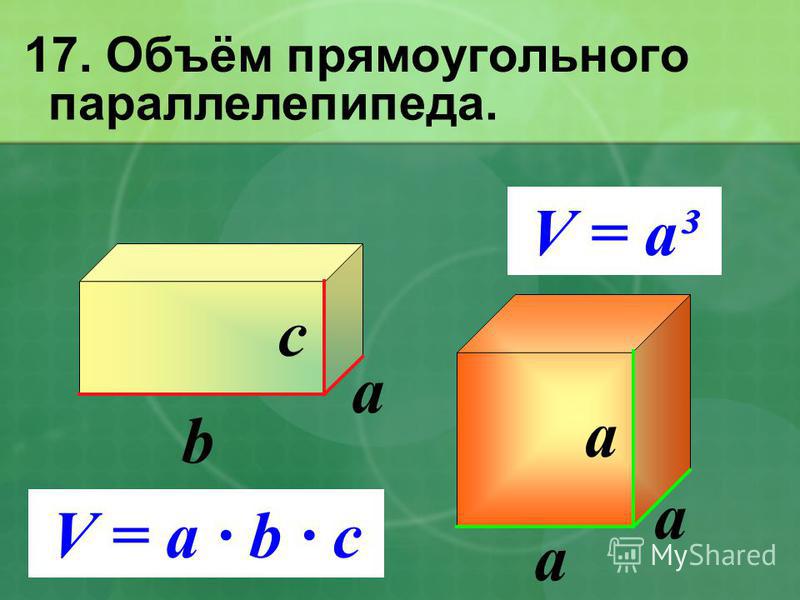
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см 3, а высота — 15 см.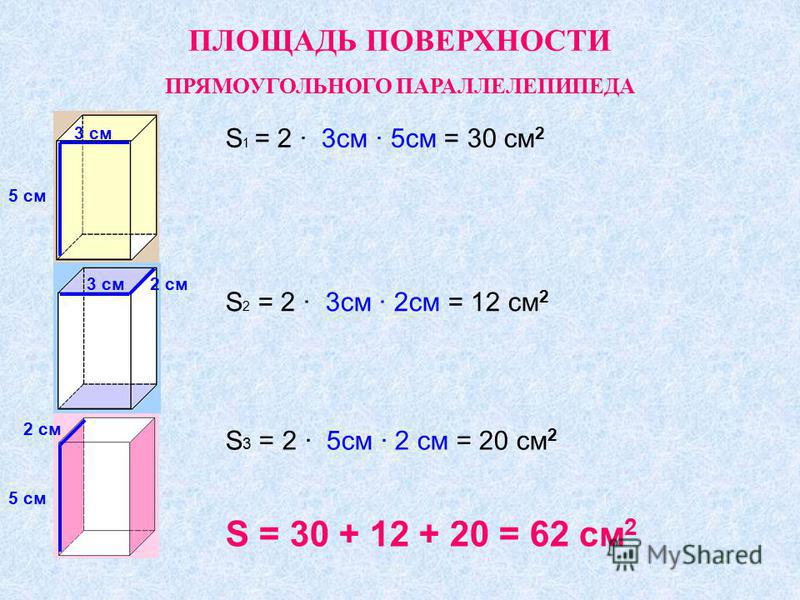
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. п. = 2 (ac + bc) |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
412.3K
Время, скорость, расстояние
К следующей статье
500. 9K
9K
Порядок действий в математике
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Площадь поверхности параллелепипеда — формула и калькулятор
{S_{полн} = 2(ab+bc+ac)}
Найти площадь
полной поверхностибоковой поверхности
Длина a
ммсмдммкмдюймы (in)футы (ft)
Ширина b
ммсмдммкмдюймы (in)футы (ft)
Высота c
ммсмдммкмдюймы (in)футы (ft)
Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.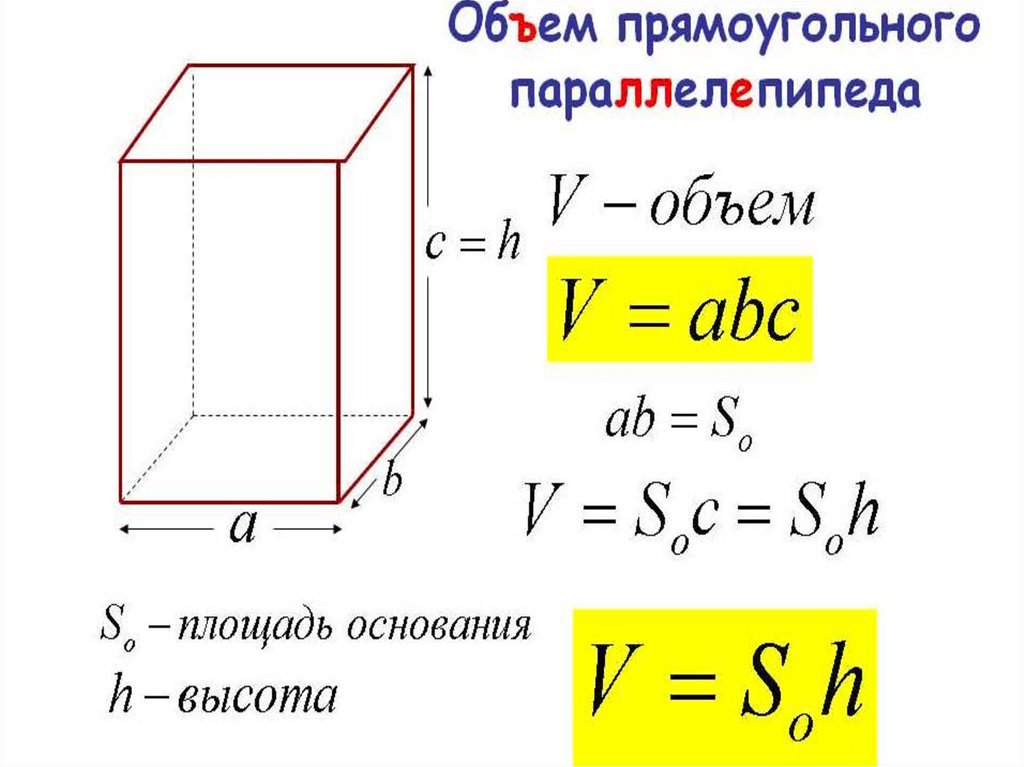 2
2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Параллелепипед – формулы, свойства, определение, примеры
Параллелепипед – это трехмерная фигура, образованная шестью параллелограммами. Слово «параллелепипед» происходит от греческого слова parallelepdon , что означает «тело, имеющее параллельные тела». Можно сказать, что параллелепипед относится к параллелограмму так же, как куб относится к квадрату. Параллелепипед имеет 6 граней в форме параллелограмма, 8 вершин и 12 ребер. Давайте разберемся со свойствами и различными формулами, связанными с площадью поверхности и объемом параллелепипеда, в следующих разделах.
| 1. | Что такое параллелепипед? |
| 2. | Свойства параллелепипеда |
| 3. | Площадь поверхности параллелепипеда |
| 4. | Объем параллелепипеда |
5. | Решенные примеры |
| 6. | Практические вопросы |
| 7. | Часто задаваемые вопросы о параллелепипеде |
Что такое параллелепипед?
Параллелепипед представляет собой трехмерную фигуру с шестью гранями, каждая из которых имеет форму параллелограмма. У него 6 граней, 8 вершин и 12 ребер. Куб, прямоугольный параллелепипед и ромбовидный — все это частные случаи параллелепипеда. Куб – это параллелепипед, все стороны которого имеют форму квадрата. Точно так же кубоид и ромбоид являются параллелепипедами с прямоугольной и ромбовидной гранями соответственно. На приведенном ниже рисунке мы можем наблюдать параллелепипед с длинами сторон «a», «b» и «c», а «h» — высотой параллелепипеда.
Свойства параллелепипеда
Существуют определенные свойства параллелепипеда, которые помогают нам отличить его от других трехмерных фигур. Эти свойства перечислены ниже:
- Параллелепипед представляет собой трехмерную твердую форму.

- Имеет 6 граней, 12 ребер и 8 вершин.
- Все грани параллелепипеда имеют форму параллелограмма.
- Параллелепипед имеет 2 диагонали на каждой грани, называемые диагоналями граней. Всего у него 12 диагоналей граней.
- Диагонали, соединяющие вершины, не лежащие на одной грани, называются телом или пространственной диагональю параллелепипеда.
- Параллелепипедом называется призма с основанием в форме параллелограмма.
- Каждая грань параллелепипеда является зеркальным отражением противоположной грани.
Площадь поверхности параллелепипеда
Площадь поверхности параллелепипеда определяется как общая площадь, занимаемая всеми поверхностями параллелепипеда. Площадь поверхности параллелепипеда выражается в квадратных единицах, например 9.0087 2 , см 2 , м 2 , фут 2 , ярд 2 и т. д. Площадь поверхности параллелепипеда может быть двух типов:
- Площадь боковой поверхности 9006
- Общая площадь поверхности
Площадь боковой поверхности параллелепипеда
Площадь боковой поверхности параллелепипеда определяется как площадь боковых или боковых граней параллелепипеда. Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Общая площадь поверхности параллелепипеда
Общая площадь поверхности параллелепипеда определяется как площадь всех граней параллелепипеда. Чтобы вычислить TSA параллелепипеда, нам нужно найти сумму площадей, покрытых 6 гранями.
Площадь поверхности параллелепипеда Формула
Формула для расчета площади боковой поверхности и общей площади поверхности параллелепипеда:
LSA параллелепипеда = P × H
TSA параллелепипеда = LSA + 2 × B = (P × H) + (2 × B)
где,
- B = Базовая площадь
- H = Высота параллелепипеда
- P = Периметр основания
Объем параллелепипеда
Объем параллелепипеда определяется как пространство, занимаемое фигурой в трехмерной плоскости. Объем параллелепипеда выражается в кубических единицах, например, 3 , см 3 , м 3 , фут 3 , ярд 3 и т.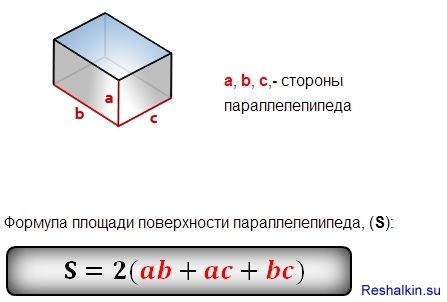 д.
д.
Объем параллелепипеда Формула
Объем параллелепипеда можно рассчитать, используя площадь основания и высоту. Формула для расчета объема параллелепипеда дается как,
В = В × Н
где
- B = Базовая площадь
- H = Высота параллелепипеда
Решенные примеры на параллелепипеде
Пример 1: Если базовая грань параллелепипеда имеет противоположные стороны размером 6 дюймов и 10 дюймов, а его высота равна 7 дюймам, найдите площадь боковой поверхности параллелепипеда.
Решение:
Используя формулу площади боковой поверхности параллелепипеда,
LSA = периметр основания × высота 90 115 ⇒ ЛСА = 2(6 + 10) × 7
= 224 в 3Ответ: Площадь боковой стороны данного параллелепипеда = 224 в 3.
Пример 2: Подарок упакован в прямоугольную коробку размером 10, 7 и 8 дюймов и должен быть обернут подарочной бумагой.
 Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки?Решение:
Размеры данной подарочной коробки,
длина, l = 10 в
ширина, w = 7 в
высота, h = 8 inЧтобы найти необходимое количество подарочной бумаги, нам нужно найти общую площадь поверхности коробки. Поскольку форму коробки можно сравнить с прямоугольным параллелепипедом,
ВПС = 2 (дв + вх + вл)
= 2 (10 × 7 + 7 × 8 + 8 × 10)
= 2 (70 + 56 + 80)
= 412 в 2 .
Ответ: Площадь необходимой подарочной бумаги = 412 в 2 .
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по параллелепипеду
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о параллелепипеде
Что такое параллелепипед?
Параллелепипед представляет собой трехмерную фигуру с 6 гранями в форме параллелограмма, 12 ребрами и 8 вершинами. Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Каков объем параллелепипеда?
Объем параллелепипеда – это емкость, форма или общее пространство, занимаемое в трехмерной плоскости. Объем параллелепипеда в кубических единицах, например, 3 , см 3 , фут 3 , 3 и т. д.
Какова общая площадь поверхности параллелепипеда?
Полная площадь поверхности параллелепипеда – это площадь, покрытая всеми гранями параллелепипеда. Выражается в квадратных единицах, например, в 2 , м 2 , см 2 , фут 2 и т. д.
Что такое площадь боковой поверхности параллелепипеда?
Площадь боковой поверхности параллелепипеда – это площадь или область, покрываемая всеми боковыми или боковыми гранями параллелепипеда. Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Что такое формулы параллелепипеда?
Формулы, связанные с параллелепипедом, даны как,
- LSA параллелепипеда = P × H
- TSA параллелепипеда = (P × H) + (2 × B)
- Объем параллелепипеда = B × H
где B — площадь основания, H — высота параллелепипеда, P — периметр основания.
Что такое прямоугольный параллелепипед?
Прямоугольный параллелепипед — тип параллелепипеда, все шесть граней которого имеют прямоугольную форму, а длины параллельных ребер равны.
Какой формы параллелепипед?
Параллелепипед — это трехмерная фигура, все стороны которой имеют форму параллелограмма. Противоположные грани параллелепипеда являются зеркальным отражением друг друга.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы для фигур
Площадь, объем, прямоугольная формула с примерами
Параллелепипед — это трехмерная фигура или призма с основанием в виде параллелограмма, состоящим из шести сторон параллелограмма. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Параллелепипед представляет собой трехмерную фигуру, образованную шестью параллелограммами, и его можно определить как многогранник с шестью гранями, также называемый шестигранником, каждая грань которого представляет собой параллелограмм. Параллелепипед также называют ромбом. По аналогии с 2D Shapes, он соотносится с параллелограммом так же, как куб соотносится с квадратом. Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда.
Объем параллелепипеда Объем параллелепипеда — это количество пространства, которое содержит параллелепипед.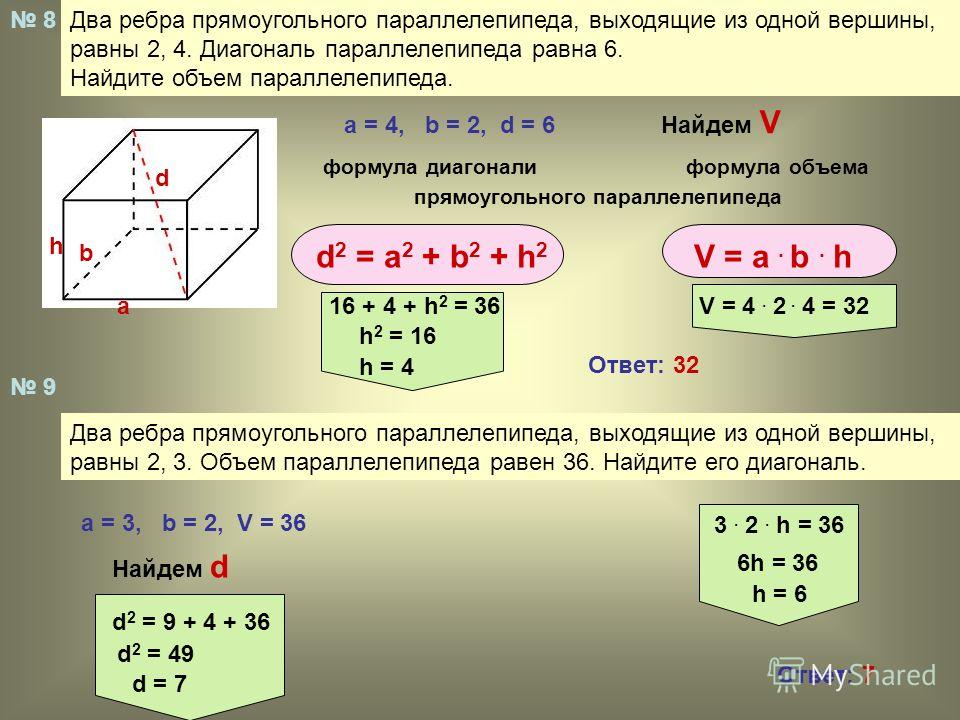 Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда.
Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда.
Объем параллелепипеда равен произведению площади основания на высоту. Из геометрического определения перекрестного произведения мы знаем, что его величина, ∥a×b∥, представляет собой площадь основания параллелограмма и что направление вектора a×b перпендикулярно основанию. Для описания параллелепипеда нам нужны три его смежные стороны и мера углов между ними, или три смежных вектора.
Формула объема параллелепипеда: Формула объема параллелепипеда, образованного векторами \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) с той же начальной точкой задается их скалярным тройным произведением:
\(V=∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\).
V – Объем параллелепипеда, образованного тремя векторами; \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\)
Первый шаг вычисления объема параллелепипеда включает в себя нахождение векторного произведения или векторного произведения \((\vec{a}\times\vec{b})\). Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.
Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.
Последующее скалярное произведение между \((\vec{a}\times\vec{b})\) и \(\vec{c}\) обозначает проекцию \(\vec{a}\times\vec {b}\) на \(\vec{c}\). Другими словами, он перемещает базовый параллелограмм вдоль \(\vec{c}\), аналогично умножению базовой площади на высоту.
Формулу можно упростить и свести к одному определителю:
\(\begin{matrix}
(\vec{a}\times\vec{b})\cdot\vec{c}
&=
\left|
\begin{array}{cc}
a_2 & a_3\\
b_2 & b_3
\end{массив}
\right|
c_1
–
\левый|
\begin{array}{cc}
a_1 & a_3\\
b_1 & b_3
\end{array}
\right|
c_2
+
\левый|
\begin{array}{cc}
a_1 & a_2\\
b_1 & b_2
\end{array}
\right|
c_3
\\
&=
\влево|
\begin{array}{ccc}
c_1 & c_2 & c_3\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{массив}
\right|.
\end{matrix}\)
Это дает нам объем параллелепипеда, когда векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) известны.
Объем параллелепипеда с использованием вершин Если мы знаем вершины параллелепипеда, мы можем найти его векторы, используя простую формулу расстояния. Если \(A < x_1, y_1, z_ 1 >, B < x_2, y_2, z_ 2 >\), \(C < x_3, y_3, z_ 3 >\) и \(D < x_4, y_4, z_ 4 > \) тогда мы можем найти векторы AB =a, AC=b и AD=c, имеющие одну и ту же начальную точку, и использовать их в качестве наших базисных векторов, образующих параллелепипед. AB будет задан как \( a =
Получив векторы a, b и c, выполните следующие простые шаги: Найдите векторное произведение между векторами \(\vec{a}\) и \(\vec{b}\), чтобы получить \(\ vec{a}\times\vec{b}\).
Вычислите скалярное произведение между векторами \(\vec{a}\times\vec{b}\) и \(\vec{c}\), чтобы получить скалярное значение \((\vec{a}\ раз\vec{b})\cdot\vec{c}\).
Определите объем параллелепипеда как абсолютное значение этого скаляра, заданного как \(∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\).
92({\gamma}))}\)
Где,
\(\alpha\) — угол между сторонами b и c;
\(\beta\) – Угол между сторонами а и с; и
\(\gamma\) – угол между сторонами a и b.
Площадь параллелепипедаПлощадь параллелепипеда равна сумме площадей всех его поверхностей. Это называется полной площадью поверхности параллелепипеда. Когда дело доходит до площади 3D-объектов, есть две важные площади поверхности:
- Общая площадь поверхности параллелепипеда
- Площадь боковой поверхности параллелепипеда
Узнайте о площади четырехугольника.
Площадь боковой поверхности параллелепипеда
Площадь боковой поверхности параллелепипеда определяется как сумма площадей поверхностей его граней без учета основания и вершины. Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда.
Площадь боковой поверхности параллелепипеда Формула: \(LSA= 2(a+b){\times}c\)
Общая площадь поверхности параллелепипеда
Полная площадь поверхности параллелепипеда определяется как общая область, покрытая всеми гранями формы.
Общая площадь поверхности параллелепипеда Формула: \(TSA=2(ab+bc+ac)\)
В векторной форме мы можем записать это как
\(A = 2{\times}( ∣\vec{a}{\times}\vec{b}∣ + ∣\vec{b}{\times}\vec{c}∣ + ∣\vec{a}{\times}\vec{c}∣ )\)
Где,
\(∣\vec{a}{\times}\vec{b}|: Величина \; из \; \; перекрестное произведение \; между \; \vec{a}\) и \(\vec{a}\)
\(∣\vec{b}{\times}\vec{c}|: Величина \; of \; \; перекрестное произведение \; между \; \vec{ b}\) и \(\vec{c}\)
\(∣\vec{c}{\times}\vec{a}|: Величина \; of \; \; перекрестное произведение \; между \; \vec{c}\) и \(\vec{b}\)
Площадь параллелепипеда с использованием сторон и углов Существует альтернативный способ расчета площади параллелепипеда с использованием длин его сторон \ (a\), \(b\) и углы. Он находится по формуле
Он находится по формуле
\(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot}sin(\beta))\), где:
\(\alpha\) – угол между b и c;
\(\beta\) – Угол между а и с; и
\(\gamma\) – Угол между a и b.
Прямоугольный параллелепипедПрямоугольный параллелепипед представляет собой многогранник с шестью гранями, также известный как шестигранник. Это трехмерная структура в виде параллелепипеда, все шесть граней которой имеют прямоугольную форму, а длины параллельных ребер равны. Это частный случай параллелепипеда. Прямоугольный параллелепипед аналогичен двумерному прямоугольнику.
Узнайте о прямоугольниках.
Формула прямоугольного параллелепипедаФормула прямоугольного параллелепипеда включает формулу площади поверхности, объема и диагоналей.
Площадь поверхности прямоугольного параллелепипеда
На фигуре прямоугольного параллелепипеда шесть прямоугольников. Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
Площадь поверхности \(= 2(l{\times}h) + 2(l{\times}w) + 2(h{\times}w)\)
\(S = 2[(l{\ times}h) + (l{\times}w) + (h{\times}w)]\)
, где
\(l\), \(w\), \(h\) — длина, ширина, высота прямоугольного параллелепипеда соответственно.
Площадь боковой поверхности прямоугольного параллелепипеда
Произведение периметра основания и высоты называется площадью боковой поверхности. Каждая грань прямоугольного параллелепипеда представляет собой прямоугольник, поэтому периметр основания равен периметру прямоугольника. Ниже приведена формула для LSA (площадь боковой поверхности):
LSA = периметр основания × высота
Поскольку периметр основания равен 2 (длина + ширина)
= 2 (длина + ширина) × высота
\(LSA = 2lh + 2wh\)
где
\(l\), \(w\), \(h\) — длина, ширина и высота прямоугольного параллелепипеда соответственно.
Площадь основания, умноженная на высоту, дает объем прямоугольного параллелепипеда. Основание прямоугольного параллелепипеда — прямоугольник, как и каждая его грань, а его площадь равна произведению его длины на ширину. Формула объема следующая: 92}\)
Решенные примеры на параллелепипедеНекоторые важные решенные примеры на параллелепипеде приведены ниже:
Пример 1: Найдите общую площадь поверхности данного параллелепипеда, если длина 13 см, ширина 12 см и высота 10 см.
Решение: Мы знаем, что
Общая площадь поверхности (TSA) = 2(ab + bc + ac), здесь a = 13 см, b = 12 см, c = 10 см
= 2(13 × 12 + 12 × 10 + 10 × 13 )
= 812 кв.см
Пример 2: Рассмотрим параллелепипед ABCDEFGH с длинами ребер a = 7, b = 5 и c = 3. Если ∠DAE=45°, ∠BAD=63° и ∠BAE=50°, то что площадь поверхности параллелепипеда?
Решение: Здесь
\(\alpha=∠BAD=63°\) – угол между b и c;
\(\beta=∠DAE=45°\) – Угол между а и с; и
\(\gamma=∠BAE=50°\) – угол между a и b.
Площадь поверхности будет равна, будет равна
\(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot} sin (\ beta)) \)
\ (A = 2 \ times (7 {\ cdot} 5 {\ cdot} sin (50) + 5 {\ cdot} 3 {\ cdot} sin (63) + 7 {\ cdot} 3 {\ cdot} sin (45)) \)
\ (A = 2 \ times (35 {\ cdot} sin (50) + 15 {\ cdot} sin (63) + 21 {\ cdot}sin(45))\)
\(A = 110,05\) квадратных единиц
Пример 3: Найти объем параллелепипеда с векторами a = (1, 1, 2), b = (2 , 1, 3) и с = (3, 1, 2).
Решение: Объем параллелепипеда определяется определителем матрицы:
\( V=
{\begin{bmatrix}
c_1 & c_2 & c_3\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{bmatrix}}
\)
Подставляя значения получаем
\( V=
{\begin{bmatrix}
3 & 1 & 2\\
1 & 1 & 2\\
2 & 1 & 3
\end{bmatrix}}
\)
Находим определитель, получаем,
\(V = |3(1\times3 – 2\times1) – 1(1\times3 – 2\times2) + 2( 1\раз1 – 1\раз2)|\)
\(V = |3\times1 – 1\times(-1) + 2\times(-1)|\)
\(V = 2 \) единиц куба.
Надеюсь, эта статья о параллелепипеде была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о параллелепипедеВ.1 Что такое параллелепипед?
Ответ 1 Параллелепипед — это трехмерная фигура или призма с основанием в виде параллелограмма, состоящим из шести сторон параллелограмма.
Q.2 Что такое объем формулы параллелепипеда?
Ответ 2 Формула объема параллелепипеда, образованного векторами \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) с одна и та же начальная точка задается их скалярным тройным произведением:
\(V=∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\)
Q.3 Что площадь параллелепипеда?
Ответ 3 Площадь параллелепипеда равна сумме площадей всех его поверхностей. Это называется полной площадью поверхности параллелепипеда.

 п.)
п.)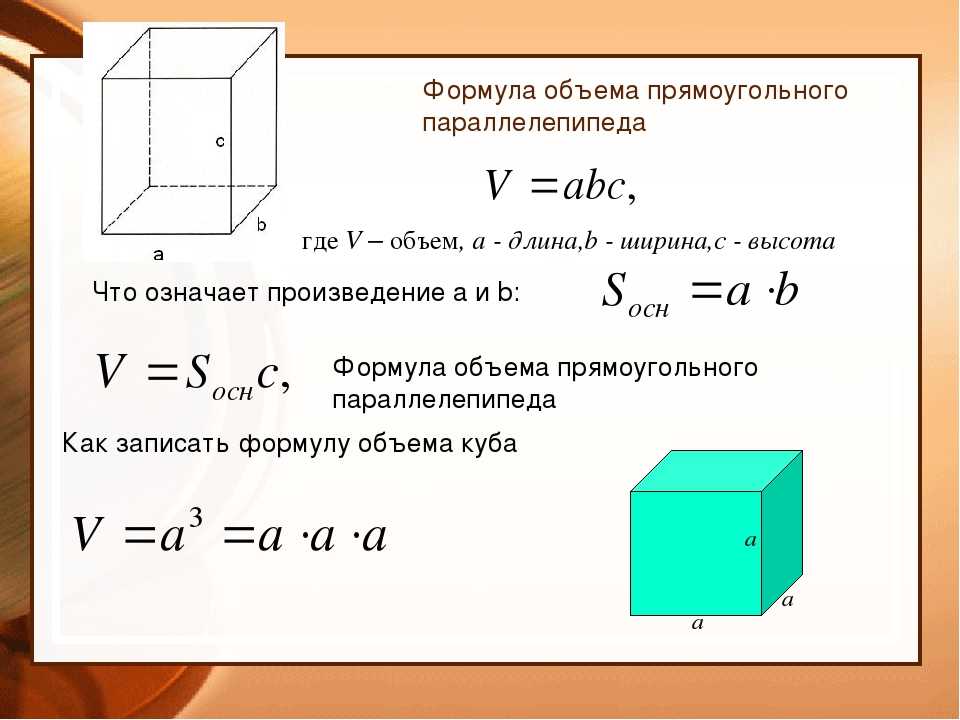
 Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки?