Площадь прямоугольного треугольника формулы все: Площадь прямоугольного треугольника — урок. Математика, 4 класс.

Площадь прямоугольного треугольника – формула через катеты для нахождения и расчета

4.5

Средняя оценка: 4.5

Всего получено оценок: 270.

4.5

Средняя оценка: 4.5

Всего получено оценок: 270.

Площадь прямоугольного треугольника можно найти несколькими способами. Прямой угол в составе любой фигуры добавляет ей свойств и это можно использовать для правильного и быстрого решения задач.

Прямоугольный треугольник

Для начала обсудим сам прямоугольный треугольник, его особенности и свойства. Прямоугольный треугольник это треугольник, в составе которого есть угол.

Прямоугольный треугольник не может быть тупоугольным, потому что тогда сумма углов треугольника превысит 180 градусов, а это невозможно.

В прямоугольном треугольнике две из трех высот совпадают со сторонами – катетами. По этой же причине точка пересечения высот прямоугольного треугольника совпадает с вершиной при прямом угле.

Рис. 1. Все высоты прямоугольного треугольника.

Эта же точка будет центром описанной окружности.

Площадь треугольника

Площадь треугольника обычно находится по стандартной формуле, как половина произведения основания на высоту, проведенную к этому основанию.

$$S={1\over2}*a*h$$

Можно найти площадь как половину произведения сторон на синус угла между ними:

$$S={1\over2}*a*b*sin(g)$$

Существуют усложненные формулы нахождения площади, но они используются крайне редко.

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника находится по тем же формулам, но в некоторых случаях эти формулы можно упростить.

Например, можно воспользоваться тем, что высоты в прямоугольном треугольнике совпадают с катетами. Тогда стандартная формула превратится в следующую:

$S={1\over2}*a*b$, где а и b это катеты прямоугольного треугольника.

Это одна из самых простых формул площади прямоугольного треугольника. Попробуем преобразовать вторую формулу.

$$S={1\over2}*a*b*sin(g)$$

Если вспомнить, что синус угла это отношение противолежащего катета к гипотенузе.

В нашем случае, противолежащий катет обозначим за букву f, потому как а это прилежащий катет, а острый угол может быть заключен только между катетом и гипотенузой. Значит b это гипотенуза.

$S={1\over2}*a*b*sin(g)= {1\over2}*a*b*{f\over{b}}={1\over2}a*f$ – получается все та же формула.

Рис. 2. Рисунок к выводу.

Значит, первый вывод мы осуществили правильно, а у прямоугольного треугольника есть только одна специальная формула для нахождения площади. Если она не подойдет можно воспользоваться общими формулами. Это и есть два возможных пути расчета площади.

Например, если по условию задачи известна гипотенуза, то можно попробовать найти высоту, падающую на гипотенузу и определить площадь по общей формуле. По тому же принципу можно найти площадь через синус, если известны гипотенузы и катет.

Рис. 3. Высота, проведенная к гипотенузе.

Главное помнить, что у любой задачи всегда есть 3 решения и решать каждую наиболее удобным способом.

Что мы узнали?

Мы поговорили о прямоугольных треугольниках и вывели формулу площади прямоугольного треугольника через катеты.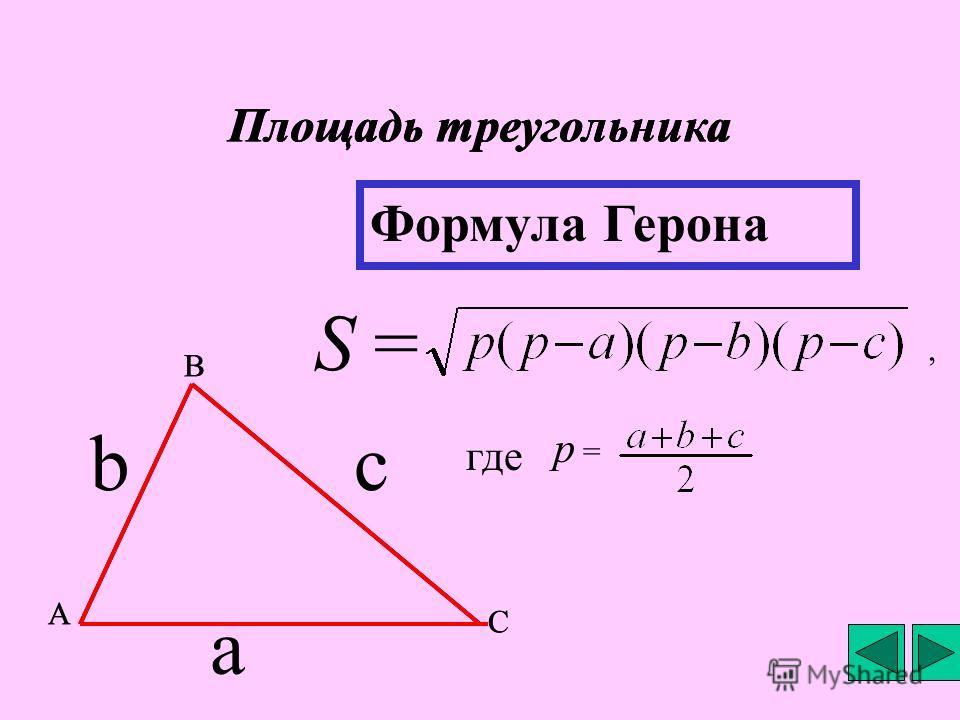 Обсудили общие формулы площади треугольников и сказали, что каждая из этих формул подойдет для решения прямоугольного треугольника.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Titas Blažys

  5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 270.

---

А какая ваша оценка?

Формула площади прямоугольного треугольника

В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90°). Прямоугольный треугольник

характеризуется целым рядом важных свойств, многие из которых составляют основу тригонометрии (например, соотношения между его сторонами и углами). Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника, а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как нахождение площади прямоугольного треугольника, часто приходится решать инженерам, конструкторам и архитекторам.

Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства. Следует заметить, что фронтоны являются обязательными элементами малоэтажных строений (загородных домов, коттеджей, дач).

Нахождение площади прямоугольного треугольника

 

S

=

1 2

ab

 

a – катет

b – катет

S – площадь прямоугольного треугольника

Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель.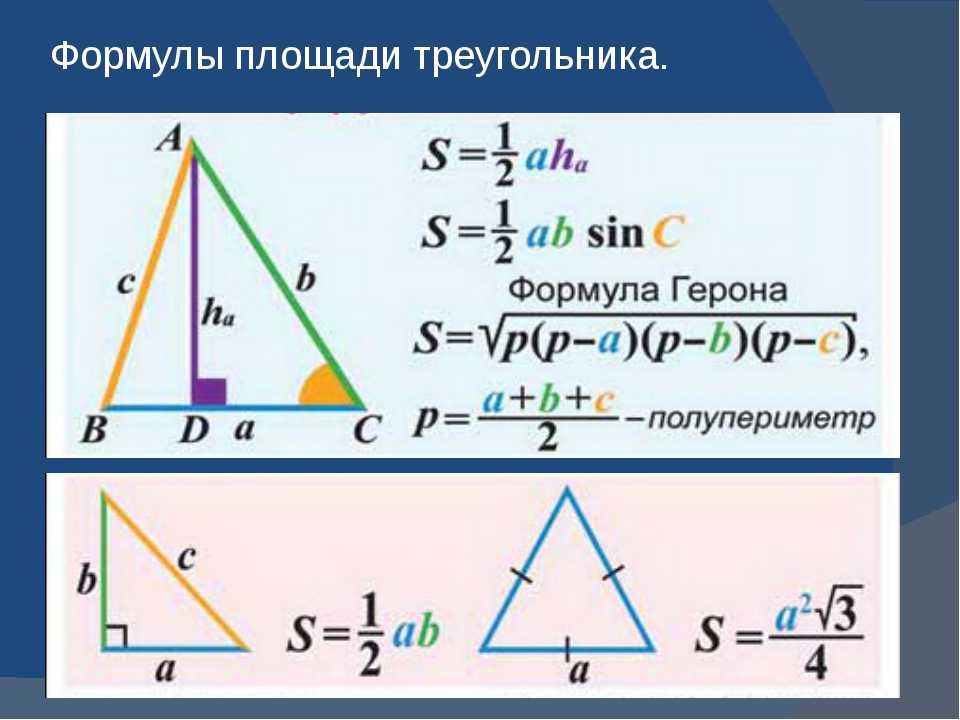 Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой

нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники.

Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины.

Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.

Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.

Как найти площадь прямоугольного треугольника (формула, видео и примеры)

Площадь прямоугольного треугольника (формула и примеры)

---

видео Определения Формула

Прямоугольный треугольник часто встречается в геометрии. Он используется снова и снова в качестве примера, так как предлагает готовый прямой угол, гипотенузу и другие замечательные части. Найти площадь прямоугольного треугольника легко и быстро.

Чему вы научитесь:

Проработав этот урок и видео, вы сможете:

• Определение прямоугольного треугольника
• Манипуляции с прямоугольным треугольником, чтобы найти все его высоты или высоты
• Вспомните и примените формулу ½ основания x высота, чтобы найти площадь прямоугольного треугольника

Прямоугольный треугольник

Давайте создадим прямоугольный треугольник , △CAS, с прямым углом ∠A.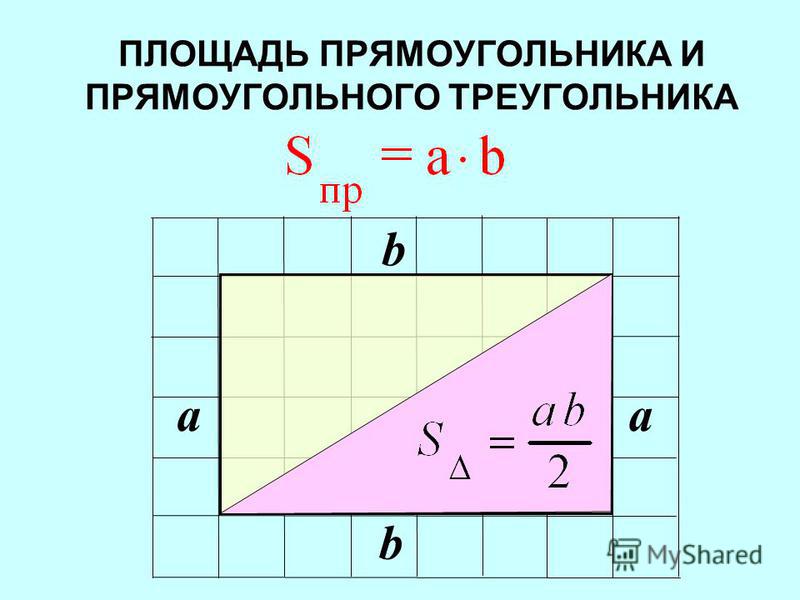 Он измеряет 90 ° и имеет гипотенузу или самую длинную сторону, противоположную ей. Это сторона SC, длиной 30 ярдов. Это прямоугольный треугольник, потому что у него прямой угол, а не потому, что он обращен вправо.

Вставьте первый рисунок: прямоугольный треугольник, △CAS, ∠A — прямой угол, ∠C ≈53,1, ∠S ≈36,8. Чертеж ориентирован так, чтобы стороны CA и AS образовывали вертикаль и горизонталь. Поверните для второго рисунка так, чтобы AS был вертикальным, а CA — горизонтальным. Поверните для третьего рисунка так, чтобы сторона SC была горизонтальной, и введите высоту от ∠A до точки H на стороне SC. Треугольник и высота образуют фигуру CASH.

Слово «правый» относится к латинскому слову rectus , что означает «вертикальный». Прямой угол показывает одну линию или отрезок прямой относительно другой; прямоугольный треугольник имеет прямой угол.

Основание

Основание любого треугольника — это сторона, используемая для создания высоты или высоты противоположной вершины. По тому, как сидит наш △CAS, вы можете легко увидеть, что сторона AS является основанием для высоты CA до ∠C. Сторона CA является основанием для высоты AS.

[вставьте второй рисунок]

Для прямоугольного треугольника стороны, прилегающие к прямому углу, выполняют двойную функцию в качестве оснований и высот, что делает вычисления площади очень, очень простыми.

Высота или высота

Высота любого треугольника — это перпендикуляр от основания (стороны) к противоположной вершине. Для нашего △CAS мы можем повернуть фигуру еще раз и положить сторону SC на горизонталь, а затем построить высоту от ∠A до основания. Точку пересечения с SC можно обозначить как H. Теперь у нас есть △CAS и точка H; ДЕНЕЖНЫЕ СРЕДСТВА!

Площадь прямоугольного треугольника Формула

Площадь прямоугольного треугольника является мерой его внутреннего пространства в квадратных единицах. Для любого треугольника формула:

A = 12 (основание × высота)

Для прямоугольного треугольника это действительно очень легко вычислить, используя две стороны, которые не являются гипотенузой. В нашем △CAS мы можем использовать сторону AS, 24 ярда, в качестве базы, составив сторону CA, 18 ярдов, высоту:

A = 12 bh

A = 12 (24 × 18)

A = 12 (432 )

A = 216 ярдов2

Если мы повернем прямоугольный треугольник и возьмем сторону CA в качестве основания, AS станет высотой, и вы получите тот же ответ!

A = 12 (18 × 24)

A = 12 (432)

A = 216 ярдов2

Поверните его еще раз и используйте сторону SC, 30 ярдов, в качестве основания, с построенной высотой AH, которая составляет 14,4 ярда в высоту:

[Вставьте третий рисунок]

A = 12 BH

A = 12 (30 × 14,4)

A = 12 (432)

A = 216 YDS2

A = 12 (432)

A = 216 YDS2

A = 12 (432)

A = 216 YDS2

A = 12 (432)

A = 216 YDS2

A = 12 (432)

A = 216 YDS2

A = 12 (432)

A = 216 YDS2

A = Все три стороны, все три высоты или высоты, и все три ответа одинаковы! Помните, что площадь всегда выражается в квадратных единицах линейного измерения (ярдах в нашем треугольнике).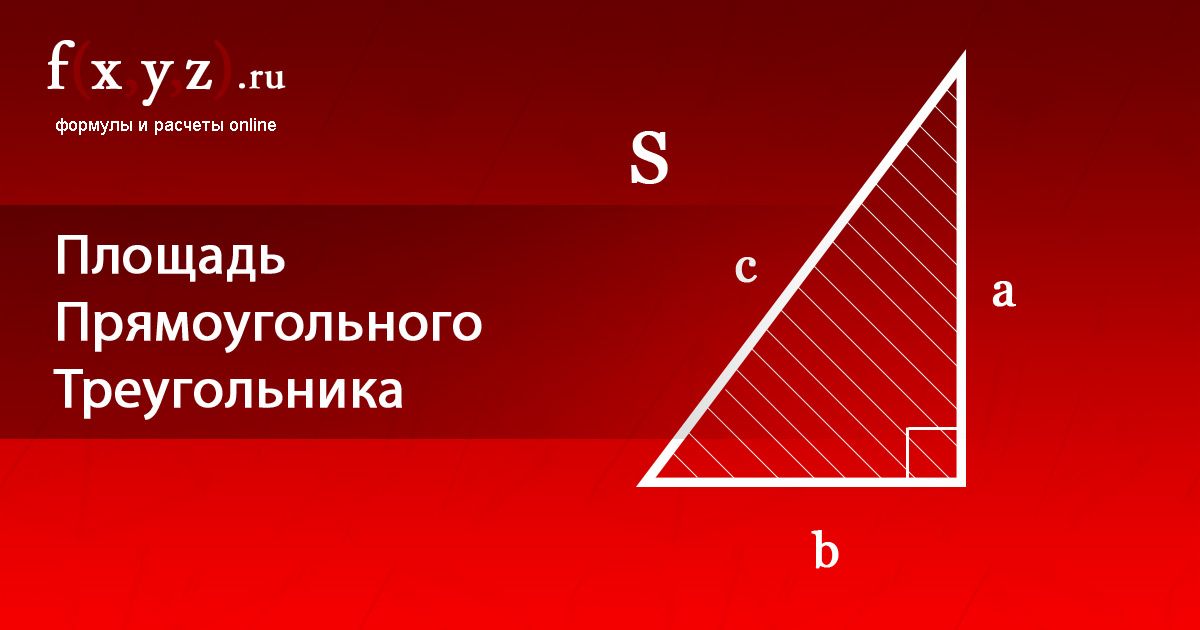

Итоги урока

После повторения этого урока вы теперь в состоянии определить прямоугольный треугольник, манипулировать прямоугольным треугольником, чтобы найти все его высоты или высоты, а также вспомнить и применить формулу ½ основания x высота, чтобы найти площадь прямоугольного треугольника. треугольник.

Следующий урок:

Как найти периметр треугольника

Как найти основание, высоту и площадь треугольников (прямоугольных, остроугольных или тупоугольных!)

Почему все треугольники не могут быть одинаковыми? Было бы неплохо, если бы равнобедренные, равнобедренные, остроугольные и тупоугольные треугольники подчинялись тем же правилам, что и прямоугольные треугольники, но, к сожалению, это не так. Пусть вас не смущают дурацкие названия фигур, у каждого типа треугольника есть простая формула для нахождения площади, основания и высоты. Возможно, самый простой способ приблизиться к этим формулам — начать с самой простой формы треугольника: прямоугольного треугольника.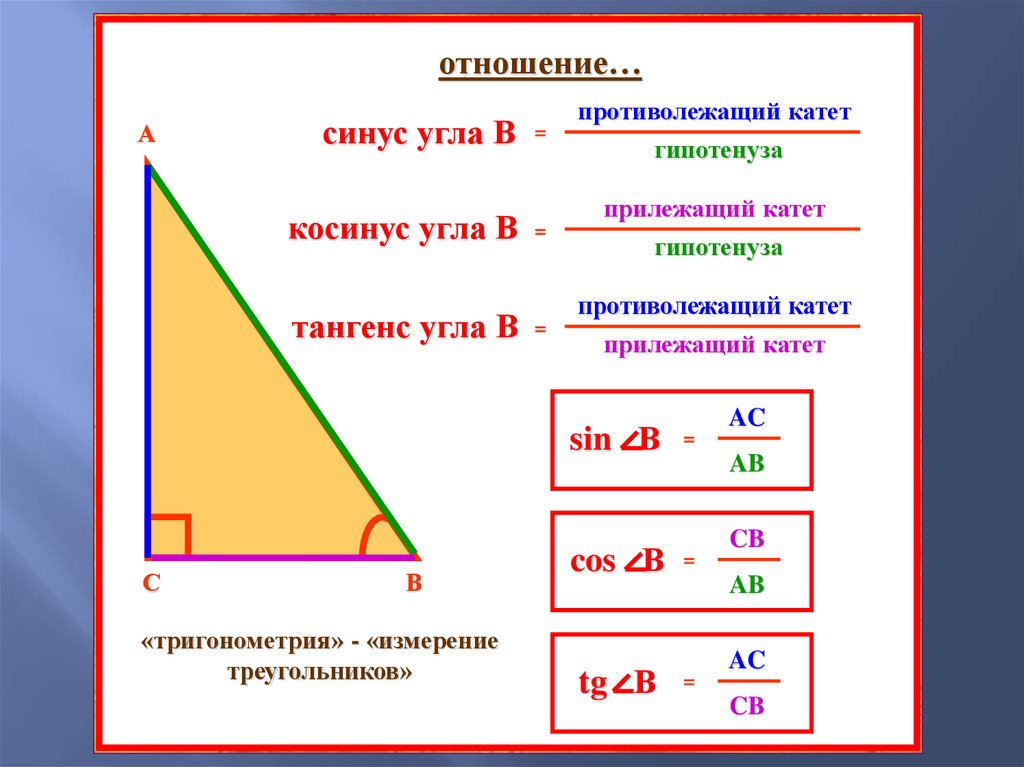

Прямоугольные треугольники

Прямоугольный треугольник характеризуется одним углом 90°, основанием, высотой и гипотенузой. Основание и высота — это две смежные стороны прямого угла. Гипотенуза — это сторона, противоположная прямому углу, и она самая длинная из трех.

Нахождение площади прямоугольного треугольника

В геометрии нам часто нужно найти площадь треугольника. Мы можем найти площадь треугольника только тогда, когда нам известны длины двух сторон. Легче всего вычислить площадь, когда мы знаем длину основания и высоту. Если у нас есть эта информация, мы можем использовать следующее уравнение для определения площади:

A = ½ Основание × Высота

Давайте используем эту формулу, чтобы найти площадь треугольника ниже:

A = ½ BASE × HEIGHT 29929 A

= = = = = = = = = = = = = = = = = = = = = = = = = = = = . ½ (6 × 7)
А = ½ (54)
А = 27

Достаточно просто, правда? Однако в геометрии нам не всегда даются размеры основания и высоты. В этом случае нам нужно сделать еще несколько шагов, чтобы найти площадь прямоугольного треугольника. Итак, давайте пройдем процесс определения основания и высоты прямоугольного треугольника, чтобы мы могли выполнить формулу A = ½ основание ×  высота .

Нахождение основания и высоты с помощью теоремы Пифагора

Мы используем теорему Пифагора для определения длин сторон прямоугольного треугольника. Уравнение выглядит следующим образом:

a ² + b ²  = c ²

Переменные a и b представляют собой основание и высоту треугольника, а переменная c представляет гипотензу. В этом примере более короткие длины треугольника (основание и высота) находятся в левой части уравнения, тогда как самая длинная сторона (гипотенуза) находится в правой части.

Воспользуемся теоремой Пифагора, чтобы найти основание треугольника ниже:

a ² + b ² = c ²
a ² + (12) ² = (15) ²
a ² ² + 144 = 225
A ² = 225 — 144
A ² = 225 — 144
A ² = 81
A = √81
a =

9

7 треугольника является целым числом 9. Поскольку все длины сторон этого треугольника являются целыми числами (целыми числами без десятичной точки), эта комбинация чисел квалифицируется как 9.0024 пифагорейская тройка . Типичными примерами пифагорейских троек являются 3:4:5, 6:8:10, 9:12:15 и 8:15:17.

Однако большинство комбинаций длин сторон не приводят к тому, что все числа являются целыми числами. Поскольку теорема Пифагора имеет дело с квадратными корнями, длина одной из сторон обычно округляется до сотого знака после запятой.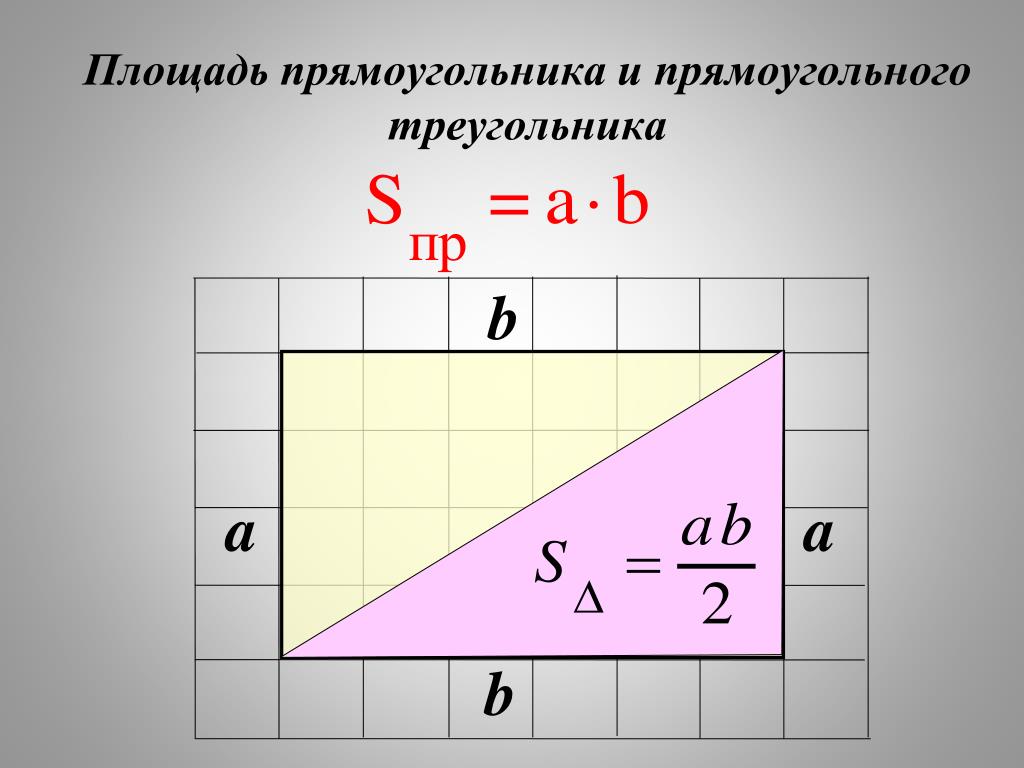

Найдем недостающую высоту треугольника, который не дает целое число:

a ² + b ² = c ²
(7) ² + b ² = (13) ²

49 + b ² = 169
b ² = 169 – 49
b ² = 169 – 49
b ² = 120
b = 120
B = 10,95

Теперь, когда мы знаем высоту треугольника, давайте решим для области:

A = ½ Основание × Высота
A = ½ (7 × .999559595959595995959959999599995999959999995995 )
А = ½ (7 ×   10,95)
А = ½ (7 ×   6,65)
A = 38,32

Это так просто!

Использование площади для определения основания и высоты

Как определить основание и высоту прямоугольного треугольника, зная только площадь и длину одной стороны? Вы не можете использовать теорему Пифагора, потому что для этого требуются две длины сторон.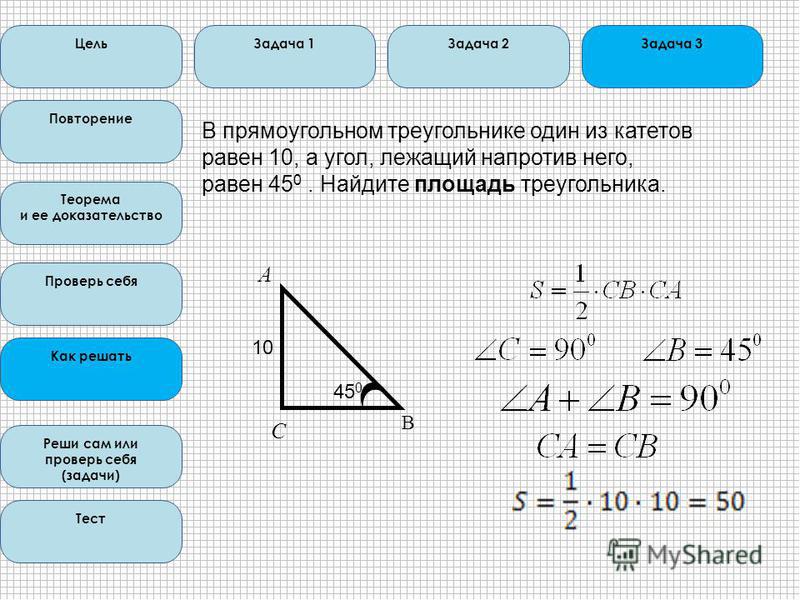 Вместо этого вы можете изменить формулу площади, чтобы найти недостающую длину стороны:

A = ½ основания × высота
2 × A = (½ основания × высота) × 2
2A = основание × высота
2A/основание = высота или 2A/высота = основание

Давайте воспользуемся приведенной выше формулой, чтобы найти высоту треугольника ниже:

Воспользуемся той же формулой для нахождения основания треугольника:

Нахождение площади остроугольного треугольника угол. Формула, которую вы используете, зависит от того, с каким типом треугольника мы работаем. Если мы хотим найти площади остроугольного треугольника , нам нужно будет применить одну из следующих трех формул синуса: ) = Площадь

Чтобы определить площадь остроугольного треугольника, мы должны знать длины двух сторон и угол, противоположный третьей стороне. Формула, которую мы используем, зависит от того, какую комбинацию сторон и углов мы знаем.

В треугольнике ниже мы знаем длины сторон a и b. Мы также знаем меру угла c. Поэтому мы можем использовать формулу ½ ab sin(c)  для определения площади этого треугольника:

½ ab sin(c) = A
½ (25 ° 22 = 90° 22) sin
½ (25 × 22) SIN (40 °) = A
½ (550) × 0,64 =
275 × 0,64 = A
176 = A

7 . Тупой угол

Нахождение площади тупоугольного треугольника требует другого метода. Вместо того, чтобы сразу использовать функцию синуса, мы создадим прямой угол, сформировав прямую линию, которая выходит из обеих точек C и A. Точка, в которой эти две линии пересекаются, образует прямой угол. Назовем новый треугольник DEF. Для обоих этих треугольников заглавные буквы обозначают углы. Строчная версия каждой буквы представляет соответствующую длину стороны для каждого угла:

Мы можем найти площадь тупоугольного треугольника, проведя линию высоты.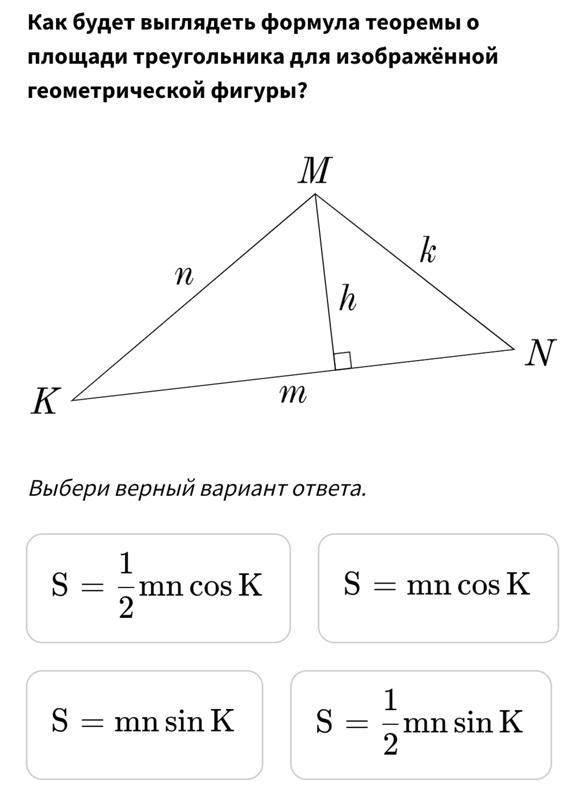 Высота треугольника ABC была создана путем формирования линии, обозначенной h (высота). Поскольку ACD — прямоугольный треугольник, мы можем найти его площадь с помощью уравнения A = ½ основания × высоты.  Мы также можем определить площадь большего треугольника ABD, используя это уравнение. Чтобы найти площадь тупоугольного треугольника ABC, мы должны затем вычесть площадь ACD из ABD:
Площадь ABC = Площадь ABD – Площадь ACD

В зависимости от предоставленной информации мы можем использовать геометрические доказательства и выполнить формулы синуса и найти недостающие длины сторон. Когда у нас будет достаточно информации, чтобы найти площади треугольника ABD и треугольника ACD, мы можем использовать вычитание, чтобы найти площадь треугольника ABC.

Нахождение площади с помощью многоэтапных формул

Давайте применим многочисленные методы определения площади к тупоугольному треугольнику DEF:

Первым шагом к нахождению площади является нахождение недостающих длин.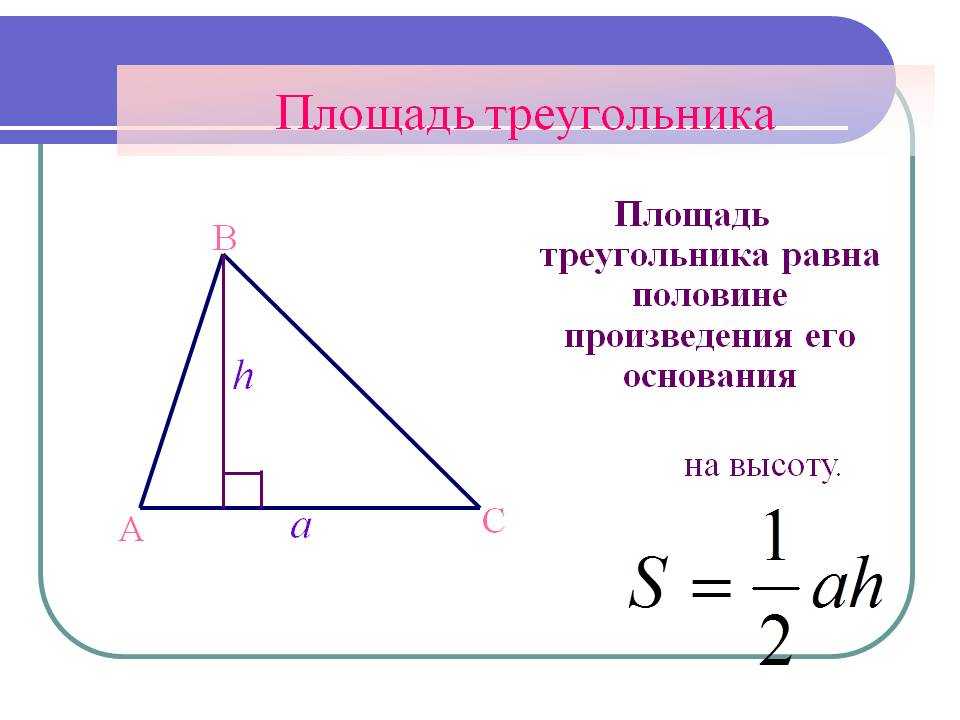 Вы можете определить длину основания меньшего прямоугольного треугольника, вычитая 28–20 = 8. Чтобы вычислить высоту этого треугольника, мы должны использовать теорему Пифагора:

8 ² + (высота) ² = 172
64 + (высота) ² = 289
(высота) ² = 289 – 64
(высота) ² = 289 – 64
(высота) ² = 225
(высота) = 225
(высота) = 15

Как видите, этот прямоугольный треугольник представляет собой квадратную тройку, поскольку все его измерения являются целыми числами. Давайте используем высоту и основание, чтобы найти площадь этого прямоугольного треугольника:

A = ½ основание × высота
A = ½ (8 × 15)
A = ½ (120)

A
A = 60

Теперь найдем площадь большего прямоугольного треугольника:

A = ½ (15 × 28)
A = ½ (15 × 28)
A = ½ (420)
A = 2 10

Наконец, давайте вычтем две площади, чтобы найти площадь треугольника DEF:

Площадь треугольника 210 – 60
Площадь DEF = 210 – 60
Площадь DEF = 150

---

Если вам все еще трудно понять площади треугольников, высоты и основания, не чувствуйте себя побежденным.

No related posts.