Площадь ромба: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.
p|number:4 $} - Площать: {$ result.s|number:4 $}
p|number:4 $}Ромб — это четырехугольник, все стороны которого одинаковы. Ромб представляет собой частный случай параллелограмма, а квадрат — частный случай ромба. Следовательно, каждый квадрат — это ромб, а каждый ромб — параллелограмм.
Геометрия ромба
Термин «ромб» с греческого языка означает «бубен», который в древности выполняли в виде четырехугольника, а не круга. Ромб — равносторонний параллелограмм с неравными углами. Любой равносторонний четырехугольник, который имеет два острых и два тупых угла может называться ромбом. Таким образом, ромб в отличие от квадрата является косоугольником. Параллелограмм будет считаться ромбом, если фигура соответствует хотя бы одному из условий:
- две смежные стороны равны, соответственно, равны все стороны;
- диагонали фигуры пересекаются под прямым углом;
- все высоты косоугольника равны;
- диагонали делят четырехугольник на 4 одинаковых прямоугольных треугольника;
- одна из диагоналей является биссектрисой для внутренних треугольников.
Данная фигура в своей классической форме не часто встречается в реальной жизни. Чаще всего ромбы можно найти в металлообработке: пластины резцов различных инструментов имеют именно ромбовидную форму. Кроме того, ромбические элементы встречаются в архитектуре и строительстве, а наиболее очевидным примером реального ромба является тротуарная плитка. Встречая ромбы в реальности, вам может понадобиться определить площадь данной фигуры для решения практических задач.
Площадь ромба
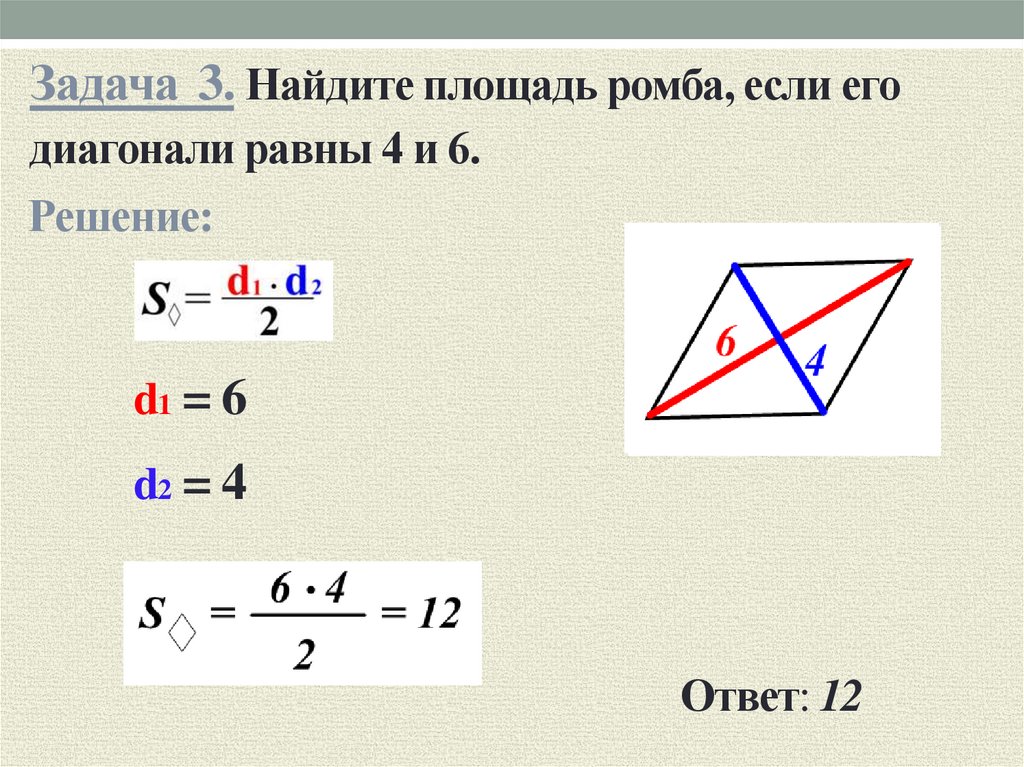
Площадь ромба — это плоскость, ограниченная периметром фигуры. Площадь такого четырехугольника можно найти шестью способами, используя для расчетов такие параметры как величины углов, длины сторон или диагоналей. Наиболее простая формула для определения площади ромбовидной фигуры оперирует диагоналями. Диагональ ромба — это отрезок, который соединяет вершины противоположных углов косоугольника. Зная длину диагоналей ромба, вы можете вычислить площадь по следующей формуле:
S = 0,5 d1 × d2
Для определения площади ромба вы можете использовать наш онлайн-сервис, который позволяет найти не только площадь или периметр фигуры, но и определяет ее углы, длину сторон и высоту.
Для вычислений вам потребуется ввести в форму два параметра на выбор:
- две диагонали;
- высоту и сторону.
Зная эти два значения, программа рассчитает все остальные свойства ромба, которые могут вам понадобиться при решении практических задач. Рассмотрим пару примеров.
Примеры из реальной жизни
Плитка
Ранее мы выяснили, что тротуарная плитка — это самый банальный пример ромбических фигур в реальной жизни. Допустим, есть участок, который вы хотите замостить такой плиткой. Для определения необходимого количества плитки, которое нужно закупить, вам потребуется узнать два параметра: площадь участка и площадь одного элемента тротуарного покрытия. Пусть площадь участка составляет 20 квадратных метров, а диагонали плитки равны 20 см и 10 см. Для правильного расчета необходимо выразить длину диагоналей в метрах (0,2 и 0,1 м) и ввести их в поля «Диагонали». Вы получите результат в виде:
S = 0,01
Следовательно, площадь одного элемента составляет 0,01 квадратных метров, и вам понадобится 2 000 маленьких ромбов для обустройства участка.
Геральдика
Большая часть гербов исполняется на ромбовидных геральдических щитах. Если вы захотите сделать собственный ромбовидный герб для фестиваля исторической реконструкции, то вам понадобится узнать, сколько ткани нужно для его создания. Вы можете прикинуть только длину стороны и высоту ромба. Пусть высота фигуры составляет 0,3 м, а сторона — 0,5 м. Тогда площадь герба будет равна:
S = 0,15
Таким образом, для создания герба вам понадобится 0,15 квадратных метров ткани.
Заключение
Ромб не занимает в реальной жизни человека значимое место: фигура встречается нечасто, в основном в машиностроении, архитектуре и дизайне. Для решения практических задач или школьных заданий вы можете воспользоваться онлайн-калькулятором, который мгновенно выдаст вам не только правильный результат, но и вычислит углы, стороны и высоту ромба.
Площадь ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти площадь ромба по известным элементам. Для нахождения площади ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить».
Теоретическую часть смотрите ниже.
Содержание
- Площадь ромба через сторону и угол
- Площадь ромба через диагонали
- Площадь ромба через сторону и высоту
- Площадь ромба через угол и противолежащую диагональ
- Площадь ромба через угол и диагональ из данного угла
- Площадь ромба через угол и радиус вписанной в ромб окружности
- Площадь ромба через сторону и радиус вписанной в ромб окружностии
1. Площадь ромба через сторону и угол
Пусть задан ромб ABCD (Рис.1). Выведем формулу вычисления площади ромба через сторону и угол.
Проведем диагональ AC. Тогда ромб делится на два треугольника ABC и ADC.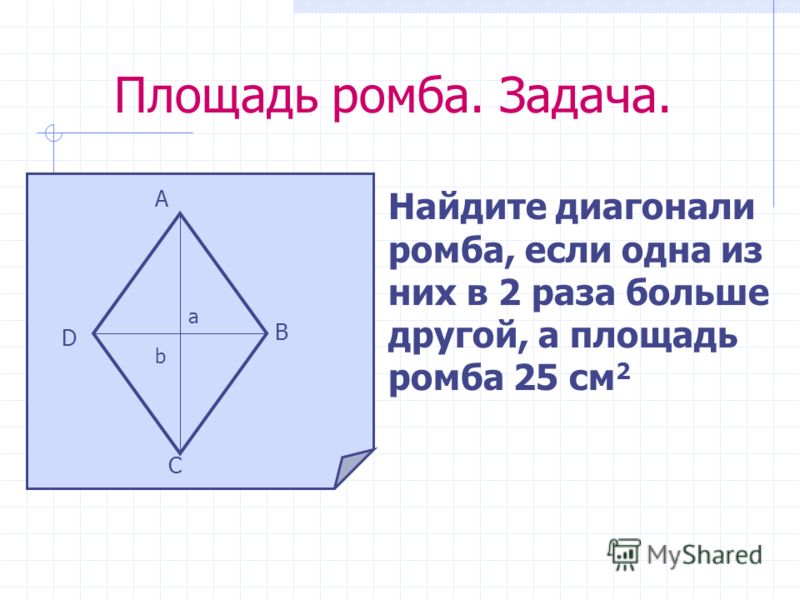
2 \cdot \sin \alpha .\)
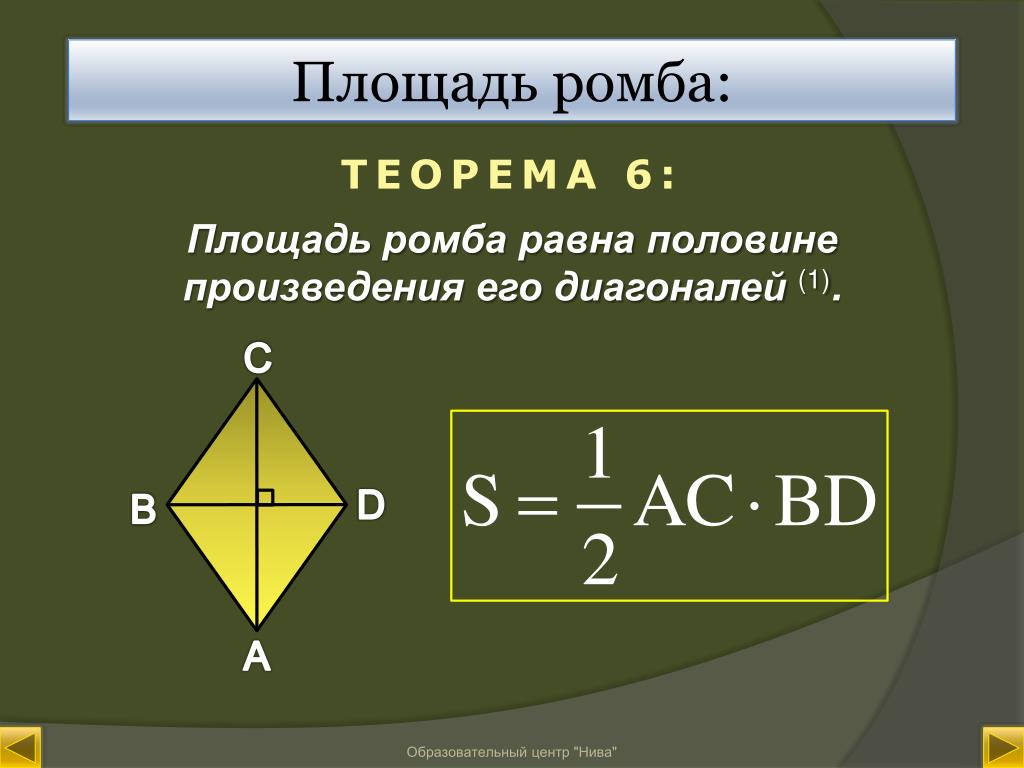
2. Площадь ромба через диагонали
Пусть известны диагонали d1 и d2 ромба ABCD (Рис.2). Выведем формулу вычисления площади ромба через диагонали.
Поскольку диагонали ромба перепендикулярны и точкой пересечения делятся пополам (свойства 6 и 5 ромба), то они разделяют ромб на четыре прямоугольных треугольника. Тогда эти прямоугольные треугольники равны по двум катетам: \( \small \frac{d_1}{2} \) и \( \small \frac{d_2}{2} \).
Площадь прямоугольного треугольника AOB равна:
| \(\small S_{AOB}=\frac{\large 1}{\large 2} \cdot \frac{\large d_1}{\large 2} \cdot \frac{\large d_2}{\large 2}\) \(\small =\frac{\large d_1 \cdot d_2}{\large 8} .\) |
Тогда площадь ромба равна:
| \(\small S=4 \cdot S_{AOB}= 4 \cdot \frac{\large d_1 \ \cdot \ d_2}{\large 8} \) |
или
\(\small S= \frac{\large d_1 \ \cdot \ d_2}{\large 2} . | (2) |
3. Площадь ромба через сторону и высоту
Пусть известны сторона a и высота h ромба (Рис.3). Так как ромб является параллелограммом, то площадь ромба вычисляется по формуле площади параллелограмма:
| \(\small S= a\cdot h.\) | (3) |
4. Площадь ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащий диагональ d=AC (Рис.4). Выведем формулу вычисления площади ромба.
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_{AOB}= \frac{\large 1 }{\large 2} \cdot AO \cdot OB .\) | (3) |
Но
| \(\small \frac{\large OB }{\large AO} = \mathrm{ctg} \ \angle ABO \) \(\small = \mathrm{ctg} \ \frac{\large \alpha}{\large 2} \) |
или
\(\small OB= AO \cdot \mathrm{ctg} \ \frac{\large \alpha}{\large 2} . 2 }{\large 2} \cdot \mathrm{ctg} \ \frac{\large \alpha}{\large 2}.\) | (6) |
5. Площадь ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠BAD ромба и диагональ из данного угла d=AC (Рис.5). Выведем формулу вычисления площади ромба.
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
| \(\small S_{AOB}= \frac{\large 1 }{\large 2} \cdot AO \cdot OB .\) |
Но
| \(\small \frac{\large OB }{\large AO} = \mathrm{tg} \ \angle BAO \) \(\small = \mathrm{tg} \ \frac{\large \alpha}{\large 2} \) |
или
| \(\small OB= AO \cdot \mathrm{tg} \ \frac{\large \alpha}{\large 2} .\) | (8) |
Подставим (8) в (7):
\(\small S_{AOB}= \frac{\large 1 }{\large 2} \cdot AO \cdot AO \cdot \mathrm{tg} \ \frac{\large \alpha}{\large 2}. 2 }{\large 2} \cdot \mathrm{tg} \ \frac{\large \alpha}{\large 2}.\) | (10) |
6. Площадь ромба через угол и радиус вписанной в ромб окружности
Пусть известны один из углов α=∠ABC ромба и радиус r вписанной в ромб окружности (Рис.6). Выведем формулу вычисления площади ромба.
Как мы отметили выше, диагонали разделяют ромб на четыре равных прямоугольных треугольника. В частности
| \( \small ⊿AOB=⊿ BOC \) | (11) |
Тогда \( \small \angle BAO=\angle BCO=90°-\frac{ \large \alpha }{\large 2} \). Треугольники AKO и CLO также прямоугольные. Следовательно
| \( \small \angle 1=90°- \angle BAO \) \( \small =90°- (90°-\frac{ \large \alpha }{\large 2}) \) \( \small =\frac{ \large \alpha }{\large 2}, \) | (12) |
\( \small \angle 2=90°- \angle BCO \) \( \small =90°- (90°-\frac{ \large \alpha }{\large 2}) \) \( \small =\frac{ \large \alpha }{\large 2}. \) | (13) |
Применим теорему синусов для прямоугольного треугольника AOB
| \( \small \frac{\large AO}{\large \sin \frac{ \alpha }{2}}= \frac{\large OB}{\large \sin \left( 90°-\frac{ \alpha }{ 2} \right) }\) \( \small =\frac{\large OB}{\large \cos \frac{ \alpha }{ 2} } \) |
Откуда
| \( \small OB=\frac{\large AO \ \cdot \ \cos \frac{ \alpha }{2} }{\large \sin \frac{ \alpha }{2}} \) | (14) |
Для прямоугольного треугольника AKO имеем:
| \( \small \frac{\large KO}{\large AO}=\cos \angle 1 \) |
или, учитывая (12) и KO=r:
| \( \small AO= \frac{\large r}{\large \cos \frac{ \alpha }{2}} \) | (15) |
Подставляя (15) в (14), получим:
| \( \small OB=\frac{\large r \ \cdot \ \cos \frac{ \alpha }{2} }{\large \cos \frac{ \alpha }{2}\ \cdot \ \sin \frac{ \alpha }{2}} \) |
или
| \( \small OB=\frac{\large r }{\large \sin \frac{ \alpha }{2}} \) | (16) |
Найдем площадь треугольника AOB:
| \( \small S_{AOB}=\frac{\large 1 }{\large 2} \cdot AO \cdot OB\) | (17) |
Подставляя (15) и (16) в (17), получим:
\( \small S_{AOB}=\frac{\large 1 }{\large 2} \cdot \frac{\large r}{\large \cos \frac{ \alpha }{2}} \cdot \frac{\large r }{\large \sin \frac{ \alpha }{2}}\) \( \small =\frac{\large r^2}{\large \s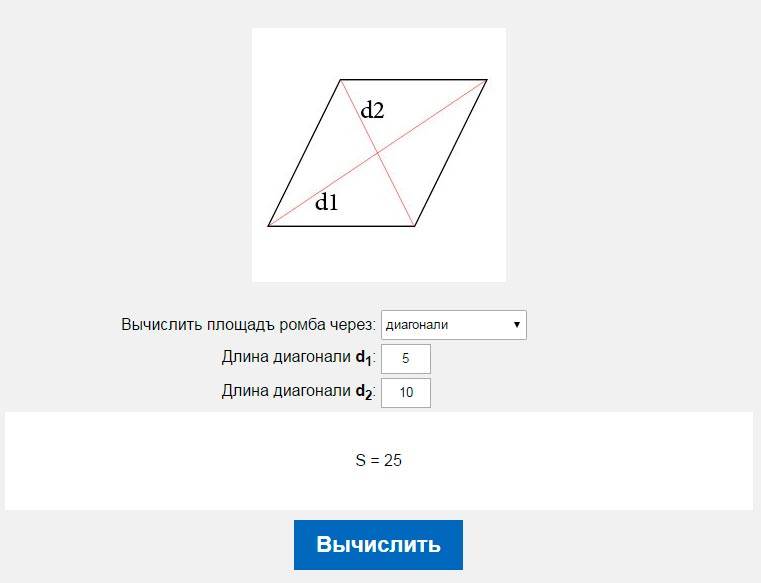in \alpha}. 2}{\large \sin \alpha}.\) | (18) |
7. Площадь ромба через сторону и радиус вписанной в ромб окружности
Пусть известны сторона a=AB ромба и радиус r вписанной в ромб окружности (Рис.7). Найдем площадь ромба.
Прямая AB является касательной к окружности вписанной в ромб. Тогда \( \small OK ⊥ AB \). Прямая CD является касательной к окружности вписанной в ромб. Тогда \( \small OL ⊥ CD \). Поэтому треугольники BKO и DLO прямоугольные. Эти треугольники равны по гипотенузе и катету (BO=OD, KO=OL). Тогда \( \small \angle BOK=\angle DOL \). Углы BOK и KOD смежные. Следовательно \( \small \angle KOD=180°-\angle BOK. \) \( \small \angle KOD+\angle DOL \) \( \small =180°-\angle BOK+\angle DOL=180°. \) Получили, что отрезки KO и OL находятся на одной прямой. То есть KL=KO+OL=2r. Поскольку \( \small KL ⊥ AB, \) то является высотой ромба.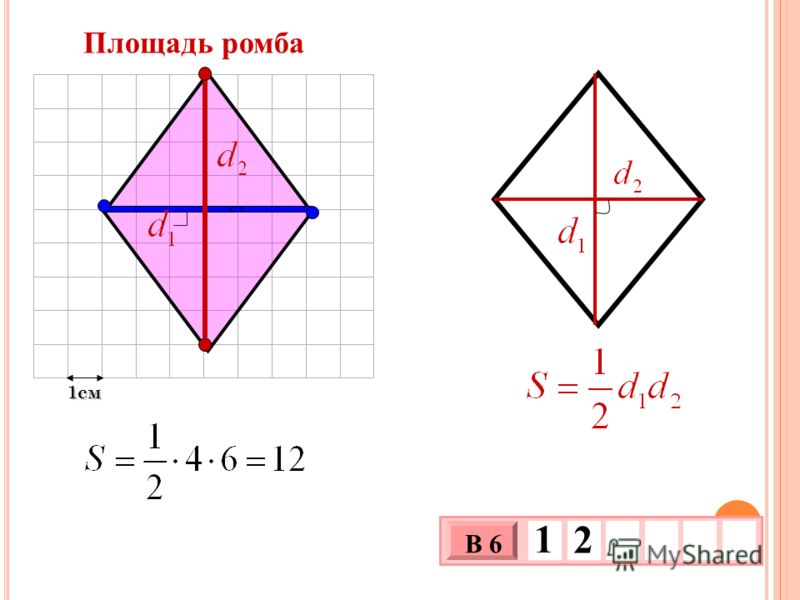
Площадь ромба по стороне и высоте вычисляется из формулы (3). Тогда имеем:
| \( \small S=AB \cdot KL=a \cdot 2r\) |
или
| \( \small S=2a r. \) | (19) |
Площадь ромба
Для полной функциональности сайта желательно включить JavaScript в настройках Вашего браузера.
Главная
→
Геометрия
→
Площадь ромба
Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.
Таблица с формулами площади ромба (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь ромба по стороне и высоте
.
.. подготовка …
a — сторона
h — высота
2
Площадь ромба по двум диагоналям
… подготовка …
d1 — диагональ
d2 — диагональ
3
Площадь ромба по углу и противолежащей диагонали
… подготовка …
d — диагональ
α° — угол между сторонами
4
Площадь ромба по углу и диагонали проведенной из этого угла
… подготовка …
d — диагональ
α° — угол между сторонами
5
Площадь ромба по стороне и углу между сторонами
.
.. подготовка …
a — сторона
α° — угол между сторонами
6
Площадь ромба по радиусу вписанной окружности и углу между сторонами
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
7
Площадь ромба по радиусу вписанной окружности и стороне
… подготовка …
a — сторона
r — радиус вписанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.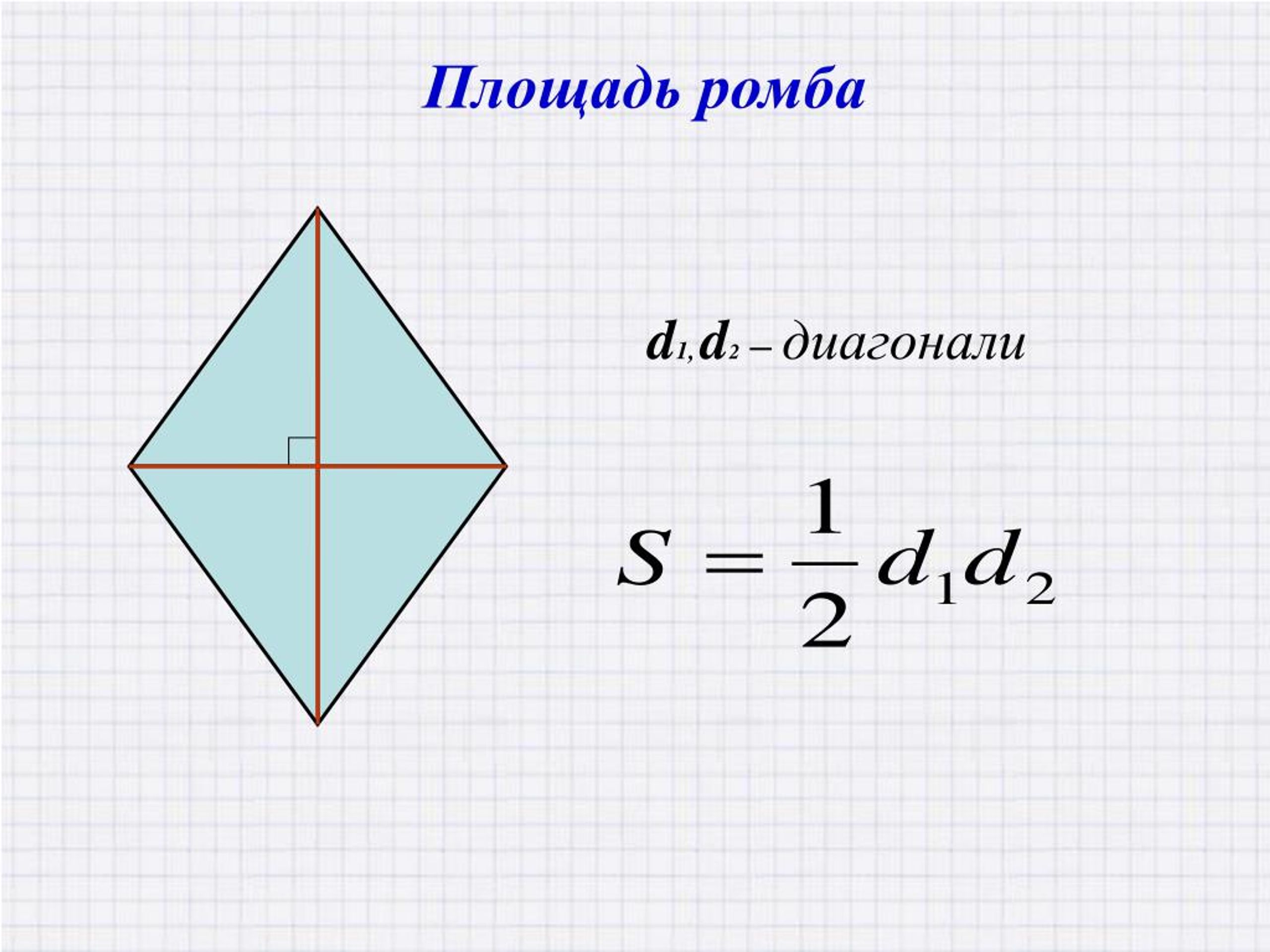
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | сторона и высота | ||
| 2 | диагонали | ||
| 3 | диагональ и угол между сторонами | ||
| 4 | диагональ и угол между сторонами | ||
| 5 | сторона и угол между сторонами | ||
| 6 | радиус вписанной окружности и угол между сторонами | ||
| 7 | сторона и радиус вписанной окружности |
Определения
Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Ромб – это частный случай параллелограмма.
Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Площадь ромба — MathCracker.com
Решатели Алгебра
Инструкции: Используйте этот калькулятор, чтобы найти площадь ромба с заданными диагоналями p и q.
Пожалуйста, укажите диагонали в форме ниже.
Одна диагональ \(p\) ромба (пример: 2 или 3/2 и т. д.)
Другая диагональ \(q\) ромба (пример: 2 или 3/2 и т. д.)
Подробнее об этой области ромбовидного калькулятора
Этот калькулятор рассчитает для вас площадь ромба для двух диагоналей ромба, которые вы предоставите. Предоставленные диагонали должны быть действительными числовыми выражения. Вы можете ввести любые допустимые выражения, включая числа, такие как «4» или «3,56», или алгебраические выражения, такие как «2/3» или «sqrt (3)».
Все, что вам нужно сделать, это указать два допустимых выражения, представляющих диагонали, а затем нажать кнопку «Рассчитать», и все шаги расчета будут показаны.
Вычисление площади ромба, пожалуй, менее распространенная задача, по крайней мере, по сравнению с вычислением площади ромба. площадь прямоугольника и площадь квадрата. Тем не менее, расчет геометрических площадей является важным навыком выучил по алгебре.
Как вычислить площадь ромба?
Используя соображения симметрии, вычисление площади ромба очень похоже на вычисление площади треугольника. формула площади прямоугольника
\[\text{Область} = \displaystyle \frac{p q}{2}\]
, где p и q соответствуют диагоналям
Каковы шаги для вычисления площади ромба? ‘д’
Есть ли приложения ромба?
Конечно Все геометрические фигуры обычно можно использовать по-разному.
Например, форма бейсбольного поля (в идеале) имеет форму правильного ромба, но
это один пример из многих.
Пример: вычислить площадь ромба
вычислить площадь ромба с заданными диагоналями, равными p = 3 и q = 4.
Решение : Шаг состоит в точном определении диагоналей. Здесь ясно сказано, что диагонали равны p = 3 и q = 4. Формула площади, которую нужно использовать:
\[ Площадь = \displaystyle \frac{pq}{2} \]
Теперь, подставив значения p = 3 и q = 4 в формулу, мы получим:
\[ Площадь = \displaystyle \frac{pq}{2} = \displaystyle \frac{3 \times 4}{2} = \displaystyle \frac{12}{2} = 6 \]
, поэтому площадь равна 6.
Пример: Площадь прямоугольника с единицами измерения
Вычислить площадь ромба с диагоналями p = 2,2 см и q = 6,1 см
Решение . Как и в предыдущем примере, первое задача соответствует выявлению диагоналей, которые в данном случае равны p = 2,2 см и q = 6,1 см, а в данном
например, диагонали поставляются с единицами длины.
Площадь: 92\]
что означает, что площадь составляет 13,42 см 2
Дополнительные калькуляторы площадей
Геометрические фигуры обычно имеют простые формулы для вычисления площадей. Вычисление площади ромба и Площадь треугольника считается базовым навыком в алгебре и геометрии. калькулятор площади круга и наш калькулятор площади эллипса.
площадь ромба Площадь эллипса Площадь круга Площадь треугольника Площадь прямоугольника площадь квадрата Калькулятор объема площади куба Калькулятор абсолютного значения
Вычислите площадь ромба — Калькулятор, формулы, упражнения и многое другое!
Вычислить площадь ромба очень просто с помощью нашего бесплатного онлайн калькулятора.
Единственные данные, которые нам нужно знать, — это значения, которые измеряют большую и малую диагонали многоугольника. Если они у вас есть, введите числа в инструмент, нажмите кнопку расчета, и вы сразу получите площадь ромба.
Помните, что крайне важно, чтобы единицы происхождения соответствовали то есть как в сантиметрах, так и в метрах или сколько угодно. Вы всегда можете воспользоваться нашим конвертером единиц длины, если вам необходимо выполнить какие-либо преобразования для выполнения этого требования.
Разделы статьи
- Как вычислить площадь ромба
- Как вычислить диагонали ромба
- Вычислить площадь ромба по периметру.
Как вычислить площадь ромба
Чтобы получить площадь ромба, нужно применить следующую математическую формулу:
Вы просто должны знать, что:
- D — длина самой длинной диагонали
- d — длина малой диагонали
С помощью этих данных мы теперь можем удалить поверхность ромба .
Если вы хотите найти площадь ромбоида, нажмите на ссылку, которую мы вам только что оставили, так как это разные фигуры.
Наконец, единица площади ромба будет возведена в квадрат. Например, если меньшая диагональ равна 2 сантиметрам, а большая — 3 сантиметрам, площадь многоугольника будет равна 3 квадратным сантиметрам.
В качестве решения задачи вычислим площадь ромба, у которого большая диагональ D = 6 см, а меньшая диагональ d = 3 см. Чтобы решить ее, мы применяем формулу, которая у вас есть над этими линиями, и мы имеем, что:
Площадь ромба = (6 см x 3 см) / 2 = 18 / 2 = 9 см 2
Как рассчитать диагонали ромба
Если нас попросят вычислить диагонали ромба , мы должны использовать эту формулу:
4a 2 = D 2 + d 2
Бытие:
- а: длина одной из сторон ромба
- D: длина наибольшей диагонали
- d: длина малой диагонали
В зависимости от диагонали ромба, который мы хотим вычислить, нам придется выделить то или иное неизвестное.
Ниже у вас есть формула , которая будет использоваться для каждой из диагоналей , на которых есть ромб…:
д = √(4а 2 — Д 2 )
D = √(4a 2 — d 2 )
Помните, что в обоих случаях квадратный корень должен применяться ко всему, что находится внутри скобок .
Вычислить площадь ромба по периметру.
Ромб – фигура, имеющая четыре равные стороны, поэтому его периметр равен:
периметр = 4а
Из периметра и длины одной из диагоналей можно получить площадь объединяет всю теорию, которую мы видели до сих пор.
Например, вычислим площадь ромба, малая диагональ которого d = 4 см, а периметр у равен 32 см.
Lo primero que haremos con los datos del enunciado es hallar cuánto mide cada lado del rombo. Para ello despejamos la incógnita ‘a’ de la fórmula anterior:
a = периметр / 4 = 32 см / 4 = 8 сантиметров.
Далее посчитаем длину диагонали , который у нас отсутствует, то есть самый крупный. Чтобы получить его длину, воспользуемся формулой, которую мы видели в предыдущем пункте:
D = √(4a 2 — d 2 ) = √(4 x 8 2 — 4 2 ) = √(256 — 16) = √240 = 15,49
Наконец, у нас есть все данные для расчета площади:
Площадь ромба = (15,49 см x 4 см) / 2 = 18 / 2 = 30 ,98 см 2
Если у вас есть вопросы о как вычислить площадь ромба Если вы не знаете, как решить упражнение, оставьте нам комментарий с упражнением, которое вы не знаете, как решить, и мы вам поможем.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré.
Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- Площадь пирамиды
- Калькулятор площади квадрата
- Калькулятор площади сферы
- Калькулятор площади круга
- Калькулятор площади прямоугольника
- Вычисление площади и апофемы пятиугольника
- Вычисление площади a4 конуса 900 трапеции
- Вычислить площадь треугольника
- Вычислить площадь цилиндра
- Вычислить площадь ромба
- Вычислить площадь и апофему правильного шестиугольника
- Вычислить сторону квадрата
- Додекаэдр
- Икосаэдр
- Ромбовид
- Круговой сектор
- Тетраэдр
Калькулятор ромба онлайн | Математические калькуляторы
Ромб — это двухмерный геометрический объект с четырьмя равными сторонами, напоминающий форму ромба или воздушного змея. Противоположные стороны параллельны и противоположные углы равны. Две диагонали пересекают друг друга под прямым углом.
Ромб классифицируется как параллелограмм.
★ ★ ★ ★ ★ [4 голоса]
Примечания использования калькулятора ромба
- Все стороны равны ромб. Изменение сторон влияет на высоту и длину диагоналей.
- Высота — это перпендикулярная высота. Изменение высоты влияет на стороны и диагонали
- Изменение длины диагонали влияет на стороны, высоту и углы
- Изменение длины диагонали влияет на стороны, высоту и углы
- Изменение угла A влияет на угол B, высоту и обе диагонали
- Изменение угла B влияет на угол A, высоту и обе диагонали
- Площадь ромба в квадратных единицах
- Внешний край ромба включает следующие алгоритмы:
Угол A = 180 — Угол B
Угол B = 180 — Угол A
Высота = sin(B) x S (синус угла B, умноженный на длину стороны)
Площадь можно рассчитать несколькими способами:
Площадь = a x S (высота x стороны)
Площадь = S 2 x sin(A) (квадрат длины стороны, умноженный на синус A )
Площадь = S 2 x sin(B) (квадрат длины стороны, умноженный на синус угла B)
Площадь = (p x q)/2 (диагональ A-A (p) умноженная на диагональ B-B ( q) тогда результат делится на два)
Периметр = 4 x S (длина стороны, умноженная на 4)
Используйте калькулятор ромбов для ежедневных расчетов — это быстро и просто
Прежде чем мы начнем говорить о калькуляторах ромбов, давайте немного поговорим о ромбе, не так ли? Но прежде чем мы это сделаем, нам нужно знать, что такое четырехугольник.
Четырехугольник – это замкнутая геометрическая фигура с 4 сторонами и 4 углами. Квадрат, прямоугольник, трапеция, ромб, все эти фигуры являются четырехугольниками.Возвращаясь к сути дела, ромб — это четырехугольник, у которого все 4 стороны равны по длине. Теперь вы можете задаться вопросом, что такое квадрат. Но вот разница, все углы квадрата под прямым углом (90°). Однако ромб имеет равные противоположные углы и параллельные противоположные стороны.
Каковы свойства ромба?
Помимо того, что воздушный змей является наиболее распространенным и наиболее близким примером ромба в жизни большинства из нас, ромб обладает некоторыми очень интересными свойствами:
- Как упоминалось ранее, противоположные стороны ромба равны .
- Сумма смежных углов ромба равна 180° (дополнительные углы).
- Ни одна из вершин ромба не равна 90°.
- Диагонали ромба перпендикулярны друг другу.
- Ромб НЕ является вписанным четырехугольником.
Как вычислить площадь ромба?
Существует 3 способа вычисления площади ромба.
- Использование диагоналей: Самый простой способ найти площадь ромба — это знать длины диагоналей. Все, что вам нужно сделать, это умножить длины и разделить произведение на 2. Вот вам и площадь ромба. Например: если длины диагоналей равны 4 см и 11 см, площадь круга будет (11×4)/2 = 22 см².
- Использование базы и высоты (высоты): Если вам известны длина основания и высота ромба, все, что вам нужно сделать, это умножить их, и произведение будет площадью ромба. Например: если основание ромба 5 см, а его высота 2 см, площадь ромба будет 5×2 = 10 см².
- С помощью тригонометрии: Возможно, это самый сложный метод вычисления площади ромба. Вам понадобится длина стороны ромба и острого угла. Умножьте длину основания на себя, а затем умножьте на синус угла. Например, если длина основания 3 см, а острый угол равен 60°, то площадь ромба будет равна (3×3) x Sin(60°) = 9х 0,30 = 2,74 см².
Четырехугольник – это замкнутая геометрическая фигура с 4 сторонами и 4 углами. Квадрат, прямоугольник, трапеция, ромб, все эти фигуры являются четырехугольниками.
