Площадь сегмента поверхности сферы: Как найти площадь поверхности сегмента шара: формула, пример

Как найти площадь поверхности сегмента шара: формула, пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади шарового сегмента

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.

• Определение сегмента шара
• Формулы для нахождения площади сегмента шара
  • Площадь основания
  • Площадь сферической поверхности
  • Площадь полной поверхности
• Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью.

На чертеже ниже закрашен зеленым цветом.

• R – радиус шара;
• r – радиус основания сегмента;
• h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Формулы для нахождения площади сегмента шара

Площадь основания

Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):

S_осн. = πr ²

Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть: r = d/2.

Площадь сферической поверхности

Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.

S_{сфер. пов.} = 2πRh

Площадь полной поверхности

Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.

S_полн. = S_осн. + S_{сфер. пов.} = π (2Rh + r ²)

Пример задачи

Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см.

Решение

Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.

S_осн. = 3,14 ⋅ (4,7 см) ² = 69,3626 см ²

S_{сфер. пов.} = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см = 90,432 см ²

S_полн. = S_осн. + S

сфер. пов. = 69,3626 см ² + 90,432 см ² = 159,7946 см ²

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Площадь поверхности шара с примерами решения

Содержание:

1. Площадь поверхности шара.
   Доказательство Архимеда
2. Площадь сегмента шара
3. Площадь шарового пояса
4. Задача пример №81

Площадь поверхности шара находится по формуле . Здесь радиус шара. В окружность радиусом впишем правильный многоугольник.

Поверхность шара, полученного при вращении относительно диаметра соответствующих кругов, можно рассматривать как сумму пределов боковых поверхностей фигур — конуса, усеченного конуса и цилиндра, образующие которых являются сторонами данного многоугольника. Покажем, что при вращении сторон многоугольника вокруг оси получается тело (конус, усеченный конус, цилиндр), площадь боковой поверхности которого равна площади боковой поверхности цилиндра, высота которого равна высоте данного тела, радиус основания равен апофеме многоугольника. Обозначим апофему многоугольника через .

— площадь боковой поверхности конуса с образующей . Так как , то .

Умножим на 2 обе части равенства . Учитывая, что , , получим .

Значит, — площадь боковой поверхности усеченного конуса. Зная, что

, получим что . Так как , то

Умножим на 2 обе части равенства . Учитывая,что , получим .

Значит, .

Понятно, что площадь боковой поверхности цилиндра с образующей равна . Аналогично получаем, что площадь боковых поверхностей усеченного конуса с образующей и конуса с образующей можно найти по формулам . Таким образом, поверхность тела, полученного вращением многоугольника вокруг диаметра, равна :

При бесконечном увеличении количества сторон многоугольника значение стремится к радиусу, а площадь поверхности полученного тела к площади поверхности шара, т.е. .

Площадь поверхности шара. Доказательство Архимеда

Найдя сумму поверхностей усеченных конусов и цилиндра, можно найти площадь поверхности шара. Рассмотрим осевое сечение одного из усеченных конусов. Пусть радиус средней окружности равен , а высота , радиус шара сторона многоугольника, описанного вокруг большего круга равна . Площадь боковой поверхности усеченного конуса будет , а также , т.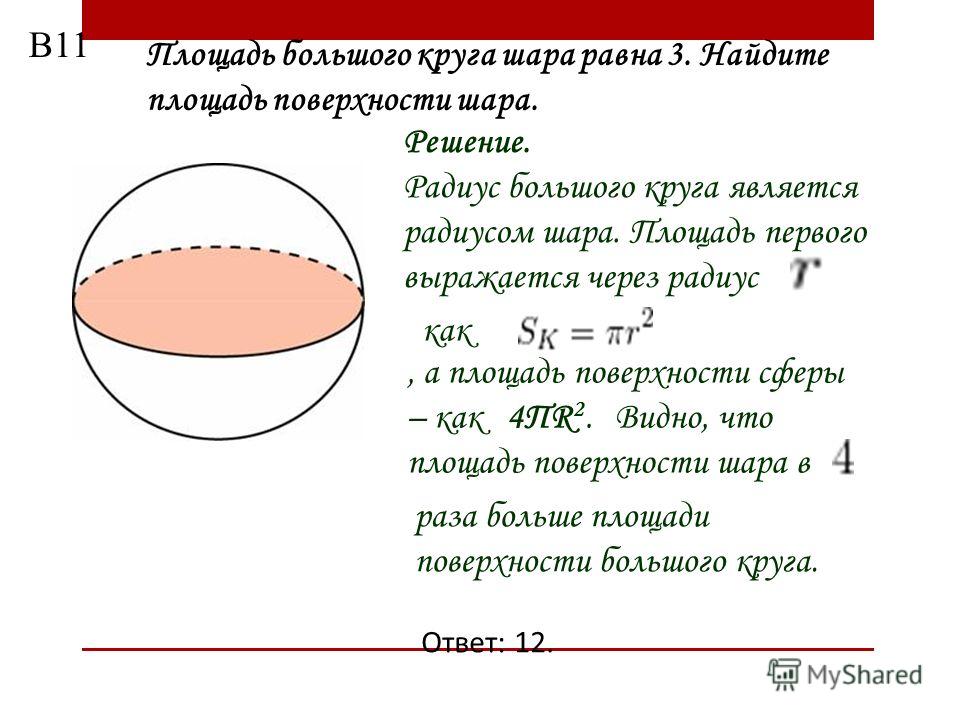 е. боковая поверхность усеченного конуса равна боковой поверхности цилиндра, радиус основания которого равен и высота . Значит, фигуру, описанную вокруг шара, можно принять за цилиндр. Отсюда получается, что площадь поверхности шара равна площади боковой поверхности цилиндра с радиусом основания и высотой Т.е.,

Площадь сегмента шара

Часть шара, отсекаемая плоскостью сечения называется сегментом. Круг, полученный при сечении плоскостью, называется основанием сегмента. Часть диаметра шара, перпендикулярного основанию сегмента, расположенная внутри него, называется высотой сегмента. Из доказательства формулы поверхности шара, аналогично, можно показать, что для шара радиуса площадь сферической поверхности сегмента высотой , вычисляется по формуле .

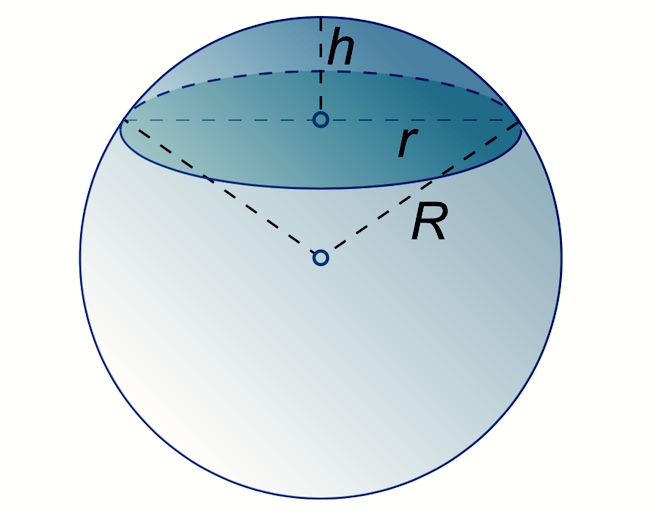
Площадь шарового пояса

Часть поверхности шара, расположенная между двумя параллельными плоскостями, называется шаровым поясом.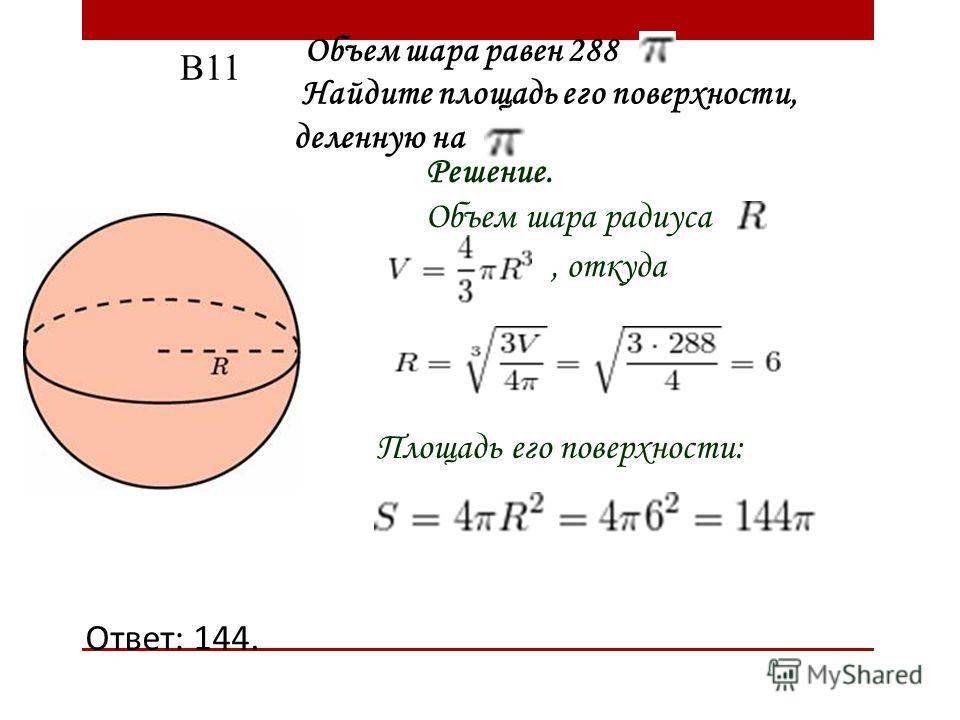 Расстояние между параллельными плоскостями называется высотой шарового пояса. Площадь поверхности шарового пояса можно найти, как разность площадей сегментов, отсекаемых параллельными плоскостями.

Площадь поверхности шарового пояса высотой отсекаемого от шара радиуса вычисляется по формуле

Задача пример №81

Радиус шара разбит на три равные части и через эти точки проведены перпендикулярные к радиусу плоскости. Зная, что радиус шара , найдите площадь поверхности шарового пояса.

Решение:

если и , то площадь поверхности шарового пояса будет .

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Усеченный конус. Поверхность усеченного конус

Шар и его части

Площадь поверхности подобных фигур

Средняя скорость изменения, мгновенная скорость изменения

Формула сферического сегмента — GeeksforGeeks

Сферический сегмент — это часть сферы, образованная, когда плоскость разрезает сферу сверху и снизу таким образом, что оба разреза параллельны друг другу. Он соответствует сферическому усеченному конусу, потому что напоминает сферическую шапку с усеченным верхом. Зона – это поверхность сферического сегмента (исключая основания).

 

Формула сферического сегмента

Сферический сегмент имеет две основные формулы: площадь и объем. Ниже приводится подробное объяснение формулы площади и объема сферического сегмента.

Площадь сферического сегмента

Площадь сферического сегмента определяется как площадь, покрываемая сферическим сегментом в трехмерном пространстве. Он равен произведению его радиуса на высоту с константой 2π.

A = 2πRh

Где

r — радиус сегмента,

h — высота сегмента.

Объем сферического сегмента

Объем сферического сегмента определяется как пространство, заключенное внутри сегмента. Он равен произведению высоты на сумму удвоенного квадрата первого радиуса, удвоенного квадрата второго радиуса и квадрата высоты с константой π/6.

V = πh(3R ₁ ² + 3R ₂ ² + h ² )/6

Where,

R ₁ is the radius of small bounded region,

R ₂ — радиус большой ограниченной области,

h — высота отрезка.

Примеры задач

Задача 1: Найдите площадь сегмента сферы, если радиус сферы 14 см, а высота 7 см.

Решение:

Имеем R = 14 и h = 7.

Используя формулу, имеем

A = 2πRh

= 2 (22/7) (190) (73)

= 2 (22) (2) (7)

= 616 кв. см

Задача 2. Найти высоту сегмента сферы, если радиус сферы равен 14 см, а площадь 176 кв. . см.

Решение:

Имеем, R = 14 и A = 176.

Используя формулу, имеем,

A = 2πRh

=> 176 = 2 (22/7) (14) (h)

=> 176 = 2 (22) (2) (h)

=> 4h = 8

=> h = 2 см

Задача 3. Найдите объем сегмента сферы, если радиус сферы 14 см, радиус основания 10 см, а высота 7 см.

Решение:

Имеем, R ₁ = 14, R ₂ = 10 и h = 7.

Используя формулу имеем,

V = πh(3R ₁ ² + 3R ₂ ² + h ² )/6

= (22/9 7) (7) (3(14) (10) ² + 7 ² )/6

= 22 (588 + 300 + 49)/6

= 20614/6

= 3435,66 куб. см

Задача 4. Найдите объем сегмента сферы, если радиус сферы равен 8 см, радиус основания 5 см, а высота 3 см.

Решение:

Имеем, R ₁ = 8, R ₂ = 5 и h = 3. ² + h ² )/6

= (22/7) (3) (3(8) ² + 3(5) ² + 3 ² )/6

66 (276)/42

= 18216/42

= 433,71 куб. см

Задача 5: Найдите объем сегмента сферы, если радиус сферы 7 см, радиус основания 14 см, а площадь 264 кв.см.

Решение:

Мы имеем, r ₁ = 14, R ₂ = 7 и A = 264

Используем формулу,

A = 2πrh

=> 264 = 2 (22/7) (14) (h)

=> 264 = 2 (22) (2) (h)

=> 4h = 12

=> h = 3 см

Итак, объем равен,

V = πh(3R ₁ ² + 3R ₂ ² + h ² )/6

= (22/7) (3) (3) (3(14)0039 2 + 3(7) ² + 3 ² )/6

= (22/7) (3) (744)/6

= 49104/42

= 1169,14 у. е. см

Задача 6. Найдите площадь сегмента сферы, если радиус сферы 20 см, а высота 10 см.

Решение:

Имеем R = 20 и h = 10.

= 2 (22/7) (200)

= 1257,14 кв. см

Задача 7. Найдите объем сегмента сферы, если радиус сферы равен 4 см, радиус основания равен 2 см, а высота равна 6 см.

Решение:

Мы имеем, r ₁ = 4, R ₂ = 2 и H = 6.

Используем формулу,

V = πh (3R ₁ ² + 3R ₂ ² + h ² )/6

= (22/7) (6) (3(4) ² + 3(2) ² + 6 ² )/6

= (22/7) (96)

= 18216/42

= 301,71 куб. см

Сферический сегмент | Обзор твердотельной геометрии в MATHalino

Сферический сегмент представляет собой твердое тело, ограниченное двумя параллельными плоскостями через сферу.