Площадь сфера: Шар, сфера — урок. Геометрия, 11 класс.

Как найти площадь поверхности шара (сферы): формула через радиус, диаметр

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади поверхности шара (сферы): формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.

• Формула вычисления площади шара/сферы
  • 1. Через радиус
  • 2. Через диаметр
• Примеры задач

Формула вычисления площади шара/сферы

1. Через радиус

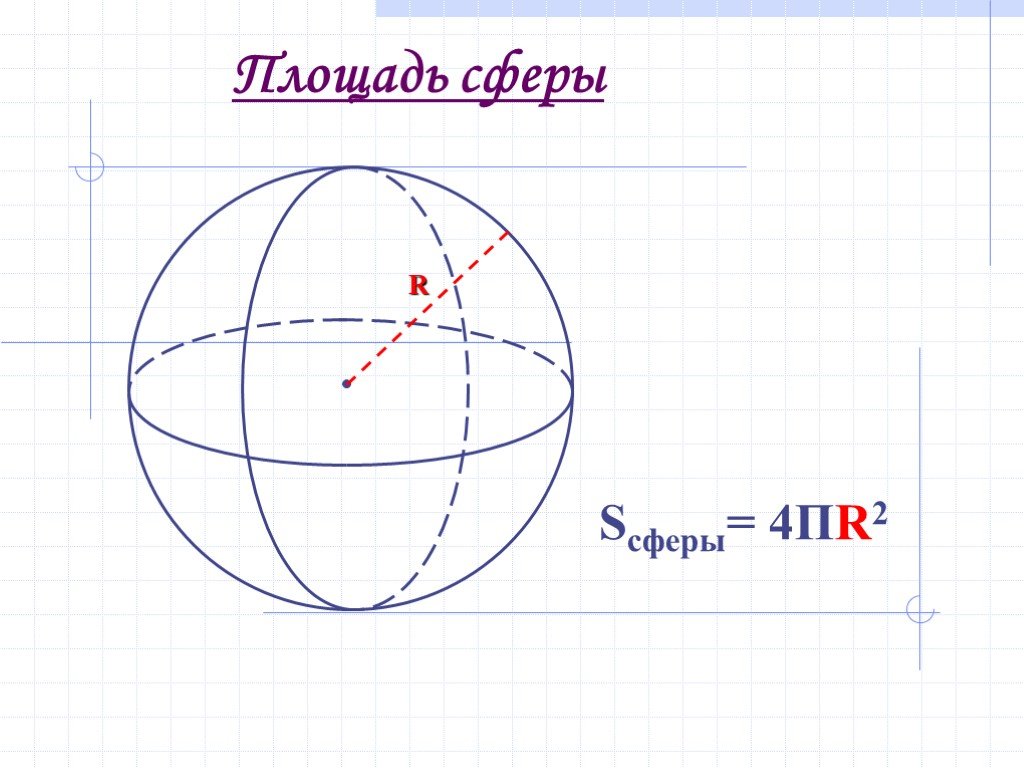
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.

S = 4 π R²

Примечание: в расчетах значение числа π округляется до 3,14.

2. Через диаметр

Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:

S = 4 π (d/2)²

Примеры задач

Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.

Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)² = 615,44 см².

Задание 2
Площадь поверхности сферы равна 200,96 см

2. Найдите ее диаметр.

Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

сферы, шапочки, кольца / Этюды // Математические этюды

Площадь на сфере: сферы, шапочки, кольца / Этюды // Математические этюды

Математические этюды

К списку

Площадь всей сферы, шапочки или кольца на сфере посчи­тать не так про­сто. 2$.

«Счи­ты­вая» с гло­буса информацию по при­ве­дён­ному алго­ритму, можно постро­ить рав­но­ве­ли­кую азиму­таль­ную кар­тографи­че­скую про­екцию Земли. Такая про­екция сохра­няет площади всех обла­стей. Раз­ра­бо­тал её матема­тик и аст­ро­ном Иоганн Лам­берт — тот самый, кото­рый дока­зал ирраци­о­наль­ность числа $\pi$. Замет­ный недо­ста­ток про­екции — зна­чи­тель­ное искаже­ние на общей карте Земли кон­ту­ров круп­ных обла­стей, напри­мер, кон­ти­нен­тов.

Круг, касающийся сферы в полюсе, можно счи­тать пре­дель­ным слу­чаем конуса, касающегося сферы.

Рас­смот­рим две вспомога­тель­ные концен­три­че­ские сферы с цен­тром в вершине конуса. И на сфере, и на конусе эти сферы высе­кают кольца. Ока­зы­ва­ется, что площади этих колец — на сфере и на конусе — равны.

Равен­ство оста­ётся вер­ным для любого положе­ния концен­три­че­ских сфер. Рас­смот­рен­ный слу­чай равен­ства площа­дей шапочки на сфере и соот­вет­ствующего круга, касающегося сферы, полу­ча­ется из кони­че­ского: радиус одной из концен­три­че­ских сфер сле­дует положить нулю, а вершину конуса поме­стить в полюс сферы.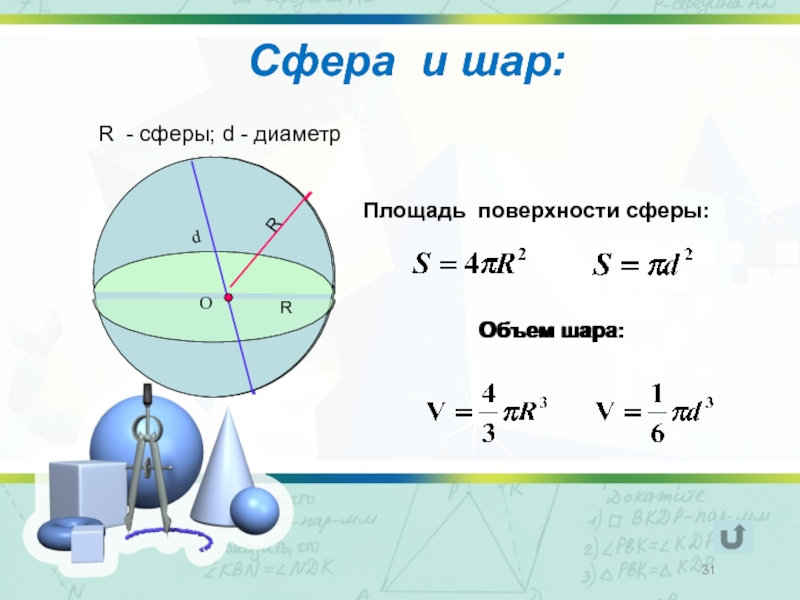

Если же вершину конуса «угнать» на бес­ко­неч­ность, то конус перей­дёт в цилиндр, касающийся сферы по эква­тору. Концен­три­че­ские вспомога­тель­ные сферы перей­дут в плос­ко­сти.

Площадь сфе­ри­че­ского кольца, выре­за­емого двумя парал­лель­ными плос­ко­стями, равна площади соот­вет­ствующего цилин­дри­че­ского кольца (плос­ко­сти перпен­ди­ку­лярны оси цилин­дра). Это при­во­дит к инте­рес­ному наблю­де­нию: площадь кольца на гло­бусе зави­сит только от рас­сто­я­ния между секущими плос­ко­стями, но не зави­сит от бли­зо­сти кольца к эква­тору или полюсу. «Съе­доб­ное» тол­ко­ва­ние: если круг­лый неочищен­ный апель­син наре­зать на лом­тики оди­на­ко­вой толщины, то и площадь шкурки у всех кус­ков будет оди­на­кова.

Срав­не­ние площади кольца на сфере и кольца на цилин­дре поз­во­ляет посчи­тать площадь всей сферы. Когда плос­ко­сти касаются полю­сов сферы рас­сто­я­ние между ними равно $2R$. А длина окруж­но­сти цилин­дра, касающегося сферы равна $2\pi R$. 2$.

Пере­нося информацию с гло­буса на сферу с сохра­не­нием высоты полу­чаем рав­но­ве­ли­кую цилин­дри­че­скую кар­тографи­че­скую про­екцию Земли. Такая про­екция, по рас­смот­рен­ному выше свойству, сохра­няет площади всех обла­стей и тоже была раз­ра­бо­тана Лам­бер­том.

Утвер­жде­ние про равен­ство площа­дей колец на сфере и на цилин­дре назы­ва­ется леммой Архимеда и известно с дав­них времён. Утвер­жде­ние про площадь сфе­ри­че­ской шапочки и площадь круга тоже довольно известно. Уди­ви­тельно, что свя­зы­вающая эти два слу­чая кон­струкция — срав­не­ние площа­дей колец на сфере и на конусе, заклю­чён­ных между концен­три­че­скими сфе­рами с цен­трами в вершине конуса — мало­из­вестна и, возможно, была открыта только в XXI веке.

Лите­ра­тура

Акопян А. Апель­сины, кана­ли­за­ци­он­ные люки и раз­ре­за­ние длин­ного прямо­уголь­ника // Жур­нал «Квант». — 2021. — № 9. — Стр. 40—43.

Vin De Silva. A Generalisation of Archimedes’ Hatbox Theorem // The Mathematical Gazette.  — 2006. — Vol. 90, № 517. — P. 132—134.

Кар­тографи­че­ские про­екции // Матема­ти­че­ская состав­ляющая / Ред.-сост. Н. Н. Андреев, С. П. Коно­ва­лов, Н. М. Паню­нин. — Вто­рое изда­ние, расши­рен­ное и допол­нен­ное. — М. : Матема­ти­че­ские этюды, 2019. — С. 136—145, 342, 343.

⁠⁠Тео­рема о косточке // Матема­ти­че­ские этюды.

Другие этюды раздела «Площади и объёмы»

  Площади фигурОбновлено  Формула ПикаТеорема Пифагора: доказательство ЕвклидаОбновлено  Теорема Пифагора: интерактивная головоломка  Объём шара: весы Архимеда  Объём шара  Теорема о косточке  Сапог Шварца

Математические этюды

Площадь поверхности сферы

Площадь поверхности сферы — это площадь, занимаемая изогнутой поверхностью сферы. Круглые формы принимают форму сферы, если рассматривать их как трехмерные структуры. Например, глобус или футбольный мяч. Давайте узнаем о формуле площади поверхности сферы и о том, как рассчитать площадь поверхности сферы в этом уроке.

1.	Какова площадь поверхности сферы?
2.	Получение площади поверхности сферы
3.	Формула площади поверхности сферы
4.	Как рассчитать площадь поверхности сферы?
5.	Часто задаваемые вопросы о площади поверхности сферы

Какова площадь поверхности сферы?

Площадь, покрытая внешней поверхностью сферы, называется площадью поверхности сферы. Сфера – это трехмерная форма круга. Разница между сферой и кругом заключается в том, что круг представляет собой 2-мерную форму (2D-форму), тогда как сфера представляет собой 3-мерную форму. Площадь поверхности сферы выражается в квадратных единицах. Обратите внимание на сферу, приведенную ниже, которая показывает центр, радиус и диаметр сферы.

Определение сферы

Сфера представляет собой трехмерный объект круглой формы без вершин и краев.

Важными аспектами этой формы являются радиус, диаметр, окружность и объем.

Вывод площади поверхности сферы

Сфера имеет круглую форму, поэтому, чтобы найти площадь ее поверхности, мы соотносим ее с изогнутой формой, например с цилиндром. Цилиндр — это форма, которая имеет криволинейную поверхность наряду с плоскими поверхностями. Теперь, если радиус цилиндра такой же, как радиус сферы, это означает, что сфера может идеально вписаться в цилиндр. Это означает, что высота цилиндра равна высоте сферы. Таким образом, эту высоту также можно назвать диаметром сферы. Поэтому этот факт был доказан великим математиком Архимедом, что если радиус цилиндра и сферы равен r, то площадь поверхности сферы равна площади боковой поверхности цилиндра.

Следовательно, соотношение между площадью поверхности сферы и площадью боковой поверхности цилиндра определяется как:

Площадь поверхности сферы = Площадь боковой поверхности цилиндра

Площадь боковой поверхности цилиндра = 2πrh, где ‘ r — радиус, а h — высота цилиндра. Теперь высоту цилиндра также можно назвать диаметром сферы, потому что мы предполагаем, что эта сфера идеально помещается в цилиндре. Следовательно, можно сказать, что высота цилиндра = диаметру сферы = 2r. Итак, в формуле площадь поверхности Сферы = 2πrh; «h» можно заменить диаметром, то есть 2r. Следовательно, площадь поверхности сферы равна 2πrh = 2πr(2r) = 4πr ²

Формула площади поверхности сферы

Формула площади поверхности сферы зависит от радиуса сферы. Если радиус сферы равен r, а площадь поверхности сферы равна S. Тогда площадь поверхности сферы выражается как:

Площадь поверхности сферы = 4πr

² ; где «r» — радиус сферы.

В пересчете на диаметр площадь поверхности сферы выражается как S = 4π(d/2)

2
где d — диаметр сферы.

Как рассчитать площадь поверхности сферы?

Площадь поверхности шара – это пространство, занимаемое его поверхностью. Площадь поверхности сферы можно рассчитать по формуле площади поверхности сферы.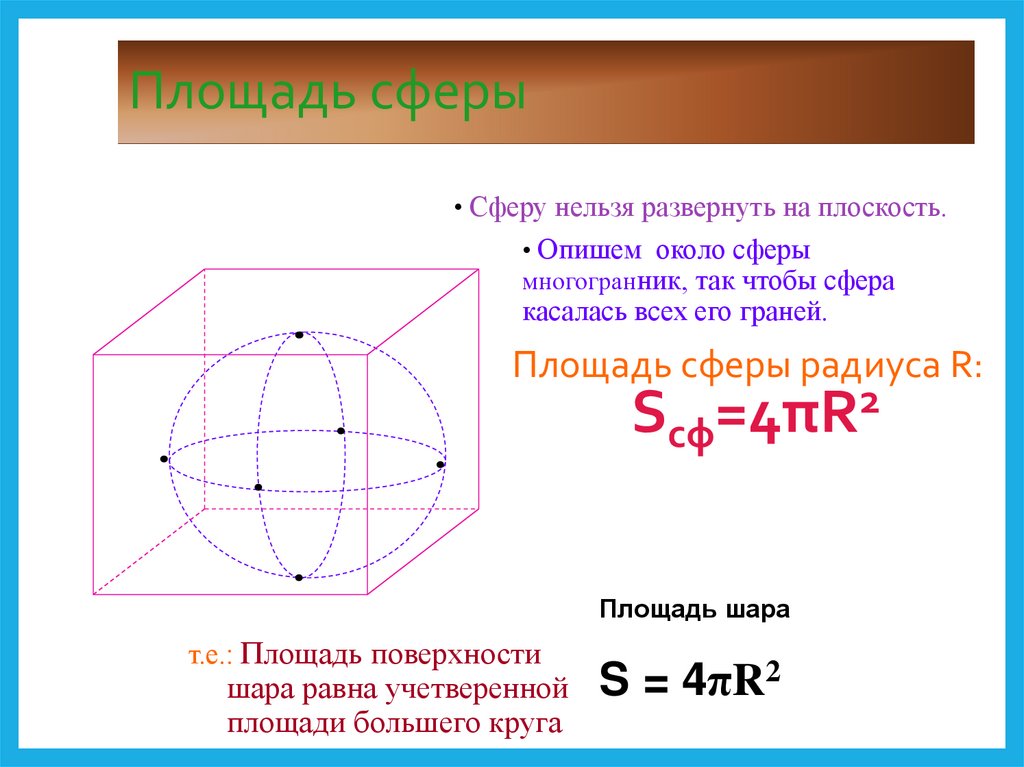 Шаги для расчета площади поверхности сферы приведены ниже.

Давайте рассмотрим пример, чтобы узнать, как рассчитать площадь поверхности сферы, используя ее формулу.

Пример: Найдите площадь поверхности сферического шара с радиусом 9 дюймов.

• Шаг 1: Обратите внимание на радиус сферы. Здесь радиус шара равен 9 дюймам.
• Шаг 2: Как мы знаем, площадь поверхности сферы = 4πr ² , поэтому после подстановки значения r = 9 мы получаем площадь поверхности сферы = 4πr ² = 4 × 3,14 × 9 ² = 4 х 3,14 х 81 = 1017,36
• Шаг 3: Следовательно, площадь поверхности сферы равна 1017,36 в ²

Площадь криволинейной поверхности сферы

Площадь криволинейной поверхности сферы — это общая площадь поверхности сферы, поскольку сфера имеет только одну изогнутую поверхность. Поскольку у сферы нет плоской поверхности, площадь криволинейной поверхности сферы равна общей площади поверхности сферы. Следовательно, формула площади криволинейной поверхности сферы выражается как Площадь криволинейной поверхности сферы = 4πr ² ; где «r» — радиус сферы.

☛ Связанные статьи

• Площадь поверхности куба
• Площадь поверхности прямоугольного параллелепипеда
• Площадь поверхности призмы
• Площадь поверхности конуса
• Разница между площадью и площадью поверхности

 

Площадь поверхности сферы Примеры

1. Пример 1: Если радиус сферы равен 20 футам, найдите площадь ее поверхности. (Используйте π = 3,14).
   Решение: Дано, радиус ‘r’ сферы = 20 футов.

   Площадь поверхности сферы = 4πr ² = 4 × π × 20 ² = 5024 фута ²

   ∴ Площадь поверхности сферы составляет 5024 фута ^{2 90 064}

2. Пример 2: Найдите площадь поверхности сферы, если ее радиус равен 6 единицам.

   Решение: Дано, радиус ‘r’ = 6 единиц. Итак, подставим значение r = 6 единиц

   ⇒ Площадь поверхности сферы = 4πr ² = 4 × π × 6 ² = 4 × 3,14 × 36 = 452,16 единица ²

   ∴ Площадь поверхности сферы равна 452.16 шт. ²

3. Пример 3: Укажите истинное или ложное значение.

   а.) Сфера представляет собой трехмерную форму круга.

   b.) Площадь криволинейной поверхности сферы – это общая площадь поверхности сферы, поскольку у сферы есть только одна криволинейная поверхность.

   Решение:

   а.) Верно, сфера — это трехмерная форма круга.

   b.) Правда, площадь криволинейной поверхности сферы равна общей площади поверхности сферы, потому что у сферы есть только одна изогнутая поверхность.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по площади поверхности сферы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади поверхности сферы

Что такое площадь поверхности сферы в математике?

Площадь поверхности сферы — это общая площадь, которая покрыта ее внешней поверхностью. Площадь поверхности сферы всегда выражается в квадратных единицах. Формула площади поверхности сферы зависит от радиуса и диаметра сферы. Это математически выражается как 4πr ² ; где «r» — радиус сферы.

Почему площадь поверхности сферы в 4 раза больше площади круга?

Нить, полностью покрывающая площадь поверхности сферы, может полностью покрыть площадь поверхности ровно четырех кругов. Таким образом, вы можете проверить, что площадь поверхности сферы в четыре раза больше площади круга. Когда мы пишем формулу площади поверхности сферы, мы пишем площадь поверхности сферы = 4πr ² = 4(πr ² ) = 4 × площадь круга.

Сколько сторон и вершин у сферы?

Сфера — это трехмерная фигура, круглая, как круг. Следовательно, у него нет ни сторон, ни вершин, ни граней.

Есть ли у сферы бесконечные грани?

Нет, у шара нет лица. Грань — это плоская поверхность, а сфера не имеет плоской поверхности. Это делает сферу безликой трехмерной формой (3D-формой).

Что такое площадь криволинейной поверхности и общая площадь поверхности сферы?

Сфера имеет только одну поверхность, и она изогнута. Поскольку у сферы нет плоской поверхности, площадь криволинейной поверхности сферы равна общей площади поверхности сферы, которая равна 4πr ² .

☛Также проверьте:

• Формулы площади поверхности
• Геометрические формулы
• Формулы измерения

Что такое площадь поверхности сферической формулы в терминах диаметра?

Формула площади поверхности сферы в пересчете на диаметр определяется как πD ² , где «D» — диаметр сферы. Он дает отношение между площадью поверхности сферы и диаметром сферы.

Как рассчитать площадь поверхности сферы по объему?

Площадь поверхности сферы можно легко рассчитать с помощью объема сферы. В этом случае мы должны знать значение радиуса сферы. Радиус сферы можно рассчитать по формуле объема сферы, то есть Объем сферы = 4/3 × πr ³ . Отсюда можно вычислить радиус и затем подставить его значение в формулу площади поверхности. Мы знаем, что площадь поверхности сферы = 4πr ² . Другой способ следить за этим заключается в следующем. Из формулы объема мы можем вывести, что r ³ = 3V/4π или r = (3V/4π) ^1/3 . После этого мы можем подставить значение r в формулу площади поверхности сферы.

Что такое Калькулятор площади поверхности сферы?

Калькулятор площади поверхности сферы — это онлайн-инструмент для детей, облегчающий их расчеты. Это созданный системой инструмент, в котором формула площади поверхности предустановлена, все, что нам нужно сделать, это ввести значение заданных параметров, таких как радиус, и мы получим площадь поверхности сферы.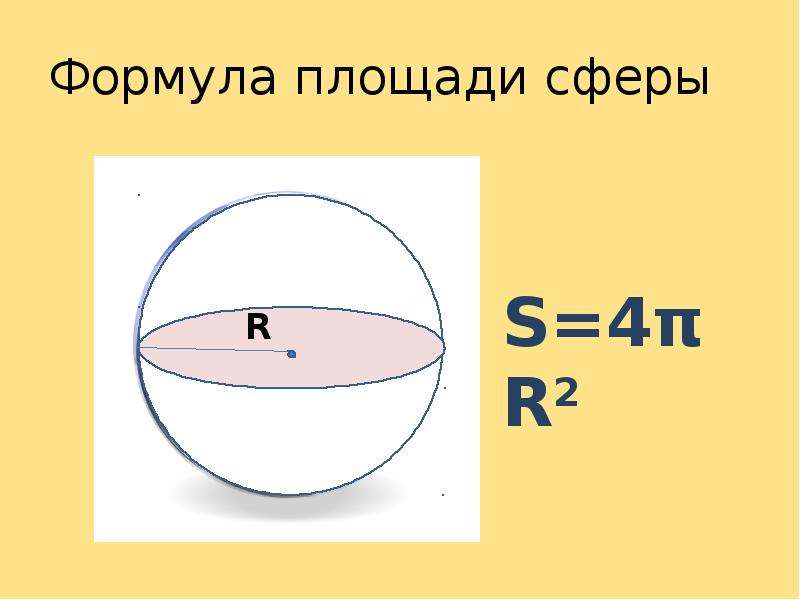 Попробуйте калькулятор площади поверхности сферы от Cuemath и получите ответы за несколько секунд.

Как изменится площадь поверхности сферы при уменьшении радиуса вдвое?

Площадь поверхности сферы увеличивается на одну четвертую, когда радиус уменьшается вдвое, потому что r становится r/2. Так как площадь поверхности сферы = 4πr ² , то, если мы заменим «r» на r/2, формула станет 4π(r/2) ² = πr ² , что составляет одну четверть площадь поверхности. Таким образом, площадь поверхности сферы становится одной четвертой, как только ее радиус уменьшается вдвое.

Как изменится площадь поверхности сферы при утроении радиуса?

Площадь поверхности сферы становится равной 36πr ² , когда радиус увеличивается втрое, потому что ‘r’ становится 3r’. Мы знаем, что площадь поверхности сферы = 4πr ² , поэтому, если мы заменим «r» на 3r, мы получим формулу: площадь поверхности = 4π(3r) ² = 4π × 9r ² = 36πr ²

Площадь поверхности сферы

Ворранат Пакорнрат, Абхинит Гоэль, Тадеуш Абий, и 92. \_\квадрат \конец{выравнивание} \]

Теорема Архимеда о шляпной коробке

Теорема Архимеда о шляпной коробке утверждает, что для любого сечения сферы ее боковая поверхность будет равна поверхности цилиндра той же высоты, что и сечение, и того же радиуса сферы.

Напомним наш последний раздел доказательства. После вращения полукруга вокруг оси \(x\) мы получим площадь поверхности сферы, и если мы вырежем только частичный участок с параллельными основаниями, новая площадь поверхности будет продемонстрирована на изображении ниже:

На изображении площадь боковой поверхности сечения окрашена в голубой цвет с двумя круглыми основаниями разного радиуса. Чтобы лучше визуализировать высоту секции, эта секция будет повернута на 90 градусов, как показано ниже:

Теперь внутри сечения есть 2 переменных угла, \(\угол a\) и \(\угол b\), которые появляются как интегральные границы сечения сечения.

9яркий] \\ &= (2\pi r)r\big[\cos (a) — \cos (b)\big] . \конец{выравнивание}\]

Рассматривая прямоугольные треугольники с радиусом \(r\) (жирный красный) на изображении, очевидно, что \(r\) является стороной гипотенузы для обоих. В результате вертикальные стороны можно вычислить как \(r\times \cos (a)\) и \(r\times \cos (b)\) для левого и правого треугольников соответственно.

Следовательно, высота сечения равна \(h = \big(r\times \cos (a)\big) — \big(r\times \cos (b)\big) = r\big[\cos ( а) — \cos (b)\big]\).

Подстановка этого члена в предыдущее уравнение дает

\[A’ = (2\pi r)r\big[\cos (a) — \cos (b)\big] = 2\pi rh. \]

Ясно, что это формула боковой поверхности цилиндра с радиусом \(r\) и высотой \(h\)!

Это означает, что площадь боковой поверхности сечения сферы равна площади боковой поверхности цилиндра с радиусом \(r\) и высотой \(h,\), как показано на рисунке, и это верно для любого уровня сферы вовлеченный. \(_\квадрат\)

Ломтик помидора Ломтик огурца Каждый срез обоих видов имеет одинаковую площадь боковой поверхности.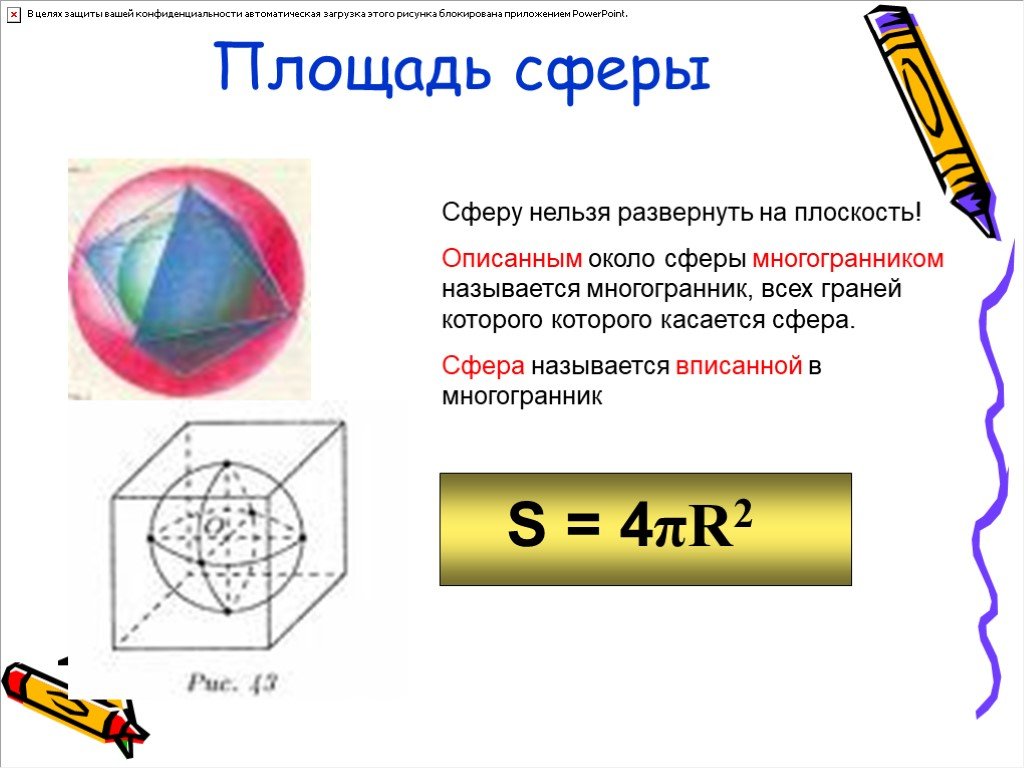 Неточно, в зависимости от уровня огранки

Сферический помидор и цилиндрическая часть огурца имеют одинаковую высоту и радиус. Затем их нарезают ломтиками одинаковой толщины, как показано выше.

Сравнивая каждого ломтика обоих видов, какой из ломтиков будет иметь большую площадь боковой поверхности кожуры?

Дыня плюс тарелка Оба варианта имеют одинаковую площадь поверхности. Мало информации Синий купол

Маленький зеленый кружок вписан в часть большого синего круга, касаясь средней хорды, как показано вверху слева. Затем графики вращаются вокруг оси \(y\), чтобы получить три фигуры: купол синей крышки, зеленую сферическую дыню и красную сервировочную тарелку.

Какой из следующих вариантов будет иметь большую площадь поверхности?

I. Синий купол
II. Дыня плюс тарелка

Магазин сладостей продает конфеты 2-х разных форм: сферический шар и купол. Куполообразная форма представляет собой сферическое сечение большей сферы с высотой \(h\) и радиусом основания \(R,\), как показано выше, в то время как леденец имеет радиус \(r\) с \(2r = R + ч\).

Если обе фигуры имеют одинаковую общую площадь поверхности, каково отношение \(\frac{R}{h}\)? 93 \) для объема сферы с радиусом \(r,\) вы знаете, что радиус арбуза равен \(r=6 \text{ см}.\) Поскольку вы разрезаете арбуз на две точные половинки, вы может подумать, что площадь поверхности половинки арбуза также равна половине площади поверхности всего арбуза. Однако это мышление ошибочно.

Как показано на диаграмме выше, площадь поверхности половины арбуза больше половины площади поверхности целого арбуза на площадь поперечного сечения \(A.