Площадь треугольника. Площадь треугольника формулы. 6 формул площади треугольника.
- Альфашкола
- Статьи
- Площадь треугольника
В этой статье собраны наиболее популярные формулы для нахождения площади треугольника.
Если известно основание и высота, проведенная к основанию треугольника, можно вычислить площадь треугольника.
\(S=\frac{1}{2}a*h\)
Основание треугольника:
Высота треугольника:
Формула Герона помогает вычислить площадь треугольника по трем сторонам треугольника:
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
где \(a,b,c\) – стороны треугольника, \(p=\frac{a+b+c}{2}\) – его полупериметр.
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Площадь треугольника можно вычислить, если известно три стороны и описанная окружность:
\(S=\frac{a*b*c}{4R}\)
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус описанной окружности R:
Площадь треугольника, когда мы знаем полупериметр и радиус вписанной окружности:
\(S=pr\)
где r — радиус вписанной окружности, \(p=\frac{a+b+c}{2}\)– его полупериметр.
Первая сторона треугольника:
Вторая сторона треугольника:
Третья сторона треугольника:
Радиус вписанной окружности R:
Формула нахождения площади по стороне и тангенсу углов треугольника:
\(S=\frac{c^2}{2(ctgA+ctgB)}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Виктория Анатольевна Шилова
Репетитор по математике
Стаж (лет)
Образование:
Северо-Казахстанский государственный университет имени Козыбаева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 5-11 классов, подготовка к ОГЭ и ЕГЭ.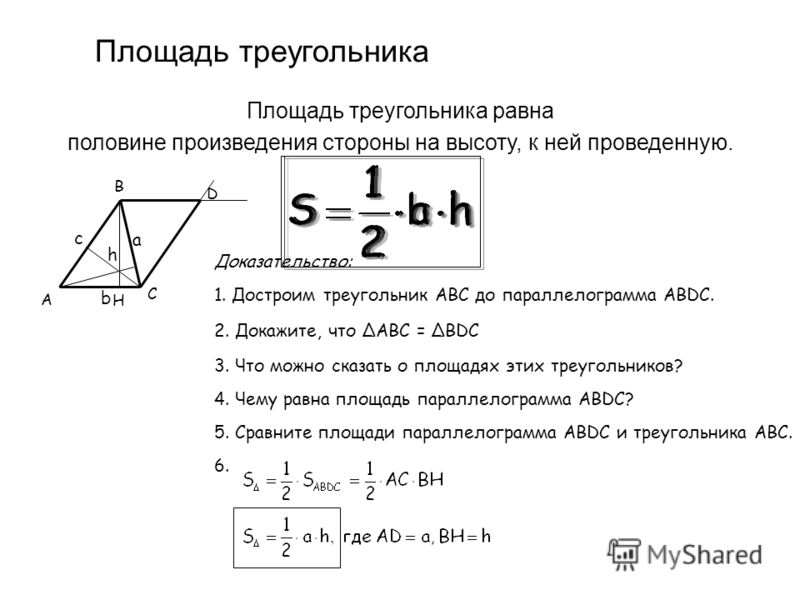 Также репетитор по истории и обществознанию 5-11 классы, готовлю к ВПР/ОГЭ/ЕГЭ. Скорочтение для 5-11 классов.
Я преподаю по авторской методике. Она включает в себя разные подходы и методы преподавания. Все мои ученики сдают выпускные экзамены .Всегда настраиваю на позитивное мышление, мотивирую на успех. Индивидуальный подход к каждому ученику.
Также репетитор по истории и обществознанию 5-11 классы, готовлю к ВПР/ОГЭ/ЕГЭ. Скорочтение для 5-11 классов.
Я преподаю по авторской методике. Она включает в себя разные подходы и методы преподавания. Все мои ученики сдают выпускные экзамены .Всегда настраиваю на позитивное мышление, мотивирую на успех. Индивидуальный подход к каждому ученику.
Людмила Владимировна Голубина
Репетитор по математике
Стаж (лет)
Образование:
Воткинский педагогический колледж Дошкольное отделение, ООО Учебный центр
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы, ВПР/ОГЭ. Всем известно, что математика обладает уникальными возможностями. Она не только «приводит ум в порядок», но и формирует внимание и память, мышление и речь, аккуратность и трудолюбие. Я считаю, что любой человек может ошибаться. Не ошибается тот, кто ничего не делает. Любой результат — это поле для роста. Математику люблю со школы. В процессе обучения стараюсь перенести математику на примеры из жизни и создать благоприятную атмосферу для учеников.
Всем известно, что математика обладает уникальными возможностями. Она не только «приводит ум в порядок», но и формирует внимание и память, мышление и речь, аккуратность и трудолюбие. Я считаю, что любой человек может ошибаться. Не ошибается тот, кто ничего не делает. Любой результат — это поле для роста. Математику люблю со школы. В процессе обучения стараюсь перенести математику на примеры из жизни и создать благоприятную атмосферу для учеников.
Иван Николаевич Лукашин
Репетитор по математике
Стаж (лет)
Образование:
Тульский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 6-11 классов и по физике 7-9 классов. Также готовлю к ОГЭ и ЕГЭ по математике и к ОГЭ по физике. Люблю свой предмет за интересные задачи, решая которые можно хорошенько «прокачать» свои мозги, научиться видеть причинно-следственные связи, развить своё логическое мышление, научиться последовательно и аргументированно выражать свои мысли.
Всегда стараюсь поддерживать открытую и позитивную атмосферу во время проведения урока. Объясняю материал на понятном и доступном для ученика языке. Вовлекаю ученика в диалог и обсуждение решения заданий. Особый упор делаю на приобретение учеником практических знаний и навыков, необходимых для решения задач.
Уделяю внимание повышению интереса ученика к предмету.
Также готовлю к ОГЭ и ЕГЭ по математике и к ОГЭ по физике. Люблю свой предмет за интересные задачи, решая которые можно хорошенько «прокачать» свои мозги, научиться видеть причинно-следственные связи, развить своё логическое мышление, научиться последовательно и аргументированно выражать свои мысли.
Всегда стараюсь поддерживать открытую и позитивную атмосферу во время проведения урока. Объясняю материал на понятном и доступном для ученика языке. Вовлекаю ученика в диалог и обсуждение решения заданий. Особый упор делаю на приобретение учеником практических знаний и навыков, необходимых для решения задач.
Уделяю внимание повышению интереса ученика к предмету.
Похожие статьи
- Свойства интегралов
- Объем сферы
- Площадь сферы
- Перевод км/час в м/с?
- Факультет Менеджмента (НИУ ВШЭ)
- Сезон аллергии: как распознать и как спасаться
- Комплексы из-за внешности: учимся любить себя на примере звезд
- Отпусти меня, мама, я уже взрослый
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Площадь треугольника — все формулы
Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Содержание
Что такое треугольник
Треугольник — это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.
Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.
Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.
Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.
Площадь треугольника
Площадь разностороннего треугольника
Вычисляем площадь треугольника без особенностей — все его стороны разные и все углы разные.
Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле «площадь треугольника через две стороны и угол между ними»:
Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:
Формула Герона определения площади треугольника
Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.
, где
Площадь равнобедренного треугольника
Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.
К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:
Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь прямоугольного треугольника
Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:
Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе
Площадь прямоугольного треугольника, если в него вписана окружность:
Площадь равностороннего треугольника
Площадь равностороннего треугольника можно найти через радиус описанной окружности.
Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:
Площадь равностороннего треугольника, если известна сторона треугольника:
Площадь равностороннего треугольника, если известна высота треугольника:
Как найти площадь треугольника если высота неизвестна.
 Как можно найти площадь треугольника
Как можно найти площадь треугольникаТреугольник — хорошо знакомая всем фигура. И это, несмотря на богатое разнообразие его форм. Прямоугольный, равносторонний, остроугольный, равнобедренный, тупоугольный. Каждый из них чем-то отличается. Но для любого требуется узнавать площадь треугольника.
Общие для всех треугольников формулы, в которых используются длины сторон или высот
Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны н а, н в, н с.
1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * н а. Аналогично следует записать формулы для двух остальных сторон.
2. Формула Герона, в которой фигурирует полупериметр (его принято обозначать маленькой буквой р, в отличии от полного периметра). Полупериметр необходимо сосчитать так: сложить все стороны и разделить их на 2. Формула полупериметра: р = (а+в+с) / 2. Тогда равенство для площади фигуры выглядит так: S = √ (р * (р — а) * (р — в) * (р — с)).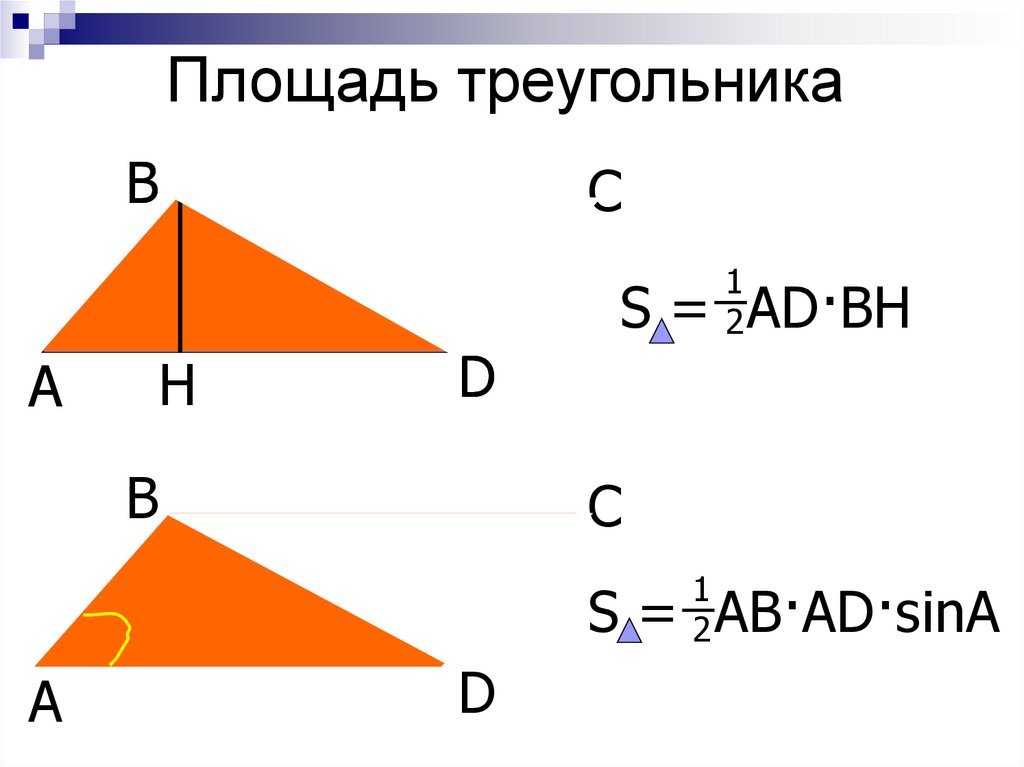
3. Если не хочется использовать полупериметр, то пригодится такая формула, в которой присутствуют только длины сторон: S = ¼ * √ ((а + в + с) * (в + с — а) * (а + с — в) * (а + в — с)). Она несколько длиннее предыдущей, но выручит, если забылось, как находить полупериметр.
Общие формулы, в которых фигурируют углы треугольника
Обозначения, которые требуются для прочтения формул: α, β, γ — углы. Они лежат напротив сторон а, в, с, соответственно.
1. По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.
2. Площадь треугольника можно вычислить по одной стороне и трем известным углам. S = (а 2 * sin β * sin γ) / (2 sin α).
3. Существует еще формула с одной известной стороной и двумя прилежащими к ней углами. Она выглядит таким образом: S = с 2 / (2 (ctg α + ctg β)).
Две последние формулы являются не самыми простыми. Запомнить их довольно сложно.
Запомнить их довольно сложно.
Общие формулы для ситуации, когда известны радиусы вписанных или описанных окружностей
Дополнительные обозначения: r, R — радиусы. Первый используется для радиуса вписанной окружности. Второй — для описанной.
1. Первая формула, по которой вычисляется площадь треугольника, связана с полупериметром. S = р * r. По-другому ее можно записать так: S = ½ r * (а + в + с).
2. Во втором случае потребуется перемножить все стороны треугольника и разделить их на учетверенный радиус описанной окружности. В буквенном выражении это выглядит так: S = (а * в * с) / (4R).
3. Третья ситуация позволяет обойтись без знания сторон, но потребуются значения всех трех углов. S = 2 R 2 * sin α * sin β * sin γ.
Частный случай: прямоугольный треугольник
Это самая простая ситуация, поскольку требуется знание только длины обоих катетов. Они обозначаются латинскими буквами а и в. Площадь прямоугольного треугольника равна половине площади достроенного к нему прямоугольника.
Математически это выглядит так: S = ½ а * в. Она запоминается проще всего. Потому что выглядит, как формула для площади прямоугольника, только появляется еще дробь, обозначающая половину.
Частный случай: равнобедренный треугольник
Поскольку у него две стороны равные, то некоторые формулы для его площади выглядят несколько упрощенными. Например, формула Герона, по которой вычисляется площадь равнобедренного треугольника, принимает следующий вид:
S = ½ в √((a + ½ в)*(a — ½ в)).
Если ее преобразовать, то она станет короче. В таком случае формула Герона для равнобедренного треугольника записывается так:
S = ¼ в √(4 * a 2 — b 2).
Несколько проще, чем для произвольного треугольника, выглядит формула площади, если известны боковые стороны и угол между ними. S = ½ a 2 * sin β.
Частный случай: равносторонний треугольник
Обычно в задачах про него известна сторона или ее можно как-либо узнать. Тогда формула, по которой находится площадь такого треугольника, выглядит следующим образом:
S = (а 2 √3) / 4.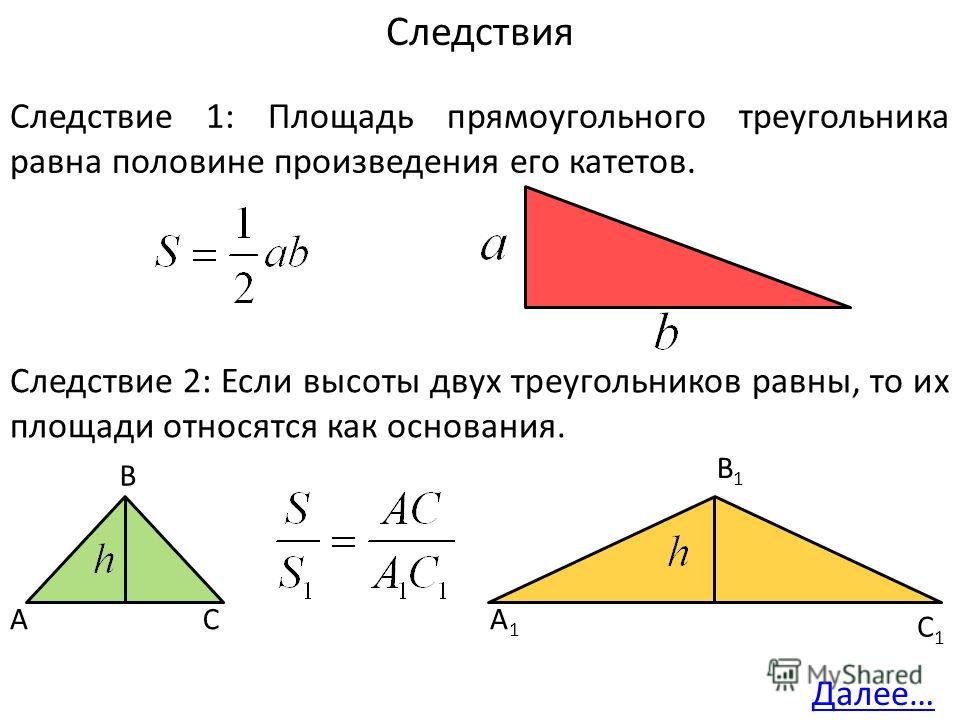
Задачи на нахождение площади, если треугольник изображен на клетчатой бумаге
Самой простой является ситуация, когда прямоугольный треугольник начерчен так, что его катеты совпадают с линиями бумаги. Тогда требуется просто посчитать число клеточек, укладывающихся в катеты. Потом перемножить их и разделить на два.
Когда треугольник остроугольный или тупоугольный, его нужно дорисовать до прямоугольника. Тогда в получившейся фигуре будет 3 треугольника. Один — тот что дан в задаче. А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.
Гораздо сложнее оказывается ситуация, в которой ни одна из сторон треугольника не совпадает с линиями бумаги. Тогда его нужно вписать в прямоугольник так, чтобы вершины исходной фигуры лежали на его сторонах. В этом случае вспомогательных прямоугольных треугольников будет три.
Пример задачи на формулу Герона
Условие. У некоторого треугольника известны стороны. Они равны 3, 5 и 6 см. Необходимо узнать его площадь.
Теперь можно вычислять площадь треугольника по указанной выше формуле. Под квадратным корнем оказывается произведение четырех чисел: 7, 4, 2 и 1. То есть площадь равна √(4 * 14) = 2 √(14).
Если не требуется большая точность, то можно извлечь квадратный корень из 14. Он равен 3,74. Тогда площадь будет равна 7,48.
Ответ. S = 2 √14 см 2 или 7,48 см 2 .
Пример задачи с прямоугольным треугольником
Условие. Один катет прямоугольного треугольника больше, чем второй на 31 см. Требуется узнать их длины, если площадь треугольника равна 180 см 2 .
Решение. Придется решить систему из двух уравнений. Первое связано с площадью. Второе — с отношением катетов, которое дано в задаче.
180 = ½ а * в;
а = в + 31.
Сначала значение «а» нужно подставить в первое уравнение. Получится: 180 = ½ (в + 31) * в. В нем только одна неизвестная величина, поэтому его легко решить. После раскрытия скобок получается квадратное уравнение: в 2 + 31 в — 360 = 0. Оно дает два значения для «в»: 9 и — 40. второе число не подходит в качестве ответа, так как длина стороны треугольника не может быть отрицательной величиной.
В нем только одна неизвестная величина, поэтому его легко решить. После раскрытия скобок получается квадратное уравнение: в 2 + 31 в — 360 = 0. Оно дает два значения для «в»: 9 и — 40. второе число не подходит в качестве ответа, так как длина стороны треугольника не может быть отрицательной величиной.
Осталось вычислить второй катет: прибавить к полученному числу 31. Получается 40. Это искомые в задаче величины.
Ответ. Катеты треугольника равны 9 и 40 см.
Задача на нахождение стороны через площадь, сторону и угол треугольника
Условие. Площадь некоторого треугольника 60 см 2 . Необходимо вычислить одну из его сторон, если вторая сторона равна 15 см, а угол между ними равен 30º.
Решение. Исходя из принятых обозначений, искомая сторона «а», известная «в», заданный угол “γ”. Тогда формула площади можно переписать так:
60 = ½ а * 15 * sin 30º. Здесь синус 30 градусов равен 0,5.
После преобразований «а» оказывается равным 60 / (0,5 * 0,5 * 15). То есть 16.
Ответ. Искомая сторона равна 16 см.
Задача о квадрате, вписанном в прямоугольный треугольник
Условие. Вершина квадрата со стороной 24 см совпадает с прямым углом треугольника. Две другие лежат на катетах. Третья принадлежит гипотенузе. Длина одного из катетов равна 42 см. Чему равна площадь прямоугольного треугольника?
Решение. Рассмотрим два прямоугольных треугольника. Первый — заданный в задаче. Второй — опирается на известный катет исходного треугольника. Они подобны, так как имеют общий угол и образованы параллельными прямыми.
Тогда отношения их катетов равны. Катеты меньшего треугольника равны 24 см (сторона квадрата) и 18 см (заданный катет 42 см вычесть сторону квадрата 24 см). Соответствующие катеты большого треугольника — 42 см и х см. Именно этот «х» нужен для того, чтобы вычислить площадь треугольника.
18/42 = 24/х, то есть х = 24 * 42 / 18 = 56 (см).
Тогда площадь равна произведению 56 и 42, разделенному на два, то есть 1176 см 2 .
Ответ. Искомая площадь равна 1176 см 2 .
Треугольник — это одна из самых распространенных геометрических фигур, с которой мы знакомимся уже в начальной школе. С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.
Виды треугольников
Найти площадь треугольника можно абсолютно разными способами, потому что в геометрии выделяется не один вид фигур, содержащих три угла. К таким видам относятся:
- Тупоугольный.
- Равносторонний (правильный).
- Прямоугольный треугольник.
- Равнобедренный.
Рассмотрим подробнее каждый из существующих типов треугольников.
Такая геометрическая фигура считается наиболее распространенной при решении геометрических задач. Когда возникает необходимость начертить произвольный треугольник, на помощь приходит именно этот вариант.
В остроугольном треугольнике, как понятно по названию, все углы острые и в сумме составляют 180°.
Такой треугольник также очень распространен, однако встречается несколько реже остроугольного. Например, при решении треугольников (т. е. известно несколько его сторон и углов и нужно найти оставшиеся элементы) иногда требуется определить, является угол тупым или нет. Косинус — это отрицательное число.
В величина одного из углов превышает 90°, поэтому оставшиеся два угла могут принимать маленькие значения (например, 15° или вовсе 3°).
Чтобы найти площадь треугольника данного типа, необходимо знать некоторые нюансы, о которых мы поговорим дальше.
Правильный и равнобедренный треугольники
Правильным многоугольником называется фигура, включающаяся в себя n углов, у которой все стороны и углы равны. Таким и является правильный треугольник. Так как сумма всех углов треугольника составляет 180°, то каждый из трех углов равен 60°.
Правильный треугольник, благодаря его свойству, также называют равносторонней фигурой.
Стоит также отметить, что в правильный треугольник можно вписать только одну окружность и около него можно описать только одну окружность, причем их центры расположены в одной точке.
Помимо равностороннего типа, можно также выделить равнобедренный треугольник, несильно от него отличающийся. В таком треугольнике две стороны и два угла равны между собой, а третья сторона (к которой прилегают равные углы) является основанием.
На рисунке показан равнобедренный треугольник DEF, углы D и F которого равны, а DF является основанием.
Прямоугольный треугольник
Прямоугольный треугольник назван так потому, что один из его углов прямой, то есть равен 90°. Другие же два угла в сумме составляют 90°.
Самая большая сторона такого треугольника, лежащая против угла в 90° является гипотенузой, остальные же две его стороны — это катеты. Для данного типа треугольников применима теорема Пифагора:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.
На рисунке изображен прямоугольный треугольник BAC с гипотенузой AC и катетами AB и BC.
Чтобы найти площадь треугольника с прямым углом, нужно знать числовые значения его катетов.
Перейдем к формулам нахождения площади данной фигуры.
Основные формулы нахождения площади
В геометрии можно выделить две формулы, которые подходят для нахождения площади большинства видов треугольников, а именно для остроугольного, тупоугольного, правильного и равнобедренного треугольников. Разберем каждую из них.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.
Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.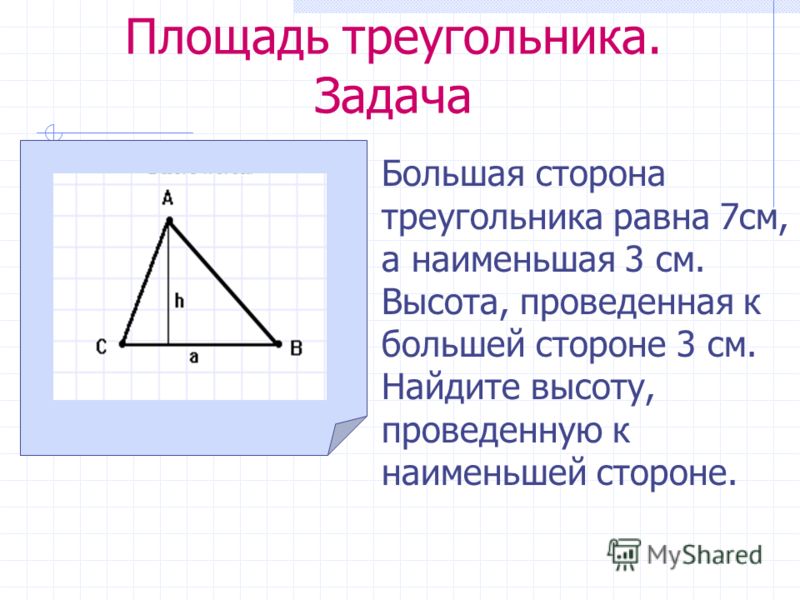
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.
На практике данная формула применяется чаще остальных.
По двум сторонам и углу
Данная формула, как и предыдущая подходит для большинства треугольников и по своему смыслу является следствием формулы нахождения площади по стороне и высоте треугольника. То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
S = ½*sinO*A*B,
где A и B — это стороны треугольника, а O — угол между сторонами A и B.
Напомним, что синус угла можно посмотреть в специальной таблице, названной в честь выдающегося советского математика В. М. Брадиса.
А теперь перейдем к другим формулам, подходящим только для исключительных видов треугольников.
Площадь прямоугольного треугольника
Помимо универсальной формулы, включающей в себя необходимость проводить высоту в треугольнике, площадь треугольника, содержащего прямой угол, можно найти по его катетам.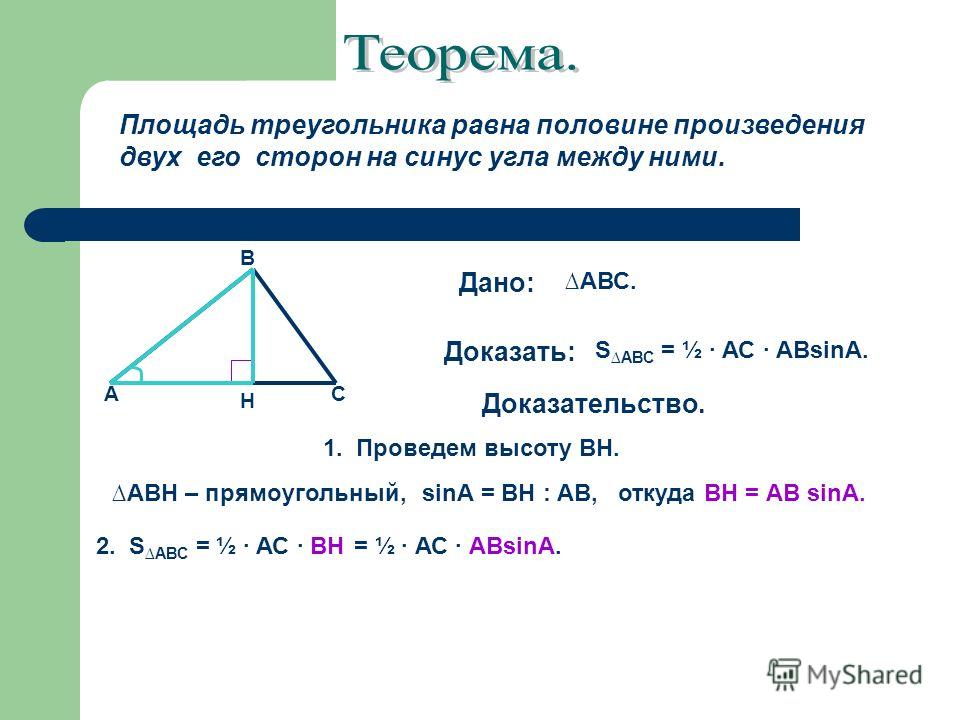
Так, площадь треугольника, содержащего прямой угол, — это половина произведения его катетов, или:
где a и b — катеты прямоугольного треугольника.
Правильный треугольник
Данный вид геометрических фигур отличается тем, что его площадь можно найти при указанной величине лишь одной его стороны (так как все стороны правильного треугольника равны). Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
S = A 2 *√3 / 4,
где A — это сторона равностороннего треугольника.
Формула Герона
Последний вариант для нахождения площади треугольника — это формула Герона. Для того чтобы ею воспользоваться, необходимо знать длины трех сторон фигуры. Формула Герона выглядит так:
S = √p·(p — a)·(p — b)·(p — c),
где a, b и c — это стороны данного треугольника.
Иногда в задаче дано: «площадь правильного треугольника — найти длину его стороны». В данном случае нужно воспользоваться уже известной нам формулой нахождения площади правильного треугольника и вывести из нее значение стороны (или ее квадрата):
A 2 = 4S / √3.
Экзаменационные задачи
В задачах ГИА по математике встречаются множество формул. Помимо этого, достаточно часто необходимо найти площадь треугольника на клетчатой бумаге.
В данном случае удобнее всего провести высоту к одной из сторон фигуры, определить по клеткам ее длину и воспользоваться универсальной формулой для нахождения площади:
Итак, после изучения представленных в статье формул, у вас не возникнут проблемы при нахождении площади треугольника любого вида.
Чтобы определить площадь треугольника, можно пользоваться разными формулами. Из всех способов самый легкий и часто применяемый — это умножение высоты на длину основания с последующим делением полученного результата на два. Однако данный метод далеко не единственный. Ниже вы сможете прочесть, как найти площадь треугольника, используя разные формулы.
Отдельно мы рассмотрим способы вычисления площади специфических видов треугольника — прямоугольного, равнобедренного и равностороннего. Каждую формулу мы сопровождаем коротким пояснением, которое поможет вам понять ее суть.
Универсальные способы нахождения площади треугольника
В приведенных ниже формулах используются специальные обозначения. Мы расшифруем каждое из них:
- a, b, c – длины трех сторон рассматриваемой нами фигуры;
- r – радиус окружности, которая может быть вписана в наш треугольник;
- R – радиус той окружности, которая может быть описана вокруг него;
- α — величина угла, образованного сторонами b и с;
- β — величина угла между a и c;
- γ — величина угла, образованного сторонами а и b;
- h – высота нашего треугольника, опущенная из угла α на сторону а;
- p – половина суммы сторон a, b и с.
Логически понятно, почему можно находить площадь треугольника этим способом. Треугольник легко достраивается до параллелограмма, в котором одна сторона треугольника будет выполнять роль диагонали. Площадь параллелограмма находится умножением длины одной из его сторон на значение высоты, проведенной к ней. Диагональ разделяет этот условный параллелограмм на 2 одинаковых треугольника.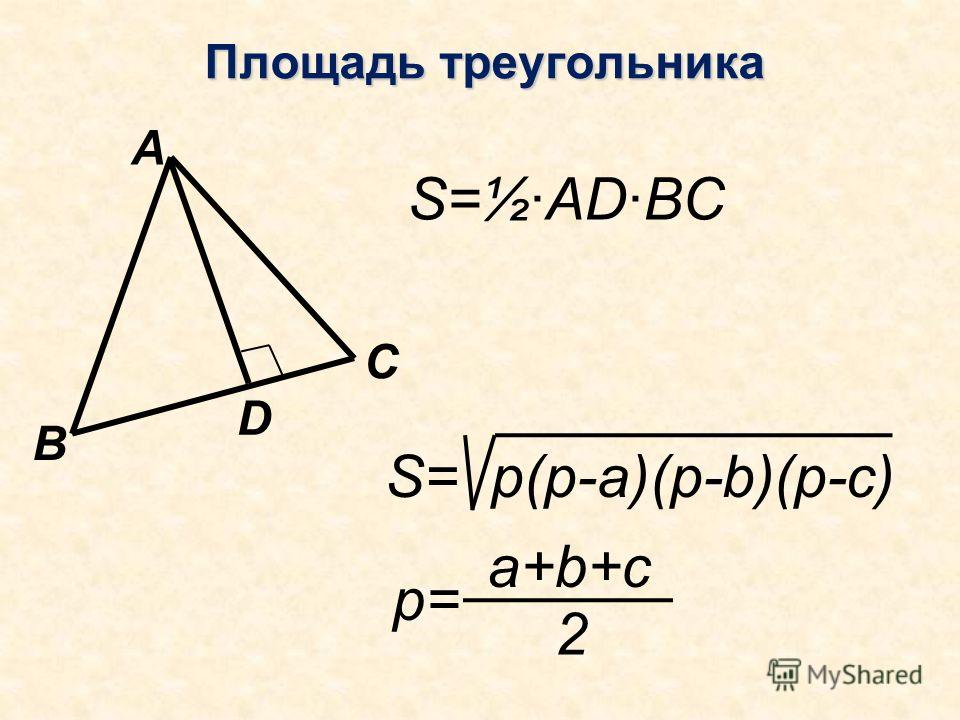 Следовательно, совершенно очевидно, что площадь нашего исходного треугольника должна равняться половине площади этого вспомогательного параллелограмма.
Следовательно, совершенно очевидно, что площадь нашего исходного треугольника должна равняться половине площади этого вспомогательного параллелограмма.
S=½ a · b·sin γ
Согласно этой формуле, площадь треугольника находится умножением длин двух его сторон, то есть а и b, на синус образованного ими угла. Эта формула логически выводится из предыдущей. Если опустить высоту из угла β на сторону b, то, согласно свойствам прямоугольного треугольника, при умножении длины стороны a на синус угла γ получаем высоту треугольника, то есть h.
Площадь рассматриваемой фигуры находим путем умножения половины радиуса окружности, которую в него можно вписать, на его периметр. Иными словами, находим произведение полупериметра на радиус упомянутой окружности.
S= a · b · с/4R
Согласно данной формуле, необходимую нам величину можно найти путем деления произведения сторон фигуры на 4 радиуса окружности, вокруг нее описанной.
Эти формулы универсальны, так как дают возможность определить площадь любого треугольника (разностороннего, равнобедренного, равностороннего, прямоугольного).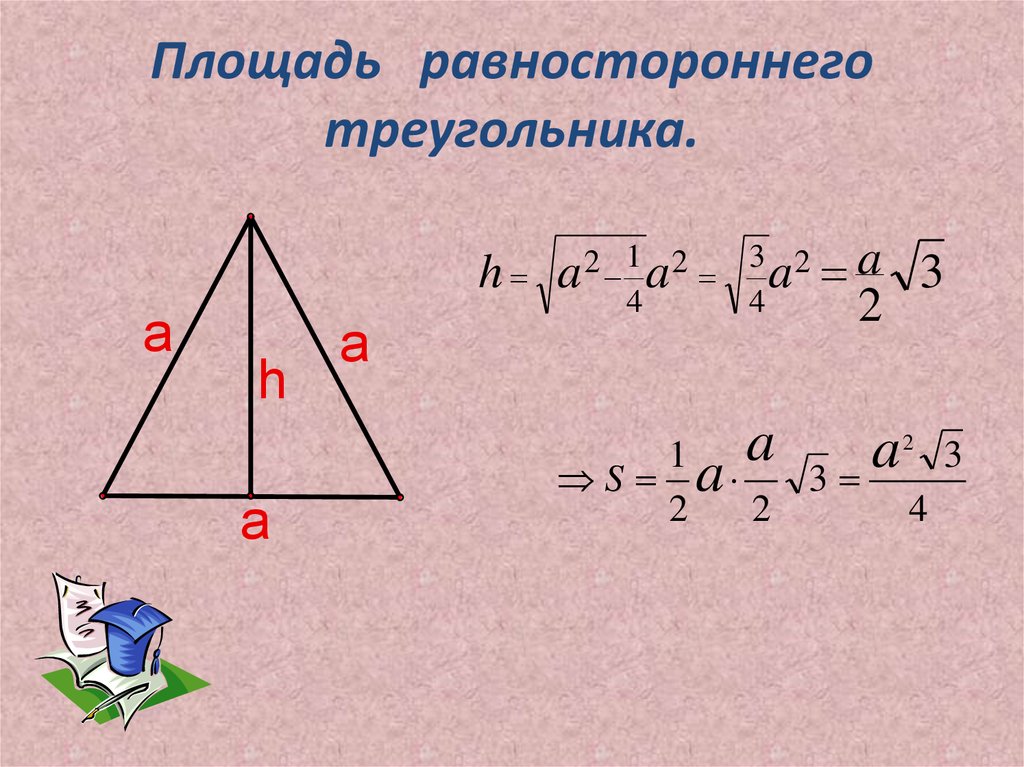 Можно это сделать и при помощи более сложных вычислений, на которых мы подробно останавливаться не станем.
Можно это сделать и при помощи более сложных вычислений, на которых мы подробно останавливаться не станем.
Площади треугольников со специфическими свойствами
Как найти площадь прямоугольного треугольника? Особенностью этой фигуры является то, что две ее стороны одновременно являются ее высотами. Если а и b являются катетами, а с становится гипотенузой, то площадь находим так:
Как найти площадь равнобедренного треугольника? В нем две стороны с длиной а и одна сторона с длиной b. Следовательно, его площадь определить можно путем деления на 2 произведения квадрата стороны а на синус угла γ.
Как найти площадь равностороннего треугольника? В нем длина всех сторон равняется а, а величина всех углов — α. Его высота равна половине произведения длины стороны а на корень квадратный из 3. Чтобы найти площадь правильного треугольника, нужно квадрат стороны а умножить на корень квадратный из 3 и разделить на 4.
Формул для вычисления площади треугольника в интернете можно найти свыше 10.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c
– стороны треугольника,
R
– радиус описанной окружности,
r
– радиус вписанной окружности,
h[b],h[a],h[c]
– высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma –
углы возле вершин.
1.
Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
То с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5.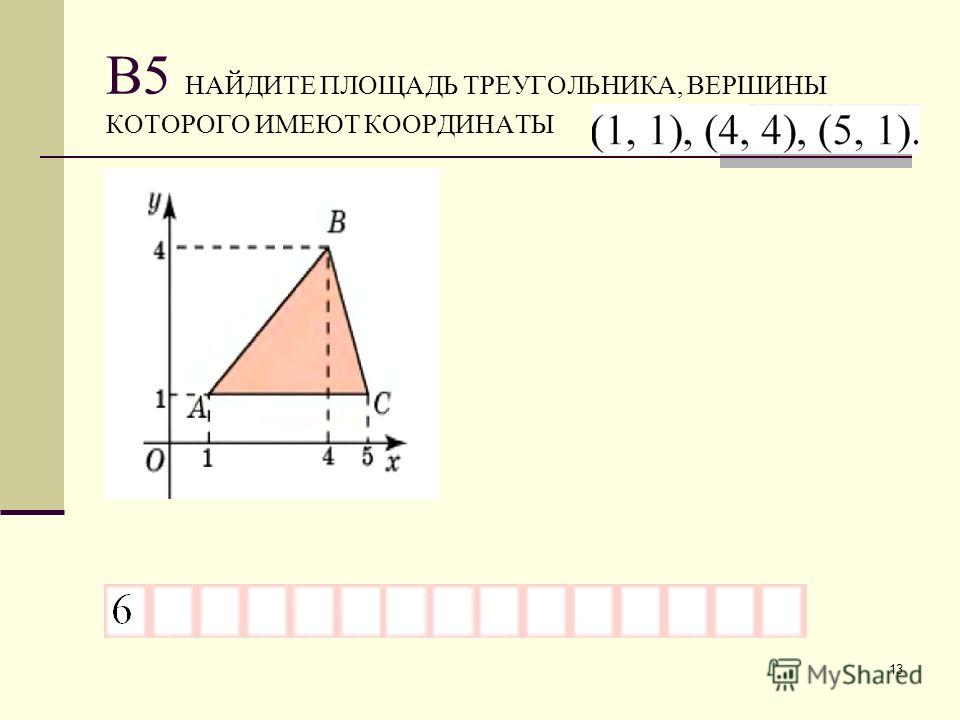 Формула площади через сторону и котангенс прилегающих углов следующая
Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона
применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
А затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9.
Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника
с катетами a
и b
равна половине их произведения
Формула площади равностороннего (правильного) треугольника
=
= одной четвертой произведения квадрату стороны на корень из тройки.
Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.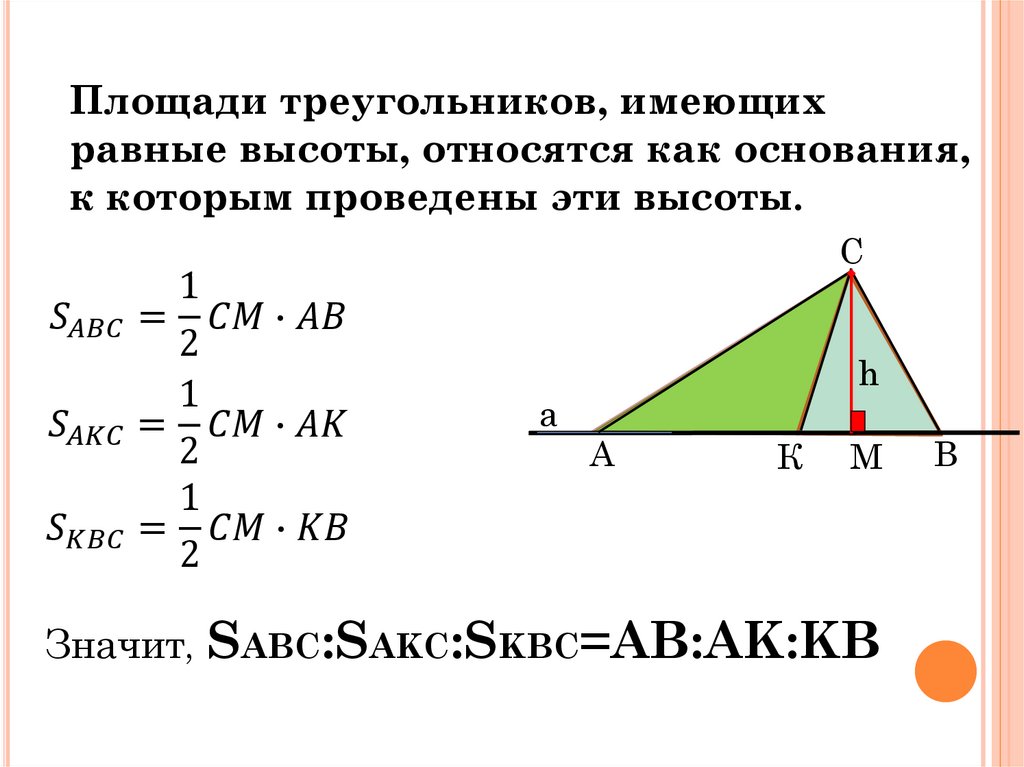
Рассмотрим пример.
Пример 1
Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется
Тогда площадь треугольника равняется
Ответ: $15$.
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Теорема 1
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=\frac{1}{2}αh$
где $a$ — длина стороны, $h$ — высота, проведенная к ней.
Доказательство.
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда
$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$
Теорема доказана.
Пример 2
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим
$S=\frac{1}{2}\cdot 9\cdot 9=40,5$
Ответ: $40,5$.
Формула Герона
Теорема 2
Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом
$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
здесь $ρ$ означает полупериметр этого треугольника. 2}}$
2}}$
$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
Как вычислить площадь треугольника. Площадь треугольника
Школьная программа предусматривает обучение детей геометрии с раннего возраста. Одно из самых базовых знаний этой области — это нахождение площади различных фигур. В этой статье мы постараемся привести все возможные способы получения этой величины, от простейших до самых сложных.
Основа
Первая формула, которую изучают дети в школе, предусматривает нахождение площади треугольника через длину его высоты и основания. Высота — это отрезок, проведённый из вершины треугольника под прямым углом к противолежащей стороне, которая будет являться основанием. Как найти площадь треугольника по этим величинам?
Если V — высота, а O — основание, тогда площадь S=V*O:2.
Другой вариант получения искомой величины требует от нас знания длин двух сторон, а также величины угла между ними.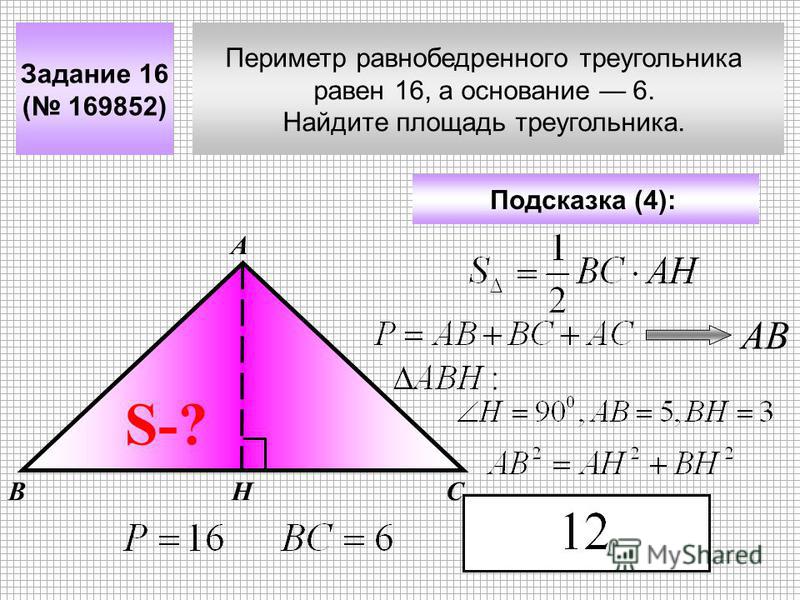 Если у нас L и M — длины сторон, а Q — угол между ними, тогда вы можете получить площадь по формуле S=(L*M*sin(Q))/2.
Если у нас L и M — длины сторон, а Q — угол между ними, тогда вы можете получить площадь по формуле S=(L*M*sin(Q))/2.
Формула Герона
Кроме всех прочих ответов на вопрос о том, как вычислить площадь треугольника, есть формула, позволяющая получить необходимое нам значение, зная исключительно длины сторон. То есть, если нам известны длины всех сторон, то нам нет необходимости проводить высоту и вычислять её длину. Мы можем воспользоваться, так называемой формулой Герона.
Если M, N, L — это длины сторон, тогда мы можем найти площадь треугольника, следующим образом. P=(M+N+L)/2, тогда необходимая нам величина S 2 =P*(P-M)*(P-L)*(P-N). В итоге, нам останется только вычислить корень.
Для прямоугольного треугольника формула Герона немного упрощается. Если M, L -это катеты, тогда S=(P-M)*(P-L).
Окружности
Другой способ, с помощью которого можно найти площадь треугольника, предусматривает использование вписанных и описанных окружностей. Чтобы получить необходимую нам величину с помощью вписанной окружности, нам потребуется узнать её радиус.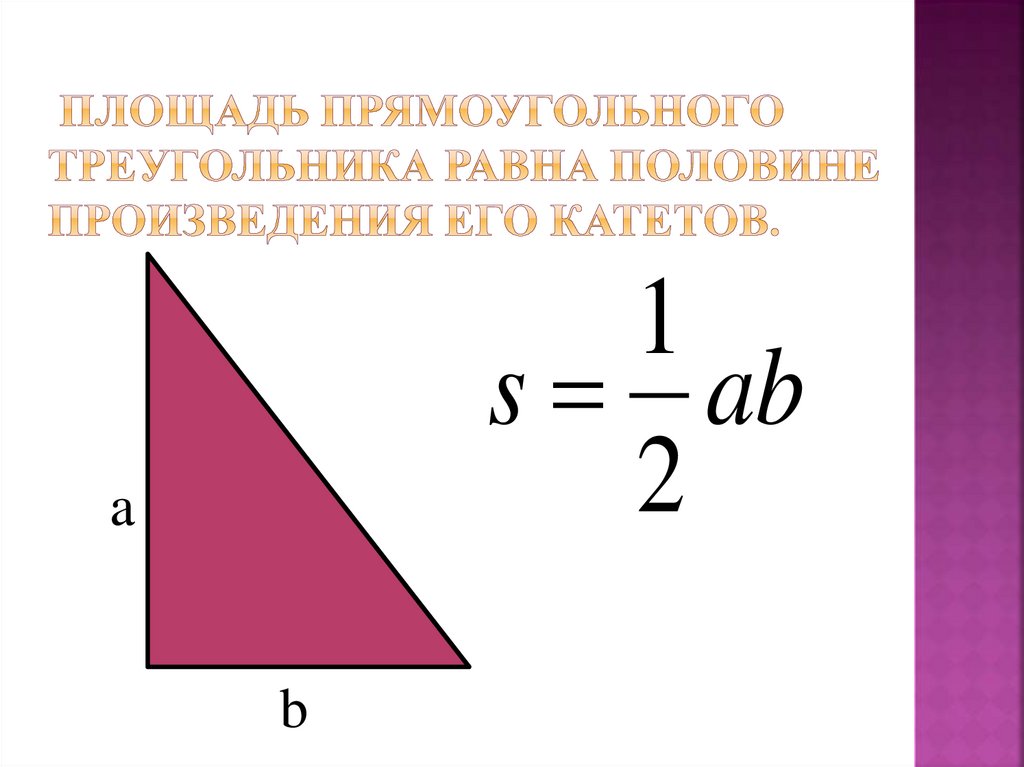 Обозначим его «r». Тогда формула, по которой мы будем проводить вычисления, примет следующий вид: S=r*P, где P — это половина от суммы длин всех сторон.
Обозначим его «r». Тогда формула, по которой мы будем проводить вычисления, примет следующий вид: S=r*P, где P — это половина от суммы длин всех сторон.
В прямоугольном треугольнике эта формула немного преобразуется. Конечно, вы можете использовать и указанную выше, однако лучше взять для вычислений другое выражение. S=E*W, где E и W — это длины отрезков, на которые делится гипотенуза, точкой касания окружности.
Говоря об описанной окружности, найти площадь треугольника, также не составит труда. Введя обозначение R, как радиус описанной окружности, можно получить следующую формулу, необходимую для вычисления искомой величины: S= (M*N*L):(4*R). Где три первые величины — это стороны треугольника.
Говоря о равностороннем треугольнике, за счет ряда простейших математических преобразований можно получить немого изменённые формулы:
S=(3 1/2 *M 2)/4;
S=(3*3 1/2 *R 2)/4;
S=3*3 1/2 *r 2 .
Во всяком случае, любая формула, позволяющая найти площадь треугольника, может быть изменена в соответствии с данными поставленной задачи. Так что все написанные выражения не являются абсолютами. При решении задач поразмышляйте, чтобы найти наиболее подходящий способ решения.
Так что все написанные выражения не являются абсолютами. При решении задач поразмышляйте, чтобы найти наиболее подходящий способ решения.
Координаты
При изучении координатных осей задачи, стоящие перед учениками, усложняются. Однако не настолько, чтобы впадать в панику. Для того чтобы найти площадь треугольника по координатам вершин, вы можете воспользоваться всё той же, но немного изменённой формулой Герона. Для координат она приобретает следующий вид:
S=((x 2 -x 1) 2 *(y 2 -y 1) 2 *(z 2 -z 1) 2) 1/2 .
Впрочем, никто не запрещает, используя координаты, вычислить длины сторон треугольника и затем, по формулам, которые были написаны выше, посчитать площадь. Для преобразования координат в длину пользуйтесь следующей формулой:
l=((x 2 -x 1) 2 +(y 2 -y 1) 2) 1/2 .
Примечания
В статье использовались стандартные обозначения величин, которые применяются в условиях большинства задач. При этом степень «1/2» означает, что вам необходимо извлечь корень из всего выражения под скобками.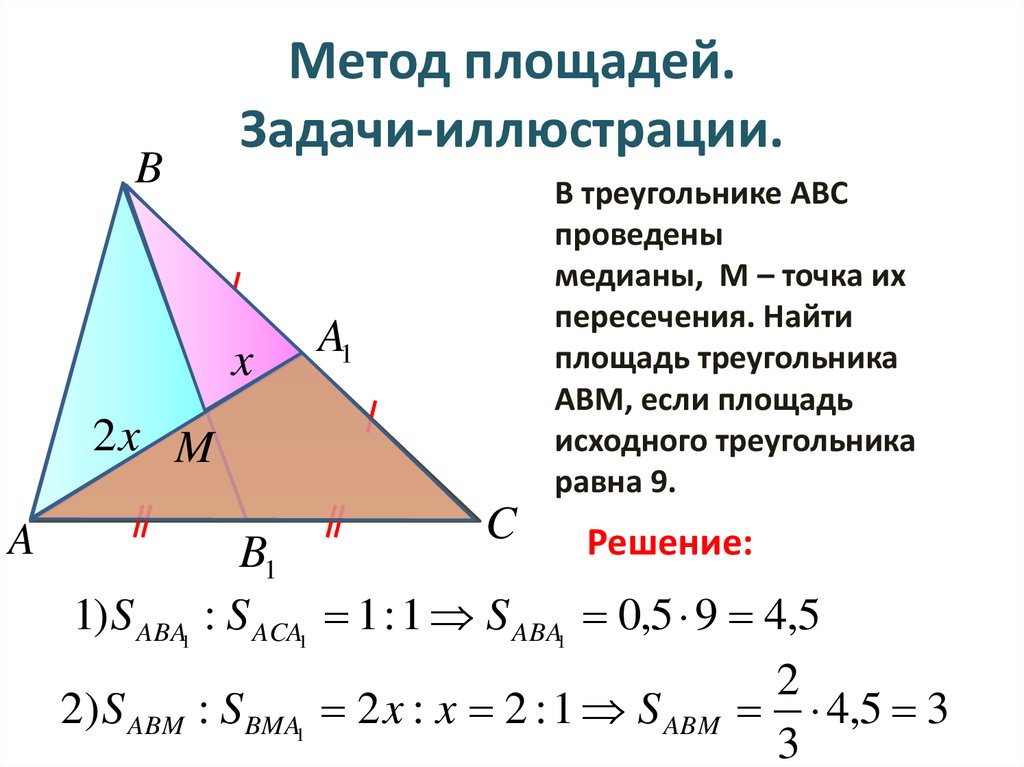
При выборе формулы будьте внимательнее. Некоторые из них теряют свою актуальность в зависимости от начальных условий. Например, формула описанной окружности. Она способна высчитать вам результат в любом случае, однако может быть такая ситуация, когда треугольника с заданными параметрами может вообще не существовать.
Если вы сидите дома и делаете домашнее задание, тогда можете воспользоваться онлайн-калькулятором. Многие сайты предоставляют возможность вычисления различных величин по заданным параметрам, причем не суть важно, каким именно. Вы просто можете вписать начальные данные в поля, и компьютер (сайт) посчитает за вас результат. Таким образом, вы сможете избежать ошибок, допущенных по невнимательности.
Надеемся наша статья ответила все ваши вопросы касательно вычисления площади самых разных треугольников, и вам не придётся искать допонительную информацию в другом месте. Удачи с учебой!
Треугольник — это одна из самых распространенных геометрических фигур, с которой мы знакомимся уже в начальной школе. С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.
С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.
Виды треугольников
Найти площадь треугольника можно абсолютно разными способами, потому что в геометрии выделяется не один вид фигур, содержащих три угла. К таким видам относятся:
- Тупоугольный.
- Равносторонний (правильный).
- Прямоугольный треугольник.
- Равнобедренный.
Рассмотрим подробнее каждый из существующих типов треугольников.
Такая геометрическая фигура считается наиболее распространенной при решении геометрических задач. Когда возникает необходимость начертить произвольный треугольник, на помощь приходит именно этот вариант.
В остроугольном треугольнике, как понятно по названию, все углы острые и в сумме составляют 180°.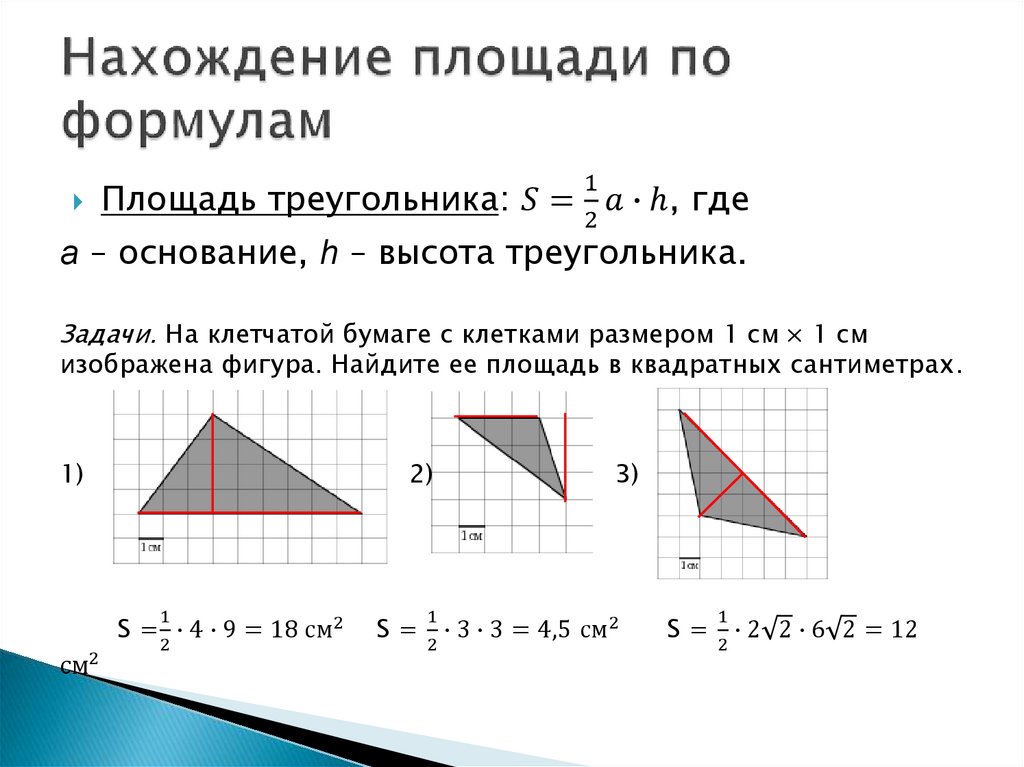
Такой треугольник также очень распространен, однако встречается несколько реже остроугольного. Например, при решении треугольников (т. е. известно несколько его сторон и углов и нужно найти оставшиеся элементы) иногда требуется определить, является угол тупым или нет. Косинус — это отрицательное число.
В величина одного из углов превышает 90°, поэтому оставшиеся два угла могут принимать маленькие значения (например, 15° или вовсе 3°).
Чтобы найти площадь треугольника данного типа, необходимо знать некоторые нюансы, о которых мы поговорим дальше.
Правильный и равнобедренный треугольники
Правильным многоугольником называется фигура, включающаяся в себя n углов, у которой все стороны и углы равны. Таким и является правильный треугольник. Так как сумма всех углов треугольника составляет 180°, то каждый из трех углов равен 60°.
Правильный треугольник, благодаря его свойству, также называют равносторонней фигурой.
Стоит также отметить, что в правильный треугольник можно вписать только одну окружность и около него можно описать только одну окружность, причем их центры расположены в одной точке.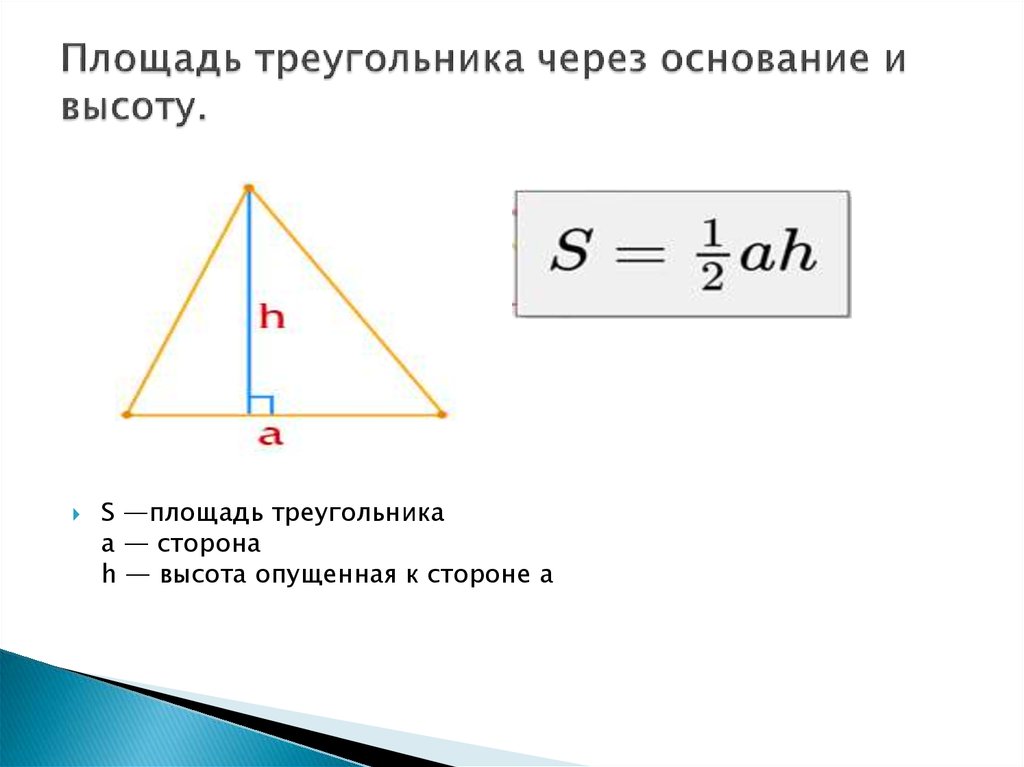
Помимо равностороннего типа, можно также выделить равнобедренный треугольник, несильно от него отличающийся. В таком треугольнике две стороны и два угла равны между собой, а третья сторона (к которой прилегают равные углы) является основанием.
На рисунке показан равнобедренный треугольник DEF, углы D и F которого равны, а DF является основанием.
Прямоугольный треугольник
Прямоугольный треугольник назван так потому, что один из его углов прямой, то есть равен 90°. Другие же два угла в сумме составляют 90°.
Самая большая сторона такого треугольника, лежащая против угла в 90° является гипотенузой, остальные же две его стороны — это катеты. Для данного типа треугольников применима теорема Пифагора:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.
На рисунке изображен прямоугольный треугольник BAC с гипотенузой AC и катетами AB и BC.
Чтобы найти площадь треугольника с прямым углом, нужно знать числовые значения его катетов.
Перейдем к формулам нахождения площади данной фигуры.
Основные формулы нахождения площади
В геометрии можно выделить две формулы, которые подходят для нахождения площади большинства видов треугольников, а именно для остроугольного, тупоугольного, правильного и равнобедренного треугольников. Разберем каждую из них.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.
Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.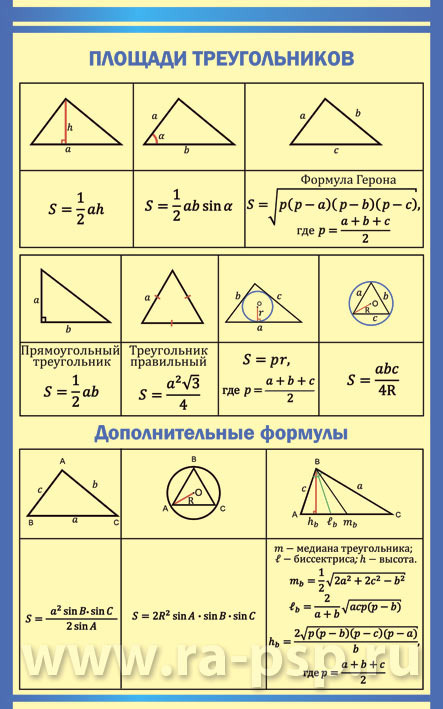
На практике данная формула применяется чаще остальных.
По двум сторонам и углу
Данная формула, как и предыдущая подходит для большинства треугольников и по своему смыслу является следствием формулы нахождения площади по стороне и высоте треугольника. То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
S = ½*sinO*A*B,
где A и B — это стороны треугольника, а O — угол между сторонами A и B.
Напомним, что синус угла можно посмотреть в специальной таблице, названной в честь выдающегося советского математика В. М. Брадиса.
А теперь перейдем к другим формулам, подходящим только для исключительных видов треугольников.
Площадь прямоугольного треугольника
Помимо универсальной формулы, включающей в себя необходимость проводить высоту в треугольнике, площадь треугольника, содержащего прямой угол, можно найти по его катетам.
Так, площадь треугольника, содержащего прямой угол, — это половина произведения его катетов, или:
где a и b — катеты прямоугольного треугольника.
Правильный треугольник
Данный вид геометрических фигур отличается тем, что его площадь можно найти при указанной величине лишь одной его стороны (так как все стороны правильного треугольника равны). Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
S = A 2 *√3 / 4,
где A — это сторона равностороннего треугольника.
Формула Герона
Последний вариант для нахождения площади треугольника — это формула Герона. Для того чтобы ею воспользоваться, необходимо знать длины трех сторон фигуры. Формула Герона выглядит так:
S = √p·(p — a)·(p — b)·(p — c),
где a, b и c — это стороны данного треугольника.
Иногда в задаче дано: «площадь правильного треугольника — найти длину его стороны». В данном случае нужно воспользоваться уже известной нам формулой нахождения площади правильного треугольника и вывести из нее значение стороны (или ее квадрата):
A 2 = 4S / √3.
Экзаменационные задачи
В задачах ГИА по математике встречаются множество формул.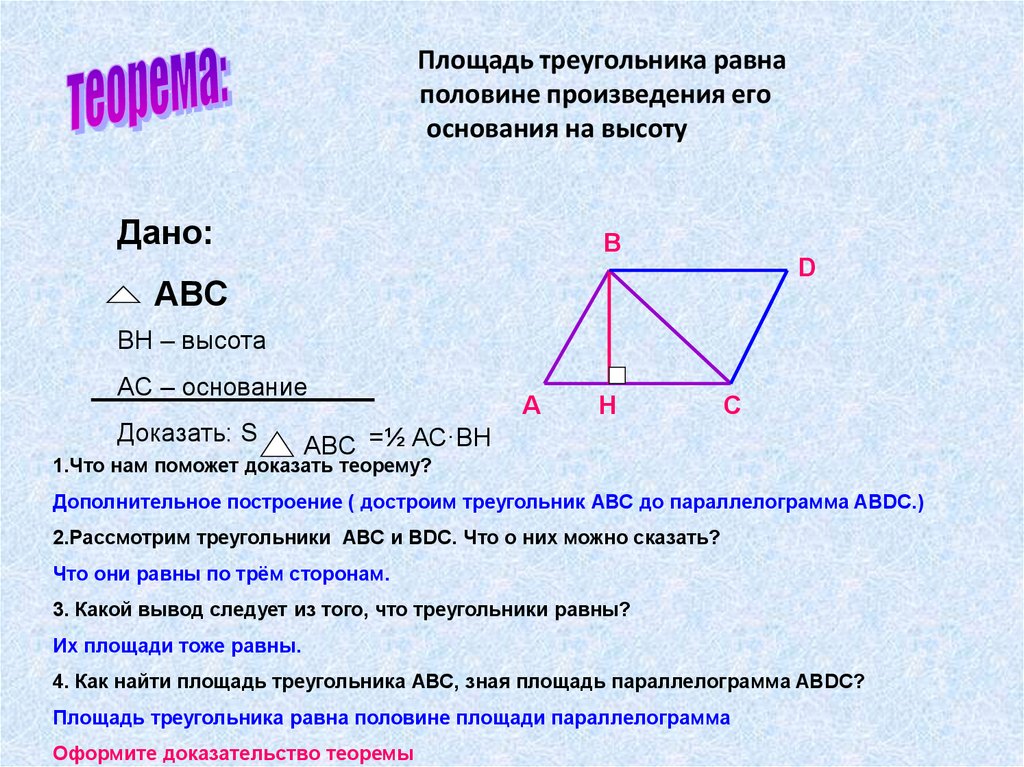 Помимо этого, достаточно часто необходимо найти площадь треугольника на клетчатой бумаге.
Помимо этого, достаточно часто необходимо найти площадь треугольника на клетчатой бумаге.
В данном случае удобнее всего провести высоту к одной из сторон фигуры, определить по клеткам ее длину и воспользоваться универсальной формулой для нахождения площади:
Итак, после изучения представленных в статье формул, у вас не возникнут проблемы при нахождении площади треугольника любого вида.
Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой. Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C). Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:
- Прямоугольный.
- Тупоугольный.
- Остроугольный.
- Разносторонний.
- Равносторонний.
- Равнобедренный.
Общие формулы для вычисления площади треугольника
Формула площади треугольника по длине и высоте
S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.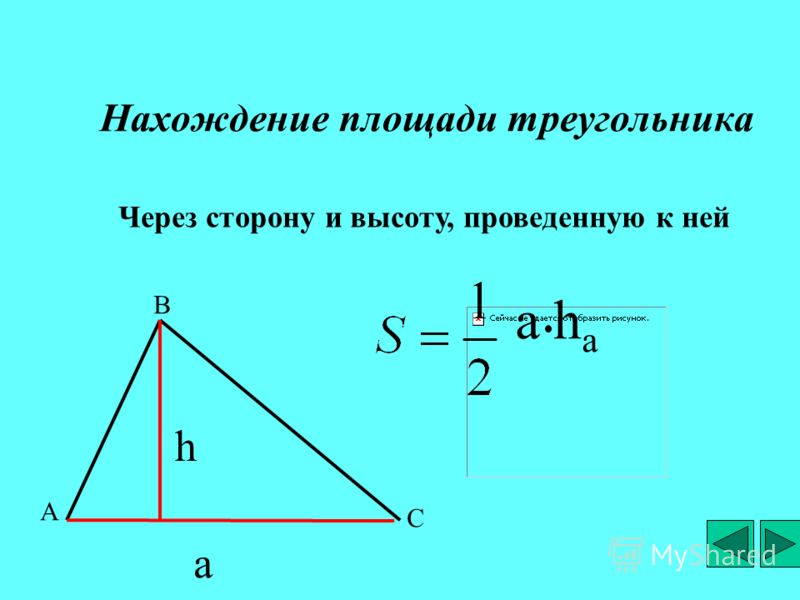
Формула Герона
S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.
Формула площади треугольника по величине угла и длине отрезка
S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.
Формула площади треугольника по радиусу вписанной окружности и трем сторонам
S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.
Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности
S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.
Формула площади треугольника по декартовым координатам точек
Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
где || обозначает модуль.
Как найти площадь прямоугольного треугольника
Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.
Формула площади прямоугольного треугольника по двум катетам
S= a*b/2,
где a,b – это длина катетов. Катетами называются стороны, прилежащие к прямому углу.
Формула площади прямоугольного треугольника по гипотенузе и острому углу
S = a*b*sin(α)/ 2,
где a, b – это катеты треугольника, а sin(α)- это синус угла, в котором пересекаются прямые a, b.
Формула площади прямоугольного треугольника по катету и противолежащему углу
S = a*b/2*tg(β),
где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.
Как вычислить площадь равнобедренного треугольника
Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.
Основная формула для вычисления площади равнобедренного треугольника
S=h*c/2,
где с – это основание треугольника, h-это высота треугольника, опущенного к основанию.
Формула равнобедренного треугольника по боковой стороне и основанию
S=(c/2)* √(a*a – c*c/4),
где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.
Как найти площадь равностороннего треугольника
Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу:
Для вычисления площади равностороннего треугольника можно использовать следующую формулу:
S = (√3*a*a)/4,
где a-это длина стороны равностороннего треугольника.
Вышеприведенные формулы позволят вычислить искомую площадь треугольника. Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления.
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c
– стороны треугольника,
R
– радиус описанной окружности,
r
– радиус вписанной окружности,
h[b],h[a],h[c]
– высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma –
углы возле вершин.
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
То с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.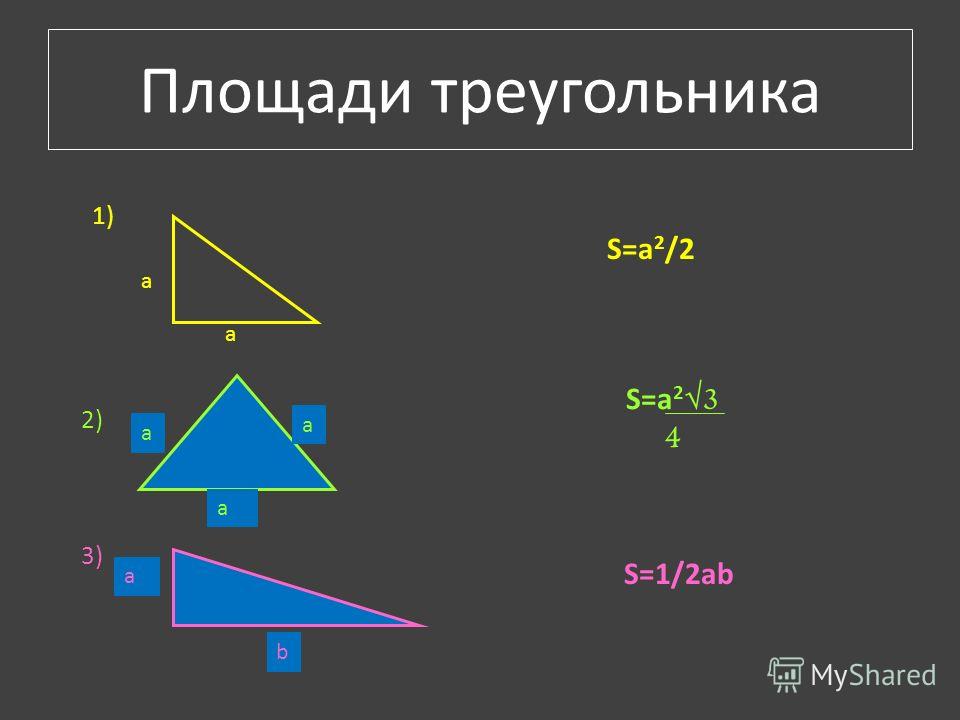
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона
применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
А затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9.
Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника
с катетами a
и b
равна половине их произведения
Формула площади равностороннего (правильного) треугольника
=
= одной четвертой произведения квадрату стороны на корень из тройки.
Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.
Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
- «Формулы площади равностороннего треугольника»
Формулы площади треугольника
Пояснения к формулам :
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a
треугольника
β — угол, противолежащий стороне b
треугольника
γ — угол, противолежащий стороне c
треугольника
h a , h b , h c — высота треугольника, опущенная на сторону a
, b
, c
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.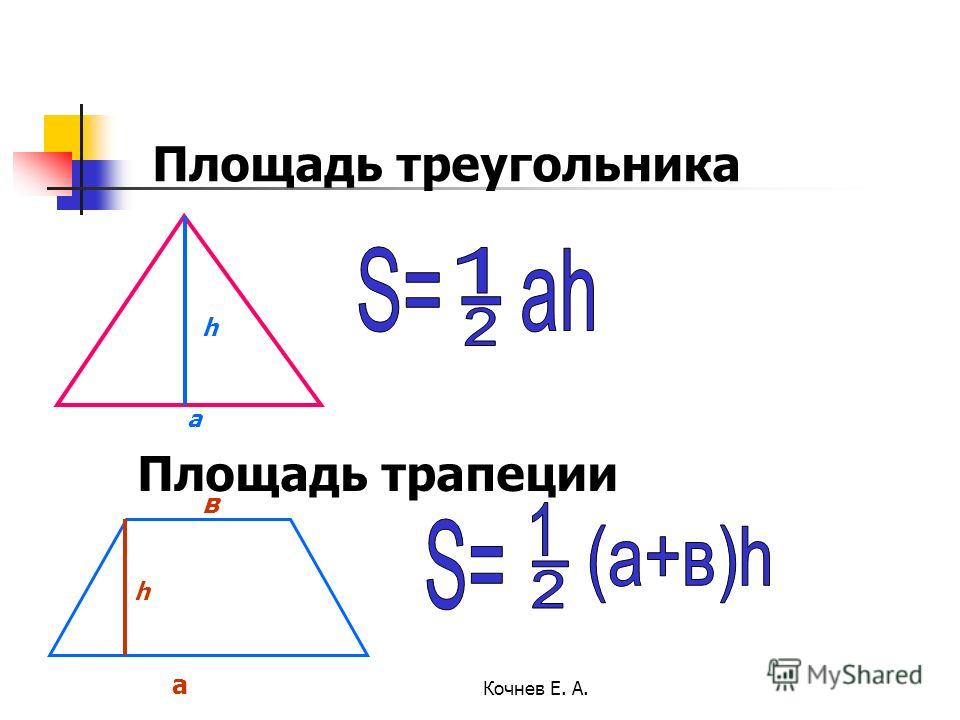
- Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
- Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
- Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
- Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
- Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
- Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
- Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов.
 (Формула 8)
(Формула 8) - Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
- Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
- Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений
Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение . Иногда для простых подкоренных выражений может использоваться символ √
Иногда для простых подкоренных выражений может использоваться символ √
Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .
Решение .
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2
Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Задача. Найти площадь равностороннего треугольникаНайти площадь равностороннего треугольника со стороной 3см.
Решение .
Площадь треугольника можно найти по формуле Герона:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
Поскольку a = b = c формула площади равностороннего треугольника примет вид:
S =
√3 / 4 * a 2
S =
√3 / 4 * 3 2
Ответ : 9 √3 / 4.
Задача. Изменение площади при изменении длины сторон
Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?
Решение .
Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.
Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.
Желающие могут сразу опуститься вниз решения.
Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. первую строку рисунка внизу)
Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c))
(см. вторую строку на рисунке внизу)
Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда
S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — четвертая строка
Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. пятую строку рисунка внизу)
пятую строку рисунка внизу)
Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.
Правило как найти площадь треугольника. Как найти площадь треугольника
Инструкция
Стороны и углы считаются основными элементами а . Треугольник полностью определяется любой из следующих своих основных элементов: либо тремя сторонами, либо одной стороной и двумя углами, либо двумя сторонами и углом между ними. Для существования треугольника , задаваемого тремя сторонами a, b, c, необходимо и достаточно выполнение неравенств, называемых неравенствами треугольника :
a+b > c,
a+c > b,
b+c > a.
Для построения треугольника по трем сторонам a, b, c, необходимо из точки С отрезка СВ=a как из провести циркулем окружность радиусом b. Затем аналогичным образом провести из точки B окружность радиусом равным стороне c. 2 v3)/4
2 v3)/4
Если треугольник является прямоугольным, то есть один из его углов равен 90°, а стороны, его образующие, катетами, третья сторона гипотенузой. В данном случае площадь равняется произведению катетов, деленному на два.
S=ab/2
Чтобы найти площадь треугольника , можно воспользоваться одной из многочисленных формул. Формулу выбирайте в зависимости от того, какие данные уже известны.
Вам понадобится
- знание формул для нахождения площади треугольника
Инструкция
Если вы знаете величину одной из сторон и величину высоты, опущенной на эту сторону из противолежащего ей угла, то можно найти площадь по следующей : S = a*h/2, где S — площадь треугольника, a — одна из сторон треугольника, а h — высота, к стороне a.
Существует известная для определения площади треугольника, если известны три его стороны. Она формулой Герона. Для упрощения ее записи вводят промежуточную величину — полупериметр: p = (a+b+c)/2, где a, b, c — . возведение в степень.
возведение в степень.
Предположим, что вам известна одна из сторон треугольника и три угла. Тогда легко найти площадь треугольника: S = a²sinα sinγ / (2sinβ), где β — угол, противолежащий стороне a, а α и γ — прилежащие к стороне углы.
Видео по теме
Обратите внимание
Самая общая формула, которая подходит для всех случаев — это формула Герона.
Источники:
Поиск площади треугольника — одна из самых распространенных задач школьной планиметрии. Знания трех сторон треугольника достаточно для определения площади любого треугольника. В частных случаях и равностороннего треугольников достаточно знать длины двух и одной стороны соответственно.
Вам понадобится
- длины сторон треугольников, формула Герона, теорема косинусов
Инструкция
Формула Герона для площади треугольника следующим образом: S = sqrt(p(p-a)(p-b)(p-c)). Если расписать полупериметр p, то получится: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c)/2)) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4. 2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.
2). Подставляя синус в формулу для площади и расписывая его, можно прийти к формуле для площади треугольника ABC.
Видео по теме
Для проведения ремонтных работ бывает необходимо измерить площадь стен. Так проще рассчитать необходимое количество краски или обоев. Для измерений лучше всего воспользоваться рулеткой или сантиметровой лентой. Замеры следует проводить уже после того, как стены были выровнены.
Вам понадобится
- -рулетка;
- -стремянка.
Инструкция
Чтобы посчитать площадь стен, вам необходимо знать точную высоту потолков, а также произвести замеры длины по полу. Делается это следующим образом: возьмите сантиметр, проложите его над плинтусом. Обычно сантиметра для всей длины не хватает, поэтому закрепите его в углу, затем размотайте на максимальную длину. В этой точке поставьте отметку карандашом, запишите полученный результат и дальнейшее измерение проводите тем же образом, начиная с последней точки замера.
Стандартная потолков в типовых — 2 метра 80 сантиметров, 3 метра и 3 метра 20 сантиметров, в зависимости от дома. Если дом был построен до 50-х годов, то, скорее всего, реальная высота несколько ниже указанной. Если вы вычисляете площадь для ремонтных работ, то небольшой запас не повредит — считайте, исходя из стандарта. Если все же необходимо знать реальную высоту — проведите замеры . Принцип аналогичен измерению длины, но потребуется стремянка.
Перемножьте полученные показатели — это и есть площадь вашей стены . Правда, при покрасочных работах или для необходимо вычесть площадь дверных и оконных проемов. Для этого проложите сантиметр вдоль проема. Если речь идет о двери, которую вы впоследствии собираетесь менять, то проводите со снятой дверной коробкой, учитывая только площадь непосредственно самого проема. Площадь окна высчитывается по периметру его рамы. После того, как площадь окна и дверного проема высчитана, вычтите результат из общей полученной площади комнаты.
Учтите, что замеры длины и ширины комнаты проводить вдвоем, так легче зафиксировать сантиметр или рулетку и, соответственно, получить более точный результат. Проводите один и тот же замер несколько раз, чтобы убедиться в точности полученных цифр.
Видео по теме
Нахождение объема треугольника действительно нетривиальная задача. Дело в том, что треугольник — двухмерная фигура, т.е. он целиком лежит в одной плоскости, а это значит, что у него попросту нет объема. Разумеется нельзя найти то, чего не существует. Но не будем опускать руки! Можно принять следующее допущение — объем двухмерной фигуры, это ее площадь. Площадь треугольника мы и будем искать.
Вам понадобится
- лист бумаги, карандаш, линейка, калькулятор
Инструкция
Начертите на листе бумаги при помощи линейки и карандаша. Внимательно рассмотрев треугольник, вы сможете убедиться, что у него действительно нет , так как он нарисован на плоскости. Подпишите стороны треугольника: пусть одна сторона будет стороной «а», другая — стороной «b», и третья — стороной «c». Подпишите вершины треугольника буквами «А», «B» и «C».
Подпишите вершины треугольника буквами «А», «B» и «C».
Измерьте линейкой любую сторону треугольника и запишите получившийся результат. После этого восстановите перпендикуляр к измеренной стороне из противоположной ей вершины, такой перпендикуляр будет высотой треугольника. В случае, представленном на рисунке, перпендикуляр «h» восстановлен к стороне «c» из вершины «A». Измерьте получившуюся высоту линейкой и запишите результат измерения.
Может случиться, что вам будет сложно восстановить точный перпендикуляр. В этом случае вам следует воспользоваться другой формулой. Измерьте все стороны треугольника линейкой. После этого подсчитайте полупериметр треугольника «p», сложив получившиеся длины сторон и разделив их сумму пополам. Имея в своем распоряжении значение полупериметра, вы можете по формуле Герона. Для этого необходимо извлечь квадратный корень из следующего : p(p-a)(p-b)(p-c).
Вы получили искомую величину площади треугольника. Задача нахождения объема треугольника не решена, но как говорилось выше, объема не . Вы можете найти объем , которая по сути треугольником в трехмерном мире. Если представить, что наш первоначальный треугольник стал трехмерной пирамидой, то объем такой пирамиды будет произведению длины ее основания на полученную нами площадь треугольника.
Вы можете найти объем , которая по сути треугольником в трехмерном мире. Если представить, что наш первоначальный треугольник стал трехмерной пирамидой, то объем такой пирамиды будет произведению длины ее основания на полученную нами площадь треугольника.
Обратите внимание
Подсчеты будут тем точнее, чем тщательнее вы будете производить измерения
Источники:
- Калькулятор “Все во все” — портал по справочным величинам
- объем треугольника в 2019
Три точки, однозначно определяющие треугольник в Декартовой системе координат — это его вершины. Зная их положение относительно каждой из координатных осей можно вычислить любые параметры этой плоской фигуры, включая и ограничиваемую ее периметром площадь . Это можно сделать несколькими способами.
Инструкция
Используйте формулу Герона для расчета площади треугольника . В ней задействованы размеры трех сторон фигуры, поэтому вычисления начините с . Длина каждой стороны должна быть равна корню из суммы квадратов длин ее проекций на координатные оси. Если обозначить координаты A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃), длины их сторон можно выразить так: AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Если обозначить координаты A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃), длины их сторон можно выразить так: AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Для упрощения расчетов введите вспомогательную переменную — полупериметр (Р). Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой. Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C). Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:
- Прямоугольный.
- Тупоугольный.
- Остроугольный.
- Разносторонний.
- Равносторонний.

- Равнобедренный.
Общие формулы для вычисления площади треугольника
Формула площади треугольника по длине и высоте
S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.
Формула Герона
S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.
Формула площади треугольника по величине угла и длине отрезка
S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.
Формула площади треугольника по радиусу вписанной окружности и трем сторонам
S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.
Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности
S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.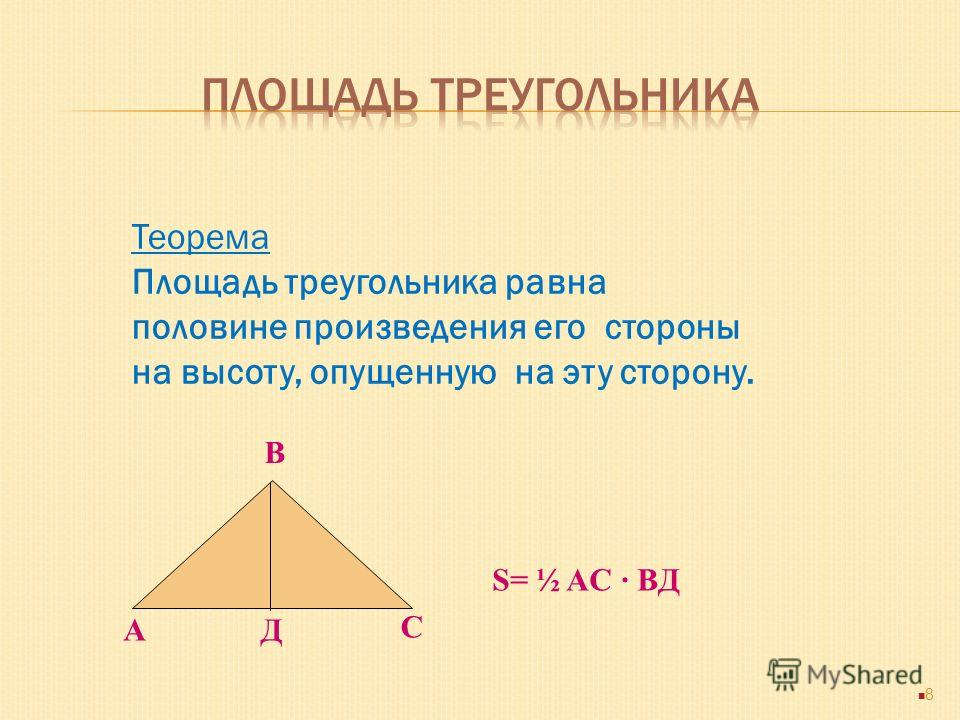
Формула площади треугольника по декартовым координатам точек
Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
где || обозначает модуль.
Как найти площадь прямоугольного треугольника
Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.
Формула площади прямоугольного треугольника по двум катетам
S= a*b/2,
где a,b – это длина катетов. Катетами называются стороны, прилежащие к прямому углу.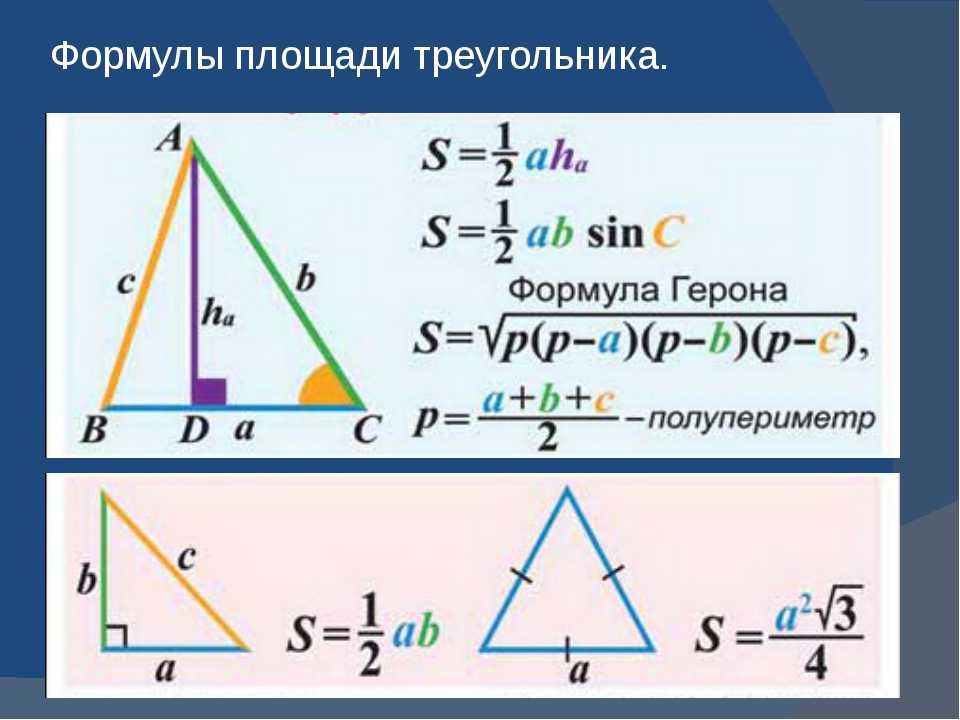
Формула площади прямоугольного треугольника по гипотенузе и острому углу
S = a*b*sin(α)/ 2,
где a, b – это катеты треугольника, а sin(α)- это синус угла, в котором пересекаются прямые a, b.
Формула площади прямоугольного треугольника по катету и противолежащему углу
S = a*b/2*tg(β),
где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.
Как вычислить площадь равнобедренного треугольника
Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.
Основная формула для вычисления площади равнобедренного треугольника
S=h*c/2,
где с – это основание треугольника, h-это высота треугольника, опущенного к основанию.
Формула равнобедренного треугольника по боковой стороне и основанию
S=(c/2)* √(a*a – c*c/4),
где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.
Как найти площадь равностороннего треугольника
Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу:
S = (√3*a*a)/4,
где a-это длина стороны равностороннего треугольника.
Вышеприведенные формулы позволят вычислить искомую площадь треугольника. Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления.
Треугольник — хорошо знакомая всем фигура. И это, несмотря на богатое разнообразие его форм. Прямоугольный, равносторонний, остроугольный, равнобедренный, тупоугольный. Каждый из них чем-то отличается. Но для любого требуется узнавать площадь треугольника.
Общие для всех треугольников формулы, в которых используются длины сторон или высот
Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны н а, н в, н с.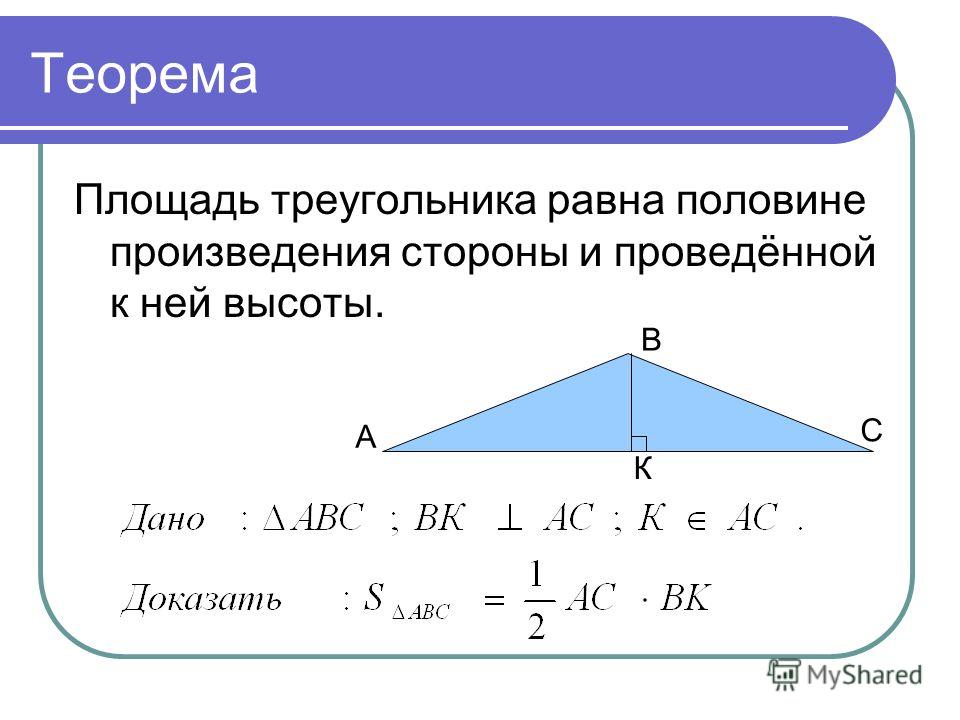
1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * н а. Аналогично следует записать формулы для двух остальных сторон.
2. Формула Герона, в которой фигурирует полупериметр (его принято обозначать маленькой буквой р, в отличии от полного периметра). Полупериметр необходимо сосчитать так: сложить все стороны и разделить их на 2. Формула полупериметра: р = (а+в+с) / 2. Тогда равенство для площади фигуры выглядит так: S = √ (р * (р — а) * (р — в) * (р — с)).
3. Если не хочется использовать полупериметр, то пригодится такая формула, в которой присутствуют только длины сторон: S = ¼ * √ ((а + в + с) * (в + с — а) * (а + с — в) * (а + в — с)). Она несколько длиннее предыдущей, но выручит, если забылось, как находить полупериметр.
Общие формулы, в которых фигурируют углы треугольника
Обозначения, которые требуются для прочтения формул: α, β, γ — углы. Они лежат напротив сторон а, в, с, соответственно.
1. По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.
По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.
2. Площадь треугольника можно вычислить по одной стороне и трем известным углам. S = (а 2 * sin β * sin γ) / (2 sin α).
3. Существует еще формула с одной известной стороной и двумя прилежащими к ней углами. Она выглядит таким образом: S = с 2 / (2 (ctg α + ctg β)).
Две последние формулы являются не самыми простыми. Запомнить их довольно сложно.
Общие формулы для ситуации, когда известны радиусы вписанных или описанных окружностей
Дополнительные обозначения: r, R — радиусы. Первый используется для радиуса вписанной окружности. Второй — для описанной.
1. Первая формула, по которой вычисляется площадь треугольника, связана с полупериметром. S = р * r. По-другому ее можно записать так: S = ½ r * (а + в + с).
2. Во втором случае потребуется перемножить все стороны треугольника и разделить их на учетверенный радиус описанной окружности. В буквенном выражении это выглядит так: S = (а * в * с) / (4R).
В буквенном выражении это выглядит так: S = (а * в * с) / (4R).
3. Третья ситуация позволяет обойтись без знания сторон, но потребуются значения всех трех углов. S = 2 R 2 * sin α * sin β * sin γ.
Частный случай: прямоугольный треугольник
Это самая простая ситуация, поскольку требуется знание только длины обоих катетов. Они обозначаются латинскими буквами а и в. Площадь прямоугольного треугольника равна половине площади достроенного к нему прямоугольника.
Математически это выглядит так: S = ½ а * в. Она запоминается проще всего. Потому что выглядит, как формула для площади прямоугольника, только появляется еще дробь, обозначающая половину.
Частный случай: равнобедренный треугольник
Поскольку у него две стороны равные, то некоторые формулы для его площади выглядят несколько упрощенными. Например, формула Герона, по которой вычисляется площадь равнобедренного треугольника, принимает следующий вид:
S = ½ в √((a + ½ в)*(a — ½ в)).
Если ее преобразовать, то она станет короче. В таком случае формула Герона для равнобедренного треугольника записывается так:
В таком случае формула Герона для равнобедренного треугольника записывается так:
S = ¼ в √(4 * a 2 — b 2).
Несколько проще, чем для произвольного треугольника, выглядит формула площади, если известны боковые стороны и угол между ними. S = ½ a 2 * sin β.
Частный случай: равносторонний треугольник
Обычно в задачах про него известна сторона или ее можно как-либо узнать. Тогда формула, по которой находится площадь такого треугольника, выглядит следующим образом:
S = (а 2 √3) / 4.
Задачи на нахождение площади, если треугольник изображен на клетчатой бумаге
Самой простой является ситуация, когда прямоугольный треугольник начерчен так, что его катеты совпадают с линиями бумаги. Тогда требуется просто посчитать число клеточек, укладывающихся в катеты. Потом перемножить их и разделить на два.
Когда треугольник остроугольный или тупоугольный, его нужно дорисовать до прямоугольника. Тогда в получившейся фигуре будет 3 треугольника. Один — тот что дан в задаче.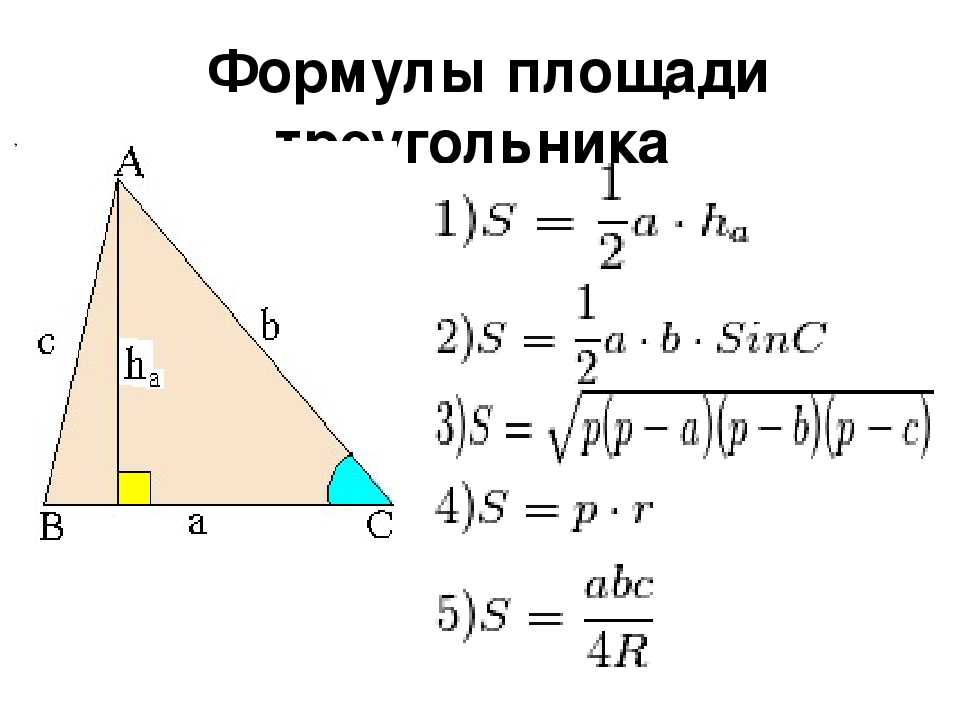 А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.
А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.
Гораздо сложнее оказывается ситуация, в которой ни одна из сторон треугольника не совпадает с линиями бумаги. Тогда его нужно вписать в прямоугольник так, чтобы вершины исходной фигуры лежали на его сторонах. В этом случае вспомогательных прямоугольных треугольников будет три.
Пример задачи на формулу Герона
Условие. У некоторого треугольника известны стороны. Они равны 3, 5 и 6 см. Необходимо узнать его площадь.
Теперь можно вычислять площадь треугольника по указанной выше формуле. Под квадратным корнем оказывается произведение четырех чисел: 7, 4, 2 и 1. То есть площадь равна √(4 * 14) = 2 √(14).
Если не требуется большая точность, то можно извлечь квадратный корень из 14. Он равен 3,74. Тогда площадь будет равна 7,48.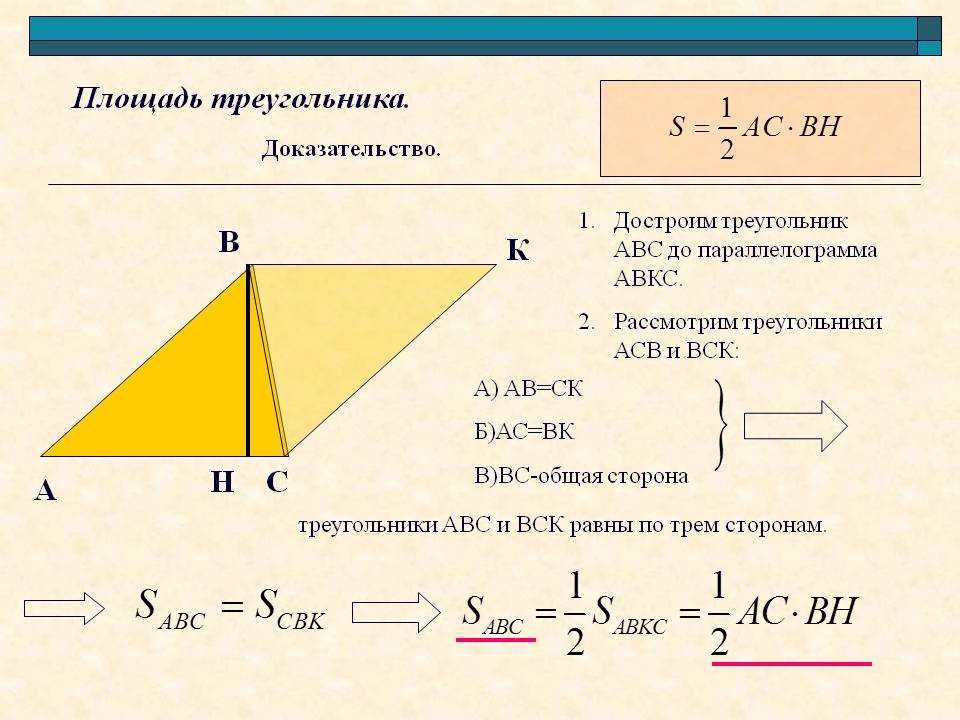
Ответ. S = 2 √14 см 2 или 7,48 см 2 .
Пример задачи с прямоугольным треугольником
Условие. Один катет прямоугольного треугольника больше, чем второй на 31 см. Требуется узнать их длины, если площадь треугольника равна 180 см 2 .
Решение. Придется решить систему из двух уравнений. Первое связано с площадью. Второе — с отношением катетов, которое дано в задаче.
180 = ½ а * в;
а = в + 31.
Сначала значение «а» нужно подставить в первое уравнение. Получится: 180 = ½ (в + 31) * в. В нем только одна неизвестная величина, поэтому его легко решить. После раскрытия скобок получается квадратное уравнение: в 2 + 31 в — 360 = 0. Оно дает два значения для «в»: 9 и — 40. второе число не подходит в качестве ответа, так как длина стороны треугольника не может быть отрицательной величиной.
Осталось вычислить второй катет: прибавить к полученному числу 31. Получается 40. Это искомые в задаче величины.
Ответ. Катеты треугольника равны 9 и 40 см.
Задача на нахождение стороны через площадь, сторону и угол треугольника
Условие. Площадь некоторого треугольника 60 см 2 . Необходимо вычислить одну из его сторон, если вторая сторона равна 15 см, а угол между ними равен 30º.
Площадь некоторого треугольника 60 см 2 . Необходимо вычислить одну из его сторон, если вторая сторона равна 15 см, а угол между ними равен 30º.
Решение. Исходя из принятых обозначений, искомая сторона «а», известная «в», заданный угол “γ”. Тогда формула площади можно переписать так:
60 = ½ а * 15 * sin 30º. Здесь синус 30 градусов равен 0,5.
После преобразований «а» оказывается равным 60 / (0,5 * 0,5 * 15). То есть 16.
Ответ. Искомая сторона равна 16 см.
Задача о квадрате, вписанном в прямоугольный треугольник
Условие. Вершина квадрата со стороной 24 см совпадает с прямым углом треугольника. Две другие лежат на катетах. Третья принадлежит гипотенузе. Длина одного из катетов равна 42 см. Чему равна площадь прямоугольного треугольника?
Решение. Рассмотрим два прямоугольных треугольника. Первый — заданный в задаче. Второй — опирается на известный катет исходного треугольника. Они подобны, так как имеют общий угол и образованы параллельными прямыми.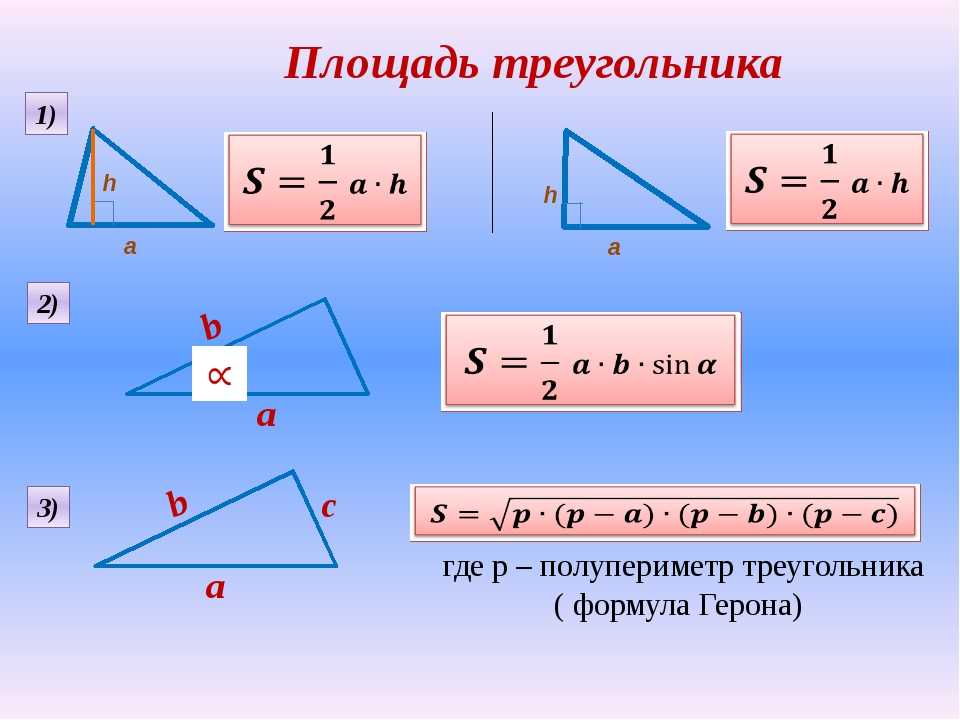
Тогда отношения их катетов равны. Катеты меньшего треугольника равны 24 см (сторона квадрата) и 18 см (заданный катет 42 см вычесть сторону квадрата 24 см). Соответствующие катеты большого треугольника — 42 см и х см. Именно этот «х» нужен для того, чтобы вычислить площадь треугольника.
18/42 = 24/х, то есть х = 24 * 42 / 18 = 56 (см).
Тогда площадь равна произведению 56 и 42, разделенному на два, то есть 1176 см 2 .
Ответ. Искомая площадь равна 1176 см 2 .
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c
– стороны треугольника,
R
– радиус описанной окружности,
r
– радиус вписанной окружности,
h[b],h[a],h[c]
– высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma –
углы возле вершин.
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
То с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b
и угол связан с третьей
С (hamma).
Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b
и угол связан с третьей
С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона
применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
А затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.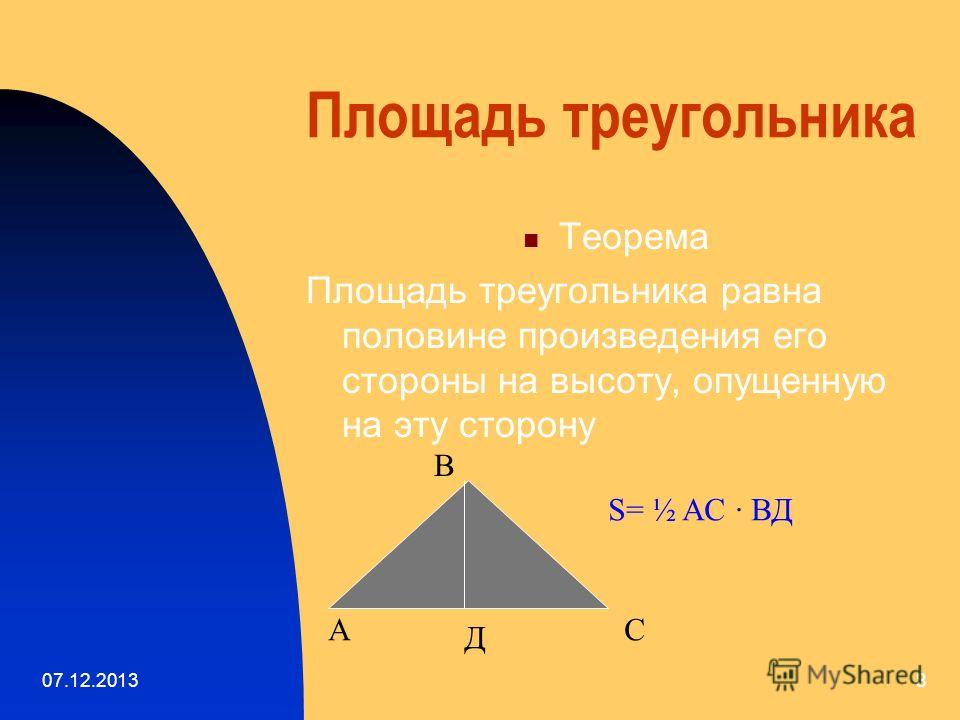
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9.
Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника
с катетами a
и b
равна половине их произведения
Формула площади равностороннего (правильного) треугольника
=
= одной четвертой произведения квадрату стороны на корень из тройки.
Некоторые из задач по геометрии, а если точнее, то по планиметрии, требуют нахождения площади какой-то заданной фигуры. Площадь любой фигуры может быть как конечной целью задачи, так и промежуточным вычислением, необходимым для подстановки в более сложную формулу. Часто в таких задачах просят найти площадь треугольника. Начальные данные могут быть разными. В одних случаях известна какая-то сторона треугольника и значение высоты, проведенной к ней, в других — периметр треугольника и так далее.
Площадь любой фигуры может быть как конечной целью задачи, так и промежуточным вычислением, необходимым для подстановки в более сложную формулу. Часто в таких задачах просят найти площадь треугольника. Начальные данные могут быть разными. В одних случаях известна какая-то сторона треугольника и значение высоты, проведенной к ней, в других — периметр треугольника и так далее.
Допустим, задано найти площадь треугольника, если известно три стороны. Для нахождения площади такого треугольника используется формула Герона. Чтобы определить площадь по этой формуле требуется сначала вычислить полупериметр треугольника (п) . Зная значения всех трех сторон, сделать это элементарно. Нужно суммировать все стороны треугольника — это будет его периметр, а затем разделить полученное значение на два. После этого надо от значения полупериметра вычесть по очереди значения длины каждой из трех заданных сторон треугольника, то есть из п вычесть а, потом из п вычесть b и, наконец, из п вычесть с.
Полученные три разности следует перемножить между собой и это произведение снова умножить на значение полупериметра. Проведя все перечисленные действия и получив результат умножения, надо из этого результата извлечь квадратный корень. То число, которое получится после извлечения квадратного корня, и будет площадью заданного треугольника. Если записать вкратце, то формула площади треугольника будет такая: площадь (S) =корень кв-ный из (п*(п-а) *(п-b) *(п-с)) . Как можно понять из формулы, решается вопрос нахождения треугольника с известными значениями сторон очень легко.
Проведя все перечисленные действия и получив результат умножения, надо из этого результата извлечь квадратный корень. То число, которое получится после извлечения квадратного корня, и будет площадью заданного треугольника. Если записать вкратце, то формула площади треугольника будет такая: площадь (S) =корень кв-ный из (п*(п-а) *(п-b) *(п-с)) . Как можно понять из формулы, решается вопрос нахождения треугольника с известными значениями сторон очень легко.
Например, как найти площадь треугольника, если известны 3 стороны: сторона а равняется 3 сантиметрам, сторона b равняется 4 сантиметрам и сторона с равняется 2 сантиметрам. Периметр этого треугольника будет равен а + b + с = 3 сантиметра + 4 сантиметра + 2 сантиметра = 9 см. Значит полупериметр равняется 9: 2=4,5 сантиметраПолучим: S=корень кв-ный из (4,5 сантиметра * (4,5 сантиметра — 3 сантиметра) * (4,5 сантиметра — 4 сантиметра) * (4,5 сантиметра — 2 сантиметра)) = 2,9 квадратных сантиметров
А что, если значения сторон не только известны, но также указано, что они равны по условию задачи? В таком случае, как найти площадь треугольника, если известны все стороны, а также они равны? Можно, конечно, тоже вычислить ее по рассмотренной выше формуле Герона, но зачем лишние расчеты, если для такого треугольника выведена другая формула, которая гораздо проще формулы Герона.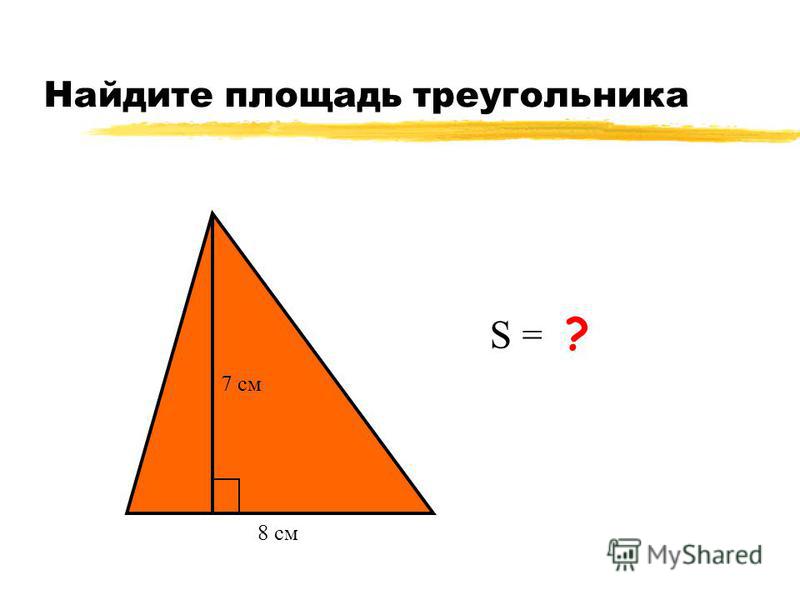 2*корень(3)) /4=3,9 квадратных сантиметров. Чтобы проверить, правильно или нет вычислено значение площади конкретного треугольника, можно провести дополнительные расчеты по ф-ле Герона и сверить полученные результаты.
2*корень(3)) /4=3,9 квадратных сантиметров. Чтобы проверить, правильно или нет вычислено значение площади конкретного треугольника, можно провести дополнительные расчеты по ф-ле Герона и сверить полученные результаты.
Полупериметр (п) =(3+3+3) /2=4,5 сантиметра. По формуле Герона находится: S=корень кв-ный из (4,5 сантиметра * (4,5 сантиметра — 3 сантиметра) * (4,5 сантиметра — 3 сантиметра) * (4,5 сантиметра — 3 сантиметра)) = 3,9 квадратных сантиметров. Оба значения площади, найденные по разным формулам, совпадают. Значит площадь треугольника определена правильно. Решая какие-нибудь другие задачи, следует учитывать данные в условии и использовать соответствующую этим данным формулу.
Площадь треугольника, формулы площадей прямоугольных, равносторонних, равнобедренных,…
Площадь треугольника, формулы площадей прямоугольных, равносторонних, равнобедренных,… Привет, сегодня поговорим про площадь треугольника, обещаю рассказать все что знаю.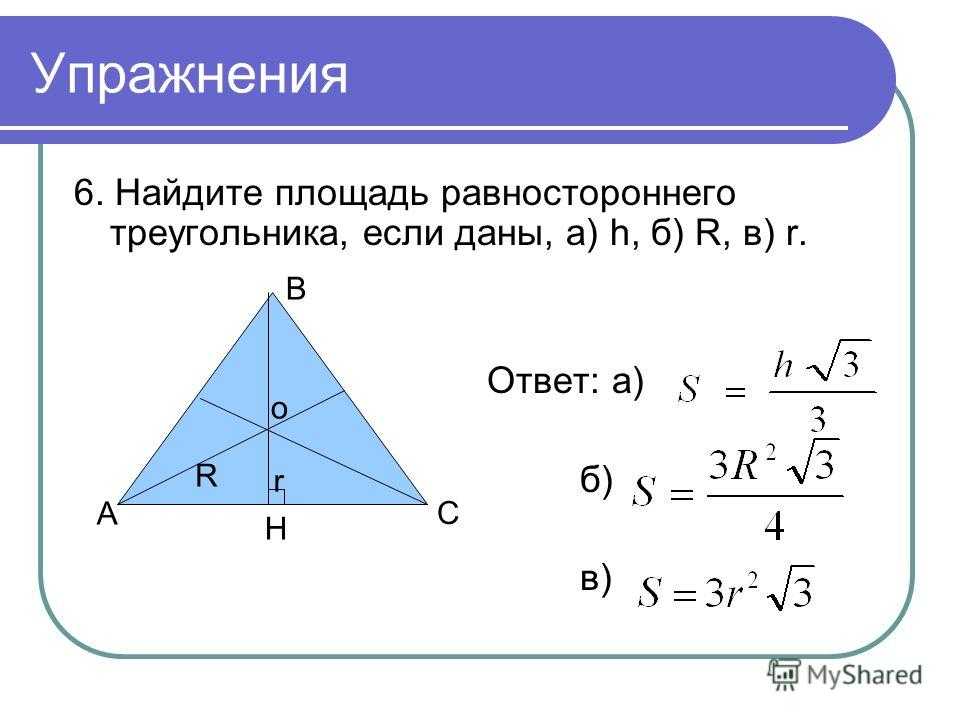 Для того чтобы лучше понимать что такое
площадь треугольника , настоятельно рекомендую прочитать все из категории Планометрия.
Для того чтобы лучше понимать что такое
площадь треугольника , настоятельно рекомендую прочитать все из категории Планометрия.
площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Теорема
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a • h.
Доказательство
Пусть ABC – данный треугольник. Дополним его до параллелограмма ABCD.
Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC. Высота параллелограмма, соответствующая стороне CB, равна высоте треугольника, проведенной к стороне CB.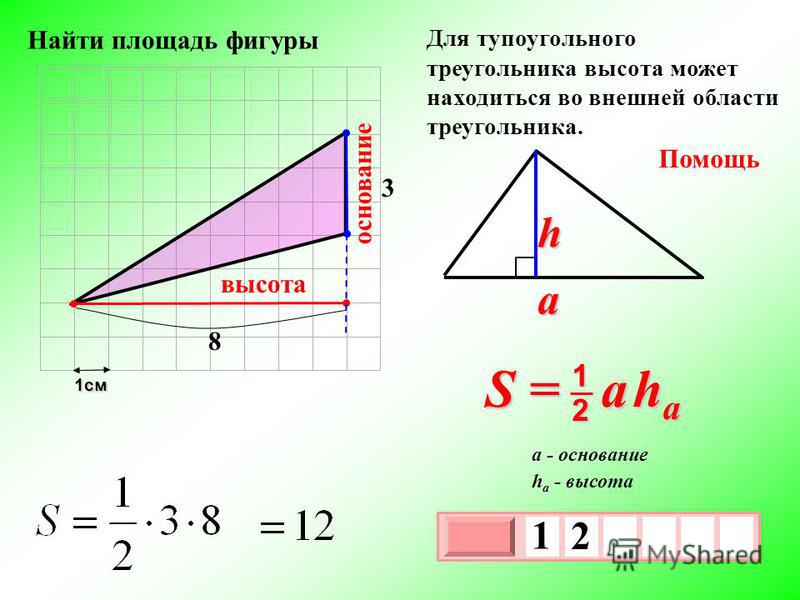 Отсюда следует утверждение теоремы, и
Отсюда следует утверждение теоремы, и
Теорема доказана.
Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных.
Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных,
Таблица с формулами площади треугольника
|
исходные данные |
Рисунок |
формула |
|
|
Площади для треугольников общего вида (любого) |
|||
|
1 |
основание и высота |
||
|
2 |
две стороны и угол между ними |
||
|
3 |
радиус вписанной окружности и три стороны |
|
|
|
4 |
радиус описанной окружности и три стороны |
|
|
|
5 |
три стороны |
|
|
|
6 |
сторона и два прилежащих угла |
||
|
Площади для равнобедренных треугольников |
|||
|
7 |
боковые стороны и основание |
||
|
8 |
боковые стороны и угол между ними |
||
|
9 |
боковые стороны, основание и угол между боковыми сторонами и основанием |
||
|
10 |
основание и угол между боковыми сторонами |
||
|
11 |
высота и основание |
||
|
Площади для равносторонних треугольников |
|||
|
12 |
сторона |
||
|
13 |
высота |
||
|
14 |
радиус вписанной окружности |
||
|
15 |
радиусу описанной окружности |
||
|
ДПлощади дляя прямоугольных треугольников |
|||
|
16 |
два катета |
||
|
17 |
гипотенуза и угол |
||
|
18 |
катет и угол |
||
|
19 |
отрезки, на которые делит гипотенузу вписанная окружность |
||
|
20 |
гипотенуза и радиус вписанной окружности |
||
|
21 |
три стороны |
|
|
Пример решения задачи на нахождение площади треугольника
две чевианы делят треугольник , как показано на рисунке на четыре части . Об этом говорит сайт https://intellect.icu . Площади трех из них равны 2, 5 ,7. Найдите площадь четвертой части треугольника.
Об этом говорит сайт https://intellect.icu . Площади трех из них равны 2, 5 ,7. Найдите площадь четвертой части треугольника.
Решение
См. также
- площадь прямоугольника , площадь квадрата ,
- вычисление площадей плоских фигур в полярных координатах ,
- площадь трапеции ,
- вычисление площадей плоских фигур ,
- площадь параллелограмма ,
- площадь кругового сектора ,
- четырехугольник , четырехугольники ,
- площадь фигуры ,
- площадь круга ,
- площадь боковой поверхности цилиндра ,
- площадь сферы ,
Понравилась статья про площадь треугольника? Откомментируйте её Надеюсь, что теперь ты понял что такое площадь треугольника
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Из статьи мы узнали кратко, но емко про площадь треугольника
Площадь треугольника – Объяснение и примеры
В этой статье вы узнаете площадь треугольника и определите площадь различных типов треугольников . Площадь треугольника – это количество пространства внутри треугольника. Измеряется в квадратных единицах.
Прежде чем перейти к теме площади треугольника , давайте ознакомимся с такими терминами, как основание и высота треугольника.
Основание — сторона треугольника, которая считается основанием, а t высота треугольника — перпендикуляр, опущенный на его основание из вершины, противоположной основанию.
На приведенном выше рисунке пунктирные линии обозначают возможные высоты △ ABC.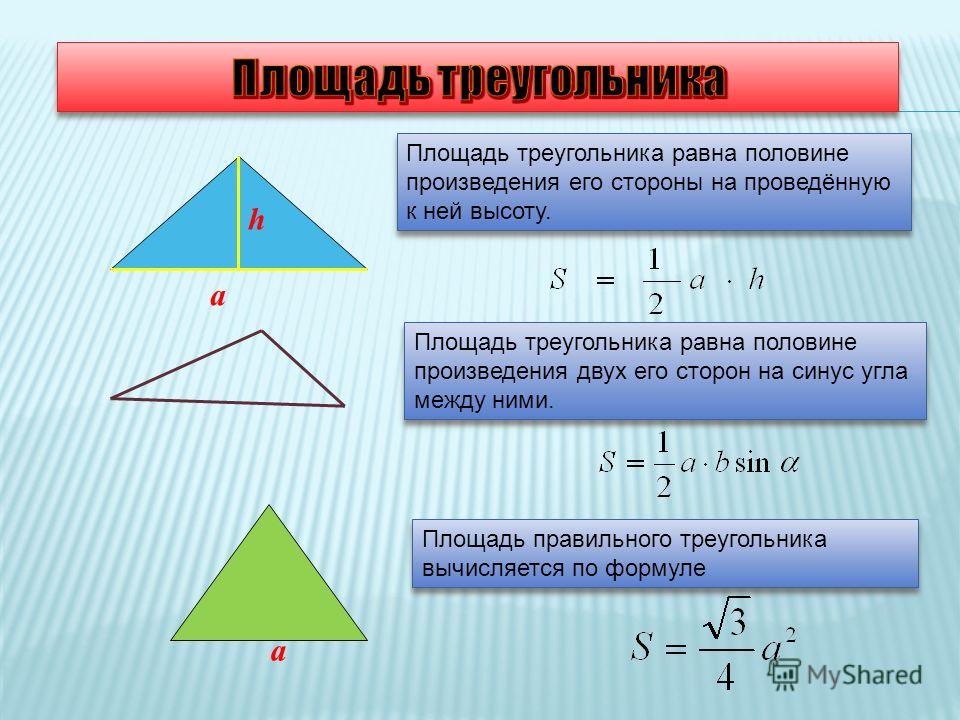 Обратите внимание, что каждый треугольник имеет, возможно, три высоты или высоты.
Обратите внимание, что каждый треугольник имеет, возможно, три высоты или высоты.
- Высота треугольника △ ABC равна h 1 , когда основание является стороной.
- Высота треугольника △ ABC равна h3 при основании AB.
- Высота треугольника △ ABC равна h 3 , когда основание равно
- Высота треугольника △ ABC может быть вне треугольника ( 4 h 49003), который равен 4 h , то же, что высота h 1 .
Из приведенных выше рисунков можно сделать следующие выводы:
- Высота треугольника зависит от его основания.
- Перпендикуляр к основанию треугольника равен высоте треугольника.
- Высота треугольника может быть вне треугольника.
Обсудив концепцию высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.
Площадь прямоугольника нам хорошо известна, т.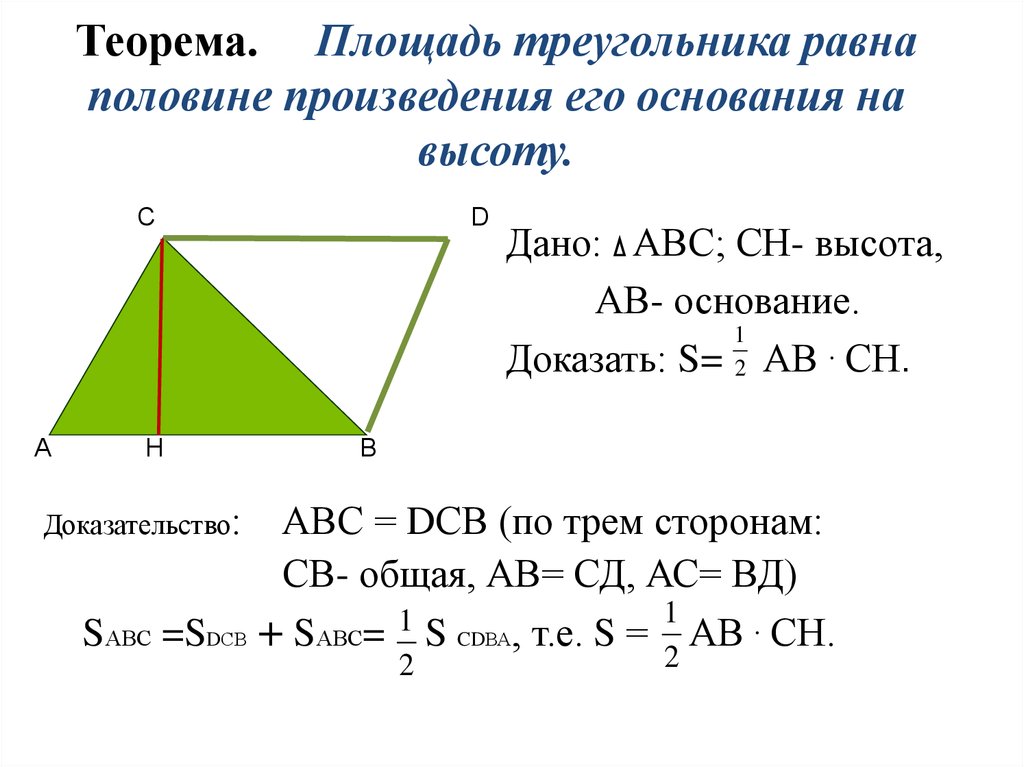 е. длина * ширина . Что произойдет, если мы разделим прямоугольник пополам по диагонали (разрежем пополам)? Какова будет его новостная область? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц соответственно площадь прямоугольника составляет 72 квадратных единицы.
е. длина * ширина . Что произойдет, если мы разделим прямоугольник пополам по диагонали (разрежем пополам)? Какова будет его новостная область? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц соответственно площадь прямоугольника составляет 72 квадратных единицы.
Теперь, если вы разделите его на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна быть 36 квадратных единиц каждая. Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезать по диагонали на две равные половины, две новые образовавшиеся фигуры будут треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Площадь треугольника – это общее пространство или область, ограниченная определенным треугольником.
Площадь треугольника равна произведению основания и высоты, деленному на 2.
Стандартной единицей измерения площади являются квадратные метры (м 2 ).
Другие единицы включают:
- квадратных миллиметров (мм 2 )
- квадратных дюймов (в 2 )
- квадратных километров (км 2 )
- 9.
Формула площади треугольника
Общая формула для вычисления площади треугольника:
Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника. Треугольники могут быть разными по своей природе, но важно отметить, что эта формула применима ко всем треугольникам. Различные типы треугольников имеют разные формулы площади.
Примечание. Основание и высота должны быть выражены в одних и тех же единицах измерения, то есть в метрах, километрах, сантиметрах и т. д.
Площадь прямоугольного треугольника
Площадь треугольника = (½ × основание × высота) квадратных единиц.
Пример 1
Найдите площадь прямоугольного треугольника, основание которого равно 9 м, а высота 12 м.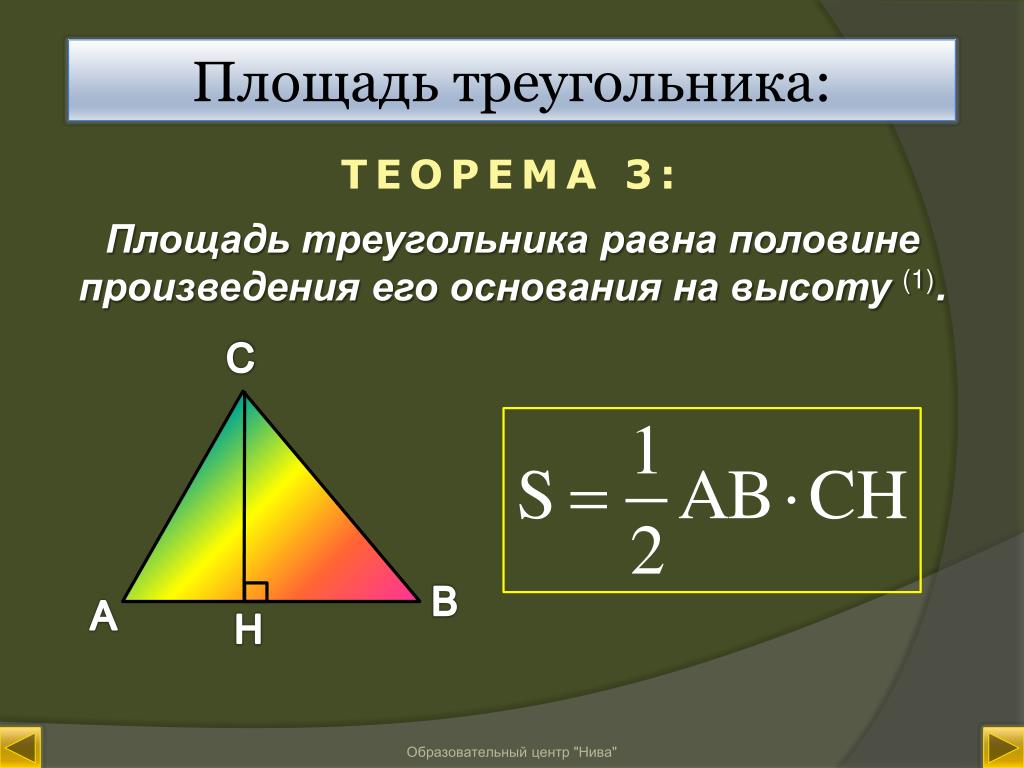
Раствор
A = ¹/₂ × основание × высота
= ¹/₂ × 12 × 9
= 54 см²
Пример 2
Основание и высота прямоугольного треугольника равны 70 см и 8 м соответственно. Чему равна площадь треугольника?
Решение
A = ½ × основание × высота
Здесь 70 см и 8 м. Вы можете выбрать работу с см или м. Давайте поработаем в метрах, заменив 70 см на метры.
Разделите 70 см на 100.
70/100 = 0,7 м.
⇒ A = (½ × 0,7 × 8) м 2
⇒ A = (½ x 5,6) м 2
⇒ A = 2,8 м 2
Площадь равнобедренного треугольника
Равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны. Формула площади равнобедренного треугольника:
⇒ A = ½ (основание × высота).
Если высота равнобедренного треугольника не указана, то для ее нахождения используется следующая формула:
Высота = √ (a 2 − b 2 /4)
Где;
b = основание треугольника
a = длина двух равных сторон.
Таким образом, площадь равнобедренного треугольника может быть;
⇒ A = ½ [√ (a 2 − b 2 /4) × b]
Кроме того, площадь равнобедренного прямоугольного треугольника определяется как:
A= ½ × a 2 ,9009 где a = длина двух равных сторон
Пример 3
Вычислите площадь равнобедренного треугольника, основание которого равно 12 мм, а высота 17 мм.
Решение
⇒A = ½ × основание × высота
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 мм 2
Пример 4
. Пример 4
. Найдите площадь равнобедренного треугольника с длинами сторон 5 м и 9 м Решение Пусть основание b = 9 м, а a = 5 м. ⇒ A = ½ [√ (a 2 − b 2 /4) × b] ⇒ ½ [√ (5 2 − 9 2 /4) × 9] = 9,81 м 2 Равносторонний треугольник — это треугольник, у которого три стороны равны и три внутренних угла равны. A = (a 2 √3)/4 Где a = длина сторон. Пример 5 Вычислите площадь равностороннего треугольника со стороной 4 см. Решение ⇒ a = (A 2 /4) √3 ⇒ (4 2 /4) √3 ⇒ (16/4) √3 = 4√3 CM 2 Пример 6 Найдите площадь равностороннего треугольника, периметр которого равен 84 мм. Решение Периметр равностороннего треугольника = 3а. ⇒ 3a = 84 мм ⇒ a = 84/3 ⇒ a = 28 мм Площадь = (a 2 /4) √3 ⇒ (28 2 /4) √3 = 196√3 мм 2 Разносторонний треугольник — это треугольник с 3 различными длинами сторон и 3 различными углами. Площадь разностороннего треугольника можно вычислить по формуле Герона. , где «p» – полупериметр, а a, b, c – длины сторон. ⇒ p = (a + b + c) / 2 Пример 7 Решение ⇒ p = (a + b + c) / 2 Из курса элементарной геометрии вы узнали, что площадь треугольника равна половине произведения основания на высоту. Предположим, что у нас есть треугольник \(\triangle\,ABC\), в котором угол \(A\) может быть либо острым, либо прямым, либо тупым, как на рис. 2.4.1. Предположим, что \(A\), \(b\) и \(c\) известны. В каждом случае мы проводим высоту \(h \) из вершины \(C \) в \(\overline{AB} \), так что площадь (которую мы будем обозначать буквой \(K\)) определяется выражением \(K = \frac{1}{2}hc \). Но мы видим, что \(h = b\;\sin\;A \) в каждом из треугольников (поскольку \(\;h=b \) и \(\sin\;A = \sin\;9\circ — A) =b\;\sin\;A \) на рис. 2.4.1(c)). Таким образом, мы получаем следующую формулу: \[\fbox{\(\text{Area} ~=~ K ~=~ \tfrac{1}{2}\,bc\;\sin\;A\)}\ label{2.23} \] Приведенная выше формула для площади \(\треугольника\,ABC\) выражена в известных частях \(A\), \(b\) и \(c\). \[ \begin{align}\text{Area} ~&=~ K =~ \tfrac{1}{2}\, ac\;\sin\;B \\ Предположим, что у нас есть треугольник \(\треугольник\,ABC \), в котором известны все три стороны. Тогда Формула Герона дает нам площадь: Для треугольника \(\треугольник\,ABC\) со сторонами \(a\), \(b\) и \(c\), пусть \(s = \frac{1}{2}\,(a+b+c) \) (т.е. \(2s = a+b+c \) — периметр треугольника). Тогда площадь \(K\) треугольника равна 92 ~=~ s\,(s-a)\,(s-b)\,(s-c) ~, \nonumber \] Найдите площадь треугольника \(\triangle\,ABC \) по данному \ (а=5\), \(b=4\) и \(с = 7\). Использование формулы Герона с \(s = \frac{1}{2}\,(a+b+c) = \frac{1}{2}\,(5+4+7) = 8 \), площадь \(K \) определяется как: Формула Герона полезна в теоретических целях (например, при выводе других формул). Однако он не подходит для использования в калькуляторе, демонстрируя так называемую численную нестабильность для «экстремальных» треугольников, как в следующем примере. ,ABC \) задано \(a=1000000\), \(b=999999,9999979 \) и \(c = 0,0000029 \). Решение: Чтобы использовать формулу Герона, нам нужно вычислить \(s = \frac{1}{2}\,(a+b+c) \). Обратите внимание, что фактическое значение \(a+b+c \) равно \(2000000,0000008 \), что имеет \(14 \) цифр. Это проблема, потому что \(a=1000000 \), поэтому мы получим \(s-a=0 \), в результате чего формула Герона даст нам площадь треугольника \(0 \)! И это действительно неправильный ответ, который возвращает TI-83 Plus. Другие калькуляторы могут дать другой неточный ответ, в зависимости от того, как они хранят значения внутри. Фактическая площадь — с точностью до \(15\) знаков после запятой — равна \(K = 0,99999999999895 \), то есть в основном равна \(1 \). Приведенный выше пример показывает, как проблематичная арифметика с плавающей запятой может быть. К счастью, есть лучшая формула для площади треугольника, когда известны три стороны: Для треугольника \(\треугольник\,ABC\) со сторонами \(a \ge b \ge c \) площадь равна : \[ \text{Площадь} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c — (a-b))\,(c + (a-b))\,(a + (b-c))}\label{2. Чтобы использовать эту формулу, отсортируйте названия сторон так, чтобы \(a \ge b \ge c \). Затем выполните операции внутри квадратного корня в точном порядке, в котором они появляются в формуле, включая использование круглых скобок . Затем извлеките квадратный корень и разделите на \(4\). Для треугольника в примере 2.16 приведенная выше формула дает точное значение \(K = 1 \) на том же калькуляторе TI-83 Plus, который не смог использовать формулу Герона. Что удивительно в этой формуле, так это то, что это просто переписанная формула Герона! Использование круглых скобок — это то, что заставляет соблюдать правильный порядок операций для числовой стабильности. Другая формула для площади треугольника с учетом его трех сторон приведена ниже: Для треугольника \(\треугольник\,ABC \) со сторонами \(a \ge b \ge c \) площадь равна: 92} \] Эта страница под названием 2.4: Площадь треугольника распространяется в соответствии с лицензией GNU Free Documentation License 1. Опубликовано Математика с мамой ПримерВидеоВопросыУрок Поделиться в Google Classroom Площадь треугольника равна 1 / 2 × основание × высота. Единицы площади измеряются в единицах, возведенных в квадрат. Площадь равностороннего треугольника
 Площадь равностороннего треугольника:
Площадь равностороннего треугольника: Площадь разностороннего треугольника

Формула Герона дается формулой;
⇒ Площадь = √ {p (p – a) (p – b) (p – c)}
Вычислите площадь треугольника, стороны которого равны 18 мм, 20 мм и 12 мм.
Подставьте значения a, b и c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Площадь = √ {p (p – a) (p – b) (p – c)}
= √ {25 x (25–12) x (25–18) x (25–20)}
= √ (25 x 13 x 7 x 5)
= 5√455 мм 2
29000 : площадь треугольника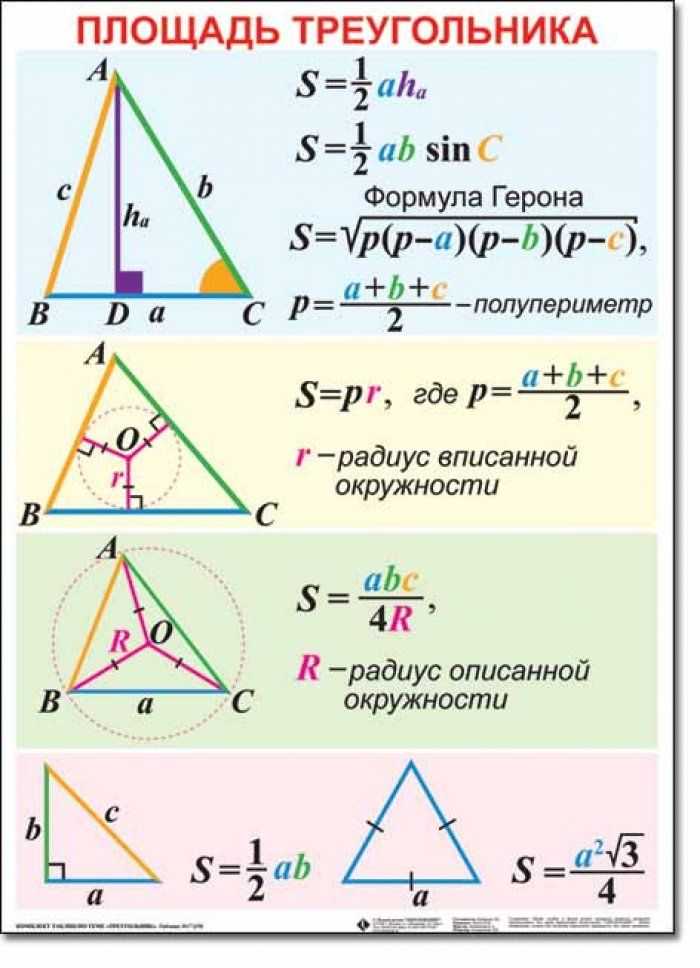 Теперь мы будем использовать это в сочетании с некоторой тригонометрией, чтобы вывести больше формул для площади при заданных частях треугольника.
Теперь мы будем использовать это в сочетании с некоторой тригонометрией, чтобы вывести больше формул для площади при заданных частях треугольника.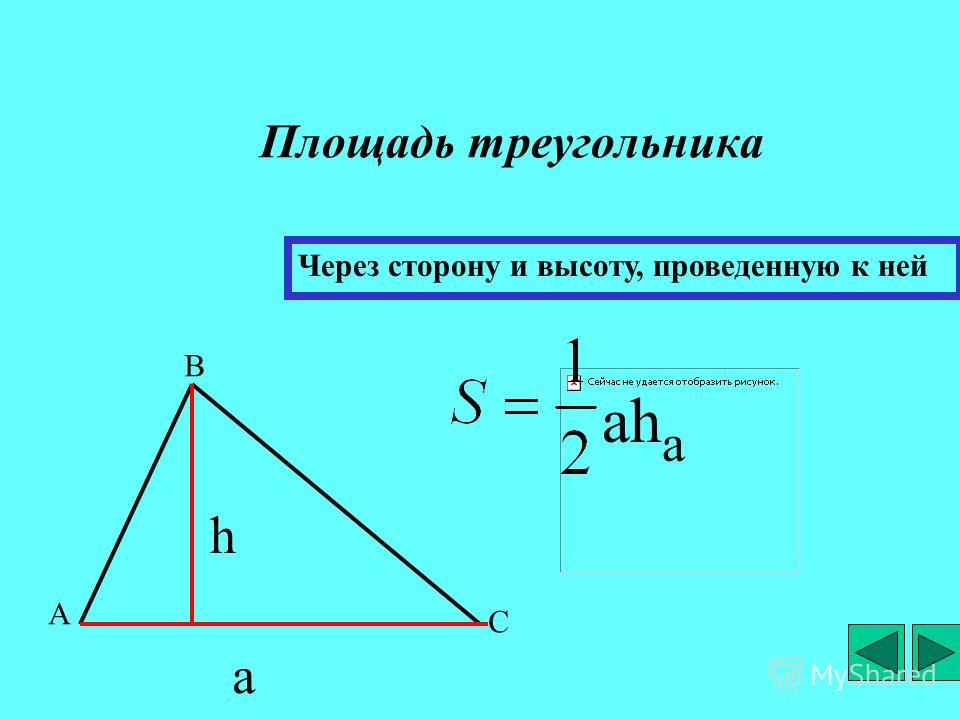 Аналогичные рассуждения для углов \(B \) и \(C \) дают нам:
Аналогичные рассуждения для углов \(B \) и \(C \) дают нам:
\text{Area} ~&=~ K =~ \tfrac{1}{2}\,ab\;\sin\;C\label{2.25} \end{align } \] 9\circ}\\
K ~&=~ 21.58
\end{align*} \] Формула Герона
поэтому при извлечении квадратных корней мы получаем
\[\nonumber K ~=~ \sqrt{s\,( s-a)\,(s-b)\,(s-c)} ~~.\quad \textbf{QED} \nonumber \] Пример 2.15

Решение
\[ \begin{align*}
K ~&=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c) }\\
&=~ \sqrt{8\,(8-5)\,(8-4)\,(8-7)} ~=~ \sqrt{96} \quad\Стрелка вправо\quad \boxed{K ~= ~ 4\,\sqrt{6}
~\приблизительно 9.8} ~.
\end{align*} \] Пример 2.16
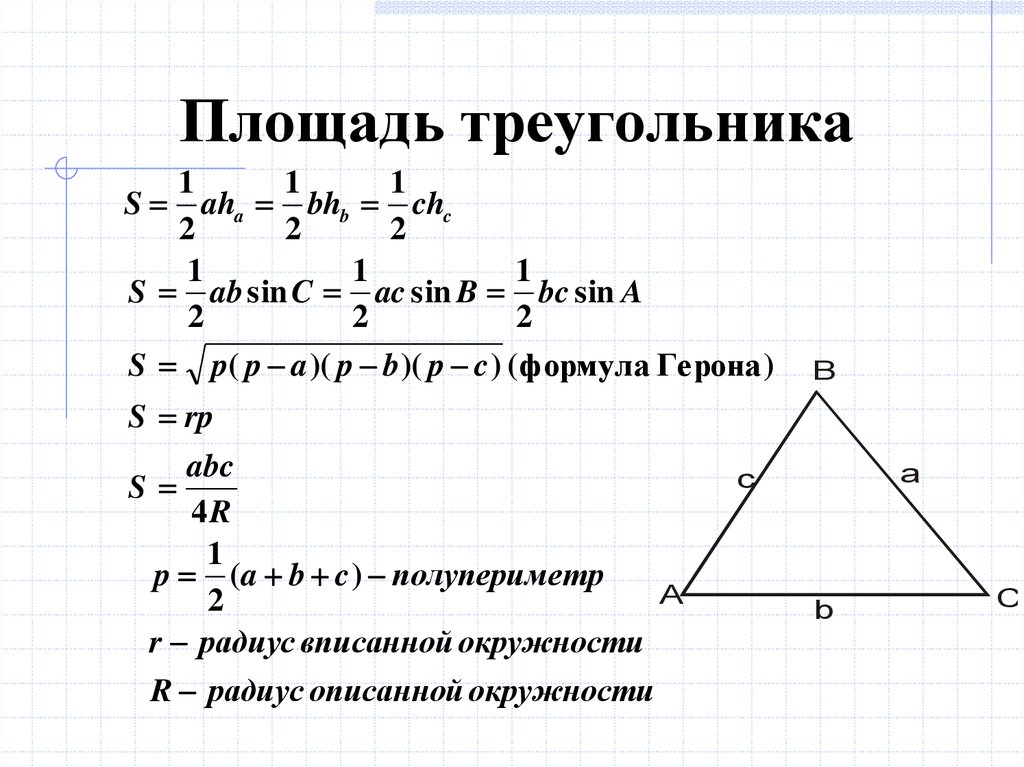 Большинство калькуляторов могут хранить \(12\)-\(14\) цифр внутри (даже если они отображают меньше), и, следовательно, могут округлять это значение \(a+b+c\) до \(2000000\). Когда мы затем разделим это округленное значение для \(a+b+c\) на \(2\), чтобы получить \(s\), некоторые калькуляторы (например, TI-83 Plus) дадут округленное вниз значение \( 1000000 \).
Большинство калькуляторов могут хранить \(12\)-\(14\) цифр внутри (даже если они отображают меньше), и, следовательно, могут округлять это значение \(a+b+c\) до \(2000000\). Когда мы затем разделим это округленное значение для \(a+b+c\) на \(2\), чтобы получить \(s\), некоторые калькуляторы (например, TI-83 Plus) дадут округленное вниз значение \( 1000000 \). 33} \]
33} \] 3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу. mecmath.net/trig/index.html
mecmath.net/trig/index.html Как найти площадь треугольника

- Площадь треугольника равна 1 / 2 × основание × высота.
- Основание 11 м, высота 8 м.
- Мы можем умножить основание и высоту, а затем разделить результат пополам.
- 11 × 8 = 88, а половина этого числа равна 44.
- Площадь треугольника равна 44 м 2 .
- Мы могли бы также сначала разделить 8 пополам, а затем умножить на 11.
- Половина 8 равна 4, а затем 4 × 11 = 44.
- Единицы измерения — м 2 , потому что длины сторон измеряются в метрах.
Площадь треугольника Рабочие листы и ответы
Как найти площадь треугольника
Чтобы найти площадь треугольника, умножьте основание на высоту, а затем разделите на 2. Либо разделите основание на 2, а затем умножьте на высоту или разделите высоту на 2, а затем умножьте на основание.
Не имеет значения, умножаете ли вы сначала основание и высоту, а затем делите ответ пополам, или сначала вы делите пополам основание или высоту, а затем умножаете.
Например, вот прямоугольный треугольник с основанием 8 см и высотой 3 см.
Умножая основание и высоту, 8 × 3 = 24. Половина этого ответа равна 12.
Площадь 12 см 2 .
Площадь треугольника измеряется в квадратах. Возьмите единицу, в которой измеряются стороны, и запишите эту единицу в квадрате после своего ответа. Если стороны измеряются в см, то единицы измерения площади см 2 . Если стороны измеряются в м, то единицы площади будут м 2 .
В этом расчете мы умножили см на см, поэтому единицы площади в этом примере равны см 2 .
Вместо того, чтобы сначала умножать основание на высоту, а затем делить на 2, мы можем сначала разделить пополам одну из длин основания или высоты.
Мы рассмотрим тот же пример и сначала разделим на 2, прежде чем умножать.
Так как 8 см четные, а 3 см нет, проще разделить длину 8 см пополам.
Половина 8 равна 4, а затем 4 × 3 = 12.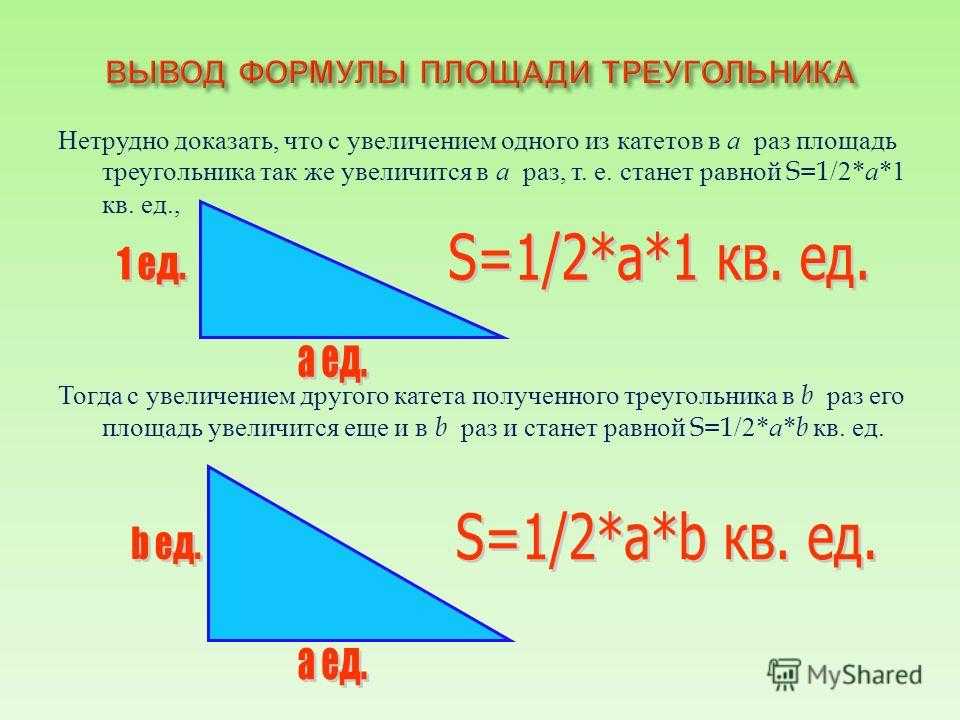 Площадь равна 12 см 2 .
Площадь равна 12 см 2 .
Ответ один и тот же независимо от того, в каком порядке умножаются числа.
Формула площади треугольника: 1 / 2 × основание × высота. Эту формулу проще записать как Площадь = 1 / 2 bh.
Формула площади = 1 / 2 bh работает для всех треугольников, независимо от их размера или формы. Если высота и основание известны, эту формулу можно использовать для вычисления площади.
Вот пример использования формулы для вычисления площади треугольника.
Основание этого треугольника равно 11 м, а высота треугольника 8 м.
Значение b = 11 и значение h = 8.
1 / 2 × b × h становится 1 / 2 × 11 × 8.
Мы можем сначала умножить 11 на 8, а затем разделить ответ пополам. 11 × 8 = 88, а затем 88 ÷ 2 = 44.
Длины сторон измеряются в метрах, значит, площадь этого треугольника равна 44 м 9 .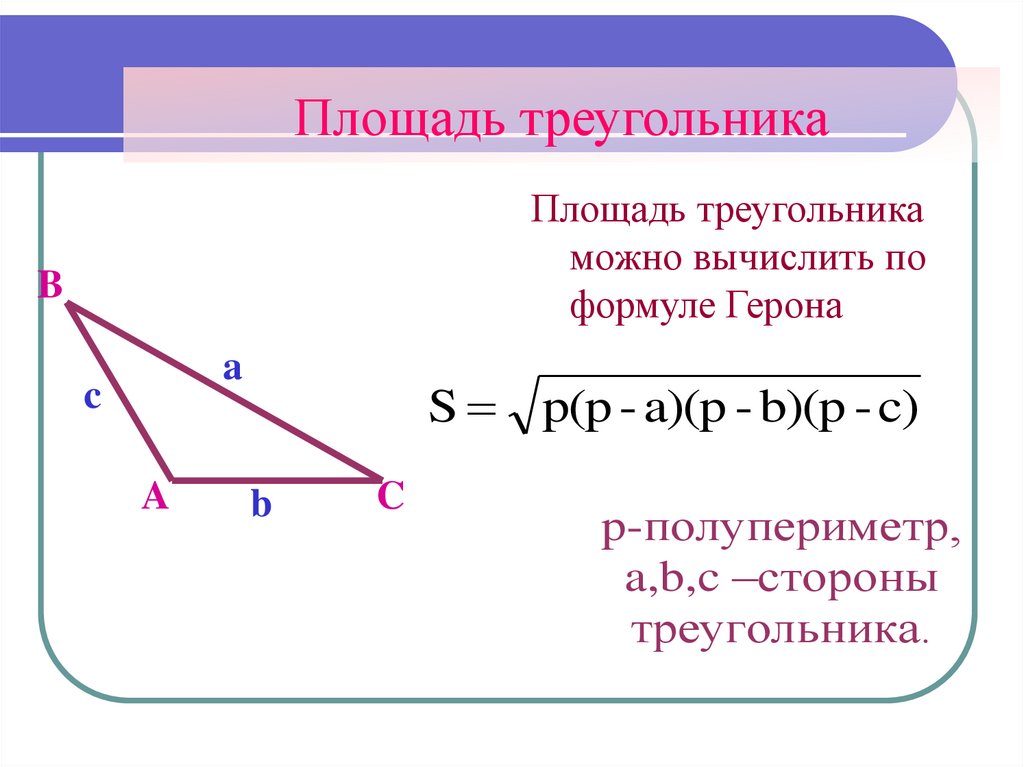 0094 2 .
0094 2 .
При обучении нахождению площади треугольника рекомендуется перед умножением сначала делить на 2, чтобы облегчить вычисление.
Легче сначала разделить 8 пополам, чтобы получить 4, а затем умножить это на 11, чтобы получить тот же ответ: 44 m 2 .
Выполняя сначала деление, сумма умножения использует меньшие числа, которые легче вычислить. Этот метод также включает в себя деление пополам меньшего числа, а не большего окончательного ответа.
При использовании формулы для нахождения площади треугольника важно убедиться, что основание и высота пересекаются под прямым углом.
Иногда вам могут быть даны все три стороны треугольника. Чтобы вычислить площадь треугольника, выберите две длины, которые находятся под прямым углом друг к другу в качестве основания и высоты. Умножьте эти длины, а затем разделите на 2. Игнорируйте любые другие длины сторон.
Почему площадь треугольника равна половине основания, умноженной на высоту
Любой треугольник можно нарисовать внутри прямоугольника, который в два раза больше его.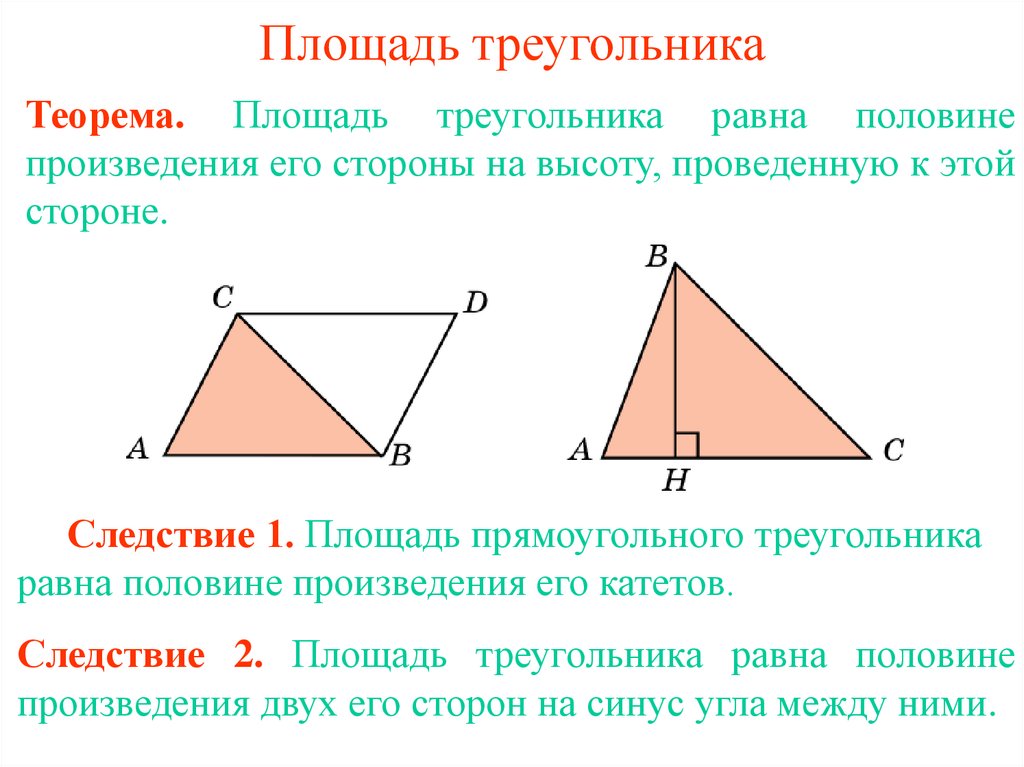 Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь треугольника равна половине основания, умноженному на высоту.
Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь треугольника равна половине основания, умноженному на высоту.
Площадь прямоугольника равна основанию × высоте, иначе записывается как длина × ширина.
Чтобы превратить прямоугольник в треугольник, разделите его пополам по диагонали.
Поскольку площадь прямоугольника равна основанию × высоте, площадь треугольника равна 1 / 2 × основание × высота.
Вот еще один пример треугольника, который в два раза меньше прямоугольника.
Площадь прямоугольника 10 × 6 = 60 мм 2 , а площадь треугольника составляет половину от этой.
Площадь треугольника 30 мм 2
Помните, что при изучении площади треугольника проще всего сначала разделить либо высоту, либо основание на 2.
Половина 10 равна 5, а затем 5 × 6 = 30 мм 2 .
Теперь попробуйте наш урок Как найти площадь параллелограмма , где мы узнаем, как найти площадь параллелограмма.
Площадь треугольника
Треугольник — это всего лишь половина прямоугольника. Чтобы найти площадь треугольника, нужно найти площадь прямоугольника, внутри которого находится треугольник, и разделить ее на 2. Вот несколько словарных слов, которые помогут в этом уроке.
- Основание : Ширина треугольника
- Перпендикуляр : 2 линии, соприкасающиеся под углом 90 градусов. (См. информационную рамку о прямых углах в уроке по периметру прямоугольника.)
- Смежные стороны : Стороны фигуры, которые сходятся в углу
Площадь треугольника
Источник видео (05:49 мин.) | Стенограмма
\(\displaystyle \text{Площадь треугольника} = \frac{1}{2}\text{основание} \times \text{высота} = \frac{1}{2}{\text{bh} }\)
Помните, что основание и высота должны быть перпендикулярны друг другу. В этом курсе мы предоставим значения основания и высоты.
Дополнительные ресурсы
- Академия Хана: Площадь треугольника (5:29{2}\)
Детали:
Мы хотим найти площадь треугольника с основанием 5 дюймов и высотой 7 дюймов.
Чтобы найти площадь треугольника, полезно посмотреть на прямоугольник со сторонами, равными основанию, и высотой, разделенной пополам следующим образом:
Как видите, площадь треугольника равна половине площади прямоугольника с той же длиной и шириной. Чтобы найти площадь прямоугольника, мы умножаем \(\цвет{синий} \текст{ширина}\) на \(\цвет{красный} \текст{длина}\). Чтобы найти площадь треугольника, мы умножаем ширину на длину, а затем делим на два. 9{2}\)
Детали:
Мы пытаемся найти площадь сада в форме треугольника с \(\color{blue} \text{шириной (или основанием) 35 футов}\) и \(\color{red} \text{длина (или высота) 55 футов}\).Помните, что площадь треугольника равна половине площади прямоугольника той же длины и ширины.
Когда мы находим площадь прямоугольника, мы умножаем длину на ширину. Чтобы найти площадь треугольника, нужно длину умножить на ширину и разделить на два. Мы часто ссылаемся на ‘\(\color{blue} \text{width}\)’ и ‘\(\color{red} \text{length}\)’ терминами ‘\(\color{red} \ text{base}\)’ и ‘\(\color{blue} \text{height}\)’, когда речь идет о треугольниках.
 9{2}\)
9{2}\)
Детали:(источник видео | расшифровка стенограммы)
) - Изучите другие уроки математики в Ресурсном центре.
- Посетите онлайн-ресурсы для обучения в Ресурсном центре.
- Свяжитесь со своим инструктором.
- Если вам все еще нужна помощь, запишитесь к репетитору.
- Научиться вычислять площадь треугольника с помощью тригонометрических функций.
- Изучить формулу Герона для расчета площади треугольника по трем сторонам.
Нужна дополнительная помощь?
Видео-урок: Площадь треугольника
Стенограмма видео
В этом видео мы увидим
как мы можем вычислить площадь треугольника, используя его основание и высоту. Мы увидим, что на самом деле
два эквивалентных способа, которыми мы можем написать формулу для нахождения площади
треугольник. Но чтобы увидеть, как мы
вычислить площадь треугольника, давайте начнем с рассмотрения того, как мы находим площадь
другая геометрическая фигура, прямоугольник.
Возьмем этот прямоугольник, который нарисовано на бумаге в клетку. Подсчитав квадраты, мы могли бы видим, что длина прямоугольника равна семи единицам, а ширина прямоугольника составляет четыре единицы. Это означает, что в нем 28 квадратов. прямоугольник. Мы бы сказали, что площадь прямоугольник 28 квадратных единиц. И в самом деле, мы можем вспомнить, что мы может вычислить площадь любого прямоугольника, если мы знаем его длину и ширину, даже если это не нарисовано на квадратной бумаге.
Чтобы найти площадь прямоугольника, мы
умножьте длину на ширину. Значит, площадь этого прямоугольника с
его длина шесть сантиметров и ширина пять сантиметров находятся путем вычисления
пять раз шесть. Это 30. И единицы измерения площади в данном случае
будут квадратные сантиметры. Итак, теперь давайте подумаем о том, как мы
может связать прямоугольники с треугольниками.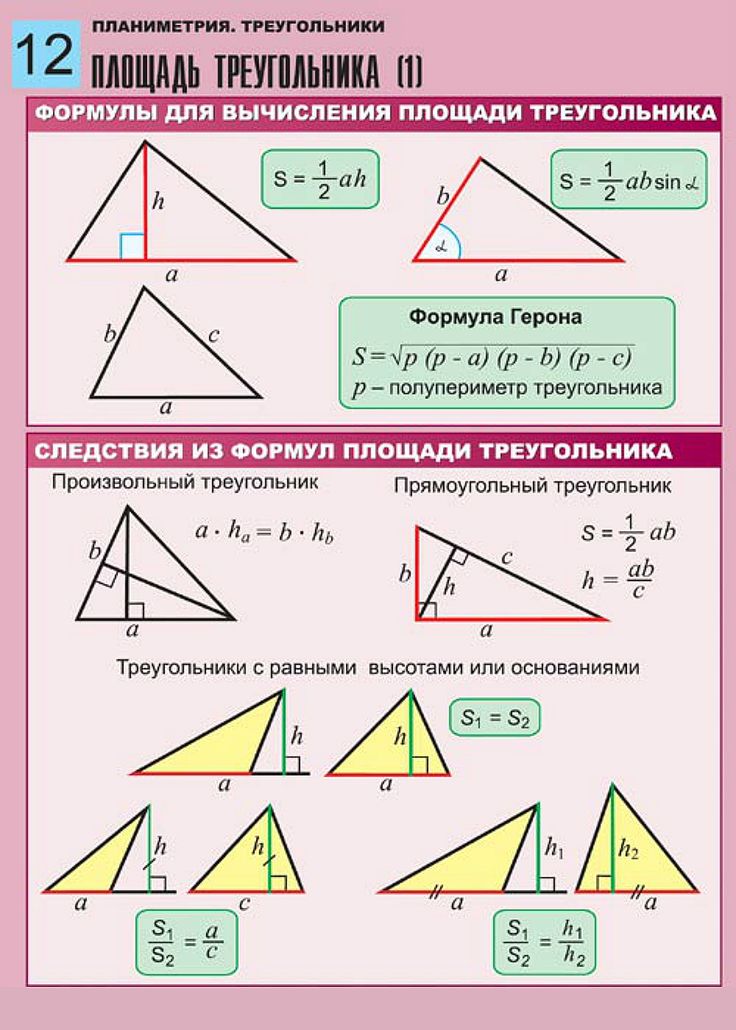
Нарисуем прямоугольный треугольник, имеет основание в пять единиц и высоту в четыре единицы. Теперь, чтобы найти площадь этого треугольник, мы могли бы попробовать считать квадраты. Но есть много частей квадраты по диагонали, которые сложно сложить точно. Итак, вместо этого давайте нарисуем прямоугольник вокруг треугольника, имеющего одинаковую длину и высоту. Это означает, что он будет иметь длина пять единиц и высота четыре единицы. Площадь треугольника будет часть площади прямоугольника.
Мы можем вычислить, что площадь прямоугольник пять раз четыре, что составляет 20 квадратных единиц. И можем ли мы увидеть, какая часть или часть этого прямоугольника, что треугольник? Это половина дела. Площадь этого треугольника равна половине 20 квадратных единиц, так что это 10 квадратных единиц.
Конечно, у нас не всегда
треугольники, нарисованные для нас на бумаге в клетку. Тем не менее, мы все еще можем применить
тот же метод, чтобы найти площадь треугольника. Например, этот прямоугольный треугольник
имеет основание девять сантиметров и высоту шесть сантиметров. Две копии треугольника объединяются
чтобы сделать прямоугольник, площадь которого в два раза больше площади исходного треугольника.
Тем не менее, мы все еще можем применить
тот же метод, чтобы найти площадь треугольника. Например, этот прямоугольный треугольник
имеет основание девять сантиметров и высоту шесть сантиметров. Две копии треугольника объединяются
чтобы сделать прямоугольник, площадь которого в два раза больше площади исходного треугольника.
Площадь прямоугольника вокруг него рассчитывается путем умножения длины на высоту. Итак, девять умножить на шесть, что дает 54 квадратных сантиметра. Следовательно, площадь треугольника составляет половину этого. Половина от 54 равна 27, поэтому площадь равна 27. квадратных сантиметров. Итак, теперь, когда мы увидели, как найти площади прямоугольных треугольников, а как насчет площадей треугольников, которые не имеют прямые углы?
Вот треугольник с основанием
10 см и перпендикуляр высотой 8 см.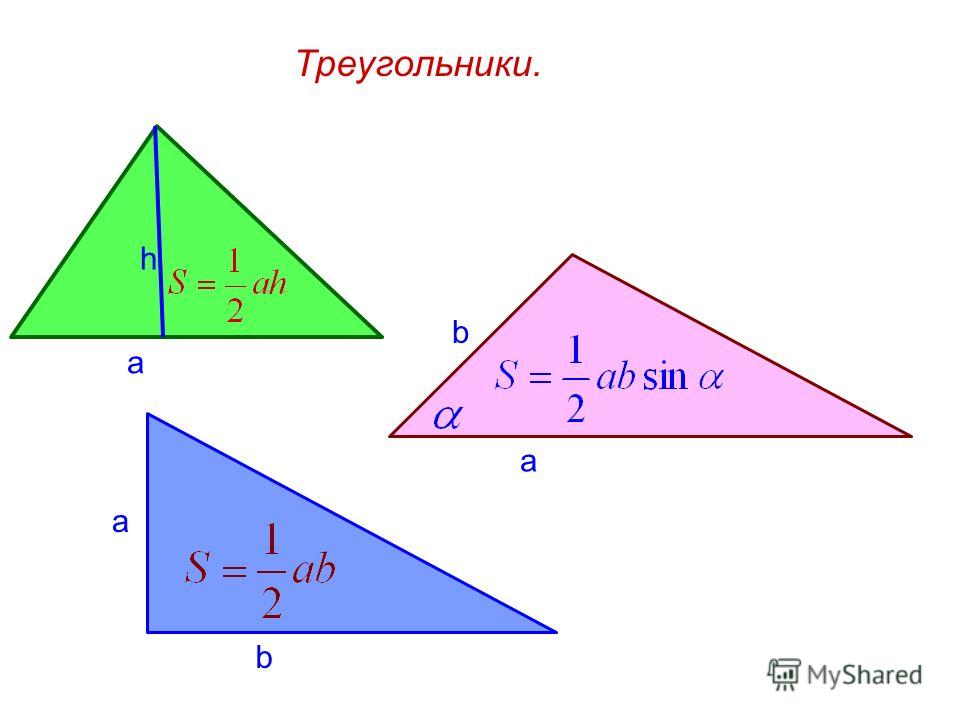 Так же, как и раньше, мы можем
начертите вокруг него прямоугольник длиной 10 см и высотой
восемь сантиметров. Но площадь треугольника
по-прежнему будет составлять половину площади прямоугольника?
Так же, как и раньше, мы можем
начертите вокруг него прямоугольник длиной 10 см и высотой
восемь сантиметров. Но площадь треугольника
по-прежнему будет составлять половину площади прямоугольника?
Затеняем правую часть треугольника. Обратите внимание, что у нас есть небольшой треугольник и маленький прямоугольник. А площадь этого маленького треугольника составляет половину площади маленького прямоугольника. И мы можем сделать то же самое для оставшаяся часть треугольника слева. Его площадь равна половине этой другой прямоугольник. Значит площадь треугольника равна половине окружающего его прямоугольника.
Теперь составим формулу
это поможет нам найти площадь треугольника без необходимости рисовать прямоугольники
каждый раз. Площадь треугольника равна
основание умножить на высоту разделить на два. Помните, что основание умножается на
высота эквивалентна нахождению длины, умноженной на ширину, чтобы найти площадь
прямоугольник.
Помните, что основание умножается на
высота эквивалентна нахождению длины, умноженной на ширину, чтобы найти площадь
прямоугольник.
Обратите внимание, что высота всегда должна быть высотой перпендикуляра. Это не обязательно будет длина стороны в треугольнике, особенно если это не прямоугольный треугольник. Нам нужно провести линию через вершина треугольника равна 90 градусов к основанию и измерьте высоту, используя эта линия.
Теперь мы также можем написать эту формулу
по-разному, и это означает то же самое. Площадь треугольника равна
половина произведения основания на высоту перпендикуляра. Итак, для нашего примера мы могли бы написать
что площадь треугольника равна половине умноженной на 10 умноженной на восемь. И мы можем решить это за несколько
различные пути. Мы могли бы умножить 10 и восемь
сначала, что равно 80, а затем разделить его пополам, чтобы получить 40 квадратных сантиметров.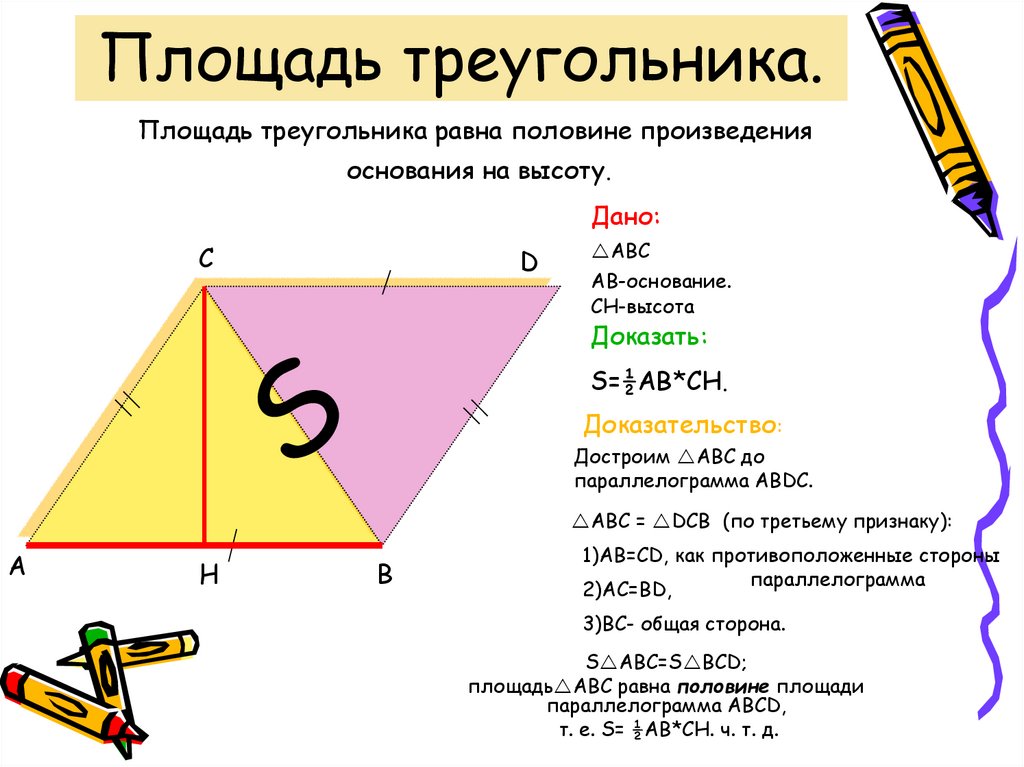 Или мы могли бы сначала сократить вдвое 10,
что равно пяти, а затем умножить пять на восемь. Это тоже 40 кв.
сантиметры.
Или мы могли бы сначала сократить вдвое 10,
что равно пяти, а затем умножить пять на восемь. Это тоже 40 кв.
сантиметры.
Если одно из оснований или перпендикуляров высота является четным числом, тогда нам может быть проще сначала разделить его пополам, прежде чем умножение на другое измерение. Итак, давайте теперь посмотрим, как мы можем поставить эти формулы на практике в следующем примере.
𝐴𝐵𝐶𝐷 — прямоугольник. Найдите площадь треугольника 𝐴𝐵𝐹.
На схеме видно, что мы есть прямоугольник с вершинами 𝐴, 𝐵, 𝐶 и 𝐷. Тем не менее, мы заинтересованы в этом треугольник 𝐴𝐵𝐹. Это треугольник, который имеет вершины 𝐴, 𝐵 и 𝐹.
Вспомним формулу для нахождения
площадь треугольника. Площадь треугольника равна
половина произведения основания на высоту. И эта высота должна быть
перпендикулярная высота.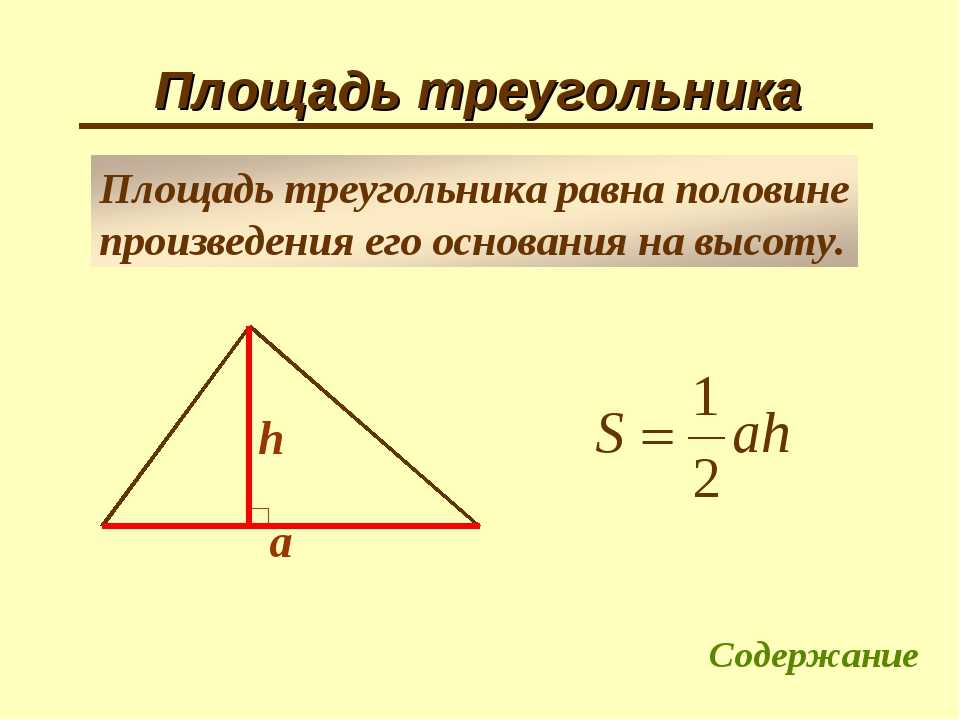 Но в этом треугольнике мы не знаем
перпендикулярная высота, или мы?
Но в этом треугольнике мы не знаем
перпендикулярная высота, или мы?
Мы знаем, что прямоугольник имеет высота пять сантиметров. А так как это прямоугольник, то расстояние от основания до вершины всегда будет равно пяти сантиметрам. Итак, отрезок 𝐴𝐵 равен пяти сантиметров ниже 𝐹, которая является вершиной треугольника. Мы можем показать это на нашей диаграмме с отрезком, проведенным из 𝐹 перпендикулярно 𝐴𝐵.
Итак, теперь мы знаем, что треугольник
имеет основание восемь сантиметров и высоту перпендикуляра пять сантиметров. Это означает, что площадь
треугольник 𝐴𝐵𝐹 равен половине, умноженной на восемь, умноженной на пять. Половина восьми это четыре, а четыре
пять умножить на 20. Не забывая о единицах измерения
площади, мы можем дать ответ, что площадь треугольника 𝐴𝐵𝐹 равна 20 кв.
сантиметры, так как обе наши длины даны в сантиметрах.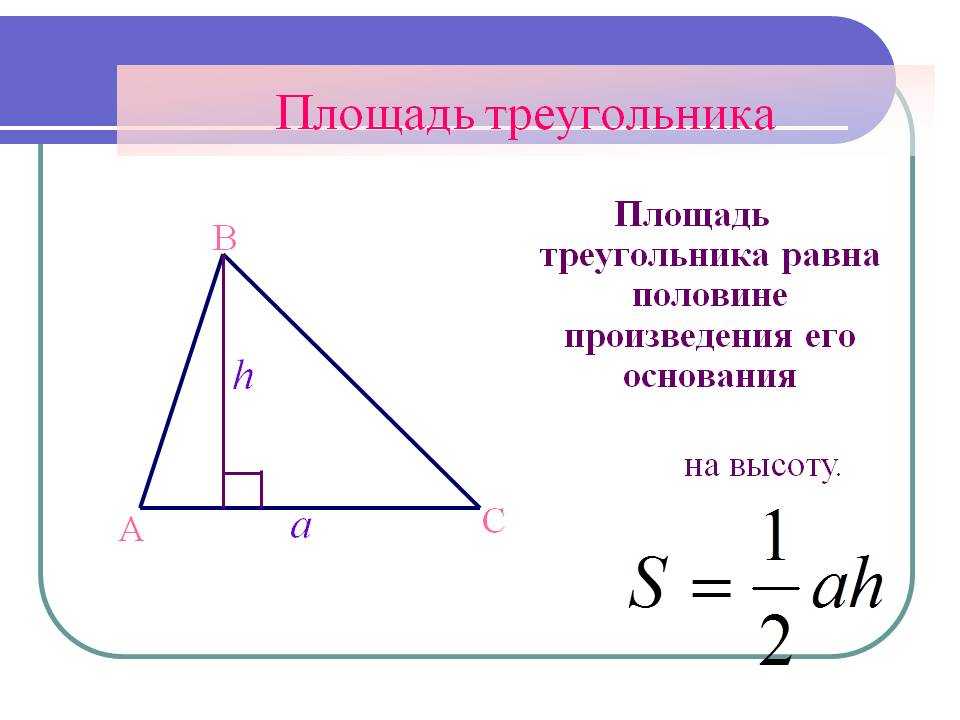
До сих пор мы видели, как найти площадь прямоугольного треугольника и треугольников, не являющихся прямоугольными. Но иногда у нас есть треугольники где вершина треугольника не выше основания, треугольник, который может выглядеть что-то вроде этого. Важно помнить, что что наша формула для нахождения площади треугольника всегда одна и та же. И высота всегда должна быть перпендикулярная высота. База будет такой же, как мы видели до. Это одна из сторон треугольник. А как же перпендикуляр высота?
Ну, мы не можем использовать эту длину стороны
оранжевым, потому что это не перпендикулярно основанию. И мы не можем провести перпендикуляр
выстройтесь от края основания вот так, потому что это не полная высота
треугольник. Вместо этого, чтобы найти перпендикуляр
высота, нам нужно считать перпендикулярное расстояние от вершины треугольника
к линии, являющейся продолжением основания. Затем мы можем использовать формулу с
основание и высота перпендикуляра.
Затем мы можем использовать формулу с
основание и высота перпендикуляра.
Давайте посмотрим, как это работает для треугольник с некоторыми заданными измерениями. Здесь у нас есть треугольник, нарисованный с помощью одна сторона длиной четыре сантиметра, а другая сторона длиной 13 сантиметров. Он имеет перпендикулярную высоту пять сантиметров от четырехсантиметрового основания. Помните, что если у нас есть один из длины сторон треугольника и его перпендикулярную высоту от этой стороны, мы можем работать вне области. Итак, мы можем взять за основу это треугольника как четыре сантиметра, а высота перпендикуляра с этой стороны как пять сантиметры.
Следовательно, площадь треугольника
можно рассчитать как половину умножить на четыре умножить на пять. Четыре умножить на пять равно 20, а
тогда нам нужно вдвое уменьшить это. Это дает нам площадь 10 кв.
сантиметры.
Это дает нам площадь 10 кв.
сантиметры.
Обратите внимание, что у нас тоже была такая длина из 13 сантиметров. Иногда у нас есть дополнительные информацию о треугольной диаграмме. Или мы можем определить длину некоторые другие стороны треугольника. Но это не значит, что у нас использовать эту дополнительную информацию. Помните, что для нахождения площади треугольника, нам просто нужно использовать длину основания и высоту перпендикуляра из этого сторона.
Еще одно важное замечание
с треугольниками, подобными этому, заключается в том, что эта дополнительная длина, которую мы продолжаем от
основание до перпендикулярной высоты не должно включаться в состав основания
длина. Например, если бы мы знали, что это
длина была восемь сантиметров, это не составляло бы основания в общей сложности 12
сантиметры. Длина основания треугольника
все равно будет четыре сантиметра.
Длина основания треугольника
все равно будет четыре сантиметра.
Теперь, прежде чем мы закончим с этим видео, есть важный момент, который действительно нужно выделить в отношении базы и перпендикулярная высота треугольника. Мы привыкли видеть треугольники нарисовано вот так, с одной из сторон, расположенной горизонтально. И поэтому, если мы хотим решить площади, мы бы умножили значение основания на значение высоты, перпендикулярной к основание и разделить его пополам.
Но мы можем выбрать любую сторону, чтобы быть
основание треугольника. Таким образом, мы могли бы принять эту сторону, чтобы быть
основание, и в этом случае мы должны найти перпендикулярную высоту от этого основания, даже
если нам нужно расширить основание, чтобы найти перпендикулярную высоту. Мы можем вызвать любую из трех сторон
основания треугольника.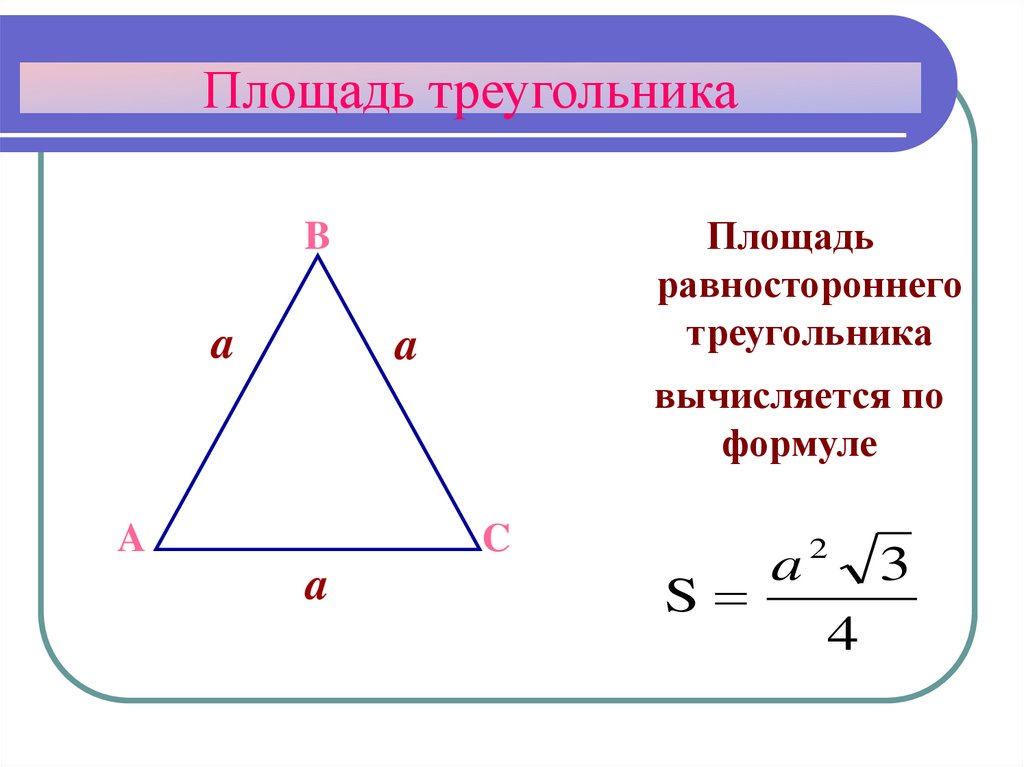 Итак, когда мы говорим о
перпендикулярная высота треугольника, мы действительно имеем в виду перпендикулярную высоту от
выбранная база. Таким образом, независимо от ориентации
треугольник начерчен или какую сторону мы называем основанием, мы еще можем вычислить площадь
треугольника с помощью одной из формул, которые мы видели.
Итак, когда мы говорим о
перпендикулярная высота треугольника, мы действительно имеем в виду перпендикулярную высоту от
выбранная база. Таким образом, независимо от ориентации
треугольник начерчен или какую сторону мы называем основанием, мы еще можем вычислить площадь
треугольника с помощью одной из формул, которые мы видели.
Давайте теперь суммируем ключевые моменты
этого видео. Мы увидели, что можем написать формулу
вычислить площадь треугольника двумя разными, но эквивалентными способами, либо как
площадь треугольника равна произведению основания на высоту, деленному на два, или площади
треугольника равно половине произведения основания на высоту. Важно помнить, что
что мы всегда используем перпендикулярную высоту от стороны, выбранной в качестве основания, к
рассчитать площадь. Имеют ли треугольники право
угол, не имеют прямого угла, или даже если нам нужно найти высоту перпендикуляра
используя расширенную линию от основания, мы все еще можем применить одну из формул выше
чтобы найти площадь треугольника.
Площадь треугольника ‹ OpenCurriculum
Цели статьи
Из курса элементарной геометрии вы узнали, что площадь треугольника равна половине произведения основания на высоту. Теперь мы будем использовать это в сочетании с некоторой тригонометрией, чтобы вывести больше формул для площади при заданных частях треугольника.
Случай 1: Две стороны и прилежащий угол. Предположим, что у нас есть треугольник △ ABC , в котором A может быть острым, прямым или тупым углом, как на рисунках 1, 2 и 3. Предположим, что A , b и c равны известен.
В каждом случае мы проводим высоту h из вершины C в AB, так что площадь (которую мы будем обозначать буквой K) равна K = 1/2hc. Но мы видим, что h = b sin A в каждом из треугольников (поскольку h = b и sin A = sin 90° = 1 на рис.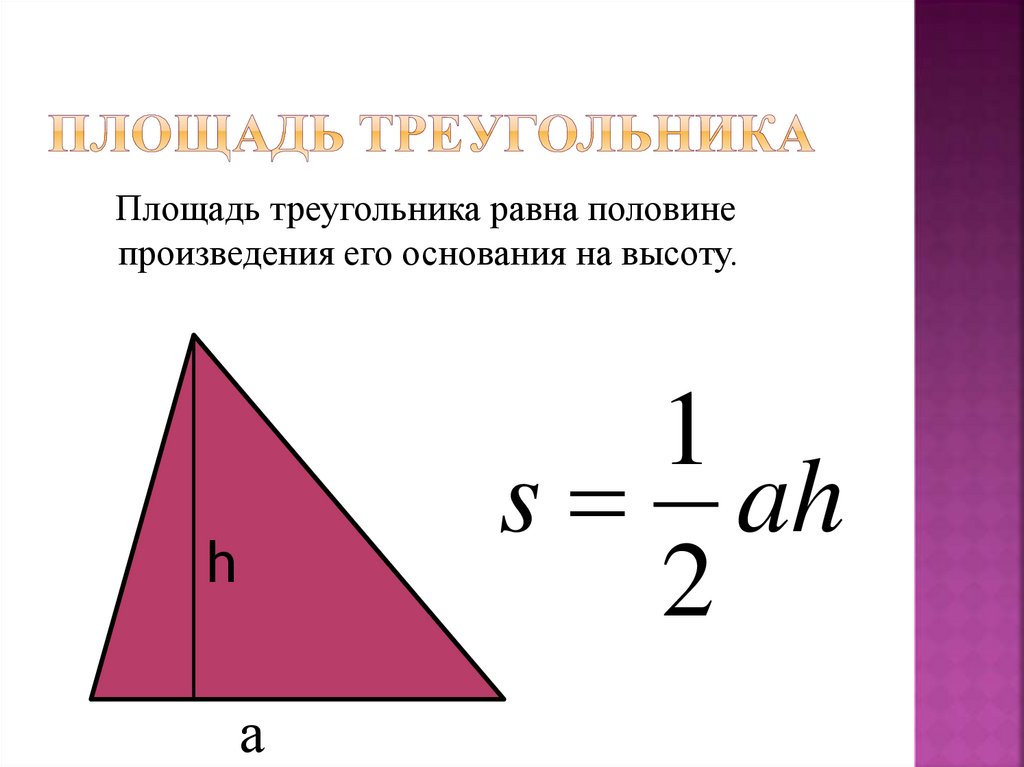 2 и h = b sin (180° − A) = b sin A на рис. 3). Таким образом, мы получаем следующую формулу:
2 и h = b sin (180° − A) = b sin A на рис. 3). Таким образом, мы получаем следующую формулу:
$$\boxed{Area = K = \frac{1}{2} bc\;sin A}\;\;\;\;\; (1)$$
Приведенная выше формула для площади △ABC основана на известных частях A, b и c. Аналогичные рассуждения для углов B и C дают нам:
$$\boxed{Area = K = \frac{1}{2} ac\;sin B} \;\;\; (2)$$ $$Area = K = \frac{1}{2} ab \; грех С \;\;\; (3)$$
Обратите внимание, что высота h не фигурирует явно в этих формулах, хотя неявно присутствует. Преимущество этих формул в том, что они основаны на частях треугольника, и нет необходимости находить h отдельно. 9\circ}$$ $$K = 21,58$$
Случай 3: Три стороны. Предположим, что у нас есть треугольник △ ABC , в котором известны все три стороны. Тогда формула Герона дает нам площадь:
Формула Герона: Для треугольника △ ABC со сторонами a , b и c пусть с = \(\frac{1}{2} (a+b+c)\) (т.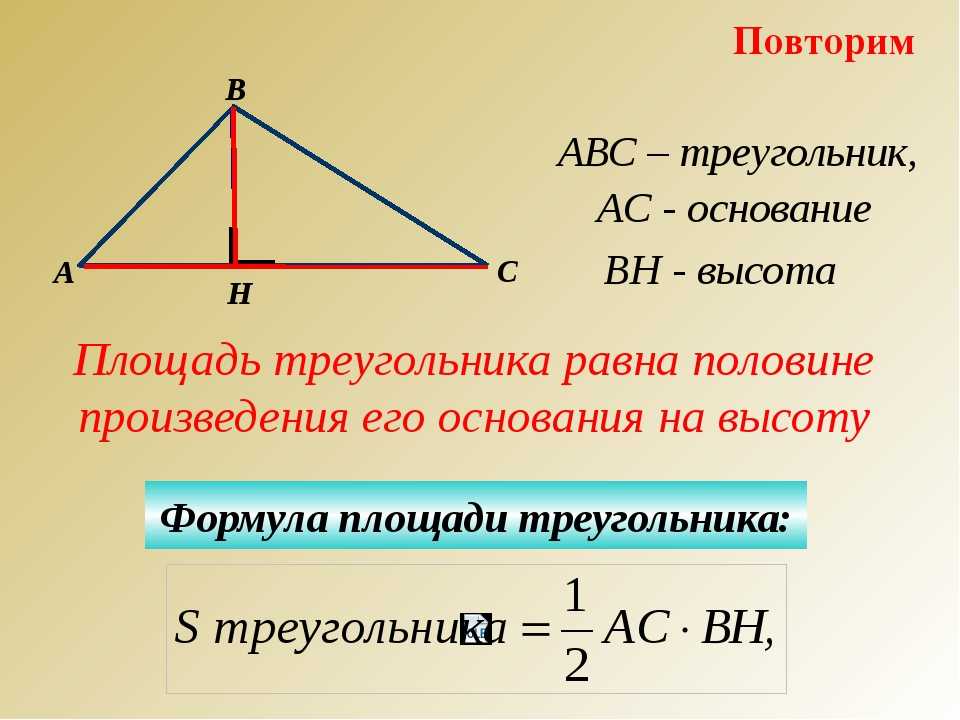 е. 2 с = a+b+ c — периметр треугольника). Тогда площадь К треугольника равна 92 = s(s−a)(s−b)(s−c) ,$$
е. 2 с = a+b+ c — периметр треугольника). Тогда площадь К треугольника равна 92 = s(s−a)(s−b)(s−c) ,$$
, поэтому при извлечении квадратных корней мы получаем
$$K = \sqrt{s(s−a)(s−b) (s− c)} .$$
Пример 3
Найдите площадь треугольника △ ABC по заданным a = 5, b = 907,5 c 4 и . Решение : Использование формулы Герона с s =\(\frac{1}{2}\) (a+b+c) = \(\frac{1}{2}\) (5+4 +7) = 8, площадь K определяется как:
$$K = \sqrt{s(s−a)(s−b)(s−c)}$$
$$= \sqrt{8(8−5)(8−4)(8−7)} = \sqrt{96} ⇒ K = 4\sqrt{6} ≈ 9,8 .$$ Формула Герона полезна в теоретических целях (например, при выводе других формул). Однако он не очень подходит для использования на калькуляторе, демонстрируя так называемую числовую нестабильность для «экстремальных» треугольников, как в следующем примере. Пример 4 Решение : Чтобы использовать формулу Герона, нам нужно вычислить s = \(\frac{1}{2}\) (a+b+ c) . Вот еще один пример, в котором формула Герона используется немного по-другому. Пример 5: Длины двух сторон треугольника равны \(4\) и \(9\), а площадь треугольника равна \(6\sqrt{5}). Найдите длину третьей стороны треугольника. Решение: Согласно формуле Герона: $$A = \sqrt{s(s — a)(s — b)(s — c)} \Rightarrow$$
$$6\sqrt{5} = \sqrt{s(s — 4)(s — 9)(s — c)}$$ Возведение в квадрат обеих частей уравнения: $$180 = s(s — 4) (s — 9)(s — c)$$ Мы должны найти \(c\). Однако полупериметр определяется как $$s = \frac{a + b + c}{2}$$ Мы уже знаем \(a\) и \(b\): $$s = \frac{4 + 9 + c}{2} = \frac{13 + c}{2}$$ Следовательно, уравнение принимает вид $$180 = \frac{13 + c}{2} \cdot (\frac{13 + c}{ 2} — 4) \cdot (\frac{13 + c}{2} — 9) \cdot (\frac{13 + c}{2} — c) \Rightarrow$$
$180 = \frac{13 + c}{2} \cdot \frac{5 + c}{2} \cdot \frac{-5 + c}{2} \cdot \frac{13 — c}{2} $$ Очистите дроби, умножив обе части уравнения на \(16\): $2880 = (13 + c)(5 + c)(-5 + c)(13 — c)$$ Вместо того, чтобы решать это уравнение алгебраически, просто подключите его к графическому калькулятору.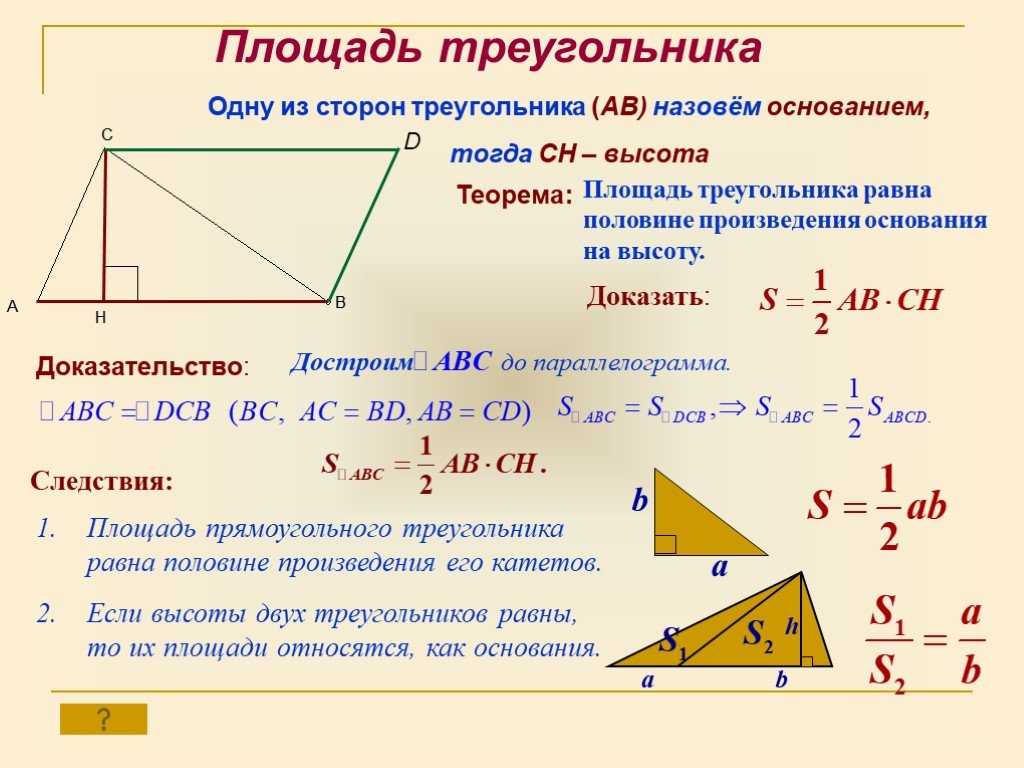 Обратите внимание, что фактическое значение a+b+c равно 2000000,0000008, которое состоит из 14 цифр. Большинство калькуляторов могут хранить 12-14 цифр (даже если они отображают меньше) и, следовательно, могут округлить это значение a+b+c до 2000000. Когда мы затем разделим это округленное значение для a+b+c на 2, чтобы получить s, некоторые калькуляторы (например, TI-83 Plus) дадут округленное в меньшую сторону значение 1000000.
Это проблема, потому что a = 1000000, и поэтому мы получим s− a = 0, в результате чего формула Герона дает нам площадь треугольника, равную 0! И это действительно неправильный ответ, который возвращает TI-83 Plus. Другие калькуляторы могут дать другой неточный ответ, в зависимости от того, как они хранят значения внутри. Фактическая площадь — с точностью до 15 знаков после запятой — равна K = 0,999999999999895, т. е. в основном 1.
Обратите внимание, что фактическое значение a+b+c равно 2000000,0000008, которое состоит из 14 цифр. Большинство калькуляторов могут хранить 12-14 цифр (даже если они отображают меньше) и, следовательно, могут округлить это значение a+b+c до 2000000. Когда мы затем разделим это округленное значение для a+b+c на 2, чтобы получить s, некоторые калькуляторы (например, TI-83 Plus) дадут округленное в меньшую сторону значение 1000000.
Это проблема, потому что a = 1000000, и поэтому мы получим s− a = 0, в результате чего формула Герона дает нам площадь треугольника, равную 0! И это действительно неправильный ответ, который возвращает TI-83 Plus. Другие калькуляторы могут дать другой неточный ответ, в зависимости от того, как они хранят значения внутри. Фактическая площадь — с точностью до 15 знаков после запятой — равна K = 0,999999999999895, т. е. в основном 1.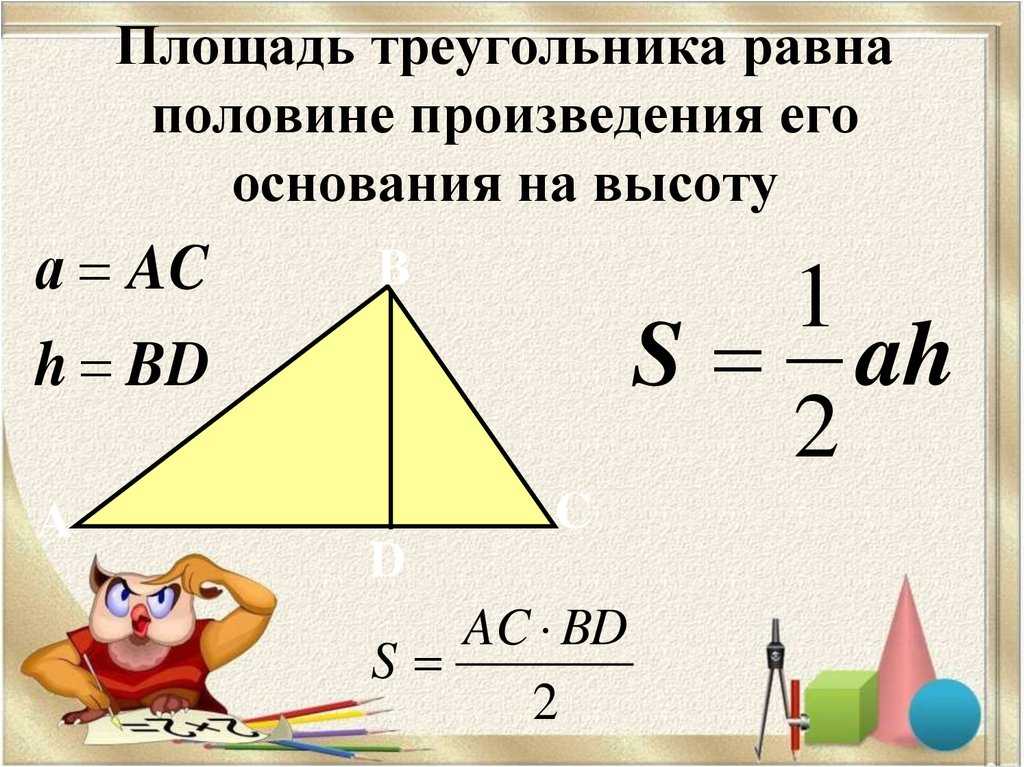


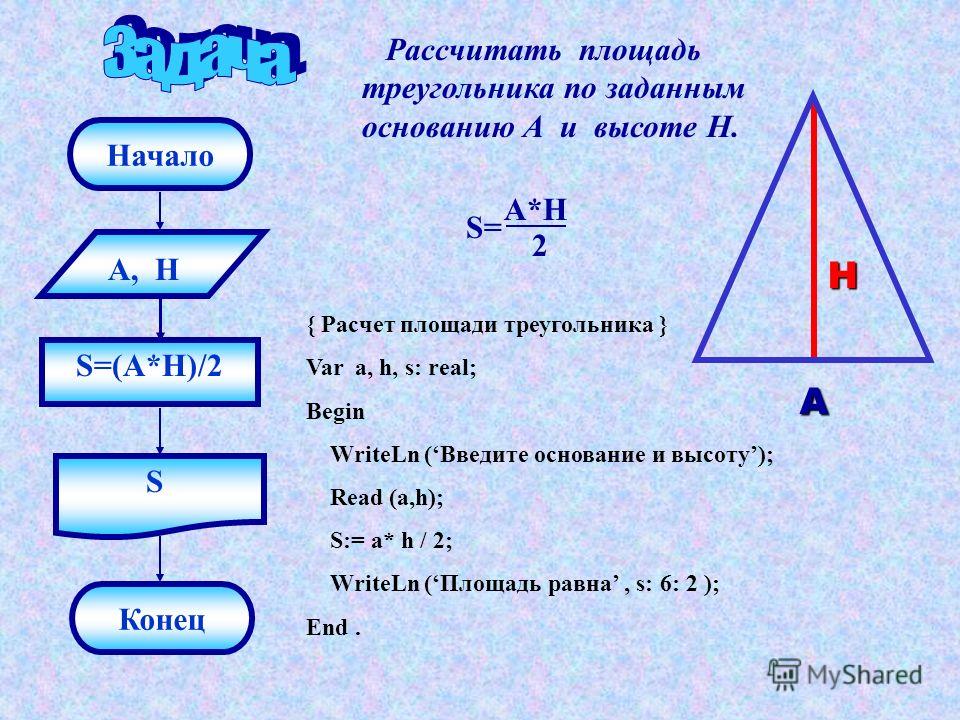
 (Формула 8)
(Формула 8)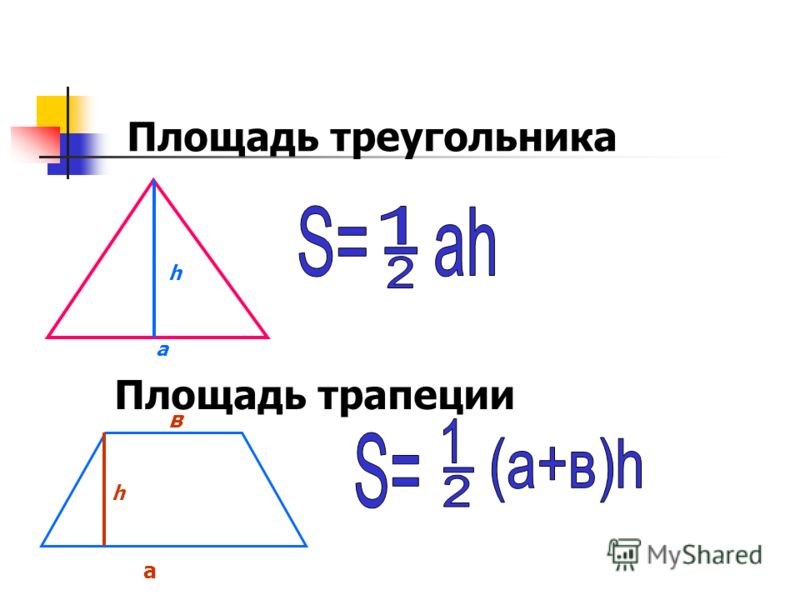

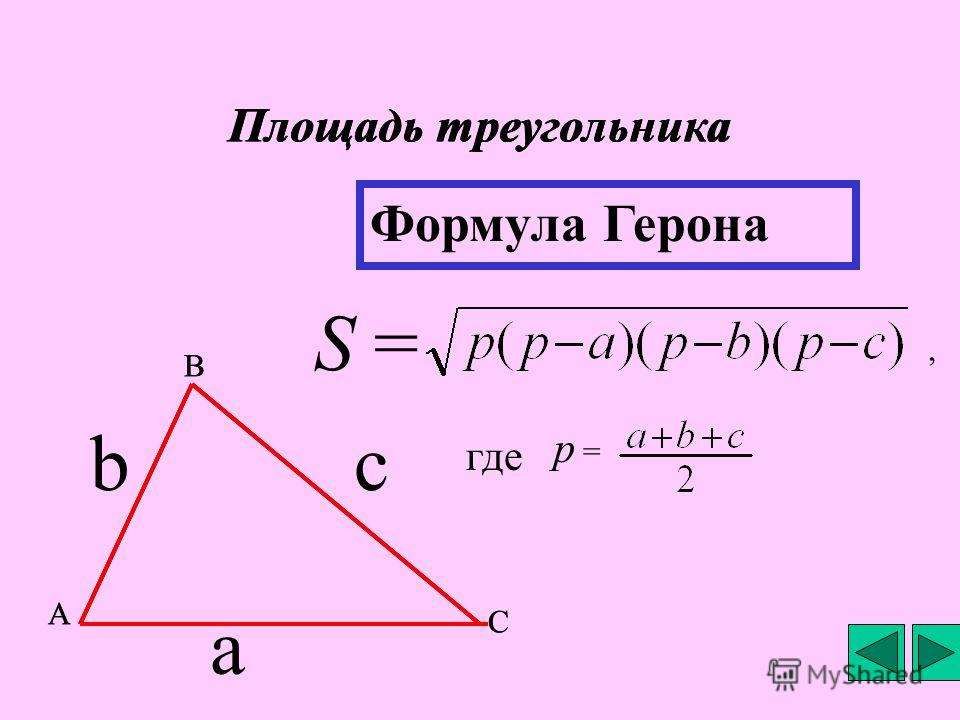 9{2}\)
9{2}\)