Площадь треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Площадь треугольника по основанию и высоте
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
| \( \small S= \frac {\large 1}{\large 2} \cdot AC \cdot BH. \) |
Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку \( \small AC \ || \ BD \) и \( \small AB\ || \ CD \), то ABDC является параллелограммой и, следовательно, \( \small AC \ = \ BD \), \( \small AB\ = \ CD . \) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
Доказательство. Пусть площадь треугольников ABC и A1B1C1 равны:
где AC и A1C1 основания треугольников ABC и A1B1C1, соответственно, а h их высоты.
Обозначим через k отношение
\( \small k= \frac {\large AC}{\large A_1C_1}. \) |
Тогда
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
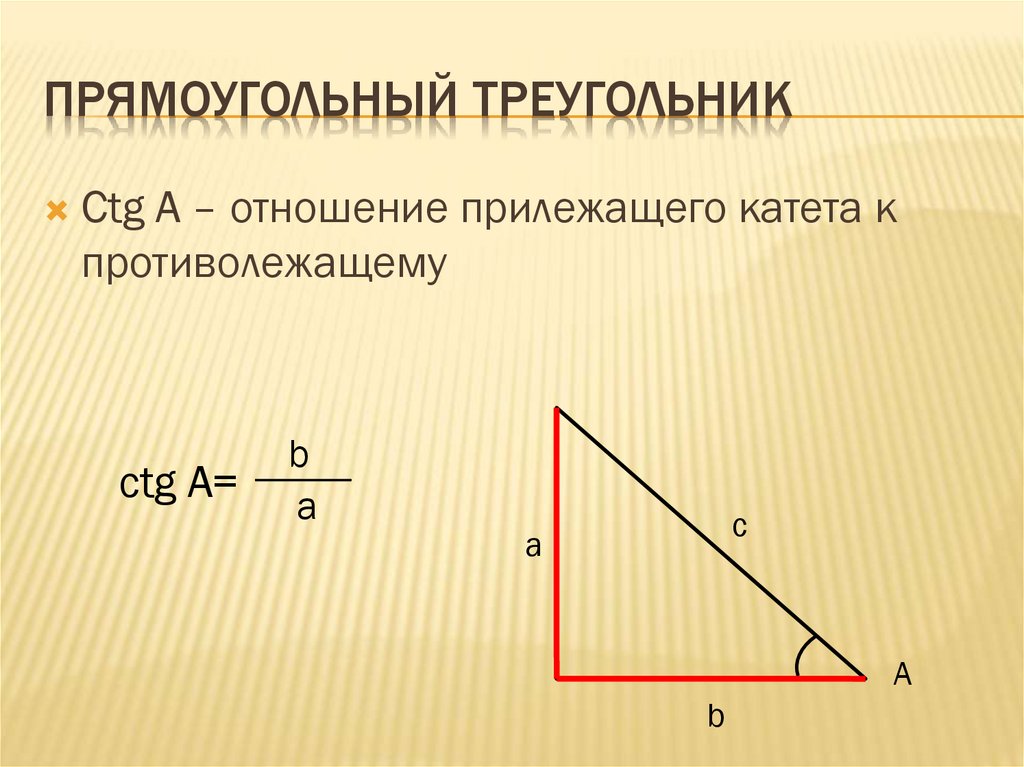
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
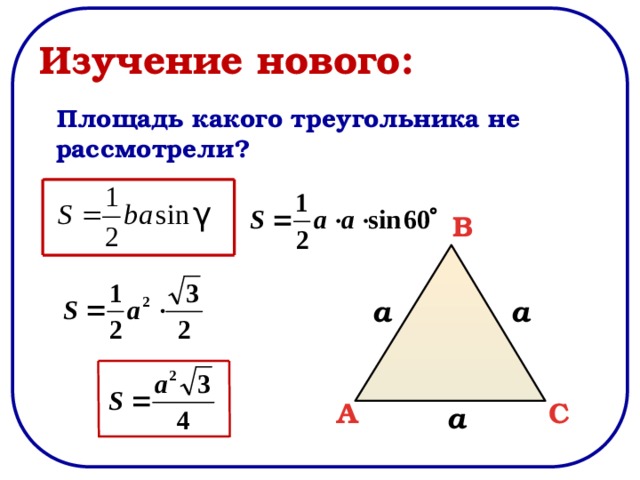
Площадь треугольника по двум сторонам и углу между ними
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
где h − высота треугольника.
Из теоремы синусов имеем:
Подставляя (2) в (1), получим:
или
Площадь треугольника по стороне и прилежащим двум углам
Пусть известна сторона треугольника и две прилежащие углы (Рис.
4).
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
Найдем сторону b используя теорему синусов:
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
Учитывая формулы приведения тригонометрических функциий, получим:
Площадь треугольника по трем сторонам. Формула Герона
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
где a, b, c − стороны треугольника, а p − полупериод треугольника:
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
Из (8) и (9) следует:
Откуда находим x:
Подставляя (10) в (8) найдем h:
Тогда площадь треугольника равна:
Преобразовав (12) получим формулу (7):
Площадь треугольника по трем сторонам и радусу описанной окружности
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.
6). Докажем, что площадь треугольника равна: \( \small S=\frac{\large abc}{\large 4R}. \)
Из теоремы синусов имеем:
| \( \small \frac {\large a}{\large \sin A}= \frac {\large b}{\large \sin B} \) \(\small =\frac {\large c}{\large \sin C}=2R. \) |
Откуда;
| \( \small \sin C=\frac {\large c}{\large 2R}. \) |
Подставляя (13) в (3), получим:
| \( \small S=\frac {\large abc}{\large 4R}. \) | (14) |
Смотрите также:
- Площадь прямоугольного треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
Площадь треугольника по двум сторонам и углу
- Главная
- Калькуляторы
- Математика
- Геометрия
- Площадь плоских фигур
- Площадь треугольника по двум сторонам и углу
- Для произвольного треугольника
- Исходные данные:
- Результат:
- Для равнобедренного треугольника
- Исходные данные:
- Результат:
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Для произвольного треугольника
Для равнобедренного треугольника
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Площадь плоских фигур Площадь Геометрия 7288
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Площадь треугольника через основание и высоту
Площадь плоских фигур Калькулятор Площадь Математика
Калькулятор площади ромба
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади круга
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади параллелограмма
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади элипса
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Калькулятор площади правильного многоугольника
Площадь плоских фигур Калькулятор Расчёт Площадь Геометрия
Сколько грамм в чайной ложечке, столовой ложке и стакане?
1 чайная ложка, 5 мл жидкости это приблизительно 5 грамм
Масса и вес Масса Физика Теория Единицы измерения
Бесплатный генератор паролей онлайн
Создать бесплатно пароль любой длины и уровня сложности для ваших приложений, аккаунтов, соц.
сетей, паролей к Windows, зашифрованным архивам и т.д.Работа с текстом Генератор Инструмент Текст Пароли
Переводчик азбуки Морзе онлайн
Азбука Морзе — перечень сигналов из точек и тире, воспроизводящихся с помощью радиосигналов или прерыванием постоянного электрического тока.
Работа с текстом Инструмент Текст
Как собрать кубик Рубика 3х3. Самая легкая схема для начинающих
Инструкции
Что такое лошадиная сила
Лошадиная сила — единица мощности. Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
Разное Мощность Сила Единицы измерения Деньги Справочник
Что такое Ом
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
Электротехника Формулы Физика Теория Электричество
Процент / доля от числа
Арифметика Калькулятор Расчёт Проценты
Что такое масса?
Массой тела называется физическая величина, характеризующая его инерционные и гравитационные свойства.
Масса и вес Масса Физика Теория Единицы измерения
Площадь треугольника SAS
LearnPracticeDownload
Площадь треугольника SAS – это общий объем пространства, заключенного в двумерной плоскости. Напомним, что треугольник SAS — это треугольник с двумя заданными сторонами и внутренним углом между ними. Таким образом, формула площади треугольника SAS помогает рассчитать пространство, занимаемое между сторонами треугольника SAS на плоскости. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Здесь «единица» означает единицу (1), а единичный квадрат – это квадрат со стороной, равной 1 единице. В этом разделе мы обсудим площадь треугольника с двумя сторонами и прилежащим углом (треугольник SAS) вместе с решенными примерами.
| 1. | Площадь треугольника SAS Формула |
| 2. | Доказательство площади треугольника SAS |
| 3. | Часто задаваемые вопросы о площади треугольника SAS Формула |
Площадь треугольника SAS Формула
«SAS», что означает «сторона, угол, сторона», является свойством треугольника, у которого заданы 2 стороны и угол между этими сторонами.
Для заданного треугольника ABC с двумя известными сторонами и внутренним углом между этими сторонами его площадь может быть рассчитана по формуле SAS. Предположим, что a, b и c — разные стороны треугольника.
Формула для расчета площади треугольника с использованием SAS представлена в виде × грех (А)
Доказательство площади треугольника SAS
Предположим, a,b и c – разные стороны треугольника.
- Когда известны стороны b и c и угол А между ними, площадь треугольника составляет: 1/2 × bc × sin(A)
- Если известны стороны «b» и «a» и угол между ними B , площадь треугольника составляет: 1/2 × ab × sin(C)
- Когда известны стороны ‘a’ и ‘c’ и угол C между ними, площадь треугольника составляет: 1/2 × ac × sin(B)
Приведенную выше формулу можно доказать, выполнив следующие действия:
Дан треугольник ABC с двумя известными сторонами BC и AC и внутренним углом C между этими сторонами. Примем высоту равной h.
Треугольник ACD прямоугольный. Используя тригонометрию, мы получаем
⇒ sin(C) = h/b
⇒ h = b sin(C)
Высота = h = AD = b sin(C)
Основание = длина BC = a (как показано на рисунке выше)
Следовательно, площадь треугольника ABC = (1/2)(основание)(высота) = (1/2)(длина BC)(высота) = (1/2)(a)(b sin(C))
-
Пример 1Найдите площадь треугольника ABC, учитывая, что стороны AB = 5 единиц, BC = 8 единиц и ∠ABC = 60°.
Решение
Длина AB = c = 5 единиц, Длина BC = a = 8 единиц
Угол между AB и BC = ∠B = 60°
Площадь ΔABC = 1/2 × a × c × sin(B) = 1/2 × 5 × 8 × sin60º = 10 √ 3 квадратных единиц : Площадь треугольника ABC = 10√3 квадратных единиц
-
Пример 2Найдите площадь четырехугольника BCED, учитывая, что AB = 30 единиц, AC = 20 единиц и ∠BAC = 30°. Кроме того, D делит AB в отношении 1:2, а E — это середина AC.
Раствор
Длина AB = 30 единиц, длина AC = 20 единиц
Угол между AB и AC = ∠A = 30°
Площадь ΔABC = 1/2 × AB × AC × sin(A) = 1/2 × 30 × 20 × sin30º = 150 квадратных единиц
Дано, D делит АВ в отношении 1:2,
AD = \( \dfrac{1}{1+2}\) AB = 1/3 × 30 = 10 квадратных единиц
Учитывая, что E является серединой AC, таким образом, AE = AC/2 = 10 единиц 2
Площадь ΔADE = 1/2 × AD × AE × sin(A) = 1/2 × 10 × 10 × sin30º = 25 квадратных единиц
Площадь (BCED) = Площадь ΔABC – Площадь ΔADE = 150–20 = 125 квадратных единиц
Ответ: Площадь (BCED) = 125 квадратных единиц
перейти к слайдуперейти к слайду
Пусть ваш ребенок решит задачи из реальной жизни, используя математику
Пусть ваш ребенок применит понятия, полученные в школе, в реальном мире с помощью наших экспертов.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади треугольника SAS
Какова площадь треугольника с двумя сторонами и углом между ними?
Треугольник SAS — это треугольник с двумя заданными сторонами и внутренним углом между ними. Площадь треугольника с двумя сторонами и внутренним углом — это общее количество пространства, которое он заключает в двумерной плоскости, которое можно рассчитать с помощью формулы треугольника SAS.
Какая формула для нахождения площади треугольника SAS?
Предположим, что a, b и c — разные стороны треугольника. Таким образом, формула площади треугольника SAS выражается как
- . Когда известны стороны b и c и угол А между ними, площадь треугольника составляет: 1/2 × bc × sin(A)
- Если известны стороны «b» и «a» и угол между ними B, площадь треугольника составляет: 1/2 × ab × sin(C)
- Когда стороны ‘a’ и ‘c’ и угол C между ними известны, площадь треугольника составляет: 1/2 × ac × sin(B)
Что означает треугольник SAS?
Угол между двумя заданными сторонами треугольника называется внутренним углом этих сторон.
Как найти площадь SAS-треугольника, если S — длина равных сторон, а θ — угол между ними?
Так как стороны равны, значит треугольник равнобедренный. Площадь заданного равнобедренного треугольника = 1/2 × s × s × sin(θ) = 1/2 s 2 sin(θ) (с использованием формулы площади треугольника SAS).
Как найти длину неизвестной стороны треугольника SAS?
Используя закон косинуса (правило косинуса или формулу косинуса), можно узнать длину неизвестной стороны. Если даны две стороны a и b и угол C между ними, то неизвестная сторона c может быть задана как c 2 = a 2 + b 2 — 2ab cos(C).
Что такое периметр треугольника SAS?
Периметр треугольника определяется как общая длина границы треугольника, т. е. Периметр = Сумма всех длин сторон треугольника. Для заданного треугольника ABC с двумя известными сторонами BC и AC и внутренним углом C между этими сторонами. Пусть a будет длиной BC, b будет длиной AC и c будет длиной AB, тогда его периметр может быть задан как Perimeter = a + b + c.
Поскольку c неизвестно, его можно определить по формуле косинуса (правило косинусов или закон косинусов) c 92 — 2ab cos(C)} \)
Какова высота треугольника SAS?
Дан треугольник ABC с двумя известными сторонами, BC и AC, и углом C между этими сторонами. Пусть a будет длиной BC, b будет длиной AC и c будет длиной AB, тогда его высота может быть определена как, h = a sin(C)
Скачать БЕСПЛАТНЫЕ учебные материалы
Лист конгруэнтного треугольника
Рабочие листы по математике и наглядный учебный план
Площадь треугольника Калькулятор SAS
Наш калькулятор SAS площади треугольника может определить площадь треугольника по любой из двух его сторон и соответствующему вписанному углу. Обратите внимание, что аббревиатура SAS расшифровывается как Side-Angle-Side.
В этой статье мы кратко обсудим следующее:
- Как найти площадь треугольника по двум сторонам и углу.
- Что такое формула SAS площади треугольника.
- Некоторые часто задаваемые вопросы.
SAS формула площади треугольника
Возможно, вы знакомы с формулой площади треугольника, учитывая его основания и высоты :
Площадь = 12×основание×высота\text{Площадь} = \frac{1}{2} \times \text{ основание} \times \text{высота}Площадь=21×основание×высота
Треугольник, у которого известны две стороны и вписанный угол.В приведенном выше треугольнике мы знаем только его две стороны , aaa и bbb, и угол γ\gammaγ между ними. Если мы рассмотрим сторону bbb как основания треугольника , используя тригонометрию, мы получаем его высоту как: формула для треугольника задается следующим образом:
Площадь = 12 × a × b × sin(γ)\text{Площадь} = \frac{1}{2} \times a × b ×\sin(\gamma) Площадь=21×a×b×sin(γ)
Мы можем использовать эту формулу для вычисления площади треугольника с двумя сторонами и углом.
Как найти площадь треугольника по двум сторонам и углу?
Чтобы найти area of a triangle given its two sides a and b , and the inscribed angle γ , follow these simple steps:
- Multiply the lengths of the two sides вместе, чтобы получить
a × b. - Умножьте это значение на синус угла
γ, чтобы получитьa × b × sin(γ). - Разделить это значение на половину , чтобы получить треугольник площадь как
A = (a × b × sin(γ))/2. - Проверьте с помощью нашего калькулятора площади треугольника SAS.
Другие соответствующие калькуляторы
Мы собрали коллекцию похожих калькуляторов, которые могут быть вам полезны:
- Калькулятор площади треугольника;
- Калькулятор подобных треугольников;
- Калькулятор площади трехстороннего треугольника;
- Квадратный фут калькулятора треугольника;
- Калькулятор площади разностороннего треугольника;
- Калькулятор площади тупоугольного треугольника;
- Калькулятор площади косоугольного треугольника;
- Калькулятор площади треугольника с координатами.
Как использовать эту площадь треугольника Калькулятор SAS
Наш калькулятор площади треугольника с двумя сторонами и углом прост и удобен в использовании:
- Введите две стороны, которые вы знаете.
- Введите значение вписанного угла. Калькулятор автоматически найдет площадь.
Точно так же можно найти площадь треугольника с двумя сторонами и углом. Обратите внимание, что эта область калькулятора SAS треугольника также может работать в обратном направлении! Поэкспериментируйте с ним, предоставляя различные входные данные в любом порядке, и наслаждайтесь результатами!
Часто задаваемые вопросы
Как найти недостающую сторону треугольника по двум его сторонам и углу?
Формула для вычисления недостающей стороны c треугольника из его двух сторон A и B и вписанный угол γ IS:
C = √ (A 2 + B 2 — 2ABCOS (γ -9036) 9036 + 9036).