Площадь треугольника формулы: Напишите формулу нахождение площади треугольника

формула, чему равна, как найти

Что такое площадь треугольника

Определение

Треугольник — это многоугольник с тремя сторонами и тремя вершинами.

Определение

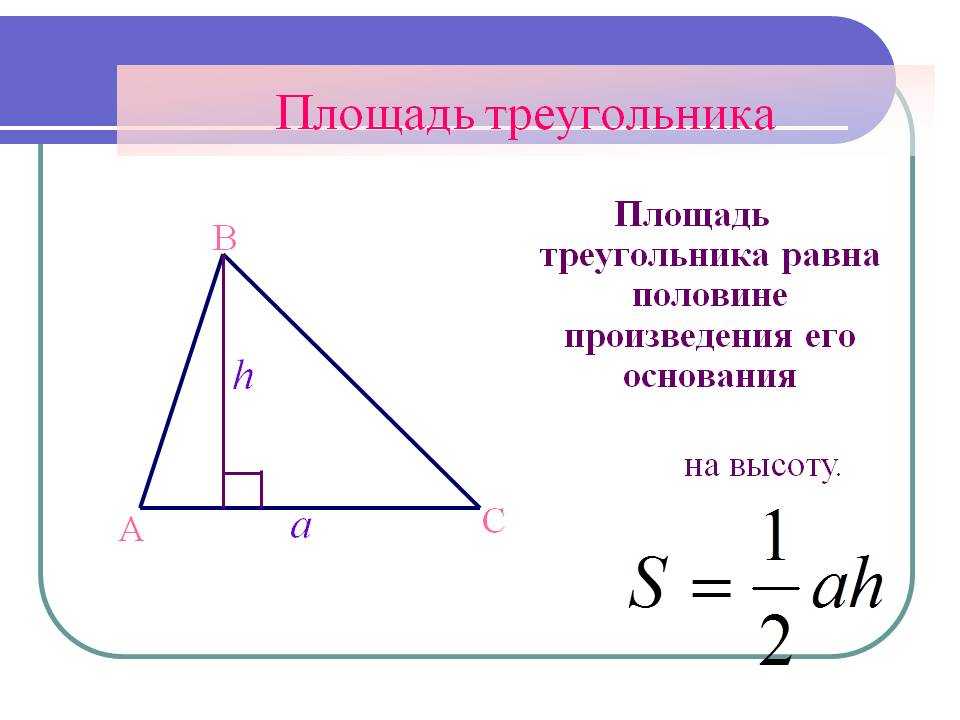
Площадь треугольника — это величина плоскости, заключенной между сторонами этой геометрической фигуры.У треугольника она равна произведению половины основания на высоту.

Математически это выглядит так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(S=\frac12a\times h\)

где a — основание треугольника, а h — его высота.

Способы нахождения площади

Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.

Через две стороны и угол

Источник: lifehacker. ru

Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:

\(S=\frac12a\times b\times\sin\alpha\)

где a и b — стороны фигуры, а α — угол между ними.

Через радиус описанной окружности и три стороны

Источник: lifehacker.ru

Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:

\(S=\frac{a\times b\times c}{4\times R}\)

где a, b и c — стороны фигуры, а R — радиус описанной окружности.

Через радиус вписанной окружности и три стороны

Источник: lifehacker.ru

В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:

\(S=r\times\frac{a+b+c}2\)

где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.

Таким образом, формулу можно выразить всего двумя множителями:

\(S=r\times p\)

где p — полупериметр треугольника.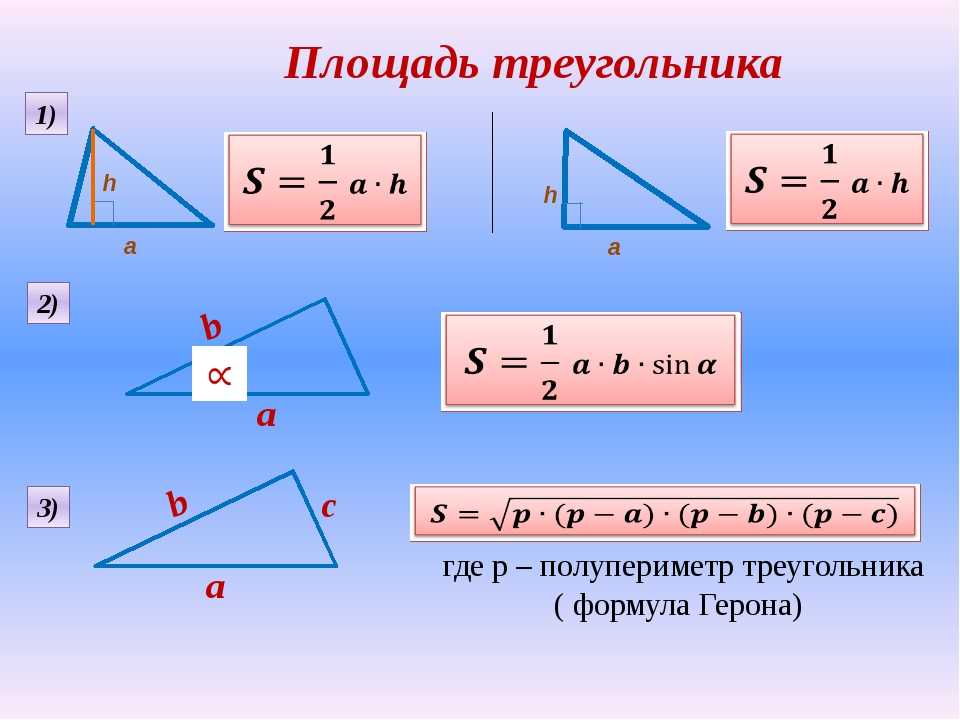 \circ-(\alpha+\beta)\)

Для прямоугольного треугольника

В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.

По двум сторонам

Источник: lifehacker.ru

Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:

\(S=\frac{a\times b}2\)

где a и b — катеты прямоугольного треугольника.

Через гипотенузу и острый угол

Источник: spravochnick.ru

Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.

Начнем с поиска катета:

\(\cos\left(\alpha\right)=\frac ac\)

\(a=c\times\cos\left(\alpha\right)\)

где c — гипотенуза треугольника, a — его катет, а α —  угол между ними.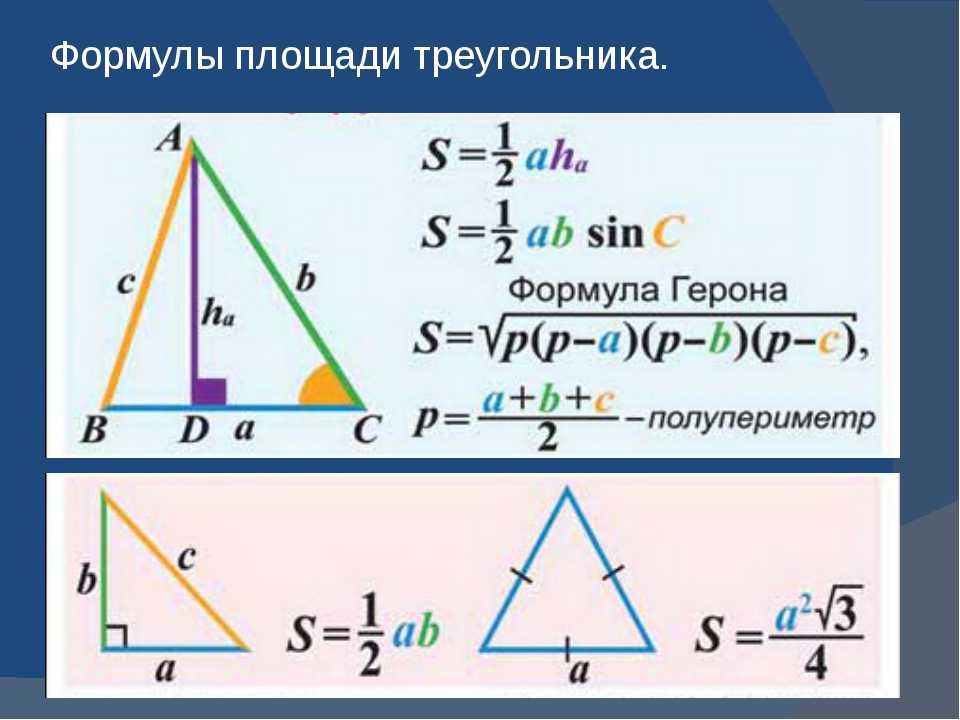 2\times\tan\left(\alpha\right)\)

Через радиус вписанной окружности и гипотенузу

Источник: mnogoformul.ru

Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:

\(S=r\times(r+c)\)

где r — радиус вписанной окружности, c — гипотенуза.

Через вписанную окружность

Источник: mnogoformul.ru

Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:

\(S=с_1\times с_2\)

где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.

По формуле Герона

Источник: mnogoformul.ru

Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:

\(S=(p-a)\times(p-b)\)

где \(p=\frac{a+b+c}2\) — полупериметр фигуры. 2\).

Как найти площадь треугольника, формула

Оглавление

Время чтения:  4 минуты

649

Понятие площади

Определение

Площадью (S) геометрической фигуры именуется численная величина, характеризующая её размер.

В этом собственно и состоит понятие площади. У неё есть следующие два свойства:

1. Площадь равных геометрических фигур имеет одно и то же числовое значение;
2. Величина площади фигуры равняется сумме единичных площадей квадратов, на которые её можно разделить.

Пример 1.

Пусть у нас имеется прямоугольник в котором укладывается 7 клеток по вертикали и 12 по горизонтали. Это значит он будет иметь стороны a=7 и b=12.

Из рисунка видно, что S нашего треугольника это половина таковой у прямоугольника.  Последняя вычисляется так \[\mathrm{S}_{\text {прям }}=\mathrm{a} * \mathrm{~b}\]. Чтобы узнать площадь треугольника, разделим \[\mathrm{S}_{\text {прям }}\] на 2, тогда получим:

Формула 1

\[S= (a*b)/2\].

Подставляем численные значения (7*12)/2 = 42.

Как найти площадь треугольника, если мы знаем его основание и высоту

Теорема

Площадь любого треугольника численно равняется половине произведения длины основания на высоту фигуры.

В нашем случае основанием считается сторона AB. Формула для S получается следующей:

Формула 2

\[S=(1/2)*AB*h   \].

Доказательство:

Посмотрите рисунок. Из него ясно видно, что высота h делит ABC на 2 прямоугольных треугольника ACH и HCB.

По формуле (1) вычисление S каждого из них идёт так.

S(ACH) = (1/2)(AH)*h

S(HCB)=(1/2)(HB)*h

Чтобы вычислить площадь треугольника abc, нужно S(ACH) и S(HCB) сложить.

S=(1/2)(AH)*h+ (1/2)(HB)*h

Выносим (1/2) и h за скобки и получаем

(1/2)*h*(AH+HB)

Но AH+HB=AB, т. е.

S = (1/2)*AB*h, что и требовалось доказать.

Как видите, формулу площади треугольника получить и доказать достаточно легко.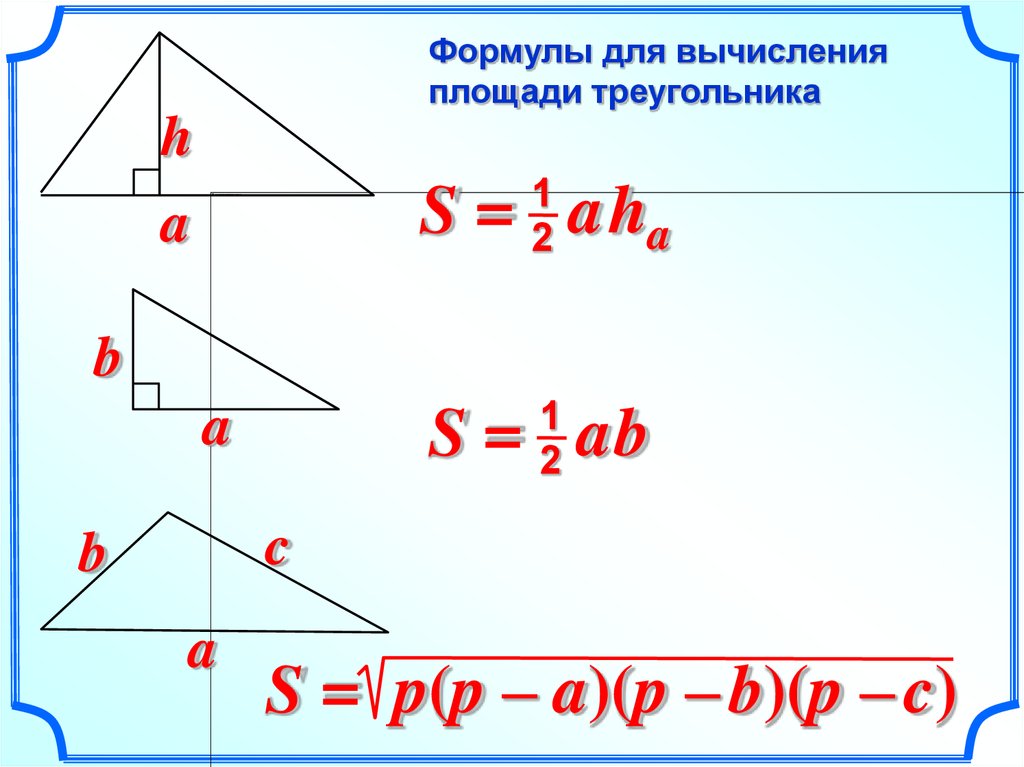 {2} \sqrt{3}}{4}\]

Что и требовалось доказать.

Оценить статью (0 оценок):

Поделиться

2.4: Площадь треугольника

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3257

• Майкл Коррал
• Колледж Скулкрафт

Из курса элементарной геометрии вы узнали, что площадь треугольника равна половине произведения основания на высоту. Теперь мы будем использовать это в сочетании с некоторой тригонометрией, чтобы вывести больше формул для площади при заданных частях треугольника.

Вариант 1: две стороны и прилежащий угол.

Предположим, что у нас есть треугольник \(\треугольник\,ABC\), в котором угол \(A\) может быть острым, прямым или тупым, как на рис.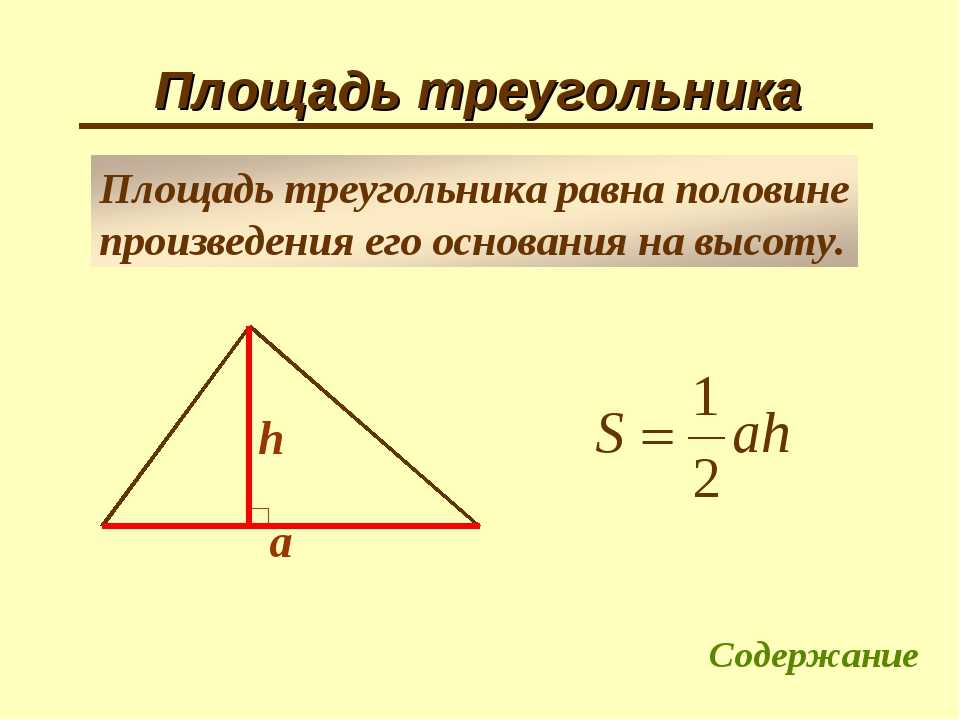 2.4.1. Предположим, что \(A\), \(b\) и \(c\) известны.

Рисунок 2.4.1 Площадь \(△ ABC\)

В каждом случае мы проводим высоту \(h \) из вершины \(C \) в \(\overline{AB} \), так что площадь (которую мы будем обозначать буквой \(K\)) определяется выражением \(K = \frac{1}{2}hc \). Но мы видим, что \(h = b\;\sin\;A \) в каждом из треугольников (поскольку \(\;h=b \) и \(\sin\;A = \sin\;9\circ — A) =b\;\sin\;A \) на рис. 2.4.1(c)). Таким образом, мы получаем следующую формулу:

\[\fbox{\(\text{Area} ~=~ K ~=~ \tfrac{1}{2}\,bc\;\sin\;A\)}\ label{2.23} \]

Приведенная выше формула для площади \(\треугольника\,ABC\) выражена в известных частях \(A\), \(b\) и \(c\). Аналогичные рассуждения для углов \(B \) и \(C \) дают нам:

\[ \begin{align}\text{Area} ~&=~ K =~ \tfrac{1}{2}\, ac\;\sin\;B \\
\text{Area} ~&=~ K =~ \tfrac{1}{2}\,ab\;\sin\;C\label{2.25} \end{align } \] 9\circ}\\
K ~&=~ 21.58
\end{align*} \]

Случай 3: Три стороны.

Предположим, что у нас есть треугольник \(\треугольник\,ABC \), в котором известны все три стороны. Тогда Формула Герона дает нам площадь:

Формула Герона

Для треугольника \(\треугольник\,ABC\) со сторонами \(a\), \(b\) и \(c\), пусть \(s = \frac{1}{2}\,(a+b+c) \) (т.е. \(2s = a+b+c \) — периметр треугольника). Тогда площадь \(K\) треугольника равна 92 ~=~ s\,(s-a)\,(s-b)\,(s-c) ~, \nonumber \]
поэтому при извлечении квадратных корней мы получаем
\[\nonumber K ~=~ \sqrt{s\,( s-a)\,(s-b)\,(s-c)} ~~.\quad \textbf{QED} \nonumber \]

Пример 2.15

Найдите площадь треугольника \(\triangle\,ABC \) по данному \ (а=5\), \(b=4\) и \(с = 7\).

Решение

Использование формулы Герона с \(s = \frac{1}{2}\,(a+b+c) = \frac{1}{2}\,(5+4+7) = 8 \), площадь \(K \) определяется как:
\[ \begin{align*}
K ~&=~ \sqrt{s\,(s-a)\,(s-b)\,(s-c) }\\
&=~ \sqrt{8\,(8-5)\,(8-4)\,(8-7)} ~=~ \sqrt{96} \quad\Стрелка вправо\quad \boxed{K ~= ~ 4\,\sqrt{6}
~\приблизительно 9.8} ~.
\end{align*} \]

Формула Герона полезна в теоретических целях (например, при выводе других формул). Однако он не подходит для использования в калькуляторе, демонстрируя так называемую численную нестабильность для «экстремальных» треугольников, как в следующем примере.

Пример 2.16

Найдите площадь треугольника ,ABC \) задано \(a=1000000\), \(b=999999,9999979 \) и \(c = 0,0000029 \).

Решение:

Чтобы использовать формулу Герона, нам нужно вычислить \(s = \frac{1}{2}\,(a+b+c) \). Обратите внимание, что фактическое значение \(a+b+c \) равно \(2000000,0000008 \), что имеет \(14 \) цифр. Большинство калькуляторов могут хранить \(12\)-\(14\) цифр внутри (даже если они отображают меньше), и, следовательно, могут округлять это значение \(a+b+c\) до \(2000000\). Когда мы затем разделим это округленное значение для \(a+b+c\) на \(2\), чтобы получить \(s\), некоторые калькуляторы (например, TI-83 Plus) дадут округленное вниз значение \( 1000000 \).

Это проблема, потому что \(a=1000000 \), поэтому мы получим \(s-a=0 \), в результате чего формула Герона даст нам площадь треугольника \(0 \)! И это действительно неправильный ответ, который возвращает TI-83 Plus. Другие калькуляторы могут дать другой неточный ответ, в зависимости от того, как они хранят значения внутри. Фактическая площадь — с точностью до \(15\) знаков после запятой — равна \(K = 0,99999999999895 \), то есть в основном равна \(1 \).

Приведенный выше пример показывает, как проблематичная арифметика с плавающей запятой может быть. К счастью, есть лучшая формула для площади треугольника, когда известны три стороны:

Для треугольника \(\треугольник\,ABC\) со сторонами \(a \ge b \ge c \) площадь равна :

\[ \text{Площадь} ~=~ K ~=~ \tfrac{1}{4}\,\sqrt{(a + (b+c))\,(c — (a-b))\,(c + (a-b))\,(a + (b-c))}\label{2.33} \]

Чтобы использовать эту формулу, отсортируйте названия сторон так, чтобы \(a \ge b \ge c \). Затем выполните операции внутри квадратного корня в точном порядке, в котором они появляются в формуле, включая использование круглых скобок . Затем извлеките квадратный корень и разделите на \(4\). Для треугольника в примере 2. 16 приведенная выше формула дает точное значение \(K = 1 \) на том же калькуляторе TI-83 Plus, который не смог использовать формулу Герона. Что удивительно в этой формуле, так это то, что это просто переписанная формула Герона! Использование круглых скобок — это то, что заставляет соблюдать правильный порядок операций для числовой стабильности.

Другая формула для площади треугольника с учетом его трех сторон приведена ниже:

Для треугольника \(\triangle\,ABC \) со сторонами \(a \ge b \ge c \) площадь равна: 92} \]

---

Эта страница под названием 2.4: Площадь треугольника распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Майкл Коррал

   Лицензия

   ГНУ ФДЛ

   Версия лицензии

   1,3

   Показать страницу TOC

   нет

2. Теги

   1. Формула Герона
   2. источник@http://www. mecmath.net/trig/index.html

Визуализация подсказок с числами по формуле площади треугольника

С помощью этого набора подсказок с числами по площади треугольника вы сможете лучше понять отношения площадей между треугольниками и прямоугольниками.

В этом наборе визуальных числовых подсказок…

Учащиеся выведут формулу площади треугольника, взяв половину площади прямоугольника.

Целеустремленность…

Эта наглядная математическая беседа и целенаправленная практика служат для более глубокого понимания следующих больших идей.

• Площадь прямоугольника можно определить, умножив длину его основания на длину его высоты;
• Площадь прямоугольника используется для определения формул площади других многоугольников;
• Использование «основания» и «высоты», а не «длины» и «ширины», может помочь учащимся понять формулу площади для треугольников и всех четырехугольников;
• Параллелограмм — это любой четырехугольник с двумя наборами параллельных сторон;
• Прямоугольник — это параллелограмм;
• Отношения между прямоугольниками, параллелограммами и треугольниками можно использовать для определения формул площади;
• Любой треугольник можно удвоить, чтобы получился параллелограмм;
• Конгруэнтные фигуры имеют одинаковый размер и форму, но не обязательно одинаковую ориентацию.

 

Подсказка с визуальным числом

Начните воспроизводить видео-подсказку с визуальным числом, а затем будьте готовы задать учащимся следующие вопросы:

Вычислите площадь каждого треугольника в квадратных метрах.

Создайте убедительный аргумент без использования калькулятора.

Как вы могли сразу заметить, мы дали учащимся два конгруэнтных треугольника и расположили их так, чтобы вместе они образовывали прямоугольник. Это делается для того, чтобы все учащиеся ясно видели, что каждый прямоугольник можно разделить по диагонали на два равных треугольника. Из этой визуальной математической подсказки мы надеемся повторить, что разделение любого прямоугольника по диагонали на два конгруэнтных треугольника приведет к тому, что каждый треугольник будет иметь половину площади прямоугольника.

Поэтому некоторым учащимся может показаться интуитивно понятным сначала найти площадь прямоугольника и просто половину этой величины, чтобы определить площадь каждого из получившихся треугольников.

Хотя некоторые учащиеся могут выполнить операцию по взятию половины площади прямоугольника (или делению площади на 2), вполне вероятно, что многие не будут естественно записывать свои мысли символически, как вы видите справа от экран. Цель здесь не обязательно состоит в том, чтобы все учащиеся «переписали» формулу, а скорее в том, чтобы они могли установить связь между интуитивными действиями, которые они выполнили, чтобы найти площадь треугольников, с символическим представлением того же мышления.

Важно четко подчеркнуть, что два треугольника, которые были созданы путем разделения прямоугольника по диагонали, приводят к конгруэнтным треугольникам, поскольку это может быть не очевидно для всех учащихся сразу.

Также было бы полезно показать учащимся, что, несмотря на то, что, взяв половину площади прямоугольника (или разделив площадь на 2), мы получим площадь каждого конгруэнтного треугольника, ту же операцию можно выполнить для определения площади другого треугольника.