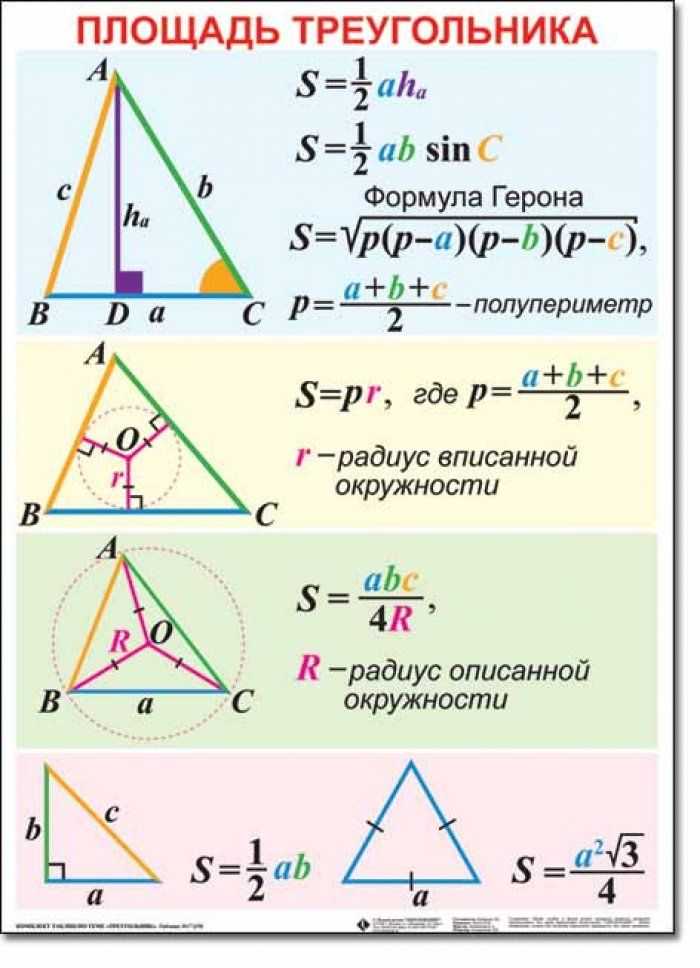
Как найти площадь зная катеты. Как найти площадь прямоугольного треугольника необычным способом. Самая простая формула определения площади прямоугольного треугольника
Прямоугольным треугольником называется треугольник, у которого один из углов равняется 90°. Его площадь можно найти, если известны два катета. Можно, конечно, пойти и длинным путем – найти гипотенузу и просчитать площадь по , но в большинстве случаев это только займет лишнее время. Именно поэтому формула площади прямоугольного треугольника выглядит так:
Площадь прямоугольного треугольника равняется половине произведения катетов.
Пример расчета площади прямоугольного треугольника.
Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см.
Вычисляем площадь:
Площадь равна: 24 см 2
Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
Формула площади равнобедренного прямоугольного треугольника вычисляется также как и обычного прямоугольного треугольника.
Пример расчета площади равнобедренного прямоугольного треугольника:
Вычисляем площадь:=8 см 2
Формула площади прямоугольного треугольника по гипотенузе может использоваться, если в условии дан один катет. Из теоремы Пифагора находим длину неизвестного катета. К примеру, дана гипотенуза c и катет a , катет b будет равен:
Далее вычисляем площадь по обычной формуле. Пример расчета формулы площади прямоугольного треугольника по гипотенузе идентичен описанному выше.
Рассмотрим интересную задачу, которая поможет закрепить знания формул для решения треугольника.
Задача : площадь прямоугольного треугольника равняется 180 кв. см. найдите меньший катет треугольника, если он меньше второго на 31 см.
Решение : обозначим катеты a и b . Теперь подставим данные в формулу площади:, еще мы знаем, что один катет меньше другого a – b = 31 см
Из первого условия получаем, что
Так как мы находили стороны, то знак минус убираем.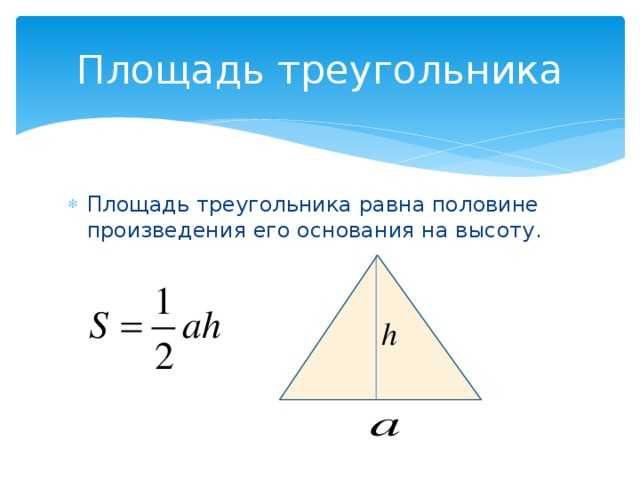
Получается, что катет a = 40 см, а b = 9 см.
На уроках геометрии в средней школе всем нам говорили о том, треугольника. Однако в рамках школьной программы мы получаем только самые необходимые знания и учимся наиболее распространенным и стандартным способам вычислений. Существуют ли необычные способы нахождения этой величины?
В качестве введения вспомним, какой треугольник считается прямоугольным, а также обозначим понятие площади.
Прямоугольным треугольником называют замкнутую геометрическую фигуру, один из углов которой равен 90 0 . Неотъемлемыми понятиями в определении являются катеты и гипотенуза. Под катетами подразумевают две стороны, которые в точке соединения образуют прямой угол. Гипотенуза — сторона, противоположная прямому углу. Прямой треугольник может быть равнобедренным (две его стороны будут иметь одинаковую величину), но никогда не будет равносторонним (все стороны одной длины). Определения высоты, медианы, векторов и прочих математических терминов подробно разбирать не будем.
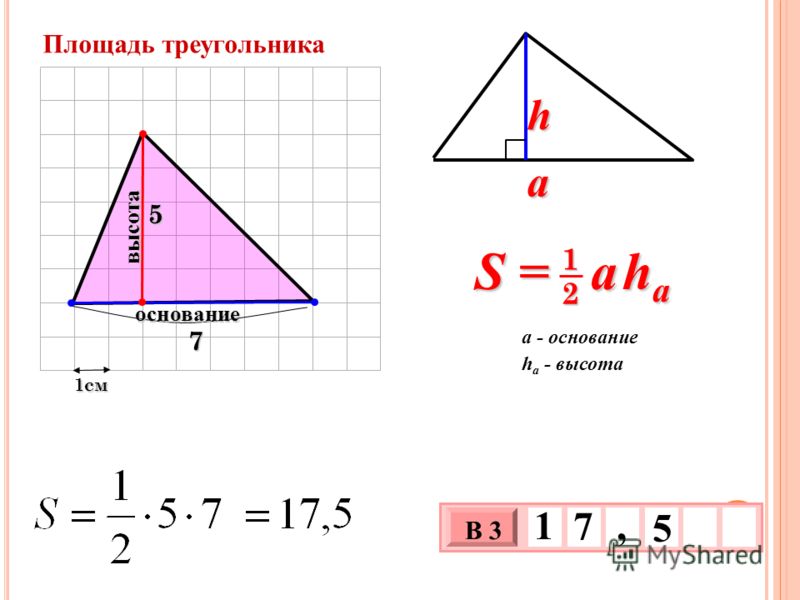
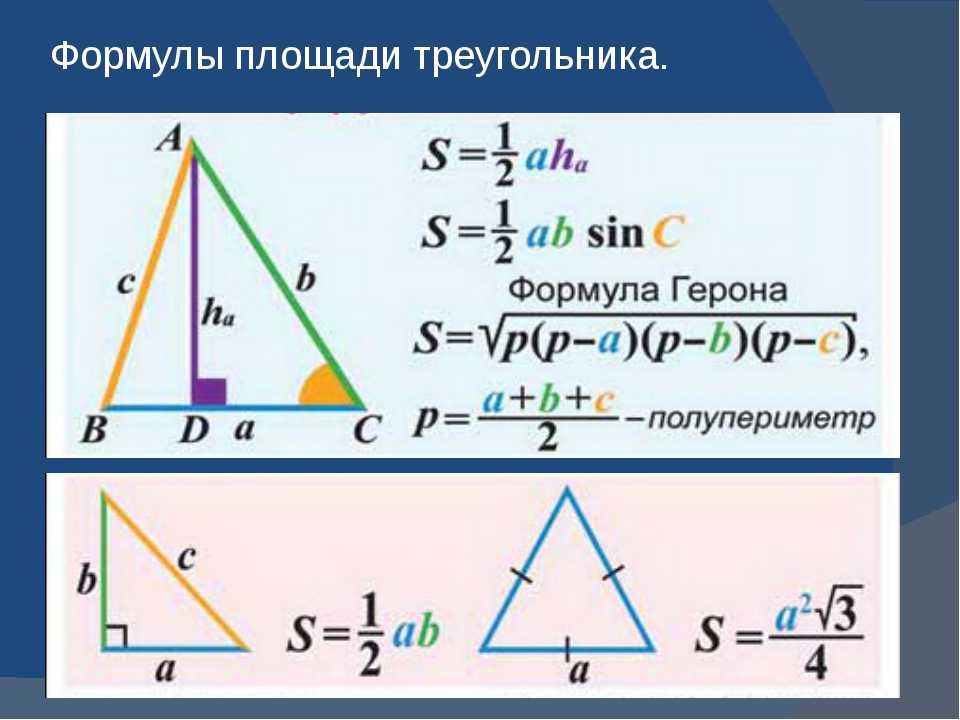
Площадь прямого треугольника. В отличие от прямоугольников, правило о
произведении сторон в определении не действует. Если говорить сухим языком терминов, то под площадью треугольника понимают свойство этой фигуры занимать часть плоскости, выраженное числом. Довольно сложно к восприятию, согласитесь. Не будем пытаться глубоко вникнуть в определение, наша цель не в этом. Перейдем к главному — как найти площадь прямоугольного треугольника? Сами вычисления производить не будем, укажем только формулы. Для этого определимся с обозначениями: A,B,C — стороны треугольника, катеты — AB, BC. Угол ACB — прямой. S — площадь треугольника, h n n — высота треугольника, где nn — сторона, на которую она опущена.
Способ 1. Как найти площадь прямоугольного треугольника, если известна величина его катетов
Способ 2. Находим площадь равнобедренного прямоугольного треугольника
Способ 3. Вычисление площади через прямоугольник
Достраиваем прямоугольный треугольник до квадрата (если треугольник
равнобедренный) или прямоугольника. Получим простой четырехугольник, составленный из 2-х идентичных прямоугольных треугольников. В этом случае значение площади одного из них будет равно половине площади полученной фигуры. S прямоугольника вычисляем произведением сторон. Обозначим эту величину M. Искомое значение площади будет равно половине M.
Получим простой четырехугольник, составленный из 2-х идентичных прямоугольных треугольников. В этом случае значение площади одного из них будет равно половине площади полученной фигуры. S прямоугольника вычисляем произведением сторон. Обозначим эту величину M. Искомое значение площади будет равно половине M.
Способ 4. «Пифагоровы штаны». Знаменитая теорема Пифагора
Мы все помним ее формулировку: «сумма квадратов катетов…». Но не все могут
сказать, причем тут некие «штаны». Дело в том, что изначально Пифагор изучал взаимосвязь построенных на сторонах прямого треугольника. Выявив закономерности в соотношении сторон квадратов, он смог вывести и известную всем нам формулу. Ее можно применять в случае, когда неизвестна величина одной из сторон.
Способ 5. Как найти площадь прямоугольного треугольника по формуле Герона
Тоже достаточно простой способ расчета. Формула предполагает выражение площади треугольника через числовые значения его сторон. Для расчетов необходимо знать величины всех сторон треугольника.
Для расчетов необходимо знать величины всех сторон треугольника.
S = (p-AC)*(p-BC), где p = (AB+BC+AC)*0.5
Кроме приведенных, существует множество других способов найти величину такой загадочной фигуры, как треугольник. Среди них: вычисление методом вписанной или описанной окружности, вычисление при помощи координат вершин, использование векторов, абсолютной величины, синусов, тангенсов.
Треугольник – плоская геометрическая фигура с одним углом равным 90 °. При этом в геометрии очень часто требуется вычислить площадь такой фигуры. Как это сделать, мы расскажем далее.
Самая простая формула определения площади прямоугольного треугольника
Исходные данные, где: a и b – стороны треугольника, выходящие из прямого угла.
То есть, площадь равна половине произведения двух сторон, которые выходят из прямого угла. Конечно, существует формула Герона, используемая для вычисления площади обычного треугольника, но для определения величины необходимо знать длину трех сторон.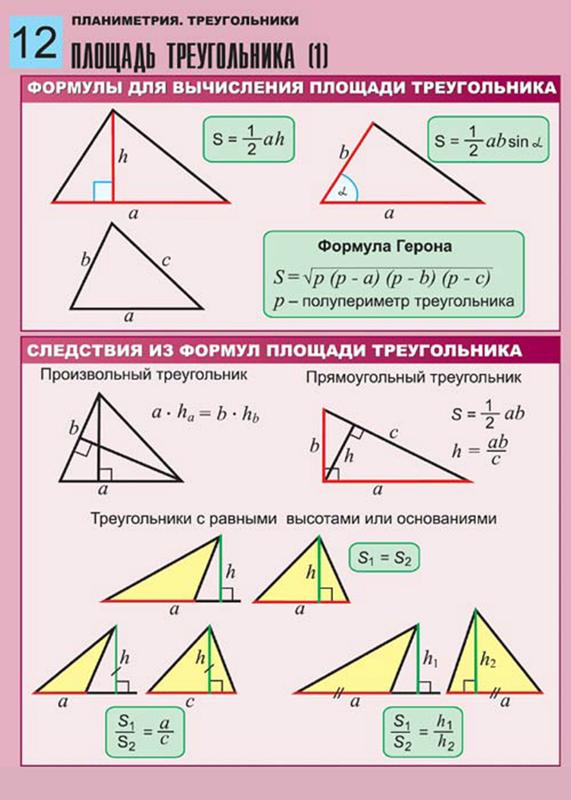 Соответственно, вам придется рассчитать гипотенузу, а это лишнее время.
Соответственно, вам придется рассчитать гипотенузу, а это лишнее время.
Найти площадь прямоугольного треугольника через формулу Герона
Это всем известная и исходная формула, но для этого вам придется посчитать гипотенузу по двум катетам, используя Теорему Пифагора.
В этой формуле: a, b, c – стороны треугольника, а p – полупериметр.
Найти площадь прямоугольного треугольника по гипотенузе и углу
Если в вашей задаче не известен ни один из катетов, то воспользоваться самым простым способом вы не сможете. Для определения величины вам нужно рассчитать длину катетов. Это сделать просто по гипотенузе и косинусу прилежащего угла.
b=c×cos(α)
Узнав длину одного из катетов, по теореме Пифагора вы сможете рассчитать вторую сторону, выходящую из прямого угла.
b 2 =c 2 -a 2
В этой формуле c и a – гипотенуза и катет соответственно. Теперь можете рассчитать площадь по первой формуле. Точно так же можно вычислить один из катетов, имея второй и угол. В таком случае одна из искомых сторон будет равна произведению катета на тангенс угла. Существуют и другие способы вычисления площади, но зная основные теоремы и правила, вы сможете легко найти искомую величину.
В таком случае одна из искомых сторон будет равна произведению катета на тангенс угла. Существуют и другие способы вычисления площади, но зная основные теоремы и правила, вы сможете легко найти искомую величину.
Если у вас нет ни одной из сторон треугольника, а имеется лишь медиана и один из углов, то вы сможете вычислить длину сторон. Для этого используйте свойства медианы делить прямоугольный треугольник на два. Соответственно, она может выступать гипотенузой, если выходит из острого угла. Воспользуйтесь теоремой Пифагора и определите длину сторон треугольника, выходящих из прямого угла.
Как видите, зная основные формулы и Теорему Пифагора, вы сможете рассчитать площадь прямоугольного треугольника, имея лишь один из углов и длину одной из сторон.
Площадь треугольника с прямым углом. Как находить площадь треугольника (формулы)
Площадь треугольника с прямым углом. Как находить площадь треугольника (формулы)
В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90°).
Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства.
Нахождение площади прямоугольного треугольника
a — катет
b — катет
S — площадь прямоугольного треугольника
Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель. Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники .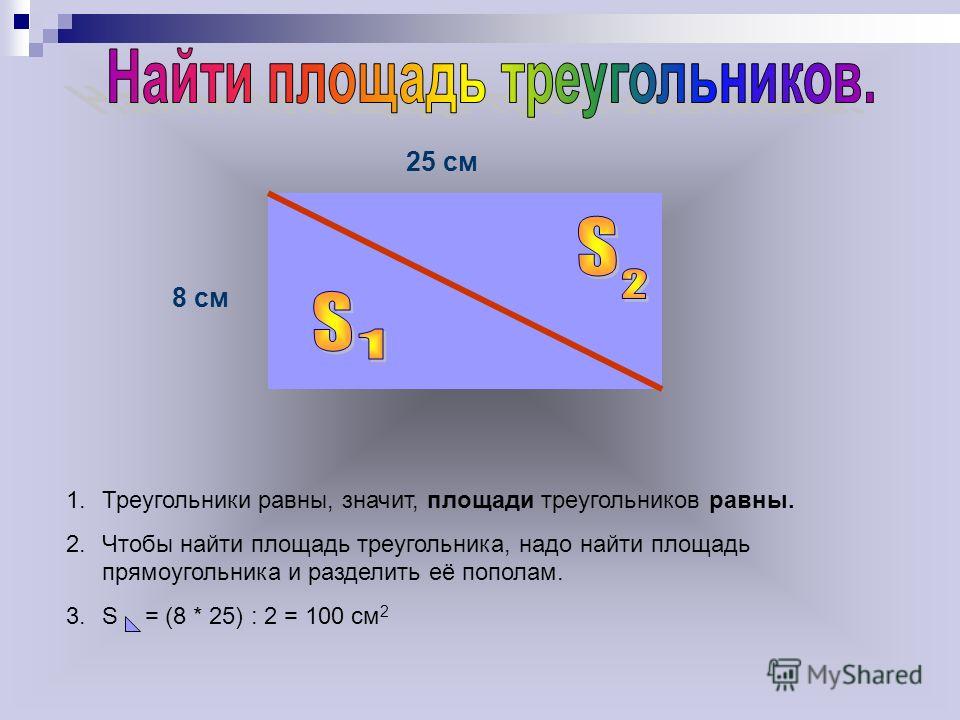
Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины. Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.
Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.
На уроках геометрии в средней школе всем нам говорили о том, треугольника. Однако в рамках школьной программы мы получаем только самые необходимые знания и учимся наиболее распространенным и стандартным способам вычислений. Существуют ли необычные способы нахождения этой величины?
В качестве введения вспомним, какой треугольник считается прямоугольным, а также обозначим понятие площади.
Прямоугольным треугольником называют замкнутую геометрическую фигуру, один из углов которой равен 90 0 . Неотъемлемыми понятиями в определении являются катеты и гипотенуза. Под катетами подразумевают две стороны, которые в точке соединения образуют прямой угол. Гипотенуза — сторона, противоположная прямому углу. Прямой треугольник может быть равнобедренным (две его стороны будут иметь одинаковую величину), но никогда не будет равносторонним (все стороны одной длины). Определения высоты, медианы, векторов и прочих математических терминов подробно разбирать не будем. Их легко найти в справочниках.
Площадь прямого треугольника. В отличие от прямоугольников, правило о
произведении сторон в определении не действует. Если говорить сухим языком терминов, то под площадью треугольника понимают свойство этой фигуры занимать часть плоскости, выраженное числом. Довольно сложно к восприятию, согласитесь. Не будем пытаться глубоко вникнуть в определение, наша цель не в этом.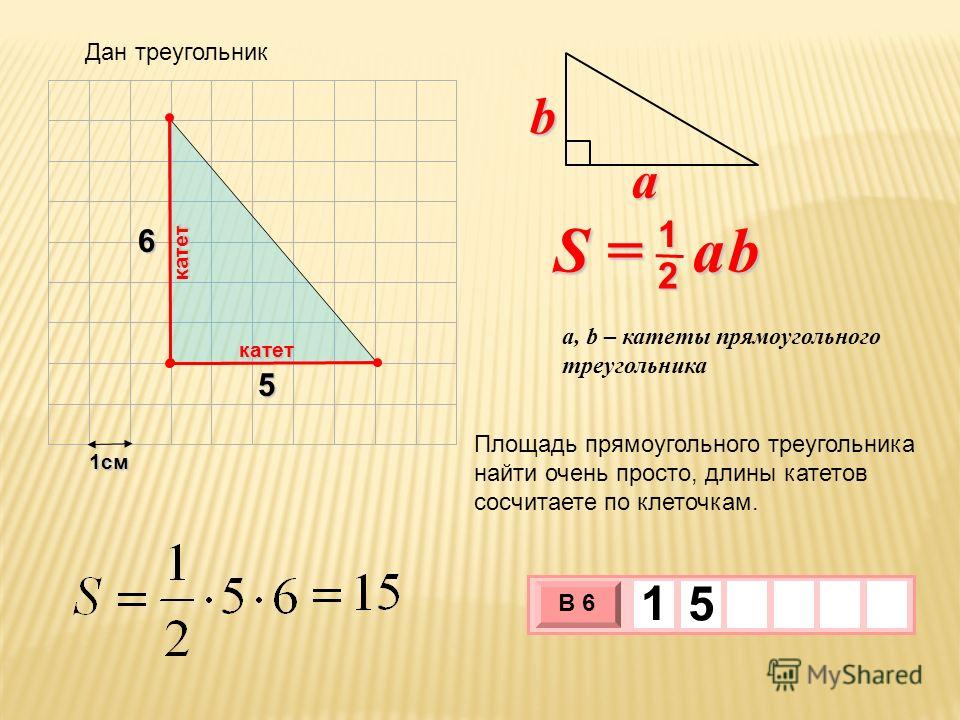 Перейдем к главному — как найти площадь прямоугольного треугольника? Сами вычисления производить не будем, укажем только формулы. Для этого определимся с обозначениями: A,B,C — стороны треугольника, катеты — AB, BC. Угол ACB — прямой. S — площадь треугольника, h n n — высота треугольника, где nn — сторона, на которую она опущена.
Перейдем к главному — как найти площадь прямоугольного треугольника? Сами вычисления производить не будем, укажем только формулы. Для этого определимся с обозначениями: A,B,C — стороны треугольника, катеты — AB, BC. Угол ACB — прямой. S — площадь треугольника, h n n — высота треугольника, где nn — сторона, на которую она опущена.
Способ 1. Как найти площадь прямоугольного треугольника, если известна величина его катетов
Способ 2. Находим площадь равнобедренного прямоугольного треугольника
Способ 3. Вычисление площади через прямоугольник
Достраиваем прямоугольный треугольник до квадрата (если треугольник
равнобедренный) или прямоугольника. Получим простой четырехугольник, составленный из 2-х идентичных прямоугольных треугольников. В этом случае значение площади одного из них будет равно половине площади полученной фигуры. S прямоугольника вычисляем произведением сторон. Обозначим эту величину M. Искомое значение площади будет равно половине M.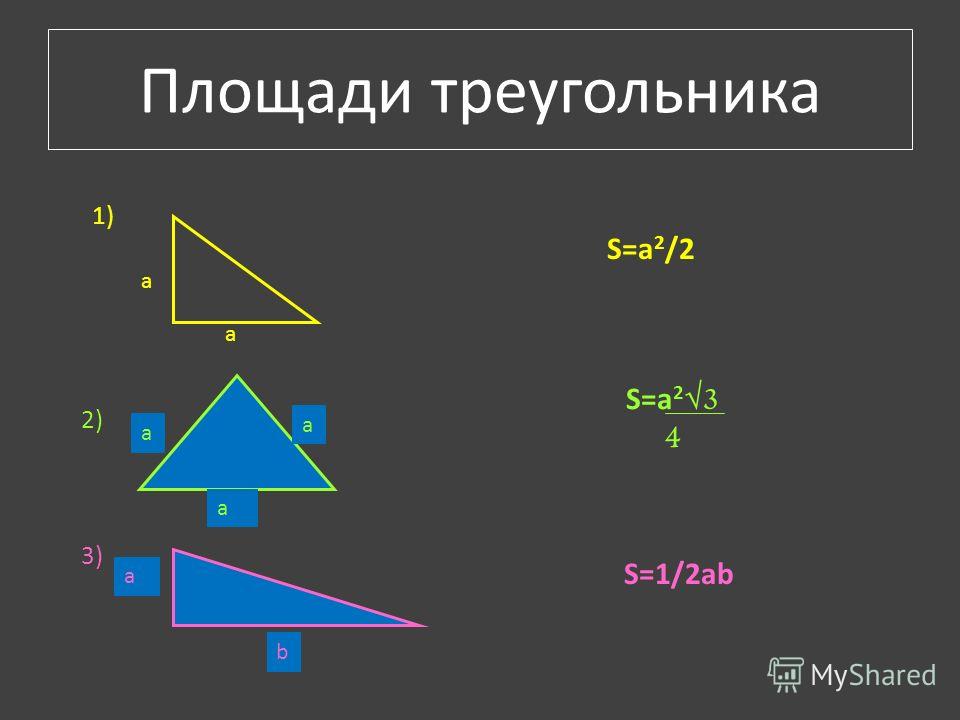
Способ 4. «Пифагоровы штаны». Знаменитая теорема Пифагора
Мы все помним ее формулировку: «сумма квадратов катетов…». Но не все могут
сказать, причем тут некие «штаны». Дело в том, что изначально Пифагор изучал взаимосвязь построенных на сторонах прямого треугольника. Выявив закономерности в соотношении сторон квадратов, он смог вывести и известную всем нам формулу. Ее можно применять в случае, когда неизвестна величина одной из сторон.
Способ 5. Как найти площадь прямоугольного треугольника по формуле Герона
Тоже достаточно простой способ расчета. Формула предполагает выражение площади треугольника через числовые значения его сторон. Для расчетов необходимо знать величины всех сторон треугольника.
S = (p-AC)*(p-BC), где p = (AB+BC+AC)*0.5
Кроме приведенных, существует множество других способов найти величину такой загадочной фигуры, как треугольник. Среди них: вычисление методом вписанной или описанной окружности, вычисление при помощи координат вершин, использование векторов, абсолютной величины, синусов, тангенсов.
Прямоугольным треугольником называется треугольник, у которого один из углов равняется 90°. Его площадь можно найти, если известны два катета. Можно, конечно, пойти и длинным путем – найти гипотенузу и просчитать площадь по , но в большинстве случаев это только займет лишнее время. Именно поэтому формула площади прямоугольного треугольника выглядит так:
Площадь прямоугольного треугольника равняется половине произведения катетов.
Пример расчета площади прямоугольного треугольника.
Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см.
Вычисляем площадь:
Площадь равна: 24 см 2
Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
Формула площади равнобедренного прямоугольного треугольника вычисляется также как и обычного прямоугольного треугольника.
Пример расчета площади равнобедренного прямоугольного треугольника:
Дан треугольник с катетами a = 4 см, b = 4 см.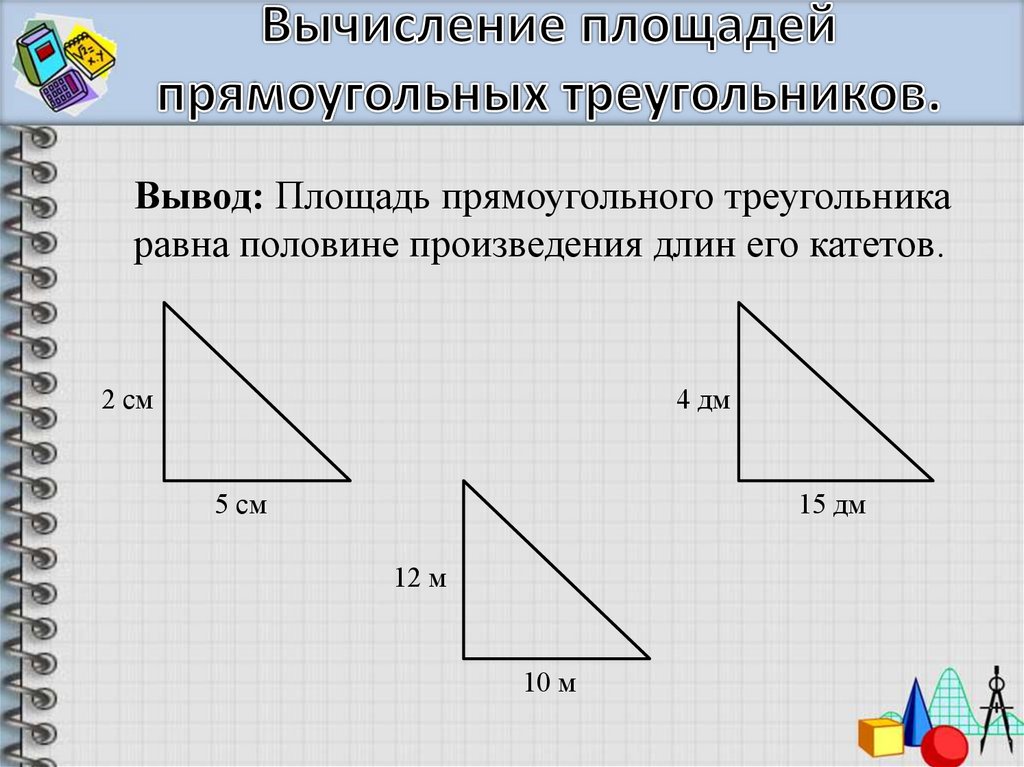 Вычисляем площадь:
Вычисляем площадь:
Вычисляем площадь:=8 см 2
Формула площади прямоугольного треугольника по гипотенузе может использоваться, если в условии дан один катет. Из теоремы Пифагора находим длину неизвестного катета. К примеру, дана гипотенуза c и катет a , катет b будет равен:
Далее вычисляем площадь по обычной формуле. Пример расчета формулы площади прямоугольного треугольника по гипотенузе идентичен описанному выше.
Рассмотрим интересную задачу, которая поможет закрепить знания формул для решения треугольника.
Задача : площадь прямоугольного треугольника равняется 180 кв. см. найдите меньший катет треугольника, если он меньше второго на 31 см.
Решение : обозначим катеты a и b . Теперь подставим данные в формулу площади:, еще мы знаем, что один катет меньше другого a – b = 31 см
Из первого условия получаем, что
Подставляем данное условие во второе уравнение:
Так как мы находили стороны, то знак минус убираем.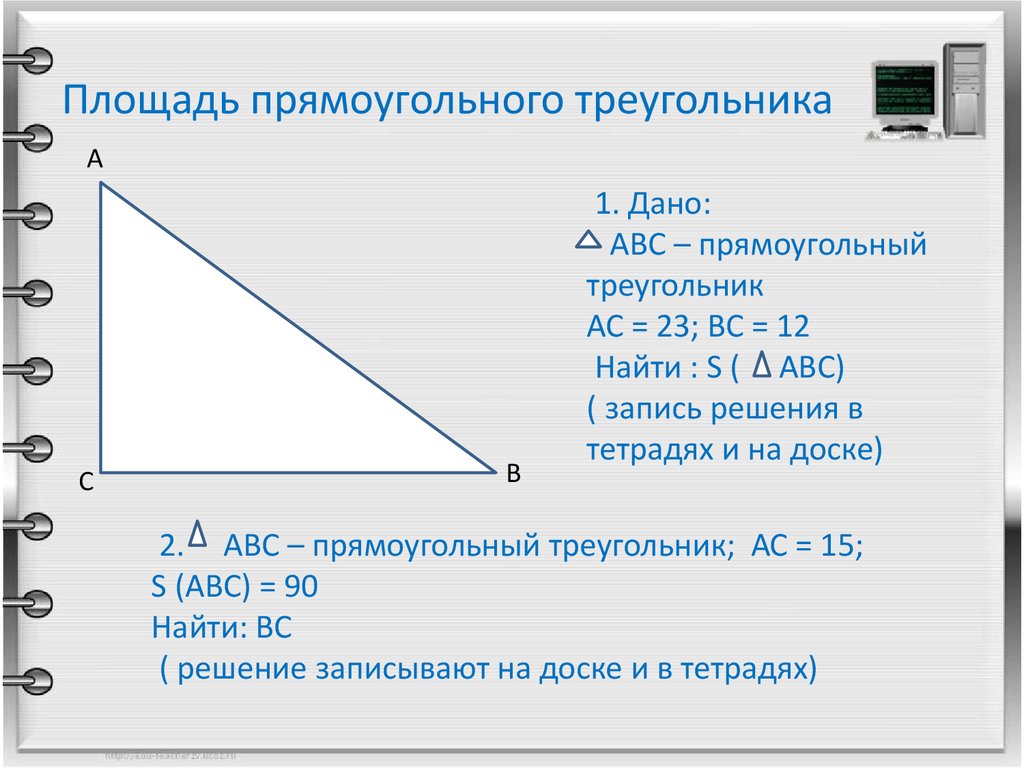 2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.
Как находить площадь равнобедренного треугольника
Площадь равнобедренного треугольника можно очень легко и быстро найти по формуле S= b*h / 2, но, при отсутствии одного из показателей, задача значительно усложняется. Ведь необходимо выполнять дополнительные действия.
Возможные варианты задач:
- Дано: длина одной из боковых сторон и длина основания. Находим через теорему Пифагора высоту, то есть длину второго катеты. При условии, что длина основания, разделенная на два, является катетом, а изначально известная боковая сторона – гипотенузой.

- Дано: основание и угол между боковой стороной и основанием. Вычисляем по формуле h=c*ctg(B)/2 высоту (не забываем сторону «c» разделить на два).
- Дано: высота и угол, который был образован основанием и боковой стороной: применяем формулу c=h*tg(B)*2 для нахождения высоты, и полученный результат умножаем на два. Далее вычисляем площадь.
- Известна: длина боковой стороны и угол, который образовался между ним и высотой. Решение: используем формулы — c=a*sin(C)*2 и h=a*cos(C) для нахождения основания и высоты, после чего считаем площадь.
Как найти площадь равнобедренного прямоугольного треугольника
Если все данные известны, то по стандартной формуле S= a* a / 2 вычисляем площадь равнобедренного прямоугольного треугольника, если же в задаче не указаны некоторые показатели, то выполняются дополнительные действия.
Например: нам не известны длины обеих сторон (мы помним, что в равнобедренном прямоугольном треугольнике они равны), но дана длинна гипотенузы. 2, где R — радиус окружности.
2, где R — радиус окружности.
Прямоугольный треугольник — формула, определение, свойства, факты
Треугольник, в котором один из внутренних углов равен 90°, называется прямоугольным треугольником. Самая длинная сторона прямоугольного треугольника, которая также является стороной, противоположной прямому углу, — это гипотенуза, а две стороны прямого угла — это высота и основание. Вот как выглядит прямоугольный треугольник:
Общая площадь или территория, покрываемая прямоугольным треугольником, известна как площадь прямоугольного треугольника. Он рассчитывается в квадратных единицах. Единицы м 2 , cm 2 , in 2 , yd 2 и другие обычно представляют площадь.
Особенности прямоугольного треугольника
- Прямой угол всегда является наибольшим углом в прямоугольном треугольнике.
- Гипотенуза, сторона, противоположная прямому углу, является самой длинной стороной.
- В прямоугольном треугольнике не может быть тупых углов.

Типы прямоугольных треугольников
В широком смысле прямоугольные треугольники можно разделить на следующие категории:
1. Равнобедренный прямоугольный треугольник : В этом треугольнике один внутренний угол равен 90°, а два других угла равны 45° каждый. Он также известен как треугольник 45-90-45.
Это равнобедренный прямоугольный треугольник, стороны которого AB и AC равны, а ∠ B составляет 90°. Здесь ∠ A и ∠ C имеют по 45° каждый, потому что свойство гласит, что углы, противоположные равным сторонам, также равны.
2. Разносторонний прямоугольный треугольник : В этом треугольнике один внутренний угол равен 90°, а два других имеют разную величину. Например:
В прямоугольном треугольнике ABC ∠ A составляет 30°, ∠ B составляет 90°, а ∠ C составляет 60°. В этом треугольнике все три стороны будут разной длины и три угла будут разной величины.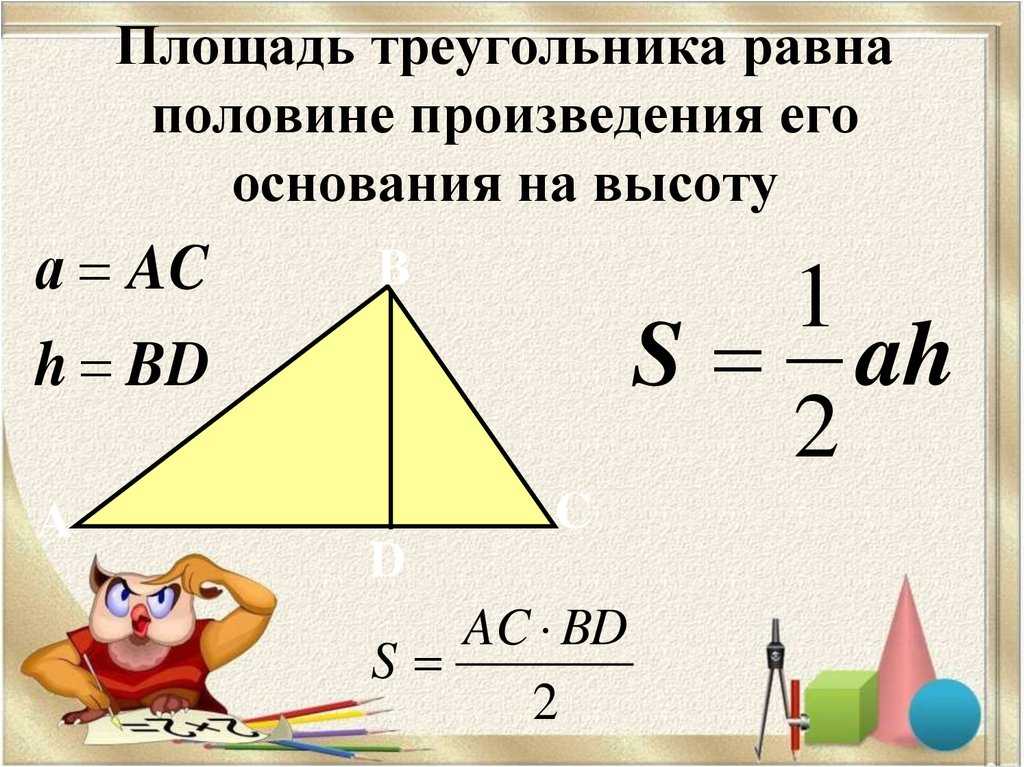
Формула прямоугольного треугольника
Теорема Пифагора
- Пифагор обнаружил, что квадрат гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника.
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника определяется как общая длина границы. Формула для периметра:
P (периметр) = a + b + c (сумма сторон треугольника)
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника определяется как пространство, занимаемое треугольником. Формула площади:
Площадь = $\frac{1}{2}\times base\time height$
Решенные примеры
- Самая большая сторона треугольника равна 10 см. Если высота треугольника 8 см, определите площадь по теореме Пифагора.
Решение:
Гипотенуза — самая длинная сторона прямоугольного треугольника.
Здесь гипотенуза ( H ) = 10 см, высота ( h ) = 8 см и основание ( b ) неизвестно.
Согласно теореме Pythagoras,
H 2 = B 2 + H 2
2 = B 2 + 2 = B 2 + 9 9 2 69 = 3 B 2 + 2 . 100 = b 2 + 64
b 2 = 36 см 2
b = = $\sqrt{6}0003
Площадь = $\frac{1}{2}\times base\times height$
= $\frac{1}{2}\times 6\times 8 = 24$
Следовательно, площадь треугольника = 24 квадратных см.
- Соотношение сторон треугольника 3:4:5. Периметр 840 м. Найдите его площадь.
Решение :
Пусть стороны треугольника равны 3 x , 4 x и 5 x соответственно.
Мы знаем, что периметр = 840 м.
3 x + 4 x + 5 x = 840
12 x = 840
x = $ \ FRAC {840} {12} $ = 70
SO SIDE треугольника:
3 х = 3(70) = 210 м
4 х = 4(70) = 280 м
5 х = 5(70) 9003 м 350 м — самая длинная сторона треугольника, это гипотенуза.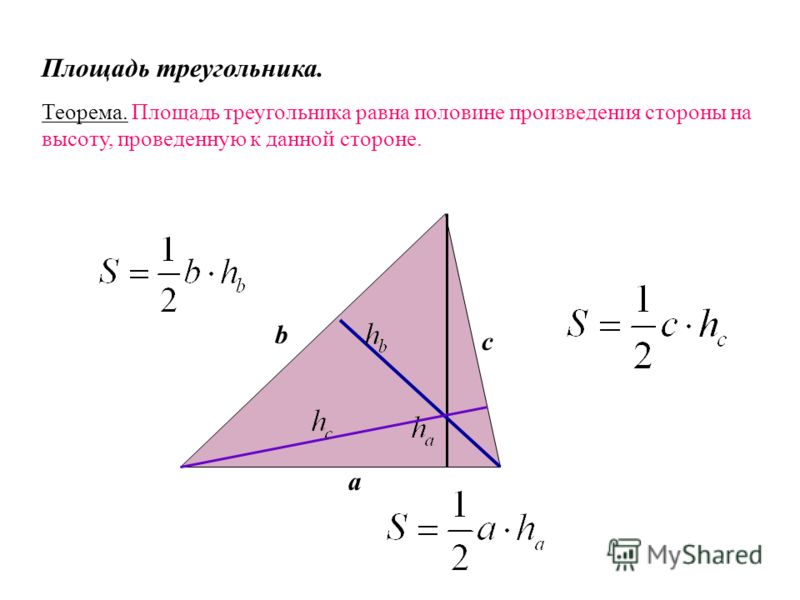
Итак, 210 м и 280 м — это основание и высота треугольника взаимозаменяемо.
Используя формулу площади прямоугольного треугольника, получаем
Площадь = $\frac{1}{2}\times base\times height = \frac{1}{2}\times 210\times 280 = 29,400$
Следовательно, площадь данного треугольника = 29,400 м 2
- Какова мера гипотенузы в прямоугольном треугольнике, высота которого равна 7 см, а основание равно 5 см?
Решение:
Перпендикулярная высота ( h ) = 7 см, основание ( b ) = 5 см и Гипотенуза ( H ) = ?
By Pythagoras Theorem,
H 2 = b 2 + p 2
H 2 = 5 2 + 7 2
H 2 = 25 + 49
H 2 = 74
H = $ \ SQRT {74} $ CM
Практические задачи
1
в правой Angle Triang и b = 32, а периметр треугольника равен 58 см.
 Найдите с, третью сторону треугольника.
Найдите с, третью сторону треугольника.44 см
50 см
12 см
14 см
Правильный ответ: 14 см
58 = 12 + 32 + c, c = 14 см = 23 см, ВС = 14 см, СА = 13 см. Чему равен периметр треугольника?
234 см
33 см
50 см
40 см
Правильный ответ: 50 см
Периметр = (23 + 14 + 13) см = 50 см Высота прямоугольного треугольника с гипотенузой 13 см и основанием 5 см? 92} = \sqrt{16 + 9} = \sqrt{25}$ = 5 см
Часто задаваемые вопросы
Может ли прямоугольный треугольник иметь две равные стороны?
Прямоугольный треугольник также может быть равнобедренным, что означает, что у него две стороны и два угла равны. Прямоугольный равнобедренный треугольник имеет угол 90° и два угла по 45°.
Могут ли 8 см, 15 см и 17 см составлять три стороны прямоугольного треугольника?
Мы можем проверить, образуют ли 8 см, 15 см и 17 см три стороны прямоугольного треугольника, используя теорему Пифагора.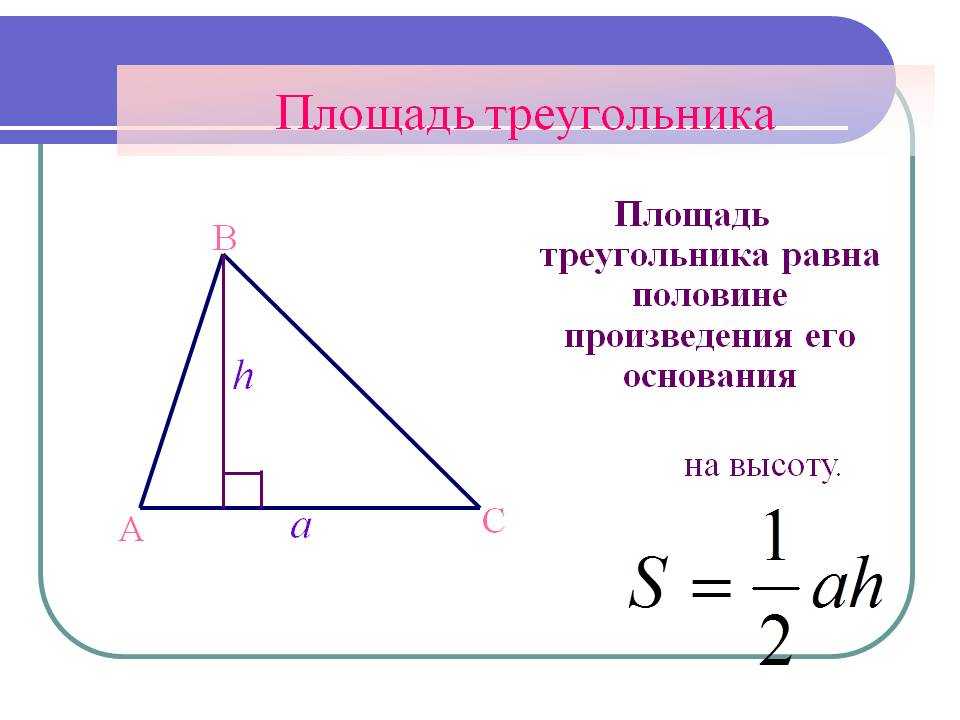
H (Hypotenuse) 2 = P (Perpendicular height) 2 + B (Base) 2
172 = 152+82
289 = 225 + 64
289 = 289
Отсюда проверено, что 8 см, 15 см и 17 см могут составить три стороны прямоугольного треугольника.
Как называются 3 стороны прямоугольного треугольника?
Основание, перпендикулярная высота и гипотенуза — три стороны прямоугольного треугольника.
Какая формула Пифагора для прямоугольного треугольника?
Теорема Pythagoras гласит следующую формулу для правого треугольника: H (гипотенуза) 2 = P (перпендикулярная высота) 2 + B (База) 2
+ B (База) 2 . Угловой треугольник: определение, формулы, примеры- Принц
- Последнее изменение 20-10-2022
Прямоугольный треугольник — одна из самых важных фигур в геометрии и основа тригонометрии. Прямоугольный треугольник — это треугольник, у которого три стороны, а именно « основание «, « гипотенуза » и « высота «, причем угол между основанием и высотой составляет 90°. Доля прямоугольного треугольника, покрытая внутренней стороной ребра треугольника, является его площадью. Прямоугольный треугольник – это треугольник, в котором один из углов равен другому (90 градусов). Его просто называют прямоугольным треугольником. Гипотенуза — это сторона, противоположная прямому углу прямоугольного треугольника, а две другие стороны называются катетами. Термины «база» и «высота» могут использоваться взаимозаменяемо для описания двух ножек. Студентам важно знать Площадь прямоугольного треугольника Существуют в основном две формулы для расчета площади прямоугольного треугольника. Мы подробно рассмотрим обе эти формулы. Поскольку математика является сложным предметом, учащимся необходимо уделять больше времени изучению и повторению тем.
Прямоугольный треугольник — это треугольник, у которого три стороны, а именно « основание «, « гипотенуза » и « высота «, причем угол между основанием и высотой составляет 90°. Доля прямоугольного треугольника, покрытая внутренней стороной ребра треугольника, является его площадью. Прямоугольный треугольник – это треугольник, в котором один из углов равен другому (90 градусов). Его просто называют прямоугольным треугольником. Гипотенуза — это сторона, противоположная прямому углу прямоугольного треугольника, а две другие стороны называются катетами. Термины «база» и «высота» могут использоваться взаимозаменяемо для описания двух ножек. Студентам важно знать Площадь прямоугольного треугольника Существуют в основном две формулы для расчета площади прямоугольного треугольника. Мы подробно рассмотрим обе эти формулы. Поскольку математика является сложным предметом, учащимся необходимо уделять больше времени изучению и повторению тем.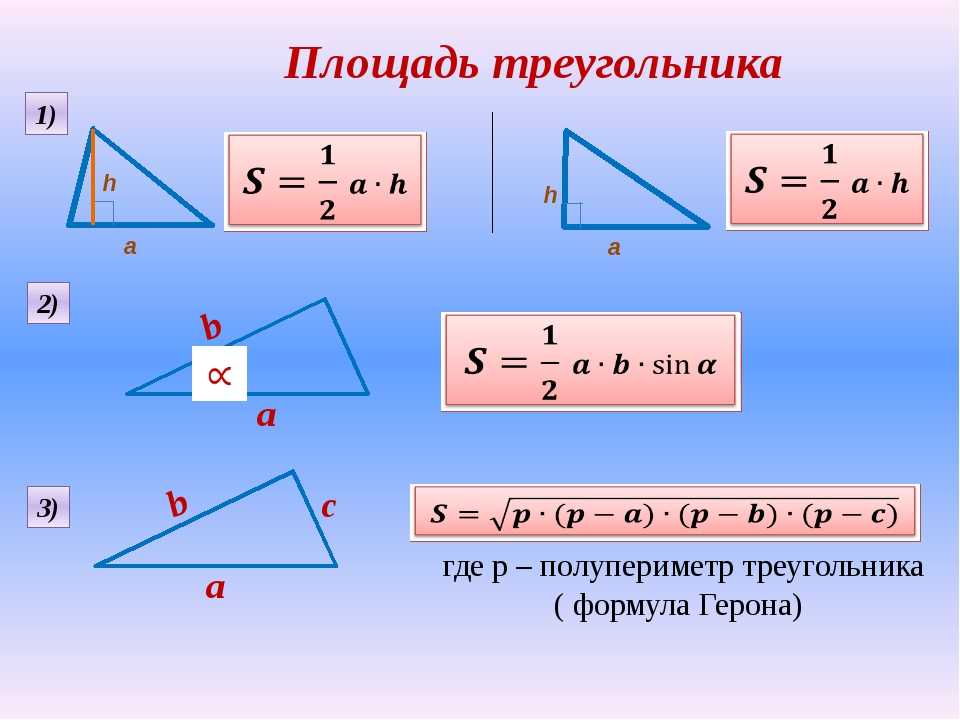 При регулярной практике можно развить скорость. Это позволит им ответить на большее количество вопросов за более короткий промежуток времени и получить более высокие оценки.
При регулярной практике можно развить скорость. Это позволит им ответить на большее количество вопросов за более короткий промежуток времени и получить более высокие оценки.
Математика состоит из алгебры и геометрии, которые одинаково важны. Ученикам важно усвоить основные понятия в старшей школе, так как понятия взаимосвязаны друг с другом в старших классах. Продолжайте читать, чтобы узнать о площади прямоугольного треугольника: определение, формула, примеры и многое другое.
Определение прямоугольного треугольника : Прямоугольный треугольник — это правильный многоугольник с тремя сторонами и тремя углами, один из которых равен 90°. Это уникальное свойство прямоугольного треугольника. Как и во всех других типах треугольников, сумма всех трех внутренних углов равна 180°.
Площадь прямоугольного треугольника — это общая площадь, заключенная между сторонами треугольника. Есть две формулы для вычисления площади в зависимости от того, даны ли нам все стороны или только основание и высота.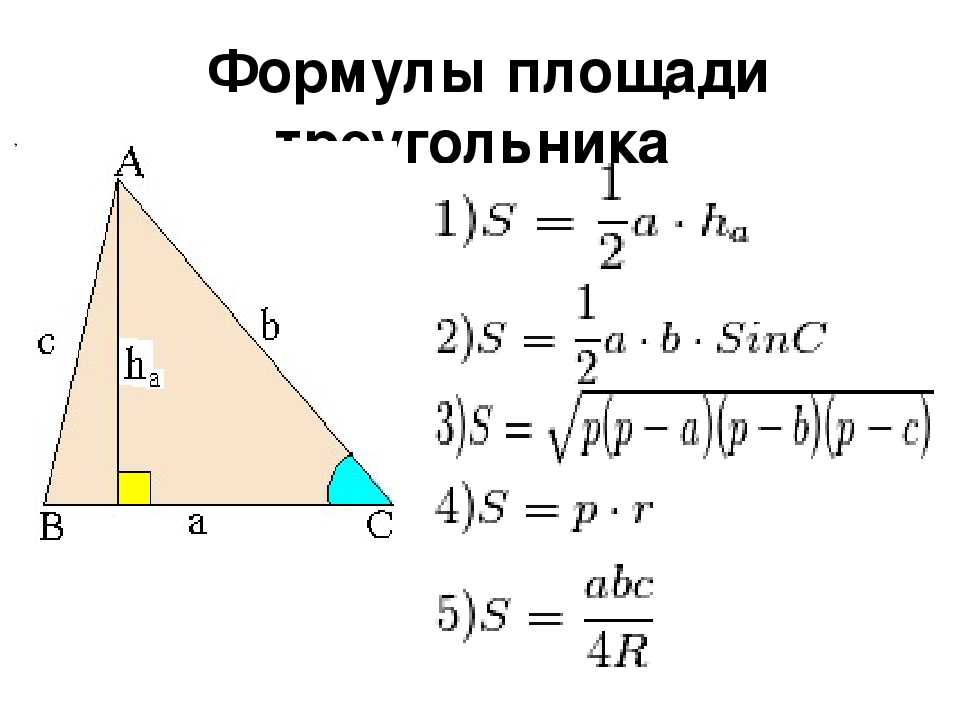 Рассмотрим две формулы подробнее.
Рассмотрим две формулы подробнее.
Площадь прямоугольного треугольника: используя основание и высоту
Мы можем вычислить площадь прямоугольного треугольника, зная основание и высоту.
| Площадь прямоугольного треугольника = ½ x основание x перпендикуляр Площадь этого прямоугольника равна b × h Однако, если провести диагональ из одной вершины, прямоугольник разобьется на два конгруэнтных или равных прямоугольных треугольника. Поскольку диагональ прямоугольника делит его пополам на два равных и конгруэнтных треугольника, площадь каждого треугольника равна половине площади прямоугольника. Следовательно, Площадь (△ABC) = Площадь (△ACD) = ½ bh Площадь прямоугольного треугольника, если даны только углы : В прямоугольном треугольнике основание всегда перпендикулярно высота. Когда стороны треугольника не даны, а даны только углы, площадь прямоугольного треугольника можно вычислить по данной формуле: $$Area = {{bc \times ba} \over 2}$$ Где a, b, c — соответствующие углы прямоугольного треугольника, где ∠b всегда равен 90°. Площадь прямоугольного треугольника с использованием формулы ГеронаКогда известны все стороны прямоугольного треугольника, мы можем использовать формулу Герона для вычисления площади. Формула площади прямоугольного треугольника: $$ Площадь = \sqrt {s(s – a)(s – b)(s – c)}$$ Где s — это полупериметр, который рассчитывается как $$ s = {{(a + b + c)} \over 2}$$ , а a, b, c — стороны треугольника. Решенные примеры площади прямоугольного треугольникаЗдесь мы предоставили некоторые вопросы о площади прямоугольного треугольника вместе с решениями.
|


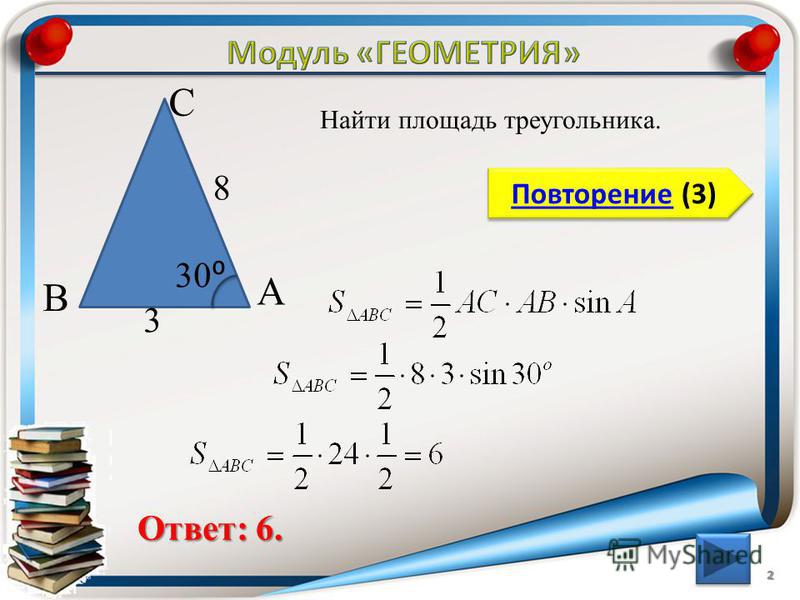
 Найдите площадь основания и высоту треугольника, если его площадь 243 см².
Найдите площадь основания и высоту треугольника, если его площадь 243 см².  Найдите его площадь.
Найдите его площадь. 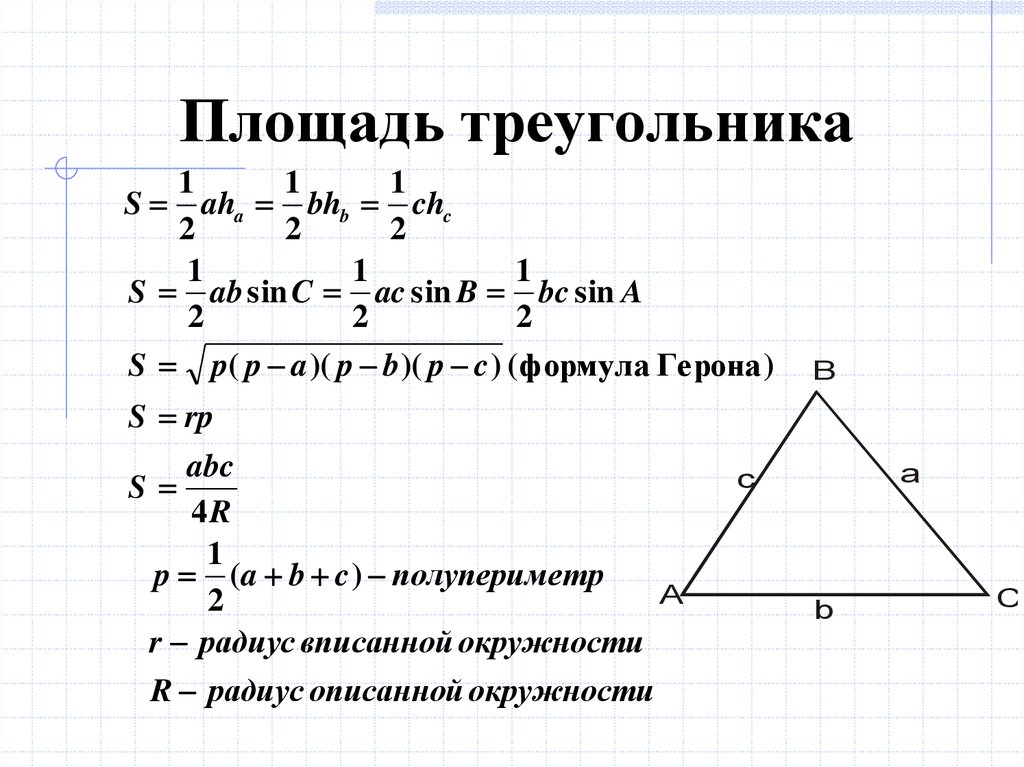
 Так как один угол равен 90°, то сумма двух других углов будет равна 90°.
Так как один угол равен 90°, то сумма двух других углов будет равна 90°.