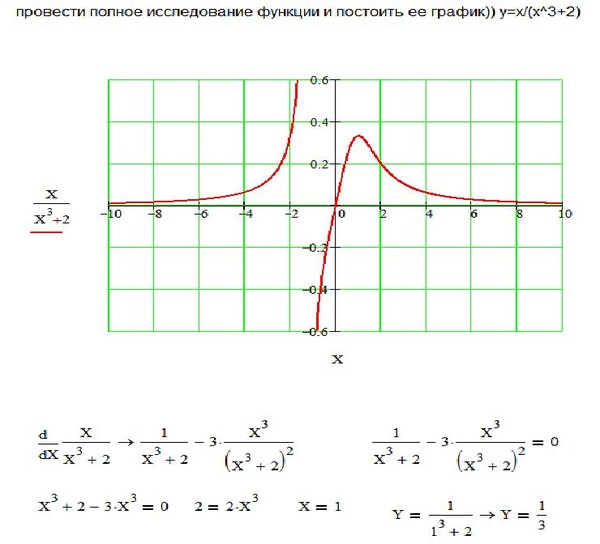
13. Общая схема исследования функций и построения графиков.
13.1 Общая схема исследования и построения графика функции заданной явно.
Общее исследование функции следует проводить по приведенной ниже схеме:
1.Определить область существования функции, область непрерывности, точки разрыва.
2. Найти асимптоты функции.
3. Выяснить вопрос о периодичности.
4. Выяснить вопрос о четности или нечетности.
В случае, если функция окажется четной или нечетнойдостаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
5.Найти точки пересечения графика функции с осями координат:
с осью абсцисс — точки , где-решение уравнения;
с
осью ординат- точки
,
где.
6. Найти промежутки монотонности и локальные экстремумы.
7.Найти интервалы выпуклости и вогнутости, точки перегиба.
8. Составить таблицу
Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | ||||
знак | знак | знак | знак | ||||
знак | знак | знак | знак |
Точки
-все найденные в п.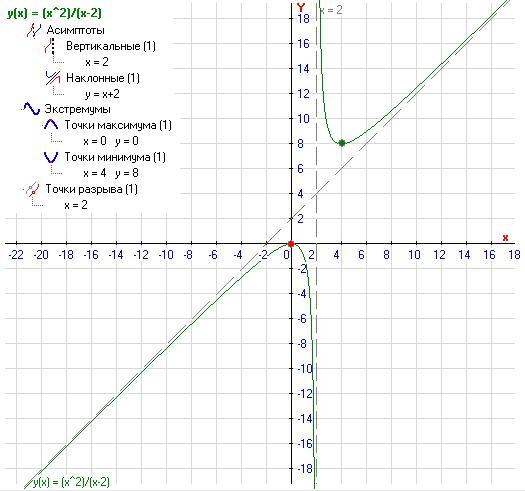
6-7 точки, в которых
производные обращаются в нуль или не
существуют.
9.На основании проведенного исследования построить график заданной функции.
Пример 26
Провести полное исследование и построить график функции .
Решение:
Область определения функции
Точка разрыва функции , функция непрерывна наи.
2. Асимптоты.
Вертикальная асимптота .
Поведение функции в окрестности :
Найдем наклонную асимптоту:
Прямая является наклонной асимптотой заданной кривой.
3. Функция не является периодической.
4. Четность функции
Условие
четности или нечетности не выполнено.
5. Точки пересечения с осями.
График функции проходит через начало координат.
6. Промежутки монотонности, локальные экстремумы.
Найдем критические точки:
Исследуем знак производной методом интервалов:
знак
Найдем значения функции в критических точках:
7.Промежутки выпуклости и вогнутости. Точки перегиба.
Найдем вторую производную.
Точки, в которых равна нулю или несуществует:
Исследуем знак второй производной методом интервалов:
8. Составляем таблицу.
0 | — | ||||||
+ | 0 | + | — | — | 0 | + | |
— | 0 | + | — | + | + | ||
перегиб | разрыв | Мин. |
13.2 Общая схема исследования и построения графика функции заданной параметрически.
Функция задана параметрически
1.Исследовать область изменения ипри изменении параметра.
2. Найти значения параметра , при которыхи.
3.а)Найти значения параметра , при котрых. Найти вертикальную асимптоту
б) Найти значения параметра , при котрых. Найти наклонную асимптоту
,
4. Вычисляем и.Находим все значения параметра, при которых хотя бы одна из полученных производных обращается в нуль или терпит разрыв. Найденные значения параметра будем называть критическими.По формуле (9) определяем знак производнойв каждом из полученных интервалов.
5.
Вычисляем вторую производную
по формуле (16) или (17). Определяем значения
параметрапри которыхобращается в нуль или терпит разрыв.
Определяем промежутки выпукдости
вогнутости согласно (40) и (41).
6. Строим таблицу
Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
7. Строим график функции.
Пример 27
Построить кривую (декартов лист), заданную параметрическими уравненниями:
Решение:
1.Обе функции определены при .
При этом
2.при
при .
3.а) При
При этом
Таким образом, вертикальных асимптот график функции не имеет.
б) Найдем наклонную асимптоту:
Таким образом, график функции имеет наклонную асимптоту:
4.
Найдем производные
и.
Найдем критические значения параметра
При обе производные терпят разрыв.
Таким образом, получаем следующие критические значения параметра :
Найдем по формуле (9):
5. Найдем :
6. Строим таблицу
Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
убывает, вогнута | ||||||||
убывает, вогнута | ||||||||
возрастает, вогнута | ||||||||
убывает, вогнута | ||||||||
возрастает, выгнута |
7.
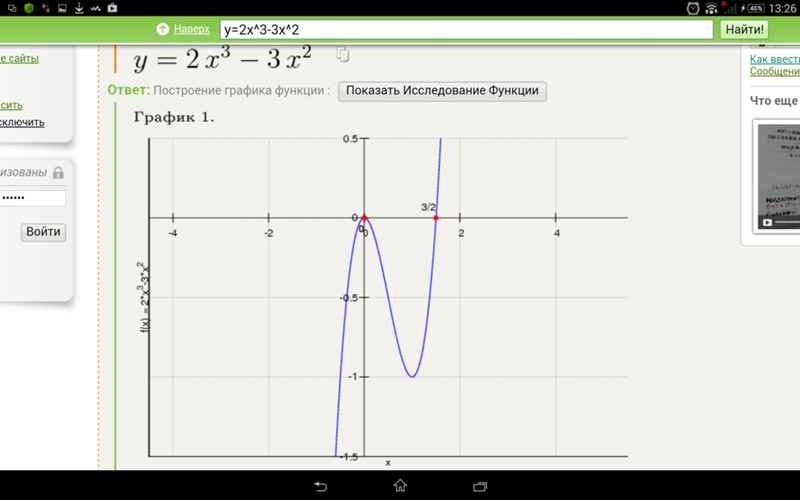Строим график
Задания 11. Провести полное исследование и построить график функции:
1. | 2. | 3. |
4. | 5. | 6. |
7. | 8. | 9. |
10. | 11. | 12. |
Исследование функций и построение их графиков. Полное исследование функции
◄Из существования первого предела следует, что f(x)
− k = β(x),
где β(
)x — бесконечно малая функция.
Тогда x
f (x) = kx + x⋅β(x). Отнимем от обеих частей величину kx и найдем предел при x →∞, lim( f (x) −kx)= limx⋅β(x). Из
x→∞ x→∞
lim( f (x) −kx)= b следует limx⋅β(x) = b. Поэтому
x→∞ x→∞ x⋅β(x) = b +α(x), где ( )α x — бесконечно малая функция. Следовательно, f (x) = kx + x⋅β(x) = kx + b +α(x).►
ПРИМЕР. Найти асимптоты графика функции y = x(x-2). f (x)
Решение. Найдем последовательно пределы lim и
x→∞ x
lim(
f (x) −kx).
Второй предел находится при условии, что первый
x→∞
f(x)x(x-2)
из них конечен. Тогда lim. x→∞ xxx
Если x > 0, то модуль раскрываем со знаком плюс, и
Если x < 0, то k
x→−∞ x
Найдем величину второго предела, домножив числитель и знаменатель (который равен единице) на сопряженное выражение:
x(x −2)− x2
lim( f (x)−kx)= lim( x(x −2) − x)= lim=
x→+∞ x→+∞x→+∞ x(x −2) + x
−2x −2
= lim= −1
⎛ 2 ⎞ x→+∞
x⎜⎜⎝ 1− x +1⎟⎟⎠
Таким образом, правая наклонная асимптота имеет вид y = x -1.
Аналогично рассматривается случай x →-∞.
x(x −2)− x2
= lim=
−∞ x→−∞ x(x −2) − x
−2x 2
lim= lim=1
x→+∞ ⎛ 2 ⎞ x→+∞
− x⎜⎜⎝ 1− x +1⎟⎟⎠
Тогда получим левую наклонную асимптоту y = -x +1. График исходной функции со своими асимптотами представлен на рис. 12.
Значительно короче можно решить пример, используя «о»-малое.
2 ⎛ 2⎞
y = =
x ⋅⎜1− ⎟ .
⎝ x⎠
Поскольку x→∞, заменим скобку асимптотическим равенством. Получим
⎛ ⎛ ⎛1⎞⎞ x y = x ⋅⎜1− ⎟ = x⎜1− + o⎜ ⎟⎟ = x − +o(1).
⎝ x⎠⎝⎝ x⎠⎠ x
Пусть x → +∞. Тогда y = x − +o(1) = x −1+o(1).
Пусть x→−∞. Тогда y = x − +o(1) = −x +1+o(1).
Как известно, о(1) есть бесконечно малая величина. Правая y = x-1 и левая y = -x +1 наклонные асимптоты получены.
Замечание 1. Прямая x = x0 не может быть вертикальной
асимптотой, если функция непрерывна в точке x = x0 .
Поэтому вертикальные асимптоты следует
искать в точках разрыва функции.
Замечание 2. Горизонтальная асимптота является частным случаем наклонной при k=0.
Замечание 3. Если при нахождении горизонтальной асимптоты получается lim f (x) = ∞, то функция может иметь
x→∞
наклонную асимптоту.
Замечание 4. Кривая y=f(x) может пересекать свою асимптоту, причем многократно.
При построении графика функции необходимо провести ее предварительное исследование. Построение сразу по точкам, за исключением элементарных случаев, может привести к потере на графике важных свойств функции. Примерная схема исследования функции с целью построения ее графика представлена ниже.
1. Область определения D(y) и область допустимых значений
E(y) функции.
2. Симметрия и периодичность.
3. Точки
разрыва и промежутки непрерывности функции.
4. Нули функции и промежутки постоянного знака.
5. Экстремумы и промежутки монотонности.
6. Точки перегиба и промежутки выпуклости.
7. Асимптоты.
Замечание 1. Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика. Однако без нахождения разрывов, экстремумов, асимптот и исследования на выпуклость часто невозможно получить график, правильно отражающий поведение функции.
Замечание2. Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание 3. Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
ПРИМЕР 1. Провести полное исследование функции
1
y = 2 и построить график.
1+ x
1. Областью определения является вся числовая ось.
2. Функция четная: f(-x) = f(x), так что ее график симметричен относительно оси ординат. Из четности функции следует, что достаточно построить ее график в правой полуплоскости, а затем отразить его в левую полуплоскость.
3. Точек разрыва нет, функция max непрерывная на всей числовой оси. y′( x ) + 4. При х=0 имеем у=1. Функция положительна при всех x, так что график Рис. 13 функции лежит в верхней полуплоскости.
2x
5. y′ = − 2 2 . Функция возрастает при х<0 и убывает при (1+ x )
х>0.
Точка х=0 — критическая. При переходе перегиб х через точку х=0 производная у'(х)
меняет y′′(
x ) — +
знак с плюса на минус (рис.
13).
Следовательно, точка х=0 — точка Рис. 14 максимума, у(0) = 1.
1—3x2
6. y′′ = —2 2 3 . Вторая производная обращается в нуль в
(1+ x )
точках x = ± Исследуем точку x = . При x имеем у» >0, т.е. кривая выпукла вниз; при
x < получаем у»<0 (кривая выпукла вверх) (рис.14). Следовательно, x = — точка перегиба
1
7. lim 2 = 0. График имеет горизонтальную асимптоту у = 0, x→+∞1+ x
наклонных асимптот нет.
Строим график в правой полуплоскости и симметрично
отражаем его в левую полуплоскость.
График функции изображен на рис. 15.
ПРИМЕР 2. Провести полное исследование функции
(x +1)3
y = 2 и построить график.
(x −1)
1.Область определения функции х≠1, т.е.D(y)=(-∞;1)∪(1;+∞).
Так как при х=-1 y<0, а при x>-1 y>0, и lim y(x) = −∞,lim y(x) = +∞, то множество значений функции
x→−∞ x→+∞
Е(у)=(-∞;+∞).
2.Функция у(х) не является периодической. Она ни четная, ни нечетная, т.е. ее график не обладает симметрией. (Этот очевидный для данной функции пункт можно было опустить).
3.В точке х=1 функция имеет разрыв y( x) — +
второго рода, -1 х
т.
к. lim y(x) =
+∞, lim y(x) =
+∞. Рис. 16 x→1−0 x→1+0
4.Точки пересечения с осями координат: х=0, у=1, и х=-1,
у=0.Промежутки постоянного знака y′( x ) + — min + представлены на рис. 16.
5.Найдем интервалы возрастания, Рис. 17
убывания и экстремумы функции. Для этого вычислим первую производную:
3(x +1)2 (x −1)2 − 2(x −1)(x +1)3 (x +1)2 (x − 5) y′ = 4 = 3 .
(x −1) (x −1)
Отсюда получим а) у′>0
при x<1 и x>5, следовательно, на этих промежутках функция возрастает,
а при х∈(1,5)
у′<0
и функция убывает.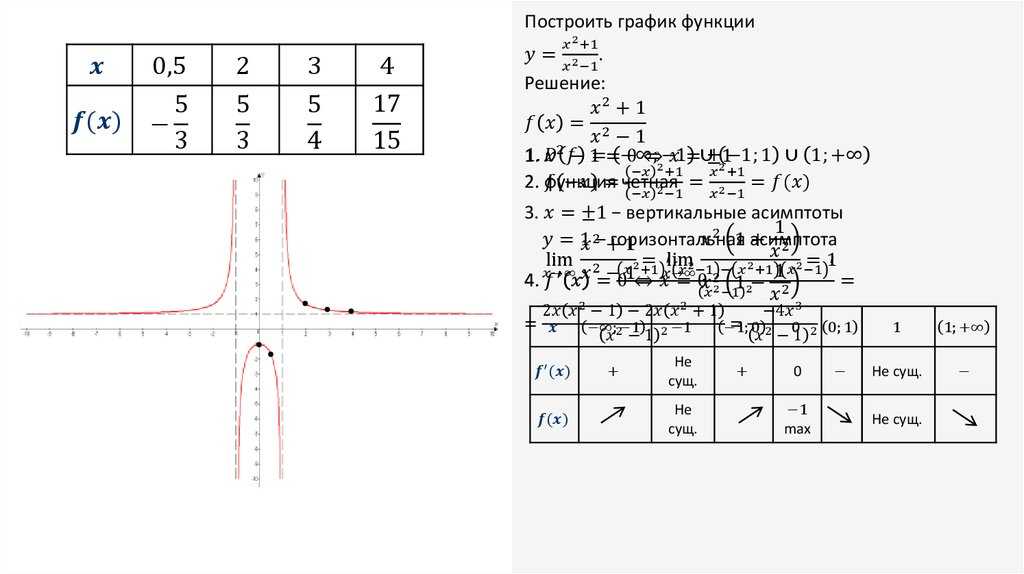
(рис.
9.17).
б) у′=0 при х=5 и в точке (5;27/2) перегиб
y′′( x ) функция имеет локальный минимум. — + + х
∩ -1 ∪ 1 ∪
Точка х=-1 тоже является критической Рис. 18.
точкой у(-1)=0, но локального экстремума функции в этой точке нет.
6. Найдем интервалы выпуклости функции. Для этого вычис24(x +1)
лим вторую производную: у′′ == 4 .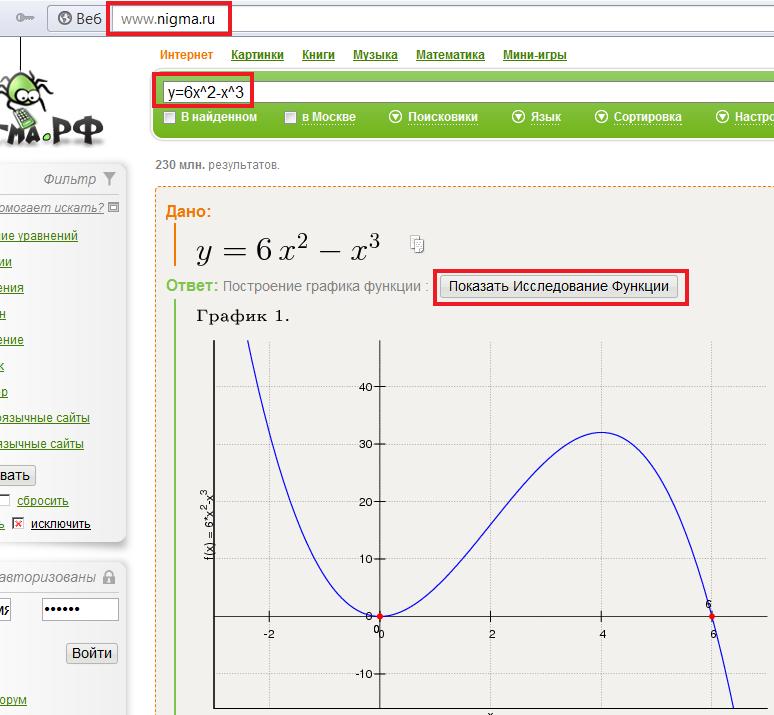
Тогда у″<0
при х<-1 и (x −1)
функция выпукла вверх, а на промежутках -1<x<1 и x>1 у″>0 и функция
Примеры графиков данных
В этом документе приведены примеры ряда графиков, которые могут используется для понимания или представления данных. Комментарии к каждому примеру предназначены для того, чтобы помочь вам понять, почему данные были нанесены на график в определенном моды, или почему это должно было быть сделано по-другому.
Вас также может заинтересовать наш туториал по использованию рисунков (графиков).
Заговор или не заговор?
Целью построения научных данных является визуализация вариаций или
показать отношения между переменными, но не все наборы данных требуют
участок. Если есть только одна или две точки, легко исследовать
цифры напрямую, и мало или совсем ничего не получается, помещая их на
график.
Точно так же, если данные не различаются, легко
достаточно, чтобы увидеть или констатировать факт, не используя график любого рода.
Если график подходит, он должен быть соответствующего типа, чтобы избежать введение читателя в заблуждение.
Рис. 1. Расходы на исследования для различных научных поля.
Оба графика на рисунке 1 показывают расходы на исследования в США по дисциплинам в
2000. Точечная диаграмма слева неверна, поскольку подразумевает
взаимосвязь между переменными по двум осям, дополнительно усиленная
по соединительным линиям. Поскольку горизонтальная ось представляет собой просто список
дисциплины без внутреннего порядка, никакие отношения не могут существовать. Категориальный
данные такого рода лучше отображать в виде гистограммы, как справа,
поскольку такой график отображает относительные величины, не подразумевая
функциональное отношение.
(Круговые диаграммы часто можно увидеть в популярных
нажмите на финансовые данные, чтобы подчеркнуть относительный размер
ассигнования. Круговые диаграммы редко используются в технических областях.)
Набор типичных ошибок
Утверждается, что курение вызывает рак легких. Один из способов проверить Эта гипотеза заключается в поиске связи между курением табака и рак легких. На рисунке ниже представлены данные о потреблении сигарет в 1930 г. и мужской смертности от рака легких в 1950 г. для ряда стран.
Рис. 2. Смертность от курения сигарет.
На рисунке 2 много ошибок, в том числе
- Отсутствующие единицы – это общее потребление и количество смертей или нормализовано для населения?
- Перевернутые оси – мы подозреваем, что курение приводит к раку, а не
обратное. Независимая или причинная переменная идет по оси x.
- Изогнутая линия, соединяющая точки, не имеет основы. Разброс данные предполагают большие случайные эффекты, а не реальные изменения от точки В точку.
- Подпись, которая не особенно полезна.
Перерисовка графика приводит к следующему результату
Рис. 3. Смертность от рака легких по сравнению с курением потребления для нескольких стран. Сплошная линия соответствует линейной данные.
Прямая линия представляет собой простую модель, которая может быть лучшей из эти сильно разбросанные данные могут поддерживать. Экстраполяция к нулевому потреблению может быть или не быть действительным, и его необходимо будет проверить с другими данными.
Весы, вводящие в заблуждение
Эксперимент проводится для определения вклада растворенного вещества
к объему полученного раствора.
Процедура заключается в добавлении взвешенного
количества соли KCl на 100 мл пробы воды. После разрешения
Чтобы система пришла в равновесие, раствор фильтруют, чтобы удалить любые
остаточного твердого вещества и измеряют объем раствора.
Рис. 4. Объем раствора в зависимости от KCl масса.
На рисунке выше данные нанесены в худшем чем бесполезен. Обратите внимание на следующие проблемы:
- Оси не имеют маркировки измеряемой величины, а также не идентифицируются единицы измерения.
- Топоры очень неравны по длине без видимой причины.
- Вертикальная шкала имеет слишком широкий диапазон для отображения диапазона данные.
- Горизонтальная шкала также слишком длинная, выходит далеко за пределы диапазон данных.
- Линии сетки добавляют беспорядок, но не информацию.
- Показана подогнанная прямая линия, но масштабы затрудняют ее определение. если это точно.
- Подгонка выходит далеко за пределы данных без обоснования.
Исправление этих ошибок дает график на рисунке 5. Теперь ясно, что объем раствора увеличивается с добавлением массы растворенного вещества, но только до тех пор, пока решение становится насыщенным, поэтому линейная подгонка ко всему набору данных это просто ерунда. Ниже насыщения шкалы теперь позволяют читателю точно оценить данные, например, чтобы увидеть, увеличивается ли объем является линейным ниже насыщения или если для принятия решения требуется больше данных.
Рис. 5. Объем раствора в зависимости от KCl масса.
Компьютер подходит для
Экспериментаторы часто используют сгенерированные компьютером линии наилучшего соответствия, чтобы продемонстрировать
согласие с какой-либо моделью или теорией.
Например, у студента есть данные
радиационного эксперимента, который состоял в наблюдении количества
гамма-излучение, испускаемое через фиксированный интервал времени. Были получены подсчеты за
много временных интервалов, а результаты отображаются в виде гистограммы. Следующий
шаг состоит в том, чтобы увидеть, соответствует ли распределение отсчетов ожидаемому гауссову
распределение. Использование значений по умолчанию в программе с плохой подгонкой может привести к
этот результат.
Рис. 6. Сравнение данных и теории для подсчета эксперимент.
Одна строка состоит из данных, другая теория, но за ней трудно следить
либо один (невозможно с монохромной версией). Подключение данных
точек также неверно, поскольку подразумевает, что данных больше, чем
на самом деле присутствует. Лучшее представление будет выглядеть как рисунок 7.
Фактические точки данных теперь четко различимы символы, показывающие, что необработанные данные для четырех значений счетчика были объединены в бины вместе и что существует некоторый разброс по теоретической кривой. сама теория отображается в виде плавной сплошной линии, поскольку значения можно рассчитать везде, и нет никаких неопределенностей в расчетах числа. Любая программа, предназначенная для построения научных графиков, должна иметь возможность для создания аналогичного сюжета.
Рис. 7. Гистограмма данных интервального счета. сплошная линия — ожидаемое распределение Гаусса, квадраты — наблюдения.
Руководство экспериментом
Графики данных часто являются полезным руководством для экспериментов. Сюжет будет
быстро показать, изменяются ли параметры, как ожидалось, и может указать
режимы, где требуется больше или меньше данных.
Рис. 8. Плотность жидкой ртути как функция температуры. Сплошная линия представляет собой линейную подгонку к наблюдениям.
График на рисунке 8 был получен путем измерения плотности жидкости ртути в зависимости от температуры. В указанном диапазоне плотность уменьшается линейно с температурой, в очень хорошем приближении, и можно определить коэффициент объемного расширения по наклону линия.
Рис. 9. Плотность жидкой воды как функция температуры.
Следующей измеряемой жидкостью была вода, которая, очевидно, представляет собой гораздо более сложную
вещество. Общее изменение от 0 до 100°C составляет всего около 5%, что показывает
необходимость хорошей точности измерения, и, конечно, не является линейным.
На самом деле, может быть полезно получить больше данных в области около 0°С,
выяснить, стремится ли плотность к нулю равномерно или имеет максимум
в регионе.
Рис. 10. Плотность жидкой воды как функция температуры, расширенная шкала.
Результаты дополнительных измерений приведены выше, четко показывает пик плотности в зависимости от температуры. Обратите внимание, что эти данные нанесены в еще более расширенном масштабе, с вертикальным диапазон всего 0,4%. Поскольку это необходимо для отображения малого максимума, оба графики, вероятно, будут включены в отчет об этом эксперименте.
Преобразование переменных
Иногда бывает полезно математически преобразовать один или оба переменные перед построением графика. Технику можно использовать для линеаризации данных. для упрощения подбора модели или для изменения способа распределения данных для уточнения отображения. Точная процедура будет зависеть от ситуации, но два примера покажут процесс.
Создание линейной связи
Луч света искривляется, когда он падает на плоскую поверхность между
разные вещества.
Угол преломления связан с углом
падения по закону Снелла,
Студент измеряет углы падения и преломления воздуха на стекло. интерфейса и хочет найти показатель преломления для стекла, n 2 , зная, что индекс для воздуха n 1 = 1.000. Веря что график был бы хорошим способом анализа данных, студент решает для угла преломления через угол падения
Компьютерная программа может соответствовать этой функции, но доступная программа не будет выполнять функцию арксинуса, поэтому студент пытается быть более умным. Отметив, что
она строит sinq r против sinq i , со следующим результатом
Рис. 11. Линеаризованные данные рефракции.
Твердое тело
линия соответствует закону Снеллиуса.
Теперь легко увидеть, что данные хорошо описываются ожидаемым прямой и получить наклон, который равен 1/ n 2 .
Изменение дистрибутива
Далее рассмотрим приведенный ниже график, на котором изображено количество государственных служащих по сравнению с общей численностью населения 50 штатов США в 2000 г. Очевидно, мелких государств гораздо больше, чем крупных, поэтому данные группируются недалеко от происхождения. Прямая проведена в предположении, что размер бюрократии просто пропорционален количеству граждан. К сожалению, это предположение не представляется верным, поскольку кажутся систематическими отклонениями в нижней части, где данные точные различать, а перехват не равен нулю. Нужен другой подход.
Рис. 2. Численность государственных служащих
по сравнению с общей численностью населения штата в 2000 г.
На следующем графике используются те же данные, но они отображаются в виде логарифма. численности как работников, так и населения. Эффект от взятия бревна разложить маленькие значения и сжать большие, что приведет к данные должны быть более равномерно распределены по осям. Это часто помогает визуализация отклонений или других проблем.
Рис. 13. Численность государственных служащих по сравнению с общей численностью населения штата в 2000 г. Линия представляет собой степенную зависимость к данным.
Логарифмические графики также полезны для демонстрации степенные или скейлинговые соотношения. Степенной закон,
г = топор б
, в котором показатель степени b не обязательно равен единице, является обобщением
знакомой пропорциональности.
Логарифмируя обе части,
мы получаем
log y = b log x + журнал а
, поэтому степенная зависимость представляет собой прямую линию на бревне y vs бревно х участок, с уклоном б . Возвращаясь к бюрократии например, наклон показанной линии равен 0,79, что указывает на то, что число государственных служащих растет несколько медленнее, чем численность населения. Экономист заметил бы, что это пример «экономики шкала’.
Эффективное использование графиков
Графики — распространенный метод визуальной иллюстрации взаимосвязей в данных. Назначение графика — представить данные, которые слишком многочисленны или сложны для адекватного описания в тексте и в меньшем объеме. Однако не используйте графики для небольших объемов данных, которые можно кратко передать в одном предложении. Точно так же не повторяйте данные в тексте, так как это противоречит цели использования графика.
Если данные показывают явные тенденции или выявляют отношения между переменными, следует использовать график. Если данные не показывают какой-либо существенной тенденции в доказательствах, график не является предпочтительным рисунком. 1
Несмотря на то, что существует множество компьютерных программ, которые могут создавать графики, автор все же должен учитывать некоторые основные принципы. Основным требованием к графику является его ясность и удобочитаемость. Это определяется не только размером шрифта и символами, но и типом самого графика. Важно предоставить четкую и описательную легенду для каждого графика. Графики могут состоять из нескольких частей, в зависимости от их формата: (1) номер рисунка, (2) подпись (не заголовок), (3) заголовок, (4) поле данных, (5) оси и масштабы, ( 6) символы, (7) легенды и (8) кредит или исходная строка. Для большинства целей создавайте график так, чтобы вертикальная ось (ордината, ось Y) представляла зависимую переменную, а горизонтальная ось (абсцисса, ось X) представляла независимую переменную.
Следовательно, время всегда находится на оси X. 2 Графики всегда должны иметь как минимум заголовок, оси и масштабы, символы и поле данных. Графические символы должны быть четкими, разборчивыми и обеспечивать хороший контраст между фигурой на переднем плане и фоном. Открытые и закрытые круги обеспечивают лучший контраст и более эффективны, чем сочетание открытых кругов и незакрашенных квадратов. 3 Как и само название статьи, каждая легенда должна в сжатой форме передавать как можно больше информации о том, что график сообщает читателю, но не должна давать краткое изложение или интерпретацию результатов или деталей эксперимента. Избегайте простого повторения меток осей, таких как «температура и время». Крайне важно выбрать правильный тип графика в зависимости от типа данных, которые должны быть представлены. Если независимые и зависимые переменные являются числовыми, используйте линейные диаграммы или диаграммы рассеяния; если только зависимая переменная является числовой, используйте гистограммы; для пропорций используйте гистограммы или круговые диаграммы.
Они кратко описаны ниже.
Точечная диаграмма используется для демонстрации взаимосвязи между двумя переменными и того, изменяются ли их значения согласованным образом, например, при анализе взаимосвязи между уровнями концентрации двух разных белков.
Линейный график похож на точечную диаграмму, за исключением того, что значения X представляют непрерывную переменную, такую как время, температура или давление. Он отображает ряд связанных значений, отображающих изменение Y в зависимости от X. Линейные графики обычно строятся с зависимой переменной по оси Y и независимой переменной по горизонтальной оси X, например, график Каплана-Мейера. анализирует графики выживания результатов времени до события. Доля лиц представлена на оси Y в виде доли или процента, оставшихся свободными или испытавших определенный результат с течением времени.
Гистограмма может состоять из горизонтальных или вертикальных столбцов. Чем больше длина полос, тем больше значение.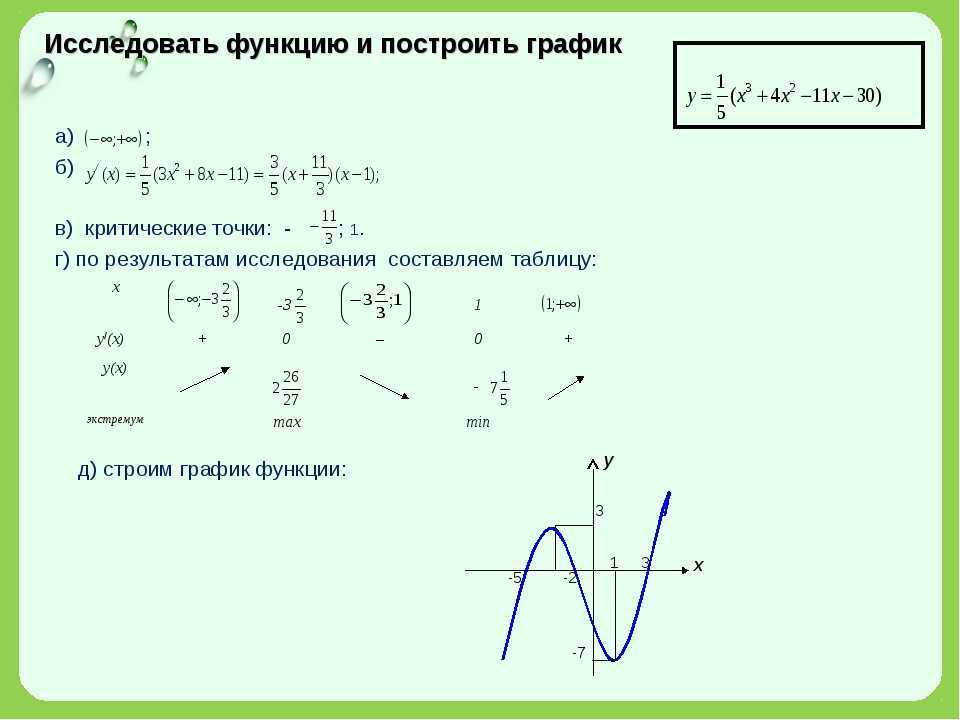
Они используются для сравнения одного значения переменной между несколькими группами, например, средних уровней концентрации белка в когорте пациентов и контрольной группе.
Гистограмма , также называемая графиком распределения частот , — это специальный тип гистограммы, который напоминает столбчатую диаграмму, но без промежутков между столбцами. Он используется для представления данных измерения непрерывной переменной. Отдельные точки данных сгруппированы в классы, чтобы показать частоту данных в каждом классе. Частота измеряется площадью столбца. Их можно использовать, чтобы показать, как измеряемая категория распределяется по измеряемой переменной. Эти графики обычно используются, например, для проверки того, соответствует ли переменная нормальному распределению, такому как распределение уровней белка между разными людьми в популяции.
Круговая диаграмма показывает классы или группы данных пропорционально всему набору данных. Вся диаграмма представляет все данные, а каждый срез или сегмент представляет отдельный класс или группу в целом.
Каждый срез должен показывать значительные вариации. Количество категорий, как правило, должно быть ограничено от 3 до 10.
Блочная диаграмма может быть как горизонтальной, так и вертикальной. Он используется для отображения статистической сводки одного или нескольких блоков и переменных, таких как минимум, нижний квартиль, медиана и максимум. Он также может идентифицировать выбросы данных. Расстояние между различными частями прямоугольника указывает на степень дисперсии и на то, является ли распределение данных симметричным или асимметричным.
Некоторые распространенные ошибки включают следующее: информация в тексте дублируется в графиках или информация в графиках дублируется в таблицах. График не имеет надлежащих легенд. Для представления данных выбран неправильный тип графика. График построен не в масштабе. Данные не помечены, непоследовательны, прерывисты или преувеличены для получения желаемого эффекта. Другой распространенной ошибкой является включение линии, которая предполагает необоснованную экстраполяцию между точками данных или за их пределами.