Формулы площадей всех основных фигур
Площадь эллипса
R — большая полуось
r — малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:
Калькулятор, вычислить площадь элипса:
Все формулы площади равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Площадь треугольника по стороне и двум углам, формула.

a, b, c — стороны треугольника
α, β, γ— противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Площадь треугольника, формула Герона
Зная длины всех трех сторон
и используя формулу Герона можно найти площадь разностороннего треугольника
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Формула (Герона) площади треугольника через полупериметр (S):
Калькулятор — вычислить, найти площадь треугольника:
a =
b =
c =
S=
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Формула расчета площади треугольника
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h — высота треугольника
a — основание
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
Высота, h =
Основание, a =
Количество знаков после запятой: 212461015
Площадь треугольника, S =
2. Площадь треугольника с тупым углом
h — высота треугольника
a — основание
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Найти площадь треугольника, угол и две стороны
Зная у треугольника
две стороны и синус угла между ними, находим по формуле, его площадь
a, b, c — стороны треугольника
α, β, γ — углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
Калькулятор — вычислить, найти площадь треугольника:
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Площадь прямоугольного треугольника
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
a, b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a, b — катеты
α, β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3.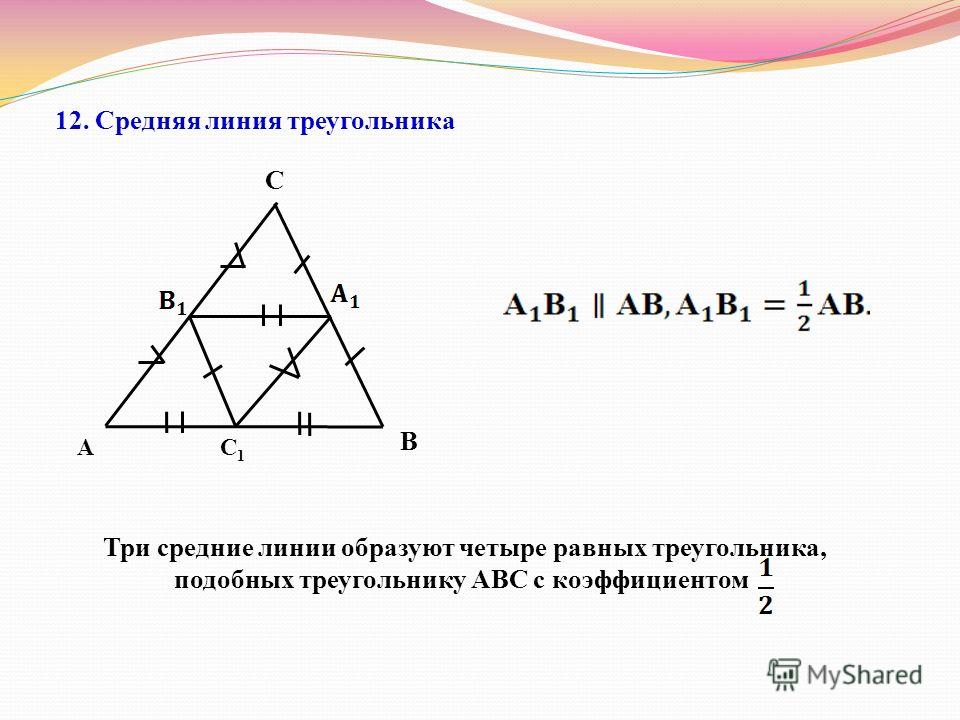 Если известны радиус вписанной окружности и гипотенуза
Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c1, c2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Калькулятор — вычислить, найти площадь треугольника через высоту и основание:
b (основание) =
h (высота)=
S (площадь) =
Формула площади треугольника через, стороны a, b, (S):
Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:
a (сторона)=
b (основание)=
S (площадь)=
b — основание треугольника
a — равные стороны
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Площадь равностороннего треугольника равна:
Если вы знаете сторону или высоту
вы можете найти площадь равностороннего треугольника
a — сторона треугольника
h — высота
Площадь треугольника через сторону a и высоту h, (S):
Площадь треугольника только через сторону a, (S):
Калькулятор для расчета площади равностороннего треугольника
Площадь треугольника только через высоту h, (S):
Калькулятор для расчета площади равностороннего треугольника
a — сторона треугольника
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Формула площади круга, диаметр
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Радиус окружности, r =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Калькулятор для расчета площади круга через диаметр
Диаметр окружности, D =
Количество знаков после запятой: 2124610F
Площадь круга, S =
L — длина окружности
О — центр круга
π ≈ 3. 14
14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
Длина окружности, L =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Найти по формуле площадь кольца
Площадь кольца равна — число π, умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности
R — радиус внешней окружности
r — радиус внутренней окружности
π ≈ 3.14
Формула площади кольца (S):
Калькулятор — вычислить, найти площадь кольца
Площадь сектора кольца
R — радиус внешней окружности
r — радиус внутренней окружности
α — угол сектора AOB, в градусах
π ≈ 3. 14
14
Формула площади сектора кольца (S):
Площадь сегмента круга
R — радиус круга
α — угол сегмента в градусах
π ≈ 3.14
Формула площади сегмента круга (S), отсекаемая хордой AC:
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Площадь сектора круга
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол
r — радиус круга
L — длина дуги AB
α — угол сектора круга AOB в градусах
π ≈ 3. 14
14
Формула площади сектора круга (S), через длину дуги (L):
Формула площади сектора круга (S), через угол (α):
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Вычислить площадь ромба
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба
h — высота
r — радиус вписанной окружности
Формула площади ромба через высоту или радиус вписанной окружности ( S ):
Все формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор — вычислить, найти площадь параллелограмма:
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d —меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор — вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
Все формулы площади произвольной трапеции
1. Формула площади трапеции через основания и высоту
Формула площади трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S ):
2. Формула площади трапеции через диагонали и угол между ними
d1, d2 — диагонали трапеции
α, β — углы между диагоналями
Формула площади трапеции, (S ):
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Формула площади трапеции, (S ):
Как рассчитать площадь квадрата через диагональ или сторону
Зная сторону
или диагональ квадрата, можно найти его площадь
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a, (S):
Калькулятор — вычислить, найти площадь квадрата:
Формула площади квадрата через диагональ c, (S):
C (диагональ)=
S=
Формула расчета площади прямоугольника
Зная длину
и ширину прямоугольника, можно вычислить его площадь
b — длина прямоугольника
a — ширина прямоугольника
Формула площади прямоугольника, (S):
Калькулятор — вычислить, найти площадь прямоугольника:
a (длина) =
b (ширина)=
S=
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Формула площади правильного многоугольника, (S):
Калькулятор — вычислить, найти площадь правильного многоугольника
Раздел долгосрочного плана: 7.3А Треугольники | Школа: | ||||
Дата: | ФИО учителя: | ||||
Класс: 7 | Количество присутствующих: | отсутствующих: | |||
Тема урока | Высоты, средняя линия, срединный перпендикуляр треугольника. | ||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 7.3.2.6 знать определения медианы, биссектрисы, высоты, серединного перпендикуляра, средней линии треугольника и умеет изображать их. | ||||
Цели урока | Знакомства с понятиями треугольника, его элементами и видами. | ||||
Критерии успеха | Ученик достиг цели, если: — знает основные и дополнительные элементы треугольников, — знает свойства элементов треугольников, — изображает треугольники различных видов, — показывает на чертеже элементы треугольника, — делает запись с использованием символики, — умеет пользоваться чертёжными инструментами. | ||||
Языковые цели | Учащиеся будут: — знать и применять свойства равнобедренного и равностороннего треугольников; — формировать навыки доказательных рассуждений с помощью аксиом и теорем. Предметная лексика и терминология: — катет, гипотенуза; — основание, боковая сторона; — угол между сторонами; — угол, прилежащий к стороне; — противолежащий угол; — катет, прилежащий к углу, катет, противолежащий углу; — медиана треугольника; — биссектриса треугольника; — высота треугольника; — серединный перпендикуляр к стороне треугольника; — средняя линия треугольника; Серия полезных фраз для диалога/письма: — определите углы, прилежащие к сторонам треугольника; — углы при основании … ; — угол между катетами … . | ||||
Привитие ценностей | Академическая честность, ответственное отношение к своим обязанностям в коллективе, терпимое отношение к мнению коллектива, толерантность. | ||||
Навыки использования ИКТ | |||||
Предварительные знания | Начальные геометрические сведения: точка, прямая, отрезок, плоскость, луч. | ||||
Ход урока | |||||
Запланиро-ванные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||
Начало урока 3 мин | Создание рабочей обстановки 1. Уроки 2. Какое число уменьшится на треть, если его перевернуть? Цифра 9 3. У квадратного стола отпилили один угол по прямой линии. Сколько теперь углов у стола? Пять Совместное определение целей урока. | ||||
Середина урока 15 мин 15 мин 5 мин | Изучение нового материала Лабораторная работа 1) Постройте произвольный треугольник 2) Измерьте основание АC, результат запишите 3) Измерьте боковые стороны АB и ВС, результат запишите 4) В середине АB и ВС поставьте соответственно точки М и N 5 ) Проведите отрезок МN и измерьте его длину (вводится определение средней линии) — Какой получили отрезок? Какие точки соединяет этот отрезок? — Так вот, отрезок соединаящий середины двух его сторон называется средней линией треугольника Поэтому: MN-средняя линия треугольника АВС (т. 6) Сравните длину отрезка МN и длину стороны АС. Какую закономерность вы здесь увидели? 7) Сформулируйте гипотезу. Попробуйте сформулировать теорему. Закрепление изученного материала Устно. 1. Чему равны средние линии треугольника со сторонами 14 см, 16 см, 20 см? 2. Дан треугольник, стороны которого равны 8 см, 5 см, 7 см. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника 3. Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно 2,5 см. Найдите меньшую сторону прямоугольника. 4. Дано: АВС – треугольник, РАВС= 18 см, F∈AB, E∈BC FE – средняя линия Найти: PFBE 5. Дано: АВС – треугольник, AM=MB, BN=NC, АC=8 см Найти: MN Формативное оценивание. Если один угол треугольника равен соответственно углу другого треугольника, то такие треугольники равны. Средняя линия треугольника соединяет середины соседних сторон.(1) Средняя линия треугольника не параллельна третьей стороне.(0) Средняя линия треугольника равна половине одной из его сторон.(1) Средняя линия треугольника в 2 раза больше основания.(0) Если стороны одного треугольника соответственно равны сторонам второго треугольника, то такие треугольники равны.(1) В итоге получите код: 010101 | ||||
Конец урока 1 мин | Рефлексия: — сегодня я узнал — сегодня я научился — мне было интересно — мне было трудно | ||||
1 мин | Домашнее задание: Выучить теорию, выполнить задания, которые не успели сделать на уроке. | ||||
Дополнительная информация | |||||
Дифференциация — как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся? | Междисциплинарные связи Безопасность жизнедеятельности ИКТ связи Связи с ценностями | ||||
Оценивание — как вы планируете проверить знания учащихся? | |||||
Используйте графу ниже, чтобы проанализировать Ваш урок. | |||||
Find -Midline -Equation -Calculator — Google Sucke
ALLBILDERVIDEOSBüchermApsNewshopping
Sucoptionen
Калькулятор синусоидальной функции — Free Online Calculator — Byju’s
ByJus.com ›Calculators Calculators› Callator Scalulators Callators
ByJus.com ›Calculators Calculators› Callator Scalulators 9000ByJus.com ›Callatoration Flactulators Flactoration Flactional. вычисления быстрее, и он отображает синусоидальную волну за доли секунды. Как использовать …
Калькулятор домена и диапазона: Калькулятор средней точки
Калькулятор объема квадратной пирамиды: Калькулятор дюймов в ярдах
Калькулятор ошибки выборки: Калькулятор обратных триггерных функций
Калькулятор веса металла: Калькулятор закона Стефана Больцмана
Ähnliche Fragen
Какое уравнение средней линии функции?
Что такое средняя линия синуса?
Как найти уравнение синусоиды?
Калькулятор тригонометрических уравнений — Symbolab
www. symbolab.com › Step-by-Step › Тригонометрия
symbolab.com › Step-by-Step › Тригонометрия
Бесплатный калькулятор тригонометрических уравнений — решайте тригонометрические уравнения шаг за шагом.
Триггерные неравенства · Sin (x)+sin (x/2)=0, 0<= x<= 2pi · Cos (x)-sin (x)=0
Калькулятор синусоидальной функции + онлайн-решатель с бесплатными шагами
www.storyofmathematics.com › математические калькуляторы › s…
Bewertung 5,0
(5)
Калькулятор синусоидальной функции строит синусоидальную функцию с учетом амплитуды, угловой частоты, фазы и вертикального сдвига ценности.
Определить уравнение средней линии функции триггерная функция. В данном случае это −2.
Калькулятор фазового сдвига
www.omnicalculator.com › математика › фазовый сдвиг
30.12.2022 · Калькулятор фазового сдвига предназначен для определения амплитуды, периода, фазового сдвига и вертикального сдвига произвольно измененного синуса или косинус . ..
..
Онлайн-калькулятор синусоидальной функции — Cuemath
www.cuemath.com › калькуляторы › синусоидальная функция… решить ваши сложные расчеты.
Амплитуда, период и фазовый сдвиг — Примеры тригонометрии — Mathway
www.mathway.com › примеры › тригонометрия › a…
Бесплатное решение математических задач отвечает на ваши домашние задания по алгебре, геометрии, тригонометрии, исчислению и статистике. .. Найдите амплитуду, период и фазовый сдвиг.
Калькулятор средней точки
www.calculatorsoup.com › Геометрия › Плоскость
Рассчитать расстояние между двумя точками и найти отсутствующую конечную точку. … решите и покажите работу, чтобы найти наклон, линейные уравнения и точки пересечения x и y …
Изображение
Все расчеты
Все расчеты
Калькулятор фазового сдвига с шагами — Диаграмма | Формулы 🥇
calconcalculator.com › математика › фазовый калькулятор
Bewertung 5,0
(3)
Как найти амплитуду и период? Амплитуда измеряет расстояние между средней линией функции и самой высокой или самой низкой точкой функции.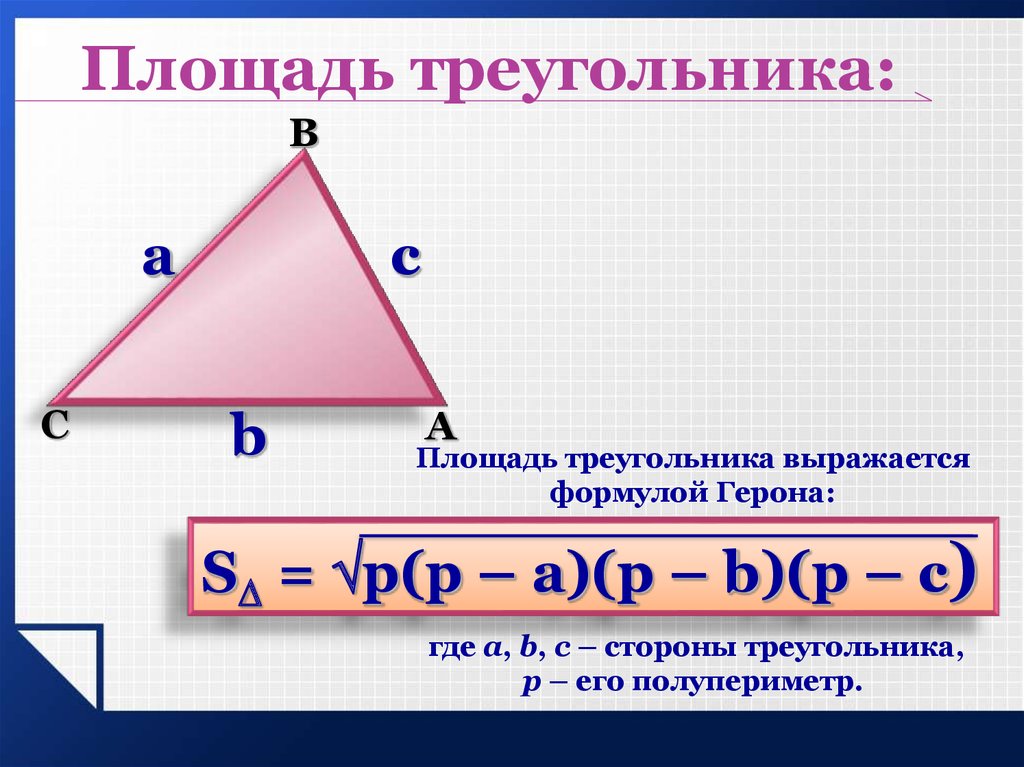



 Что можно приготовить, но нельзя съесть?
Что можно приготовить, но нельзя съесть? к. М – середина АВ и N – середина ВС)
к. М – середина АВ и N – середина ВС) (0)
(0) Ответьте на самые актуальные вопросы о проведенном уроке.
Ответьте на самые актуальные вопросы о проведенном уроке. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.
Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.