Площади фигур шпаргалка формулы: Несуществующая страница

alexxlab / / Разное

Содержание

Урок геометрии по теме «Площадь фигур»

nataadm Материалы для уроков, Подготовка к ГИА

Урок геометрии по теме «Площадь фигур». 9 класс(подготовка к ОГЭ)

 Цель урока: создать условия для развития умений вычислять площади фигур, применяя известные свойства фигур и формулы.

Задачи:

Обучающие

  • повторить основные теоретические факты по теме;
  • закрепить навыки вычисления площади фигур по формуле;
  • грамотно применять известные свойства фигур для решения задач на вычисление площадей

Развивающие

  • способствовать развитию мыслительной операции анализа, сравнения, обобщения;
  • способствовать развитию коммуникативных качеств личности

Воспитательные

  • способствовать воспитанию трудолюбия, настойчивости в достижении цели, аккуратности, культуру поведения при групповой и индивидуальной работе

Педагогические задачи формирования УУД:

  • Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности, мотивация учебной деятельности
  • Регулятивные УУД: оценивать результаты деятельности (своей – чужой), анализировать собственную работу, планировать свое действие в соответствии с поставленной задачей, определять цель учебной деятельности (этапа) в сотрудничестве с учителем, контролировать и оценивать процесс и результаты деятельности.
  • Коммуникативные УУД: слушать собеседника, формулировать собственное мнение и позицию, с точностью и достаточной полнотой выражать свои мысли.
  • Познавательные УУД: систематизировать материал, полученный при изучении темы

«Площади» в 8, 9 классах, ориентироваться в учебнике, находить нужную информацию, уметь составлять алгоритмы деятельности при решении проблемы.

Тип урока – урок закрепления знаний, умений и отработки навыков

Форма урока – урок-практикум

Формы работы – парная, индивидуальная, групповая

Организационный момент.

  • Актуализация опорных знаний.
  • Блиц-работа в парах «Мини-задачи на применение формул».
  • Решение задач по готовым чертежам.
  • «Нестандартный» метод вычисления площади многоугольник.
  • Итог урока.
  1. Организационный момент. (1 минута)

Здравствуйте ребят.

2.     Актуализация знаний. (7 минут)

Вы прекрасно знаете, что наибольшие затруднения при решении экзаменационных вариантов вызывают задачи по геометрии. Сегодня на нашем очередном элективном занятии мы поговорим о вычислении площади плоской фигуры. Как вы думаете, с чего мы должны начать разговор о площади? (должны повторить теорию)

Начнем с теоретических фактов.

Площадь – это положительная величина, характеризующая размеры различных фигур.

Вспомним свойства площади: 1) Равные фигуры имеют равные площади;

  • Если фигура разбивается на части, то площадь этой фигуры равна сумме площадей ее частей.
  • Площадь квадрата равна квадрату его стороны.

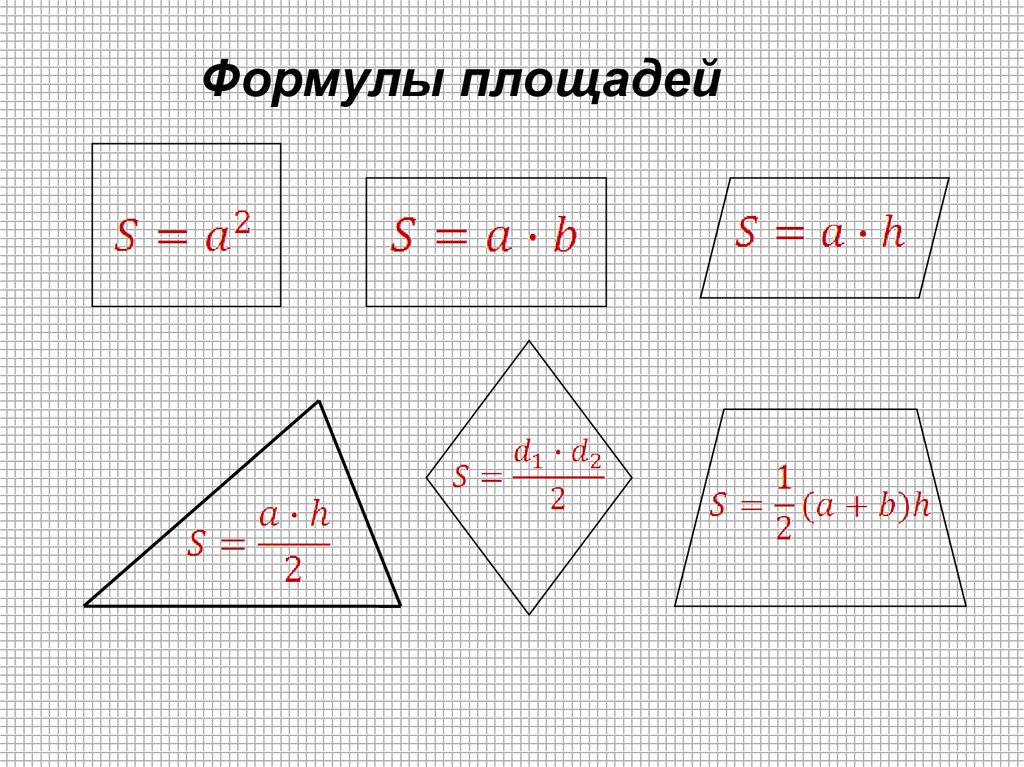
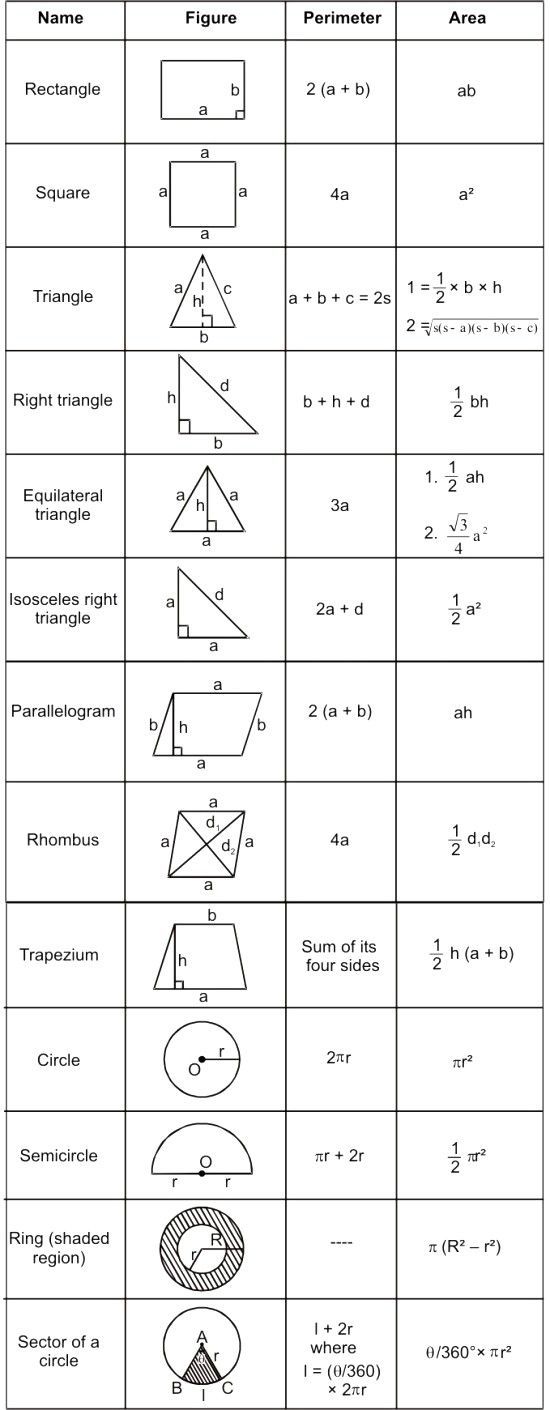
Что необходимо знать для решения задач по этой теме? (формулы)

Давайте вспомним основные формулы для вычисления площадей плоских фигур. Для этого выполним задание (в тетради).

Вам нужно найти соответствие между изображенными фигурами и формулой, по которой вычисляется площадь данной фигуры. В тоже время каждой формуле соответствует буква. Выполнив верно задание, вы получите фразу. Попробуйте это сделать в элективных тетрадях. Давайте проверим.

А теперь заполним таблицу формул площадей, которая останется у вас и будет помогать при подготовке к экзамену.

3.     Блиц-работа в парах «Мини-задачи на применение формул»

  1. Периметр квадрата равен 32. Найдите площадь этого квадрата. (64 см²)
  1. Найти площадь параллелограмма, изображенного на рисунке. (192)
  1. Найти площадь треугольника, изображенного на рисунке. (102)
  1. Найти площадь прямоугольного треугольника, два катета которого равны 4см и 10см. (20см²)
  1. Найдите площадь треугольника. (6)
  1. Найти площадь трапеции, изображенной на рисунке. (75)
  1. Найдите площадь ромба, если его диагонали равны 14 и 6. (42)

Выполним проверку полученных вами ответов. За каждое верно выполненное задание вы зарабатываете 1 балл. (Слайды).

Теперь самостоятельно оцените свою работу.

  1. Решение задач по готовым чертежам. Задачи взяты из открытого банка заданий ОГЭ сайта ФИПИ.

5.        «Нестандартный» метод вычисления площади многоугольника.

А что вы можете мне сказать о площади вот такой фигуры?

Сможем ли мы найти её площадь по формулам, которые мы сегодня повторяли? Как найти площадь нестандартной фигуры?

(Слайд) Для этого часто используют формулу, которая названа в честь австрийского математика Георга Александра Пика. Формула для расчёта площади многоугольника была открыта им в 1899 году. В Германии эта теорема включена в школьные учебники.

В=15, Г=13, S=20,5

А теперь выполните небольшую самостоятельную работу по вычислению площади по формуле Пика.

6.     Итог урока

Заканчивая сегодняшнее занятие, я хочу вас спросить:

Какие методы вычисления площадей мы сегодня повторили? Что-то новое вы сегодня узнали?

Было ли вам интересно?

Как вы думаете, помогут ли эти знания вам лучше сдать экзамен?

скачать презентацию

Нахождение площади фигуры

Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y).

В разделе геометрический смысл определенного интеграла мы разобрались с нахождением площади криволинейной трапеции G. Вот полученные формулы:

Однако при решении задач на нахождение площади очень часто приходится иметь дело с более сложными фигурами.

В этой статье мы поговорим о вычислении площади фигур, границы которых заданы функциями в явном виде, то есть, как y=f(x) или x=g(y), и подробно разберем решение характерных примеров.

Навигация по странице.

  • Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).

  • Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y

    ).

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).

Теорема.

Пусть функции  и  определены и непрерывны на отрезке [a;b], причем  для любого значения x из [a;b]. Тогда площадь фигуры G, ограниченной линиями x=a, x=b,  и  вычисляется по формуле .

Аналогичная формула справедлива для площади фигуры, ограниченной линиями y=c,y=d,  и : .

Доказательство.

Покажем справедливость формулы для трех случаев:

В первом случае, когда обе функции неотрицательные, в силу свойства аддитивности площади сумма площади исходной фигуры G и криволинейной трапеции  равна площади фигуры .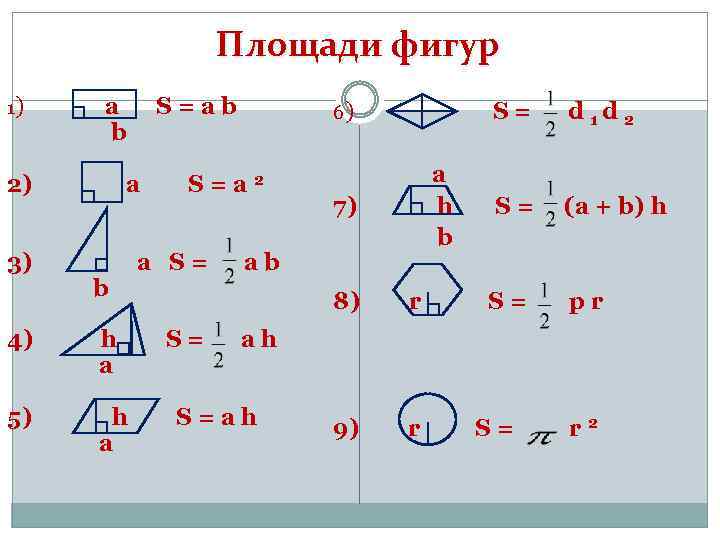 Следовательно,

Поэтому, . Последний переход возможен в силу третьего свойства определенного интеграла.

Аналогично, во втором случае справедливо равенство . Вот графическая иллюстрация:

В третьем случае, когда обе функции неположительные, имеем . Проиллюстрируем это:

Теперь можно переходить к общему случаю, когда функции  и пересекают ось Ox.

Обозначим точки пересечения . Эти точки разбивают отрезок [a; b]на n частей , где . Фигуру Gможно представить объединением фигур . Очевидно, что на своем интервале  попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как

Следовательно,

Последний переход справедлив в силу пятого свойства определенного интеграла.

Графическая иллюстрация общего случая.

Таким образом, формула  доказана.

Пришло время перейти к решению примеров на нахождение площади фигур, ограниченных линиями y=f(x) и x=g(y).

К началу страницы

Примеры вычисления площади фигуры, ограниченной линиямиy=f(x) или x=

g(y).

Решение каждой задачи будем начинать с построения фигуры на плоскости. Это нам позволит сложную фигуру представить как объединение более простых фигур. При затруднениях с построением обращайтесь к статьям: основные элементарные функции, их свойства и графики; геометрические преобразования графиков функций и исследование функции и построение графика.

Пример.

Вычислить площадь фигуры, ограниченной параболой  и прямыми , x=1, x=4.

Решение.

Построим эти линии на плоскости.

Всюду на отрезке [1;4] график параболы  выше прямой . Поэтому, применяем полученную ранее формулу для площади и вычисляем определенный интеграл по формуле Ньютона-Лейбница:

Немного усложним пример.

Пример.

Вычислить площадь фигуры, ограниченной линиями .

Решение.

В чем здесь отличие от предыдущих примеров? Ранее у нас всегда были две прямых, параллельных оси абсцисс, а сейчас только одна x=7. Сразу возникает вопрос: где взять второй предел интегрирования? Давайте для этого взглянем на чертеж.

Стало понятно, что нижним пределом интегрирования при нахождении площади фигуры является абсцисса точки пересечения графика прямой y=x и полу параболы . Эту абсциссу найдем из равенства:

Следовательно, абсциссой точки пересечения является x=2.

Обратите внимание.

В нашем примере и по чертежу видно, что линии  и y=x пересекаются в точке(2;2) и предыдущие вычисления кажутся излишними. Но в других случаях все может быть не так очевидно. Поэтому рекомендуем всегда аналитически вычислять абсциссы и ординаты точек пересечения линий.

Очевидно, график функции y=x расположен выше графика функции  на интервале [2;7]. Применяем формулу для вычисления площади:

Еще усложним задание.

Пример.

Вычислить площадь фигуры, ограниченной графиками функций  и .

Решение.

Построим график обратной пропорциональности  и параболы .

Прежде чем применять формулу для нахождения площади фигуры, нам нужно определиться с пределами интегрирования. Для этого найдем абсциссы точек пересечения линий, приравняв выражения  и .

При отличных от нуля значениях x равенство  эквивалентно уравнению третьей степени  с целыми коэффициентами. Можете обратиться к разделу решение кубических уравнений чтобы вспомнить алгоритм его решения.

Легко проверить, что x=1 является корнем этого уравнения: .

Разделив выражение  на двучлен x-1, имеем:

Таким образом, оставшиеся корни находятся из уравнения :

Теперь из чертежа стало видно, что фигура G заключена выше синей и ниже красной линии на интервале .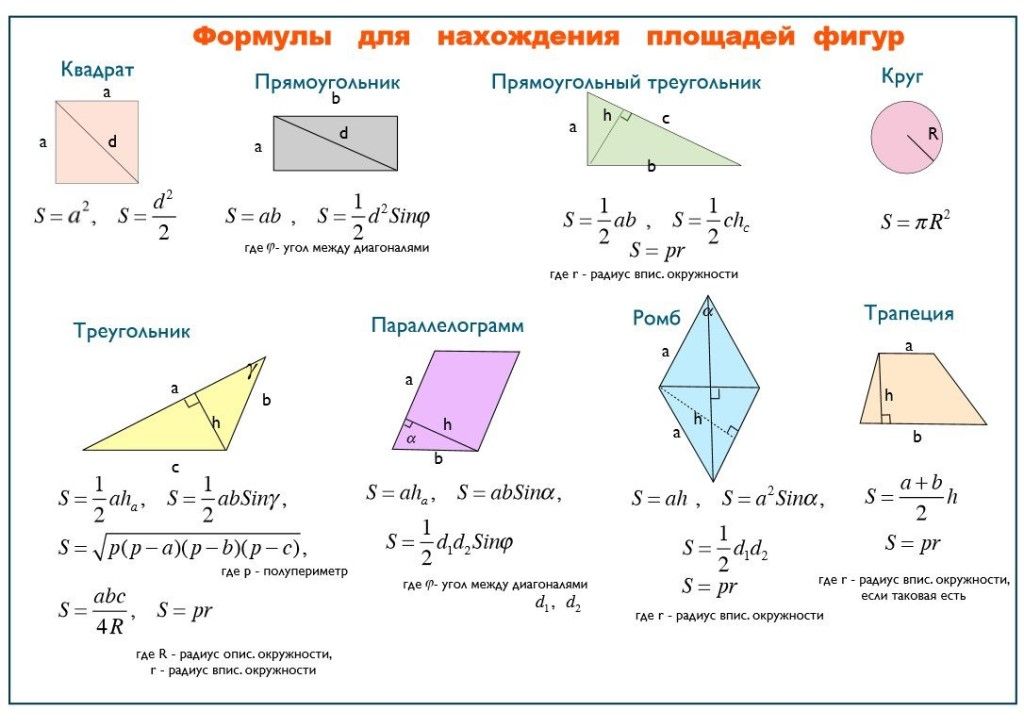 Таким образом, искомая площадь будет равна

Рассмотрим еще один характерный пример.

Пример.

Вычислить площадь фигуры, ограниченной кривыми  и осью абсцисс.

Решение.

Сделаем чертеж.

 — это обычная степенная функция с показателем одна треть, график функции  можно получить из графика  отобразив его симметрично относительно оси абсцисс и подняв на единицу вверх.

Найдем точки пересечения всех линий.

Ось абсцисс имеет уравнение y=0.

Графики функций  и y=0 пересекаются в точке (0;0) так как x=0 является единственным действительным корнем уравнения .

Графики функций  и y=0 пересекаются в точке (2;0), так как x=2является единственным корнем уравнения .

Графики функций  и  пересекаются в точке (1;1), так как x=1является единственным корнем уравнения . Это утверждение не совсем очевидно, но  — функция строго возрастающая, а  — строго убывающая, поэтому, уравнение  имеет не более одного корня.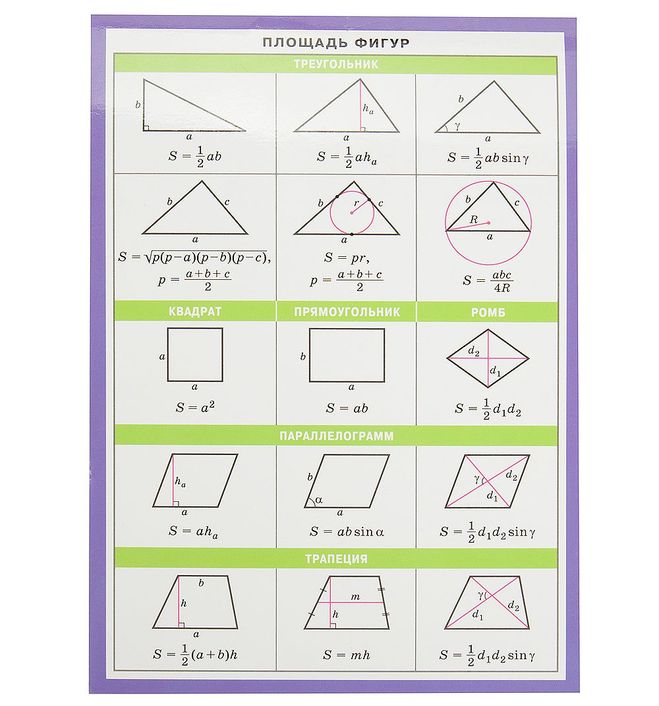

Как же действовать дальше? Здесь есть несколько вариантов.

  1. Можно фигуру G представить суммой двух криволинейных трапеций. Первая фигура расположена выше оси абсцисс и ниже синей линии на отрезке , вторая фигура расположена выше оси абсцисс и ниже красной линии на отрезке . Следовательно, искомая площадь будет равна .

  2. Можно фигуру G представить разностью двух фигур. Первая фигура является криволинейной трапецией и расположена выше оси 

    Ox и ниже синей линии на отрезке , вторая фигура расположена выше красной и ниже синей линии на отрезке . В этом случае площадь представляем как .

  3. А можно фигуру G рассматривать на отрезке , заключенной правее синей линии и левее красной. Вот на этом варианте и остановимся.

Единственное замечание: в этом случае для нахождения площади придется использовать формулу вида . То есть, ограничивающие линии нужно представить в виде функций от аргумента y. Это сделать в нашем случае достаточно легко. Разрешим уравнения  и  относительно x:

Таким образом, искомая площадь равна

Мы бы пришли к этому же результату и в двух других случаях.

Можно переходить к последнему примеру.

Пример.

Вычислить площадь плоской фигуры, ограниченной линиями .

Решение.

С построением этих линий проблем возникнуть не должно. На чертеже красной линией изображен график функции , синей линией , а черной линией .

Определим точки пересечения линий.

Начнем с графиков функций  и :

Найдем точку пересечения графиков функций  и :

Осталось найти точку пересечения прямых  и :

Дальше можно поступить двояко:

Тогда площадь фигуры равна:

Для этого случая, перед применением формулы для вычисления площади фигуры, разрешим уравнения линий относительно x:

Таким образом, площадь равна:

Как видите, значения совпадают.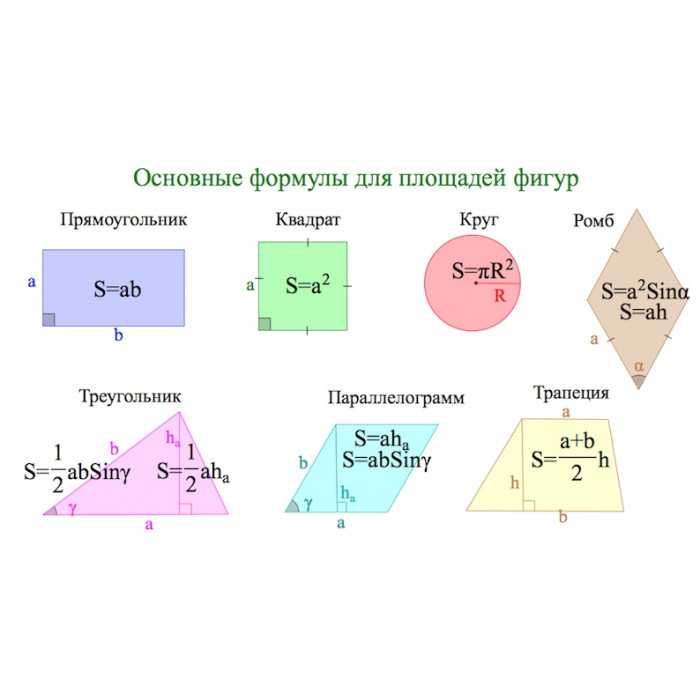

К началу страницы

Подведем итог.

Мы разобрали все наиболее часто встречающиеся случаи нахождения площади фигуры, ограниченной явно заданными линиями. Для этого нужно уметь строить линии на плоскости, находить точки пересечения линий и применять формулу для нахождения площади, что подразумевает наличие навыков вычисления определенных интегралов.

Шпаргалка по математическим формулам для розничной торговли

+ скачать бесплатно

Это шпаргалка по наиболее важным математическим формулам, используемым в розничной торговле и электронной коммерции. Не стесняйтесь загружать бесплатные копии PDF и Excel ниже.

Пройдите онлайн-видеокурс по математике в сфере розничной торговли и узнайте, как различные метрики связаны друг с другом, и посмотрите на приложения на бизнес-примерах. Пройдите курс и получите сертификат об окончании.

РОЗНИЧНАЯ МАТЕМАТИКА ФОРМУЛЫ

  • Уравнение продаж
  • квадроцикл
  • МПК
  • Преобразование
  • Трафик
  • СПФ
  • LFL рост
  • Открыт для покупки (OTB)
  • GMROI
  • Продать через
  • Инвентарь старения
  • Оборачиваемость запасов
  • ДСИ
  • Усадка
  • Обложка форвардного запаса
  • Валовая прибыль
  • Уценка
  • Разметка
  • EBITDA
  • Рентабельность по чистой прибыли

Уравнение продаж

Продажи = Трафик x Конверсия x ATV

ATV = Общий объем продаж ÷ Количество транзакций

РЕКОМЕНДУЕМЫЙ КУРС