Подобные треугольники. Отношение площадей подобных треугольников 8 класс онлайн-подготовка на Ростелеком Лицей |
Подобные треугольники. Отношение площадей подобных треугольников.
При сравнении двух величин возникает вопрос: во сколько раз одна больше другой?
Например, во сколько раз собака пробежит быстрее некоторое расстояние, чем это же расстояние проползёт жук? Или какую часть всех деревьев парка составляют дубы?
Ответ в таких случаях дается в виде частного двух чисел, которое называют отношением. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Отношением отрезков АВ и СD называется отношение их длин, т. е. ABCD (или AB:CD).
На рисунке отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если AB:A1B1 = CD:C1D1.
В геометрии фигуры одинаковой формы называют подобными.
А какие два треугольника называют подобными? Возьмём два треугольника ABC и A1B1C1, у которых угол А равен углу A1, угол B равен углу B1, а угол C равен углу C1.
Тогда стороны AB и A1B1, BC и B1C1, AC и A1C1 называются сходственными. И если эти сходственные стороны пропорциональны, то есть AB:A1B1 = BC:B1C1 = AC:A1C1, то треугольники ABC и A1B1C1 являются подобными. Подобие треугольников обозначается следующим образом ⊿ABC∼⊿A1B1C1.
Подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.
Отношение сходственных сторон называют коэффициентом подобия.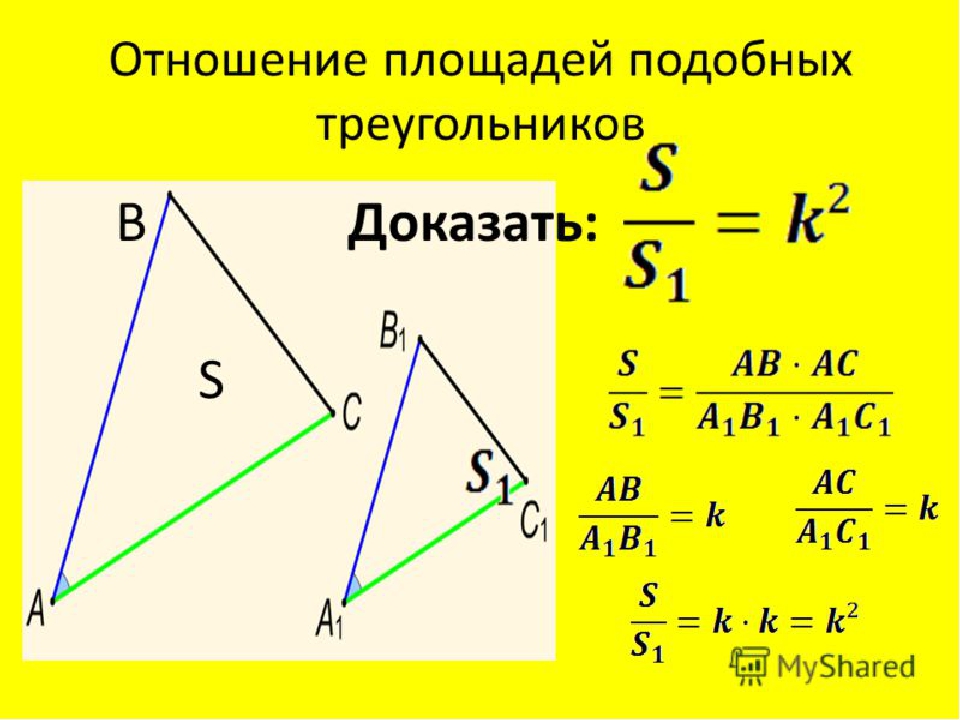 Если стороны треугольника ABC в два раза больше сторон треугольника A1B1C1, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Если стороны треугольника ABC в два раза больше сторон треугольника A1B1C1, то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Подобие треугольников можно установить, проверив только некоторые из равенств:
AB:A1B1 = BC:B1C1 = AC:A1C1 = 2, то есть k=2.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано: ⊿ABC∼⊿A1B1C1, k — коэффициент подобия.
Найти: отношение площадей ABC и A1B1C1
Решение:
Обозначим SABC= S, SA1B1C1 = S
∠A = ∠A1, значит, SS1=AB∙ACA1B1∙A1C1 (площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол).
ABA1B1=k
ACA1C1=k
Следовательно, SS1=k2.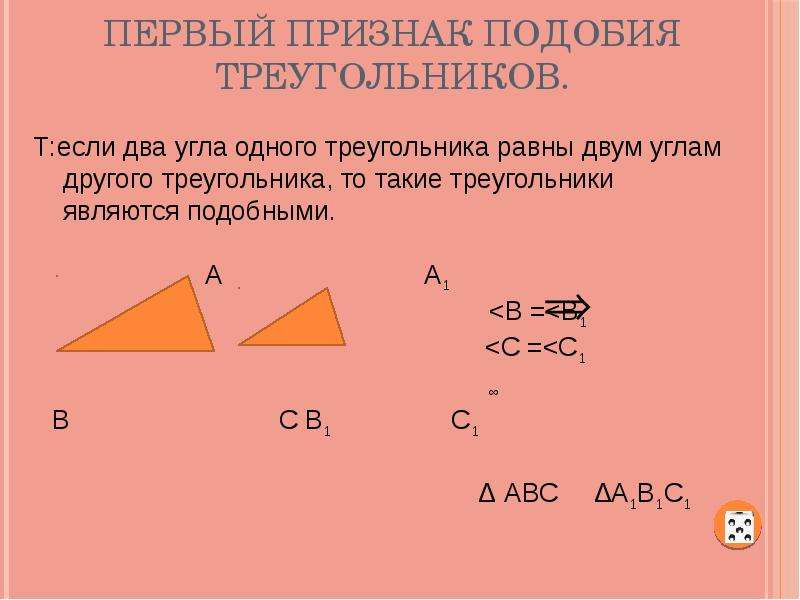
Задача. Площади подобных треугольников АВС и А1В1С1 равны соответственно 20 см2 и 5 см2. Сторона А1В1 = 2 см. Найдите сходственную ей сторону АВ треугольника АВС.
Выше мы доказали, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
SS1=k2, значит, 205=k2, следовательно k=2.
k=ABA1B1=2, значит, AB=2∙A1B1=2∙4=8 см.
Ответ: 8 см.
Площади подобных треугольников относятся как коэффициент подобия. Отношение площадей подобных треугольников
1.3. Отношение площадей подобных треугольников. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Доказательство. Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то.
Слайд 11 из презентации ««Подобные треугольники» 8 класс» . Размер архива с презентацией 1756 КБ.
Размер архива с презентацией 1756 КБ.Геометрия 8 класс
краткое содержание других презентаций«Прямоугольники» — Диагональ. Картины. Стороны прямоугольника. Периметр прямоугольника. Человек. Площадь прямоугольника. Прямоугольник в жизни. Определение. Сторона прямоугольника. Диагонали. Сказка о прямоугольнике. Прямоугольник. Противоположные стороны.
«Скалярное произведение в координатах» — Вектор. Теорема Наполеона. Следствие. Свойства скалярного произведение векторов. Обменяйтесь карточками. Решим задание. Геометрия. Скалярное произведение в координатах и его свойства. Математический тест. Новый материал. Решение треугольника. Математическая разминка. Имя автора теоремы. Доказательство теоремы Пифагора.
«Нахождение площади параллелограмма» — Площадь параллелограмма. Устные упражнения. Высота. Определение высоты параллелограмма. Высоты параллелограмма. Найдите площадь параллелограмма. Площадь треугольника. Площадь квадрата. Свойства площадей. Найдите площадь треугольника. Найдите периметр квадрата. Основание. Найдите площадь прямоугольника. Найдите площадь квадрата. Признаки равенства прямоугольных треугольников.
Найдите периметр квадрата. Основание. Найдите площадь прямоугольника. Найдите площадь квадрата. Признаки равенства прямоугольных треугольников.
«Векторы 8 класс» — Назовите равные и противоположные векторы. Векторы на уроках физики. Абсолютная величина вектора. Абсолютная величина вектора. Прямоугольник, у которого все стороны равны. Понятие вектора. Определите координаты вектора. Найдите и назовите равные векторы на данном рисунке. Равные вектора. Самостоятельная работа в парах. Координаты вектора. Девиз урока. Скалярные физические величины, такие как сила трения, скорость.
«Разные виды симметрии» — Требование. Скользящая симметрия. Равнобедренный треугольник с зеркальной симметрией. Теория групп. Симметрия в биологии. Вращательная симметрия. Двулучевая радиальная симметрия. Что такое симметрия. Суперсимметрия. Симметрия в геометрии. Симметрия в физике. Верхушка колокола. Появление билатеральной симметрии. Билатеральная симметрия. Теорема Нётер. Отсутствие симметрии. Симметрия физике. Центральная симметрия.
Центральная симметрия.
«Квадрат в жизни» — Квадраты находят нас везде. Индия. Магический квадрат Альбрехта Дюрера. История. Квадраты. Магический квадрат Ло Шу. Черный квадрат. Загадка «Квадрат». Интересные факты о квадрате. Геометрическая фигура квадрат. Квадрат Малевича. Магический квадрат. Прямоугольник. Квадрат. Основное понятие. Интересные факты. Китай.
Тип урока:
Цель урока: Доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач.
Задачи урока:
- обучающие – доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач; развивающие – развивать умение анализировать и подбирать аргументацию при решении задачи, способ решения которой неизвестен; воспитательные – воспитывать интерес к предмету через содержание учебного процесса и создание ситуации успеха, воспитывать умение работать в группе.
Учащийся владеет следующими знаниями:
1. Определение подобных треугольников;
Определение подобных треугольников;
2. Применение определения подобных треугольников при решении задач;
3. Теорема об отношении площадей треугольников имеющих по равному углу;
Единица деятельностного содержания, которое нужно усвоить учащимся:
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
3. Работа с проблемной ситуацией.
4. Подведение итогов урока и запись домашнего задания, рефлексия.
Методы обучения: словесные, наглядные, проблемно-поисковые.
Формы обучения: фронтальная работа, работа в мини-группы, индивидуальная и самостоятельная работа.
Технологии: задачно-целевая, информационные технологии , компетентностный подход.
Оборудование:
- компьютер, проектор для демонстрации презентации, интерактивная доска, документ камера; компьютерная презентация в Microsoft PowerPoint; опорный конспект;
Здравствуйте ребята! Садитесь. Сегодня у нас необычный урок. У нас на уроке присутствуют гости. Повернитесь, пожалуйста, и поприветствуйте их кивком головы. Спасибо ребята. Садитесь.
Сегодня на уроке мы будем работать не в тетрадях, а в опорных конспектах, которые будете заполнять на продолжение всего урока. Подпишите его. Оценка за урок будет состоять из двух составляющих: за опорный конспект и за активную работу на уроке.
2. Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.Мы продолжаем с вами изучать тему «подобие треугольников». Поэтому давайте вспомним то, что изучали на прошлом уроке.
Теоретическая разминка. Тест. В ваших опорных конспектах первое задание имеет тестовый характер. Ответьте на вопросы, выбирая один из предложенных вариантов ответа, где необходимо впишите свой ответ. 1) Учитель: Что называется отношением двух отрезков? Ответ: Отношением двух отрезков двух отрезков называется отношение их длин.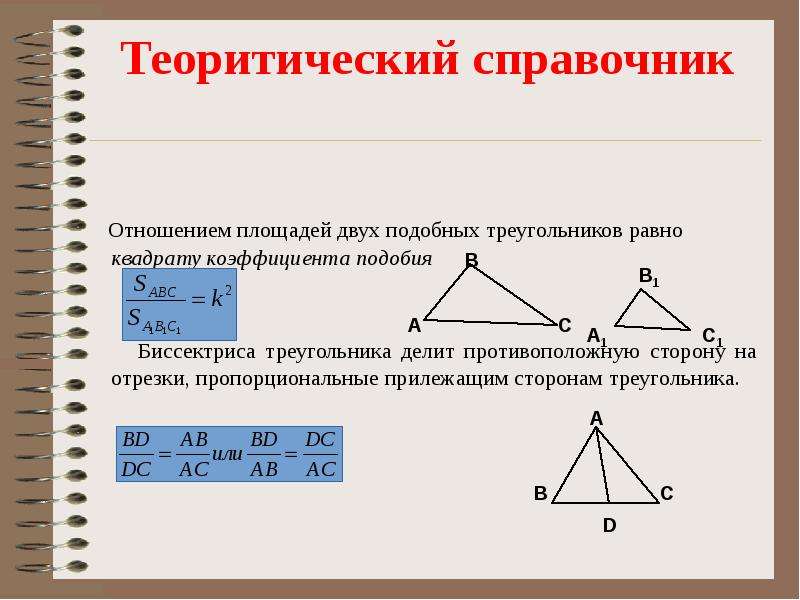 2) Учитель: В каком случае отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 Ответ: отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 , если Ваши варианты. Хорошо. Не забудьте исправить у кого не так. 3) Учитель: Дайте определение подобных треугольников? Обратитесь к вашему опорному конспекту. У Вас три варианта ответа на этот вопрос. Выберите правильный. Обведите его. Так, пожалуйста, какой вариант выбрал ты_______
2) Учитель: В каком случае отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 Ответ: отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 , если Ваши варианты. Хорошо. Не забудьте исправить у кого не так. 3) Учитель: Дайте определение подобных треугольников? Обратитесь к вашему опорному конспекту. У Вас три варианта ответа на этот вопрос. Выберите правильный. Обведите его. Так, пожалуйста, какой вариант выбрал ты_______ Ответ: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.
Молодцы! Исправьте у кого не так.4)
Учитель: Чему равно отношение площадей двух треугольников, имеющих по равному углу?Ответ: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Решение задач по готовым чертежам. Далее наша разминка будет происходить в ходе решения задач по готовым чертежам. Эти задачи так же вы видите в ваших опорных конспектах.
https://pandia.ru/text/80/368/images/image005_101.gif»>
Ответ: стороны бермудского треугольника 2000 км, 1840 км, 2220 км. Длина границы 6060 км.
Рефлексия.
Возможный ответ: у подобных треугольников сходственные стороны пропорциональны.
2. Ситуация успеха.
С размерами Бермудского треугольника мы разобрались. Ну а теперь выясним измерения цветочной клумбы. Переворачиваем опорные конспекты. Вторая задача. Эту задачу решаем, работая в парах. Проверяем аналогичным способом, но только результат будет представлять уже пара первая справившаяся с заданием.
Ответ: стороны треугольной клумбы 10м и 11м 20 см.
Итак, сверяемся. Все ли согласны? Кто решал другим способом?
Рефлексия.
Каким способом действия вы пользовались при решении этой задачи? Запишите в свой опорный конспект.
Возможный ответ:
· у подобных треугольников соответственные углы равны;
· площади треугольников имеющих по равному углу относятся как произведения сторон заключающих равные углы.
3. Ситуация сбоя.
5. Изучение нового материала.При решении третьей задачи учащиеся сталкиваются с проблемой. У них не получается решить задачу, так как по их мнению недостаточно полное условие задачи или получают необоснованный ответ.
С таким типом задач учащиеся не встречались ранее, поэтому произошел сбой при решении задачи.
Рефлексия.
Каким методом пытались решить?
Почему не получилось решить последнее уравнение?
Ученики: Мы не можем найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.
Таким образом, цель нашего урока найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.
Давайте переформулируем задачу на геометрический язык. Решим ее, а затем вернемся к этой задаче.
Вывод: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Ну а теперь давайте вернемся к задаче №3 и решим ее, опираясь на доказанный факт.
7. Итог урока
Что сегодня вы научились делать нового?
Решать задачи, в которых известны коэффициент подобия и площадь одного из подобных треугольников.
Какое геометрическое свойство нам в этом помогло?
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Домашнее задание.
П. 58 стр.139 № 000, 548
Творческое задание.
Найдите чему равно отношение периметров двух подобных треугольников (№ 000)
Цель урока: дать определение подобных треугольников, доказать теорему об отношении подобных треугольников.
Задачи урока:
- Образовательные: учащиеся должны знать определение подобных треугольников, теорему об отношении подобных треугольников, уметь применять их при решении задач, реализовывать межпредметные связи с алгеброй и физикой.

- Воспитательные: воспитывать трудолюбие, внимательность, прилежание, воспитывать культуру поведения учащихся.
- Развивающие: развитие у учащихся внимания, развития умения рассуждать, логически мыслить, делать выводы, развития у учащихся грамотной математической речи и мышления, развивать навыки самоанализа и самостоятельности.
- Здоровьесберегающие: соблюдение санитарно-гигиенических норм, смена видов деятельности на уроке.
Оборудование: компьютер, проектор, дидактический материал: самостоятельные и контрольные работы по алгебре и геометрии для 8 класса А.П. Ершова, и др.
Тип урока: изучение нового материала.
Ход урока
I. Организационный момент (приветствие, проверка готовности к уроку).
II. Сообщение темы урока.
Учитель: В повседневной жизни встречаются предметы одинаковой формы, но разных размеров.
Пример: футбольный и теннисный мячи.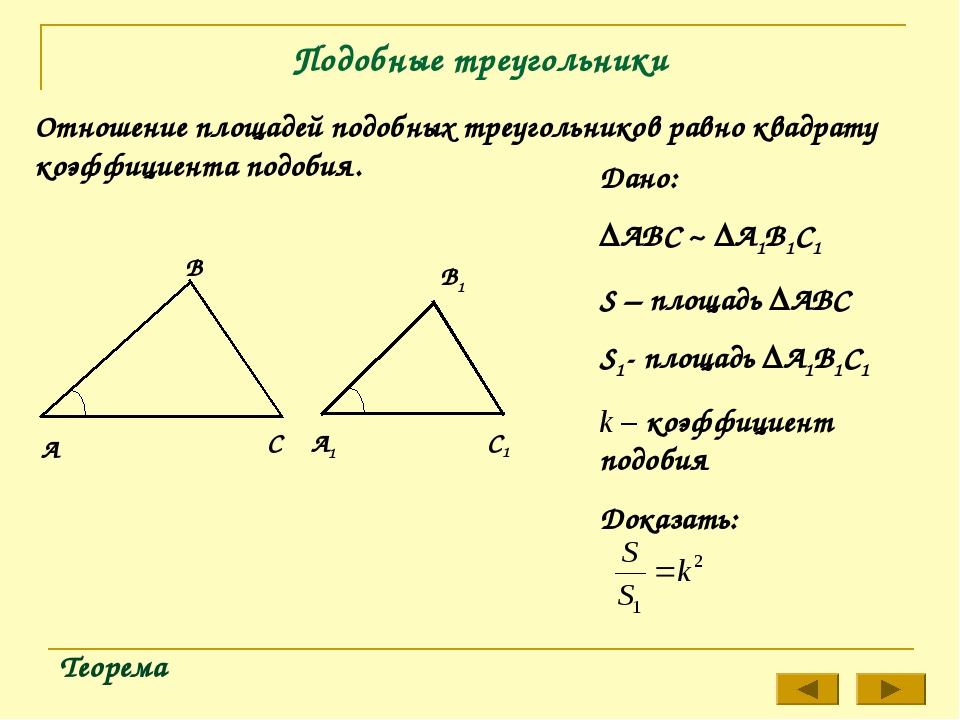
В геометрии фигуры одинаковой формы называют подобными: любые два круга, любые два квадрата.
Введем понятие подобных треугольников.
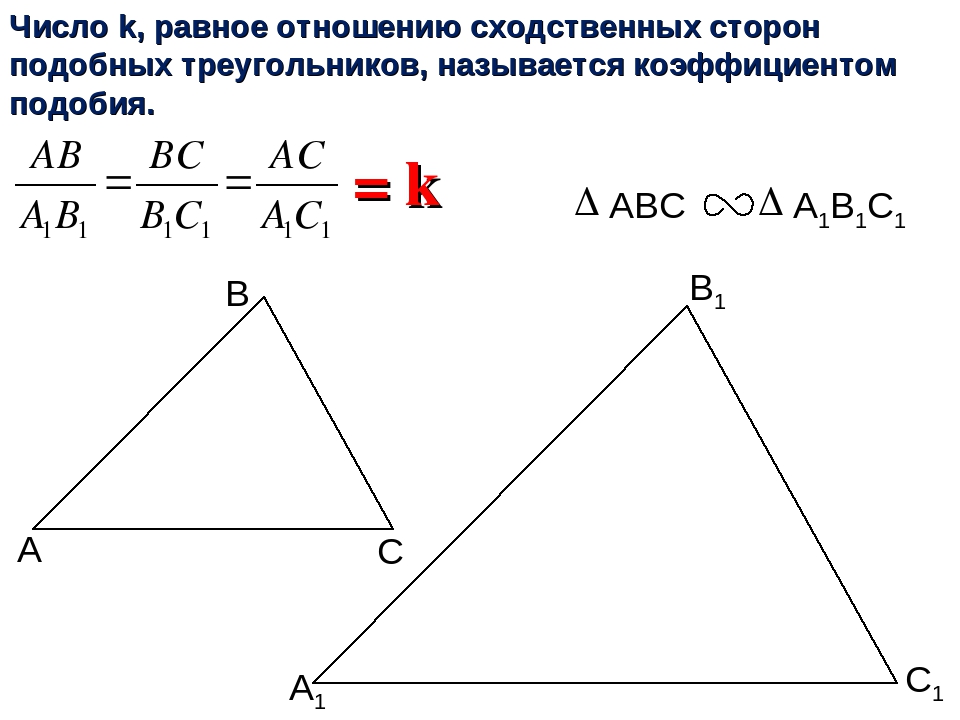
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. ΔABC ~ A 1 B 1 C 1
1. Устно: Подобны ли треугольники? Почему? (заготовленный чертеж на экране).
а) Треугольник ABC и треугольник A 1 B 1 C 1 , если AB = 7, BC = 5, AC = 4, ∠A = 46˚, ∠C = 84˚, ∠A 1 = 46˚, ∠B 1 = 50˚, A 1 B 1 = 10,5 , B 1 C 1 = 7,5, A 1 C 1 = 6.
б) В одном равнобедренном треугольнике угол при вершине равен 24˚, а в другом равнобедренном треугольнике угол при основании равен 78˚.
Ребята! Вспомним теорему об отношении площадей треугольников, имеющих по равному углу.
Теорема: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.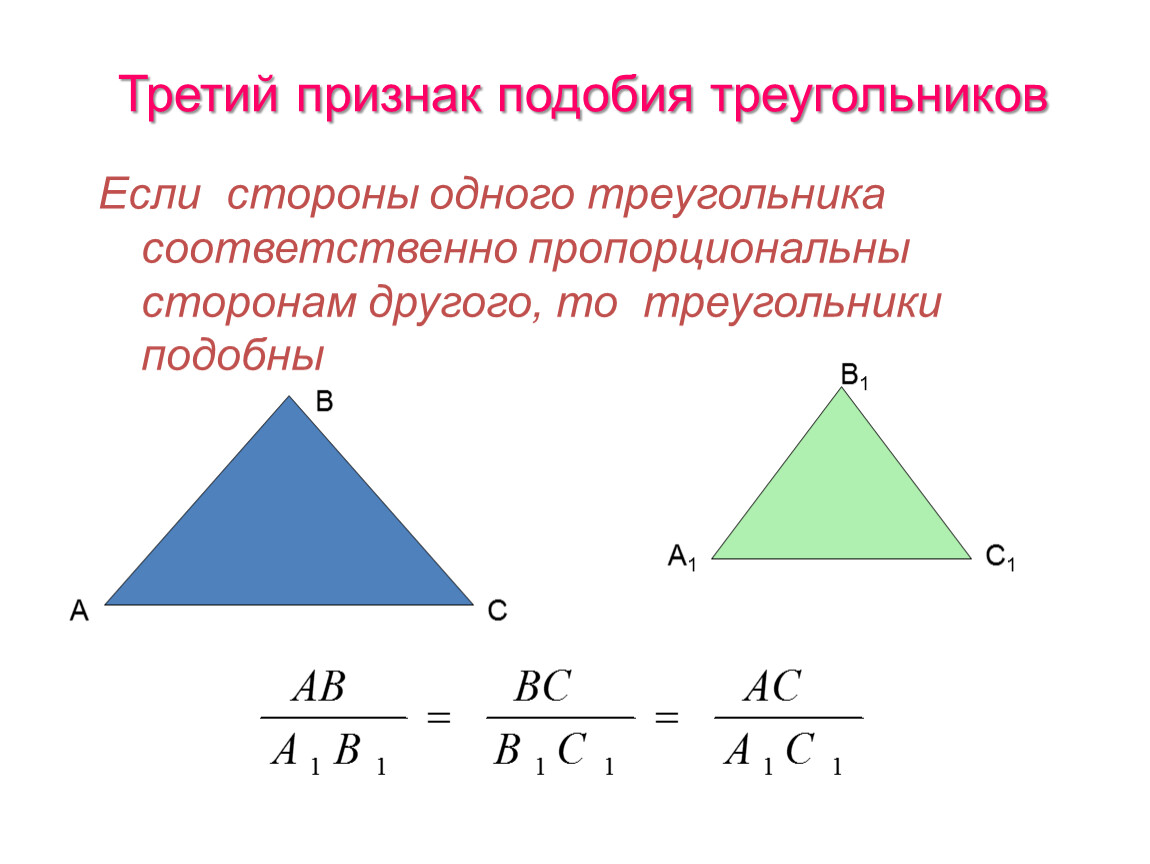
2. Письменная работа по заготовленным чертежам.
На экране чертеж:
а) Дано: BN: NC = 1:2,
BM = 7 см, AM = 3 см,
S MBN = 7 см 2 .
Найти: S ABC
(Ответ: 30 см 2 .)
б) Дано: AE = 2 см,
S AEK = 8 см 2 .
Найти: S ABC
(Ответ: 56 см 2 .)
3. Докажем теорему об отношении площадей подобных треугольников (доказывает теорему ученик на доске, помогает весь класс ).
Теорема: Отношение двух подобных треугольников равно квадрату коэффициента подобия.
4. Актуализация знаний.
Решение задач:
1. Площади двух подобных треугольников равны 75 см 2 и 300 см 2 . Одна из сторон второго треугольника равна 9см. Найти сходственную ей сторону первого треугольника. (Ответ: 4,5 см.)
2. Сходственные стороны подобных треугольников равны 6см и 4см, а сумма их площадей равна 78 см 2 . Найти площади этих треугольников. (Ответ: 54 см 2 и 24 см 2 . )
)
При наличии времени самостоятельная работа обучающего характера.
Вариант 1
У подобных треугольников сходственные стороны равны 7 см и 35 см.
Площадь первого треугольника равна 27 см 2 .
Найти площадь второго треугольника. (Ответ: 675 см 2 .)
Вариант 2
Площади подобных треугольников равны 17 см 2 и 68 см 2 . Сторона первого треугольника равна 8см. Найти сходственную сторону второго треугольника. (Ответ: 4 см.)
5. Домашнее задание: учебник геометрии 7-9 Л.С. Атанасян и др., п. 57, 58, № 545, 547.
6. Подведение итогов урока.
Урок 34. Теорема об отношении площадей подобных треугольников. ТЕОРЕМА. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. где k – коэффициент подобия. Отношение периметров двух подобных треугольников равно коэффициенту подобия. В. А. С. Р. М. К. Решение задач: № 545, 549. Домашнее задание: п. 56-58, № 544, 548.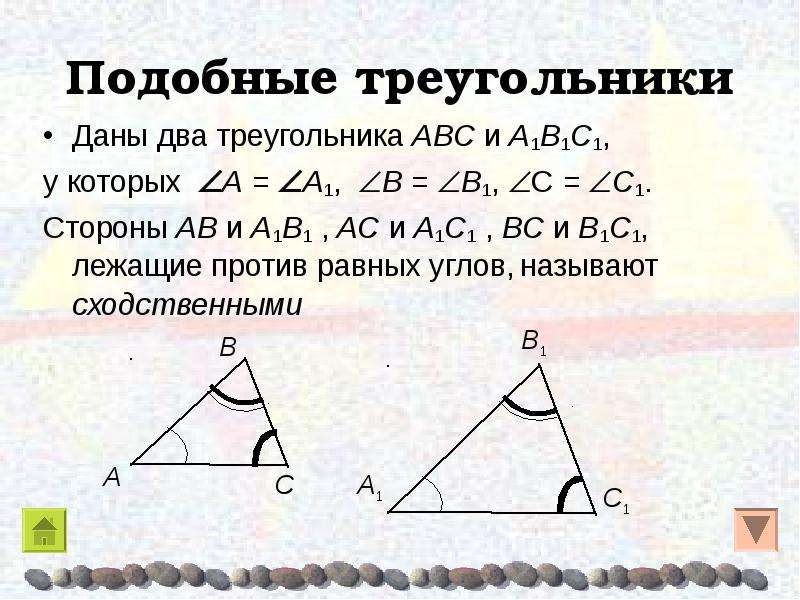
Геометрия 8 класс
краткое содержание других презентаций«Определение осевой симметрии» — Симметрия в природе. Подсказка. Оси симметрии. Изобразите точку. Построение точки. Построение треугольника. Построение отрезка. Народы. Симметрия в поэзии. Фигуры, не обладающие осевой симметрией. Фигуры, обладающие двумя осями симметрии. Прямоугольник. Симметрия. Прямая. Постройте точки. Осевая симметрия. Отрезок. Ось симметрии. Начертите две прямые. Точки, лежащие на одном перпендикуляре. Соразмерность.
«Нахождение площади параллелограмма» — Найдите площадь параллелограмма. Площадь параллелограмма. Высота. Найдите площадь квадрата. Площадь квадрата. Высоты параллелограмма. Найдите площадь треугольника. Признаки равенства прямоугольных треугольников. Найдите площадь прямоугольника. Определение высоты параллелограмма. Основание. Площадь треугольника. Найдите периметр квадрата. Свойства площадей. Устные упражнения.
Свойства площадей. Устные упражнения.
«Задачи на нахождение площади» — Урок -объяснение нового материала, выполнен в виде презентации «Power point». Основная цель. «Площадь параллелограмма». «Площадь трапеции». ПрОВЕРКА УСВОЕННОГО МАТЕРИАЛА. Решить задачу. Рабочая тетрадь №42, повторить все изученные формулы. Вывести формулы площадей прямоугольника, параллелограмма, трапеции, треугольника. Расширить и углубить представления об измерении площадей. Сформировать у учащихся понятие площади.
«Геометрия «Подобные треугольники»» — Два треугольника называются подобными. Пропорциональность сторон угла. Значения синуса, косинуса и тангенса. Первый признак подобия треугольников. Пропорциональные отрезки в прямоугольном треугольнике. Свойство биссектрисы треугольника. Математический диктант. Найти площадь равнобедренного прямоугольного треугольника. Пропорциональные отрезки. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.
«Прямоугольники» — Человек. Противоположные стороны. Сторона прямоугольника. Сказка о прямоугольнике. Стороны прямоугольника. Прямоугольник в жизни. Периметр прямоугольника. Прямоугольник. Диагонали. Картины. Диагональ. Определение. Площадь прямоугольника.
Сторона прямоугольника. Сказка о прямоугольнике. Стороны прямоугольника. Прямоугольник в жизни. Периметр прямоугольника. Прямоугольник. Диагонали. Картины. Диагональ. Определение. Площадь прямоугольника.
««Площадь прямоугольника» 8 класс» — Площадь заштрихованного квадрата. Стороны каждого из прямоугольников. АBCD и DСМK – квадраты. На стороне АВ построен параллелограмм. Единицы измерения площадей. Найдите площадь квадрата. Площадь прямоугольника. ABCD – параллелограмм. Свойства площадей. Найдите площадь четырехугольника. Площади квадратов, построенных на сторонах прямоугольника. Пол комнаты, имеющий форму прямоугольника. Площадь квадрата равна квадрату его стороны.
Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Определение 1
Отношением двух отрезков называется отношение их длин.
Понятие пропорциональности отрезков имеет место и для большего числа отрезков.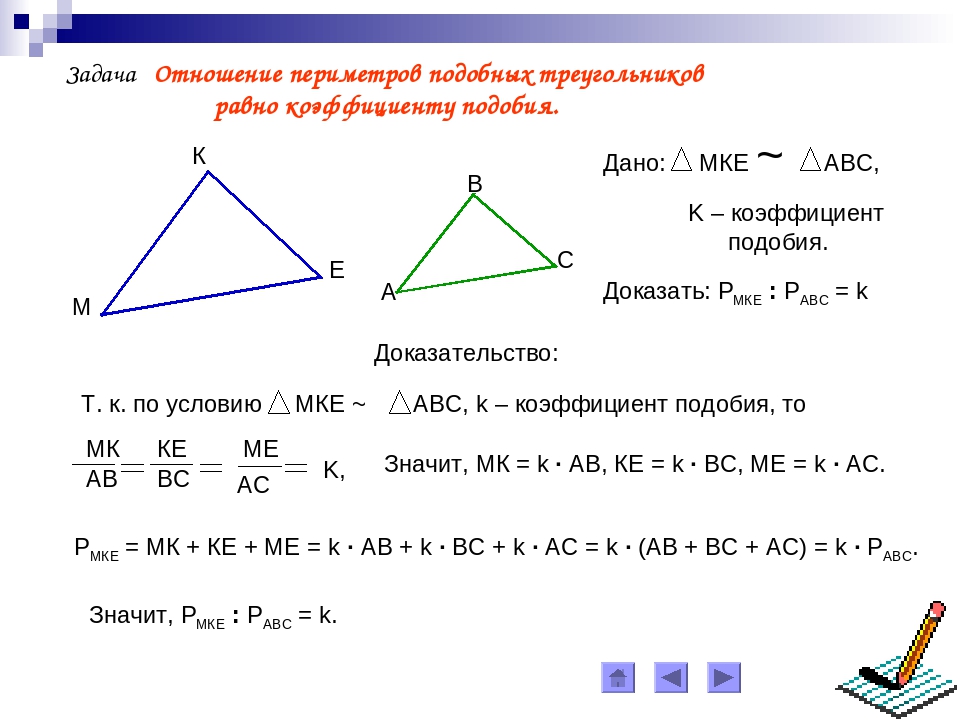 Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Определение 3
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.
Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Определение 4
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Определение 5
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]
На рисунке 1 изображены подобные треугольники.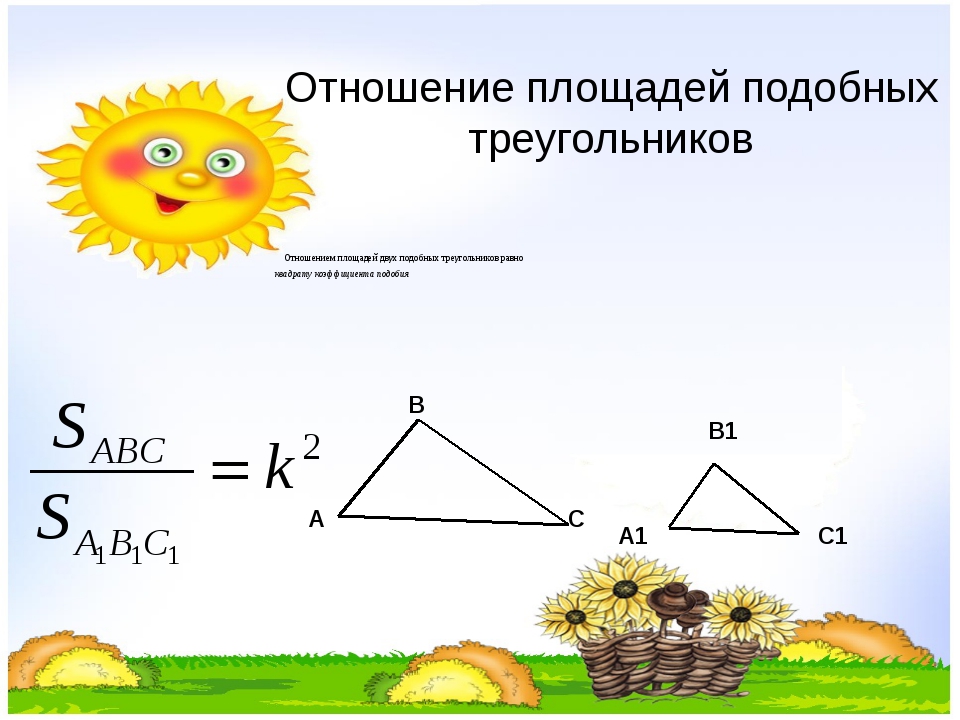 2\]
2\]
Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).
Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Теорема 2
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Пример 1
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
- Образовательные: учащиеся должны знать определение подобных треугольников, теорему об отношении подобных треугольников, уметь применять их при решении задач, реализовывать межпредметные связи с алгеброй и физикой.
- Воспитательные: воспитывать трудолюбие, внимательность, прилежание, воспитывать культуру поведения учащихся.
- Развивающие: развитие у учащихся внимания, развития умения рассуждать, логически мыслить, делать выводы, развития у учащихся грамотной математической речи и мышления, развивать навыки самоанализа и самостоятельности.
- Здоровьесберегающие: соблюдение санитарно-гигиенических норм, смена видов деятельности на уроке.
Создайте треугольник \ (poly1 = \ bigtriangleup AED \) и треугольник \ (poly2 = \ bigtriangleup BED \).Обозначим через \ (poly1 \) и \ (poly2 \) площади треугольников. Каково соотношение \ (poly1 \) и \ (poly2 \)? Подтвердите свой ответ!
Создайте треугольник \ (poly3 = \ bigtriangleup DEC \). Каково соотношение \ (poly3 \) и \ (poly1 \)? Подтвердите свой ответ!
Каково соотношение \ (poly3 \) и \ (poly2 \)? Подтвердите свой ответ!
Покажите, что \ (\ dfrac {a} {b} = \ dfrac {c} {d} \)!
\ (\ угол ABD = \ угол CED \)
треугольник \ (\ bigtriangleup BCE \) — равнобедренный треугольник, поэтому \ (BC = CE \).
\ (\ угол BDA = \ угол CDE \)
\ (\ bigtriangleup ABD \ sim \ bigtriangleup CED \)
\ (\ dfrac {AB} {AD} = \ dfrac {CE} {CD} \)
\ (\ dfrac {AB} {AD} = \ dfrac {BC} {CD} \)
- Решать приложения, используя свойства треугольников
- Используйте теорему Пифагора
- Решение приложений с использованием свойств прямоугольника
- Прочтите задачу и убедитесь, что все слова и идеи понятны.Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите то, что мы ищем.
- Этикетка то, что мы ищем, выбирая переменную для его представления.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в уравнение, решенное на шаге 5, и убедившись, что он имеет смысл в контексте проблемы.
- Ответьте на вопрос полным предложением.
- Сумма углов треугольника равна .
- Периметр — это сумма длин сторон треугольника.
- Площадь треугольника равна половине основания, умноженной на высоту.
- геометрическая последовательность : упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением. Также известна как геометрическая прогрессия.
- Положительно, все условия будут того же знака, что и начальный термин
- Отрицательный, члены будут чередоваться между положительным и отрицательным
- Больше, чем [latex] 1 [/ latex], будет экспоненциальный рост в сторону положительной бесконечности ([latex] + \ infty [/ latex]).
- [latex] 1 [/ latex], последовательность будет постоянной
- Между [latex] -1 [/ latex] и [latex] 1 [/ latex], но не [latex] 0 [/ latex], будет экспоненциальный спад в сторону [latex] 0 [/ latex]
- [latex] -1 [/ latex], прогрессия — чередующаяся последовательность (см. Чередующиеся серии)
- Меньше [latex] -1 [/ latex], для абсолютных значений наблюдается экспоненциальный рост в сторону положительной и отрицательной бесконечности (из-за чередования знака)
- геометрическая серия : Бесконечная последовательность добавляемых чисел, члены которой находятся путем умножения предыдущего члена на фиксированное ненулевое число, называемое обычным отношением.
- геометрическая прогрессия : серия чисел, в которой каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обычным отношением.
- [латекс] 4 + 40 + 400 + 4000 + \ точки [/ латекс] имеет общее соотношение [латекс] 10 [/ латекс]
- [латекс] \ displaystyle {9 + 3 + 1 + \ frac {1} {3} + \ frac {1} {9} + \ dots} [/ latex] имеет общее соотношение [латекс] {\ frac {1 } {3}} [/ латекс]
- [латекс] 3 + 3 + 3 + 3 + \ точки [/ латекс] имеет общее соотношение [латекс] 1 [/ латекс]
- [латекс] \ displaystyle {1- \ frac {1} {2} + \ frac {1} {4} — \ frac {1} {8} + \ dots} [/ latex] имеет общее соотношение [латекс] — \ frac {1} {2} [/ latex]
- [латекс] 3-3 + 3-3 + \ точки [/ латекс] имеет общее соотношение [латекс] -1 [/ латекс]
- Если [латекс] r [/ латекс] находится между [латекс] -1 [/ латекс] и [латекс] +1 [/ латекс], члены ряда становятся все меньше и меньше, приближаясь к нулю в пределе, и ряд сходится к сумме.Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.
- Если [latex] r [/ latex] больше, чем [latex] 1 [/ latex] или меньше, чем [latex] -1 [/ latex], члены ряда становятся все больше и больше по величине. Сумма членов также становится все больше и больше, и в серии нет суммы. Сериал расходится.
- Если [latex] r [/ latex] равно [latex] 1 [/ latex], все члены серии совпадают.Сериал расходится.
- Если [latex] r [/ latex] равно [latex] -1 [/ latex], термины принимают поочередно два значения [latex] \ left (\ text {eg}, 2, -2,2, -2,2 , -2, \ cdots \ right) [/ латекс]. Сумма членов колеблется между двумя значениями [latex] \ left (\ text {eg.}, 2,0,2,0,2,0, \ cdots \ right) [/ latex]. Это другой тип дивергенции, и снова у ряда нет суммы.
- Сумма геометрического ряда конечна, пока члены стремятся к нулю; поскольку числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
- Для бесконечного геометрического ряда, который сходится, его сумму можно вычислить по формуле [latex] \ displaystyle {s = \ frac {a} {1-r}} [/ latex].
- сходиться : приблизиться к конечной сумме.
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно изменяются с общим соотношением.
- Повторяющаяся десятичная дробь может рассматриваться как геометрическая последовательность, общее отношение которой равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].
- Архимед использовал сумму геометрического ряда, чтобы вычислить площадь, ограниченную параболой и прямой линией.
- Внутренняя часть снежинки Коха представляет собой союз бесконечного множества треугольников.При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры.
- Знание бесконечных рядов позволяет нам решать древние проблемы, такие как парадоксы Зенона.
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно меняются с общим соотношением.
- фрактал : природное явление или математический набор, который демонстрирует повторяющийся узор, который можно увидеть в любом масштабе.
Шаг 2. Нарисуйте специальный прямоугольный треугольник 45 45 90 и определите, что говорит триггерная функция. В этом случае для «sin 45» функция синуса и соответствующее правило, которому мы следуем: SOH , то есть sin = противогипотенуза \ sin = \ frac {противоположный} {гипотенуза} sin = гипотенузапротивоположный
Пример 1. Специальный прямоугольный треугольник 45-45-90, изображающий особые соотношения и углы.Шаг 3. Подставьте значения, полученные с помощью соответствующей тригонометрической формулы, и упростите.Помните, что вопрос требует точных значений, поэтому в этом случае вы можете оставить свой ответ в виде дроби.
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$.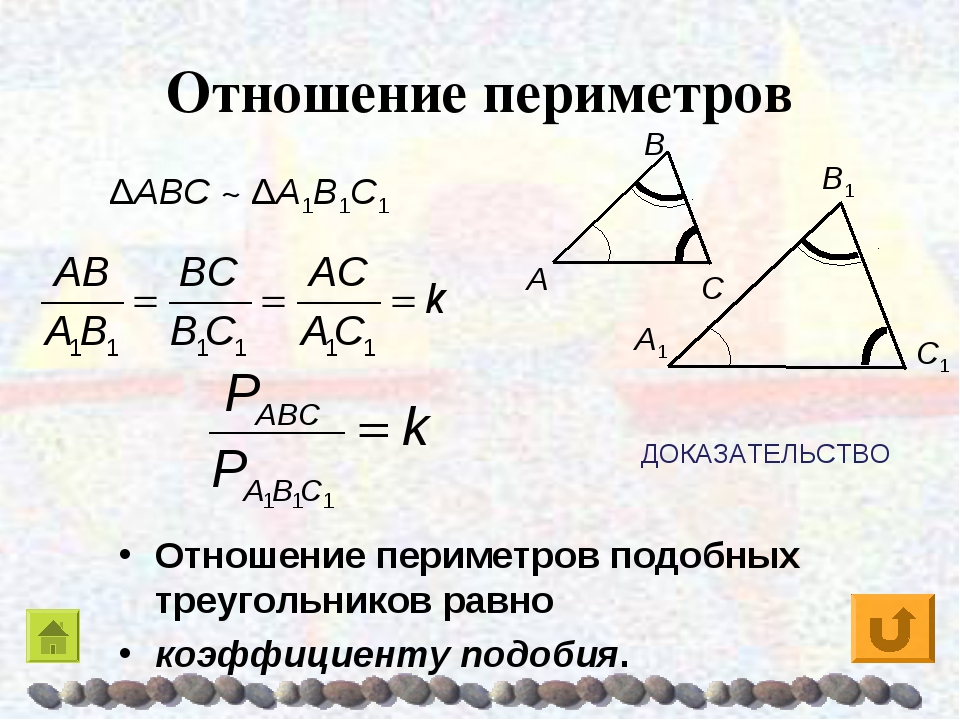 2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
Подобие треугольников, отношение площадей, сторон. Коэффициент подобия. Тест
Всего вопросов: 10
Вопрос 1. Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см.
Вопрос 2. Отрезок ВD является биссектрисой треугольника ABC. Найдите AB, если ВС=9см, AD=7,5см, DC=4,5см.
Вопрос 3. Отрезок AD является биссектрисой треугольника ABC. Найдите BD, если АВ=14 см, ВС=20 см, АС=21 см.
Вопрос 4. Биссектриса AD треугольника АВС делит сторону BC на отрезки CD и BD, равные соответственно 4,5 см и 13,5 см. Найдите АВ, если периметр треугольника АВС равен 42 см.
Вопрос 5. В подобных треугольниках АВС и KМN стороны АВ и КМ, BC и MN являются сходственными. Найдите наименьшую сторону треугольника KMN, если АВ=4 см, ВС=5 см, СА=7 см, КМ/АВ=2,1
Вопрос 6. Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второго треугольника равна 9 м. Найдите сходственную ей сторону первого треугольника.
Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второго треугольника равна 9 м. Найдите сходственную ей сторону первого треугольника.
Вопрос 7. Треугольники АВС и A1B1C1 подобны, и их сходственные стороны относятся как 6:5. Площадь треугольника АВС больше площади треугольника A1B1C1 на 77 см2. Найдите площадь меньшего треугольника.
Вопрос 8. Треугольники АВС и A1B1C1 подобны. Сходственные стороны ВС и B1C1 соответственно равны 1,4 м и 56 см. Найдите отношение периметров треугольников АВС и A1B1C1 .
Вопрос 9. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите наибольшую сторону треугольника, подобного данному, если его периметр 26 см.
Вопрос 10. Через точку М, взятую на медиане АD треугольника ABC, и вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите отношение АК/КС, если M — середина отрезка AD.
Через точку М, взятую на медиане АD треугольника ABC, и вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите отношение АК/КС, если M — середина отрезка AD.
Видеоурок по геометрии 8 класс тема Отношение площадей подобных треугольников
Скорость воспроизведения04:17
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.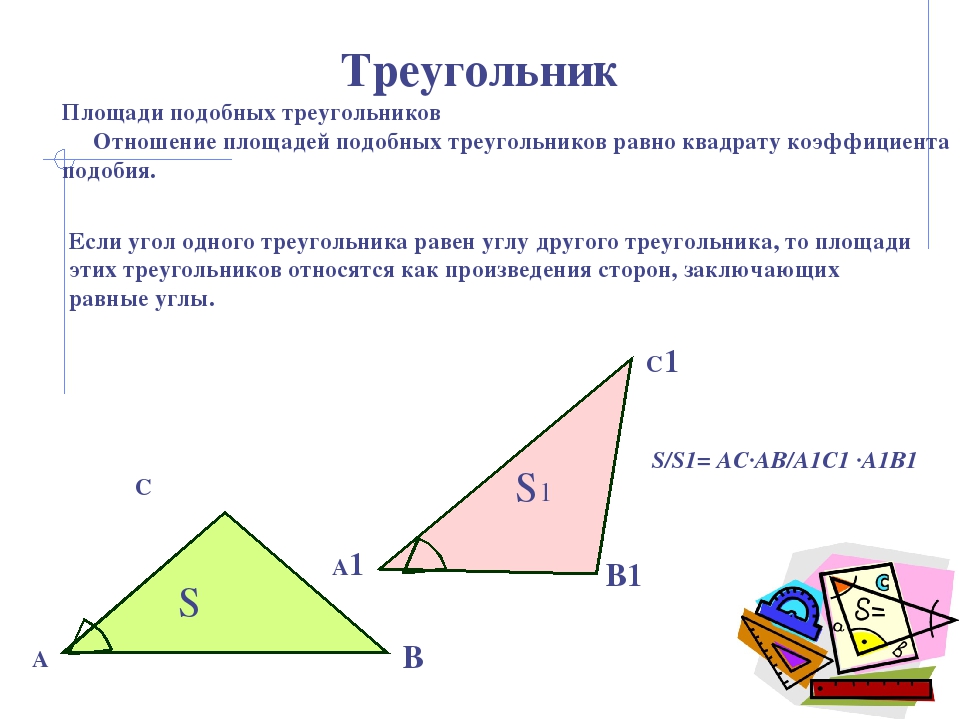
Следующие уроки
03:23
06:16
07:25
08:14
07:01
Определение подобных треугольников
Два треугольника называются подобными, если отношения всех их соответствующих сторон равны.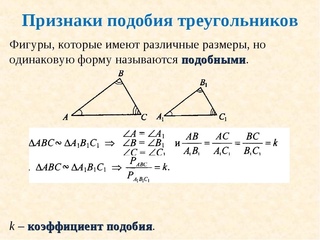 Отношение \(k\) соответствующих сторон подобных треугольников называется коэффициентом подобия этих треугольников.
Отношение \(k\) соответствующих сторон подобных треугольников называется коэффициентом подобия этих треугольников.
$$ \triangle{ABC} \backsim \triangle{A_1B_1C_1} \Leftrightarrow \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}; $$ $$ k=\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} $$
Первый признак подобия треугольников
Если отношения двух сторон треугольников и равны углы между этими сторонами, то такие треугольники подобны.
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}, \, \angle{A}=\angle{A_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$
Второй признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
$$ \angle{A}=\angle{A_1}, \, \angle{B}=\angle{B_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$
Третий признак подобия треугольников
Если отношения всех соответствующих сторон треугольников равны, то такие треугольники подобны.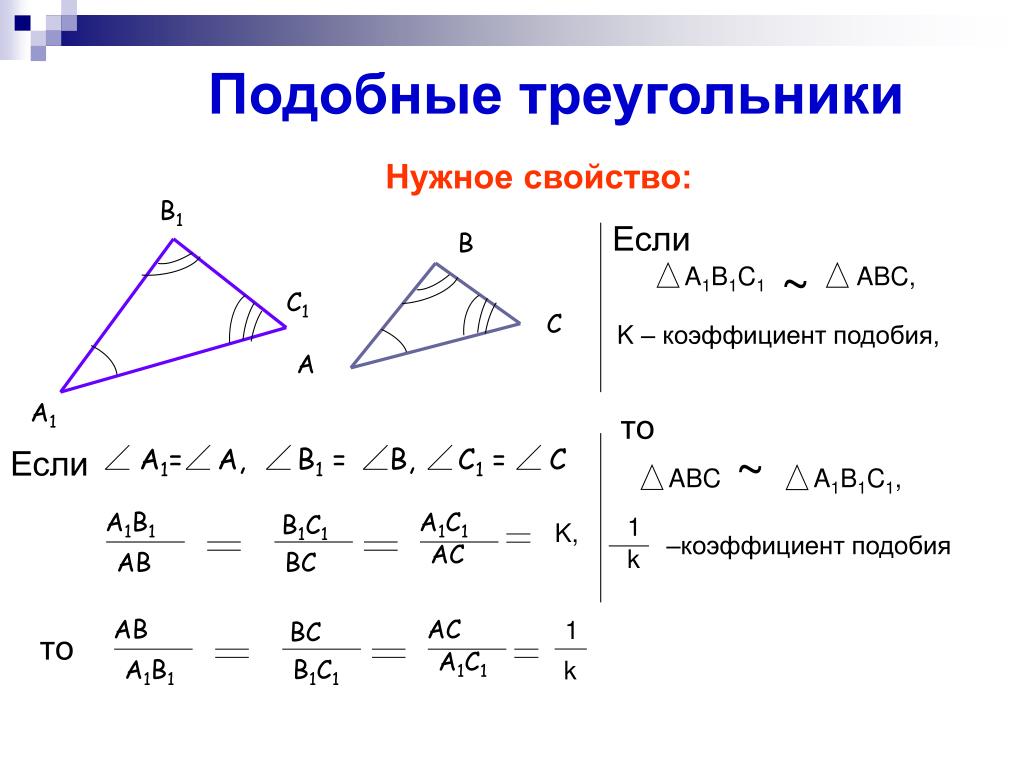
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$
Отношение соответствующих линейных элементов подобных треугольников
Отношение любых двух соответствующих линейных элементов подобных треугольников равно коэффициенту подобия этих треугольников. (Соответствующие линейные элементы – это отрезки подобных фигур, полученные одинаковой конструкцией. Например, медианы треугольников, проведённые к соотвествующим сторонам, радиусы описанных окружностей, периметры, и так далее.)
$$ \frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1} \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1} $$
Параллельные прямые и подобие треугольников
Если стороны двух треугольников лежат на соответственно параллельных или совпадающих прямых, то такие треугольники подобны.
В частности, параллельные прямые отсекают от угла, либо вертикальных углов, подобные треугольники.
$$ AB || A_1B1, \, AC || A_1C_1, \, BC ||B_1C_1 \Rightarrow \triangle{ABC} \backsim \triangle{A_1B_1C_1}; $$ $$ AB || A_1B_1, \, D=AA_1 \cap BB_1 \Rightarrow \triangle{ABD} \backsim \triangle{A_1B_1D} $$
Трапеция и подобные треугольники
При пересечении диагоналей трапеции, а также продолжений её боковых сторон, образуются подобные треугольники, прилежащие к основаниям трапеции. Коэффициент подобия в обоих случаях равен отношению оснований трапеции.
$$ \triangle{AOD} \backsim \triangle{COB}, \quad k=\frac{AD}{BC}; $$ $$ \triangle{AED} \backsim \triangle{BEC}, \quad k=\frac{AD}{BC} $$
Подобие треугольников. Третий признак подобия
В этом уроке, вы найдете решение задач по геометрии, которые используют правила подобия треугольников и являются интересными для решения. Я их размещаю здесь если они вызывают некоторые трудности при решении у школьников.
Треугольники ABC и A1B1C1 подобны. Соотношение сторон теругольников 3:4 . Площадь одного из них больше площади другого на 14 см2. Найдите площади треугольников.
Решение
Для решения данной задачи будем руководствоваться основным свойством подобия треугольников — все размеры одного теругольника подобны размерам другого. Сначала опустим на сторону а каждого треугольника высоту h. Таким образом площадь первого треугольника будет выражаться формулой S1=1/2ah, а площадь второго треугольника формулой S2=1/2*3/4a*3/4h. Таким образом, можно определить соотношение площадей треугольников:
S1/S2 = 1/2 ah / ( 1/2 * 9/16 ah)
S1/S2 = ah / ( 9/16 ah)
S1/S2 = 16/9
Выше перечисленные преобразования мы могли бы не проводить, если нам известна теорема: «площади подобных треугольников относятся как квадрат соотношения их сторон»
Выразим площадь одного треугольника через площадь другого:
S1=16S2/9
По условию задачи S1-S2=14, таким образом
16S2/9-S2=14
7/9S2=14
S2=18, следовательно S1 = 14+18=32
Ответ: 18 и 32
Задача
Стороны AB и DC трапеции ABCD продлили так, что прямые AB и DC пересеклись в точке E. Таким образом, продолжения сторон трапеции образовали треугольник площадью 98 квадратных сантиметров. Найти площадь трапеции, если ее основания относятся друг к другу как 5 к 7.
Таким образом, продолжения сторон трапеции образовали треугольник площадью 98 квадратных сантиметров. Найти площадь трапеции, если ее основания относятся друг к другу как 5 к 7.
Решение
Начало решения.
Из условия задачи видно, что у нас получились треугольники EAD и EBC. Поскольку оба треугольника имеют общий угол E, а основания трапеции, являющиеся параллельными, согласно теореме Фалеса, отсекают на сторонах AE и DE пропорциональные отрезки отрезки, то треугольники EAD и EBC являются подобными.
Способ 1.
Опустим из вершины E высоту на основание AD. Она же будет высотой для основания BC, поскольку основания трапеции параллельны. Обозначим высоту для треугольника EAD как h1, а для треугольника EBC как h2.
Таким образом:
Площадь треугольника EAD будет равна SEAD=1/2*AD*h1.
Площадь треугольника EBC будет равна SEBC=1/2*BC*h2.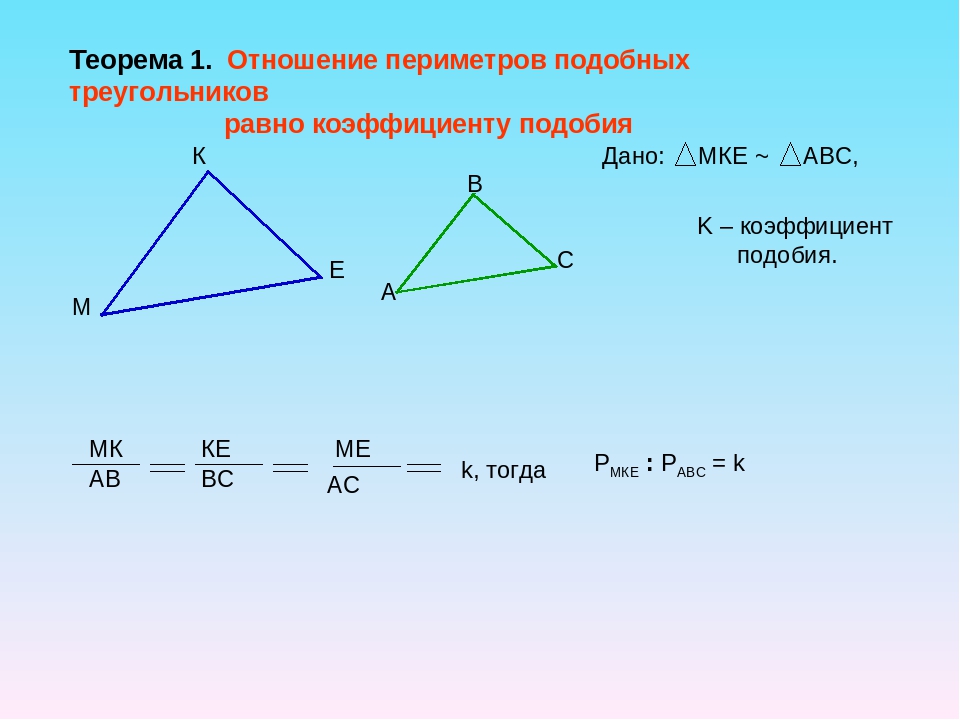
Поскольку треугольники подобны, то все стороны относятся друг к другу с одним и тем же коэффициентом подобия. Поскольку основания трапеции относятся дрцг к другу как 5:7, то и все остальные стороны относятся друг к другу с тем же соотношением. Из этого следует:
BC / AD = 5 / 7
BC = 5AD / 7
аналогично:
h2 / h1 = 5 / 7
h2 = 5h1 / 7
Таким образом:
SEBC=1/2*BC*h2.
Подставим значения сторон меньшего подобного треугольника через значения сторон большего подобного треугольника:
SEBC=1/2*(5AD / 7)*(5h1 / 7)
SEBC=1/2*AD*h1*25 / 49
Заметим, что по условию задачи площадь получившегося треугольника EAD равна 98 сантиметрам, одновременно SEAD=1/2*AD*h1.
Подставим вместо указанного выражения его значение:
SEBC = 98*25/49
SEBC = 50 см2
Способ 2.
Если нам известна теорема: «площади подобных треугольников относятся как квадрат соотношения их сторон», то площади подобных треугольников AED и BEC будут соотноситься как 52 : 72. То есть:
SEBC / SEAD = 52 / 72
SEBC / SEAD = 25 / 49
SEBC = SEAD * 25 / 49
Поскольку площадь треугольника EAD известна нам по условию и составляет 98 см2 , то
SEBC = 98 * 25 / 49
SEBC = 50 см2
Продолжение решения.
Площадь трапеции ABCD равна разности площадей треугольников AED и BEC. Таким образом, площадь трапеции равна 98 — 50 = 48 см2.
Ответ: 48 см2.
Подобие треугольников. Первый признак подобия | Описание курса | Подобие треугольников. Использование в задачах
Урок по теме «Определение подобных треугольников, отношение площадей подобных треугольников»
Цель урока: дать определение подобных треугольников, доказать теорему об отношении подобных треугольников.
Задачи урока:
Оборудование: компьютер, проектор, дидактический материал: самостоятельные и контрольные работы по алгебре и геометрии для 8 класса А. П. Ершова, и др.
П. Ершова, и др.
Тип урока: изучение нового материала.
Ход урока
I. Организационный момент (приветствие, проверка готовности к уроку).
II. Сообщение темы урока.
Учитель: В повседневной жизни встречаются предметы одинаковой формы, но разных размеров.
Пример: футбольный и теннисный мячи.
В геометрии фигуры одинаковой формы называют подобными: любые два круга, любые два квадрата.
Введем понятие подобных треугольников.
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. ΔABC ~ A1B1C1
1. Устно: Подобны ли треугольники? Почему? (заготовленный чертеж на экране).
Устно: Подобны ли треугольники? Почему? (заготовленный чертеж на экране).
а) Треугольник ABC и треугольник A1B1C1, если AB = 7, BC = 5, AC = 4, ∠A = 46˚, ∠C = 84˚, ∠A1 = 46˚, ∠B1 = 50˚, A1B1 = 10,5 , B1C1 = 7,5, A1C1 = 6.
б) В одном равнобедренном треугольнике угол при вершине равен 24˚, а в другом равнобедренном треугольнике угол при основании равен 78˚.
Ребята! Вспомним теорему об отношении площадей треугольников, имеющих по равному углу.
Теорема: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
2. Письменная работа по заготовленным чертежам.
На экране чертеж:
а) Дано: BN : NC = 1:2,
BM = 7 см, AM = 3 см,
SMBN = 7 см2.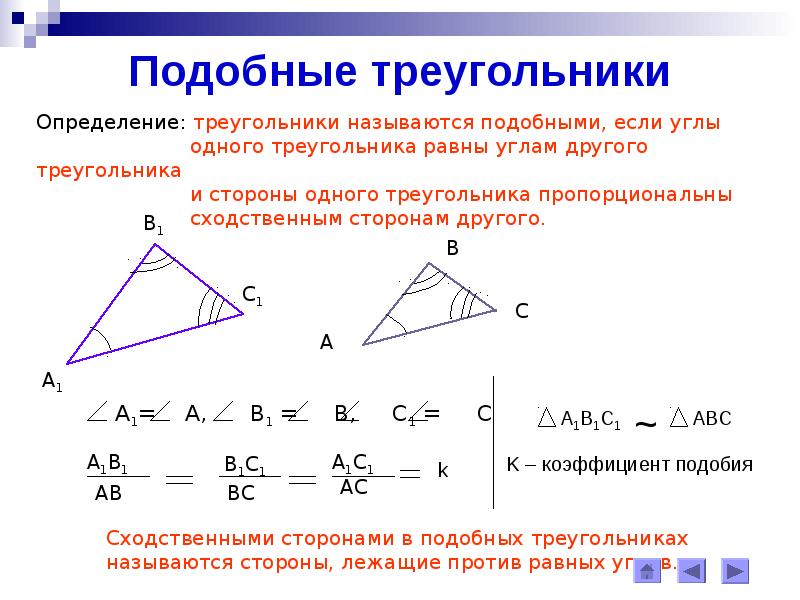
Найти: SABC
(Ответ: 30 см2.)
б) Дано: AE = 2 см,
EB = 5 см,
AK = KC,
SAEK = 8 см2.
Найти: SABC
(Ответ: 56 см2.)
3. Докажем теорему об отношении площадей подобных треугольников (доказывает теорему ученик на доске, помогает весь класс).
Теорема: Отношение двух подобных треугольников равно квадрату коэффициента подобия.
4. Актуализация знаний.
Решение задач:
1. Площади двух подобных треугольников равны 75 см2 и 300 см2. Одна из сторон второго треугольника равна 9см. Найти сходственную ей сторону первого треугольника. (Ответ: 4,5 см.)
2. Сходственные стороны подобных треугольников равны 6см и 4см, а сумма их площадей равна 78 см2. Найти площади этих треугольников. (Ответ: 54 см2 и 24 см2.)
Найти площади этих треугольников. (Ответ: 54 см2 и 24 см2.)
При наличии времени самостоятельная работа обучающего характера.
Вариант 1
У подобных треугольников сходственные стороны равны 7 см и 35 см.
Площадь первого треугольника равна 27 см2.
Найти площадь второго треугольника. (Ответ: 675 см2.)
Вариант 2
Площади подобных треугольников равны 17 см2 и 68 см2. Сторона первого треугольника равна 8см. Найти сходственную сторону второго треугольника. (Ответ: 4 см.)
5. Домашнее задание: учебник геометрии 7-9 Л.С. Атанасян и др., п. 57, 58, № 545, 547.
6. Подведение итогов урока.
Геометрия — похожие треугольники
Определение
Два треугольника подобны, если соответствующие углы совпадают и если отношение соответствующих сторон равно
постоянный.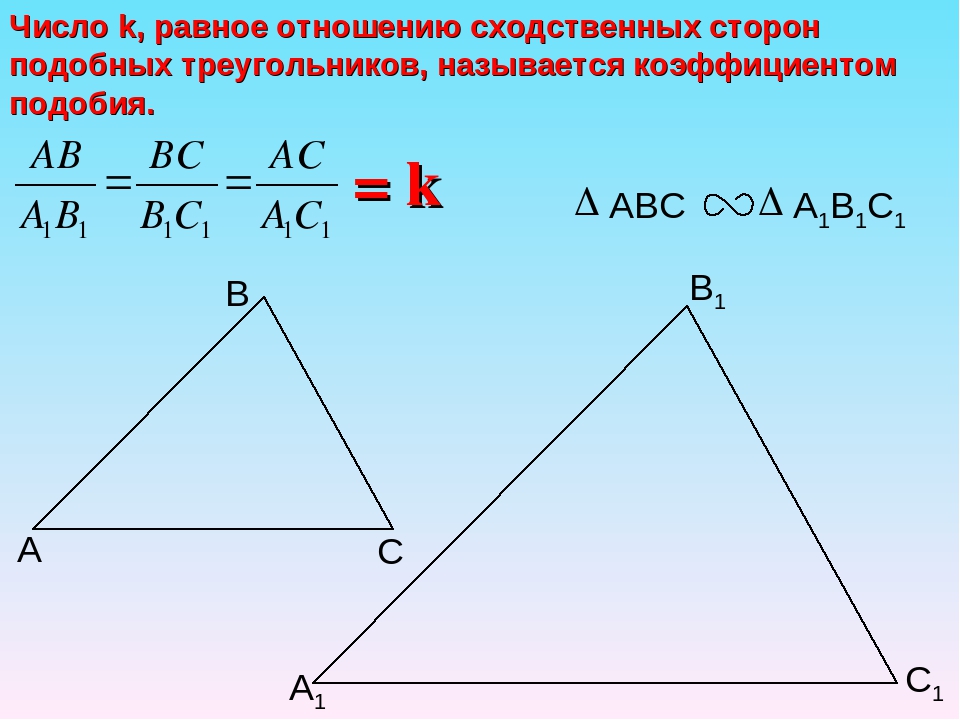 Если треугольники \ (\ bigtriangleup ABC \) и \ (\ bigtriangleup DEF \) равны
аналогично, мы можем записать это соотношение как
Если треугольники \ (\ bigtriangleup ABC \) и \ (\ bigtriangleup DEF \) равны
аналогично, мы можем записать это соотношение как
Разница между подобными и совпадающими треугольниками состоит в том, что похожие треугольники не обязательно должны быть одинакового размера.
\ (\ cong \) congruence такая же форма и такой же размер
\ (\ sim \) подобие такая же форма
Теорема о пропорциональности треугольника
Интерактивная помощь в доказательстве теоремы о пропорциональности треугольника.Поперечная линия — это линия, пересекающая две или несколько линий.
Теорема: Трансверсаль, параллельная одной из сторон в треугольнике пропорционально делит две другие стороны.
Доказательство: Все, что вам нужно знать, чтобы доказать теорему состоит в том, что площадь треугольника равна \ [A = \ frac {w \ cdot h} {2} \]
где \ (w \) — ширина, а \ (h \) — высота треугольника. Сравните площади трижды!
Сравните площади трижды!
Следствие теоремы о пропорциональности
Следствие: Трансверсаль, параллельная стороне треугольника. определяет новый меньший треугольник, похожий на исходный треугольник.
Проба:
Покажите, что соответствующие углы в двух треугольниках совпадают (равны).
Затем покажите, что \ [\ frac {a + b} {a} = \ frac {c + d} {c} \]
Нарисуйте еще одну поперечину параллельно другой стороне
и покажите, что \ [\ frac {a + b} {a} = \ frac {c + d} {c} = \ frac {AB} {DE} \]
Три случая, которые дают сходство
Сторона-угол-Сторона (SAS) Если две стороны треугольника находятся на одной стороне
отношение к двум соответствующим сторонам другого треугольника, и если включенные углы
в обоих треугольниках одинаковые, значит, треугольники похожи.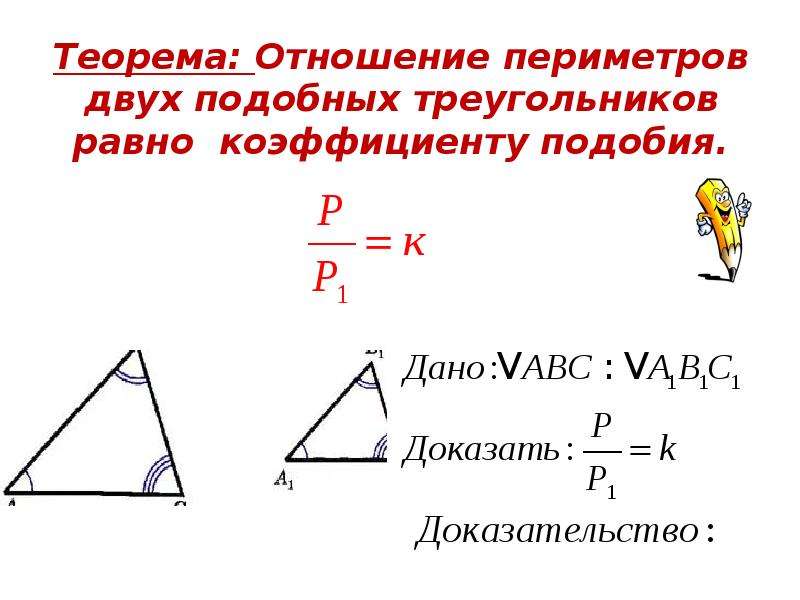
Доказательство
Поместите точку \ (G \) так, чтобы \ (AG = DE \).
Нарисуйте \ (GH \) так, чтобы \ (GH \) был параллелен \ (BC \).
Теперь \ (\ bigtriangleup AGH∼ \ bigtriangleup ABC \).
Покажите, что \ (AH = DF \)!
Тогда случай сравнения Side-Angle-Side дает \ (\ bigtriangleup AGH≅ \ bigtriangleup DEF \) и доказательство сделано.
Доказательства двух других случаев аналогичны.
Сторона-сторона-сторона (SSS) Если три пары соответствующих сторон находятся в такое же соотношение, тогда треугольники похожи.
Угол-угол-угол (AA) Если углы в треугольнике совпадают (равны) соответствующим углам другого треугольника, то треугольники равны похожий.
Также обратите внимание, что достаточно, чтобы два угла были равны (почему?).
Теорема о биссектрисе угла
Прямая, проходящая через C, параллельна AB.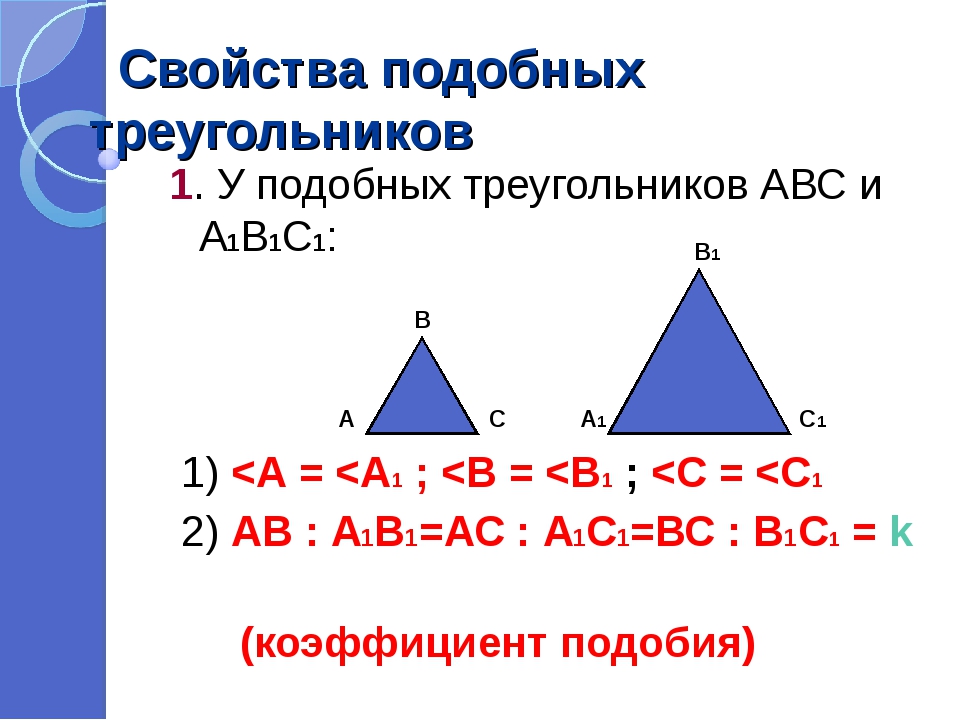
Теорема: В треугольнике \ (\ bigtriangleup ABC \) проводится биссектриса угла в точке \ (B \). Биссектриса угла пересекает \ (AC \) в точке \ (D \).Теорема биссектрисы угла утверждает, что:
\ [\ frac {AB} {AD} = \ frac {BC} {CD} \]
Проба: Проведите линию, параллельную от \ (AB \) до \ (C \). Пусть \ (E \) — пересечение новой прямой и биссектрисы угла. Объясните почему:
Упражнения
Упражнение 1
Высоты в треугольниках
\ (AC \) параллельно \ (EF \).\ (AB \) параллельно \ (DF \). 2} = \ frac {9} {16} $$
2} = \ frac {9} {16} $$
Давайте посмотрим на два похожих треугольника ниже, чтобы увидеть это правило в действии.
Пример 1
Проще всего понять, что это правда, если вы посмотрите на некоторые конкретные примеры реальных подобных треугольников.
Треугольник 1
$$ Площадь = \ frac {1} {2} \ cdot {12} \ cdot {4} \\ Площадь = 24 $$
Треугольник 2
$$ Площадь = \ frac {1} {2} \ cdot {24} \ cdot {8} \\ Площадь = 96 $$
Уведомление: $$ \ frac {24} {96} = \ frac {1} {4} $$
Следовательно, если вы знаете коэффициент подобия, все, что вам нужно сделать, это возвести его в квадрат, чтобы определить соотношение площадей треугольника.
Раздел 4.1 Обсуждение
Определение похожих многоугольников: два многоугольника подобны тогда и только тогда, когда существует взаимно однозначное соответствие между вершинами одного многоугольника и вершинами другого многоугольника, так что соответствующие углы конгруэнтны и отношение длин соответствующих сторон является константой.
Масштабный коэффициент — соотношение соответствующих длин. Также называется (в другом месте) коэффициентом сходства , коэффициентом сходства или коэффициентом разбавления .
Теперь решим это 4.1
1. Опишите и нарисуйте два четырехугольника и два выпуклых пятиугольника, у которых соответствующие стороны пропорциональны, но многоугольники не похожи.
Квадрат и ромб, например, имеют пропорциональные стороны, но они не похожи, если ромб не является квадратом.
Другие?
2. Если два многоугольника P1 и P2 одинаковы, сделайте сторону P! пропорциональны сторонам P2 с масштабным коэффициентом r, с каким масштабным коэффициентом стороны P2 пропорциональны сторонам P1?
1 / р? Почему или почему нет?
Теорема 4.1
Параллельная проекция сохраняет соотношение длин сегментов. То есть
Напомним, что теорема 1.29 ДОКАЗЫВАЕТ, ЧТО ПАРАЛЛЕЛЬНОЕ ПРОЕКТИРОВАНИЕ СОХРАНЯЕТ КОНГРЕУНОСТЬ СЕГМЕНТОВ.
Открыть файл GSP .
Доказательство: Доказательство, представленное в тексте, предполагает, что AB и BC каждый может быть разбит на некоторое количество сегментов одинаковой длины. Если каждый из этих сегментов на AB и BC имеет длину x с AB с i из них и BC с j из них, то мы можем записать AB = ix и до н.
э. = jx .То есть AC покрыт i + j сегментами длиной x каждый.
Параллельная проекция сохраняет совпадений сегментов, поэтому каждый из этих i + j сегментов отображается на i + j сегментов на A’C ‘. Все отрезки на A’C ‘будут конгруэнтными, скажем, длины y, поэтому A’B’ = iy и B’C ‘= jy. Итак
Было показано, что каждое отношение длин сегментов равно отношению числа конгруэнтных сегментов некоторой общей меры, составляющих каждый сегмент.Аргумент предполагает, что сегменты соизмеримы (что существует общая мера.
Известное доказательство того, что это иррационально, является примером того, что отрезки длины 1 и несоизмеримы.
Два сегмента, каждый из которых имеет рациональную длину, соизмеримы . Просто запишите каждую длину обоснования с общим знаменателем и используйте единичную дробь с этим общим знаменателем в качестве общей меры.
Теорема 4.2 Теорема
о расщеплении сторонЛиния, параллельная стороне треугольника, которая пересекает две другие стороны в различных точках, разделяет стороны на пропорциональные сегменты. То есть
План: мы можем попытаться найти треугольники с одинаковой высотой по сравнению с сегментами, которые мы хотим сравнить в качестве оснований. Открыть файл GSP
Triangle AQP и Triangle APQ — это два названия одного и того же треугольника.Следовательно, альтернативные выражения для площади равны.
Принимая PQ как общую основу для треугольника PQB и треугольника QPC, высота до этой базы равна расстоянию между параллельными линиями. Следовательно, площади этих двух треугольников равны. QED
Теорема 4. 3 Обратное к теореме о боковом расщеплении
3 Обратное к теореме о боковом расщеплении
Если прямая делит две стороны треугольника пропорционально (соотношение сегментов на одной стороне равно отношению соответствующих сегментов на другой стороне, то прямая параллельна третьей стороне. Открыть файл GSP
Следствие теоремы о разделении сторон (открытый файл GSP)
Теперь решим это 4.2
1. Сформулируйте и докажите , обратное следствия к теореме о разделении сторон
2.Используйте теорему о боковом расщеплении, чтобы доказать, что параллельная проекция сохраняет соотношение сегментов. Предлагается следующая цифра:
План : A’BCD, E’BCF и A’E’FD — параллелограммы.
Соответствующие стороны совпадают.
По теореме о боковом расщеплении BE: AE = BE ‘: A’E’
Поскольку BE ‘конгруэнтно CF, а E’A’ конгруэнтно FD, тогда BE: EA = CF: FD
Использование теоремы о боковом разделении позволяет обойти предыдущие вопросы о счетности единиц измерения в составляющих сегментах отношения.
Теорема 4.4: Условие AA подобия треугольников
Если два угла одного треугольника совпадают с двумя углами другого треугольника, то треугольники подобны.
ПЛАН: Мы даем два треугольника с двумя конгруэнтными углами. Если мы можем показать, что один треугольник может быть встроен в другой, сопоставив один из заданных углов, то мы можем использовать теорему о расщеплении сторон . Откройте файл GSP .
Теперь решим это 4. 3
3
Докажите пропорцию, вложенную в доказательство теоремы 4.4. . .
Теорема 4.5: условие подобия SSS (обратное условию подобия AA)
Теорема 4.6. Условие сходства SAS
Для двух треугольников, если две пары соответствующих сторон пропорциональны, а включенные углы конгруэнтны, то треугольники подобны.
Решить теперь 4.4
Докажите теорему 4.6
Пример 4.2 Среднее гармоническое
Формула длины EG — отрезка прямой, параллельного основанию трапеции через пересечение диагоналей, — это гармоническое среднее значений a и b.
Когда мы рассматривали M и N как середины сторон трапеции, длина MN была средним арифметическим a и b. Проверьте это .
Анимация предлагает теорему
Теорема: Если a ≥ b> 0, то
AM ≥ HM с равенством, если a = b
Докажите это алгебраически.То есть
Доказательство
GSP файл?
Откройте файл GSP для примера 4.3. В приведенном выше доказательстве используется подобие треугольников ADE и ABC. Что, если бы вы использовали подобие треугольников ABC и EFB?
ДОПОЛНИТЕЛЬНО: Для треугольника ABC ПОСТРОИТЕ ромб CDEF так, чтобы ромб делил вершину в C с треугольником, D находился на AC, E находился на AB и F находился на BC.
Если хотите, показывается конструкция ЗДЕСЬ
НАБОР ПРОБЛЕМ 4.1 (19 проблем)
треугольников, прямоугольников и теорема Пифагора — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
Решение приложений с использованием свойств треугольников
В этом разделе мы будем использовать некоторые общие геометрические формулы.Мы адаптируем нашу стратегию решения проблем, чтобы мы могли решать геометрические приложения. Формула геометрии назовет переменные и даст нам уравнение для решения.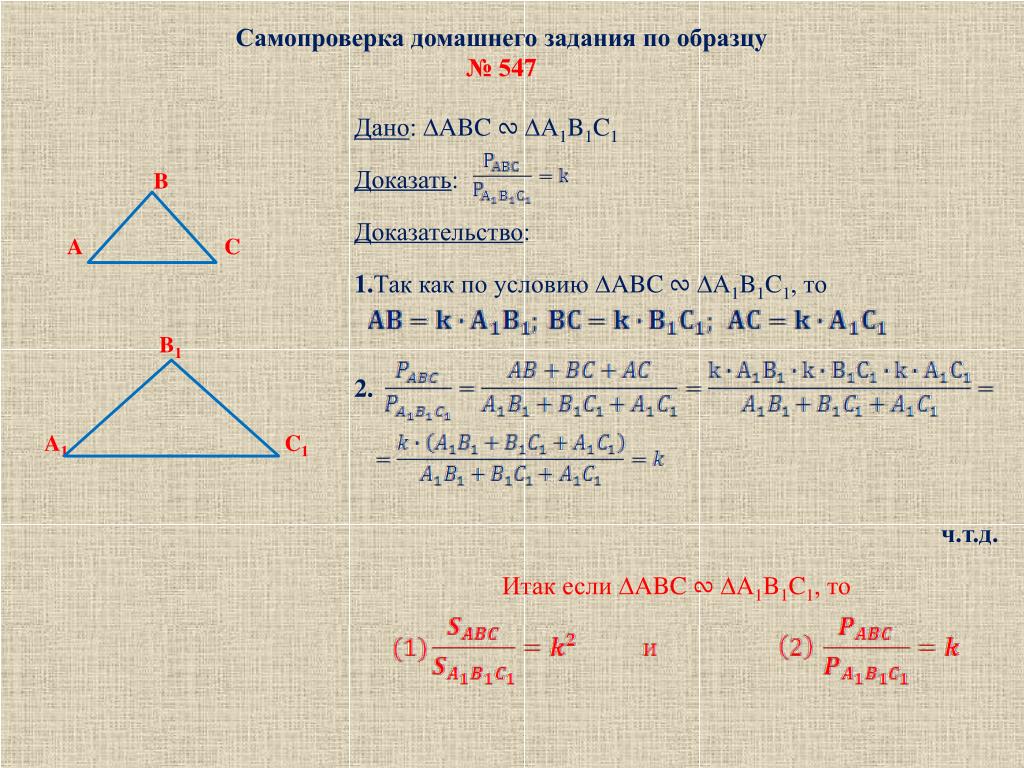 Кроме того, поскольку все эти приложения будут включать в себя какие-то формы, большинство людей находят полезным нарисовать фигуру и пометить ее с заданной информацией. Мы включим это в первый шаг стратегии решения проблем для геометрических приложений.
Кроме того, поскольку все эти приложения будут включать в себя какие-то формы, большинство людей находят полезным нарисовать фигуру и пометить ее с заданной информацией. Мы включим это в первый шаг стратегии решения проблем для геометрических приложений.
Приложения для решения геометрии.
Мы начнем с геометрических приложений, изучив свойства треугольников. Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла. Обычно каждая сторона помечена строчной буквой, которая соответствует прописной букве противоположной вершины.
Множественное число слова вершина составляет вершин . У всех треугольников по три вершины.Треугольники названы по их вершинам: Треугольник на (Рисунок) называется
.Треугольник ABC имеет вершины A, B и C. Длины сторон равны a, b и c.
Три угла треугольника связаны особым образом. Сумма их мер равна. Обратите внимание, что мы читаем как «мера угла А.» Итак, на (рисунок),
Поскольку периметр фигуры равен длине ее границы, периметр фигуры равен сумме длин трех ее сторон.
Чтобы найти площадь треугольника, нам нужно знать его основание и высоту. Высота — это линия, которая соединяет основание с противоположной вершиной и составляет угол с основанием. Нарисуем еще раз, а теперь покажем высоту, х . См. (Рисунок).
Формула для вычисления площади: b — основание, а h — высота.Свойства треугольника
для
Размеры угла:
Периметр:
Площадь:
Размеры двух углов треугольника — 55 и 82 градуса. Найдите размер третьего угла.
Размеры двух углов треугольника — 31 и 128 градус. Найдите размер третьего угла.
Размеры двух углов треугольника — 49 и 75 градусов. Найдите размер третьего угла.
Периметр треугольного сада составляет 24 фута. Длина двух сторон четыре фута и девять футов. Какова длина третьей стороны?
Периметр треугольного сада составляет 48 футов. Длина двух сторон 18 футов и 22 фута. Какова длина третьей стороны?
Длина двух сторон треугольного окна составляет семь футов пять футов. По периметру 18 футов. Какова длина третьей стороны?
Площадь треугольного церковного окна — 90 квадратных метров.База окна 15 метров. Какая высота окна?
Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов. Какая высота?
Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота пять футов. Что такое база?
Свойства треугольника, которые мы использовали до сих пор, применимы ко всем треугольникам. Теперь мы рассмотрим один конкретный тип треугольника — прямоугольный треугольник. Прямоугольный треугольник имеет один угол, который мы обычно отмечаем маленьким квадратом в углу.
Прямой треугольник
Прямоугольный треугольник имеет один угол, который часто отмечается квадратом в вершине.
Измеряет один угол прямоугольного треугольника. Какова мера третьего угла?
Размер одного угла прямоугольного треугольника Какова мера другого малого угла?
Размер одного угла прямоугольного треугольника Какова мера другого малого угла?
В примерах, которые мы видели до сих пор, мы могли нарисовать фигуру и пометить ее сразу после прочтения задачи.В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражения для всех искомых углов.
Размер одного угла прямоугольного треугольника на 20 градусов больше меры наименьшего угла. Найдите размеры всех трех углов.
Размер одного угла прямоугольного треугольника на 50 ° больше размера наименьшего угла. Найдите размеры всех трех углов.
Размер одного угла прямоугольного треугольника на 30 ° больше, чем размер наименьшего угла.Найдите размеры всех трех углов.
Используйте теорему Пифагора
Мы узнали, как соотносятся друг с другом размеры углов треугольника. Теперь мы узнаем, как длины сторон соотносятся друг с другом. Важное свойство, которое описывает соотношение между длинами трех сторон прямоугольного треугольника, называется теоремой Пифагора. Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.
Прежде чем сформулировать теорему Пифагора, нам нужно ввести некоторые термины для сторон треугольника. Помните, что у прямоугольного треугольника есть угол, отмеченный маленьким квадратом в углу. Сторона треугольника, противоположная углу, называется гипотенузой , а каждая из других сторон называется катетом .
Теорема Пифагора говорит, как длины трех сторон прямоугольного треугольника соотносятся друг с другом. В нем говорится, что в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.В символах мы говорим: в любом прямоугольном треугольнике, где — длины катетов, а — длина гипотенузы.
Написание формулы в каждом упражнении и произнесение ее вслух во время написания может помочь вам запомнить теорему Пифагора.
Теорема Пифагора
В любом прямоугольном треугольнике
, где a и b — длина катетов, c — длина гипотенузы.
Чтобы решить упражнения, в которых используется теорема Пифагора, нам нужно найти квадратные корни.Мы использовали обозначения и определение:
Если то за
Например, мы обнаружили, что это 5, потому что
Поскольку теорема Пифагора содержит возведенные в квадрат переменные, чтобы найти длину стороны прямоугольного треугольника, нам придется использовать квадратные корни.
Используйте теорему Пифагора, чтобы найти длину гипотенузы, показанной ниже.
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину ноги, показанной ниже.
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.
Джон ставит основание 13-футовой лестницы в пяти футах от стены своего дома, как показано ниже. Как далеко до стены поднимается лестница?
Рэнди хочет прикрепить 17-футовую гирлянду фонарей к вершине 15-футовой мачты своей парусной лодки, как показано ниже. На каком расстоянии от основания мачты он должен прикрепить конец световой струны?
Решение приложений с использованием свойств прямоугольника
Возможно, вы уже знакомы со свойствами прямоугольников.Прямоугольники имеют четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы называем одну сторону прямоугольника длиной L , а прилегающую к нему сторону шириной W .
Расстояние вокруг этого прямоугольника равно или Это периметр прямоугольника P .
А как насчет площади прямоугольника? Представьте себе прямоугольный коврик длиной 2 фута и шириной 3 фута. Его площадь составляет 6 квадратных футов. На рисунке шесть квадратов.
Площадь равна длине, умноженной на ширину.
Формула площади прямоугольника
Свойства прямоугольников
Прямоугольник имеет четыре стороны и четыре прямых угла.
Длины противоположных сторон равны.
Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины.
Площадь прямоугольника равна произведению длины и ширины.
Длина прямоугольника 32 метра, ширина 20 метров.Какой периметр?
Длина прямоугольника составляет 120 ярдов, а ширина — 50 ярдов. Какой периметр?
Длина прямоугольника 62 фута, ширина 48 футов. Какой периметр?
Площадь прямоугольной комнаты составляет 168 квадратных футов. Длина 14 футов. Какая ширина?
Площадь прямоугольника составляет 598 квадратных футов. Длина 23 фута. Какая ширина?
Ширина прямоугольника 21 метр.Площадь 609 квадратных метров. Какая длина?
Найдите длину прямоугольника с периметром 50 дюймов и шириной 10 дюймов.
Найдите длину прямоугольника с периметром 80 и шириной 25.
Найдите длину прямоугольника с периметром 30 и шириной 6.
Мы решили задачи, в которых задавалась длина или ширина, а также периметр или площадь; Теперь мы научимся решать задачи, в которых ширина определяется длиной.Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.
Ширина прямоугольника на два фута меньше его длины. Периметр — 52 фута. Найдите длину и ширину.
Ширина прямоугольника на семь метров меньше его длины. Периметр — 58 метров. Найдите длину и ширину.
Длина прямоугольника на восемь футов больше ширины. Периметр 60 футов.Найдите длину и ширину.
Длина прямоугольника на четыре сантиметра больше ширины в два раза. По периметру 32 сантиметра. Найдите длину и ширину.
Длина прямоугольника в восемь раз больше ширины в два раза. Периметр равен 64. Найдите длину и ширину.
Ширина прямоугольника в шесть раз меньше двойной длины. Периметр равен 18. Найдите длину и ширину.
Периметр прямоугольного бассейна составляет 150 футов.Длина на 15 футов больше ширины. Найдите длину и ширину.
Периметр прямоугольного бассейна составляет 200 футов. Длина на 40 футов больше ширины. Найдите длину и ширину.
Длина прямоугольного сада на 30 ярдов больше ширины. Периметр 300 ярдов. Найдите длину и ширину.
Практика ведет к совершенству
Решение приложений с использованием свойств треугольника
В следующих упражнениях решите, используя свойства треугольника.
Размеры двух углов треугольника — 26 и 98 градусов. Найдите размер третьего угла.
Размеры двух углов треугольника 61 и 84 градуса. Найдите размер третьего угла.
Размеры двух углов треугольника — 105 и 31 градус. Найдите размер третьего угла.
Размеры двух углов треугольника — 47 и 72 градуса. Найдите размер третьего угла.
Периметр треугольного бассейна — 36 ярдов.Длина двух сторон составляет 10 ярдов и 15 ярдов. Какова длина третьей стороны?
Треугольный двор имеет периметр 120 метров. Длина двух сторон 30 метров и 50 метров. Какова длина третьей стороны?
Если треугольник имеет стороны 6 футов и 9 футов, а периметр равен 23 футам, какова длина третьей стороны?
Если треугольник имеет стороны 14 и 18 см, а периметр равен 49 см, какова длина третьей стороны?
Треугольный флаг имеет основание одна ножка и высоту 1.5 футов. Какая у него площадь?
Треугольное окно имеет основание восемь футов и высоту шесть футов. Какая у него площадь?
Что такое основание треугольника площадью 207 квадратных дюймов и высотой 18 дюймов?
Какова высота треугольника с площадью 893 квадратных дюйма и основанием 38 дюймов?
Один угол прямоугольного треугольника составляет 33 градуса. Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 51 градус.Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 22,5 градуса. Какова мера другого малого угла?
Один угол прямоугольного треугольника составляет 36,5 градуса. Какова мера другого малого угла?
Периметр треугольника составляет 39 футов. Одна сторона треугольника на один фут длиннее второй стороны. Третья сторона на два фута длиннее второй. Найдите длину каждой стороны.
Периметр треугольника составляет 35 футов.Одна сторона треугольника на пять футов длиннее второй. Третья сторона на три фута длиннее второй. Найдите длину каждой стороны.
Одна сторона треугольника вдвое короче. Третья сторона на пять футов больше самой короткой. Периметр — 17 футов. Найдите длины всех трех сторон.
Одна сторона треугольника в три раза длиннее самой короткой стороны. Третья сторона на три фута больше самой короткой. Периметр — 13 футов.Найдите длины всех трех сторон.
Два меньших угла прямоугольного треугольника имеют равные размеры. Найдите размеры всех трех углов.
Размер наименьшего угла прямоугольного треугольника на 20 ° меньше размера следующего большего угла. Найдите размеры всех трех углов.
Углы в треугольнике таковы, что один угол в два раза больше наименьшего угла, а третий угол в три раза больше наименьшего угла.Найдите размеры всех трех углов.
Углы в треугольнике таковы, что один угол на 20 ° больше наименьшего угла, а третий угол в три раза больше наименьшего угла. Найдите размеры всех трех углов.
Используйте теорему Пифагора
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину гипотенузы.
В следующих упражнениях используйте теорему Пифагора, чтобы найти длину ноги.При необходимости округлите до ближайшей десятой.
В следующих упражнениях решите, используя теорему Пифагора. При необходимости с точностью до десятых долей.
13-футовая гирлянда огней будет прикреплена к вершине 12-футовой стойки для праздничной демонстрации, как показано ниже. На каком расстоянии от основания столба должен быть закреплен конец гирлянды?
Пэм хочет повесить плакат на двери своего гаража, как показано ниже, чтобы поздравить сына с окончанием колледжа.Дверь гаража имеет высоту 12 футов и ширину 16 футов. Какой длины должен быть баннер, чтобы подходить к воротам гаража?
Чи планирует проложить дорожку из брусчатки в своем цветнике, как показано ниже. Цветник представляет собой квадрат со стороной 10 футов. Какой будет длина пути?
Брайан одолжил 20-футовую удлинительную лестницу, чтобы использовать ее, когда красит свой дом. Если он установит основание лестницы на расстоянии 6 футов от дома, как показано ниже, насколько высоко поднимется верх лестницы?
Решение приложений с использованием свойств прямоугольника
В следующих упражнениях решите, используя свойства прямоугольника.
Длина прямоугольника составляет 85 футов, а ширина — 45 футов. Какой периметр?
Длина прямоугольника составляет 26 дюймов, а ширина — 58 дюймов. Какой периметр?
Прямоугольная комната 15 футов шириной и 14 футов длиной. Каков его периметр?
Подъездная дорога имеет форму прямоугольника 20 футов шириной и 35 футов длиной. Каков его периметр?
Площадь прямоугольника 414 квадратных метров. Длина 18 метров.Какая ширина?
Площадь прямоугольника 782 квадратных сантиметра. Ширина 17 сантиметров. Какая длина?
Ширина прямоугольного окна 24 дюйма. Площадь — 624 квадратных дюйма. Какая длина?
Длина прямоугольного плаката составляет 28 дюймов. Площадь составляет 1316 квадратных дюймов. Какая ширина?
Найдите длину прямоугольника с периметром 124 и шириной 38.
Найдите ширину прямоугольника с периметром 92 и длиной 19.
Найдите ширину прямоугольника с периметром 16,2 и длиной 3,2.
Найдите длину прямоугольника с периметром 20,2 и шириной 7,8.
Длина прямоугольника на девять дюймов больше ширины. По периметру 46 дюймов. Найдите длину и ширину.
Ширина прямоугольника на восемь дюймов больше его длины. По периметру 52 дюйма. Найдите длину и ширину.
Периметр прямоугольника 58 метров.Ширина прямоугольника на пять метров меньше длины. Найдите длину и ширину прямоугольника.
Периметр прямоугольника 62 фута. Ширина на семь футов меньше длины. Найдите длину и ширину.
Ширина прямоугольника на 0,7 метра меньше длины. Периметр прямоугольника 52,6 метра. Найдите размеры прямоугольника.
Длина 13,5 м, ширина 12,8 м
Длина прямоугольника равна 1.На 1 метр меньше ширины. Периметр прямоугольника 49,4 метра. Найдите размеры прямоугольника.
Периметр прямоугольника составляет 150 футов. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.
Длина прямоугольника в три раза больше ширины. Периметр прямоугольника 72 фута. Найдите длину и ширину прямоугольника.
Длина прямоугольника на три метра меньше двойной ширины.Периметр прямоугольника 36 метров. Найдите размеры прямоугольника.
Длина прямоугольника на пять дюймов больше, чем в два раза ширины. По периметру 34 дюйма. Найдите длину и ширину.
Периметр прямоугольного поля 560 ярдов. Длина на 40 ярдов больше ширины. Найдите длину и ширину поля.
Периметр прямоугольного атриума составляет 160 футов. Длина на 16 футов больше ширины. Найдите длину и ширину атриума.
Прямоугольная автостоянка имеет периметр 250 футов. Длина на пять футов больше, чем в два раза ширины. Найдите длину и ширину парковки.
Прямоугольный коврик имеет периметр 240 дюймов. Длина на 12 дюймов больше, чем в два раза ширины. Найдите длину и ширину коврика.
Повседневная математика
Криста хочет поставить забор вокруг своей треугольной клумбы. Стороны клумбы шесть футов, восемь футов и 10 футов. Сколько футов ограды ей понадобится, чтобы ограждать клумбу?
Хосе только что убрал детский игровой набор со своего заднего двора, чтобы освободить место для прямоугольного сада.Он хочет поставить забор вокруг сада, чтобы не пускать собаку. У него в гараже есть 50-футовый рулон забора, который он планирует использовать. Чтобы поместиться на заднем дворе, ширина сада должна составлять 10 футов. Как долго он сможет сделать другую длину?
Письменные упражнения
Если вам нужно положить плитку на пол на кухне, вам нужно знать периметр или площадь кухни? Объясните свои рассуждения.
Если вам нужно поставить забор вокруг вашего заднего двора, вам нужно знать периметр или площадь заднего двора? Объясните свои рассуждения.
Посмотрите на две цифры ниже.
ⓐ Какая фигура имеет большую площадь?
ⓑ Какая из них, похоже, имеет больший периметр?
ⓒ Теперь вычислите площадь и периметр каждой фигуры.
ⓓ У кого площадь больше?
ⓔ У кого периметр больше?
ⓐ Ответы могут быть разными.
ⓑ Ответы могут быть разными.
ⓒ Ответы могут быть разными.
ⓓ Площади такие же.
ⓔ Прямоугольник 2 × 8 имеет больший периметр, чем квадрат 4 × 4.
Напишите задачу о геометрии, которая относится к вашему жизненному опыту, затем решите ее и объясните все свои шаги.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
геометрических последовательностей и серий | Безграничная алгебра
Геометрические последовательности
Геометрическая последовательность — это упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на константу, называемую [латекс] r [/ латекс], обычное отношение.{n-1} [/ латекс].
Ключевые термины
Определение геометрических последовательностей
Геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обычным соотношением [латекс] r [/ латекс ].{n-1} [/ латекс]
Такая геометрическая последовательность также следует рекурсивному соотношению:
[латекс] a_n = ra_ {n-1} [/ латекс]
для каждого целого числа [латекс] n \ ge 1. [/ Latex]
Поведение геометрических последовательностей
Обычно, чтобы проверить, является ли данная последовательность геометрической, просто проверяют, все ли последовательные записи в последовательности имеют одинаковое соотношение. Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Поведение геометрической последовательности зависит от значения общего отношения. Если общее отношение:
Геометрические последовательности (с общим соотношением, не равным [латекс] -1 [/ латекс], [латекс] 1 [/ латекс] или [латекс] 0 [/ латекс]) показывают экспоненциальный рост или экспоненциальное затухание, в отличие от линейный рост (или снижение) арифметической прогрессии, такой как [латекс] 4, 15, 26, 37, 48, \ cdots [/ латекс] (с общим отличием [латекс] 11 [/ латекс]).Этот результат был получен T.R. Мальтуса в качестве математической основы его принципа народонаселения. Обратите внимание, что два вида прогрессии связаны между собой: возведение в степень каждого члена арифметической прогрессии дает геометрическую прогрессию, а логарифм каждого члена в геометрической прогрессии с положительным общим отношением дает арифметическую прогрессию.
Интересным результатом определения геометрической прогрессии является то, что для любого значения общего отношения любые три последовательных термина [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс] удовлетворяет следующему уравнению:
[латекс] {b} ^ {2} = ac [/ латекс]
Суммирование первых n членов геометрической последовательности
Используя обычное отношение и первый член геометрической последовательности, мы можем суммировать его члены.{n}} {1-r}} [/ латекс].
Ключевые термины
Геометрические серии — это примеры бесконечных серий с конечными суммами, хотя не все из них обладают этим свойством.Исторически геометрические ряды играли важную роль в раннем развитии исчисления, и они по-прежнему занимают центральное место в изучении сходимости рядов. Геометрические ряды используются в математике и имеют важные приложения в физике, инженерии, биологии, экономике, информатике, теории очередей и финансах.
Члены геометрического ряда образуют геометрическую прогрессию, что означает, что соотношение следующих друг за другом членов в ряду постоянно. {n}}}} [/ латекс]
является геометрическим, потому что каждый последующий член может быть получен умножением предыдущего члена на [latex] \ displaystyle {\ frac {1} {2}} [/ latex].{n}}} [/ латекс]
Эту концепцию можно визуализировать с помощью диаграммы:
Бесконечная геометрическая серия: Каждый из фиолетовых квадратов получается путем умножения площади следующего большего квадрата на [latex] \ displaystyle {\ frac {1} {4}} [/ latex]. Площадь первого квадрата составляет [латекс] \ displaystyle {\ frac {1} {2} \ cdot \ frac {1} {2} = \ frac {1} {4}} [/ latex], а площадь второй квадрат — [латекс] \ displaystyle {\ frac {1} {4} \ cdot \ frac {1} {4} = \ frac {1} {16}} [/ latex].
Ниже приведены несколько геометрических рядов с разными общими отношениями.Поведение терминов зависит от общего соотношения [латекс] г [/ латекс]:
Значение [latex] r [/ latex] предоставляет информацию о характере серии:
Мы можем использовать формулу, чтобы найти сумму конечного числа членов в последовательности. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
Бесконечная геометрическая серия
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Вычислить сумму бесконечного геометрического ряда и определить, когда геометрический ряд сойдется.
Основные выводы
Ключевые моменты
Ключевые термины
Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрической прогрессии или чьи последовательные члены имеют общее отношение. Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной. Когда числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
Говорят, что геометрический ряд с конечной суммой сходится. Ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы:
.[латекс] \ левый | г \ право | <1 [/ латекс]
Что следует на примере бесконечного ряда с конечной суммой. Подсчитаем сумму [latex] s [/ latex] следующей серии:
[латекс] \ displaystyle {s = 1+ \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ cdots} [/ latex]
Эта серия имеет общее соотношение [латекс] \ displaystyle {\ frac {2} {3}} [/ latex].Если мы умножим на это обычное соотношение, то начальный член [латекс] 1 [/ latex] станет [latex] \ displaystyle {\ frac {2} {3}} [/ latex], [latex] \ displaystyle {\ frac {2} {3}} [/ latex] становится [latex] \ displaystyle {\ frac {4} {9}} [/ latex] и так далее:
[латекс] \ displaystyle {\ frac {2} {3} s = \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ frac {16} { 81} + \ cdots} [/ латекс]
Эта новая серия такая же, как и исходная, за исключением того, что отсутствует первый термин. Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
[латекс] \ displaystyle {\ begin {align} s- \ frac {2} {3} s & = 1 \\ \ поэтому s & = 3 \ end {align}} [/ latex]
Подобный метод можно использовать для вычисления любого самоподобного выражения.n \ rightarrow 0 \\ & = \ frac {a} {1-r} \ end {align}} [/ latex]
Следовательно, для [latex] | r | <1 [/ latex] мы можем записать бесконечную сумму как:
[латекс] \ Displaystyle {s = \ frac {a} {1-r}} [/ латекс]
Пример
Найдите сумму бесконечного геометрического ряда [латекс] 64+ 32 + 16 + 8 + \ cdots [/ latex]
Сначала найдите [latex] r [/ latex], или постоянное соотношение между каждым членом и тем, что ему предшествует:
[латекс] \ displaystyle {\ begin {align} r & = \ frac {32} {64} \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Подставьте [латекс] a = 64 [/ latex] и [latex] \ displaystyle r = \ frac {1} {2} [/ latex] в формулу суммы бесконечного геометрического ряда:
[латекс] \ displaystyle {\ begin {align} s & = \ frac {64} {1- \ frac {1} {2}} \\ & = \ frac {64} {\ frac {1} {2} } \\ & = 128 \ end {align}} [/ latex]
Применения геометрической серии
Геометрические ряды применяются в математике и естественных науках и являются одним из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Применение геометрических последовательностей и рядов к различным физическим и математическим темам
Основные выводы
Ключевые моменты
Ключевые термины
Геометрические ряды сыграли важную роль в раннем развитии исчисления и продолжают оставаться центральной частью изучения сходимости рядов. Геометрические ряды используются во всей математике. У них есть важные приложения в физике, инженерии, биологии, экономике, информатике, теории массового обслуживания и финансах.
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством.
Повторяющаяся десятичная дробь
Повторяющееся десятичное число можно рассматривать как геометрический ряд, общее отношение которого равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].Например:
[латекс] \ displaystyle {0,7777 \ cdots = \ frac {7} {10} + \ frac {7} {100} + \ frac {7} {1000} + \ frac {7} {10000} + \ cdots} [/ латекс]
Формула суммы геометрического ряда может использоваться для преобразования десятичной дроби в дробь:
[латекс] \ displaystyle {\ begin {align} 0,7777 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {7} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {7} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {7} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {7} {9} \ end {align}} [/ latex]
Формула работает для любого повторяющегося термина.Еще несколько примеров:
[латекс] \ displaystyle {\ begin {align} 0.123412341234 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1234} {10000}} {1- \ frac {1 } {10000}} \\ & = \ frac {\ left (\ frac {1234} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left ( \ frac {1234} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1234} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,0
0909 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {100}} {1- \ frac {1 } {100}} \\ & = \ frac {\ left (\ frac {9} {100} \ right)} {\ left (\ frac {99} {100} \ right)} \\ & = \ left ( \ frac {9} {100} \ right) \ left (\ frac {100} {99} \ right) \\ & = \ frac {9} {99} \\ & = \ frac {1} {11} \ конец {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0.143814381438 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1438} {10000}} {1- \ frac {1} {10000}} \\ & = \ frac { \ left (\ frac {1438} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left (\ frac {1438} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1438} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,9999 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {9} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {9} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {9} {9} \\ & = 1 \ end {align}} [/ латекс]
То есть повторяющаяся десятичная дробь с повторяющейся частью длины [латекс] n [/ latex] равна частному повторяющейся части (как целое число) и [латекс] 10 ^ n — 1 [/ latex].
Квадратура Параболы Архимеда
Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.
Теорема Архимеда: Разбиение Архимеда параболического сегмента на бесконечное количество треугольников.
Теорема Архимеда утверждает, что общая площадь под параболой равна [latex] \ displaystyle {\ frac {4} {3}} [/ latex] площади синего треугольника.{3} + \ cdots} [/ латекс]
Первый член представляет площадь синего треугольника, второй член — площади двух зеленых треугольников, третий член — площади четырех желтых треугольников и так далее. Упрощение дробей дает:
[латекс] \ displaystyle {1+ \ frac {1} {4} + \ frac {1} {16} + \ frac {1} {64} + \ cdots} [/ latex]
Это геометрическая серия с общим соотношением [латекс] \ displaystyle {\ frac {1} {4}} [/ latex], а дробная часть равна [latex] \ displaystyle {\ frac {1} {3} }[/латекс].
Фрактальная геометрия
Снежинка Коха: Внутренняя часть снежинки Коха состоит из бесконечного количества треугольников.
Снежинка Коха — это фрактальная форма, внутренность которой состоит из бесконечного количества треугольников. При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры. В случае снежинки Коха ее площадь можно описать геометрическим рядом.
Построение снежинки Коха: первые четыре итерации: каждая итерация добавляет набор треугольников снаружи формы.
Область внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников. На диаграмме выше треугольники, добавленные во второй итерации, имеют размер [латекс] \ displaystyle {\ frac {1} {3}} [/ latex], равный размеру стороны наибольшего треугольника, и поэтому они имеют ровно [латекс ] \ displaystyle {\ frac {1} {9}} [/ latex] область. Точно так же каждый треугольник, добавленный во второй итерации, имеет [latex] \ displaystyle {\ frac {1} {9}} [/ latex] площадь треугольников, добавленных в предыдущей итерации, и так далее.{3} + \ cdots} [/ латекс]
Первый член этого ряда представляет площадь первого треугольника, второй член — общую площадь трех треугольников, добавленных во второй итерации, третий член — общую площадь двенадцати треугольников, добавленных в третьей итерации, и т. Д. . За исключением начального члена [латекс] 1 [/ латекс], этот ряд является геометрическим с постоянным соотношением [латекс] \ displaystyle {r = \ frac {4} {9}} [/ latex]. Первый член геометрического ряда — [латекс] \ displaystyle {a = 3 \ frac {1} {9} = \ frac {1} {3}} [/ latex], поэтому сумма составляет:
[латекс] \ displaystyle {\ begin {align} 1+ \ frac {a} {1-r} & = 1 + \ frac {\ frac {1} {3}} {1- \ frac {4} {9 }} \\ & = \ frac {8} {5} \ end {align}} [/ latex]
Таким образом, снежинка Коха имеет [латекс] \ displaystyle {\ frac {8} {5}} [/ latex] площади основного треугольника.
Парадоксы Зенона
Парадоксы Зенона — это набор философских проблем, разработанных древнегреческим философом для поддержки учения о том, что истина противоречит нашим чувствам. Проще говоря, один из парадоксов Зенона гласит: существует точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за один раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний.
Как использовать специальный прямоугольный треугольник 45-45-90
Специальные прямоугольные треугольники 45 45 90
Специальные треугольники — это способ получить точные значения для тригонометрических уравнений. На большинство триггерных вопросов, которые вы задавали до сих пор, требовалось округлить ответы в конце.Когда числа округляются, это означает, что ваш ответ неточный, а это то, что математикам не нравится. Специальные треугольники берут те длинные числа, которые требуют округления, и дают для них точные соотношения.
Не так много углов, которые дают чистые и аккуратные тригонометрические значения. Но тем, кто это делает, вам придется запоминать значения их углов в тестах и экзаменах. Это те, которые вы чаще всего будете использовать и в математических задачах. Список всех различных специальных треугольников, с которыми вы встретитесь в математике.
Одним из таких треугольников является треугольник 45 45 90. Это равнобедренный треугольник с двумя равными сторонами. Поскольку вы также обнаружите, что этот треугольник является прямоугольным, мы знаем, что третья сторона, не равная остальным, является гипотенузой. Вы также знаете хорошую формулу для определения длины гипотенузы (теорема Пифагора), и мы покажем вам, как ее использовать. Если вы хотите взглянуть на другие примеры треугольника 45 45 90, взгляните на этот интерактивный онлайн-справочник по этому специальному прямоугольному треугольнику.
Свойства прямоугольного треугольника 45-45-90Как решить треугольник 45 45 90
Чтобы продемонстрировать, как выглядит специальный прямоугольный треугольник с углами 45 45 90, а также объяснить значения, с которыми вам придется работать в будущем, мы воспользуемся приведенным ниже примером. Он показывает стандартный треугольник 45 45 90, который может помочь вам понять отношения, возникающие при использовании этого треугольника.
1 выбрано в качестве длины сторон, равных в этом специальном треугольнике, поскольку с ним проще всего работать.2 = 1 + 1 = 2c2 = 1 + 1 = 2
c = 2c = \ sqrt {2} c = 2
С гипотенузой у нас есть информация для определения следующего:
sin45 \ sin 45sin45 ° = 12 = \ frac {1} {\ sqrt {2}} = 2 1
cos45 \ cos 45cos45 ° = 12 = \ frac {1} {\ sqrt {2}} = 2 1
tan45 \ tan 45tan45 ° = 11 = 1 = \ frac {1} {1} = 1 = 11 = 1
Вы можете видеть, что мы смотрим на «тэту» 45 градусов, и вы должны помнить SOHCAHTOA, который помогает вам запомнить, какие стороны вам нужно будет выбрать, чтобы найти синус, косинус и тангенс. Вот как мы получили, что синус равен 12 \ frac {1} {\ sqrt {2}} 2 1, поскольку 1 — это длина стороны, противоположной 45 градусам, а гипотенуза равна 2 \ sqrt {2} 2.Для косинуса вам понадобится смежное значение над гипотенузой, что дает вам 12 \ frac {1} {\ sqrt {2}} 2 1. Наконец, касательная противоположна соседней, что дает вам 11 \ frac {1} {1} 11, или, в более упрощенной форме, всего 1.
Зная, что вам нужно запомнить эти значения, вы можете сохранить их в памяти или перерисовать этот треугольник и использовать SOHCAHTOA, чтобы найти соотношения углов. В любом случае, мы надеемся, что, объясняя вам компоненты треугольника, вы теперь лучше понимаете особый треугольник 45 45 90 и то, как возникли его соотношения.
Что такое теорема треугольника 45 45 90?
Теорема треугольника 45 45 90 утверждает, что 45 45 90 специальных прямоугольных треугольников, стороны которых имеют длину в специальном соотношении 1: 1: 21: 1: \ sqrt {2} 1: 1: 2 и два 454545 Углы ° и один прямой угол
0 °.
Давайте подробнее рассмотрим взаимосвязь этих соотношений и спросим, почему все особые прямоугольные треугольники 45 45 90 обладают следующими свойствами:
Стандартные размеры и свойства особого треугольника 45 45 90.1. У равнобедренных треугольников длина двух сторон любого специального треугольника 45 45 90 всегда будет одинаковой. Это обозначено буквой a на диаграмме выше. Вследствие того, что эти две стороны имеют одинаковую длину, соответствующим свойством является то, что они имеют одинаковые углы. Это можно определить по двум углам 454545 ° на диаграмме выше. Поскольку общая сумма углов в треугольнике всегда равна 180180180 °, оставшийся угол составляет
0 °, всегда называемый прямым углом.Отсюда и произошло название этого особенного треугольника.
2. Гипотенуза любого специального треугольника 45 45 90 будет иметь длину a2a \ sqrt {2} a2. Это особые отношения, обнаруженные в 45 45 90 треугольниках. Это значение получается путем умножения длины любой из двух равных сторон (т.е. aaa) на радикал 2 \ sqrt {2} 2. Этот радикал представляет собой простейшую форму длины гипотенузы в треугольнике 45 45 90. Его можно вычислить с помощью теоремы Пифагора, как было показано выше, когда мы узнали, как решать треугольники 45 45 90 градусов.
Работает ли теорема Пифагора для 45 45 90 треугольников?
Как обсуждали наши опытные преподаватели в StudyPug, теорема Пифагора описывает соотношение длин каждой стороны прямоугольных треугольников. Это лишь одно из многих уравнений треугольника, которые вы можете вспомнить в геометрии. Поскольку треугольник 45 45 90 действительно является примером прямоугольного треугольника, мы можем использовать теорему Пифагора, чтобы определить длину любой из сторон. Что делает стороны специального прямоугольного треугольника 45 45 90 особенно легкими для решения, так это то, что две стороны имеют одинаковую длину.2a2 + b2 = c2, где ccc — гипотенуза, а aaa и bbb — две равные стороны треугольника 45 45 90.
Как доказать теорему о треугольнике 45-45-90?
Есть два способа проверить теорему треугольника 45-45-90. Помните, что для треугольников 45-45-90 нам предоставлены углы и отношения длин сторон. Это сразу говорит нам о том, что нам нужно будет решить просто размеры треугольника 45-45-90, чтобы подтвердить теорему о треугольнике 45-45-90.Зная эту информацию, мы можем дважды проверить нашу работу, работая в обратном направлении, чтобы показать, что длина сторон соответствует соотношениям. Помните, что для равнобедренного треугольника половина работы заключается в простом нахождении длины смежных или противоположных сторон треугольника 45-45-90. Эти значения будут эквивалентны!
Два способа проверить теорему треугольника 45-45-90:
1. Использование теоремы Пифагора2. Использование специального соотношения 1: 1: 21: 1: \ sqrt {2} 1: 1: 2
Каковы длины сторон треугольника 45 45 90?
Использование теоремы Пифагора — В прямоугольном треугольнике длину сторон треугольника 45 45 90 можно легко вычислить с помощью теоремы Пифагора.2a2 + b2 = c2. В любой задаче вам будет предоставлено значение aaa, bbb или ccc. Поскольку aaa и bbb, противоположные и смежные стороны любого треугольника 45 45 90 эквивалентны, зная длину стороны aaa, можно получить длину стороны bbb или наоборот. Зная это, мы можем просто подставить эти значения в формулу теоремы Пифагора, чтобы найти значение ccc, длины гипотенузы.
А что, если мы имеем просто с учетом длины гипотенузы (т.е.е. ccc)? Мы можем упростить формулу Пифагора, чтобы найти длину как aaa, так и bbb, противоположных и смежных сторон треугольника 45-45-90. Длина обоих aaa и bbb равна, поскольку мы имеем дело с равнобедренным треугольником.
Уравнение 1: упрощенное уравнение формулы Пифагора, когда a2 эквивалентно b2Используя упрощенное уравнение, мы можем просто подставить значение ccc, которое нам было дано изначально, и решить как aaa, так и bbb, двух других сторон треугольника 45-45-90.Зная длины сторон треугольника 45 45 90, мы можем теперь показать, что они находятся в особом соотношении 1: 1: 21: 1: \ sqrt {2} 1: 1: 2.
Метод 2: Использование специального соотношения 1: 1: 21: 1: \ sqrt {2} 1: 1: 2 — Теперь этот метод намного быстрее и дает точные значения. Если в вопросе вас просят оставить ответы в упрощенной радикальной форме или ответить с точными значениями, воспользуйтесь этим методом! Имейте в виду, что из-за этой особой связи это соотношение также можно обобщить и записать как x: x: x2x: x: x \ sqrt {2} x: x: x2 (см. Изображение ниже).
Соотношение соотношений между длинами сторон треугольника 45-45-90.Теперь предположим, что нам дано значение одной стороны, равное 8.
Треугольник 45-45-90, длина сторон 8Взяв это значение и вставив в нашу стандартную формулу отношения, x: x: x2x: x: x \ sqrt {2} x: x: x2, мы видим, что мы быстро и легко решили для всех сторон нашего 45 45 90 треугольник — 8: 8: 828: 8: 8 \ sqrt {2} 8: 8: 82.
Теперь, как упростить эти отношения, чтобы показать, что размеры этого прямоугольного треугольника соответствуют отношениям треугольника 45 45 90? Поскольку наибольший общий множитель между этими отношениями равен 8, мы можем разделить и упростить это соотношение на 8.
88: 88: 828 \ frac {8} {8}: \ frac {8} {8}: \ frac {8 \ sqrt {2}} {8} 88: 88: 882= 1: 1 : 12 = 1: 1: 1 \ sqrt {2} = 1: 1: 12
= 1: 1: 2 = 1: 1: \ sqrt {2} = 1: 1: 2
Теперь мы показали, что этот прямоугольный треугольник удовлетворяет требованиям теоремы о прямоугольном треугольнике 45 45 90.
Что, если бы нам дали значение гипотенузы (т.е. x2 x \ sqrt {2} x2) равным 2?
45-45-90 прямоугольный треугольник, гипотенуза равна 2Для этих типов вопросов есть дополнительный шаг решения для xxx:
x2 = 2x \ sqrt {2} = 2×2 = 2x = 22 = 22⋅22 = 222 = 2x = \ frac {2} {\ sqrt {2}} = \ frac {2} {\ sqrt {2} } \ cdot \ frac {\ sqrt {2}} {\ sqrt {2}} = \ frac {2 \ sqrt {2}} {2} = \ sqrt {2} x = 2 2 = 2 2 ⋅2 2 = 222 = 2
Итак, вставив эти значения в нашу формулу обобщенного соотношения, мы получим 2: 2: 2 \ sqrt {2}: \ sqrt {2}: 22: 2: 2.Для упрощения мы можем разделить на 2 \ sqrt {2} 2.
22: 22: 22 \ frac {\ sqrt {2}} {\ sqrt {2}}: \ frac {\ sqrt {2}} {\ sqrt {2}}: \ frac {2} {\ sqrt {2} } 2 2: 2 2: 2 2= 1: 1: 22 = 1: 1: \ frac {2} {\ sqrt {2}} = 1: 1: 2 2
Чтобы упростить 22 \ frac {2} {\ sqrt {2}} 2 2 , мы умножаем знаменатель и числитель на 2 \ sqrt {2} 2
Это включает рационализацию знаменателя:
22⋅22 = 222 = 2 \ frac {2} {\ sqrt {2}} \ cdot \ frac {\ sqrt {2}} {\ sqrt {2}} = \ frac {2 \ sqrt {2}} {2 } = \ sqrt {2} 2 2 ⋅2 2 = 222 = 2Таким образом, мы снова видим, что получаем соотношение 1: 1: 21: 1: \ sqrt {2} 1: 1: 2, что соответствует стандартным отношениям специального прямоугольного треугольника 45 45 90!
Используйте любой из этих методов или формулы треугольника 45-45-90, чтобы решить любую задачу треугольника 45-45-90!
Что такое гипотенуза треугольника 45 45 90?
Гипотенуза треугольника 45 45 90 действительно может быть любым числом — единственное, что имеет значение, это то, что значение гипотенузы относительно других сторон треугольника следует особому соотношению, которое мы обсуждали ранее: 1: 1: 21 : 1: \ sqrt {2} 1: 1: 2.
Поскольку значение гипотенузы может быть любым рациональным, иррациональным или действительным числом, треугольник 45 45 90 может иметь наименьшую гипотенузу среди всех треугольников! Однако бесконечно малый характер таких чисел дает множество возможностей для длины гипотенузы треугольника 45 45 90. Это не позволяет утверждать, что у 45 45 90 треугольников наименьшие гипотенусы. Посмотрите на этот интерактивный треугольник 45 45 90, чтобы увидеть это в действии!
Итак, как найти длины гипотенузы 45 45 90 треугольников? Прокрутите вверх, чтобы увидеть, как мы вычисляем гипотенузы 45 45 90 треугольников!
Каковы соотношения треугольника 45 45 90
В простейшей форме отношение длин сторон специального прямоугольного треугольника 45 45 90 должно быть 1: 1: 21: 1: \ sqrt {2} 1: 1: 2.Напомним, что специальный прямоугольный треугольник 45 45 90 — это равнобедренный треугольник с двумя равными сторонами и одной большей стороной (то есть определение гипотенузы).
Как рассчитать площадь прямоугольного треугольника 45-45-90
Как и многие другие фундаментальные формулы треугольника, формула для вычисления площади треугольника должна быть такой, которую вы можете запомнить: A = 12⋅b⋅hA = \ frac {1} {2} \ cdot b \ cdot hA = 21 ⋅ бах. Эта же формула может быть применена к специальным прямоугольным треугольникам с углами 45 45 90.
Давайте рассмотрим это в нашем простейшем прямоугольном треугольнике 45-45-90:
Простой треугольник 45-45-90 с размерами 1,1, квадрат2.A = 12⋅b⋅hA = \ frac {1} {2} \ cdot b \ cdot h A = 21 ⋅b⋅h= 12⋅1⋅1 = \ frac {1} {2} \ cdot 1 \ cdot 1 = 21 ⋅1⋅1
A = 0,5 A = 0,5 A = 0,5
Альтернативный способ найти площадь прямоугольного треугольника 45-45-90 включает использование специальной формулы треугольника 45 45 90, полученной из формулы, используемой для вычисления площади квадрата.
Простой треугольник 45-45-90 с начерченным контуром его зеркального отражения.Глядя на изображение выше, мы видим, что причина, по которой мы можем адаптировать формулу для вычисления площади квадрата, заключается в том, что прямоугольный треугольник 45-45-90 составляет половину площади квадрата .2} {2} A = 2s2, потому что прямоугольный треугольник 45-45-90 составляет только половину площади квадрата.
Используйте этот калькулятор треугольников 45 45 90, чтобы проверить свою работу и более внимательно изучить особую взаимосвязь между соотношением размеров, периметром и площадью 45 45 90 треугольников. Этот решатель прямоугольного треугольника — всего лишь помощник, так что не забудьте сначала потренироваться самостоятельно!
Образует ли ромб 45-45-90 треугольников?
Хотя пересечение обеих диагоналей в ромбе может образовывать 4 прямоугольных треугольника (см. Ниже), другие углы в этих прямоугольных треугольниках не равны и не обязательно равны 454545 °.Кроме того, эти прямоугольные треугольники не равнобедренные, поэтому длины сторон треугольника (без учета гипотенузы) не равны. Следовательно, поскольку эти прямоугольные треугольники не соответствуют углам треугольников 45-45-90, а также имеют стороны, которые находятся в соотношении 1: 1: 21: 1: \ sqrt {2} 1: 1: 2, a ромб не образует 45-45-90 треугольников.
Простой треугольник 45-45-90 с начерченным контуром его зеркального отражения.Используйте этот интерактивный инструмент для изучения различных свойств различных ромбов.
Пример и практика с 45 45 90 треугольниками
Прежде чем мы рассмотрим пример, вот несколько советов, которые помогут вам при решении вопросов по тригонометрии 45 45 90 треугольников:
1. Если триггерный вопрос запрашивает ответ в форме « точное значение », это, вероятно, потребует использования специального треугольника. Это может быть треугольник 45 45 90 или 30 60 90. Напомним, что в специальной тригонометрии треугольника нам не нужно округлять или использовать десятичные дроби из-за уникального соотношения между длинами сторон.Однако всегда не забывайте упростить ответ, рационализируя знаменатель, упрощая радикал или дробь.
2. Запомните соотношение длин сторон 45 45 90 треугольников — 1: 1: 21: 1: \ sqrt {2} 1: 1: 2. Легкий способ запомнить это соотношение состоит в том, что, поскольку у вас есть два эквивалентных угла (например, 454545 °, 454545 °), длина / соотношение двух сторон также должны быть эквивалентными.
3. Еще одно запоминающее устройство, которое нужно держать под рукой — SOHCAHTOA . Хотя мы можем знать базовое соотношение длин сторон в треугольниках 45 45 90, нам также необходимо знать, как использовать эту информацию и как подставлять значения в правильную тригонометрическую формулу.23 (sinθ) 2 = 3 (sin45) 2
Уже чувствуете себя уверенно с 45 45 90 специальными прямоугольными треугольниками? Давайте вместе исследуем другие особые прямоугольные треугольники и попрактикуемся в тригонометрии прямоугольных треугольников! Другой тип специального прямоугольного треугольника, который вы часто встретите в тригонометрии, — это 30 60 90 специальных треугольников.
Эффекты формы при перетаскивании
Коэффициент лобового сопротивления — это число, которое аэродинамики используют для моделирования всех сложных зависимостей перетащите на форму , наклон и некоторые условия потока.2 * А)
Это слайд-шоу некоторые типичные значения коэффициента лобового сопротивления для различных форм. Показанные здесь значения были определены экспериментально путем размещения модели в аэродинамическая труба и измерение величина сопротивления, туннельные условия скорости и плотности, а также эталонная область модели. В уравнение сопротивления приведенное выше было затем использовано для расчета коэффициента лобового сопротивления. Прогнозируемая фронтальная Площадь каждого объекта использовалась в качестве эталонной.Плоская пластина имеет Cd = 1,28, призма клиновидная, обращенная клином ниже по потоку Cd = 1,14, у сферы Cd изменяется от 0,07 до 0,5, пуля Cd = .295 и типичный профиль Cd = .045.
Мы можем изучить влияние формы на перетаскивание, сравнив значения коэффициента сопротивления для любых двух объектов до тех пор, пока одна и та же ссылка площадь используется и число Маха а также Число Рейнольдса совпадают. Все коэффициенты лобового сопротивления на этом слайде были получены на низкой скорости. (дозвуковых) аэродинамических труб и при аналогичном числе Рейнольдса, за исключением для сферы.Быстрое сравнение показывает, что плоская пластина дает самый высокий лобовое сопротивление, а обтекаемый симметричный аэродинамический профиль дает наименьшее сопротивление за счет фактор почти 30! Форма очень сильно влияет на количество сопротивление произведено. Сравнивая плоскую пластину и призму, а также сферу и пули, мы видим, что форма нисходящего потока может быть изменена, чтобы уменьшить тащить.

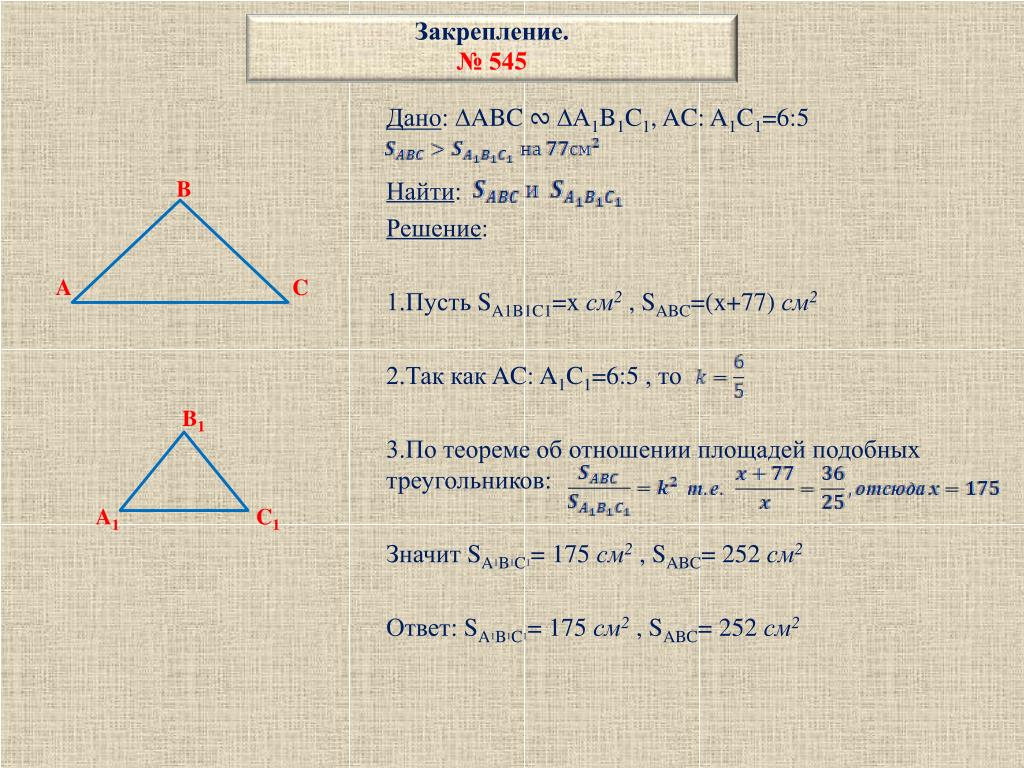
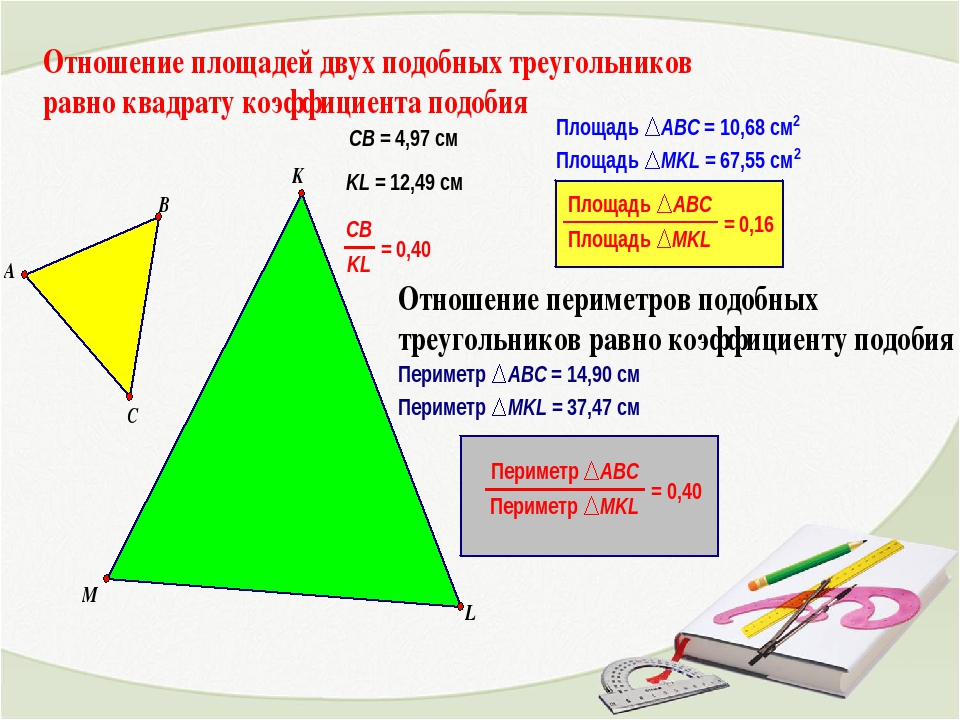
 э. = jx .То есть AC покрыт i + j сегментами длиной x каждый.
э. = jx .То есть AC покрыт i + j сегментами длиной x каждый.
 Соответствующие стороны совпадают.
Соответствующие стороны совпадают. Когда мы рассматривали M и N как середины сторон трапеции, длина MN была средним арифметическим a и b. Проверьте это .
Когда мы рассматривали M и N как середины сторон трапеции, длина MN была средним арифметическим a и b. Проверьте это .