Декартово произведение
Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а; b). Элемент а называют первой координатой (компонентой) пары, а элемент b — второй координатой (компонентой) пары.
Пары (а; b) и (с; d) равны в том и только в том случае, когда a =c и b = d.
В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, 4 = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая- множеству В. Если мы перечислим все такие пары, то получим множество:
{(1;3),(1;5),(2;5),(3;3),(3;5)}.
Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств Аи В.
Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают Ах В. Используя это обозначение, определение декартова произведения можно записать так:
А х В= {(х;у) |х А и у В}.
З а д а ч а 1. Найдите декартово произведение множеств А и В, если:
a)A = {m;p},B={e,f,k};
б)А=В={3,5}.
Решение. а) Действуем согласно определению- образуем все пары, первая компонента которых выбирается из А, а вторая — из В:
А х В= {( m; е), (m; f), (m; k), (p; e), (p;f), (p; к)}.
б) Декартово произведение равных множеств находят, образуя всевозможные пары из элементов данного множества:
А х А={(3;3), (3;5), (5;3), (5;5)}
Операцию нахождения декартова произведения множеств называют декартовым умножением. Выясним, какими свойствами обладает эта операция. Так как декартовы произведения А х В и В х А состоят из различных элементов, то декартово умножение множеств А и В свойством коммутативности не обладает. Можно доказать, что для декартова умножения не выполняется и свойство ассоциативности. Но декартово произведение дистрибутивно относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:
(А В) х С = (А х С) (В х С),
(А \ В) х С = (А х В) \ (В х С).
З а д а ч а 2. Проверьте справедливость свойства дистрибутивности декартова умножения относительно объединения, если:
А = {3; 4; 5}, В ={5; 7}, С ={7; 8}.
Решение. Найдем объединение множеств А и В: А В = {3,4,5,7}. Далее перечислим элементы множества (А В) х С, используя определение декартова произведения: (А В) х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Чтобы найти элементы множества (А х С) (В х С), перечислим сначала элементы множеств А х С и В х С:
А х С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)}
В х С={(5;7),(5;8),(7;7),(7;8)}.
Найдем объединение полученных декартовых произведений: (А х С) (В х С) = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Видим, что множества (А В) х С и (А х С) (В х С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (А В) х С = = (А х С) (В х С).
Выясним теперь, как можно наглядно представлять декартово произведение множеств.
Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке 17(а, б).
| В А | ||
| (1,3) | (1,5) | |
| (2,3) | (2,3) | |
| (3,3) | (3,3) |
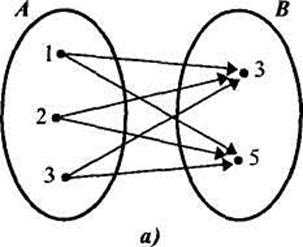
б) Рис. 17
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение А хВ множеств А = {1, 2, 3} и В = = (3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке 18.
у
5
3
0 1 2 3 х Рис.18
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В — на оси Оу.
Такой способ наглядного представления декартова произведения двух числовых множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.
Задача 3. Изобразить на координатной плоскости декартово произведение Ах В, если:
а) А = {1,2,3},В = [3,5];
б) А = [1,3], В = [3,5];
в) A = R, В = [3,5];г) А = R, В = R.
Р е ш е н и е, а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А х В будет состоять из бесконечного множества нар, первая компонента которых либо 1, либо 2, либо 3, а вторая-любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 19).
у
5
3
0 1 2 3 х Рис. 19
б) В этом случае бесконечны оба множества А и В. Поэтому первой координатой пары, принадлежащей множеству Ах В, может быть любое число из промежутка [1,3], и, следовательно, точки, изображающие элементы декартова произведения данных множеств А и В, образуют квадрат (рис. 20).
у
5
3
0 1 2 3 х Рис. 20
Чтобы подчеркнуть, что элементы декартова произведения изображаются и точками, лежащими внутри квадрата, этот квадрат можно заштриховать.
в) Этот случай отличается от предыдущего тем, что множество А состоит из всех действительных чисел, т.е. абсцисса точек, изображающих элементы множества А х В, принимает все действительные значения, в то время как ордината выбирается из промежутка [3,5]. Множество таких точек образует полосу (рис. 21).
у
5
0 х Рис. 21
г) Декартово произведение R x R состоит из всевозможных действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, декартово произведение R x R содержит столько же элементов, сколько точек находится на координатной плоскости.
В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367- это упорядоченный набор из трех элементов, а запись слова «математика» — это упорядоченный набор из 10 элементов.
Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа — это число элементов, из которых он состоит. Например, (3; 6; 7) — это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) — это кортеж длины 10.
Рассматривают в математике и декартово произведение трех, четырех и вообще и множеств.
Определение. Декартовым произведением множеств A1, А2,…, Аn называется множество всех кортежей длины n, первая компонента которых принадлежит множеству A
Декартово произведение множеств A1, А2,…, Аnобозначают так: A1 х А2 х… х Аn.
З а д а ч а 4. Даны множества: A1 = {2, b), А2 = {3, 4, 5}, А3 = {6,7}. Найти A1 х А2 х А3.
Ре ш е н и е. Элементами множества A1х А2х А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству A1, вторая — множеству А2, третья — множеству А3.
A1х А2х А3 = {(2, 3, 6), (2, 3, 7), (2, 4, 6), (2, 4, 7),
(2, 5, 6), (2, 5,7), (3,3,6), (3,3, 7),
(3,4, 6), (3,4,7), (3,5,6), (3,5,7)}.
Похожие статьи:
poznayka.org
1.5. Декартово произведение множеств
Пусть даны два произвольных непустых множества и, элементы которых мы будем обозначать,.
Определение. Прямым произведением (или декартовым произведением) двух непустых множеств называется множество упорядоченных пар, где,. Упорядоченность пары означает, что если мы будет рассматривать декартово произведение, то соответствующая пара будет иметь вид, где,.
В частности, декартово произведение множества действительных чисел на себя представляет собой множество всевозможных упорядоченных пар действительных чисел.
Пример 1. Даны множества и. Найдите множестваи,и соответствующие мощности.
Решение
;
.
.
.
Найдем мощность: .
Пример 2. Даны множества ,,.Найдите число элементов декартова произведения множеств и укажите эти элементы.
Решение
Найдем пересечение множеств , содержащее общие элементы обоих множеств:. Так как множествосодержит четыре элемента, а множество– два элемента, то количество соответствующих пар декартова произведения будет. Перечислим всевозможные пары:,,,,,,,.
Пример 3. Даны множества и. Найдите и изобразите на координатной плоскости.
Решение
В соответствии с определением декартова произведения – множество точек, расположенных в квадрате с вершинами,,и(рис. 10).
Понятие декартова произведения можно обобщить на случай множеств. Если– произвольные непустые множества, то их декартово произведениесостоит из всевозможных упорядоченных наборов, где,, …,.
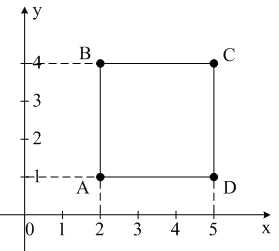
Рис. 10
Замечание. Если – конечные множества, то
.
Декартово произведение множеств само является множеством, и поэтому к нему применимы все изученные ранее способы задания и операции.
Вопросы и задачи для самостоятельного решения
Дайте определение декартова произведения множеств.
Пусть и. Найдите множества,,и соответствующие мощности.
Декартово произведение имеет вид
. Тогда чему равны множества и ?
1.6. Бинарные отношения. Свойства бинарных отношений
Определение 1. Бинарным отношением на множествахиназывается любое подмножество декартова произведения множестви:. При этом множествоназываютобластью определения отношения , а множество–областью значений.
Если элементы имножествинаходятся в отношении, то пишут, или. Если, тоназывается бинарным отношением на.
Например:
а) если , тогда записьозначает, чтои в качестве обозначения этого отношения можно взять сам символ «≤». Множество определения и множество значений совпадают с множеством натуральных чисел;
б) если – множество товаров в магазине, а– множество целых положительных чисел из некоторого диапазона, то – отношение множеств и. Множество определения – товары в магазине, а множество значений – действительные числа, каждое из которых совпадает с ценой некоторого товара;
c) если – множество действительных чисел, тоесть бинарное отношение – точки плоскости, лежащие внутри или на границе круга радиуса 2 с центром в начале координат. Множество определенияи множество значений .
Свойства бинарных отношений
1. Бинарное отношение на множестверефлексивное, если для всякого выполняется.
2. Бинарное отношение на множествеантирефлексивное, если для любых и, для которых выполнено, следует, что.
3. Бинарное отношение на множествесимметричное, если из выполнения следует, что, т. е. из принадлежности отношению парыследует принадлежность этому отношению также пары.
4. Бинарное отношение на множествеантисимметричное, если из выполнения иследует, что .
5. Бинарное отношение на множестветранзитивное, если из выполнения иследует выполнение.
Определение 2. Рефлексивное, симметричное и транзитивное отношение на множественазываетсяотношением эквивалентности.
Определение 3. Рефлексивное, антисимметричное и транзитивное отношение на множественазываетсяотношением нестрогого порядка.
Определение 4. Антирефлексивное, антисимметричное и транзитивное отношение на множественазываетсяотношением строгого порядка.
Пример. Проверьте, какими свойствами обладает отношение
(т.е. кратно трем).
Решение:
а) рефлексивность: для инеобходимо показать, что.
Действительно, отношение рефлексивно;
б) симметричность: для инеобходимо показать, что.
Обозначим , подставим:
отношение симметрично;
в) транзитивность: для и,необходимо показать, что.
Обозначим , и, подставим:
отношение транзитивно.
Так как отношение рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
Вопросы и задачи для самостоятельного решения
1. Какие отношения называют отношением эквивалентности, отношением нестрогого порядка, отношением строгого порядка?
2. Найдите область определения и множество значений отношений:
а) ;
б) .
3. Даны множества и. Найдите количество пар, удовлетворяющих бинарному отношению.
studfiles.net
9. Декартово произведение множеств
Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и b, принято записывать, используя круглые скобки: (а;b). Элемент а называют первой координатой (компонентой) пары, а элементb– второй координатой (компонентой) пары.
Пары (а; b) и (с;d) равны в том и только в том случае, когда а = с иb=d.
В упорядоченной паре (а; b) может быть, что а =b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Пусть, например, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая компонента – множеству В. Если мы перечислим все такие пары, то получим множества:
{(1; 3), (1; 5) (2; 3), (2; 5), (3; 3), (3; 5)}.
Видим, что, имея два множества А.и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.
Определение.Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, записывают:
А х В = {х; у) / х ∈ А и у∈В}.
Выясним, какими свойствами обладает операция нахождения декартова произведения. Так как декартовы произведения А х В и В х А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.
Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности. Но она дистрибутивна относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства:
(А∪В) х С = (А х С)∪(В х С),
(А / В) х С = (А х С) / (В х С).
Доказывать эти свойства мы не будем, но проверить их можно на конкретных примерах.
Выясним теперь, как можно наглядно представить декартово произведение множеств.
Если множества А и В конечны и содержат небольшое количество элементов, то его можно изобразить при помощи графа или таблицы. Например, декартово произведение множеств
А = {1, 2, 3} и В = {3, 5} можно представить так, как показано на рисунке.
А В
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изобразить на координатной плоскости, так как каждая пара чисел может быть единственным образом изображена точкой на этой плоскости. Например, декартово произведение выше названных множеств на координатной плоскости будет выглядеть так:
1 2 3
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В – на оси Оу.
Такой способ наглядного изображения декартова произведения множеств удобно использовать в случае, когда хотя бы одно из них бесконечное.
В математике и других науках рассматривают не только упорядоченные пары, но и упорядоченные наборы из трех, четырех и т.д. элементов. Например, запись числа 367 – это упорядоченный набор из трех элементов, а запись слова «математика» — это упорядоченный набор из 10 элементов.
Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа – это число элементов, из которых он состоит. Например, (3; 6; 7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10.
Рассматривают в математике и декартово произведение трех, четырех и вообще nмножеств.
Определение.Декартовым произведением множеств А₁, А₂, …, Аnназывается множество всех кортежей длиныn, первая компонента которых принадлежит множеству А₁, вторая – множеству А₂, …, n-я — множеству Аn.
Декартово произведение множеств А₁, А₂, …, Аnобозначают так:
А₁х А₂ х …х Аn.
Лекция 4. Число элементов множеств
План:
1. Число элементов в объединении и разности конечных множеств
2. Число элементов в декартовом произведении конечных множеств
3. Основные выводы
studfiles.net
Декартово произведение множеств — это… Что такое Декартово произведение множеств?
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества {в, и, к} на множество цветов радуги | |||||||
Пусть дано два множества X и Y. Прямое произведение множества X и множества Y есть такое множество , элементами которого являются упорядоченные пары (x,y) для всевозможных и .
Отображения произведения множеств в его множители ( и ) называют координатными функциями.
Аналогично строятся произведения нескольких множеств.
Декартова степень
| 000 | 001 | 002 | 010 | 011 | 012 | 020 | 021 | 022 |
| 100 | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 |
| 200 | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 |
| {0, 1, 2}3, 33 = 27 элементов | ||||||||
|---|---|---|---|---|---|---|---|---|
n-я Декартова степень множества X определяется для целых неотрицательных n, как n-кратное Декартово произведение X на себя:
При положительных n Декартова степень Xn состоит из всех упорядоченных наборов (кортежей) элементов из X длины n.
При n = 0, Декартова степень X0 по определению содержит единственный элемент — пустой кортеж.
Прямое произведение семейства множеств
Дальнейшее обобщение понятия прямого произведения приводит к произведениям по индексному множеству I (возможно, бесконечному): X = ΠXi, элементы которого сопоставляют каждому индексу i из I элемент множества Xi.
Прямое произведение отображений
Пусть f — отображение из A в B, а g — отображение из X в Y. Их прямым произведением называется отображение из в : .
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Прямое (декартово) произведение двух групп (G, * ) и — это группа из всех пар элементов (g,h) с операцией поэлементного умножения: . Эта группа обозначается как . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, и соответственно. Пересечение этих подгрупп состоит из одного элемента (1G,1H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, , где и . (Операция в правой части — это операция группы Gi.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: . Например, для счётного числа групп: , где в правой части стоит множество всех бесконечных двоичных последовательностей.
Подгруппа на множестве всех f, носитель которых (то есть множество ) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Пусть X и Y — два топологических пространства. Топология произведения задаётся базой, состоящей из всевозможных произведений , где U — открытое подмножество X и V — открытое подмножество Y.
Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения X = ΠXi определение усложняется. Определим открытый цилиндр , где и U — открытое подмножество Xi.
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
| — | | |
| | — | |
| | | |
| | — | |
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
- , где g и g‘ — соединённые ребром вершины графа G, а h — произвольная вершина графа H;
- , где g — произвольная вершина графа G, а h и h‘ — соединённые ребром вершины графа H.
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Дальнейшее развитие идея прямого произведения получила в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов A и B — это наиболее общий объект в данной категории, для которого существуют проекции на A и B. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Декартово произведение — это… Что такое Декартово произведение?
Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.
Прямое произведение в теории множеств
Произведение двух множеств
| в | в | в | в | в | в | в | в |
|---|---|---|---|---|---|---|---|
| и | и | и | и | и | и | и | и |
| к | к | к | к | к | к | к | к |
| Произведение множества {в, и, к} на множество цветов радуги | |||||||
Пусть дано два множества X и Y. Прямое произведение множества X и множества Y есть такое множество , элементами которого являются упорядоченные пары (x,y) для всевозможных и .
Отображения произведения множеств в его множители ( и ) называют координатными функциями.
Аналогично строятся произведения нескольких множеств.
Декартова степень
| 000 | 001 | 002 | 010 | 011 | 012 | 020 | 021 | 022 |
| 100 | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 |
| 200 | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 |
| {0, 1, 2}3, 33 = 27 элементов | ||||||||
|---|---|---|---|---|---|---|---|---|
n-я Декартова степень множества X определяется для целых неотрицательных n, как n-кратное Декартово произведение X на себя:
При положительных n Декартова степень Xn состоит из всех упорядоченных наборов (кортежей) элементов из X длины n.
При n = 0, Декартова степень X0 по определению содержит единственный элемент — пустой кортеж.
Прямое произведение семейства множеств
Дальнейшее обобщение понятия прямого произведения приводит к произведениям по индексному множеству I (возможно, бесконечному): X = ΠXi, элементы которого сопоставляют каждому индексу i из I элемент множества Xi.
Прямое произведение отображений
Пусть f — отображение из A в B, а g — отображение из X в Y. Их прямым произведением называется отображение из в : .
Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.
Воздействие на математические структуры
Прямое произведение групп
Прямое (декартово) произведение двух групп (G, * ) и — это группа из всех пар элементов (g,h) с операцией поэлементного умножения: . Эта группа обозначается как . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, и соответственно. Пересечение этих подгрупп состоит из одного элемента (1G,1H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.
Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.
Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, , где и . (Операция в правой части — это операция группы Gi.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: . Например, для счётного числа групп: , где в правой части стоит множество всех бесконечных двоичных последовательностей.
Подгруппа на множестве всех f, носитель которых (то есть множество ) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.
Прямое произведение других алгебраических структур
Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.
Прямое произведение топологических пространств
Пусть X и Y — два топологических пространства. Топология произведения задаётся базой, состоящей из всевозможных произведений , где U — открытое подмножество X и V — открытое подмножество Y.
Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения X = ΠXi определение усложняется. Определим открытый цилиндр , где и U — открытое подмножество Xi.
Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).
Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).
Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).
Прямое произведение графов
| — | | |
| | — | |
| | | |
| | — | |
Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
- , где g и g‘ — соединённые ребром вершины графа G, а h — произвольная вершина графа H;
- , где g — произвольная вершина графа G, а h и h‘ — соединённые ребром вершины графа H.
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
Вариации и обобщения
Дальнейшее развитие идея прямого произведения получила в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов A и B — это наиболее общий объект в данной категории, для которого существуют проекции на A и B. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Тема 1.1.4 Декартово произведение множеств(1ч.) — Мегаобучалка
Запишем с пом. цифр 3 и 5 четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов а и Ь, принято записывать, используя круглые скобки: {а; Ь). Элемент а называют первой координатой (компонентой) пары, а элемент b второй координатой (компонентой) пары.
Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, определение декартова произведения можно записать так:
АхВ= {(х; у) | х А и у В}.
Операцию нахождения декартова произведения множеств называют декартовым умножением.
Рассмотрим два одинаковых мн-ва А={3,5}, тогда АхА={(3;3),(3;5),(5;3),(5;5)}
Примечание:
Можно изобразить декартово произведение множеств :
1) при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3,5} можно представить так, как показано на рисунке :
2) Декартово произведение двух числовых множеств (конечных и бесконечных) :
А) А = {1, 2, 3} и В= {3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке:
Заметим, что элементы множества А мы изобразили на оси Ох, а элементы множества В — на оси Оу.
Декартово произведение представлено точками.
б) ) А = {1, 2, 3} и В= [3, 5]
Решение, а) Так как множество А состоит из трех элементов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведение А х В будет состоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо 3, а вторая -любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками
В) бесконечны оба множества А=[1, 3] и В=[3, 5] тогда АхВ это все, что внутри квадрата, т.е. этот квадрат (его нужно заштриховать):
Г) А=RиВ=R,т.е. на мн-ве действительных чисел. То АхВ это вся координатная плоскость.
Д) А=R и В=[3, 5], то АхВ– полоса. (рис.)
Упражнения
1. Перечислите элементы декартова произведения А хВ, если:
а)А = {a, b,c,d},B= {b,k,l}
д)А=В= {а, Ь, с};
ъ)А = {а,Ь,с},В = 0.
2.Изобразите в прямоугольной системе координат множество Ах В, если:
а) А = [-2, 2], В ={2, 3,4};
2. Изобразите в прямоугольной системе координат декартово произведение множеств и , если
1)
2)
megaobuchalka.ru
Декартово произведение множеств
Поиск ЛекцийОсновные операции над множествами
| 1) Дополнение: Дополнение множества A — множество, состоящее из всех элементов универсума, не принадлежащих A. | |
| 2) Пересечение: Пересечение множеств A и B — множество, состоящее из всех элементов, принадлежащих одновременно и A, и B. | |
| 3) объединение: Объединение множеств A и B — множество, состоящее из элементов, принадлежащих хотя бы одному из указанных множеств. | |
| 4) Дизъюнктивная сумма (симметрическая разность): Дизъюнктивная сумма множеств A и B — это множество, состоящее из элементов, принадлежащих либо только A, либо только B. | |
| 5) Разность: Разность множеств A и B — это множество, состоящее из элементов, принадлежащих A, но не принадлежащих B. |
Свойства операций над множествами
Операции над множествами, сформулированные в (1.4) обладают некоторыми свойствами, приведенными в табл. 1. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств, являющихся подмножествами некоторого универсума U.
Таблица 1
Основные свойства операций над множествами
Тождества (1а)-(3а) выражают соответственно коммутативный, ассоциативный и дистрибутивный законы для объединения, а тождества (1б)-(3б) — те же законы для пересечения. Соотношения (4а)-(7а) определяют свойства пустого множества Æ и универсума U относительно объединения, а соотношения (4б)-(7б) — относительно пересечения.
Выражения (8а) и (8б), называемые законами идемпотентности, позволяют записывать формулы с множествами без коэффициентов и показателей степени. Зависимости (9а) и (9б) представляют законы поглощения, а (10а) и (10б) — законы де Моргана.
Соотношения (11)-(20) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.
Первые десять свойств в табл. 1 представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом символов: È на Ç и Ç наÈ , а также Æ на U и U на Æ. Соответствующие пары символов È, Ç и Æ, U называются двойственными (дуальными) символами.
При замене в любой теореме входящих в нее символов дуальными получим новое предложение, которое также является теоремой (принцип двойственности или дуальности). Тождество (11) не изменяется при замене символов дуальными, поэтому его называют самодвойственным.
Декартово произведение множеств
Декартово произведение множеств A и B – это множество упорядоченных пар, первый элемент которых принадлежит A, а второй – принадлежит B.
Пример.
Свойства декартова произведения:
1) — некоммутативность
2) = — ассоциативность
Свойство ассоциативности позволяет использовать сокращенную запись для декартова произведения нескольких множеств:
3) — дистрибутивность относительно объединения
— дистрибутивность относительно пересечения
— дистрибутивность относительно разности
Доказательство: Докажем, например, дистрибутивность декартова произведения относительно операции пересечения множеств.
1) ;
2) , ,
Особым случаем декартова произведения является произведение множества самого на себя. В этом случае говорят о декартовом квадрате множества или декартовой n-ой степени множества А.
;
Пример. Þ
Теорема. Если множество A содержит n элементов, а B – m элементов, т.е.: , то содержит элементов.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
