Плотность распределения и функция распределения: Плотность распределения вероятностей

b { f( x )dx=1 } $

Геометрически это означает, что площадь под кривой распределения равна 1.

Далее:

Теорема о предполных классах

Лемма о построении множества $[F]_{x1,x2}$

Теорема об аналоге СДНФ в Pk

Механические приложения двойного интеграла

Решение задач с помощью алгебры высказываний

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Класс $S$. Теорема о замкнyтости класса $S$

Гармонические поля

Вычисление криволинейного интеграла второго рода. Примеры.

Частные случаи векторных полей

Условия независимости криволинейного интеграла от пути интегрирования

Булевы функции от $n$ переменных

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Механические приложения криволинейного интеграла 1-го рода

Вычисление площади поверхности

Огравление $\Rightarrow $

28 сентября 2016, 22:40    проектирование км, кмд, кж Теория вероятности [Калинин В.М., Тихомиров С.Р.] 0    9858 0

Функция и плотность распределения

Для количественной характеристики распределения вероят-ностей удобней пользоваться не вероятностью того события, что случайная величина примет значение,т.е., а ве-роятностью события, т.е. того, что случайная величинапримет значение, меньшее некоторой текущей переменной. Вероятность этого события зависит от значения, т.е. является функцией от . Эта функция называется функцией распределения

случайной величины и обозначается:

(1.6)

Функция распределения случайной величины  самая универ-сальная характеристика случайной величины, она существует как для дискретных случайных величин, так и для непрерывных.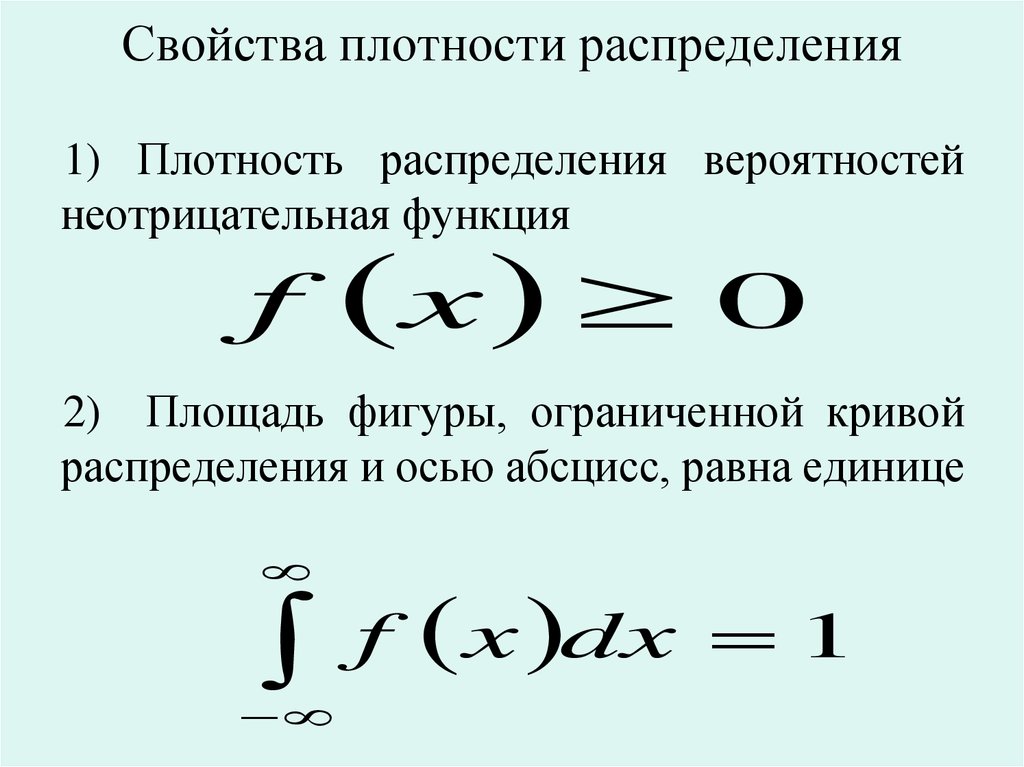 Функ-ция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Функции распределения обладают некоторыми об-щими свойствами:

1. Функция распределения есть неубывающая функция сво-его аргумента, т.е. привыполняется.

2. На минус бесконечности функция распределения равна нулю: .

3. На плюс бесконечности функция распределения равна едини-це: .

График функции распределения в общем случае может быть представлен как график неубывающей функции (рис.1), значения которой начинаются от 0 и доходят до 1, причем в отдельных точ-ках функция может иметь скачки (разрывы).

Пусть имеется непрерывная случайная величина с функцией распределения, которую мы предположим непрерывной и дифференцируемой. Посколькудля непрерывной случайной величи—ны вероятность принятия случайной величиной любого отдельного значения равна нулю, то вычислим вероятность попадания этой

случайной величины на участок от до:

(1. 7)

Вероятность попадания в указанный интервал рассчитывается как приращение функции распределения на этом участке. Рассмот-рим отношение этой вероятности к величине интервала, т.е. сред-нюю вероятность, приходящуюся на единицу длины на этом участ-ке, и будем приближать к нулю. В пределе получим производ-ную от функции распределения:

(1.8)

Введем обозначение для производной от функции распределе-ния:

(1.9)

Функцияхарактеризует как бы плотность, с которой рас-пределяется значение случайной величины в данной точке (а на самом деле отражает быстроту возрастания функции распределе-ния). Функцияназывается плотностью распределения (или плотностью вероятности) непрерывной случайной величины. В отличие от функции распределения, плотность распределения не является универсальной– она существует только для непрерывных величин. Кривая, изображающая плотность распределения случай-ной величины, называется кривой распределения (рис.

2).

Геометрически вероятность попадания величины в участокравна площади кривой распределения,опирающейся на этот участок.Значение же функции распределенияесть не что иное,как площадь кривой распределения, лежащей левее точки.

Для дискретных величин аналогом графика распределения может служить гистограмма, отображающая величину прироста функции распределения (рис.3).

Плотность распределения обладает следующими свойствами:

1. Плотность распределения есть неотрицательная функция: . Это свойство вытекает непосредственно из того, чтоесть функция неубывающая.

2. Интеграл в бесконечных пределах от плотности вероятности равен единице: (условие нормировки). Условие говорит о том, что вероятность принятия случайной величиной какого–ли-бо значения равна единице.

Разница между функцией распределения вероятностей и функцией плотности вероятностей

Функция распределения вероятностей и функция плотности вероятностей
 

Вероятность – это вероятность того, что событие произойдет. Эта идея очень распространена и часто используется в повседневной жизни, когда мы оцениваем наши возможности, сделки и многое другое. Распространить эту простую концепцию на более широкий набор событий немного сложнее. Например, мы не можем легко вычислить шансы на выигрыш в лотерею, но удобно, довольно интуитивно, сказать, что существует вероятность один из шести, что мы собираемся получить номер шесть в кости.

Когда количество событий, которые могут произойти, становится больше или количество отдельных возможностей велико, эта довольно простая идея вероятности не работает. Следовательно, прежде чем приступать к задачам более высокой сложности, необходимо дать твердое математическое определение.

Когда количество событий, которые могут произойти в одной ситуации, велико, невозможно рассматривать каждое событие в отдельности, как на примере брошенного игрального кубика. Таким образом, вся совокупность событий суммируется введением понятия случайной величины. Это переменная, которая может принимать значения различных событий в данной конкретной ситуации (или в пространстве выборки). Он придает математический смысл простым событиям в ситуации и математический подход к событию. Точнее, случайная величина — это функция действительного значения элементов выборочного пространства. Случайные величины могут быть дискретными или непрерывными. Обычно они обозначаются заглавными буквами английского алфавита.

Функция распределения вероятностей (или просто распределение вероятностей) — это функция, присваивающая значения вероятности каждому событию; то есть он обеспечивает отношение к вероятностям значений, которые может принимать случайная величина. Функция распределения вероятностей определена для дискретных случайных величин.

Функция плотности вероятности является эквивалентом функции распределения вероятностей для непрерывных случайных величин, дает вероятность того, что определенная случайная величина примет определенное значение.

Если X является дискретной случайной величиной, функция, заданная как f ( x ) = P ( X = x ) для каждого x в пределах диапазона 800190 равна 19 X 90190 называется функцией распределения вероятностей. Функция может служить функцией распределения вероятностей тогда и только тогда, когда она удовлетворяет следующим условиям.

1. f ( x ) ≥ 0

2. ∑ f ( x ) = 1

Функция f ( x ), которая определена для множества действительных чисел, называется функцией плотности вероятности непрерывной случайной величины X тогда и только тогда, когда

P ( A ≤ x ≤ B ) = _A ∫ ^B F ( x ) DX для любых реальных конститутов A и B .

Функция плотности вероятности также должна удовлетворять следующим условиям.

1. F ( x ) ≥ 0 для всех x : -∞ < x < +∞

2. _-∞ ∫ ^+∞ F ( x ^+∞ F ( x ^+∞ F ( x ^+∞ F ( x ^{) dx = 1}

И функция распределения вероятностей, и функция плотности вероятности используются для представления распределения вероятностей по выборочному пространству. Обычно их называют вероятностными распределениями.

Для статистического моделирования выводятся стандартные функции плотности вероятности и функции распределения вероятности. Нормальное распределение и стандартное нормальное распределение являются примерами непрерывных распределений вероятностей. Биномиальное распределение и распределение Пуассона являются примерами дискретных распределений вероятностей.

В чем разница между функцией распределения вероятности и функцией плотности вероятности?

• Функция распределения вероятностей и функция плотности вероятности — это функции, определенные в пространстве выборки, чтобы присвоить соответствующее значение вероятности каждому элементу.

• Функции распределения вероятностей определены для дискретных случайных величин, а функции плотности вероятности определены для непрерывных случайных величин.

• Распределение значений вероятности (т. е. распределение вероятности) лучше всего изображается с помощью функции плотности вероятности и функции распределения вероятности.

• Функция распределения вероятностей может быть представлена ​​в виде значений в таблице, но это невозможно для функции плотности вероятности, поскольку переменная является непрерывной.

• При построении графика функция распределения вероятностей дает гистограмму, а функция плотности вероятности дает кривую.

• Высота/длина столбцов функции распределения вероятности должна составлять 1, а площадь под кривой функции плотности вероятности должна быть равна 1.

• В обоих случаях все значения функции должны быть неотрицательными.

Путаница между функцией распределения вероятности и функцией плотности вероятности

настоящая сложность здесь совместное распределение вероятности $X$ и $Y$. На вводных курсах изучают совместную плотность вероятности двух непрерывных случайных величин или совместную плотность плотности массы двух дискретных случайных величин. Упомянутый вами смешанный случай, когда одна переменная непрерывна, а другая дискретна, обычно не упоминается во вступительных текстах, хотя некоторым удается проникнуть в нее, не привлекая внимания к тому, с чем они имеют дело.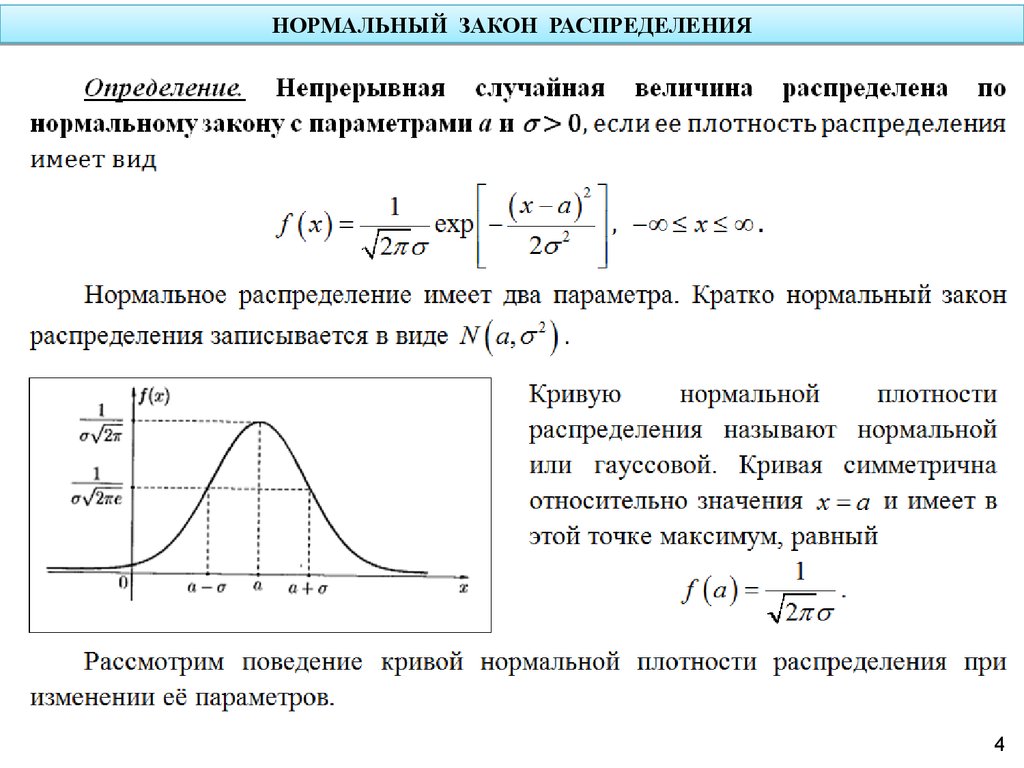

Типичный пример: предположим, что $X$ имеет биномиальное распределение bin($n,u$), где $u$ — вероятность успеха. Каждый день наблюдается новый $X$. Однако значение $u$ изо дня в день меняется случайным образом: оно выбирается каждый раз случайным образом равномерно из интервала (0,1). Поскольку вероятность успеха $u$ также является случайной, мы должны обозначать эту случайную величину [до ее выбора] через $U$. [В байесовском контексте это равномерное распределение для $U$ называется «априорной PDF» для $U$. однако, в отличие от байесовского контекста, который фокусируется на $U$, здесь мы фокусируемся на $X$.] 9{n-x},\quad x = 0,1,\cdots, n.$$

получается, что совместная [смешанная] pmf-pdf $(X,U)$ может быть записана как произведение маргинального PDF для $U$ и условный pmf для $X|U$, аналогично тому, что делается в случае, когда обе переменные дискретны или обе непрерывны. [обоснование этого включает в себя то, на что Кахен ссылается в своем ответе, но это выходит за рамки этого ответа.

No related posts.