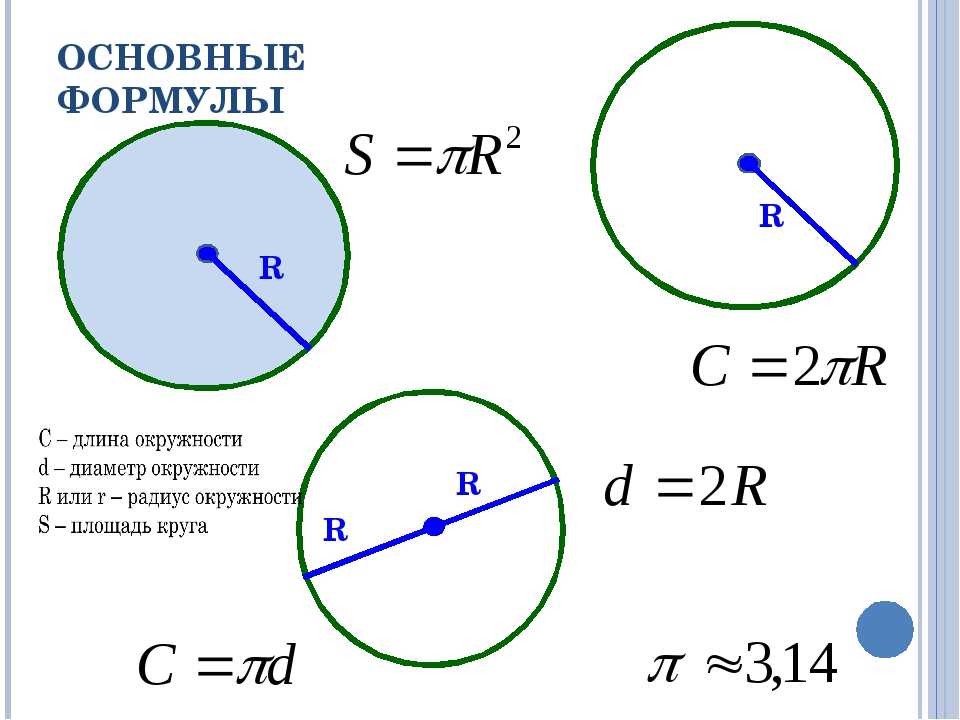
формула через длину окружности, площадь
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
- Формулы вычисления радиуса круга
- 1. Через длину окружности/периметр круга
- 2. Через площадь круга
- Примеры задач
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2πR
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π, умноженному на квадрат его радиуса:
S = πR2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см2
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Радиус круга с учетом площади Калькулятор
✖Площадь круга — это количество двумерного пространства, занимаемого кругом. | акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad | +10% -10% |
|
✖Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности.ⓘ Радиус круга с учетом площади [r] |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Радиус круга с учетом площади Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Площадь круга: 80 Квадратный метр —> 80 Квадратный метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
5.04626504404032 метр —> Конверсия не требуется
< 4 Радиус круга Калькуляторы
Радиус круга с учетом площади формула
Радиус круга = sqrt(Площадь круга/pi)
r = sqrt(A/pi)
Что такое Круг?
Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга.
Чему равен радиус круга, если дана площадь?
Радиус — это линия от центра круга до точки на круге или расстояние от центра круга до точки на круге. Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). Иногда слово «радиус» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисовать радиус круга». Чтобы вычислить радиус круга, когда дана площадь, вам нужно взять квадратный корень из площади круга, деленный на число Пи.
Share
Copied!
Площадь круга – формула, вывод, примеры
Площадь круга – это пространство, занимаемое кругом на двумерной плоскости. В качестве альтернативы пространство, занимаемое в пределах границы/окружности круга, называется площадью круга.
Формула площади круга: A = πr 2 , где r — радиус круга. Единицей площади является квадратная единица, например, м 2 , см 2 , дюймы 2 и т. д.
Формула площади круга полезна для измерения области, занимаемой круглым полем или сюжет. Предположим, если у вас есть круглый стол, то формула площади поможет нам узнать, сколько ткани нужно, чтобы полностью его покрыть. Имеет ли круг объем? Нет, у круга нет объема. Круг — это двумерная фигура, у него нет объема. У круга есть только площадь и периметр/окружность. Давайте подробно узнаем о площади круга, площади поверхности и его окружности на примерах.
| 1. | Круг и части круга |
| 2. | Какова площадь круга? |
| 3. | Формулы площади круга |
| 4. | Вывод формулы площади круга |
| 5. | Площадь поверхности круга Формула |
6. | Различия между площадью и окружностью круга |
| 7. | Реальный пример площади круга |
| 8. | Часто задаваемые вопросы по площади круга |
Какова площадь круга?
Площадь круга — это пространство, ограниченное границами круга. Область внутри границы круга — это площадь, занимаемая кругом. Его также можно назвать общим количеством квадратных единиц внутри этого круга. Площадь круга = πr 2 или πd 2 /4 в квадратных единицах, где
- (Pi) π = 22/7 или 3,14.
- r = радиус окружности
- d = диаметр окружности
Пи (π) — отношение длины окружности к диаметру любого круга. Это специальная математическая константа.
Круг и части круга
Давайте вспомним круг и его части, прежде чем подробно узнать о площади круга. Окружность — это совокупность точек, находящихся на фиксированном расстоянии от центра окружности.
Круг представляет собой замкнутую геометрическую фигуру. Мы видим круги в повседневной жизни, такие как колесо, пицца, круглая площадка и т. Д. Мера пространства или области, заключенной внутри круга, известна как площадь круга.
Радиус: Расстояние от центра до точки на границе называется радиусом окружности. Обозначается буквой «р» или «р». Радиус играет важную роль в формуле площади и длины окружности, которую мы изучим позже.
Диаметр: Линия, которая проходит через центр и ее концы лежат на окружности, называется диаметром окружности. Обозначается буквой «d» или «D».
Формула диаметра: Формула диаметра круга равна удвоенному его радиусу. Диаметр = 2 × Радиус. d = 2r или D = 2R. Если известен диаметр круга, его радиус можно рассчитать как: r = d/2 или R = D/2.
Окружность: Длина окружности равна длине ее границы. Это означает, что периметр круга также называют его окружностью.
Длина веревки, идеально обвивающей границу круга, будет равна его длине окружности. Приведенный ниже рисунок поможет вам визуализировать то же самое. Окружность можно измерить, используя данную формулу:
, где «r» — радиус окружности, а π — математическая константа, значение которой приблизительно равно 3,14 или 22/7. Для круга с радиусом «r» и окружностью «C»:
- π = длина окружности/диаметр
- π = C/2r = C/d
- С = 2πr
Давайте разберемся с различными частями круга на следующем примере из реальной жизни.
Рассмотрим парк круглой формы, как показано на рисунке ниже. Мы можем определить различные части круга с помощью рисунка и таблицы, приведенных ниже.
| По кругу | В нашем парке | Назван по букве |
|---|---|---|
| Центр | Фонтан | Ф |
| Окружность | Граница | |
| Хорд | Вход в игровую зону | ПК |
| Радиус | Расстояние от фонтана до Въездных ворот | ФА |
| Диаметр | Расстояние по прямой линии между входными и выходными воротами через фонтан | авиабаза |
| Малый сегмент | Меньшая часть парка, показанная как игровая площадка | |
| Основной сегмент | Большая площадь парка, кроме игровой площадки | |
| Внутренняя часть круга | Зеленая зона всего парка | |
| Внешняя часть круга | Территория за пределами парка | |
| Дуга | Любая изогнутая часть по окружности. |
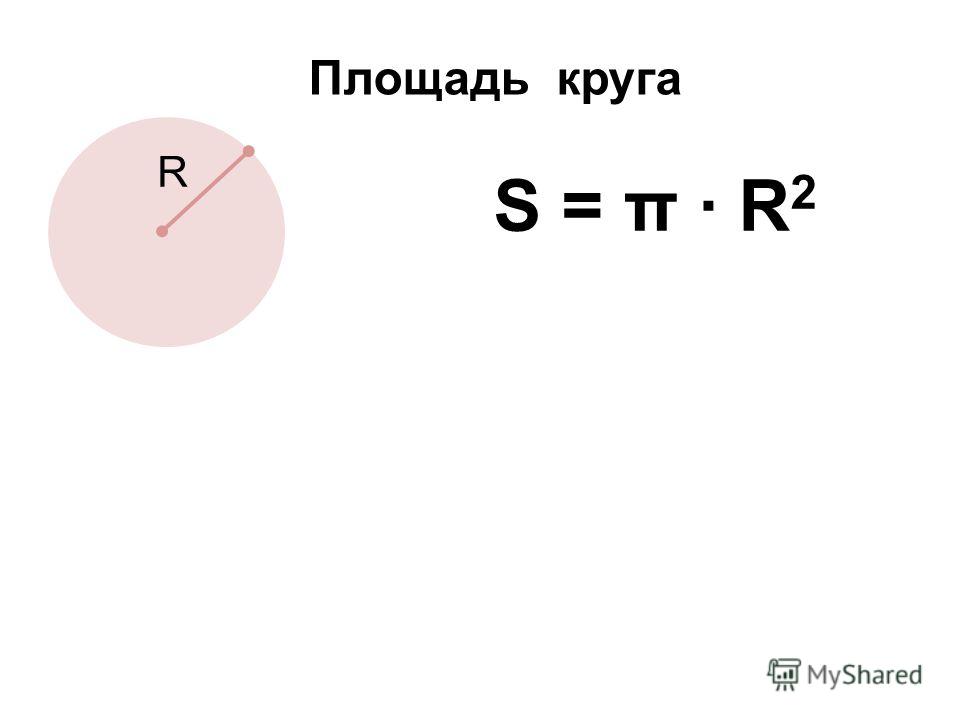
Формула площади круга
Площадь круга можно вычислить промежуточными шагами, исходя из диаметра и длины окружности. Из диаметра и окружности мы можем найти радиус, а затем найти площадь круга. Но эти формулы обеспечивают кратчайший способ найти площадь круга. Предположим, что круг имеет радиус «r», тогда площадь круга = πr 2 или πd 2 /4 в квадратных единицах, где π = 22/7 или 3,14, а d — диаметр.
Площадь круга, A = πr 2 квадратных единиц
Окружность / периметр = 2πr единиц
Площадь круга можно рассчитать по формуле:
- Площадь = π × r 2 , где ‘r’ — радиус.
- Площадь = (π/4) × d 2 , где d — диаметр.
- Площадь = C 2 /4π, где C — длина окружности (иногда называемая периметром).
Примеры использования формулы площади круга
Рассмотрим следующие иллюстрации на основе формулы площади круга.
Пример 1: Если длина радиуса окружности составляет 4 единицы. Вычислите его площадь.
Решение:
Радиус (r) = 4 единицы (данные)
Используя формулу площади круга,
Площадь круга = πr 2
2 A = π1 900 (4) 2A =π × 16
A = 16π ≈ 50,27
Ответ: Площадь круга равна 50,27 квадратных единиц.
Пример 2: Длина наибольшей хорды окружности равна 12 единицам. Найдите площадь круга.
Решение:
Диаметр (d) = 12 единиц (дано)
Используя формулу площади круга, ,
A = (π/4) × 12 2
A = (π/4) × 144
A = 36π ≈ 113,1
Примечание: Альтернативно, мы можем сначала найти радиус (r) а затем применить πr 2 формула.
Ответ: Площадь круга 113,1 квадратных единиц.
Площадь круга с использованием диаметра
Формула площади круга через диаметр: Площадь круга = πd 2 /4.
Здесь d — диаметр окружности. Диаметр круга в два раза больше радиуса круга. д = 2р. Как правило, из диаметра нам нужно сначала найти радиус круга, а затем найти площадь круга. С помощью этой формулы мы можем напрямую найти площадь круга по измерению диаметра круга, как показано в приведенном выше примере. 92}{4\пи}\). Обычно есть два простых шага, чтобы найти площадь круга по заданной окружности круга. Длина окружности сначала используется для нахождения радиуса окружности. Этот радиус также полезен для нахождения площади круга. Но используя эту формулу, мы сможем напрямую найти площадь круга из длины окружности круга.
Площадь круга — расчет
Площадь круга удобно вычислять по радиусу, диаметру или длине окружности. Константа, используемая при вычислении площади круга, равна пи и имеет дробное числовое значение 22/7 или десятичное значение 3,14. Любое из значений pi может быть использовано в зависимости от требований и необходимости уравнений. В приведенной ниже таблице показан список формул, если мы знаем радиус, диаметр или длину окружности.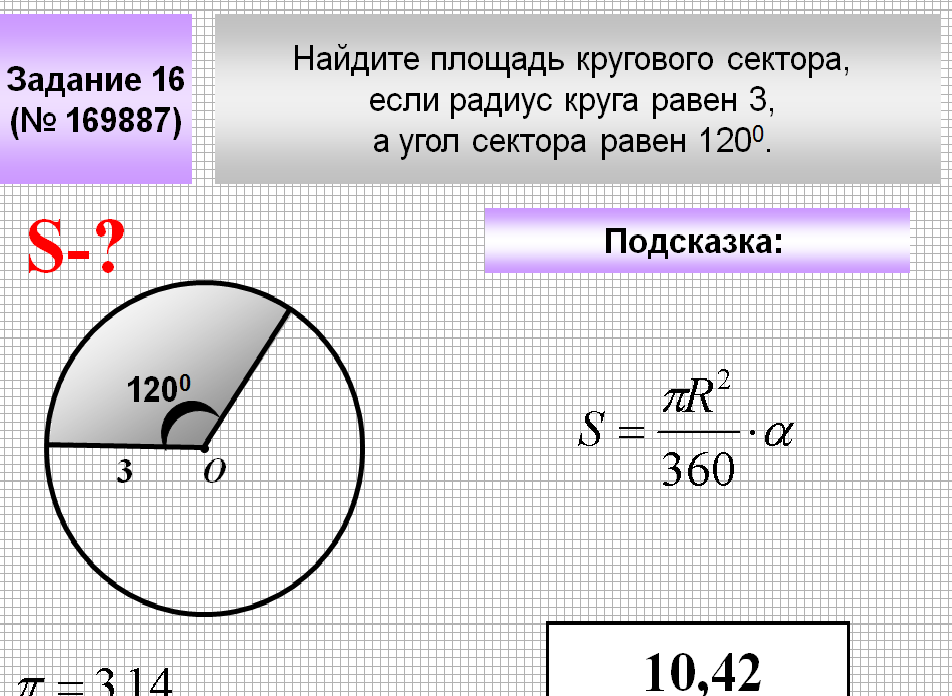
| Площадь круга, когда известен радиус. | πr 2 |
|---|---|
| Площадь круга, когда известен диаметр. | πd 2 /4 |
| Площадь круга, когда известна длина окружности. | С 2 / 4π |
Вывод площади круга
Почему площадь круга πr 2 ? Чтобы понять это, давайте сначала разберемся, как выводится формула площади круга.
Внимательно посмотрите на приведенный выше рисунок, если мы разделим круг на более мелкие части и расположим их систематически, он образует форму параллелограмма. Когда круг делится на еще более мелкие сектора, он постепенно принимает форму прямоугольника. Чем больше у него секций, тем больше он имеет форму прямоугольника, как показано выше.
Площадь прямоугольника = длина × ширина
Ширина прямоугольника = радиусу круга (r)
Сравнив длину прямоугольника и длину окружности, мы увидим, что длина = ½ длины окружности
Площадь круга = Площадь образовавшегося прямоугольника = ½ (2πr) × r
Следовательно, площадь круга равна πr 2 , где r — радиус круга, а значение π равно 22/7 или 3,14.
Площадь поверхности круга Формула
Площадь поверхности круга равна площади круга. На самом деле, когда мы говорим о площади круга, мы имеем в виду не что иное, как общую площадь его поверхности. Площадь поверхности — это площадь, занимаемая поверхностью трехмерной формы. Поверхность сферы будет иметь сферическую форму, но круг — это простая плоская двумерная форма. Так что технически мы не используем фразу «площадь поверхности» для обозначения площади круга, вместо этого мы просто называем ее «площадью круга».
Если дана длина радиуса или диаметр или даже длина окружности, то мы можем узнать площадь поверхности. Он представлен в квадратных единицах. Площадь поверхности круга по формуле = πr 2 где ‘r’ — радиус окружности, а значение π приблизительно равно 3,14 или 22/7.
Различия между площадью и окружностью круга
Вот некоторые важные различия между окружностью (периметром) и площадью круга.
| Окружность (С) | Зона (А) | |
|---|---|---|
| Определение | Длина границы круга.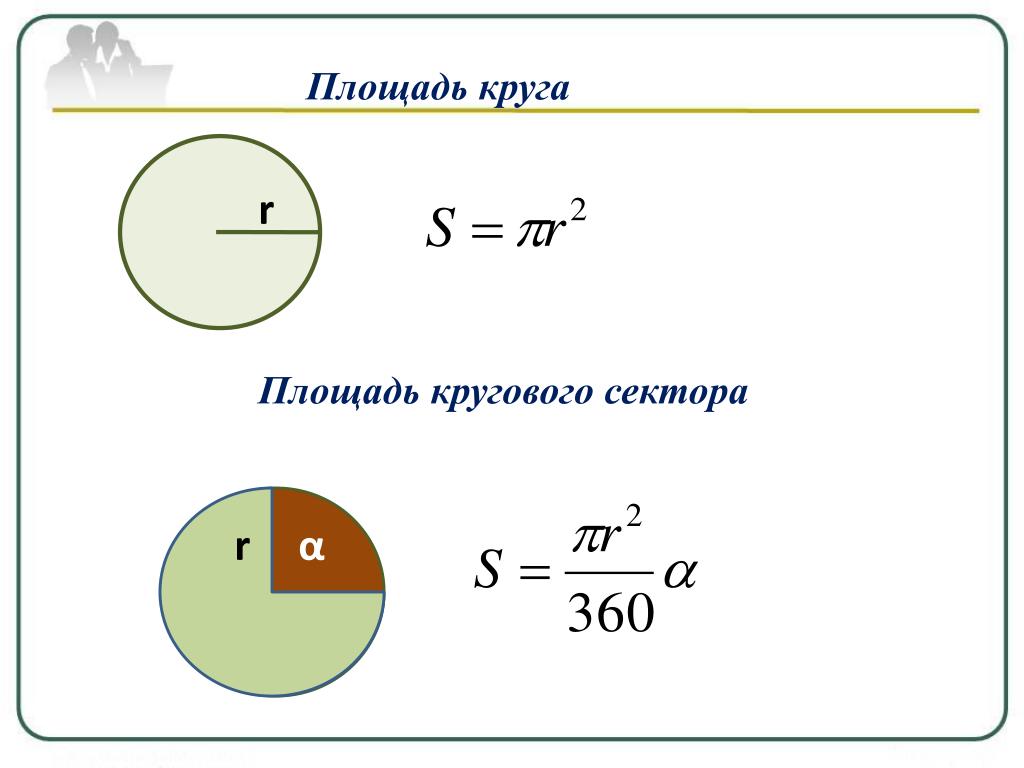 | Количество свободного места внутри круга. |
| Единицы | Такой же длины, как у блока. Пример: см, дюйм, фут и т. д. | Измеряется в квадратных единицах. Пример: см 2 , дюйм 2 , фут 2 и т. д. |
| Формула | 2πr | πr 2 |
| Связь с радиусом | Окружность прямо пропорциональна радиусу. | Площадь прямо пропорциональна квадрату радиуса. |
| Связь с диаметром | Окружность прямо пропорциональна диаметру. | Площадь прямо пропорциональна квадрату диаметра. |
Реальный пример площади круга
Рон и его друзья заказали пиццу в пятницу вечером. Длина каждого кусочка была 15 см.
Вычислите площадь пиццы, которую заказал Рон. Можно считать, что длина куска пиццы равна радиусу пиццы.
Решение:
Пицца имеет круглую форму. Таким образом, мы можем использовать формулу площади круга для вычисления площади пиццы. Радиус 15 см.
Формула площади круга = πr 2 = 3,14 × 15 × 15 = 706,5
Площадь пиццы = 706,5 кв. см.
☛ Похожие темы:
- Калькулятор круга
- Калькулятор радиуса окружности
- Калькулятор длины окружности
- Калькулятор площади круга
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Примеры площади круга
Пример 1: Найдите длину окружности и площадь круга, радиус которого равен 14 см.
Решение:
Дано: Радиус окружности = 14 см
Длина окружности = 2πr
= 2 × 22/7 × 14
= 2 × 22 × 21
Используя формулу площади круга = πr 2
= 22/7 × 14 × 14
= 22 × 2 × 14
= 616 кв.см.
Площадь круга = 616 кв. см.
Ответ: Длина окружности = 88 см, площадь = 616 кв. см.
Пример 2: Соотношение площадей двух кругов составляет 4:9. С помощью формулы площади круга найдите отношение их радиусов.
Решение:
Предположим следующее:
Радиус 1-го круга = R1
Площадь 1-го круга = A1
Радиус 2-го круга = R2
Площадь 2-го круга = A2
Дано, что A1:A2 = 4:9
Площадь круга = πr 2
π\(R_1\ ) 2 : π\(R_2\) 2 = 4 : 9
Извлечение квадратных корней из обеих сторон,
R1 : R2 = 2 : 3
Ответ: Отношение радиусов = 2: 3
Пример 3: Гоночная трасса имеет форму круглого кольца.
Внутренний радиус гусеницы составляет 58 ярдов, а внешний радиус — 63 ярда. Найдите площадь гоночной трассы.Решение:
Дано: R = 63 ярда, r = 56 ярдов.
Пусть площадь внешнего круга равна A 1 , а площадь внутреннего круга равна A 2
Площадь гоночной трассы = A 1 — A 2 904 —
πr
2 = π(63 2 — 56 2 ) = 22/7 × 833 = 2618 квадратных ярдов.Ответ: Площадь гоночной трассы составляет 2618 квадратных метров.
Пример 4: Провод имеет форму равностороннего треугольника. Каждая сторона треугольника составляет 7 дюймов. Проволока согнута в форме круга. Найдите площадь образовавшегося круга.
Решение:
Периметр равностороннего треугольника: Периметр треугольника = 3 × сторона = 3 × 7 = 21 дюйм.
Так как периметр равностороннего треугольника = длина окружности образовавшегося круга.
Таким образом, периметр треугольника равен 21 дюйму.
Длина окружности = 2πr = 2 × 22/7 × r = 21
r = (21 × 7)/(44) = 3,34.
Следовательно, радиус окружности равен 3,34 см. Площадь круга = πr 2 = 22/7 × (3,34) 2 = 35,042 квадратных дюйма.
Ответ: Площадь круга равна 35,042 квадратных дюйма.
Пример 5: Время, показанное на круглых часах, равно 15:00. Длина минутной стрелки составляет 21 единицу. Найдите расстояние, пройденное кончиком минутной стрелки в 15:30.
Решение:
Когда минутная стрелка находится в 15:30, она покрывает половину круга. Таким образом, расстояние, пройденное минутной стрелкой, на самом деле составляет половину окружности. Расстояние \(= \pi\) (где r — длина минутной стрелки). Отсюда пройденное расстояние = 22/7 × 21 = 22 × 3 = 66 единиц.
Ответ: Пройденное расстояние равно 66 единицам.
Внутренний радиус гусеницы составляет 58 ярдов, а внешний радиус — 63 ярда. Найдите площадь гоночной трассы.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Пусть ваш ребенок решит задачи из реальной жизни, используя математику
Пусть ваш ребенок применит понятия, полученные в школе, в реальном мире с помощью наших экспертов.
Записаться на бесплатный пробный урок
Практические вопросы по области круга
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади круга
Как вычислить площадь круга?
Площадь круга можно рассчитать, если мы знаем радиус (r), диаметр (d) или длину окружности (C), используя одну из следующих формул:
- Площадь = π × r 2
- Площадь = (π/4) × d 2
- Площадь = C 2 /4π
Формула площади круга?
Формула площади круга = π × r 2 . Площадь круга равна π, умноженному на квадрат радиуса.
Площадь круга при заданном радиусе r составляет πr 2 . Площадь круга, если известен диаметр d, равна πd 2 /4. π составляет ок. 3.14 или 22/7. Площадь (A) также можно найти по формуле A = (π/4) × d 2 , где «d» — радиус, а A = C 2 /4π, где «C» — длина окружности.
Что такое периметр и площадь круга?
Длина окружности равна длине ее границы. Это означает, что периметр круга равен его окружности. Площадь круга составляет πr 2 , а периметр (длина окружности) равен 2πr, когда радиус составляет «r» единиц, π составляет приблизительно 3,14 или 22/7. Длина окружности и длина радиуса круга являются важными параметрами для определения площади этого круга. Для круга с радиусом «r» и окружностью «C»:
- π = окружность ÷ диаметр
- π = C/2r
- Следовательно, C = 2πr
Почему формула площади круга равна πr
2 ? Круг можно разделить на множество маленьких секторов, которые затем можно переставить соответствующим образом, чтобы получился параллелограмм.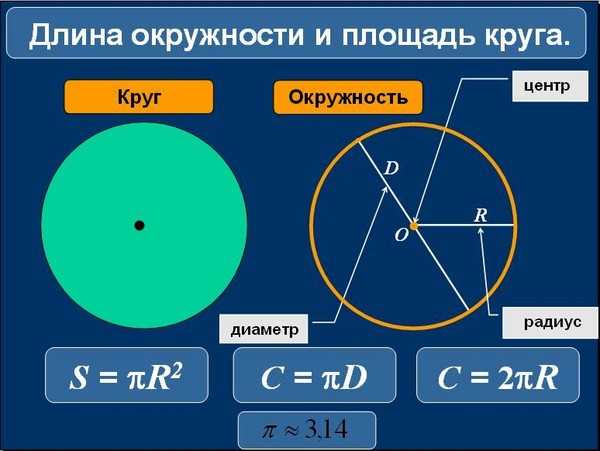
Когда круг делится на еще более мелкие сектора, он постепенно принимает форму прямоугольника. Мы можем ясно видеть, что одна из сторон прямоугольника будет радиусом, а другая будет половиной длины окружности, т. е. π. Как мы знаем, площадь прямоугольника равна его длине, умноженной на ширину, которая равна π, умноженному на «r». Следовательно, площадь круга равна πr 2 .
Чему равна формула площади круга, выраженная числом π?
Значение числа пи (π) приблизительно равно 3,14. Пи — иррациональное число. Это означает, что его десятичная форма не заканчивается (например, 1/5 = 0,2) и не повторяется (например, 1/3 = 0,3333…). Пи равно 3,141592653589793238… (всего до 18 знаков после запятой). Следовательно, формула площади круга, выраженная в числах пи, равна πr 2 квадратных единиц.
Как найти длину окружности и площадь круга?
Площадь и длину окружности можно рассчитать по следующим формулам. Окружность = 2πr; Площадь = πr 2 .
Окружность круга можно взять как π, умноженное на диаметр круга. А площадь круга в π раз больше квадрата радиуса круга.
Как рассчитать площадь круга с диаметром?
Диаметр круга в два раза больше радиуса круга. Следовательно, формула площади круга с использованием диаметра равна π/4, умноженному на квадрат диаметра круга. Формула площади круга с использованием диаметра круга π/4 × диаметр 2 .
Как найти площадь круга, зная длину окружности?
Площадь круга также можно найти, используя длину окружности круга. Радиус круга можно найти из длины окружности круга, и это значение можно использовать для нахождения площади круга. Предположим, что длина окружности равна «С». Имеем C = 2πr или r = C/2π. Теперь, применяя это значение «C» к формуле площади, мы получаем A = πr 2 = π × (C/2π) 2 = C 2 /4π.
Что такое формулы площади и периметра круга?
Для окружности радиусом r:
- Периметр (длина окружности), C = 2πr
- Площадь, A = πr 2
Какова площадь круга, вписанного в квадрат длиной 6 м?
Если в квадрат вписан круг, то диаметр круга = длина стороны квадрата = 6 м.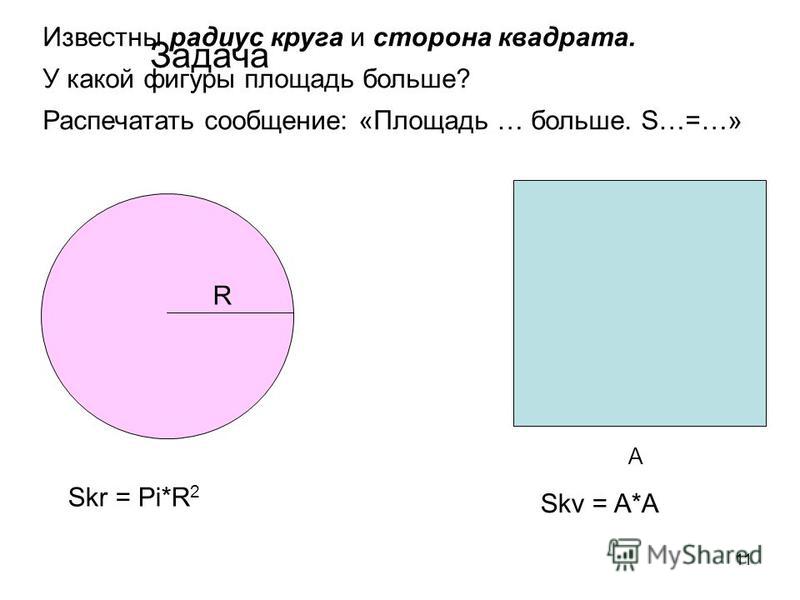
Тогда его радиус = 3 м. Следовательно, площадь круга, вписанного в данный квадрат = 3,14 × 3 × 3 = 28,26 кв.м.
Длина окружности данного круга равна 16 см. Какова будет его площадь?
Длина окружности = 16 см
Мы знаем формулу длины окружности, C =2πr
Итак,
2πr = 16
или r = 16/2π = 8/π
Подставляя значение ‘r ‘ в формуле площади круга получаем:
A = πr 2
A = π(8/π) 2 = 64/π
Решая,
Площадь = 20,38 кв.см.
Каково отношение диаметра к площади круга?
Рассмотрим круг радиуса ‘r’. Тогда его диаметр = 2r и площадь = πr 2 . Тогда отношение диаметра к площади равно 2r : πr 2 = 2 : πr.
Площадь круга | Формула радиуса, диаметра и окружности
Автор:
Malcolm McKinsey
2 дюймовый велосипедное колесо
самая большая пицца имела радиус 61 фут , 4 дюйма ( 736 дюймов )
Ответы
{2}11 817,97 футов 2 пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?
Площадь круга с помощью длины окружности
Если вы не знаете, что такое радиус или диаметр, но знаете длину окружности, C , вы можете еще найти площадь.
Формула площади и длины окружности
Длина окружности (расстояние вокруг окружности) находится по следующей формуле:
Это означает, что мы можем взять формулу длины окружности и «найти r », что дает нам:
Мы можем заменить r в нашей исходной формуле новым выражением:
Это выражение упрощается до следующего:
Как эта формула работает каждый раз1! 900 найдите площадь с окружностью
Подумайте о красивой, разумного размера пицце, которую вы и трое друзей можете разделить.
