Урок математики в 1 классе на тему «Знаки плюс, минус, равно» | План-конспект урока по математике (1 класс) на тему:
ГБОУ ООШ № 2
п.г.т. Новосемейкино Красноярского района Самарской области
Урок по математике в 1 классе по теме :
Знаки +, -, =.
Разработан учителем начальных классов:
Костиной А. А.
2016 год
Цель:
познакомить с названиями и значением знаков +, -, =.
Планируемые результаты:
— предметные: уметь понимать значение знаков +, -, =; читать полученные равенства;
метапредметные
— регулятивные: уметь организовывать своё рабочее место под руководством учителя; определять цель выполнения заданий на уроке;
— коммуникативные: уметь обмениваться мнениями, слушать другого ученика, учителя, обсуждать, делать умозаключения;
— познавательные: уметь самостоятельно выделять и формулировать познавательную цель, сравнивать, группировать;
— личностные: уметь оценивать себя, границы своего знания и незнания, работать в паре, оценивать товарища, стремиться к повышению культуры речевого общения.
Материально-техническое обеспечение:
Проектор, экран, компьютер, слайды, учебник, тетрадь на печатной основе, карточки со знаками и цифрами, знаки дорожного движения – картинки, ободки для выступления, раздаточный материал – геометрические фигуры, тренажёр Базарного.
Ход урока
- Организационный момент.
Проверить готовность принадлежностей, приветствие учителя стоя.
Парта – это не кровать
И на ней нельзя лежать.
Прозвенел звонок и смолк.
Начинается урок.
Тихо девочки за парты сели,
Тихо мальчики за парты сели,
На меня все посмотрели.
- Повторение изученного материала.
— Прежде, чем мы приступим к изучению новой темы, предлагаю вам математическую разминку.
а) логическая разминка:
— Сколько хвостов у трех китов? (3 хвоста)
— Сколько ушей и двух мышей? (4 уха)
— У кого больше лап, у утки или у утенка? (одинаково, по 2 лапы)
б) устный счет:
— Посчитайте:
От 1 до 10 и обратно хором;
На доске корзина с грибами
— Составьте вопросы со словом «сколько» и ответьте на них.
(сколько грибов в корзине, сколько грибов на поляне, сколько грибов всего в корзине и на поляне)
- Работа по теме урока.
- Целеполагание.
На доске знаки (+, -, =, 1, 2, 3 и знаки дорожного движения «Автобусная остановка», «Пешеходный переход», «Пункт первой медицинской помощи», «Осторожно, дети!»)
— Что изображено на первом рисунке? (Автобусная остановка)
— Как вы понимаете значение слова «знак»?
— Представьте, что вы оказались в незнакомом районе города, спросить не у кого, но вы знаете, что в ваш район идет автобус № 410. Что вы будете делать?
(Предлагают найти автобусную остановку с помощью знака.)
— Верно. Знак молчит, но и сообщает нам о чем- то. Указывает на место, где останавливается автобус.
— А какие еще дорожные знаки вы знаете и что они сообщают?
— Теперь вы можете мне сказать, что такое знак?
Рефлексия: Знак — это указание или сообщение о каком-либо объекте.
— Нас окружает множество знаков.
Посмотрите на карточки (на доске знаки плюс, минус, равно, цифры) и скажите, что это?
(Версии разные: цифры, числа, знаки.)
— Эти записи являются тоже знаками, но математическими. Цифра это тоже математический знак, который используют для записи чисел.
— Какие из этих знаков вам знакомы?
— Какие новые? Кто знает, что это за знаки? (Гипотеза, предположение)
— Догадались, какая тема сегодняшнего урока? (Знаки плюс, минус, равно)
— Чему вы хотели бы научиться сегодня? (пользоваться знаками: плюс, минус, равно).
- Знакомство со знаками «плюс» (+), «минус» (–), равно (=).
Практическая работа.
— Положите два оранжевых треугольника.
Какой цифрой мы это обозначим? ( один ученик к доске находит и крепит цифру 2)
— Рядом положите синий квадрат.
Какой цифрой обозначим?( 1).
— Фигур стало больше или меньше? Сколько фигур получилось?
— Какими словами можно заменить слово положили? (прибавили, добавили)
— Чтобы записать это выражение в математике используются цифры и математический знак «+».
А действие при этом называется сложение.
запись: 2+1
— Плюс – знак добрый, он всем дает, прибавляет и всего становится больше.
Ученик (Сизяков Рома) рассказывает стихотворение:
Я – плюс,
И этим я горжусь.
Я для сложения гожусь
Я – добрый знак соединенья
И в том мое предназначение.
— Какую работу он выполняет? (Он всем дает, прибавляет, всего становится больше.)
— Сколько у вас т фигур на столе? (3 фигуры)
Уберите синий квадрат. Фигур стало больше или меньше? Сколько фигур осталось? (2 фигуры)
— Слово уберите, тоже можно заменить знаком. Этот математический знак называется – минус.
Запись: 3-1
— Этот знак у всех отбирает, отнимает и всего становится меньше. Действие при этом называется вычитание.
Ученик (Спиридонов Никита) рассказывает стихотворение:
Я – минус.
Тоже добрый знак.
Ведь не со зла я отнимаю
Я свою роль лишь выполняю.
— Как называется математический знак, который у всех отнимает и при этом всего становится меньше? (Знак минус)
— Посмотрите на записи, которые у нас получились. Кто сможет их прочитать? (читают записанные на доске выражения)
Запись: 2+1 3
3 – 1 2
— Какого знака не хватает?
— Чтобы записать слово получится, используют знак равно (=) .
Запись: 2+1=3
3 – 1=2
Такие записи называют выражения.
— Давайте вместе прочитаем выражения, используя новые термины.
— Итак, какие же знаки используют математики, для записи выражений?
- Работа в тетради на печатной основе.
— Откройте тетрадь на стр.10.
«Я тетрадь свою открою
И наклонно положу.
А ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.»
— Посмотрите на клеточки, какие знаки написаны?
— Посмотрите внимательно, а по какому правилу расположены здесь знаки? (через клетку)
(Показ, как правильно пишутся знаки «+», «–».
Затем учащиеся обводят их по точечным контурам и пишут с а м о с т о я т е л ь н о.)
— Поменяйтесь тетрадями со своим соседом. Оцените работу. Посмотрите внимательно, получилось ли прописать красиво, аккуратно? Сохранили ли вы закономерность, все ли знаки у вас прописаны через клетку? Если всё верно – зелёный светофорик, если ошибка – жёлтый, если совсем неверно – красный.
- Закрепление.
- Работа по учебнику.
— Откройте учебник на стр.28.
— Посмотрите, о ком мы сейчас будем говорить? (О ежах.)
— Сколько было ежиков сначала? (1 ёжик)
— Что изменилось потом? (подбежал еще 1)
— Сколько их стало? (2)
(Чтение под картинкой рассказа) – Правильно вы ответили на вопросы?
— Какое слово заменили знаком «плюс» (подбежал). Прочитайте полученное выражение в учебнике.
2) Работа в парах:
— Посмотрите на картинку ниже и составьте рассказ. О ком вы будете составлять рассказ? Аналогично разбирается рисунок с зайцами.
– Данную запись можно прочитать так: «Три минус два равно одному». (Чтение детьми вслух.) Или по-другому: «Из трёх вычесть два, получится один». (Чтение детьми вслух.)
V. Подведение итогов.
– Давайте вспомним, что мы хотели узнать в начале урока? (Хотели узнать, как пользоваться знаками плюс, минус, равно)
— Вы достигли результата?
– Каким знаком будем пользоваться, если услышим слова: «убежали, убрали»? (Знаком минус)
— Каким знаком будет пользоваться, если услышите слова: «добавили, пришли»? (Знаком плюс)
— А какие это знаки + и – и =? (дорожные или математические)
VI. Рефлексия.
— оцените себя с помощью светофора: если вы всё поняли, всё удалось выполнить – зелёный свет;
если что-то осталось непонятно и были допущены ошибки – жёлтый. И после урока подойдёте ко мне – я ещё раз вам объясню;
если всё было непонятно – красный, и тогда нужно подробно ещё раз разобрать тему.
Спасибо вам большое за урок, завтра мы продолжим учиться пользоваться нашими новыми знаками и познакомимся с новой цифрой.
Урок окончен.
Приложение.
В течении урока, проводится 2-3 физминутки. Время проведения первой через 7-10 минут после начала урока, следующие по усмотрению учителя и временной промежуток зависит от работоспособности класса.
Физминутка
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
Головою три кивка.
На четыре руки шире,
Пять – руками помахать,
Шесть за парту тихо сесть.
Пальчиковая физминутка
Этот пальчик бабушка, (большие)
Этот пальчик дедушка, (указательные)
Этот пальчик мамочка, (средние)
Этот пальчик папочка. (безымянные)
Этот пальчик я. (мизинцы)
Это вся моя семья! (хлопки и встряхивание кистями рук)
Физминутка для глаз
Тренажёр Базарного на доске
Математика. Сложение и вычитание | Сайт Леонида Некина
«Вот смотри, я написал на бумаге
$6 + 2$
Это называется шесть плюс два. Это значит, что ты вначале берешь у папы шесть конфет, а потом еще две.
Сколько всего конфет тебе достанется? Раз ты пока этого не знаешь, то давай сначала потренируемся на счетах. Мы откладываем на счетах шесть бусинок и затем добавляем к ним еще две. Сколько всего бусинок получилось? Правильно, восемь. Записываем ответ:
$6 + 2 = \underline{\,8\,}$
Шесть плюс два равно восемь. Мы решили пример на сложение: мы сложили числа $6$ и $2$ и в результате получили $8$. Вот, держи восемь конфет. (Разумеется, речь идет о крошечных конфетах-горошинах.)
А теперь, смотри, я написал
$5 — 3$
Это называется пять минус три. Это значит, что у нас на двоих пять конфет. Три из них я отдаю тебе. Сколько же тогда конфет остается у меня? Давай отложим на счетах вначале пять бусинок, а потом из них в обратную сторону переложим три. Что получается в результате? Правильно, пять минус три равно два:
$5 — 3 = \underline{\,2\,}$
Мы решили пример на вычитание. Из числа $5$ вычли число $3$ и получили $2$».
После такого объяснения ребенок уже способен самостоятельно делать упражнения на сложение и вычитание. Взрослый вручает ему листок бумаги, на котором написано, например, следующее:
$7 + 3 =$
$7 — 3 =$
$10 + 2 =$
$10 — 2 =$
и так далее.
В задачу ребенка входит выполнить на счетах указанные действия и записать ответ. После того как все ответы будут записаны, он показывает их взрослому. Взрослый восхищается правильными ответами, обводит их в кружочек, а неправильные просит пересчитать еще раз. Если один и тот же неправильный ответ появляется снова и снова, взрослый разбирается вместе с ребенком, где источник ошибки. Постепенно числа в примерах становятся всё больше и больше, однако второе число нет смысла делать больше тридцати, пока ребенку приходится пересчитывать его по бусинкам от начала до конца. Важно, чтобы ребенок не просто понял принцип сложения и вычитания, но и выработал соответствующий навык, то есть почти никогда не ошибался. Движения руки должны стать уверенными, — чтобы, откладывая одну бусинку, не задевать соседние.
И еще один принцип: если сбился со счета, то не надо продолжать наобум — начинай всё сначала.
После того как ребенок начнет обращаться со счетами более или менее уверенно, ему можно подсказать одну «хитрость» (если он сам до нее не додумается): второе число, точно так же, как и первое, необязательно пересчитывать по бусинкам от начала до конца: можно вначале отложить десятки (пусть даже десяток получится «рваный» — часть бусинок с одного ряда, часть — со следующего) и только потом продолжать считать по отдельным бусинкам.
Еще на одно открытие можно натолкнуть ребенка, давая ему примеры такими парами:
$1 + 26 =$
$26 + 1 =$
Оказывается, удобнее вначале отложить большее число, а потом прибавлять к нему меньшее. Результат всё равно остается один и тот же.
Необязательное дополнение 1: «уравнения»
Постепенно можно переходить к более сложным заданиям. В следующем примере вместо многоточия надо поставить такое число, чтобы получился правильный ответ:
$\ldots + 3 = 9$
Подобного рода задачи решаются методом обращения времени вспять.
Допустим, мы только что решили обычный пример «какое-то число плюс $3$» и в результате получили $9$. Откладываем на счетах $9$ бусинок. Теперь как бы движемся по времени назад, воспроизводя решение примера в обратном порядке. Перекладываем бусинки обратно и считаем: три-бусинка, два-бусинка, раз-бусинка. Остается $6$ бусинок. Значит, вместо многоточия надо поставить шестерку:
$\underline{\,6\,} + 3 = 9$
Впрочем, очень скоро становится ясно, что перекладываемые бусинки можно считать и обычным образом: раз-бусинка, два-бусинка, три-бусинка. Результат от этого не изменится. Интересно отметить, что мы выполняем в точности такие же действия, как если бы решали пример «${9 — 3}$».
Подобным же образом можно найти, какое число должно стоять вместо многоточия в таком примере:
$\ldots — 2 = 5$
Снова обращаем время вспять, и обнаруживается, что мы выполняем такие действия, как будто решаем пример «${5 + 2}$». В итоге получаем:
$\underline{\,7\,} — 2 = 5$
Но вот еще один пример с многоточием:
$9 + \ldots = 12$
Здесь многоточие стоит не на первом месте, а на втором, поэтому вспять обратить время не получится.
Давайте, для начала, решим этот пример методом подбора. Попробуем вместо многоточия поставить единицу. Откладываем сперва девять бусинок, потом добавляем еще одну. Получился правильный ответ? Нет. Выходит, маловато добавили. Добавляем вторую бусинку. Снова маловато. Добавляем третью — теперь в самый раз. Всего добавили три бусинки. Значит, мы можем написать:
$9 + \underline{\,3\,} = 12$
Тут можно ввести небольшое усовершенствование. Давайте, после того как мы отложили $9$ бусинок, пометим еще как-нибудь бусинку номер двенадцать. Например, сдвинем ее чуть-чуть влево — не до конца, а так, чтобы сразу после нее в ряду бусинок образовался небольшой разрыв. Теперь мы сразу видим, какие именно бусинки надо добавить к первым девяти, чтобы всего получилось двенадцать. Остается их только пересчитать: раз, два, три — ответ готов. Но посмотрим внимательно на счеты. Здесь у нас отмечено $12$ бусинок, поскольку именно после $12$-ой бусинки идет разрыв. Из них $9$ стоят особняком — сдвинуты до упора влево, — а остальные нам надо было пересчитать. То есть получается, что мы на самом-то деле отвечали на вопрос, сколько будет «${12 — 9}$».
Теперь мы так же легко можем справиться и с таким примером:
$14 — \ldots = 8$
Откладываем $14$ бусинок, помечаем бусинку номер $8$ — например, сдвигая ее немножко вправо — и сразу видим, какие бусинки надо отнять от четырнадцати, чтобы получить восемь. Простым пересчетом находим, что их ровно $6$. Таким образом, многоточие надо заменить на шестерку:
$14 — \underline{\,6\,} = 8$
И снова приглядимся к счетам. По расположению бусинок мы видим, что фактически решали пример «${14 — 8}$».
Необязательное дополнение 2: «отрицательные числа»
Пусть теперь дано:
$3 — 3 =$
Тут всё просто: откладываем сначала три бусинки, а потом те же три бусинки отправляем обратно. В результате получается «ничто» — ноль. А как быть, если встретится такое задание?
$3 — 5 =$
Мы привычным движением откладываем справа налево три бусинки, затем начинаем перекладывать по бусинке обратно: раз-бусинка, два-бусинка, три-бусинка — мы еще не успели переложить столько бусинок, сколько требуется, а они уже кончились.
Что делать? Берем и разворачиваем счеты обратной стороной. Теперь все бусинки у нас оказались слева, и мы можем продолжить наше перекладывание: четыре-бусинка, пять-бусинка. С правой стороны у нас оказалось две бусинки. Вот это мы и напишем в качестве ответа. Только мы должны честно сознаться, что немножко схитрили, развернув счеты другой стороной Поэтому мы напишем не просто двойку, а еще поставим перед ней черточку — знак минус:
$3 — 5 = \underline{-2\,}$
Такие числа со знаком минус впереди, полученные хитрым способом, называются отрицательными. Нам еще предстоит много иметь с ними дело в будущем. Заметим, что мы всего переложили слева направо $5$ бусинок, из них $3$ на лицевой стороне счет, а остальные на обратной. Поэтому мы с тем же успехом могли бы решить пример «${5 — 3}$» и приписать к ответу знак минус.
Но вот еще один пример с многоточием:
$7 — \ldots = -3$
Откладываем $7$ бусинок и начинаем действовать методом подбора. Отнимаем для начала одну бусинку.
Мало. Еще одну. Опять мало. Впрочем, ясно, что даже если сразу отнять все $7$ бусинок, это всё равно будет мало. Поэтому единым махом перекладываем назад все оставшиеся бусинки и говорим «семь». Переворачиваем счеты обратной стороной. Тут нам надо переложить еще $3$ бусинки. Так сразу и делаем. А теперь, поочередно касаясь их пальцем, продолжаем счет: «восемь», «девять», «десять». Это и есть ответ, который мы ищем:
$7 — \underline{\,10\,} = -3$
Поучается, что с лицевой стороны мы насчитали $7$ бусинок, а с обратной стороны — еще $3$ бусинки. Значит, мы фактически решили пример «$7 + 3$».
Конспект
1. Сложение. Пусть у нас в одной кучке шесть конфет, а в другой — две. Смешаем эти кучки в одну. Сколько в ней оказалось конфет? Ответ на эту задачу записывается в виде ${6 + 2 = 8}$ (шесть плюс два равно восемь). Мы выполнили пример на сложение: сложили шесть и два и получили восемь. Для решения этого примера на счетах откладываем вначале шесть бусинок, потом две и пересчитываем отложенные бусинки.
2. Вычитание. Пусть у нас есть кучка из пяти конфет. Мы взяли из нее три конфеты. Сколько осталось? Ответ записывается в виде ${5 — 3 = 2}$ (пять минус три равно два). Это пример на вычитание: мы вычли из пяти три и получили два. Для решения этого примера на счетах откладываем пять бусинок, возвращаем обратно три и пересчитываем оставшиеся.
3. Уравнения. Допустим в решенном примере на сложение «потерялось» первое число: ${\ldots + 3 = 9}$. Какое число потерялось? Представляем себе, что мы решили этот пример на счетах, и после этого «обращаем время вспять», фактически выполняя те же действия, которые мы совершаем при решении примера ${9 — 3 = 6}$. Подобным же образом, обращая время вспять, можно найти «потерянное» число в примере на вычитание: ${\ldots — 2 = 5}$, а именно: ${5 + 2 = 7}$. Глядя на бусинки, нетрудно также установить, что в примере ${9 + \ldots = 12}$ потерялось число ${12 — 9 = 3}$, а в примере ${14 — \ldots = 8}$ потерянным оказалось число ${14 — 8 = 6}$.
4. Отрицательные числа. Решая на счетах пример ${3 — 5}$, обнаруживаем, что из трех отложенных бусинок можно в обратную сторону переложить только три. Оставшиеся две бусинки перекладываем, развернув счеты обратной стороной. Ответ записываем в виде: ${3 — 5 = -2}$ (три минус пять равно минус два). С тем же успехом мы могли бы вычесть из пяти три и приписать перед результатом знак минус.
Задачи
1.2.1. «Мама дала Денису $7$ конфет, а папа $5$ конфет. Сколько конфет стало у Дениса?» Такого рода задач можно придумать множество, и хорошо, если они поначалу будут полностью соответствовать реальности. Главное действующее лицо — сам ребенок, и речь идет о приятных вещах. Мама в самом деле дает ему вкусные конфеты и спрашивает: «Сколько конфет я тебе дала?» Ребенок отвечает: «Семь». Потом он получает конфеты от папы, пересчитывает их и говорит: «Пять». Теперь он готов с радостью подумать над вопросом: «А сколько у тебя всего конфет?». Опять-таки, имеются в виду маленькие конфетки, не больше горошины.
1.2.2. Задачи на вычитание придумывать несколько труднее. Не следует повторять ошибку Мальвины, взявшуюся обучать арифметике Буратино. Если ребенок не любит делиться конфетами с младшим братиком, то это неподходящая тема для первых занятий по математике. Не слишком хорошо начинать и с таких задачек: «У Дениса было $10$ конфет. $4$ из них он съел. Сколько конфет осталось?» Здесь недостает наглядности: съеденных конфет-то не видно! Пожалуй, лучше так: «У папы было $10$ конфет. $4$ из них он оставил себе, а остальные дал Денису. Сколько конфет папа дал Денису?»
1.2.3. К вычитанию можно подойти еще и с другой стороны.
— Денис, сколько тебе дать конфет, — спрашивает папа.
— Двенадцать, — отвечает Денис.
— Хорошо, — говорит папа и дает Денису девять конфет. — Сколько конфет я должен тебе еще дать, чтобы получилось двенадцать?
Примеры из «динамических» прописей
Сложение и вычитание в пределах 20-ти («серый» шрифт для обводки)
То же с «уравнениями» (т.
е. пробелами для вставки чисел)
Сложение и вычитание в пределах 20-ти (разность может быть отрицательной)
То же с «уравнениями»
Origin Story: «+» и «-» основные знаки арифметики | от Edtech Board | Edtech Board
Мы никогда не сможем думать о математике без знаков «+» плюс и «-» минус. Хотя у нас есть множество математических символов для деления (÷), умножения (×), интеграла (∫) и т. д., по своей сути это всегда символы «+» и «-». С самого раннего детства нас учили этим двум неотъемлемым символам. Их можно было бы рассматривать как азбуку математики, и без них все было бы иначе. Одни и те же символы используются везде, по всему миру. Немного любопытства, чтобы узнать, как они возникли и эволюционировали в нынешнюю форму, не повредит.
Знаки плюс и минус (+ и −) — это математические символы, используемые для обозначения операций сложения и вычитания, а также понятий положительного и отрицательного. Более того, плюс и минус — это латинские термины, означающие «больше» и «меньше» соответственно.
Происхождение этих двух символов восходит к египетским иероглифам, где они использовали символы, напоминающие «пару ходячих ног», которые либо уходят, либо приближаются, представляя сложение или вычитание. Точно так же, как и у греков, у индусов тоже не было особого знака для сложения и вычитания. Много раз они использовали «ю» для обозначения сложения. «Ю» использовалось в арифметике бахшалинской рукописи, относящейся к периоду III или IV века. Было отмечено, что в Европе начала 15 века буквы «P» и «M» использовались для обозначения одного и того же.
Зарегистрировано, что знак «+» происходит от латинского слова «et», означающего «и». Николь д’Оресм, астроном и автор книги «Книга неба и мира» 14 века, использовала знак «+» в качестве сокращения для слова «et». Использование знака «-» впервые было зарегистрировано в 1481 году в рукописи по немецкой алгебре, хранящейся в Дрезденской библиотеке. Иоганнес Видман, знаменитый немецкий математик, опубликовал первую печатную книгу под названием «Торговая арифметика» в Лейпциге, 1489 г.
, где он использовал знаки «+» и «-». В начале 17 века эти два символа также использовались математиками Кавальери и Глориози, а также астрономом Кристофером Клавиусом.
Но именно Роберт Рекорд, известный валлийский математик и создатель знака равенства (=), ввел в Британии в 1557 году те же плюс и минус, которыми мы пользуемся до сих пор. Он описал эти два знака следующими словами:
«Есть еще два часто используемых знака, из которых первый сделан таким образом + и означает большее; другой сделан таким образом — и означает меньшее».
Кажется, разные люди использовали разные версии этих знаков, но именно Роберт Рекорд дал нам знаки, которыми мы пользуемся до сих пор, которые передавались из поколения в поколение, прежде чем получили всеобщее признание.
Первое уравнение, когда-либо написанное Робертом Рекордом в его трактате «Точильный камень Витте» в 1557 году. Уравнение, представленное в современных терминах, «14x+15=71» с помощью , и его решение равно 4.
A Еврейская традиция, которая восходит к 1920-го века пишет символ плюса, используя что-то, напоминающее перевернутую букву Т, и даже сейчас используется в еврейских начальных школах. Объяснение этому заключается в том, что он избегает обычного символа «+», который выглядит ужасно похожим на христианский крест.
Первоначально опубликовано по адресу www.edtechboard.com 20 марта 2013 г.
Где и когда появились символы «+» и «–»?
Символы для арифметических операций сложения (плюс; «+») и вычитания (минус; «–») настолько распространены сегодня, что мы вряд ли когда-нибудь задумываемся о том, что они не всегда существовали. На самом деле кто-то должен был сначала изобрести эти символы (или, по крайней мере, другие символы, которые позже превратились в текущую форму), и, безусловно, должно было пройти некоторое время, прежде чем символы стали общепринятыми. Когда я начал изучать историю этих знаков, я с удивлением обнаружил, что они не имеют своего происхождения в древности.
Многое из того, что нам известно, основано на впечатляюще всесторонних и до сих пор непревзойденных исследованиях (в 1928–1929) под названием History of Mathematical Notations швейцарско-американского историка математики Флориана Каджори (1859–1930).
Древние греки выражали сложение в основном путем сопоставления, но время от времени использовали косую черту «/» для сложения и полуэллиптическую кривую для вычитания. В знаменитом египетском папирусе
Нет никаких сомнений в том, что наш знак + имеет свои корни в одной из форм слова » et , что означает «и» на латыни.
Первый человек, который, возможно, использовал знак + как аббревиатуру для и — астроном Николь д’Оресм (автор книги «Книга неба и мира
Advertisement
Происхождение знака — гораздо менее ясно, и предположения варьируются от иероглифического или александрийского грамматического происхождения до символа полосы, используемого торговцами для отделения тары от общего веса товаров.
Первое использование современного алгебраического знака появляется в немецкой рукописи по алгебре 1481 года, которая была найдена в Дрезденской библиотеке. В латинском манускрипте того же периода (также в Дрезденской библиотеке) встречаются оба символа + и –. Известно, что Йоханнес Видман изучил и прокомментировал обе эти рукописи. В 1489 году в Лейпциге он издал первую печатную книгу ( Торговая арифметика ), в которой встречались два знака + и – (рис.
1). Тот факт, что Видман использовал символы, как если бы они были общеизвестны, указывает на возможность того, что они были получены из практики торговцев. В анонимной рукописи — вероятно, написанной примерно в то же время — также использовались те же символы, и она послужила материалом для двух дополнительных книг, опубликованных в 1518 и 1525 годах.0003
Рис. 1. Первое использование символов + и – в печати в книге Йоханнеса Видмана Behëde und Lubsche Rechenung auff allen Kauffmanschafft, Аугсбургское издание 1526 года.
В Италии символы + и – были приняты астрономом Кристофером Клавиус (немец, живший в Риме), математики Глориози и Кавальери в начале XVII века.
Реклама
Первое появление + и – в английском языке было в 1551 году в книге по алгебре Точильный камень Витте оксфордского математика Роберта Рекорда, который также ввел знак равенства как более длинный, чем сегодняшний символ «═». Описывая знаки «плюс» и «минус», Рекорд писал: «Есть два других знака, при частом использовании которых первый сделан таким образом + и означает больше: другой сделан таким образом — и означает меньше».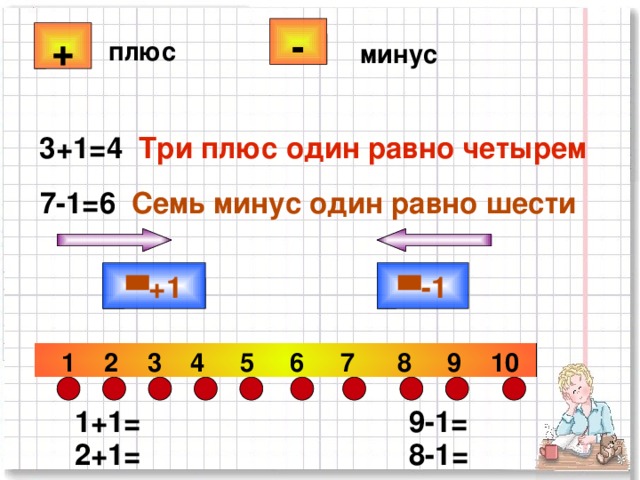
В качестве исторического любопытства я должен отметить, что даже после принятия не все использовали один и тот же символ для +. Сам Видман представил его как греческий крест + (знак, который мы используем сегодня), с горизонтальной чертой, иногда немного более длинной, чем вертикальная. Эту форму использовали такие математики, как Рекорд, Харриот и Декарт. Другие (например, Юм, Гюйгенс и Ферма) использовали латинский крест «✝», иногда располагаемый горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Де Ортега, Галлей) использовали более декоративную форму «✠».
Практика обозначения вычитания была несколько менее причудливой, но, возможно, более запутанной (по крайней мере, для нас), поскольку вместо простого – в немецких, швейцарских и голландских книгах иногда использовался символ «÷», который мы теперь используем для разделение. В нескольких книгах семнадцатого века (например, Декарта и Мерсенна) для вычитания использовались две точки «∙∙» или три точки «∙∙∙».