Теперь, как обычно, сам.
Как построить параболу | Алгебра
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция.
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
y=x²+2x-3
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т.
y= -x²+2x+8
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Примеры.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
y=x²+5x+4
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
y= -x²-3x
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Квадратичная функция, как построить Параболу
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения.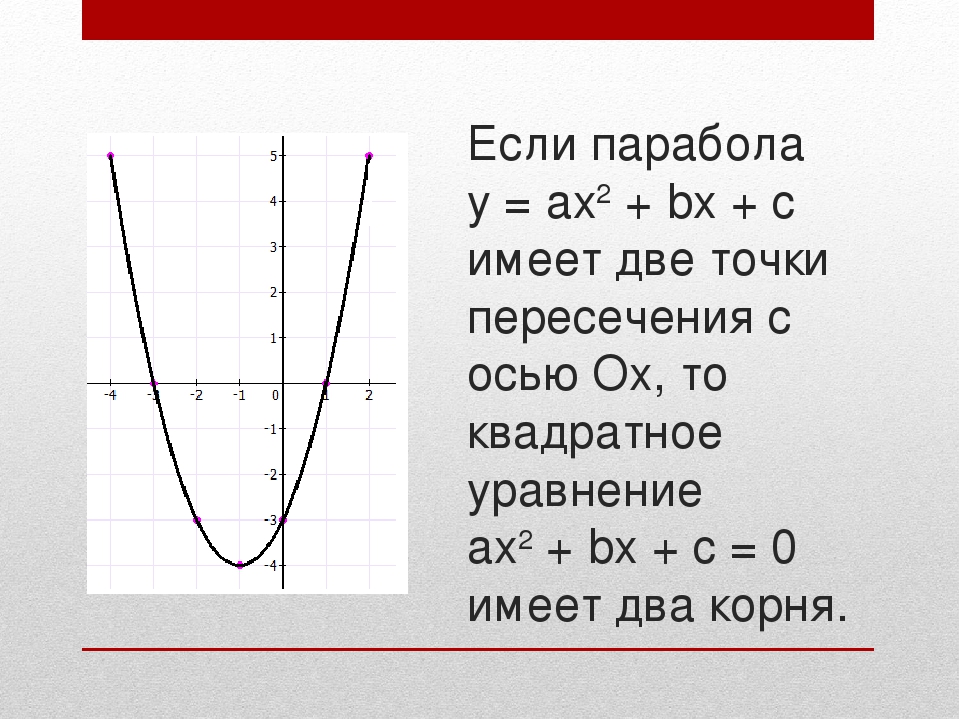 Вот, какими способами ее можно задать:
Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.
График функции y = –x2
выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x | -2 | -1 | 0 | 1 | 2 |
y | -4 | -1 | 0 | -1 | -4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax
2 + bx + c.Разберем общий алгоритм на примере y = 2x2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
Уравнение квадратичной функции имеет вид y = a * (x — x₀)
2 + y₀Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Рассмотрим следующий пример: y = (x — 2) * (x + 1).
Как строим:
- Данный вид уравнения позволяет быстро найти нули функции:
(x — 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.
- Определим координаты вершины параболы:
- Найти точку пересечения с осью OY:
с = ab =(-2) * (1)= -2 и ей симметричная.
- Отметим эти точки на координатной плоскости и соединим плавной прямой.
 3 + k\).
3 + k\).- Если \(k > 0\), то график сдвигается на \(k\) единиц вверх; если \(k < 0\), то график сдвигается на \(k\) единиц вниз.
- Если \(h > 0\),то график сдвигается на \(h\) единиц вправо; если \(h < 0\), то график смещается на \(h\) единиц влево.
- Если \(a < 0\), график переворачивается.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Пермский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.
Оставить заявку Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.Репетитор по математике
Запорожский национальный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.
Оставить заявку При обучении всегда стараюсь приводить примеры из реальной жизни и показываю, как из жизненных ситуаций построить математическую модель.
Считаю, что при изучении математики нельзя изучать новый материал, пока дети не усвоили предыдущий. Я люблю математику за то, что она развивает логическое и алгоритмическое мышление, пространственное воображение.
При обучении всегда стараюсь приводить примеры из реальной жизни и показываю, как из жизненных ситуаций построить математическую модель.
Считаю, что при изучении математики нельзя изучать новый материал, пока дети не усвоили предыдущий. Я люблю математику за то, что она развивает логическое и алгоритмическое мышление, пространственное воображение.Репетитор по математике
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов.
 Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!Векторы
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Построение графика квадратичной функции
Построение графика квадратичной функции, заданной формулой
Предмет: алгебра
Класс: 8 «Б»
Тема: Построение графика квадратичной функции, заданной формулой
Тип: комбинированный урок.
Форма организации учебной деятельности: индивидуально-групповая.

Цели
Обучающие
· проверить знания, умения и навыки построения графика квадратичной функции, заданной формулой
· внедрить алгоритм построения графика квадратичной функции, заданной формулой
· отработать алгоритм при построении графиков квадратичной функции.
Развивающая
· продолжить работу по развитию умения работать с книгой, сравнивать; развивать коммуникативные связи, информационную грамотность, логику.
Воспитательная
· стимулировать учащихся к самооценке образовательной деятельности, вызывая чувство самопознания, самоопределения и самореализации.
Оборудование
· Доска, компьютеры, экран с проектором, карточки с алгоритмами.
Ход урока
1) Организационный момент (2 мин)
· Учитель формулирует тему и цели урока, сообщает план работы, который проецируется на экран и по мере выполнения стираются пункты плана.
 Учащиеся записывают число и тему урока в тетради.
Учащиеся записывают число и тему урока в тетради.Работа по плану
1) Работая устно, вспоминаем решение уравнений.
2) Учащиеся проверяют свои знания по построению графика квадратичной функции способом перемещения.
3) Знакомство с алгоритмом.
4) Отработка алгоритма при построении графиков функции, заданной формулой
2) Актуализация знаний учащихся (13 мин).
1) Фронтальная устная работа.
1. Что является графиком функции у = аx2. (парабола)
2. Как зависит график функции у = аx2 от коэффициента а.а) Сформулируйте правило переноса графика функции вдоль оси абсцисс.
б) Сформулируйте правило переноса графика функции вдоль оси ординат.
(если а>0, то происходит растяжение графика функции от оси Ох вдоль оси Оу, ели 0<a<1, то происходит сжатие графика функции к оси Ох вдоль оси Оу)
3. Вспомни алгоритм построения графиков функций , если известен график функции у = аx2.
(График функции является парабола, получаема сдвигом параболы у = аx2:
вдоль оси абсцисс вправо на х0, если х0>0, влево на , если х0<0;
вдоль оси ординат вверх на у0, если у0>0, вниз на , если у0<0).
4. Как определить координаты вершины параболы?
5. Как определить точку, через которую проходит ось симметрии параболы?
6. Как определить направление «ветвей» параболы?
· Заполни пропуски (работа с интерактивной доской): все записывают в тетради. Взаимопроверка.
1. Функция у = aх2 + bx + c, где а, b, c – заданные действительные числа, а ¹ 0,
х – действительная переменная, называется … функцией. (квадратичной)
2. График функции у = ах2 при любом а ¹ 0 называют … .(параболой)
3. Функция у = х2 является … (возрастающей, убывающей) на промежутке
х £ 0. (убывающей)
4. Значения х, при которых квадратичная функция равна нулю, называют … функции (нулями функции)
5.
 Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы)
Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы)6. При а >0 ветви параболы у = ах2 направлены … . (вверх)
7. Если а< о и х ¹ 0, то функция у = ах2 принимает … (отрицательные)
(положительные, отрицательные) значения.
Работа у доски (индивидуальны карточки у доски)
1. Найдите координаты вершины параболы у=х2-4х+4 Ответ: (2;0)
2.Найдите нули квадратичной функции у=х2+х-2 Ответ: -2; 1
3. Выдели полный квадрат x2 — 4х + 5. И постройте график полученной функции.
Ответ: х2 — 4х + 5 = (х2 — 4х + 4) + 1 = (х — 2)2 + 1
Фронтальная работа с классом. (Презентация)
3.Учитель поясняет задание. Для каждой из функций, графики которых изображены, выберите соответствующее условие и отметьте знаком «+». Ученики выполняют работу на распечатанных листочках, осуществляя самопроверку. Листочки заранее раздать ученикам.
После того, как учащиеся закончили решение теста, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, один ученик выполняет задание на интерактивной доске, на экране с помощью анимации появляются правильные ответы.
 ( Презентация)
( Презентация)После проверки учащиеся оценивают работу соседа по следующему критерию:
- «5» — нет ошибок;
- «4» — 1 ошибка;
- «3» — 2 ошибки;
- «2» — 3 и более ошибки.
Проверка работ учащихся у доски
4.
Ответ:
(Находим нули функции: =0 х1=0; х2=-5, ветви параболы направлены вверх а>0).
Ответ: (3,0) ;
2) Индивидуальное задание
· Индивидуальная работа на компьютерах. Первая группа, проверяет свои знания по построению графиков функции – в течение 4 минут выполняет теств Excel. (11 человек). Ученикам раздаются по окончанию работы образцы для проверки.
Образец для проверки
· Фронтальная устная работа (проверка работы, анализ и комментирование). Учащиеся второй группы выполняют тест с помощью системы голосования Verdict. На экране появляется изображение соответствующего графика с указанной функцией. (15 человек).

Тест
«Квадратичная функция»
В системе Verdict
10. Функция задана формулой . Найдите .
1) 24 2) 0 3) 8 4) -8
1. График какой функции изображен на рисунке?
1) 2)
3) 4)
4. Найдите нули функции .
1) 2 и 3 2) -6 и -1 3) 1 и 6 4) -3 и -2
2. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
3. График какой функции изображен на рисунке?
График какой функции изображен на рисунке?1) 2)
3) 4)
0
1
1
у
х
8. На каком промежутке функция, изображенная на рисунке убывает?1) 2) 3) 4)
5. График какой функции изображен на рисунке?
1) 2)
3) 4)
6. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
SHAPE \* MERGEFORMAT0
1
1
у
х
0
1
1
у
х
7. График какой функции изображен на рисунке?
График какой функции изображен на рисунке?1) 2)
3) 4)
0
1
Формула вершины параболы
☰
Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.
Квадратичная функция имеет вид: y = ax2 + bx + c.
Ее график — это парабола с вершиной, координаты которой определяются по формулам:
Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.
Например, если дана функция y = 2x2 – 4x + 5, то координата x ее вершины будет равна:
x = –(–4 / (2 × 2)) = 1
Координату же y вычислим, подставив найденный x в саму функцию:
y = 2 × 12 – 4 × 1 + 5 = 3
Таким образом, вершина графика функции y = 2x2 – 4x + 5 находится в точке с координатами (1; 3).

В остальном парабола квадратичной функции вида y = ax2 + bx + c такая же как функции вида y = ax2. Отличие лишь в сдвиге вершины по сравнению с функцией y = ax2. Так в приведенном выше примере (y = 2x2 – 4x + 5) парабола будет по форме и направлению ветвей такой же, как для функции y = 2x2. Разница лишь в координатах вершин парабол.
Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b2) / 4a. То есть l и m — это координаты x0 и y0 соответственно.
Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax2 + bx + c.
 При этом выполняются следующие преобразования:
При этом выполняются следующие преобразования:- Объединим первые два члена многочлена: y = (ax2 + bx) + c
Вынесем коэффициент a за скобку, при этом b разделится на a:
Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:
Выделим квадрат суммы:
Умножим на a:
Приведем к общему знаменателю свободные члены:
Поменяем знак:
Таким образом, мы привели функцию y = ax2 + bx + c к виду y = a(x + l)2 + m, что соответствует функции y = f(x + l) + m, где f(x) = ax2. А как строить графики последней известно.

Схематично рисуем параболу по исходному выражению. Построение графика квадратичной функции. Визуальный гид (2019)
Наступает первое сентября, и счастливые родители ведут свое чадо первый раз в первый класс. А дальше дорога для большинства учащихся длиною в 11 лет. Математика с ними на всем пути, но не у всех детей прирожденная склонность к ней.
Перед учителем встает ряд нелегких проблем. Выделим три из них:
1. Искать те крупицы воздействия на учащихся, которые способствовали бы стремлению приобретать знания, расширять их, а значит помогать начинать мыслить, включаться в урок.
2. Сделать урок таким, чтобы осталась пища для размышлений.
3. Предвидеть, что есть учащиеся с тягой к гуманитарным наукам, и стремиться помочь пробудить в них желание погрузиться в математический мир, но одновременно не забывать увлеченных математикой и давать пищу жаждущему ее уму.
Мы обратим внимание на материал статьи “Рисуем графиками функций” . Автор, А. Я. Цукарь из Новосибирска предлагает выполнить 6 рисунков в качестве упражнений для домашних заданий, заметив, что они будут полезны школьникам с гуманитарной направленностью. Там же приведен список изображаемых объектов (зонтик, очки, кит, шахматный король, лягушка, бабочка ) и перечень функций, графики которых участвуют в этом изображении. Заметим, что продолжение, в смысле новых рисунков, напечатано в газете “Математика” .
О том, как этот материал можно использовать с целью попытки решения тех проблем, которые выделили выше, дальше пойдет речь.
Наш век – век компьютеров, значит, они должны работать и на уроках математики, а не только на уроках информатики. Мы предлагаем воспользоваться программой, по которой возможно выполнить эти 6 рисунков. Программа выполнена в формате интернет-страниц.
Все графики вычерчиваются исходя из математических формул. На экране отображается координатная сетка и оси.
 При нажатии на
изображение уравнения происходит вычерчивание
графика, причем это построение можно повторить
несколько раз. Размер чертежа можно увеличить
или уменьшить, что позволяет уточнить координаты
той или иной точки. Программу, выполняющую данные
построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru
При нажатии на
изображение уравнения происходит вычерчивание
графика, причем это построение можно повторить
несколько раз. Размер чертежа можно увеличить
или уменьшить, что позволяет уточнить координаты
той или иной точки. Программу, выполняющую данные
построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ruПриводим наши предложения о том, что можно добавить к материалу при изучении квадратичных функций и как это сделать.
Начнем с фрагмента начала урока перед рассмотрением построения графика квадратичной функции «y=ax 2 «.
На экране телевизора или компьютера медленно вырисовываются в разных цветах части парабол, которые в итоге дают изображение лягушки.
Учитель замечает, что детали для рисунка предоставила нам очень интересная функция, называемая квадратичной , построение графиков которой – цель нашего урока. После освоения материала (на него уйдет не один урок) каждый сможет сам рисовать, а проверять свои художества можно, используя компьютер.
 Учитель
примерно так вводит учащихся в новую тему.
Учитель
примерно так вводит учащихся в новую тему.Какая задумка была у учителя в самом начале урока? Вызвать эмоциональные переживания через удивление. На это работает необычность приводимого факта, красота обозреваемого объекта, скорость получения результата…
В этом случае внутренние переживания ученика подключаются к таким процессам, как запоминание, внимание, осмысливание. Они будут протекать более интенсивно и способствовать достижению решаемых задач в обучении.
В конце урока в качестве итога учитель обращает внимание на материал стенда, который до этого был закрыт “Изучаем на уроке”.
На нем привлекает внимание лягушонок , который запомнился учащимся и держит их в ожидании нового урока. Этого нам очень хотелось бы достичь. Потому приведены все функции, принимавшие участие в выполнении рисунка. Они отличаются от тех, с которыми учащиеся имели дело на прошедшем уроке, что особо подмечал учитель.
Там же запечатлена хроника начала урока с конкретизацией ряда моментов в шутливой стихотворной форме и подчеркнута возможность ученика, усвоившего изучаемый материал, в дальнейшем так же, как компьютер, рисовать графиками функции.

Творчески работающий учитель найдет, где и как использовать при изучении программного материала нижеследующие задания. Они будоражат фантазию, развивают эстетические наклонности, приобщают к поиску, пониманию математических истин, увлекают в загадочный мир знаний.
Задание 1.
1) Построить график функции и сделать трафарет.
2) С помощью трафарета дорисовать построенную параболу до того, на чем остановится Ваша фантазия. При этом трафарет можно переворачивать, перемещать влево или вправо, вверх или вниз, использовать любую его часть и оси координат.
3) Записать формулы парабол, прямых, которые определили Ваш рисунок.
Приводим пример выполнения задания 1. Парабола построена .После несложных размышлений принято решение рисовать тюльпан . Из параболы получается цветок, если ее прервать, проведя вверху изящную волнистую линию. Ось игреков от точки О вниз – это стебелек, справа и слева от него можно сделать по листочку.

Наши действия: трафарет переворачиваем (т.е. ветви направляем вниз) и перемещаем по параболе…
Находятся такие точки С, D, Е , которые после совмещения (трижды) с точкой О (на трафарете) дадут нужную линию.
Запишем формулы трех парабол, позволившие это сделать. Работает формула , где точка (m; n) — вершина параболы. У нас первая точка С (-4; 19) – вершина одной из парабол, а именно . Мы обводим только участок параболы при . Аналогичным будет подход в описании всех остальных случаев.
В итоге тюльпан рисовали семь квадратичных функций и одна линейная:
1.
2.
3.
4.
5.
6.
7.
8.
Задание 2.
Графиками функций сделать рисунок, дать ему название.
Например. Даны функции:
1.
2.
Инструкция
Для начала, начертите на листе координатные оси: ось абсцисс и ось ординат. Подпишите их. После этого, поработайте над данной квадратичной функцией.
 2 — (1;1), (-1;1) и (2;4), (-2;4).
2 — (1;1), (-1;1) и (2;4), (-2;4).После нанесения точек на координатную плоскость, соедините их плавной линией, придавая ей округлые . Не заканчивайте график в верхних точках, а продлите его, так как парабола бесконечна. Не забудьте подписать график на , а также напишите необходимые координаты на осях, в противном случае, это вам могут за ошибку и снять определенное количество баллов.
Источники:
- как нарисовать параболу
В элементарной и высшей математике встречается такой термин, как гипербола. Так называют график функции, который не проходит через начало координат и представляет собой две параллельные друг другу кривые. Существует несколько способов построения гиперболы.
Инструкция
Гипербола так же, как и другие кривые может быть двумя способами. Первый из них заключается в построении по прямоугольнику, а второй — функции f(x)=k/x.
Начинать строить гиперболу следует с построения прямоугольника по оси x, именуемыми A1 и A2, и с противоположными концами по оси y, именуемыми B1 и B2. 2
2
У равнобочной гиперболы асимптоты перпендикулярны друг другу. Кроме того, между y и x имеется пропорциональная , заключающаяся в том, что если x уменьшить в заданное число раз, то y увеличится во столько же раз, и наоборот. Поэтому, по-другому уравнение гиперболы записывается в виде:
y=k/xЕсли в условии дана функция f(x)=k/x, то целесообразнее строить гиперболу . Учитывая, что k — величина постоянная, а знаменатель x≠0, можно придти к выводу, что график функции не проходит через начало координат. Соответственно, интервалы функции равны (-∞;0) и (0;∞), так как при обращении x в ноль функция теряет . При увеличении x функция f(x) убывает, а при уменьшении возрастает. При приближении x к нулю соблюдается условие y→∞. График функции показан на основном рисунке.
Для построения гиперболы методом расчета удобно использовать . Если он способен работать по программе или хотя бы запоминать , можно заставить его осуществить расчет несколько раз (по числу точек), не набирая выражение каждый раз заново.
 Еще удобнее в этом смысле графический калькулятор, который возьмет на себя, помимо расчета, и построение графика.
Еще удобнее в этом смысле графический калькулятор, который возьмет на себя, помимо расчета, и построение графика.Источники:
- что такое график и как его построить
Чтобы речь была более яркой и выразительной, люди используют образные средства языка и стилистические приемы: метафору, сравнение, инверсию и другие. В системе способов художественной выразительности стоит и гипербола, или преувеличение — стилистический прием, который очень часто используется как в живой разговорной речи, так и в языке художественной литературы.
Гипербола (в переводе с греческого — преувеличение) — это стилистическая фигура, или художественный прием, который заключается в намеренном преувеличении некоторых свойств изображаемого предмета или явления для создания большей выразительности и, соответственно, усиления эмоционального воздействия от них. Гипербола может проявлять себя в количественном преувеличении (например, «мы не виделись сто лет») и воплощаться в образном выражении (например, « мой»).
 Это художественное средство выразительности нельзя назвать , так как гипербола — это только преувеличение, она лишь выделяет, подчеркивает те или иные свойства предмета или явления, не изменяя их образного содержания.
Это художественное средство выразительности нельзя назвать , так как гипербола — это только преувеличение, она лишь выделяет, подчеркивает те или иные свойства предмета или явления, не изменяя их образного содержания.Гиперболу можно считать одним из основных способов создания художественного образа : живописи и литературе. Благодаря тому, что ее главной функцией является воздействие на эмоции, она широко используется авторами в качестве средства выразительности для усиления впечатления на читателя. Этот стилистический прием характерен для риторического и романтического стилей и является важнейшим способом формирования сюжета и обрисовки характеров в литературных произведениях. Гипербола как художественный прием широко распространена в фольклоре: в былинах, сказках, песнях (например, в «У страха глаза велики», былине «Илья Муромец и Соловей-разбойник»), в русской литературе как средство передачи авторской мысли. В русской литературной традиции гипербола свойственна и поэтической речи (М.
 Ю. Лермонтов, В.В. Маяковский), и прозе (Г.Р. Державин, Н.В. Гоголь, Ф.М. Достоевский, М.Е. Салтыков-Щедрин).
Ю. Лермонтов, В.В. Маяковский), и прозе (Г.Р. Державин, Н.В. Гоголь, Ф.М. Достоевский, М.Е. Салтыков-Щедрин).В разговорной речи гипербола реализуется с помощью различных языковых средств: лексических (например, с помошью слов «совсем», «совершенно», «все» и так далее), фразеологических (например, «это и ежу понятно»), морфологических (употребление множественного числа вместо единственного, например, «некогда чаи распивать»), синтаксических (количественнных конструкциий, например, «миллион дел»). В художественной гипербола часто употребляется непосредственно с другими тропами и стилистическими фигурами, прежде всего с метафорой и сравнением, и сближается с ними, образуя гиперболические фигуры (например, гиперболическая метафора «Весь мир — театр, и люди в нем »). Этот стилистический прием также играет большую роль не только в литературном творчестве, но и в риторике, так как способствует повышению эмоционального воздействия на слушателя.
Видео по теме
Источники:
Гипербола – график обратной пропорциональности y=k/x, где k — коэффициент обратной пропорциональности не равен нулю.
 Графически гипербола являет собой две плавные изогнутые линии. Каждая из них зеркально отображает другую относительно точки начала декартовых координат.
Графически гипербола являет собой две плавные изогнутые линии. Каждая из них зеркально отображает другую относительно точки начала декартовых координат.Вам понадобится
- — карандаш;
- — линейка.
Инструкция
Начертите оси координат. Нанесите все необходимые обозначения. Если y=k/x, коэффициент k — больший нуля, то ветви будут размещаться в первой и третьей четвертях. В этом случае на всей области определения, которая состоит из двух промежутков: (-∞; 0) и (0; +∞).
Постройте сначала ветвь гиперболы на промежутке (0; +∞). Найдите координаты точек, необходимые для построения кривой. Для этого задайте переменной x несколько произвольных значений и вычислите значения переменной y. Например, для функции y=15/x при x=45 получим y=1/3; при x=15, y=1; при x=5, y=3; при x=3, y=5; при x=1, y=15; при x=1/3, y=45. Чем больше точек вы определите, тем точнее графическое изображение .
Нанесите полученные точки на координатную плоскость и соедините их плавной линией.
 Это и будет ветвь функции y=k/x на промежутке (0; +∞). Обратите внимание на то, что кривая никогда не пересекает осей координат, а лишь к ним приближается, т. к. при x=0 функция не определена.
Это и будет ветвь функции y=k/x на промежутке (0; +∞). Обратите внимание на то, что кривая никогда не пересекает осей координат, а лишь к ним приближается, т. к. при x=0 функция не определена.Постройте вторую кривую гиперболы на промежутке (-∞; 0). Для этого задайте переменной x несколько произвольных значений из данного числового промежутка. Вычислите значения переменной y. Так, для функции y=-15/x при x=-45 получим y=-1/3; при x=-15, y=-1; при x=-5, y=-3; при x=-3, y=-5; при x=-1, y=-15; при x=-1/3, y=-45.
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция, и с чем ее едят. Если ты считаешь себя профи по части квадратичных функций, добро пожаловать. Но если нет, тебе стоит прочитать тему .
Начнем с небольшой проверки :
- Как выглядит квадратичная функция в общем виде (формула)?
- Как называется график квадратичной функции?
- Как влияет старший коэффициент на график квадратичной функции?
Если ты сходу смог ответить на эти вопросы, продолжай читать.
 Если хоть один вопрос вызвал затруднения, перейди по .
Если хоть один вопрос вызвал затруднения, перейди по .Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: .
Давай вкратце вспомним, что делают коэффициенты .
- Старший коэффициент отвечает за «крутизну» параболы, или, по-другому, за ее ширину: чем больше, тем парабола у́же (круче), а чем меньше, тем парабола шире (более пологая).
- Свободный член — это координата пересечения параболы с осью ординат.
- А коэффициент каким-то образом отвечает за смещение параболы от центра координат. Вот об этом сейчас подробнее.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина . А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
Вот так: чем больше , тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив в функцию:
Подставь сам и посчитай.
 Что получилось?
Что получилось?Если сделать все правильно и максимально упростить полученное выражение, получится:
Получается, что чем больше по модулю , тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ — строить параболу, начиная с вершины.Пример:
Построить график функции.
Решение:
Для начала определим коэффициенты: .
Теперь вычислим координаты вершины:
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково. Значит, если мы построим параболу и переместим ее вершиной в точку, получится нужный нам график:
Просто, правда?
Остается только один вопрос: как быстро рисовать параболу? Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить.
 Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.Рассмотрим простейшую параболу. Построим ее по точкам:
Закономерность здесь такая. Если из вершины сместиться вправо (вдоль оси) на, и вверх (вдоль оси) на, то попадем в точку параболы. Дальше: если из этой точки сместиться вправо на и вверх на, снова попадем в точку параболы. Дальше: вправо на и вверх на. Дальше что? Вправо на и вверх на. И так далее: смещаемся на вправо, и на следующее нечетное число вверх. То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным. Например, нам стало известно, что вершина параболы находится в точке. Построй (самостоятельно, на бумаге) эту параболу.
Построил?
Должно получиться так:
Теперь соединяем полученные точки:
Вот и все.

ОК, ну что же, теперь строить только параболы с?
Конечно, нет. Сейчас разберемся, что с ними делать, если.
Рассмотрим несколько типичных случаев.
Отлично, параболу рисовать научились, давай теперь потренируемся на настоящих функциях.
Итак, нарисуй графики таких функций:
Ответы:
3. Вершина: .
Помнишь, что делать, если старший коэффициент меньше?
Смотрим на знаменатель дроби: он равен. Значит, будем двигаться так:
- вправо — вверх
- вправо — вверх
- вправо — вверх
и так же влево:
4. Вершина: .
Ой, а что с этим делать? Как отмерять клетки, если вершина где-то между линиями?..
А мы схитрим. Нарисуем сперва параболу, а уже потом переместим ее вершиной в точку. Даже нет, поступим еще хитрее: Нарисуем параболу, а потом переместим оси: — на вниз , а — на вправо :
Этот прием очень удобен в случае любой параболы, запомни его.

Напомню, что мы можем представить функцию в таком виде:
Например: .
Что это нам дает?
Дело в том, что число, которое вычитается из в скобках () — это абсцисса вершины параболы, а слагаемое за скобками () — ордината вершины.
Это значит, что, построив параболу, нужно будет просто сместить ось на влево и ось на вниз.
Пример: построим график функции.
Выделим полный квадрат:
Какое число вычитается из в скобках? Это (а не, как можно решить не подумав).
Итак, строим параболу:
Теперь смещаем ось на вниз, то есть на вверх:
А теперь — на влево, то есть на вправо:
Вот и все. Это то же самое, как переместить параболу вершиной из начала координат в точку, только прямые ось двигать намного легче, чем кривую параболу.
Теперь, как обычно, сам:
И не забывай стирать ластиком старые оси!
Я в качестве ответов для проверки напишу тебе ординаты вершин этих парабол:
Все сошлось?
Если да, то ты молодец! Уметь обращаться с параболой — очень важно и полезно, и здесь мы выяснили, что это совсем не трудно.

ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ. КОРОТКО О ГЛАВНОМ
Квадратичная функция — функция вида, где, и — любые числа (коэффициенты), — свободный член.
График квадратичной функции — парабола .
Вершина параболы:
, т.е. чем больше \displaystyle b , тем левее смещается вершина параболы.
Подставляем в функцию, и получаем:
, т.е. чем \displaystyle b больше по модулю , тем выше будет вершина параболыСвободный член — это координата пересечения параболы с осью ординат.
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это — не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но, думай сам…
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время .
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.

Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.
Как? Есть два варианта:
- Открой доступ ко всем скрытым задачам в этой статье —
- Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника — Купить учебник — 899 руб
Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.
Доступ ко всем скрытым задачам предоставляется на ВСЕ время существования сайта.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т.
 д.):
д.):Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем .
 В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.

При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Парабола
Когда вы пинаете футбольный мяч (или стреляете стрелой, запускаете ракету или бросаете камень), он поднимается вверх по дуге и снова падает …
… по пути параболы!
(Кроме того, как воздух влияет на него.)
Попробуй ударить по мячу:
images / parabola-ball.
 js? mode = мяч
js? mode = мячОпределение
Парабола — это кривая, в которой любая точка находится на равном расстоянии от:
- фиксированная точка ( фокус ) и
- фиксированная прямая ( директрикс )
Возьмите лист бумаги, нарисуйте на нем прямую линию, затем сделайте большую точку для фокуса (не на линии!).
Теперь поэкспериментируйте с некоторыми измерениями, пока не получите еще одну точку, которая находится на таком же расстоянии от фокуса и прямой линии.
Продолжайте, пока у вас не будет много маленьких точек, затем соедините маленькие точки, и у вас будет парабола!
Имена
Вот важные имена:
- г. директрикс и focus (объяснено выше)
- ось симметрии (проходит через фокус, перпендикулярно директрисе)
- г.
 вершина (где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой.
вершина (где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой.
Отражатель
А парабола обладает удивительным свойством:
Любой луч, параллельный оси симметрии, отражается от поверхности по прямой к фокусу .
И это объясняет, почему эта точка называется фокусом …
… потому что там фокусируются все лучи!
Таким образом, параболу можно использовать для:
- спутниковые антенны,
- антенна радарная,
- концентрирует солнечные лучи, чтобы создать горячую точку,
- отражатель на точечные светильники и фонари,
- и т. Д.
Мы также получаем параболу, когда разрезаем конус (разрез должен быть параллелен стороне конуса).
Итак, парабола — это коническое сечение (сечение конуса).
Уравнения
Простейшее уравнение параболы: y = x 2
В перевернутом виде получается y 2 = x
(или y = √x только для верхней половины)
Немного шире:
y 2 = 4ax
, где a — это расстояние от исходной точки до фокуса (а также от исходной точки до директрисы)
Пример: Найдите фокус для уравнения y
2 = 5x
Преобразуя y 2 = 5x в y 2 = 4ax , мы получаем y 2 = 4 (5/4) x ,, поэтому a = 5/4 , а фокус y 2 = 5x равен:
Уравнения парабол в разной ориентации следующие:
y 2 = 4ax
y 2 = −4ax
x 2 = 4 дня
x 2 = −4 дняИзмерения параболической тарелки
Если вы хотите построить параболическую тарелку с фокусом на 200 мм над поверхностью, какие измерения вам нужны?
Чтобы упростить сборку, давайте сделаем так, чтобы он был направлен вверх, и поэтому мы выберем уравнение x 2 = 4ay.
И мы хотим, чтобы «a» было 200, поэтому уравнение принимает следующий вид:
x 2 = 4ay = 4 × 200 × y = 800y
Переставляем так, чтобы можно было вычислить высоту:
y = x 2 /800
А вот измерения высоты, пока вы бежите:
Расстояние вдоль («x») Высота («y») 0 мм 0.0 мм 100 мм 12,5 мм 200 мм 50,0 мм 300 мм 112,5 мм 400 мм 200.0 мм 500 мм 312,5 мм 600 мм 450.0 мм Попробуйте построить его сами, это может быть весело! Только будьте осторожны, отражающая поверхность может сконцентрировать много тепла в фокусе.
567 568 833 834, 2088, 2089, 2086, 2087, 3334, 3335
предварительное вычисление алгебры — Построение параболы по двум точкам и оси симметрии
Георг и футуролог однозначно ответили на мой вопрос, и я публикую здесь еще один ответ, который я получил из намеков Георга, просто чтобы добавить немного разнообразия.
Думаю, я заметил эту конструкцию, потому что у меня было более поверхностное понимание теоремы Паскаля, ха: P
Прежде чем описывать конструкцию, сделаю несколько замечаний с двумя фигурами.
Шестиугольник в теореме Паскаля можно образовать, соединив точки в любом порядке, а чуть ниже — более простое расположение на эллипсе.
На этом рисунке выше точки в нижней половине $ ~ P_1 ‘~ $ и $ ~ P_2’ ~ $ являются зеркальными отображениями $ ~ P_1 ~ $ и $ ~ P_2 ~ $, поэтому при симметрии линия Паскаля перпендикулярна к оси симметрии $ L $, здесь также оси $ x $.
Теперь мы доводим самую правую вершину $ P _ {\ infty} $ до бесконечности и получаем параболу с неизменной симметрией и ортогональностью, как показано на рисунке ниже:
Здесь синяя линия $ \ overline {P _ {\ infty} P_2} $ (а также зеленая зеркальная линия $ \ overline {P _ {\ infty} P_2 ‘} $) становится параллельной оси $ L $, как ключевой момент в решении Георга и футуролога.
Здесь начинается строительство (см. Рисунок ниже):
- Постройте $ \ overrightarrow {P_2P_1} $ так, чтобы они пересекались с осью симметрии $ L $ в точке $ Q_0 $
- Постройте прямую через $ Q_0 $, которая перпендикулярна $ L $ и пересекает $ \ overline {P _ {\ infty} P_2} $ в точке $ Q_1 $. (Здесь синий $ \ overline {P _ {\ infty} P_2} $ построен как линия, проходящая через $ P_2 $ и параллельная $ L $; аналогично для зеленого $ \ overline {P _ {\ infty} P_2 ‘} $ )
- Постройте $ \ overleftrightarrow {Q_1P_1 ‘} $ так, чтобы они пересекались с $ L $ в точке $ P_0 ~ $.Этот $ P_0 $ будет вершиной. (пока что до этого шага это в основном другая версия той же конструкции, что и у Георга и футуролога)
- Постройте из точки $ P_0 $ прямую, перпендикулярную зеленому цвету $ \ overline {P _ {\ infty} P_2 ‘} $ и пересекающую ее в точке $ Q_2 $
- Средняя точка $ \ overline {P_0Q_2} $ будет обозначена как $ M $, так что $ \ overline {P_0M} = \ overline {Q_2M} $
- Соедините отрезок линии $ \ overline {P_2’M} $ так, чтобы получился прямоугольный треугольник $ \ треугольник Q_2MP_2 ‘$, где $ \ angle MQ_2P_2’ = \ pi / 2 $ — прямой угол.
- Найдите точку $ N $ на другой стороне $ Q_2 $ (противоположную $ P_2 ‘$), чтобы получился такой же прямоугольный треугольник, $ \ angle NMP_2’ = \ angle MQ_2P_2 ‘= \ pi / 2 ~ $ и $ \ angle MNQ_2 = \ angle Q_2MP_2 ‘$
- Длина $ \ overline {NQ_2} $ дает фокусное расстояние. Директива $ \ Gamma $ и фокус можно сделать легко. Смотрите рисунок.
Эта конструкция сама по себе показывает, почему она работает: есть равнобедренный треугольник, показывающий $ ~ \ overline {NP_2 ‘} = d (\ Gamma, \, P_2’) = d (F, \, P_2 ‘) ~ $, где точка $ F $ — это фокус (оранжевая точка справа; для ясности не обозначена).
Обратите внимание, что шаги с 4 по 8 основаны на $ P_2 ‘$, но можно сделать то же самое для любой из точек $ ~ P_1, \, P_1’, \, P_2 $.
Я алгебраически проверил правильность этой конструкции. Интересно, есть ли способ НЕ использовать теорему Паскаля в аргументации этой конструкции. По сути, мне нужно было бы доказать, что пара директриса-фокус, построенная на основе $ P_2 ‘$ через эту особую точку $ P_0 $ (которая, как мы знаем, является вершиной параболы), является той же парой директриса-фокус, основанной на $ P_1’ $ .
% PDF-1.6 % 1 0 obj> эндобдж 2 0 obj> эндобдж 3 0 obj> эндобдж 5 0 obj> / Font> / ProcSet [/ PDF / Text] / Properties> / MC1 >>> / ExtGState >>> / Type / Page >> эндобдж 6 0 obj> эндобдж 7 0 obj> эндобдж 8 0 obj> поток application / pdfAdobe Illustrator CS22007-03-16T15: 08: 49-04: 002007-03-23T18: 48: 07-04: 002007-03-23T18: 48: 07-04: 00
- 184256JPEG / 9j / 4AAQSkZJRgABAgEASABIAAD / 7QAsUGh4wIDQMuG9za 0AAAAAABAASAAAAAEA AQBIAAAAAQAB / + 4ADkFkb2JlAGTAAAAAAf / bAIQABgQEBAUEBgUFBgkGBQYJCwgGBggLDAoKCwoK DBAMDAwMDAwQDA4PEA8ODBMTFBQTExwbGxscHx8fHx8fHx8fHwEHBwcNDA0YEBAYGhURFRofHx8f Hx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8f / 8AAEQgBAAC4AwER AAIRAQMRAf / EAaIAAAAHAQEBAQEAAAAAAAAAAAAQFAwIGAQAHCAkKCwEAAgIDAQEBAQEAAAAAAAAA AQACAwQFBgcICQoLEAACAQMDAgQCBgcDBAIGAnMBAgMRBAAFIRIxQVEGE2EicYEUMpGhBxWxQiPB UtHhMxZi8CRygvElQzRTkqKyY3PCNUQnk6OzNhdUZHTD0uIIJoMJChgZhJRFRqS0VtNVKBry4 / PE 1OT0ZXWFlaW1xdXl9WZ2hpamtsbW5vY3R1dnd4eXp7fh2 + f3OEhYaHiImKi4yNjo + Ck5SVlpeYmZ qbnJ2en5KjpKWmp6ipqqusra6voRAAICAQIDBQUEBQYECAMDbQEAAhEDBCESMUEFURNhIgZxgZEy obHwFMHR4SNCFVJicvEzJDRDghaSUyWiY7LCB3PSNeJEgxdUkwgJChgZJjZFGidkdFU38qOzwygp 0 + PzhJSktMTU5PRldYWVpbXF1eX1RlZmdoaWprbG1ub2R1dnd4eXp7fh2 + f3OEhYaHiImKi4yNjo + DlJWWl5iZmpucnZ6fkqOkpaanqKmqq6ytrq + v / aAAwDAQACEQMRAD8A9U4q7FXYq7FXYq7FXYq7 FWM / mTrGvaR5J1W90C2a61lIStkqgEI7bGZuVFCxLVzy22piqVWGt + cdR826BF8VjY3GmC / 1 / TJI l9S2mTnEsIcqT + / llr9o7QbUDGqrO8VdirsVdirsVdirsVdirsVdirsVdirsVQ2p6ja6Zpt3qV23 C0soZLi4frSOJS7n6FXFUl1 / zxaaHYafe3mnXzx6hFPIkcSRNLG9vZS3xgkT1Q3qPFbyBeHIchQk VBKrtP8APOn3sHl6eO0uBD5kklgtZOVtIsMsMMs5jnMU0lGZLaT + 750YUbicVQ3k38yNH81PHHaW t1ZyywyXEcV2IA / GF0SVWWGWYxunrRlkfiwDqab4qyzFXYq7FXYqlfmv / lFtY / 5gbn / ky2Kppirs VdirsVdirHtc87afpGqwabLa3NzJI1ms80AiMduNRuxZWzS + pJG1HmqPgVjQE02xVAn8zNK / Rvmf UBYXhj8qSTJqEH + iiaRLdnEk0UZnDenxiZlMnDmB8AY7YqjZvPGlw6rd6dLBcK9le2WnzTER8PU1 BFaCQD1PU9Iu6xc + h39hWjEKsixV2KuxV2KuxV2KoHXdJg1nRNQ0i4JW31K2mtJmXqEnjMbEfQ2K oIeUdIlsreK7hQ3ccjXc15ac7J5L2W2e1muq27q6yPFK4rzJFetQDiqDi8seUvL0UdxPcPBaW90b qz + uXbmOC5lhlgkaN5H5F5hcSs / JmLO5b7WKr9I8jabpPmAatZyScRbzQ + nNJNcTPLcvCZppbmeS WWQlLOBFDfZCeGwVZJirsVeUeedJ / NefzlLqehQPPaWcIh0wLPb28QjludOllFeSTGUm2uOfqho + AQBTVwVUObf / AJyCn0uGRbp7O + itZA8LLpbmWcfpJ4jIwVkDH09PjbhRfjcgChKqoXW4f + chX816 zd2kUj6PDHcwaJaQ3GmrFMJLiNleQTRll / 0RCqGQOVm / 4qZlxVPW0380rv8AKeeDV5bl / PN28pT6 jJbwC1b1WWEo8E9kpjEaqx5SOaturgcMVQem6b + cdnd38t1LdSW016nqraz2c87Q + pePzsVvT6EK CN7ON0kAJ4SMo5UZlU18n2P5txXGm3HmLUXuENxGmo2ZjsFjW3fShLLJygRXLR6n + 5QK32NyGB5B V6HirsVSDU / LOnTa1ca3fyr9Ta2tFuoHBVQ + l3TXtpP6gZePpSO5IIodq7ChVQsfkvynqZutRhnn vLTWbea3v6Xs9xBd284ZeBZpJP3cfqSeksbKqc24jfFUTq3kywvrv61G7Qzz3lhd6hIzSTGVNMlN xbQJzfjCiz / HRBT7W1WJxVkGKuxV2KuxV2KuxV2KuxV5r5q8s + XfNH5ixaR5jsxHc21pDqflnVba R45qwTFbmNuRMTtG7RsBwPwt7YqzT / Cmgf8ALL / yUk / 5qw2rv8KaB / yy / wDJST / mrG1d / hTQP + WX / kpJ / wA1Y2rv8KaB / wAsv / JST / mrG1d / hTQP + WX / AJKSf81Y2qF1bQtA0 / S7y / 8AqXq / VIJJ / T9W ReXpoX41qaVp4Y2qK / wpoH / LL / yUk / 5qxtXf4U0D / ll / 5KSf81Y2rv8ACmgf8sv / ACUk / wCasbV3 + FNA / wCWX / kpJ / zVjau / wpoH / LL / AMlJP + asbVTn8n6DLBJEsLRNIrKJUkfkpIpyXkWWo7VBGNqw 7yPZeVPJepeYdG0KyW00Dy / ZxT6zqcskksz3jo07KSzEUjt6O1AN2GBWTfl152tvOnlS212GFraS VpIrm0f7cMsbFSrfNaMPYjFWS4q7FXYq7FXYq7FXYq7FWHfmbp16NLtPM2lxmXWPK8 / 6RghX7U9s FKXlsD / xbAWp / lBcVZRpmpWWqaba6lYyiazvYkntpV6NHIoZT9IOKonFXYq7FXYqlfmv / lFtY / 5g bn / ky2KppirsVdirsVdiqV + aPMNp5d8v32s3YLRWcRdYl3eSQ7RxIB1aRyEUeJxVLfy / 8uXOj + WI 4tT4y6xqMkmo61JQUe8uj6kop / LHtGv + SoxVH + U1UaDbEAAsZCxHc + owqfoGEqm + BXYq7FXYq7FX Yq7FXYq7FWAeTn / wp5pvPI09V0y79XU / Kjn7PoM3K6shXvbyNzQb / u2 / ycVZ / irsVeMaR + desWVo y6xZx3V5NcsGLXSQpbpK44TFVtVZNNiWiyXTl2WTktGoDhVOdF / NifX / ADbaaLZxQwx2 + ppbXs9t P9bhuIZdO1Gb4HeGEqFnskYMv2lKmtGpgVnPmwV8q6yK0 / 0G53H / ABhbFW / 0PqP / AFfb7 / gLH / sm xVMokZIkRpGlZVCtK / EMxApybiFWp9gBiq7FXYq7FWBXx / xf5 / h05Pj8v + UJUu9QcbrPqzLW3gB6 EWyN6r / 5ZQdsVZ7iqU + VP + OBa / 8APT / k42Eqm2BXYq7FXYq7FXYq7FXYq7FWOee / KsvmHSEFlMLP XNOmW90S / Ir6N1F9nlTcxyAlJB3UnFVTyT5si8y6N9ZeI2mqWkjWmsacx + O1vItpYj4j9pG / aUg4 qn + KvJf + Vk / mPPf6klhoiXNhaXt7bWtylleOJpbO8mto7LksnEGVIVdrz + 5jJKMtRiqFsPOX5y3E mircaa9hYySWwv7iXTZ7i6CiGxab1hF6SUkkvZV / dxLw9JvBqKvT / Nlf8K6zTY / UbmhO / wDulsVb + reaf + rhY / 8ASFN / 2V4qmUQlESCZleUKBI6KUUtTcqpLECvap + eKrsVdirF / Pnmi70i0ttN0dBce aNadrbRbY7qrgVkuZR2ht1PNz8l74qmHlLyzaeWtCt9Kt5GndOUl3eSf3txcSkvNPKe7SOSfw7Yq nGKvPf0Prl1awz6fNex2k + h6tZT / AFO4COt3JcQmzkgillihE6r6 / GT4fBmpxwlUuhsfzcisNKsI ZLy0AS3ikuY5LG5aMfpFxcy3zX8l3M0v6P4Mghd1EnIVK8cCsr / LyLzxHo8q + cZvX1IyQvE9LdaK 9lbvMlLcKlI7tp0UncqB12OKsoxV2KuxV2KuxV2KuxV2KsH83aFq + la0PO / laA3OorGsOvaOhC / p K0j + yVrt9ZgFfSb9ofB0pirKPL + v6Xr + kW2raXMJrO5Xkh6MpGzI6ndXRvhZTuDtiqIOn2JtJrMQ Iltcer60UY4BjOzNK3w0 + J2dmY9STXriqUC6vfL54ahI93og + xqT / FLbD + W67vGP9 / dh / edDIVUB qPm / Qtc8v + ZrfSpZbh9Otr23uZjb3MduJoUeOREuJI1hkKsN + DNircnna9judStTYwtdaTHHNe26 NqDyiOYssbxImns06sY2FYgw2PhiqroX5l + T9Ztp54L9USytoLq / uJYriC1hS5iSaMm5uYoI / iSR WFaNQ1oMVR1t548l3VxHbW2v6bPczSCGGCO7gd3kNaIqq5JY06DFV / mnzPp3lvSX1C8DysWWK0s4 Rynubh9o4IE / bdz0H09BiqT + SvLOqR3dz5q8y8W8z6ogjMCnlFYWgPKOyhPQ0PxSuPtv7AYqy / FX YqlPlT / jgWv / AD0 / 5ONhKptgV2KuxV2KuxV2KuxV2KuxV2KuxVhGt + UtZ0jWZ / NHkoR / Xrohta0G VhHa6hxFPUVqUhuqdJPst + 344qnHlXzvovmNZYrYva6rabaho92vpXls3hJEd + Pg61U9jiqf4qwX Vfy78raX5N84wQWvMa6t9f6jIwRZZJJfUmCepGsbFI2Y + mGJoO + Koc + Toxc6pcRWGtQNq8EdndCG TSY / 9FiiaJIQyuHbir7SOzSCgAfjthVHz / lpot / cPqDyXdlcSW8EFpDGLNDZrbSwTxcDHE / qsktn ER67SgUIHwkghWO61pPkzyxcNZQG913zZqcttcxabAYGvJpbTVJdYWSUxxJHBE1zch2HYKvAADcY qyXyz5P1FtVHmnzZMl35jZClpaxEmz06FusVsG3aRhtJMd26Ci7YqzDFXYq7FUp8qf8AHAtf + ru / ACcbCVTbArsVdirsVdirsVdiqBu9Zs7SYwyx3TOADWG0uZl3 / wAuKN1 / HFULJ5r0iN4kkS9VpmKR KbC9qzBS9B + 568UJ + jFXT + a9It4JJ5kvY4YlLySNYXoCqoqST6PQDFVT / Eunf75vv + 4fff8AVHFV OHzXpEyF4kvXUM6FlsL0jlGxRx / c9VZSDiqReYrTyP5iukN5a30esWSrJa6ja2d / b31uJCwVo5o4 Q4VijfCaqabg4qkx17z95faKGC6Hmi0duFvFqOn3 + n37EKzcBPBbSwStwQmpiTvXCqnrn5oaxL5e 1O3vvIuv2zy2k6GeKGKaBQ0bAuztJE4Ve / wV9sVR835ra29FsPIXmBnNfivIYreMeG6PcP8A8JgV BR6r568xoxv9Rby5pjM6Pb6Lp9 / d3p4OUeNr24tkjRlKlSUgrXvhVPvLEXkjy569ppNneJeSBJr + 5ksr + a7nLlgsk88kTSOWKNTkfGmBU6k816RG8SSJeq0zFIlNhe1Zgpeg / c9eKE / Rirp / NekW8Ek8 yXscMSl5JGsL0BVUVJJ9HoBiqp / iXTv9833 / AHD77 / qjiqCvNf0vU9Mura3k1Gh20ltxdW9lfLJF IOUbMjCEUaNwfpGKsf8AyzuNT0Pybb2vmOa / vdcZpZruRrG89NWZjwSPjBxVAgWvEdanvhVS0z86 LHU / Jd95mtNGvl + oGMNa3CNEtwXkEfGznCvHOxr + 7UULGg + GtcCs40LUxquiafqYVEF9bxXISKT1 UHqoHoslE5gV68RXFUdirsVdirsVdirsVQl7Ym5ubCYOFFlO05FK8g0EsNPb + 9r9GKu1exN / pN7Y q4ja7glgEhFQpkQrWntXFUXiqE0uxNlbPCXDl57ieoFNrid5gPo9SmKuisSmrXN9zBWeCCAR03Bh eZq19 / W / DFXXtibm5sJg4UWU7TkUryDQSw09v72v0YqhvNf / ACi2sf8AMDc / 8mWxVRu9KvbG4l1H QwvqSsZL3THbjDcE9XQ / 7qm / yvst + 2OjKql + nea / Lum29va3l09vdX91cmG2lhlWUTTXi1gZVVhz V7yMdfiHxrVPixVKYvzU8jN5hleyvLjUJ7oWNg8NpZXUnpGSSdoZJH9MLwlEnJKfaUclqu + KprpX nHyp5s1eC30TUfrNzo8xurqL0Z0oj27xIeUiIvGQXAeNujqCVqKkKsg1exN / pN7Yq4ja7glgEhFQ pkQrWntXFUXiqE0uxNlbPCXDl57ieoFNrid5gPo9SmKosgEUO4PUYq4AAUGwHQYq7FXYq7FXYq7F XYq7FXYq7FXYq7FXYq7FUDr1pNe6HqNnAAZrm1mhiBNBykjKrU / M4qjsVQOo6FpGpXVhdX1qk9xp cxubCRq1ilKNHyFCP2XPXbv1AxVj + j / lL + Xuixzx6TpIsVuZ4LqUwT3CMZrV3khYMJOS8DK2ykCh 4n4dsVRHlP8ALXyR5Rubm58uaWunTXfL6wUkmYOGINCru60Ur8IAou / GnI1VZNirsVdirsVdirsV dirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVd irsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdi rsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdir sVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirs VdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsV dirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVd irsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdi rsVdirsVdirsVdiqC1jWdM0exN9qVwltaCSKIzOaKHnkWJAfm7jFV8mq6ZHeLYyXkCXrcONq0iCU + oHKUQnl8QhkI234t4HFUVirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVa5LyC1HIgkL3IFK n8cVczKilmIVVFWY7AAdzireKtcl5FajkACV7gGtD + GKuZlRSzEKqirMdgAO5xVif5m + U9I8z6Bb 2GrrJJZC / s2eCORow5kuEhPIpRtllYih60PbFVWTyfE3nHStfuZRImj2DWdrJIxM8s87BDJMaBCV jqqU3Jkf2xVlGKtBlJYAglTRgOxpWh + g4q4soKgkAsaKD3NK0H0DFW8VaVlYVUgipFRvuDQj6Dir eKuxV2KuxV2KuxV2KuxV2KuxV2KoSX / jrW3 / ABgn / wCJw4q7V / 8Ajk3v / GCX / iBxVF4qhIv + Otc / 8YIP + JzYq7V / + OTe / wDGCX / iBxVDeZf + OdD / AMx2n / 8AUdDiqJ1T / eZP + M9v / wAn0xVF4qhLL / en UP8AjOv / ACYixV17 / vTp / wDxnb / kxLiqLxVCaX / vM / 8AxnuP + T74qi8VdirsVdirsVdirsVdirsV dirsVQkv / HWtv + ME / wDxOHFXav8A8cm9 / wCMEv8AxA4qi8VQkX / HWuf + MEH / ABObFXav / wAcm9 / 4 wS / 8QOKobzL / AMc6H / mO0 / 8A6jocVeXXH5vaxpWtalZazYreRyajJHY8rlYLe3ggupII5mYW3qCG JrfndSu7 + nyjoKPRSqY + YPz0t9J1I6ctha3EsfBp7gahxgEMkFjKk0RWB5J1ka / ZIxHGWf0yQvXi Fek2X + 9Oof8AGdf + TEWKuvf96dP / AOM7f8mJcVReKoTS / wDeZ / 8AjPcf8n3xVF4q7FXYq7FXYq7F XYq7FXYq7FWN3 / mS90 / z5pujXSxrpOs2cv1Ceh5i / tW5yRM1aUkgbkop + w2KpzL / AMda2 / 4wT / 8A E4cVdq // AByb3 / jBL / xA4qi8VQkX / HWuf + MEH / E5sVUteureDSbsTSKheCURqT8THgdlHVj7DFWL fmR5qvrHQ1Olac15eLd2UiJO3oIVS6ic12aQh5aboPHfapVkMnmGB7KOcB7cNLCpeQAoFeVA3J1L otVb9og / hiqbo6OiujBkYAqwNQQdwQRgVC2X + 9Oof8Z1 / wCTEWKuvf8AenT / APjO3 / JiXFUXiqBs ZooLCeaZxHDFLdPJIxoqqs8hJJPQAYqlvkPXdS1 / y5Drd7EkCahJNPp8SqVYWTSN9VMlSau8IVzT bfFWQYq7FXYq7FXYq7FXYq7FXYqx3z75bude8vtFYSi31qwlTUNFuW6R3tvVouX + Q9TG / wDkscVW eU / M9t5lttO1SKMwTNBcxXtm / wDeW91FJCk8Dj + aNwR79cVTbXrm3g0m79aVY + cEoQMQCx4HYV6n FUk87a15wttDa68o6ct7qMckarbXkThJVkcRlVpJDJGVLhi7KV4g18QqitHtddllP6duYhfm2gN1 HpweKDkXmPFWcvNt / MGWvhiqrqUUS6bqCWMaxj0JRcXlKklVNRyapkbxJ2B8TthVKPMVlb3NvZAp SGa8tZI6kkmH61DESSfi5SmfmSTWgAO4xQjGSRbO1YMEuJntpI36KX9aMywyKP5XJZe43A2Bqqm0 VtZzO5VDaXgPKYRNwYsdw540WUV6FgR1BFajAliXmy8 / MrSxNP5UhstVj + uRx3sd5HKbhFkihX1k EDxLIqVJZAoNBtXCrJbjUVSXThehreRZj6jyLwjJ + ryiocNIi1PRS9cVTdWV1DKQysKqw3BB7jAr zzzjcS6ybXyDYuRPrU1zNrUibGDSI7pxOSR0a4b9wnzbwwq9BhhighSGFBHDEoSONRRVVRQAAdAB gVfirsVdirsVdirsVdirsVdirsVeb + a9Om8oeZH86WQl / wAPXw4ebLO3 + 1FsoGoxqBX4QirPwoxU BuqnFWZTJpj6Fc3lh6csVzaO6XUZEnqo0ZZW9WpLgjcGuKpszBQWYgKBUk9AMVYL548nHzxHcael / d6XCEtWFzazSxGWP1pPVBRGCOjR8gvMHfcUHUqgvN + sa7p2p6T5N0bQzb + XZoHiutWLI0MdvBaS yJbxxozOnNbfhykAHYV64qrDzxonmLzBruk6c / rP5dvNGt55a1Uyy34Mqx / 6pjCsfEewwKhrrz3Y 6pZeb9G0dl / xF5Wuy8Ecg5F5DIJY5FQUYoJWaJwDXbtyGFWptFvfzT8jaZc6xZXPlXW7eeK4gmil Uyx0YCb0nhf1FWWLkvF + LBqVHwgkKzPQQtm9zp8jNzilVIpJJJJTKFt4t / UlZ5Gam7cmJ9z1xVG3 v + 9On / 8AGdv + TEuKpL5x1nSPLOltqDRyfXp3EOn2NmeM93dyH93FHH9l3Y9SymgqT0xVQ / L7yjd6 La3Wp6y63HmfW5PrOr3C7oh4MdtF / wAVQhiB / Mat3xVlmKuxV2KuxV2KuxV2KuxV2KuxV2KtMqup VgGVhRlO4IPY4q801PRtb8hQX0mgW0mp + TLtZWudDhBa4055AeUtktf3kDMeTwjdeqdxirM9D1bT PM2nw6rZXMd3pcvxW6xMGBI / 39Toy / 77P2T13pRVFvMkGoXcr / ZS3gJA3J + OagA7k9AMVUruF49F v3lp9Ymhlkmp0BMZAUeyqAvvSuKpVe6dp8dl9fit4o7mbUbOMyoiqTFHqMKIoIh3aIG + ZJ74VRVz p9jZXrehbxwm5eGUGNVUmRr1XuGNO7tIhY9 / oxVM5P8ARrwTf7ouSqS + 0uyo3 + yHwn34 ++ BVkEMU 02oRyLyU3CnwIIgioQRuCOxGKsc83ecbfy7cadaTRyapqk8rNpum2nFru4 / dSJQx1HFQW + KU / ABU mnQqteV / KGpSav8A4s82vHc + YnQpY2cRLWumQP8AahtyftyN / u2alW6Ci9VWZYq7FXYq7FXYq7FX Yq7FXYq7FXYq7FXYq7FWIax + XVs + pS635avpfLevzb3Fzaqr21yR0 + t2jfupf9ccX / ysVSs69560 jUvW80eXZNQtEjRRqHl6t0jvGWKs9nIVuUoJDsgk + Km + FUVe / mz + Xt1pl / BHrdvDei2lK2N6Wsrg ng1FEVyIn5HwpgVMdR1TRhoFlFDqNtOIbrTkMkcsbA + ndwAnZj4YVXeZfMOgWpsJpdTtYf8ASYkk Z541AiMiuxNW2HONN8VQF3 + a / kK4WWz066k8wztWNrTRYJr9mr1 / eW6tGu37TOB74FQVi35p64JR HBF5TsLlucl7d + nd6myiNYwY7eIm2gZuFSXd6V + ztirI / LHkjQvLrT3Foslzql3 / AL3aveOZ724o aj1Jm34jsi0Udhiqf4qoC / sTemwFzF9eEYmNrzX1RGSVD8K8uJIIrSmKqdnq + lXs00FnewXM1uaX EUMqSNGebR0dVJK / HG6791I7Yqi8VdirsVdirsVdirsVdirsVS + 80DSbydp7mDnK1Azc3HQUGwYD FVH / AApoH / LL / wAlJP8AmrDau / wpoH / LL / yUk / 5qxtXf4U0D / ll / 5KSf81Y2rv8ACmgf8sv / ACUk / wCasbVRufJPlW6Thc6dHOn8shdx9zMcbVjXmL8pvy0WzjmXy1p / qtd2UbP6CklXu4kZansVYjAq aQflL + Wlu3K38t2ELeMcKqdvliqax + UPLkaBI7MIi9FV5AB9AbDarv8ACmgf8sv / ACUk / wCasbV3 + FNA / wCWX / kpJ / zVjau / wpoH / LL / AMlJP + asbVJbz8pvJN75ltPMN3aSTXtggSyjaVxDEwYsXCqQ WY1oeZI9sCpnoHk / T9E1XWNTtZ55bjXJluL5ZjGU9VeQVkCIhWiMqUr0UftcmZVPcVdirsVdirsV dirsVdirsVdirsVdirsVdirsVSvzL / xzof8AmO0 // qOhxVNMVdirsVdirsVdirsVdirsVdirsVdi rsVdir // 2Q == uuid: D9B7665ED55811DB9D7DD61D329D7703 uuid: 914cefa6-d990-11db-ac45-0014516728a0 конечный поток эндобдж 9 0 obj> поток application / pdfAdobe Illustrator CS22007-03-16T15: 08: 49-04: 002007-03-23T18: 48: 07-04: 002007-03-23T18: 48: 07-04: 00
- 184256JPEG / 9j / 4AAQSkZJRgABAgEASABIAAD / 7QAsUGh4wIDQMuG9za 0AAAAAABAASAAAAAEA AQBIAAAAAQAB / + 4ADkFkb2JlAGTAAAAAAf / bAIQABgQEBAUEBgUFBgkGBQYJCwgGBggLDAoKCwoK DBAMDAwMDAwQDA4PEA8ODBMTFBQTExwbGxscHx8fHx8fHx8fHwEHBwcNDA0YEBAYGhURFRofHx8f Hx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8f / 8AAEQgBAAC4AwER AAIRAQMRAf / EAaIAAAHAQEBAQEAAAAAAAAAAAQFAwIGAQAHCAkKCwEAAgIDAQEBAQEAAAAAAAAA AQACAwQFBgcICQoLEAACAQMDAgQCBgcDBAIGAnMBAgMRBAAFIRIxQVEGE2EicYEUMpGhBxWxQiPB UtHhMxZi8CRygvElQzRTkqKyY3PCNUQnk6OzNhdUZHTD0uIIJoMJChgZhJRFRqS0VtNVKBry4 / PE 1OT0ZXWFlaW1xdXl9WZ2hpamtsbW5vY3R1dnd4eXp7fh2 + f3OEhYaHiImKi4yNjo + Ck5SVlpeYmZ qbnJ2en5KjpKWmp6ipqqusra6voRAAICAQIDBQUEBQYECAMDbQEAAhEDBCESMUEFURNhIgZxgZEy obHwFMHR4SNCFVJicvEzJDRDghaSUyWiY7LCB3PSNeJEgxdUkwgJChgZJjZFGidkdFU38qOzwygp 0 + PzhJSktMTU5PRldYWVpbXF1eX1RlZmdoaWprbG1ub2R1dnd4eXp7fh2 + f3OEhYaHiImKi4yNjo + DlJWWl5iZmpucnZ6fkqOkpaanqKmqq6ytrq + v / aAAwDAQACEQMRAD8A9U4q7FXYq7FXYq7FXYq7 FWM / mTrGvaR5J1W90C2a61lIStkqgEI7bGZuVFCxLVzy22piqVWGt + cdR826BF8VjY3GmC / 1 / TJI l9S2mTnEsIcqT + / llr9o7QbUDGqrO8VdirsVdirsVdirsVdirsVdirsVdirsVQ2p6ja6Zpt3qV23 C0soZLi4frSOJS7n6FXFUl1 / zxaaHYafe3mnXzx6hFPIkcSRNLG9vZS3xgkT1Q3qPFbyBeHIchQk VBKrtP8APOn3sHl6eO0uBD5kklgtZOVtIsMsMMs5jnMU0lGZLaT + 750YUbicVQ3k38yNH81PHHaW t1ZyywyXEcV2IA / GF0SVWWGWYxunrRlkfiwDqab4qyzFXYq7FXYqlfmv / lFtY / 5gbn / ky2Kppirs VdirsVdirHtc87afpGqwabLa3NzJI1ms80AiMduNRuxZWzS + pJG1HmqPgVjQE02xVAn8zNK / Rvmf UBYXhj8qSTJqEH + iiaRLdnEk0UZnDenxiZlMnDmB8AY7YqjZvPGlw6rd6dLBcK9le2WnzTER8PU1 BFaCQD1PU9Iu6xc + h39hWjEKsixV2KuxV2KuxV2KoHXdJg1nRNQ0i4JW31K2mtJmXqEnjMbEfQ2K oIeUdIlsreK7hQ3ccjXc15ac7J5L2W2e1muq27q6yPFK4rzJFetQDiqDi8seUvL0UdxPcPBaW90b qz + uXbmOC5lhlgkaN5H5F5hcSs / JmLO5b7WKr9I8jabpPmAatZyScRbzQ + nNJNcTPLcvCZppbmeS WWQlLOBFDfZCeGwVZJirsVeUeedJ / NefzlLqehQPPaWcIh0wLPb28QjludOllFeSTGUm2uOfqho + AQBTVwVUObf / AJyCn0uGRbp7O + itZA8LLpbmWcfpJ4jIwVkDH09PjbhRfjcgChKqoXW4f + chX816 zd2kUj6PDHcwaJaQ3GmrFMJLiNleQTRll / 0RCqGQOVm / 4qZlxVPW0380rv8AKeeDV5bl / PN28pT6 jJbwC1b1WWEo8E9kpjEaqx5SOaturgcMVQem6b + cdnd38t1LdSW016nqraz2c87Q + pePzsVvT6EK CN7ON0kAJ4SMo5UZlU18n2P5txXGm3HmLUXuENxGmo2ZjsFjW3fShLLJygRXLR6n + 5QK32NyGB5B V6HirsVSDU / LOnTa1ca3fyr9Ta2tFuoHBVQ + l3TXtpP6gZePpSO5IIodq7ChVQsfkvynqZutRhnn vLTWbea3v6Xs9xBd284ZeBZpJP3cfqSeksbKqc24jfFUTq3kywvrv61G7Qzz3lhd6hIzSTGVNMlN xbQJzfjCiz / HRBT7W1WJxVkGKuxV2KuxV2KuxV2KuxV5r5q8s + XfNH5ixaR5jsxHc21pDqflnVba R45qwTFbmNuRMTtG7RsBwPwt7YqzT / Cmgf8ALL / yUk / 5qw2rv8KaB / yy / wDJST / mrG1d / hTQP + WX / kpJ / wA1Y2rv8KaB / wAsv / JST / mrG1d / hTQP + WX / AJKSf81Y2qF1bQtA0 / S7y / 8AqXq / VIJJ / T9W ReXpoX41qaVp4Y2qK / wpoH / LL / yUk / 5qxtXf4U0D / ll / 5KSf81Y2rv8ACmgf8sv / ACUk / wCasbV3 + FNA / wCWX / kpJ / zVjau / wpoH / LL / AMlJP + asbVTn8n6DLBJEsLRNIrKJUkfkpIpyXkWWo7VBGNqw 7yPZeVPJepeYdG0KyW00Dy / ZxT6zqcskksz3jo07KSzEUjt6O1AN2GBWTfl152tvOnlS212GFraS VpIrm0f7cMsbFSrfNaMPYjFWS4q7FXYq7FXYq7FXYq7FWHfmbp16NLtPM2lxmXWPK8 / 6RghX7U9s FKXlsD / xbAWp / lBcVZRpmpWWqaba6lYyiazvYkntpV6NHIoZT9IOKonFXYq7FXYqlfmv / lFtY / 5g bn / ky2KppirsVdirsVdiqV + aPMNp5d8v32s3YLRWcRdYl3eSQ7RxIB1aRyEUeJxVLfy / 8uXOj + WI 4tT4y6xqMkmo61JQUe8uj6kop / LHtGv + SoxVH + U1UaDbEAAsZCxHc + owqfoGEqm + BXYq7FXYq7FX Yq7FXYq7FWAeTn / wp5pvPI09V0y79XU / Kjn7PoM3K6shXvbyNzQb / u2 / ycVZ / irsVeMaR + desWVo y6xZx3V5NcsGLXSQpbpK44TFVtVZNNiWiyXTl2WTktGoDhVOdF / NifX / ADbaaLZxQwx2 + ppbXs9t P9bhuIZdO1Gb4HeGEqFnskYMv2lKmtGpgVnPmwV8q6yK0 / 0G53H / ABhbFW / 0PqP / AFfb7 / gLH / sm xVMokZIkRpGlZVCtK / EMxApybiFWp9gBiq7FXYq7FWBXx / xf5 / h05Pj8v + UJUu9QcbrPqzLW3gB6 EWyN6r / 5ZQdsVZ7iqU + VP + OBa / 8APT / k42Eqm2BXYq7FXYq7FXYq7FXYq7FWOee / KsvmHSEFlMLP XNOmW90S / Ir6N1F9nlTcxyAlJB3UnFVTyT5si8y6N9ZeI2mqWkjWmsacx + O1vItpYj4j9pG / aUg4 qn + KvJf + Vk / mPPf6klhoiXNhaXt7bWtylleOJpbO8mto7LksnEGVIVdrz + 5jJKMtRiqFsPOX5y3E mircaa9hYySWwv7iXTZ7i6CiGxab1hF6SUkkvZV / dxLw9JvBqKvT / Nlf8K6zTY / UbmhO / wDulsVb + reaf + rhY / 8ASFN / 2V4qmUQlESCZleUKBI6KUUtTcqpLECvap + eKrsVdirF / Pnmi70i0ttN0dBce aNadrbRbY7qrgVkuZR2ht1PNz8l74qmHlLyzaeWtCt9Kt5GndOUl3eSf3txcSkvNPKe7SOSfw7Yq nGKvPf0Prl1awz6fNex2k + h6tZT / AFO4COt3JcQmzkgillihE6r6 / GT4fBmpxwlUuhsfzcisNKsI ZLy0AS3ikuY5LG5aMfpFxcy3zX8l3M0v6P4Mghd1EnIVK8cCsr / LyLzxHo8q + cZvX1IyQvE9LdaK 9lbvMlLcKlI7tp0UncqB12OKsoxV2KuxV2KuxV2KuxV2KsH83aFq + la0PO / laA3OorGsOvaOhC / p K0j + yVrt9ZgFfSb9ofB0pirKPL + v6Xr + kW2raXMJrO5Xkh6MpGzI6ndXRvhZTuDtiqIOn2JtJrMQ Iltcer60UY4BjOzNK3w0 + J2dmY9STXriqUC6vfL54ahI93og + xqT / FLbD + W67vGP9 / dh / edDIVUB qPm / Qtc8v + ZrfSpZbh9Otr23uZjb3MduJoUeOREuJI1hkKsN + DNircnna9judStTYwtdaTHHNe26 NqDyiOYssbxImns06sY2FYgw2PhiqroX5l + T9Ztp54L9USytoLq / uJYriC1hS5iSaMm5uYoI / iSR WFaNQ1oMVR1t548l3VxHbW2v6bPczSCGGCO7gd3kNaIqq5JY06DFV / mnzPp3lvSX1C8DysWWK0s4 Rynubh9o4IE / bdz0H09BiqT + SvLOqR3dz5q8y8W8z6ogjMCnlFYWgPKOyhPQ0PxSuPtv7AYqy / FX YqlPlT / jgWv / AD0 / 5ONhKptgV2KuxV2KuxV2KuxV2KuxV2KuxVhGt + UtZ0jWZ / NHkoR / Xrohta0G VhHa6hxFPUVqUhuqdJPst + 344qnHlXzvovmNZYrYva6rabaho92vpXls3hJEd + Pg61U9jiqf4qwX Vfy78raX5N84wQWvMa6t9f6jIwRZZJJfUmCepGsbFI2Y + mGJoO + Koc + Toxc6pcRWGtQNq8EdndCG TSY / 9FiiaJIQyuHbir7SOzSCgAfjthVHz / lpot / cPqDyXdlcSW8EFpDGLNDZrbSwTxcDHE / qsktn ER67SgUIHwkghWO61pPkzyxcNZQG913zZqcttcxabAYGvJpbTVJdYWSUxxJHBE1zch2HYKvAADcY qyXyz5P1FtVHmnzZMl35jZClpaxEmz06FusVsG3aRhtJMd26Ci7YqzDFXYq7FUp8qf8AHAtf + ru / ACcbCVTbArsVdirsVdirsVdiqBu9Zs7SYwyx3TOADWG0uZl3 / wAuKN1 / HFULJ5r0iN4kkS9VpmKR KbC9qzBS9B + 568UJ + jFXT + a9It4JJ5kvY4YlLySNYXoCqoqST6PQDFVT / Eunf75vv + 4fff8AVHFV OHzXpEyF4kvXUM6FlsL0jlGxRx / c9VZSDiqReYrTyP5iukN5a30esWSrJa6ja2d / b31uJCwVo5o4 Q4VijfCaqabg4qkx17z95faKGC6Hmi0duFvFqOn3 + n37EKzcBPBbSwStwQmpiTvXCqnrn5oaxL5e 1O3vvIuv2zy2k6GeKGKaBQ0bAuztJE4Ve / wV9sVR835ra29FsPIXmBnNfivIYreMeG6PcP8A8JgV BR6r568xoxv9Rby5pjM6Pb6Lp9 / d3p4OUeNr24tkjRlKlSUgrXvhVPvLEXkjy569ppNneJeSBJr + 5ksr + a7nLlgsk88kTSOWKNTkfGmBU6k816RG8SSJeq0zFIlNhe1Zgpeg / c9eKE / Rirp / NekW8Ek8 yXscMSl5JGsL0BVUVJJ9HoBiqp / iXTv9833 / AHD77 / qjiqCvNf0vU9Mura3k1Gh20ltxdW9lfLJF IOUbMjCEUaNwfpGKsf8AyzuNT0Pybb2vmOa / vdcZpZruRrG89NWZjwSPjBxVAgWvEdanvhVS0z86 LHU / Jd95mtNGvl + oGMNa3CNEtwXkEfGznCvHOxr + 7UULGg + GtcCs40LUxquiafqYVEF9bxXISKT1 UHqoHoslE5gV68RXFUdirsVdirsVdirsVQl7Ym5ubCYOFFlO05FK8g0EsNPb + 9r9GKu1exN / pN7Y q4ja7glgEhFQpkQrWntXFUXiqE0uxNlbPCXDl57ieoFNrid5gPo9SmKuisSmrXN9zBWeCCAR03Bh eZq19 / W / DFXXtibm5sJg4UWU7TkUryDQSw09v72v0YqhvNf / ACi2sf8AMDc / 8mWxVRu9KvbG4l1H QwvqSsZL3THbjDcE9XQ / 7qm / yvst + 2OjKql + nea / Lum29va3l09vdX91cmG2lhlWUTTXi1gZVVhz V7yMdfiHxrVPixVKYvzU8jN5hleyvLjUJ7oWNg8NpZXUnpGSSdoZJH9MLwlEnJKfaUclqu + KprpX nHyp5s1eC30TUfrNzo8xurqL0Z0oj27xIeUiIvGQXAeNujqCVqKkKsg1exN / pN7Yq4ja7glgEhFQ pkQrWntXFUXiqE0uxNlbPCXDl57ieoFNrid5gPo9SmKosgEUO4PUYq4AAUGwHQYq7FXYq7FXYq7F XYq7FXYq7FXYq7FXYq7FUDr1pNe6HqNnAAZrm1mhiBNBykjKrU / M4qjsVQOo6FpGpXVhdX1qk9xp cxubCRq1ilKNHyFCP2XPXbv1AxVj + j / lL + Xuixzx6TpIsVuZ4LqUwT3CMZrV3khYMJOS8DK2ykCh 4n4dsVRHlP8ALXyR5Rubm58uaWunTXfL6wUkmYOGINCru60Ur8IAou / GnI1VZNirsVdirsVdirsV dirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVd irsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdi rsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdir sVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirs VdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsV dirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVd irsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdi rsVdirsVdirsVdiqC1jWdM0exN9qVwltaCSKIzOaKHnkWJAfm7jFV8mq6ZHeLYyXkCXrcONq0iCU + oHKUQnl8QhkI234t4HFUVirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVa5LyC1HIgkL3IFK n8cVczKilmIVVFWY7AAdzireKtcl5FajkACV7gGtD + GKuZlRSzEKqirMdgAO5xVif5m + U9I8z6Bb 2GrrJJZC / s2eCORow5kuEhPIpRtllYih60PbFVWTyfE3nHStfuZRImj2DWdrJIxM8s87BDJMaBCV jqqU3Jkf2xVlGKtBlJYAglTRgOxpWh + g4q4soKgkAsaKD3NK0H0DFW8VaVlYVUgipFRvuDQj6Dir eKuxV2KuxV2KuxV2KuxV2KuxV2KoSX / jrW3 / ABgn / wCJw4q7V / 8Ajk3v / GCX / iBxVF4qhIv + Otc / 8YIP + JzYq7V / + OTe / wDGCX / iBxVDeZf + OdD / AMx2n / 8AUdDiqJ1T / eZP + M9v / wAn0xVF4qhLL / en UP8AjOv / ACYixV17 / vTp / wDxnb / kxLiqLxVCaX / vM / 8AxnuP + T74qi8VdirsVdirsVdirsVdirsV dirsVQkv / HWtv + ME / wDxOHFXav8A8cm9 / wCMEv8AxA4qi8VQkX / HWuf + MEH / ABObFXav / wAcm9 / 4 wS / 8QOKobzL / AMc6H / mO0 / 8A6jocVeXXH5vaxpWtalZazYreRyajJHY8rlYLe3ggupII5mYW3qCG JrfndSu7 + nyjoKPRSqY + YPz0t9J1I6ctha3EsfBp7gahxgEMkFjKk0RWB5J1ka / ZIxHGWf0yQvXi Fek2X + 9Oof8AGdf + TEWKuvf96dP / AOM7f8mJcVReKoTS / wDeZ / 8AjPcf8n3xVF4q7FXYq7FXYq7F XYq7FXYq7FWN3 / mS90 / z5pujXSxrpOs2cv1Ceh5i / tW5yRM1aUkgbkop + w2KpzL / AMda2 / 4wT / 8A E4cVdq // AByb3 / jBL / xA4qi8VQkX / HWuf + MEH / E5sVUteureDSbsTSKheCURqT8THgdlHVj7DFWL fmR5qvrHQ1Olac15eLd2UiJO3oIVS6ic12aQh5aboPHfapVkMnmGB7KOcB7cNLCpeQAoFeVA3J1L otVb9og / hiqbo6OiujBkYAqwNQQdwQRgVC2X + 9Oof8Z1 / wCTEWKuvf8AenT / APjO3 / JiXFUXiqBs ZooLCeaZxHDFLdPJIxoqqs8hJJPQAYqlvkPXdS1 / y5Drd7EkCahJNPp8SqVYWTSN9VMlSau8IVzT bfFWQYq7FXYq7FXYq7FXYq7FXYqx3z75bude8vtFYSi31qwlTUNFuW6R3tvVouX + Q9TG / wDkscVW eU / M9t5lttO1SKMwTNBcxXtm / wDeW91FJCk8Dj + aNwR79cVTbXrm3g0m79aVY + cEoQMQCx4HYV6n FUk87a15wttDa68o6ct7qMckarbXkThJVkcRlVpJDJGVLhi7KV4g18QqitHtddllP6duYhfm2gN1 HpweKDkXmPFWcvNt / MGWvhiqrqUUS6bqCWMaxj0JRcXlKklVNRyapkbxJ2B8TthVKPMVlb3NvZAp SGa8tZI6kkmH61DESSfi5SmfmSTWgAO4xQjGSRbO1YMEuJntpI36KX9aMywyKP5XJZe43A2Bqqm0 VtZzO5VDaXgPKYRNwYsdw540WUV6FgR1BFajAliXmy8 / MrSxNP5UhstVj + uRx3sd5HKbhFkihX1k EDxLIqVJZAoNBtXCrJbjUVSXThehreRZj6jyLwjJ + ryiocNIi1PRS9cVTdWV1DKQysKqw3BB7jAr zzzjcS6ybXyDYuRPrU1zNrUibGDSI7pxOSR0a4b9wnzbwwq9BhhighSGFBHDEoSONRRVVRQAAdAB gVfirsVdirsVdirsVdirsVdirsVeb + a9Om8oeZH86WQl / wAPXw4ebLO3 + 1FsoGoxqBX4QirPwoxU BuqnFWZTJpj6Fc3lh6csVzaO6XUZEnqo0ZZW9WpLgjcGuKpszBQWYgKBUk9AMVYL548nHzxHcael / d6XCEtWFzazSxGWP1pPVBRGCOjR8gvMHfcUHUqgvN + sa7p2p6T5N0bQzb + XZoHiutWLI0MdvBaS yJbxxozOnNbfhykAHYV64qrDzxonmLzBruk6c / rP5dvNGt55a1Uyy34Mqx / 6pjCsfEewwKhrrz3Y 6pZeb9G0dl / xF5Wuy8Ecg5F5DIJY5FQUYoJWaJwDXbtyGFWptFvfzT8jaZc6xZXPlXW7eeK4gmil Uyx0YCb0nhf1FWWLkvF + LBqVHwgkKzPQQtm9zp8jNzilVIpJJJJTKFt4t / UlZ5Gam7cmJ9z1xVG3 v + 9On / 8AGdv + TEuKpL5x1nSPLOltqDRyfXp3EOn2NmeM93dyH93FHH9l3Y9SymgqT0xVQ / L7yjd6 La3Wp6y63HmfW5PrOr3C7oh4MdtF / wAVQhiB / Mat3xVlmKuxV2KuxV2KuxV2KuxV2KuxV2KtMqup VgGVhRlO4IPY4q801PRtb8hQX0mgW0mp + TLtZWudDhBa4055AeUtktf3kDMeTwjdeqdxirM9D1bT PM2nw6rZXMd3pcvxW6xMGBI / 39Toy / 77P2T13pRVFvMkGoXcr / ZS3gJA3J + OagA7k9AMVUruF49F v3lp9Ymhlkmp0BMZAUeyqAvvSuKpVe6dp8dl9fit4o7mbUbOMyoiqTFHqMKIoIh3aIG + ZJ74VRVz p9jZXrehbxwm5eGUGNVUmRr1XuGNO7tIhY9 / oxVM5P8ARrwTf7ouSqS + 0uyo3 + yHwn34 ++ BVkEMU 02oRyLyU3CnwIIgioQRuCOxGKsc83ecbfy7cadaTRyapqk8rNpum2nFru4 / dSJQx1HFQW + KU / ABU mnQqteV / KGpSav8A4s82vHc + YnQpY2cRLWumQP8AahtyftyN / u2alW6Ci9VWZYq7FXYq7FXYq7FX Yq7FXYq7FXYq7FXYq7FWIax + XVs + pS635avpfLevzb3Fzaqr21yR0 + t2jfupf9ccX / ysVSs69560 jUvW80eXZNQtEjRRqHl6t0jvGWKs9nIVuUoJDsgk + Km + FUVe / mz + Xt1pl / BHrdvDei2lK2N6Wsrg ng1FEVyIn5HwpgVMdR1TRhoFlFDqNtOIbrTkMkcsbA + ndwAnZj4YVXeZfMOgWpsJpdTtYf8ASYkk Z541AiMiuxNW2HONN8VQF3 + a / kK4WWz066k8wztWNrTRYJr9mr1 / eW6tGu37TOB74FQVi35p64JR HBF5TsLlucl7d + nd6myiNYwY7eIm2gZuFSXd6V + ztirI / LHkjQvLrT3Foslzql3 / AL3aveOZ724o aj1Jm34jsi0Udhiqf4qoC / sTemwFzF9eEYmNrzX1RGSVD8K8uJIIrSmKqdnq + lXs00FnewXM1uaX EUMqSNGebR0dVJK / HG6791I7Yqi8VdirsVdirsVdirsVdirsVS + 80DSbydp7mDnK1Azc3HQUGwYD FVH / AApoH / LL / wAlJP8AmrDau / wpoH / LL / yUk / 5qxtXf4U0D / ll / 5KSf81Y2rv8ACmgf8sv / ACUk / wCasbVRufJPlW6Thc6dHOn8shdx9zMcbVjXmL8pvy0WzjmXy1p / qtd2UbP6CklXu4kZansVYjAq aQflL + Wlu3K38t2ELeMcKqdvliqax + UPLkaBI7MIi9FV5AB9AbDarv8ACmgf8sv / ACUk / wCasbV3 + FNA / wCWX / kpJ / zVjau / wpoH / LL / AMlJP + asbVJbz8pvJN75ltPMN3aSTXtggSyjaVxDEwYsXCqQ WY1oeZI9sCpnoHk / T9E1XWNTtZ55bjXJluL5ZjGU9VeQVkCIhWiMqUr0UftcmZVPcVdirsVdirsV dirsVdirsVdirsVdirsVdirsVSvzL / xzof8AmO0 // qOhxVNMVdirsVdirsVdirsVdirsVdirsVdi rsVdir // 2Q == uuid: D9B7665ED55811DB9D7DD61D329D7703 uuid: 914cefa6-d990-11db-ac45-0014516728a0 конечный поток эндобдж 10 0 obj> эндобдж 11 0 obj> эндобдж 12 0 obj> поток Hbd`ab`ddwNNIN + quIəf! [?? — `9sfn] Vx% ߗ ~ Mus ~ AeQfzFJCKKĢPYTW_WZX_P a̤ĢJ = s2JSRs܂ = uZ2y) я% E Из 99 `+1
Квадратичная функция через три точки
В этой статье Норман Вильдбергер объясняет, как определить квадратичную функцию, проходящую через три точки.2 + bx + c} \) задается тремя числами, разумно предположить, что мы могли бы подогнать параболу к трем точкам на плоскости. Это действительно так, и это полезная идея. На этом шаге мы увидим, как алгебраически подогнать параболу к трем точкам на декартовой плоскости. Это включает в себя вспоминание или обучение тому, как решить три уравнения с тремя неизвестными. Это полезный навык сам по себе.
Уникальный круг, проходящий через три неколлинеарных точки
Линия определяется двумя точками.Круг, с другой стороны, определяется тремя точками, если эти точки не лежат на одной прямой (все три точки не могут лежать на одной линии). Построение круга, проходящего через три точки, является стандартным упражнением в евклидовой геометрии: мы строим серединные перпендикуляры отрезков прямых, определяемых этими тремя точками, а затем эти три прямые пересекаются в центре описанной окружности треугольника \ (\ normalsize { ABC} \), а именно центр единственной окружности, проходящей через все три точки.2 + bx + c} \), который проходит через точки \ (\ normalsize {[0,1], [1,5]} \) и \ (\ normalsize {[2,3]} \). Подставляя каждую из трех точек в уравнение, получаем \ [\ Large {1 = c} \] \ [\ Large {5 = a + b + c} \] \ [\ Large {3 = 4a + 2b + c} \] Это три уравнения с тремя неизвестными. Это более сложно, но в данном конкретном случае все проще, поскольку первое уравнение уже говорит нам, что \ (\ normalsize {c = 1} \), поэтому два других уравнения становятся \ (\ normalsize {a + b = 4 } \) и \ (\ normalsize {2a + b = 1} \).2 + 7x + 1} \). Вот график:Решение трех линейных уравнений с тремя неизвестными
Поскольку два линейных уравнения представляют собой две прямые на плоскости, их общее решение соответствует геометрическому пересечению этих двух линий. Для трех линейных уравнений с тремя неизвестными ситуация фактически соответствует общей точке пересечения трех плоскостей в трехмерном пространстве! К счастью, древние китайцы смогли разработать общую методику решения таких систем уравнений. Здесь мы просто пытаемся найти простой практический метод.2 + bx + c} \), который проходит через точки \ (\ normalsize {[1,3], [2, -1]} \) и \ (\ normalsize {[4,1]} \). Это означает, что у нас есть три уравнения, по одному для каждой точки — поскольку мы знаем, что данные точки должны удовлетворять неизвестному уравнению. Три уравнения: \ [\ Large {3 = a + b + c} \ label {b1p} \ tag {1} \] \ [\ Large {-1 = 4a + 2b + c} \ label {b2p} \ tag {2} \ ] \ [\ Большой {1 = 16a + 4b + c}. \ label {b3p} \ tag 3 \] Какая стратегия? Это просто: мы пытаемся исключить одну из переменных, оставляя нам два уравнения с двумя неизвестными.Мы знаем, как решить эту проблему. Чтобы получить два уравнения с двумя переменными, давайте исключим \ (\ normalsize {c} \) из первых двух уравнений. Мы делаем это, вычитая одно из другого, скажем, вычитая первое из второго: \ [\ Large {-4 = 3a + b} \ label {b4p} \ tag {4} \] Пожалуйста, убедитесь, что вы понимаете, как мы это получили. Теперь сделаем то же самое с двумя последними уравнениями: возьмем третье уравнение и вычтем второе: \ [\ Large {2 = 12a + 2b} \] Мы можем сделать это немного проще, разделив все коэффициенты на \ (\ normalsize {2} \), чтобы получить \ [\ Large {1 = 6a + b}.\ label {b5p} \ tag {5} \] Теперь мы рассматриваем \ (\ normalsize {(\ ref {b5p})} \) и \ (\ normalsize {(\ ref {b4p})} \) как новые уравнения и используем их для нахождения \ (\ normalsize {a} \) и \ (\ normalsize {b} \). Если мы возьмем \ (\ normalsize {(\ ref {b5p})} \) — \ (\ normalsize {(\ ref {b4p})} \), мы получим \ (\ normalsize {5 = 3a} \), так что \ (\ normalsize {a = 5/3} \), а затем снова подключиться к \ (\ normalsize {(\ ref {b3p})} \) или \ (\ normalsize {(\ ref {b4p})} \ ) дает \ (\ normalsize {b = -9} \). Затем поместив их обратно в, скажем, \ (\ normalsize {(\ ref {b1p})} \), получим \ (\ normalsize {3 = 5 / 3-9 + c} \), так что \ (\ normalsize {c = 31/3} \).2-20л + 17 \ вправо) \). Обратите внимание, что это не функция.парабол
Почему спутниковые антенны параболические?
Харли Уэстон,
Кафедра математики и статистики,
Университет Реджайны
Спутниковая тарелка предназначена для сбора сигнала со спутника и сфокусируйте его на приемнике.Чтобы определить оптимальную форму блюда, вы необходимо найти поверхность, которая будет отражать входящий сигнал на приемник из каждой точки на поверхности блюда.
Из физики мы знаем, что луч, падающий на плоскую поверхность, отражает так, что угол отражения равен углу падения. Если поверхность изогнутый, то верен тот же физический закон, где плоскость отражения является плоскость, касающаяся поверхности в точке контакта. Чтобы показать это параболическая форма оптимальна для спутниковой антенны, это необходимо знать физический факт, определение параболы, некоторая элементарная геометрия и один факт из исчисления.
Парабола — это геометрическое место точек, которые равноудалены от фиксированной точки, фокус и фиксированная линия — директриса. Чтобы найти уравнение такой кривой построить систему координат на плоскости так, чтобы фокус был точкой (0, p), а директрисой является горизонтальная линия y = -p. Таким образом, точка (x, y) на кривой тогда и только тогда, когда расстояние от (x, y) до (0, p) равно расстояние от (x, y) до линии y = -p. Приравнивая квадраты этих расстояния (чтобы вам не приходилось иметь дело с квадратными корнями), это требование является
(x-0) 2 + (y-p) 2 = (y + p) 2 .
Расширение обоих стороны и упрощение дает
4 п г = x 2 или
как уравнение параболы.
Предположим, что спутник находится прямо над головой, и поэтому парабола построенный направлен на спутник. Спутник находится достаточно далеко, чтобы можно предположить, что сигнал приближается к тарелке вертикально. Предположим, что конкретный сигнал попадает на тарелку в точке P с координатой X a, тогда точка P — (a, a 2 / (4p)).Продлите вертикальную линию через P до направляющая в Q, которая тогда имеет координаты (a, -p). У фокуса есть координаты (0, p) и, следовательно, средняя точка S отрезка FQ имеет координаты (a / 2,0) и поэтому находится на оси X.
Из исчисления требуется тот факт, что касательная к параболе в точке точка P имеет наклон 2 a / 4 p , и, следовательно, уравнение касательной линия на этом точка
Найти точку где эта касательная линия пересекает ось X, заданную y = 0, и упростить чтобы найти, что x = a / 2 .Но это S, середина отрезка FQ. Поскольку | FP | = | PQ | (определение параболы) треугольники FPS и QPS совпадают и, следовательно, углы FPS и QPS равны. Но угол QPS равен углу падения и, таким образом, сигнал будет отражаться вдоль линии PF и проходить через фокус. Размещение приемника в фокусе параболы, таким образом, приведет к а тарелка, которая будет отражать все сигналы со спутника на приемник.
Решение проблемы на параболические зеркала, отправленные в Quandaries and Queries, подразумевают, что каждое сигнал от спутника, который попадает в тарелку и, таким образом, отражается на фокус перемещается на одно и то же расстояние независимо от того, где он встряхивает тарелку. 2 + 3.2 — 20x + 23
после объединения одинаковых терминов.
а. Построение параболы путем приложения областей …
Context 1
… Pedemonte, & Robotti, 1997) таким образом, чтобы читатель «узнал» обычный параболический значок, вертикально расположенный на ортогональном оси координат. Однако, поскольку метод приложения площадей одинаково хорошо работает и в неортогональном случае, рисунок 5а ниже лучше иллюстрирует эту интерпретацию (т.е.е. создание смысла) предложения, упомянутого Архимедом. …
Контекст 2
… параметр AB формирует параболу как более или менее «открытую». Для «левой части» параболы на рисунке 5a, рисунок 5b иллюстрирует симметричную конструкцию (где AB ‘равно AB, а AE’ равно AE). С помощью режима перетаскивания в программном обеспечении динамической геометрии эту «наклонную» параболу можно выпрямить до 8. Представленный здесь метод построения (точек) параболы отличается от «концептуальной реконструкции» в Sardelis and Valahas (2012), который основан на (стандартной) конструкции средней пропорции в Евклиде II.14. …
Context 3
… режим перетаскивания в программном обеспечении динамической геометрии эту «наклонную» параболу можно выпрямить до 8 Представленный здесь метод построения (точек) параболы отличается от «концептуальной реконструкции» в Sardelis and Valahas (2012), которая основывается на (стандартной) конструкции средней пропорции в Евклиде II. 14. С точки зрения математического языка функций, Сарделис и Валахас строят функцию квадратного корня, в то время как рисунок 4 (и рисунок 5a) строят (обратную) квадратичную функцию (хотя и то, и другое путем применения площадей).«Реконструкция» Сарделиса и Валахаса (2012) больше соответствует формулировке Аполлония (в связи с рисунком 6), хотя они утверждают, что их «концептуальная реконструкция» поддерживает точку зрения о том, что коники, вероятнее всего, были обнаружены как плоские кривые путем слияния метод приложения площадей с понятием локуса задолго до того, как Аполлоний изучал их как конические сечения »(https://scirate.com/arxiv/1210.6842). …
Контекст 4
… Метод также охватывает применение площадей для двух других коник (рисование на конструкциях в Евклиде).Следует отметить, что метод, использованный на рисунке 5a, основанный на предложении, представленном в тексте Архимеда (см. Выше), поддерживает ту же точку зрения, и также может быть легко распространен на две другие коники с использованием Евклида II14. за одну ступень строительства. …
Контекст 5
… Этот рисунок можно назвать парабелограммой. В формуле y = k ⋅ x 2 для параболы на рисунке 5a, где AE = x и AH = y, k ≈ 0,2. Размер постоянной k не зависит от угла наклона параллелограмма, а только от длины параметра AB (увеличение AB приводит к уменьшению k)….
Контекст 6
… Как найти ось и точку фокусировки параболы, построенной путем наложения площадей, как на рисунке 5a? …
Контекст 7
… в этом примере может быть установлен мост между параболой, как определено свойством равноудаленности, где задана точка фокусировки, и как определено применением областей в не- прямоугольный случай на рисунке 5a (который находится в том же математическом регистре и организации евклидовой геометрии).Этот пример поднимает некоторые важные вопросы о значении и его зависимости от справочной базы знаний. …
Контекст 8
… пример поднимает некоторые важные вопросы о значении и его зависимости от справочной базы знаний. Рисунок 5a сам по себе не дает подробных советов о том, как действовать. Однако на рисунке 5b показано, что прямая, проходящая через A и D, проходит через середины параллельных хорд к параболе и, таким образом, является диаметром параболы, параллельным оси (рисунок Аполлония)….
Контекст 9
… приступить к решению проблемы, поэтому необходимо ввести дополнительные теоретические знания, такие как определения и свойства диаметров и оси параболы, а также знания о том, где на оси точка фокусировки находится. Рисунок 8. Построение оси и фокуса параболы, как показано на рисунке 5a. Как показано в предварительных инструкциях выше, расстояние от вершины до точки фокуса составляет одну четверть параметра (равное длине прямой кишки).


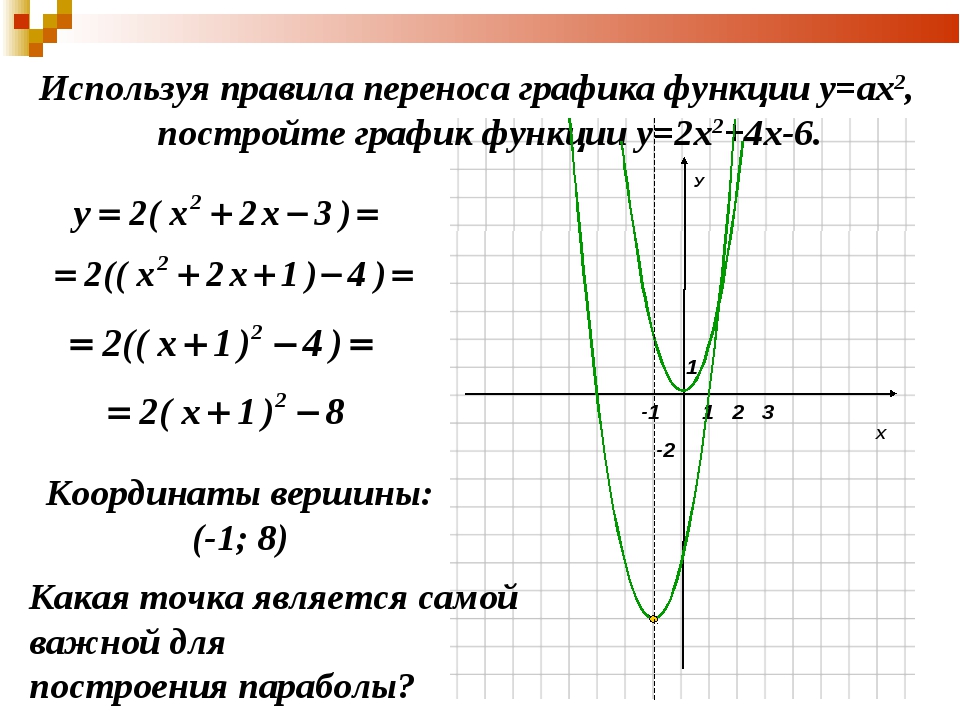 3 + k\).
3 + k\).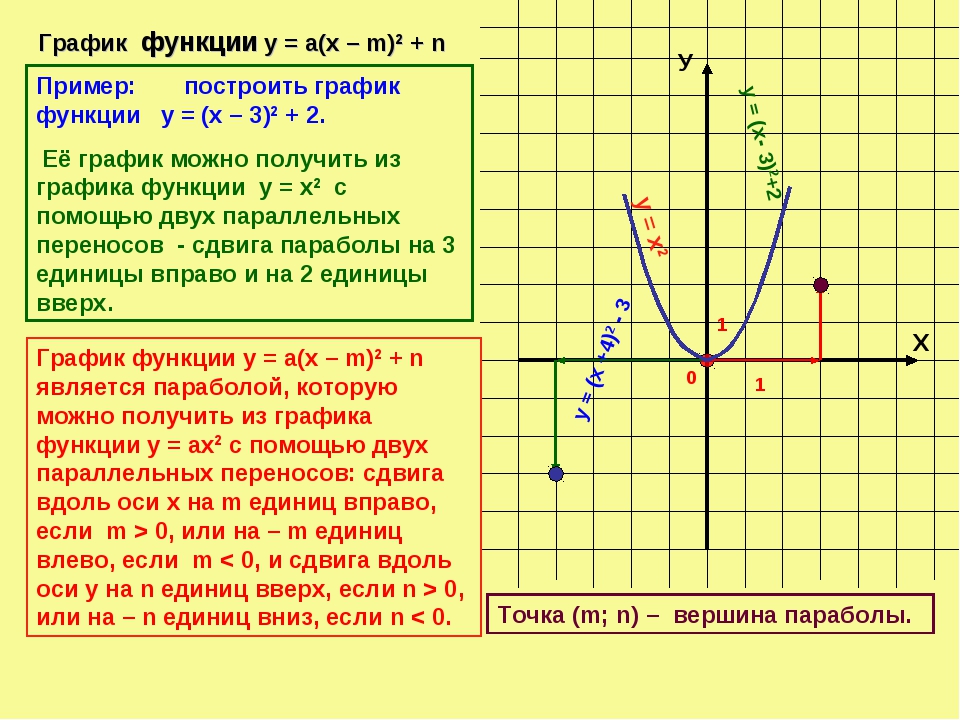 Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике. При обучении всегда стараюсь приводить примеры из реальной жизни и показываю, как из жизненных ситуаций построить математическую модель.
Считаю, что при изучении математики нельзя изучать новый материал, пока дети не усвоили предыдущий. Я люблю математику за то, что она развивает логическое и алгоритмическое мышление, пространственное воображение.
При обучении всегда стараюсь приводить примеры из реальной жизни и показываю, как из жизненных ситуаций построить математическую модель.
Считаю, что при изучении математики нельзя изучать новый материал, пока дети не усвоили предыдущий. Я люблю математику за то, что она развивает логическое и алгоритмическое мышление, пространственное воображение. Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!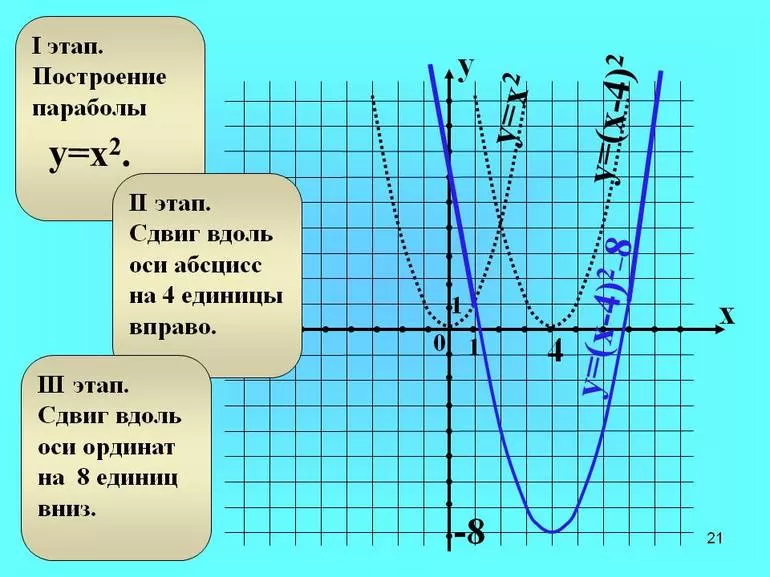
 Учащиеся записывают число и тему урока в тетради.
Учащиеся записывают число и тему урока в тетради.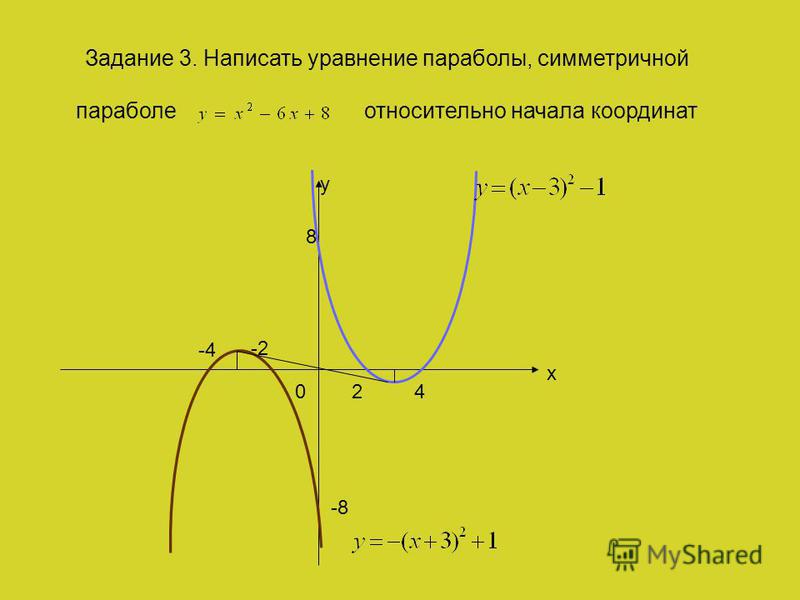
 Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы)
Точку пересечения параболы с осью симметрии называют … параболы. (вершина параболы) ( Презентация)
( Презентация)
 График какой функции изображен на рисунке?
График какой функции изображен на рисунке? График какой функции изображен на рисунке?
График какой функции изображен на рисунке?
 При этом выполняются следующие преобразования:
При этом выполняются следующие преобразования:

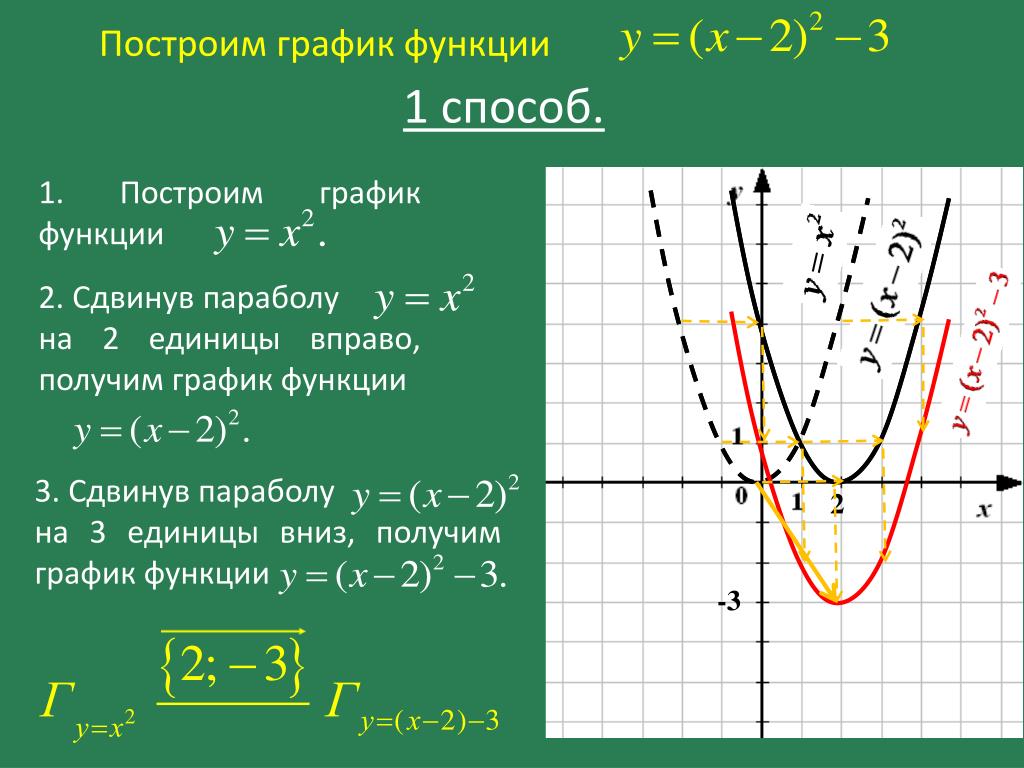 При нажатии на
изображение уравнения происходит вычерчивание
графика, причем это построение можно повторить
несколько раз. Размер чертежа можно увеличить
или уменьшить, что позволяет уточнить координаты
той или иной точки. Программу, выполняющую данные
построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru
При нажатии на
изображение уравнения происходит вычерчивание
графика, причем это построение можно повторить
несколько раз. Размер чертежа можно увеличить
или уменьшить, что позволяет уточнить координаты
той или иной точки. Программу, выполняющую данные
построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru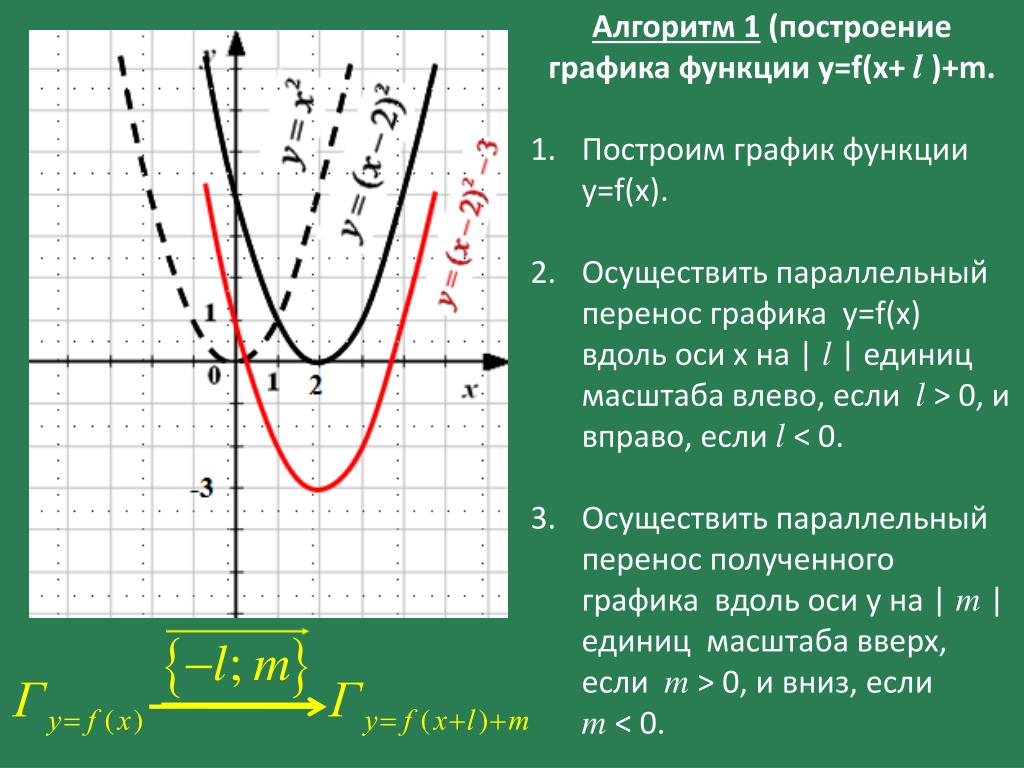 Учитель
примерно так вводит учащихся в новую тему.
Учитель
примерно так вводит учащихся в новую тему.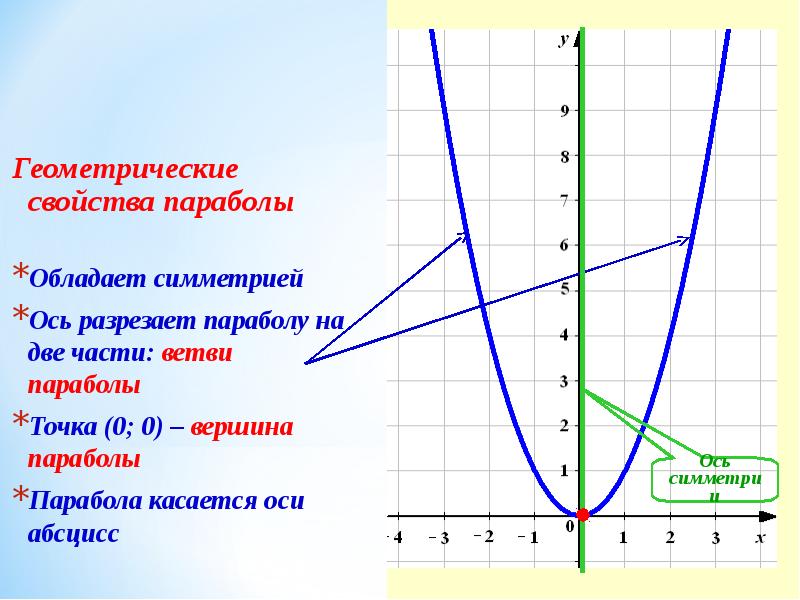

 2 — (1;1), (-1;1) и (2;4), (-2;4).
2 — (1;1), (-1;1) и (2;4), (-2;4).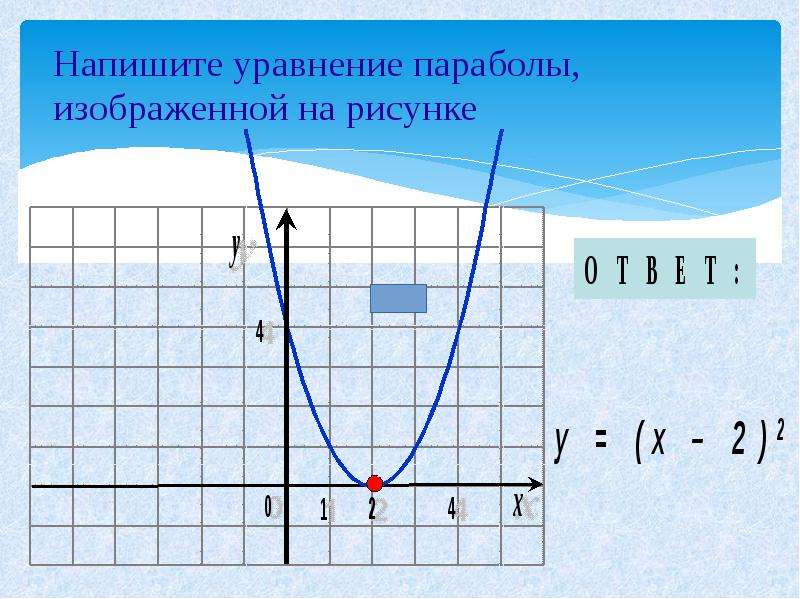 2
2 Еще удобнее в этом смысле графический калькулятор, который возьмет на себя, помимо расчета, и построение графика.
Еще удобнее в этом смысле графический калькулятор, который возьмет на себя, помимо расчета, и построение графика. Это художественное средство выразительности нельзя назвать , так как гипербола — это только преувеличение, она лишь выделяет, подчеркивает те или иные свойства предмета или явления, не изменяя их образного содержания.
Это художественное средство выразительности нельзя назвать , так как гипербола — это только преувеличение, она лишь выделяет, подчеркивает те или иные свойства предмета или явления, не изменяя их образного содержания. Ю. Лермонтов, В.В. Маяковский), и прозе (Г.Р. Державин, Н.В. Гоголь, Ф.М. Достоевский, М.Е. Салтыков-Щедрин).
Ю. Лермонтов, В.В. Маяковский), и прозе (Г.Р. Державин, Н.В. Гоголь, Ф.М. Достоевский, М.Е. Салтыков-Щедрин). Графически гипербола являет собой две плавные изогнутые линии. Каждая из них зеркально отображает другую относительно точки начала декартовых координат.
Графически гипербола являет собой две плавные изогнутые линии. Каждая из них зеркально отображает другую относительно точки начала декартовых координат. Это и будет ветвь функции y=k/x на промежутке (0; +∞). Обратите внимание на то, что кривая никогда не пересекает осей координат, а лишь к ним приближается, т. к. при x=0 функция не определена.
Это и будет ветвь функции y=k/x на промежутке (0; +∞). Обратите внимание на то, что кривая никогда не пересекает осей координат, а лишь к ним приближается, т. к. при x=0 функция не определена.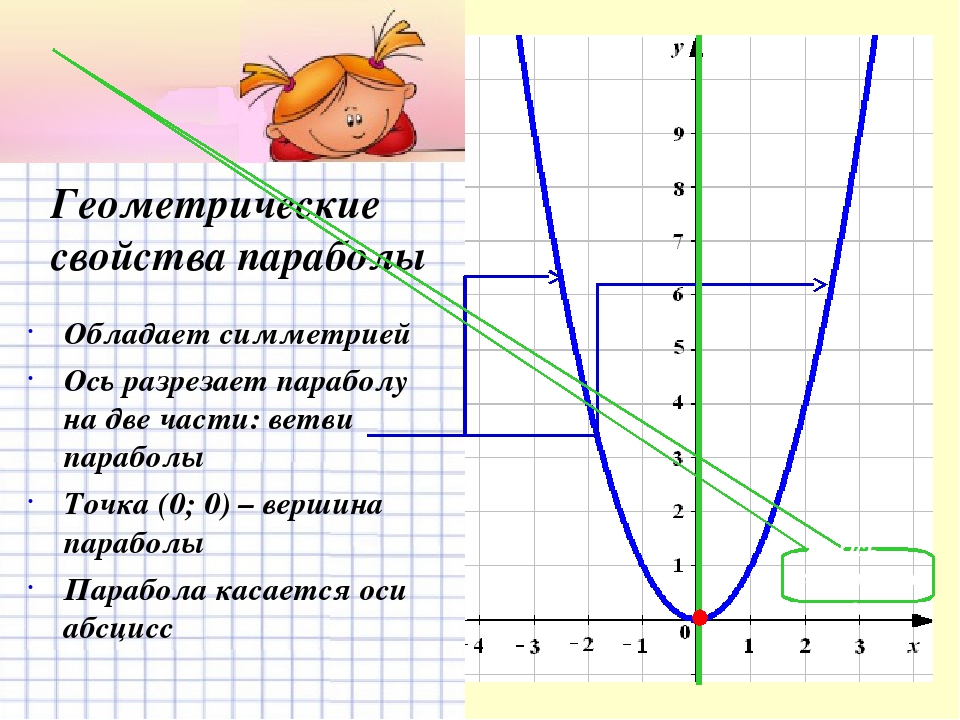 Если хоть один вопрос вызвал затруднения, перейди по .
Если хоть один вопрос вызвал затруднения, перейди по .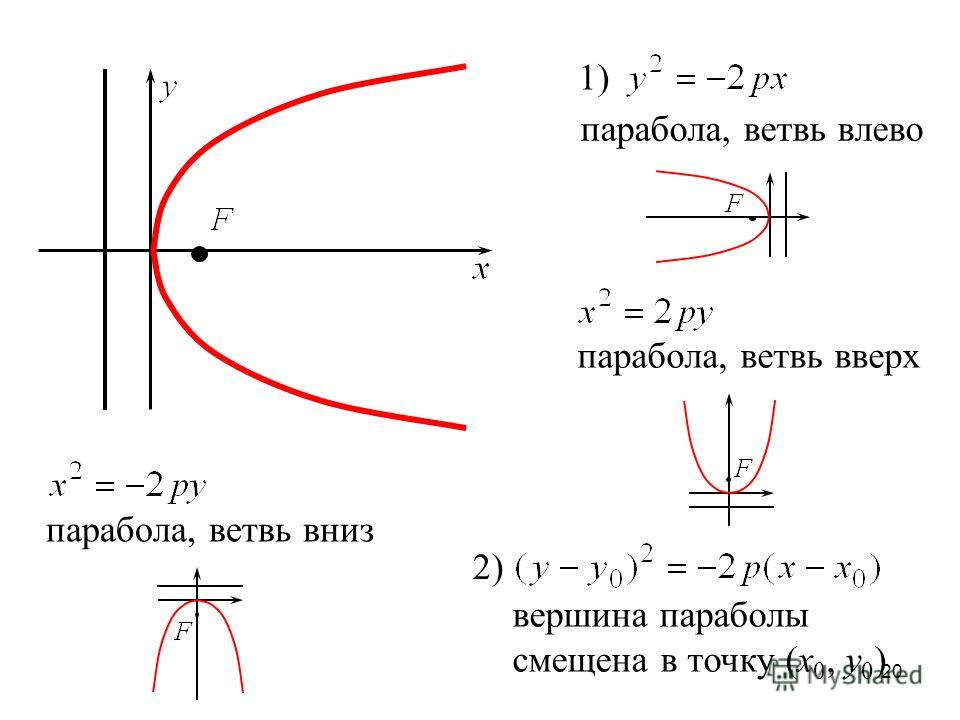 Что получилось?
Что получилось? Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.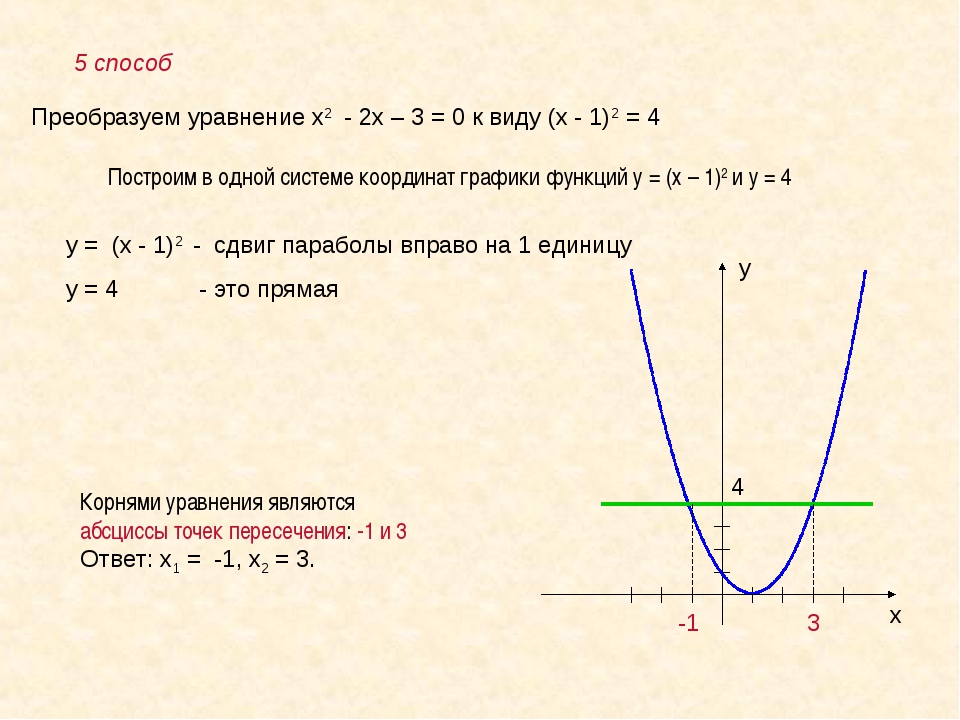

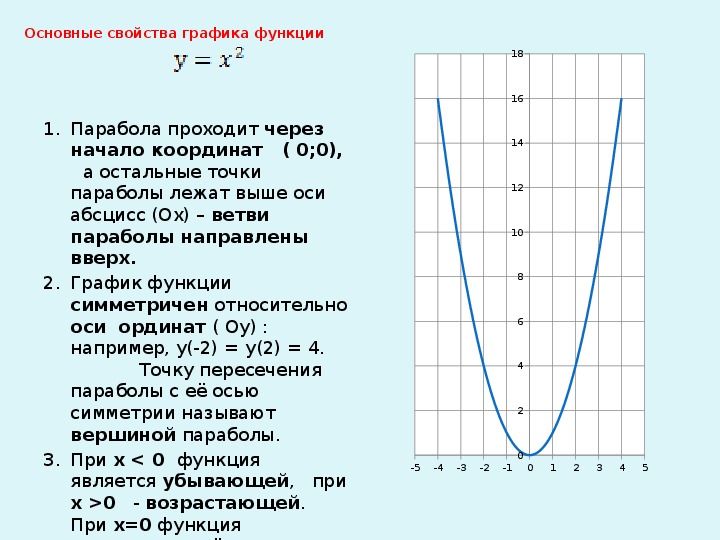

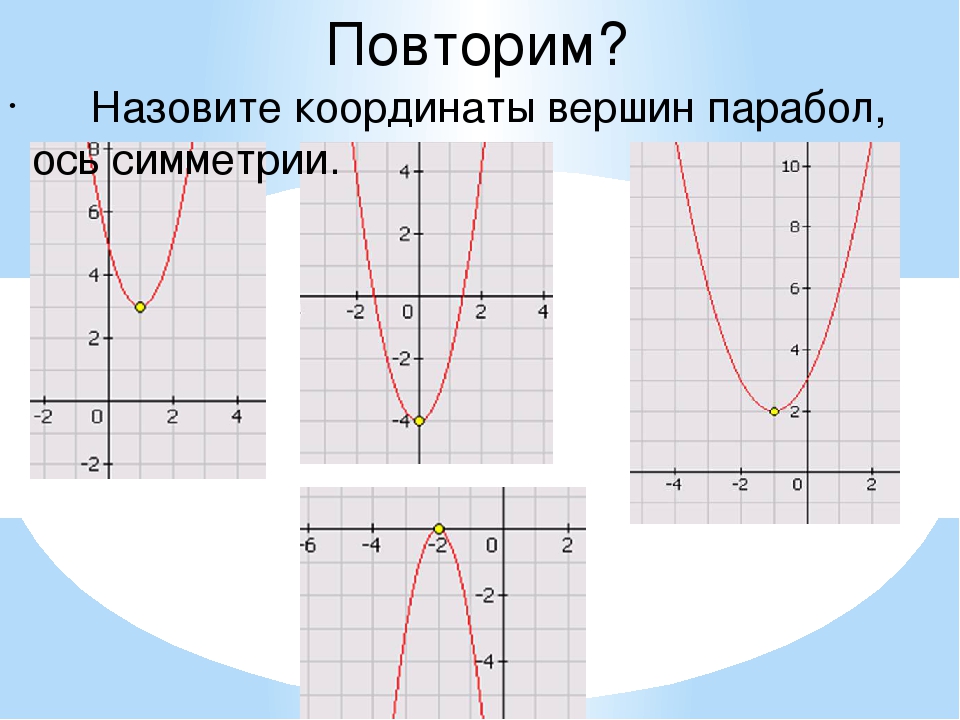 д.):
д.): В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).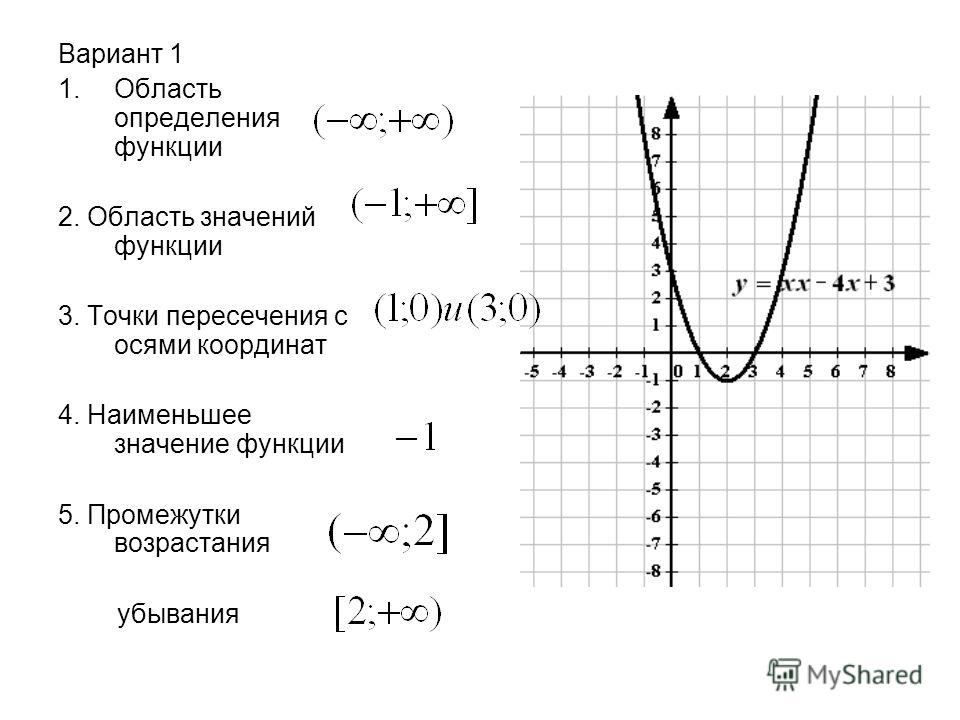
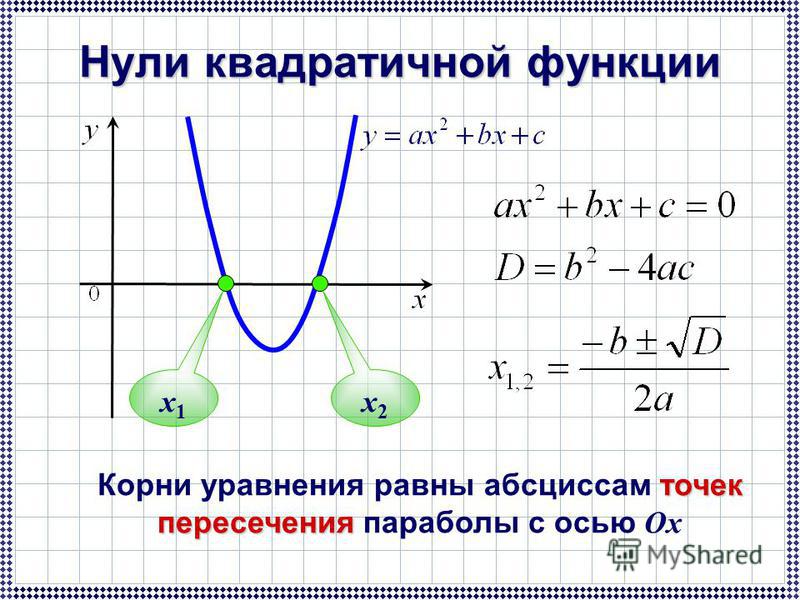 js? mode = мяч
js? mode = мяч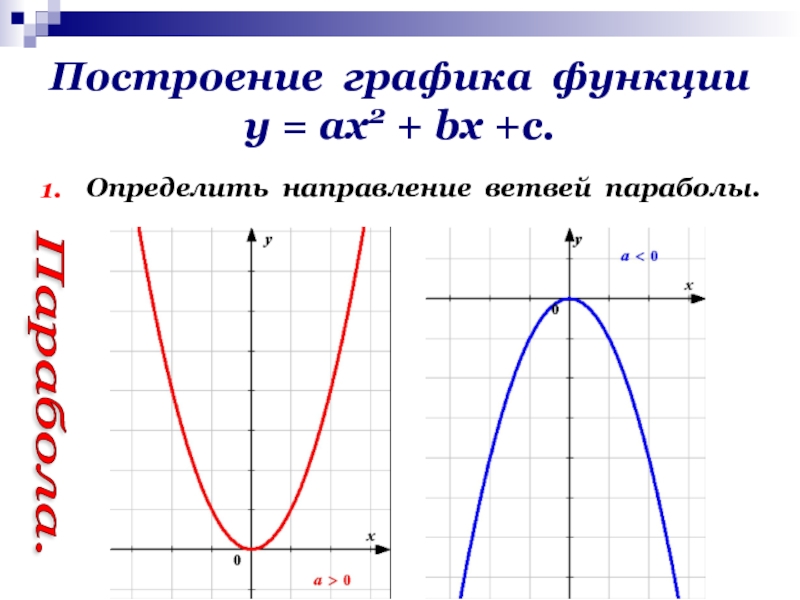 вершина (где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой.
вершина (где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой.