Признаки подобия прямоугольных треугольников (тема математики, 5 класс)
4
Средняя оценка: 4
Всего получено оценок: 126.
4
Средняя оценка: 4
Всего получено оценок: 126.
Подобие – это следующее понятие после равенства: как в математике после сложения идет умножение, так в геометрии после равенства треугольников изучают подобие. В реальной жизни подобие помогает, за счет вычислений по тени, определять реальные размеры зданий или высоких сооружений. В задачах на эту тему, благодаря подобию, можно найти значение сторон, воспользовавшись знакомым отношением.
Определения
Подобными называются треугольники, отношение сторон которых соответственно равны. Предположим треугольник АВС равен треугольнику DРН. Это значит, что:
$${АВ\over{DP}}={BC\over{PH}}={AC\over{DH}}=k$$
k это коэффициент подобия.
Для обычного треугольника существует три признака подобия. Именно через них доказываются признаки подобия прямоугольных треугольников.
Первый признак подобия:
Второй признак: по трем сторонам. Если три стороны одного треугольника пропорциональны соответственным сторонам другого треугольника, то такие треугольники подобны.
Рис. 2. Второй признак подобия.Третий признак: по двум сторонам и углу. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то такие треугольники подобны.
Рис. 3. Третий признак подобия.Эти определения необходимо знать, чтобы без проблем разобраться с подобием прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
- Первый признак по острому углу: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Доказать этот признак очень просто. Достаточно вспомнить, что прямоугольным треугольником называется треугольник, который содержит в себе прямой угол. Значит, у двух прямоугольных треугольников, один из углов всегда равен другому. А один из острых углов так же равен соответственному углу в другом треугольнике. Значит, в таких треугольниках есть два равных между собой угла, и треугольники подобны по первому признаку подобия.
- Второй признак: по двум катетам. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. Между двумя катетами всегда заключен прямой угол. Значит, у нас имеется две пропорциональные стороны и равные углы между ними. Тогда треугольники подобны по третьему признаку подобия.
- Третий признак:
 Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.
Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.
$$cos(ACB)={BC\over{AC}}$$
$$cos(DHP)={PH\over{DH}}$$
При этом по условию: $${AC\over{DH}}={BC\over{PH}}$$. Из условия выразим ВС и подставим в значение косинуса.
$$ВС=РН*{АC\over{DН}}$$
$$cos(ACB)={BC\over{AC}}={PH*{AC\over{DH}}\over AC}={PH\over{AC}}$$ – то есть косинусы углов равны, оба угла острые, значит и углы равны. Тогда треугольники подобны по двум сторонам и углу между ними.
Что мы узнали?
Мы разобрали понятие подобия, выделили все определения и теоремы, необходимые для доказательства трех признаков подобия прямоугольных треугольников. Мы показали, что эти признаки лишь следствие основных, т.е. эти свойства созданы чтобы упростить и сделать быстрее решение. А это значит, что если вдруг вы забыли признаки для прямоугольного треугольника, то всегда можно воспользоваться общими.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 126.
А какая ваша оценка?
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Подобные треугольники |
| Признаки подобия треугольников |
| Признаки подобия прямоугольных треугольников |
Подобные треугольники
Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.
Рис.1
Обозначим
a1 , b1 , c1
длины сторон треугольника KLM, расположенные в порядке возрастания.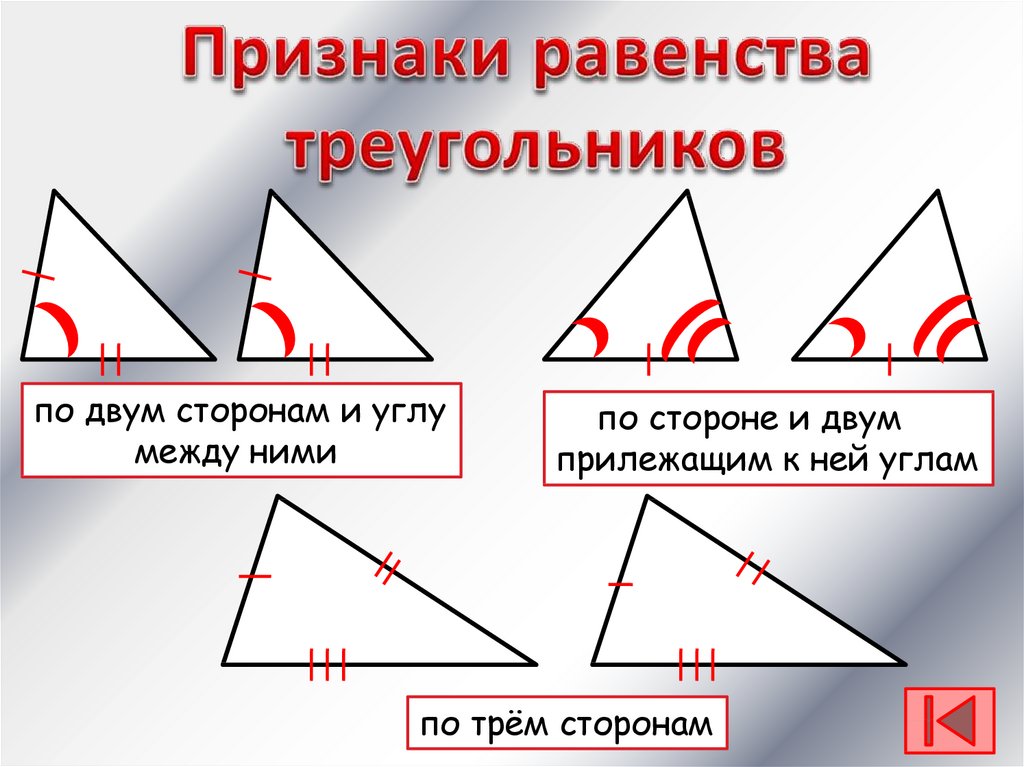
Обозначим
a2 , b2 , c2
длины сторон треугольника TRP, расположенные в порядке возрастания.
Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2.
Рис.2
На рисунке 2 треугольник KLM обозначается как треугольник A1B1C1, а треугольник TRP обозначается как треугольник A2B2C2.
Определение 1. В треугольниках A1B1C1 и A2B2C2, изображённых на рисунке 2,
- вершины A1 и A2, B1 и B2, C1 и C2 называют сходственными вершинами,
- стороны A1B1 и A2B2, A1C1 и A2C2, B1C1 и B2C2 называют сходственными сторонами,
- углы A1 и A2, B1 и B2, C1 и C2 называют сходственными углами
Определение 2. Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Другими словами, треугольники A1B1C1 и A2B2C2 подобны, если, во-первых,
а, во-вторых, существует положительное число k, такое, что справедливы равенства:
| a1 = k a2 , b1 = k b2 , c1 = k c2 . | (1) |
Определение 3. В случае, когда треугольники A1B1C1 и A2B2C2 подобны, число k, заданное формулами (1), называют коэффициентом подобия треугольников A1B1C1 и A2B2C2 .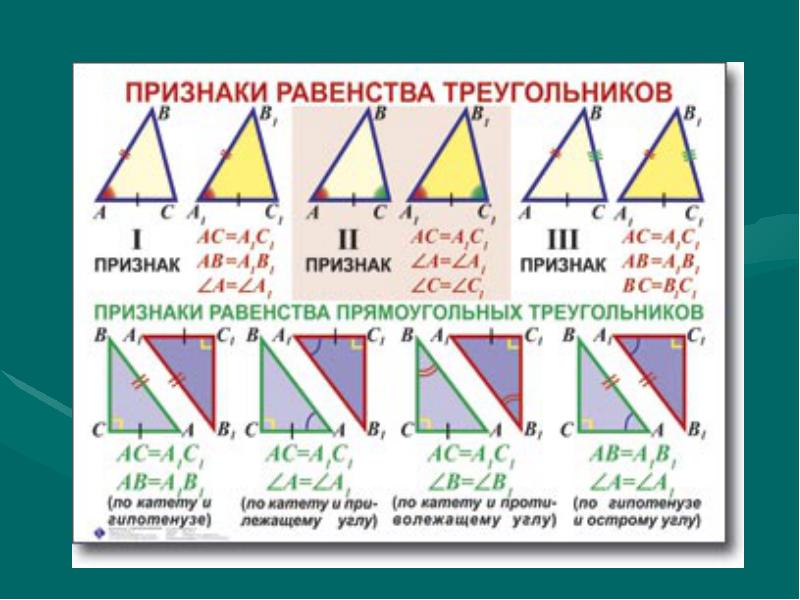
Признаки подобия треугольников
| Название признака | Рисунок | Формулировка признака |
Признак подобия треугольников по двум сторонам и углу между ними | Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. | |
Признак подобия треугольников по двум углам | Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. | |
Признак подобия треугольников по трём сторонам | Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны |
| Признак подобия треугольников по двум сторонам и углу между ними |
Формулировка признака подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. |
| Признак подобия треугольников по двум углам |
Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. |
| Признак подобия треугольников по трём сторонам |
Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны |
Признаки подобия прямоугольных треугольников
| Название признака | Рисунок | Формулировка признака |
Признак подобияпрямоугольных треугольников по двум катетам | Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. | |
Признак подобия прямоугольных треугольников по острому углу | Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. | |
Признак подобия прямоугольных треугольников по гипотенузе и катету | Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по двум катетам |
Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по острому углу |
Формулировка признака подобия прямоугольных треугольников: Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по гипотенузе и катету |
Формулировка признака подобия прямоугольных треугольников: Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
Следствие 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).
Рис.3
Следствие 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)
Рис.4
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как определить, подобны ли прямоугольники
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как определить, подобны ли прямоугольники
Примечание: цифра , а не нарисована в масштабе.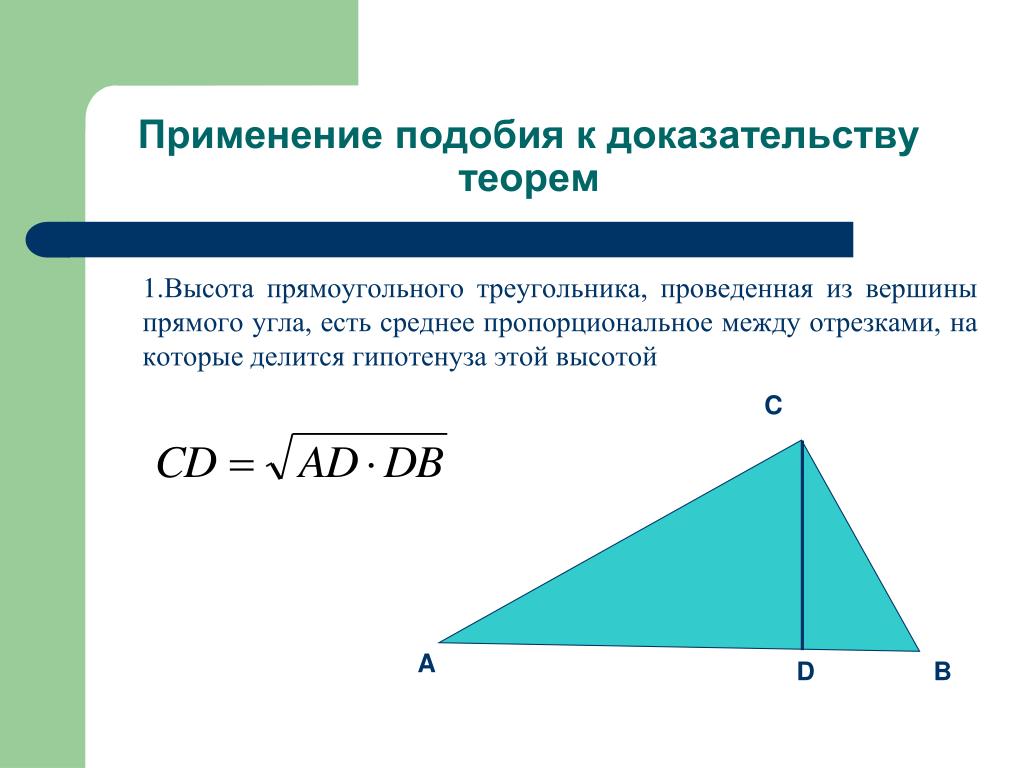
Посмотрите на рисунок выше.
Что такое?
Возможные ответы:
Из предоставленной информации определить невозможно.
Правильный ответ:
Объяснение:
По сходству можно составить пропорцию:
Заменить:
Сообщить об ошибке
Два прямоугольника подобны. Один прямоугольник имеет размеры сантиметры и 100 сантиметров; другой имеет размеры 400 сантиметров и сантиметров.
Какое значение делает это утверждение верным?
Возможные ответы:
Невозможно
Правильный ответ:
4
45
Объяснение:
Чтобы многоугольники были похожи, длины сторон должны быть пропорциональны.
Случай 1:
и 100 в первом прямоугольнике соответствуют и 400 во втором соответственно.
Полученная пропорция будет:
Это невозможно, так как должна быть положительная длина стороны.
Случай 2:
и 100 в первом прямоугольнике соответствуют 400 и во втором соответственно.
Правильная формулировка пропорции должна быть:
Перемножить, чтобы найти:
200 см — единственно возможное решение.
Сообщить об ошибке
Какое из следующих условий не является необходимым условием для того, чтобы прямоугольники A и B были похожи?
Возможные ответы:
Соответствующие стороны A и B имеют одинаковую длину
Каждой стороне каждого прямоугольника соответствует сторона другого прямоугольника
Все углы равны
Отношение длины к ширине эквивалентно
Правильный ответ:
Соответствующие стороны A и B имеют одинаковую длину
Объяснение:
Равенство всех сторон является условием конгруэнтности, а не сходства. Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сообщить об ошибке
Какое значение делает два прямоугольника похожими?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы два прямоугольника были похожи, их стороны должны быть пропорциональны (соотношение сторон равно). Отношение двух более длинных сторон должно быть равно отношению двух более коротких сторон.
Однако левое соотношение в нашей пропорции уменьшается.
Затем мы можем решить путем перекрестного умножения.
Затем мы решаем делением.
Сообщить об ошибке
Следующие изображения не в масштабе.
Чтобы сделать эти два прямоугольника похожими, какой должна быть ширина прямоугольника справа?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы два прямоугольника были похожи, их стороны должны быть в одинаковом соотношении.
Эту задачу можно решить с помощью соотношений и перекрестного умножения.
Неизвестную ширину правого прямоугольника обозначим через x.
Сообщить об ошибке
Два прямоугольника похожи. Один имеет площадь , а другой – . Если первый имеет базовую длину , какова высота второго прямоугольника?
Возможные ответы:
Правильный ответ: Объяснение:
Цель состоит в том, чтобы найти высоту второго прямоугольника.
Подобные прямоугольники функционируют по принципу пропорциональности, то есть отношения сторон между двумя прямоугольниками будут одинаковыми. Чтобы определить высоту, мы будем использовать эту концепцию отношений путем решения переменных из области.
Во-первых, полезно получить полные размеры для первого прямоугольника.
Известно, что длина его основания равна 5, а площадь равна 20.
Это означает, что первый прямоугольник имеет размеры 5×4.
Теперь мы можем использовать понятие отношений подобия. Длина сторон первого прямоугольника равна 5×4, поэтому стороны второго прямоугольника должны быть пропорциональны сторонам первого.
У нас есть информация для первого прямоугольника, поэтому данные можно подставить.
– коэффициент отношения, который будет использоваться для определения высоты второго прямоугольника. Это можно подставить в формулу площади второго прямоугольника.
Следовательно, высота второго прямоугольника — 10.
Отчет о ошибке
Есть два прямоугольника. У одного периметр , а у второго периметр . Первый прямоугольник имеет высоту . Если два прямоугольника подобны, чему равно основание второго прямоугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Цель этой задачи — выяснить, какая длина основания второго прямоугольника сделает его похожим на первый прямоугольник.
Подобные прямоугольники функционируют на основе пропорциональности, то есть отношения сторон между двумя прямоугольниками будут одинаковыми. Чтобы определить базу, мы будем использовать эту концепцию отношений путем решения переменных из периметра.
Сначала необходимо рассчитать все размеры первого прямоугольника.
Это можно сделать с помощью уравнения периметра:
Это означает, что размеры первого прямоугольника равны 10×5. Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
— коэффициент отношения, который мы будем использовать для определения основания второго прямоугольника.
Это потребует пересмотра уравнения периметра для второго прямоугольника.
Сообщить об ошибке
На прикрепленном изображении представлены размеры линолеума двух разных марок. Если две плитки подобны, какова будет длина большой плитки, учитывая информацию на рисунке ниже?
Возможные ответы:
Правильный ответ:
Объяснение:
Два прямоугольника подобны, если их длина и ширина образуют одинаковое отношение. Маленькая плитка имеет ширину и ширину , что дает нам следующее соотношение:
Поскольку длина подобных треугольников вдвое превышает их соответствующую ширину, длину большой плитки можно определить как такую:
Сообщить об ошибке
Эти прямоугольники похожи?
Возможные ответы:
Да — Масштабная фактор 2
Да — Масштабная коэффициент
Да — Масштабная коэффициент
Нет
Правильный ответ:
NO
. Объяснение:
Объяснение:
Чтобы определить, подобны ли эти прямоугольники, задайте пропорцию:
Эта пропорция сравнивает отношение длинных сторон в каждом прямоугольнике с отношением коротких сторон в каждом прямоугольнике. Если они одинаковы, перекрестное умножение даст истинное утверждение, и прямоугольники подобны:
Эти прямоугольники не похожи.
Сообщить об ошибке
Эти прямоугольники похожи?
Возможные ответы:
Да — Масштабная коэффициент 2,5
Да — Масштабная коэффициент
Да — Масштаб 3
Нет
Правильный ответ:
Да.
Объяснение:
Чтобы определить, подобны ли прямоугольники, задайте пропорцию, сравнивающую короткие и длинные стороны каждого прямоугольника:
перекрестно умножить
так как это правда, прямоугольники подобны.
Чтобы найти масштабный коэффициент, разделите 25 на 10 или 7,5 на 3. В любом случае вы получите 2,5.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Как определить, подобны ли прямоугольники
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- Репетиторство по программе SAT
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Learn by Concept
ACT Math Help »
Геометрия »
Плоская геометрия »
Четырехугольники »
Прямоугольники »
Как определить, подобны ли прямоугольники
Два прямоугольника подобны. Периметр первого прямоугольника равен 36. Периметр второго равен 12. Если длина основания второго прямоугольника равна 4, какова высота первого прямоугольника?
Периметр первого прямоугольника равен 36. Периметр второго равен 12. Если длина основания второго прямоугольника равна 4, какова высота первого прямоугольника?
Возможные ответы:
4
2
6
8
10
Правильный ответ:
6
Пояснение:
Найдите высоту второго прямоугольника.
Периметр = 2В + 2Н
12 = 2(4) + 2H
12 = 8 + 2H
4 = 2H
H = 2
Если они подобны, то основание и высота пропорционально равны.
B 1 /H 1 = B 2 /H 2
4/2 = B 2 /H 2
2 = B 2 /H 2
B 2 = 2H 2
Используйте уравнение периметра, затем найдите H:
Периметр = 2B + 2H
36 = 2 B 2 + 2 H 2
36 = 2 (2H 2 ) + 2 H 2
36 = 4H 2 + 2 H 2
36 = 6H 2
H 2 = 6
Сообщить об ошибке
Два прямоугольника похожи. Периметр первого прямоугольника равен , а периметр второго – . Если длина первого прямоугольника равна , какова длина второго прямоугольника?
Периметр первого прямоугольника равен , а периметр второго – . Если длина первого прямоугольника равна , какова длина второго прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
1. Создайте пропорцию, сравнивая два данных прямоугольника:
2. Решить длину второго прямоугольника путем перекрестного мультиплиза ширина прямоугольника в 5 раз больше длины прямоугольника. Ширина прямоугольника равна 30. Чему равен периметр прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Если ширина в 5 раз больше длины, а ширина равна 30, то длина равна 6. Периметр прямоугольника равен 2 х ширина + 2 х длина.

 Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.


 Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций. Объяснение:
Объяснение:
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- Репетиторство по программе SAT
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
 Периметр первого прямоугольника равен 36. Периметр второго равен 12. Если длина основания второго прямоугольника равна 4, какова высота первого прямоугольника?
Периметр первого прямоугольника равен 36. Периметр второго равен 12. Если длина основания второго прямоугольника равна 4, какова высота первого прямоугольника?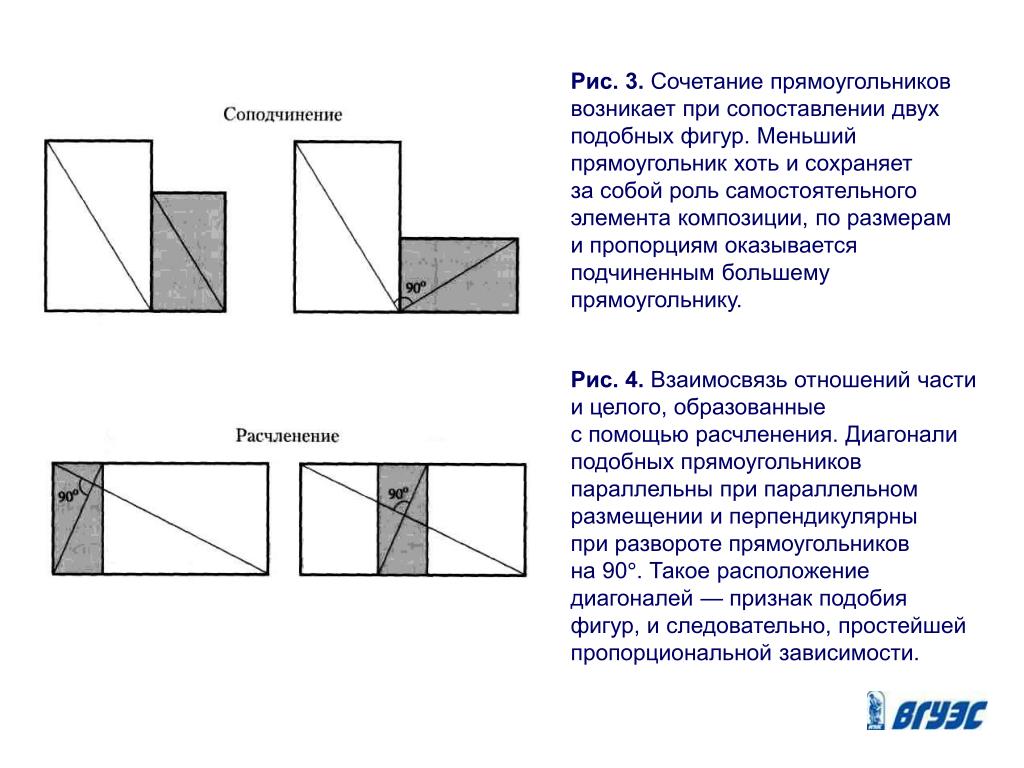 Периметр первого прямоугольника равен , а периметр второго – . Если длина первого прямоугольника равна , какова длина второго прямоугольника?
Периметр первого прямоугольника равен , а периметр второго – . Если длина первого прямоугольника равна , какова длина второго прямоугольника?

 Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.
Для доказательства признака нужно вспомнить понятие косинуса. Косинус угла это отношения прилежащего катета к гипотенузе.