Подобие треугольников | это… Что такое Подобие треугольников?
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Содержание
|
Признаки подобия треугольников
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Первый признак
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. |
То есть
Дано: и
Доказать:
Доказательство
Второй признак
Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны. |
Дано: и Доказать:
Доказательство
Третий признак
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны. |
Дано: ∆ABC и ∆A1B1C1, = = .
Доказать: ∆ABC ∆A1B1C1.
Доказательство
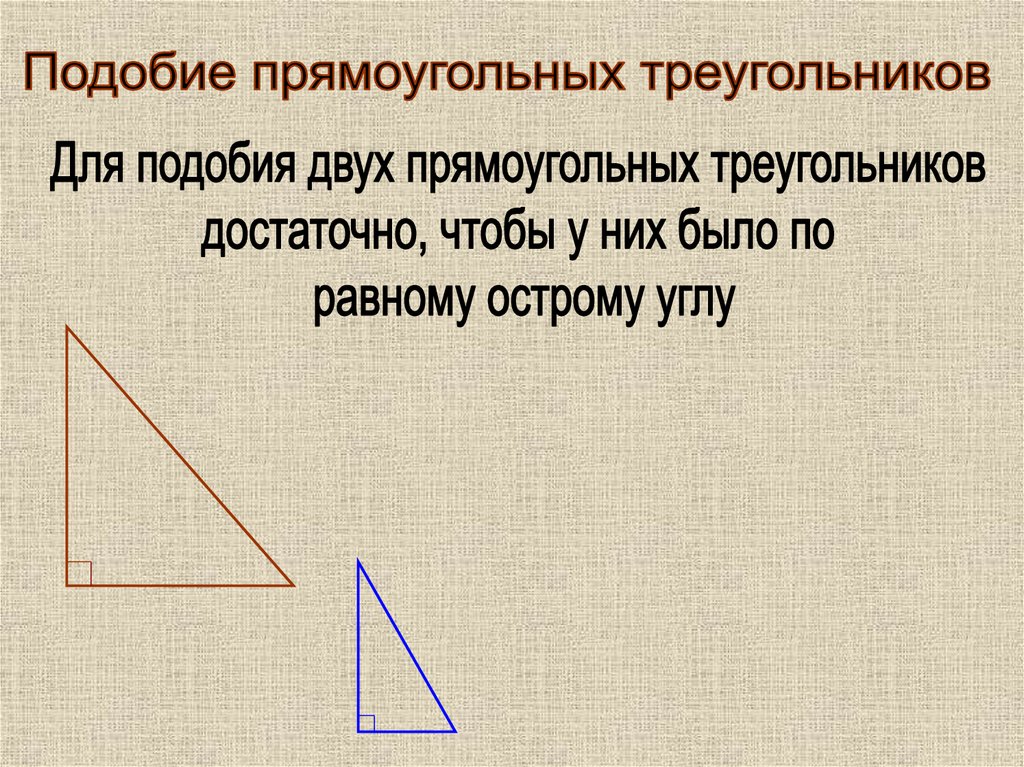
Признаки подобия прямоугольных треугольников
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. третий признак.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия
- Отношение объёма подобных стереометрических фигур равно кубу коэффициента подобия
- Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
Литература
- Геометрия 7-9/Л.
 С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
См. также
- Подобие
- Среднее геометрическое
- Треугольник
Ссылки
- Подобие треугольников
- Признаки подобия из учебника за восьмой класс
Подобие треугольников — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
ПОДОБИЕ
ТРЕУГОЛЬНИКОВ.
03.10.2018
РЕШЕНИЕ ЗАДАЧ. Обработка информации…
Обработка информации…
R
S
1) Δ DRS
Δ FHP
12
15
S = 35°, F = 70°.
x
D
Найти все углы и стороны
этих треугольников.
y
35°
70°
S
F
B1
2)
1
S
B
А
H
9
8
PA1B1C1
y
x
= 54
х , y, z — ?
C
А1
z
C1
7
5
P
Следствие продолжается…
3) Две стороны подобных треугольников
относятся как 2:5. Найти периметр
k? большего Δ,если периметр меньшего
Δ равен 16 см.
S
Главная информация…
К!
Признаки подобия треугольников
Повторим…
Сравним…
6. Подобие прямоугольных треугольников
Запомните!Высота треугольника
Высота
прямоугольного
треугольника,
проведенная из вершины прямого угла,
разделяет треугольник на два подобных
прямоугольных треугольника, каждый из
которых подобен данному треугольнику. C
ABC ACD,
ABC CBD
ACD CBD
A
D
B
9. Определение
• Средним геометрическим(пропорциональным) чисел a и b
называется квадратный корень из их
произведения.

10. Утверждение 1
1.Высотапрямоугольного
треугольника,
проведенная из вершины прямого угла, есть
среднее пропорциональное между отрезками, на
которые делится гипотенуза этой высотой
C
CD AD DB
A
D
B
11. Утверждение 2
2. Катет прямоугольного треугольника естьсреднее
пропорциональное
между
гипотенузой и проекцией этого катета на
гипотенузу.
C
AC AB AD ,
BC AB DB
A
D
B
12. Утверждение 3
• Биссектриса треугольника делитпротиволежащую сторону на отрезки,
сторонам
Задачи, в которых «живёт» подобие
Т.о среднем пропорциональном
MN ║ BC
(отсекает
подобный ∆)
∆MAN
S
∆BAC
A
B
AB 2 BC BD
AС 2 BC СD
D
C
Свойство
биссектрисы
B
O
AB
AL
BC
LC
1 2
S
∆BOC
∆DOA
A
L
AD 2 BD CD
C
Итог урока
Домашнее задание
• П.104, 105, 106 учить!
• Утверждения из п.
 106 записать в
106 записать втетрадь
• Схему подобия на карточку
• № 38, 40, 44, 48*
English Русский Правила
Подобные прямоугольные треугольники
Два треугольника подобны, если два их соответствующих угла конгруэнтны.
Пример:
На схеме, показанной выше,
ΔABC ∼ ΔXYZ
Напомним, что соответствующие длины сторон подобных треугольников пропорциональны.
Теорема
Если высота проведена к гипотенузе прямоугольного треугольника, то два образовавшихся треугольника подобны исходному треугольнику и друг другу.
На приведенной выше диаграмме
ΔCBD ∼ ΔABC
ΔACD ∼ ΔABC
ΔCBD ∼ ΔACD
Доказательство вышеизложенной теоремы:
Дано : ΔABC — прямоугольный треугольник; высота CD проведена к гипотенузе AB.
Доказательство:
ΔCBD ∼ ΔABC, ΔACD ∼ ΔABC, ΔCBD ∼ ΔACD
Доказательство:
Первое доказательство того, что ΔCBD ∼ ΔABC. В каждом треугольнике есть прямой угол, и каждый включает ∠B. Треугольники подобны в соответствии с постулатом подобия АА.
Треугольники подобны в соответствии с постулатом подобия АА.
Мы можем использовать аналогичные рассуждения, чтобы показать, что ΔACD ∼ ΔABC.
Чтобы показать, что ΔCBD ∼ ΔACD, начните с демонстрации того, что ∠ACD ≅ ∠B, поскольку оба они дополняют ∠DCB. Затем вы можете использовать постулат подобия АА.
Использование среднего геометрического для решения задач
В правом ΔABC, показанном выше, высота CD проведена к гипотенузе, образуя два меньших прямоугольных треугольника, которые подобны ΔABC. Из приведенной выше теоремы мы знаем, что ΔCBD ∼ ΔACD ∼ ΔABC.
Обратите внимание, что CD — это более длинная часть ΔCBD, а более короткая — ΔACD. Когда мы пишем пропорцию, сравнивающую длины катетов ΔCBD и ΔACD, мы видим, что CD — это среднее геометрическое BD и AD.
Стороны CB и AC также встречаются более чем в одном треугольнике. Длины их сторон также являются средними геометрическими, как показано ниже в пропорциях:
. Эти результаты выражены в теоремах ниже.
Теоремы о среднем геометрическом
Теорема 1 :
В прямоугольном треугольнике высота от прямого угла до гипотенузы делит гипотенузу на два сегмента.
В правом ΔABC, показанном выше, длина высоты CD представляет собой среднее геометрическое длин двух сегментов. АД и БД.
То есть
BD/CD = CD/AD
CD 2 = AD ⋅ BD
CD = √(AD ⋅ BD)
Теорема 2 :
В прямоугольном треугольнике высота от Прямой угол к гипотенузе делит гипотенузу на два отрезка.
Длина каждого катета прямоугольного треугольника равна среднему геометрическому длин гипотенузы и отрезка гипотенузы, примыкающего к катету.
Справа ΔABC , показанном выше,
CB = √(AB ⋅ DB)
AC = √(AB ⋅ AD)
Определение высоты крыши
Пример:
Поперечное сечение крыши представляет собой прямоугольный треугольник. На схеме показаны примерные размеры этого сечения.
а. Найдите подобные треугольники.
б. Найдите высоту h крыши.
Решение (a) :
Мы можем счесть полезным нарисовать три подобных прямоугольных треугольника так, чтобы соответствующие углы и стороны имели одинаковую ориентацию. Отметьте равные углы.
Обратите внимание, что некоторые стороны встречаются более чем в одном треугольнике.
Например, BC — это гипотенуза в ΔBCA и более короткий катет в ΔBDC.
На приведенной выше диаграмме
ΔBCA ∼ ΔCDA ∼ ΔBDC
Решение (b) :
Используйте тот факт, что ΔBCA ∼ ΔBDC, чтобы написать пропорцию.
Соответствующие длины сторон пропорциональны:
CA/DC = BC/BD
Замена.
h/5,5 = 3,1/6,3
Применение свойства перекрестного произведения.
6,3h = 3,1 (5,5)
Решите для h.
h ≈ 2,7
Отсюда высота крыши около 2,7 метра.
Использование среднего геометрического
Пример 1:
Найдите значение x на диаграмме, показанной ниже.
Решение:
Применить теорему о среднем геометрическом 1.
x/3 = 6/x
Применить свойство векторного произведения.
x 2 = 18
Найдите x.
х = √18
х = √(3 ⋅ 3 ⋅ 2)
x = 3√2
Пример 2:
Найдите значение y на диаграмме, показанной ниже.
Решение:
Применить теорему 2 о среднем геометрическом.
y 2 = 14
Найдите x.
x = √14
Использование косвенных измерений
Пример:
Чтобы оценить высоту монорельса, ваш друг держит картонный квадрат на уровне глаз. Ваш друг выравнивает верхний край квадрата с дорожкой, а нижний край — с землей. Вы измеряете расстояние от земли до глаза вашего друга и расстояние от вашего друга до дорожки.
На приведенной ниже диаграмме XY = h – 5,75 – это разница между высотой трека h и уровнем глаз вашего друга. Найдите высоту дорожки.
Решение:
Используйте теорему 2 о среднем геометрическом, чтобы написать пропорцию, содержащую XY. Тогда вы можете решить для h.
Теорема о среднем геометрическом 2 :
XY/WY = WY/ZY
Замена.
(h — 5,75)/16 = 16/5,75
Применение свойства перекрестного произведения.
5,75(ч — 5,75) = 16 2
Распределительное имущество.
5,75ч — 33,0625 = 256
Добавьте 33,0625 на каждую сторону.
5,75h = 289,0625
Разделите каждую сторону на 5,75.
h ≈ 50
Следовательно, высота пути составляет около 50 футов.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Подобные прямоугольные треугольники: определение и примеры
MathSimilar Right Triangles9 класс
13 сентября 2022 г.
Ключевые понятия
- Определение подобных треугольников
Прямой угол
угол, ограниченный двумя линиями, перпендикулярными друг другу: угол 90° или ¹/₂ π радиан.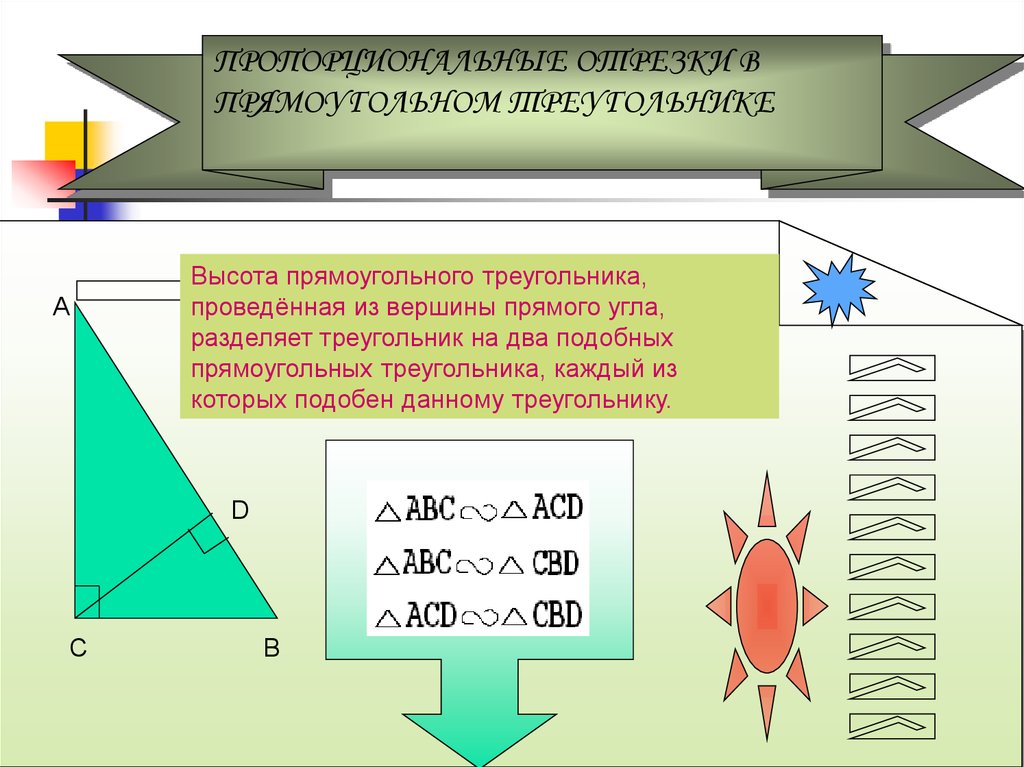
Если высота проведена к гипотенузе прямоугольного треугольника, то два образовавшихся треугольника подобны исходному треугольнику и друг другу.
Определение подобных треугольников
Пример 1:
Определите подобные треугольники на диаграмме.
Решение:
Нарисуйте три подобных прямоугольных треугольника так, чтобы соответствующие углы и стороны имели одинаковую ориентацию.
ΔQRS ~ ΔPQS ~ Δ PRQ
Пример 2:
Найдите длину высоты до гипотенузы. Округлите десятичные ответы до десятых.
Решение:
Нарисуйте диаграмму.
x/23 = 12,8 / 26,6
26,6 (x) = 294,4
x = 11,1 фута
Пример 3: 90 004
Найдите значение y . Запишите ответ в простейшей радикальной форме.
Решение:
Шаг 1: Нарисуйте три подобных треугольника
Шаг 2: Напишите пропорцию.
6/x = x/2 (замена)
12 = x 2 (свойство перекрестного произведения)
√12 = x (извлеките положительный квадратный корень из каждой стороны)
2√3= x (упрощение)
Пример 4:
Здание высотой 30 футов отбрасывает тень длиной 75 футов. Ближайшее дерево отбрасывает тень длиной 35 футов. Насколько высокое дерево?
Решение:
𝟑𝟎 / 𝟕𝟓 = 𝒉/𝟑𝟓 (соответствующие стороны подобных фигур пропорциональны)
75h = 1050 (Найти перекрестные произведения)
𝟕𝟓 / 𝒉𝟕𝟓 = 𝟏𝟎𝟓𝟎 / 𝟕𝟓 (делит обе стороны на 75)
h = 14
Высота дерева 14 футов.
Упражнение
- Найдите подобные треугольники. Затем найдите значение х.
- Чармин ростом 5,5 футов. На каком расстоянии от стены на изображении ниже она должна стоять, чтобы измерить его рост?
- Определение подобных треугольников: Найдите три подобных прямоугольных треугольника на данном рисунке.

- Найдите длину высоты до гипотенузы. Округлите десятичные ответы до десятых.
- Напишите утверждение о сходстве трех подобных треугольников на диаграмме. Затем выполните пропорцию.
- Найдите значение (значения) переменной (переменных).
- Используя теоремы: Скажите, является ли треугольник прямоугольным. Если да, то найдите длину высоты до гипотенузы. Округлите десятичные ответы до десятых.
- Опишите и исправьте ошибку в написании пропорции для данной диаграммы.
- Нахождение длин: Используйте теоремы о среднем геометрическом, чтобы найти AC и BD.
- Используйте схему. Найдите ФХ.
Концептуальная карта
Чему мы научились
- Определить подобные треугольники
- Поймите, как найти длину высоты до гипотенузы
- Понимать среднее геометрическое
- Простейшая радикальная форма.

- Узнайте, как найти высоту с помощью непрямого измерения.
Похожие темы
Как найти площадь квадрата?
Площадь квадрата можно определить по тому, сколько пространства он занимает внутри себя. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как […]
Подробнее >>
Числовые последовательности: определение и типы
Числовые последовательности — важный математический инструмент для оценки чьего-либо IQ. Большинство тестов на управленческие способности часто включают вопросы числового ряда. Вы когда-нибудь замечали закономерность в числах, отведенных домам в ряду, в номерах страниц в книге или в прибавке к зарплате, которую работник получает каждый год? Если да, вы […]
Подробнее >>
Что означает координатная сетка? — Полное руководство
Плоскость – это плоская поверхность.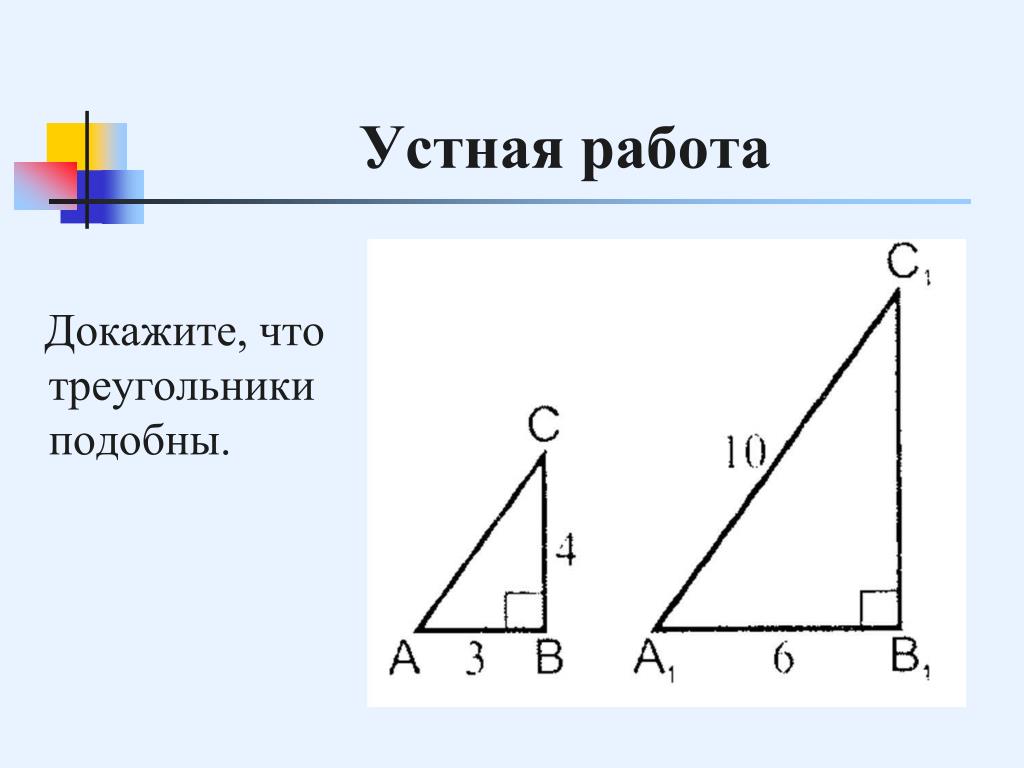


 С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.
