GU10 – НАКЛАДНЫЕ СВЕТИЛЬНИКИ ЦИЛИНДРЫ PDL-R И ПРЯМОУГОЛЬНИКИ PDL-S от JAZZWAY
2 Февраля 2021 г., 15:22
Магия белого и черного. Подобные решения всегда выглядят актуально.
Практически в любом интерьере уместны подобные цвет и форма.
Коллекцию оживляют декоративные отражатели: чёрный и белый, золото и хром.
Накладные светильники JAZZWAY изготовлены из алюминия.
Легко монтируются на ровную потолочную поверхность. Монтажная планка входит в комплект.
- Рекомендуемые источники света: PLED DIM GU10 JAZZWAY, PLED-SP GU10 JAZZWAY
- Максимальная мощность используемых ламп: 50 Вт
- Угол светораспределения: 90°
- Входное напряжение: 230 В
- Гарантийный срок: 2 года
Характеристики светильников PDL-R
|
Код РС |
Код для заказа
|
Штрих-код |
Артикул |
Цвет Корпуса/ рефлектора |
Размеры øA×B, мм |
Вес, кг |
Упак. шт. |
|
1365743 |
5031401 |
4895205031401 |
PDL-R 14080 GU10 BL/CH 230V IP20 |
черный / хром |
Ø80х140 |
0,23 |
1/20 |
|
1365744 |
5031364 |
4895205031364 |
PDL-R 14080 GU10 BL/GL 230V IP20 |
|
Ø80х140 |
0,23 |
1/20 |
|
1365745 |
5031425 |
4895205031425 |
PDL-R 14080 GU10 BL/WH 230V IP20 |
черный / белый |
Ø80х140 |
0,23 |
1/20 |
|
1365746 |
5031340 |
4895205031340 |
PDL-R 14080 GU10 WH/BL 230V IP20 |
белый / черный |
Ø80х140 |
0,23 |
1/20 |
|
1365747 |
5031388 |
4895205031388 |
PDL-R 14080 GU10 WH/GL 230V IP20 |
белый / золотой |
Ø80х140 |
0,23 |
1/20 |
|
1365748 |
5031326 |
4895205031326 |
PDL-R 14080 GU10 WH/WH 230V IP20 |
белый / белый |
Ø80х140 |
0,23 |
1/20 |
Характеристики светильников PDL-S
|
Код РС |
Код для
заказа
|
Штрих-код |
Артикул |
Цвет Корпуса/ рефлектора |
Размеры A×А×B, мм |
Вес, кг |
Упак. шт. |
|
1365750 |
5031449 |
4895205031449 |
PDL-S 14074 GU10 WH/BL 230V IP20 |
белый / черный |
74х74х140 |
0,28 |
1/20 |
|
1365749 |
5031463 |
4895205031463 |
PDL-S 14074 GU10 BL/WH 230V IP20 |
черный / белый |
74х74х140 |
0,28 |
1/20 |
Ссылка на карточку
Подскажите идею решения следующей задачи : Computer Science
| Amigo |
| ||
11/03/06 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| Amigo |
| ||
11/03/06 |
| ||
| |||
| juna |
| |||
07/03/06 |
| |||
| ||||
| Amigo |
| ||
11/03/06 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| Amigo |
| ||
11/03/06 |
| ||
| |||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| juna |
| |||
07/03/06 |
| |||
| ||||
| Amigo |
| ||
11/03/06 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Как определить, подобны ли прямоугольники
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как определить, подобны ли прямоугольники
Примечание: цифра , а не нарисована в масштабе.
Посмотрите на рисунок выше.
Что такое?
Возможные ответы:
Из предоставленной информации определить невозможно.
Правильный ответ:
Объяснение:
По сходству можно составить пропорцию:
Заменить:
Сообщить об ошибке
Два прямоугольника подобны. Один прямоугольник имеет размеры сантиметры и 100 сантиметров; другой имеет размеры 400 сантиметров и сантиметров.
Какое значение делает это утверждение верным?
Возможные ответы:
Невозможно
Правильный ответ:
4
44
Объяснение:
Чтобы многоугольники были похожи, длины сторон должны быть пропорциональны.
Случай 1:
и 100 в первом прямоугольнике соответствуют и 400 во втором соответственно.
Полученная пропорция будет:
Это невозможно, так как длина стороны должна быть положительной.
Случай 2:
и 100 в первом прямоугольнике соответствуют 400 и во втором соответственно.
Правильная формулировка пропорции должна быть:
Перемножить, чтобы найти:
200 см — единственно возможное решение.
Сообщить об ошибке
Какое из следующих условий не является необходимым условием для того, чтобы прямоугольники A и B были похожи?
Возможные ответы:
Все углы равны
Отношение длины к ширине равно
Каждой стороне каждого прямоугольника соответствует сторона другого прямоугольника
Соответствующие стороны A и B имеют одинаковую длину
Правильный ответ:
Соответствующие стороны A и B имеют одинаковую длину
Объяснение:
Равенство всех сторон является условием конгруэнтности, а не сходства. Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сообщить об ошибке
Какое значение делает два прямоугольника похожими?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы два прямоугольника были похожи, их стороны должны быть пропорциональны (соотношение сторон равно). Отношение двух более длинных сторон должно быть равно отношению двух более коротких сторон.
Однако левое соотношение в нашей пропорции уменьшается.
Затем мы можем решить путем перекрестного умножения.
Затем мы решаем делением.
Сообщить об ошибке
Следующие изображения не в масштабе.
Чтобы сделать эти два прямоугольника похожими, какой должна быть ширина прямоугольника справа?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы два прямоугольника были похожи, их стороны должны быть в одинаковом соотношении.
Эту задачу можно решить с помощью соотношений и перекрестного умножения.
Неизвестную ширину правого прямоугольника обозначим через x.
Сообщить об ошибке
Два прямоугольника похожи. Один имеет площадь , а другой – . Если первый имеет базовую длину , какова высота второго прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Цель состоит в том, чтобы найти высоту второго прямоугольника.
Подобные прямоугольники функционируют по принципу пропорциональности, то есть отношения сторон между двумя прямоугольниками будут одинаковыми. Чтобы определить высоту, мы будем использовать эту концепцию отношений путем решения переменных из области.
Во-первых, полезно получить полные размеры для первого прямоугольника.
Известно, что длина его основания равна 5, а площадь равна 20.
Это означает, что первый прямоугольник имеет размеры 5×4.
Теперь мы можем использовать понятие отношений подобия. Длина сторон первого прямоугольника равна 5×4, поэтому стороны второго прямоугольника должны быть пропорциональны сторонам первого.
У нас есть информация для первого прямоугольника, поэтому данные можно подставить.
– коэффициент отношения, который будет использоваться для определения высоты второго прямоугольника. Это можно подставить в формулу площади второго прямоугольника.
Следовательно, высота второго прямоугольника — 10.
Отчет о ошибке
Есть два прямоугольника. У одного периметр , а у второго периметр . Первый прямоугольник имеет высоту . Если два прямоугольника подобны, чему равно основание второго прямоугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Цель этой задачи — выяснить, какая длина основания второго прямоугольника сделает его похожим на первый прямоугольник.
Подобные прямоугольники функционируют на основе пропорциональности, то есть отношения сторон между двумя прямоугольниками будут одинаковыми. Чтобы определить базу, мы будем использовать эту концепцию отношений путем решения переменных из периметра.
Сначала необходимо рассчитать все размеры первого прямоугольника.
Это можно сделать с помощью уравнения периметра:
Это означает, что размеры первого прямоугольника равны 10×5. Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
— коэффициент отношения, который мы будем использовать для определения основания второго прямоугольника.
Это потребует пересмотра уравнения периметра для второго прямоугольника.
Сообщить об ошибке. Если две плитки подобны, какова будет длина большой плитки, учитывая информацию на рисунке ниже?
Возможные ответы:
Правильный ответ:
Объяснение:
Два прямоугольника подобны, если их длина и ширина образуют одинаковое отношение. Маленькая плитка имеет ширину и ширину , что дает нам следующее соотношение:
Поскольку длина подобных треугольников в два раза больше их соответствующей ширины, длину большой плитки можно определить как таковую:
Сообщить об ошибке
Эти прямоугольники похожи?
Возможные ответы:
Да — Масштабная коэффициент
Да — Масштабной коэффициент
Да — Масштабная коэффициент 2
NO
Правильный ответ:
NO
4 . Объяснение:
Объяснение:
Чтобы определить, подобны ли эти прямоугольники, задайте пропорцию:
Эта пропорция сравнивает отношение длинных сторон в каждом прямоугольнике с отношением коротких сторон в каждом прямоугольнике. Если они одинаковы, перекрестное умножение даст истинное утверждение, и прямоугольники подобны:
Эти прямоугольники не похожи.
Сообщить об ошибке
Эти прямоугольники похожи?
Возможные ответы:
№
Да — Шкал Фактор 3
Да — Масштабная коэффициент 2.5
Да — Шкал
Правильный ответ:
Да — шкале.
Объяснение:
Чтобы определить, подобны ли прямоугольники, задайте пропорцию, сравнивающую короткие и длинные стороны каждого прямоугольника:
перекрестно умножить
так как это правда, прямоугольники подобны.
Чтобы найти масштабный коэффициент, разделите 25 на 10 или 7,5 на 3. В любом случае вы получите 2,5.
В любом случае вы получите 2,5.
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Подобные многоугольники, прямоугольники, четырехугольники и многое другое!
Содержание 1. Введение 2. Похожие полигоны 3. Подобные четырехугольники 4. Подобные прямоугольники 5. Резюме 6. Часто задаваемые вопросы
03 ноября 2020 г.
Время чтения: 5 минут
Введение Геометрия позвоночника. Одной из наиболее часто встречающихся форм в геометрии являются многоугольники. Греческое слово «многоугольник» состоит из Poly , означающего «много», и gon , означающего «угол».
Одной из наиболее часто встречающихся форм в геометрии являются многоугольники. Греческое слово «многоугольник» состоит из Poly , означающего «много», и gon , означающего «угол».
Многоугольники — это двумерные фигуры, состоящие из прямых линий. Говорят, что они имеют «замкнутую форму», поскольку все линии соединены. В этой статье мы обсудим понятие сходства в полигонах.
Похожие полигоны — PDF Если вы когда-нибудь захотите прочитать его столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.
Похожие полигоны Во-первых, давайте разберемся, что значит «похожие». Две вещи называются подобными, когда они оба имеют много одинаковых свойств, но все же могут не быть идентичными. То же самое можно сказать и о полигонах.
Конгруэнтные многоугольники Как вы, возможно, уже знаете, конгруэнтные формы — это фигуры, которые точно совпадают. Конгруэнтные многоугольники имеют одинаковый размер, и они полностью совпадают, так как все соответствующие части конгруэнтны или равны.
Конгруэнтные многоугольники имеют одинаковый размер, и они полностью совпадают, так как все соответствующие части конгруэнтны или равны.
Определение подобных многоугольников С другой стороны, в подобных многоугольниках соответствующие углы конгруэнтны, но соответствующие стороны пропорциональны. Таким образом, подобные многоугольники имеют одинаковую форму, но разные размеры. В подобных полигонах должны быть определенные одинаковые соотношения.
Свойства подобных многоугольников Есть два важных свойства подобных многоугольников:
- Соответствующие углы равны/конгруэнтны. (Внутренний и внешний углы одинаковы)
- Соотношение соответствующих сторон одинаково для всех сторон. Следовательно, периметры разные.
На изображении выше показаны два похожих многоугольника (треугольника), ABC и A’B’C’. Мы видим, что соответствующие углы равны.
\[ Соответствующие стороны имеют одинаковые соотношения.
\[\frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}\]
Подобные четырехугольники Четырехугольники – это многоугольники, имеющие четыре стороны. Сумма внутренних углов четырехугольника равна 360 градусов. Два четырехугольника являются подобными четырехугольниками, когда три соответствующих угла одинаковы (четвертые углы автоматически становятся равными, так как сумма внутренних углов составляет 360 градусов), и две смежные стороны имеют равные отношения.
Все ли квадраты одинаковы? Обсудим подобие квадратов. Согласно подобию четырехугольников, соответствующие углы подобных четырехугольников должны быть равны. Мы знаем, что в квадрате все углы равны 90 градусов, поэтому все соответствующие углы любых двух квадратов будут одинаковыми.
Все стороны квадрата равны. Если, скажем, у квадрата1 длина стороны равна «а», а у квадрата2 длина стороны равна «b», то все отношения соответствующих сторон будут одинаковыми и эквивалентны a/b.
Следовательно, все квадраты подобны квадратам.
Все ли ромбы одинаковы? У ромба все стороны равны. Итак, как и квадраты, ромбы удовлетворяют условию равенства соответствующих сторон.
В ромбе противоположные стороны параллельны, а значит и противоположные углы равны. Но значение этих углов может быть любым. Итак, очень может случиться так, что два ромба имеют разные углы. Следовательно, не все ромбы подобны.
Подобные прямоугольники Два прямоугольника подобны, если соответствующие смежные стороны имеют одинаковое отношение. Нам не нужно проверять углы, так как все углы в прямоугольнике равны 90 градусам.
На изображении выше отношения смежной стороны равны . Следовательно, это подобные прямоугольники.
Все ли прямоугольники подобны? Нет, все прямоугольники не являются подобными прямоугольниками. Соотношение соответствующих смежных сторон может быть различным. Например, возьмем прямоугольник 1 на 2 и возьмем другой прямоугольник размерами 1 на 4. Здесь соотношения не будут равными.
Например, возьмем прямоугольник 1 на 2 и возьмем другой прямоугольник размерами 1 на 4. Здесь соотношения не будут равными.
\[\frac{1}{1}\ne\frac{4}{2}\]
Конгруэнтные прямоугольники Два прямоугольника называются конгруэнтными прямоугольниками, если соответствующие смежные стороны равны. Это значит, что они должны быть одного размера. Площадь и периметр равных прямоугольников также будут одинаковыми.
Резюме Подобие и конгруэнтность — некоторые важные понятия геометрии. Твердое понимание этих тем помогает в создании хорошей основы в геометрии. В этой статье обсуждались концепции сходства многоугольников с учетом некоторых конкретных случаев подобных четырехугольников, таких как похожие квадраты, подобные прямоугольники и подобные ромбы.
Часто задаваемые вопросы (FAQ) Что такое похожие полигоны?
Два многоугольника подобны, если соответствующие углы равны/конгруэнтны, а соответствующие стороны находятся в одинаковой пропорции.

 Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.
Сходство фокусируется на соотношении между прямоугольниками, а не на эквивалентности всех сторон. Что касается утверждения о равных углах, все прямоугольники, независимо от сходства или конгруэнтности, имеют четыре угла по 90 градусов.


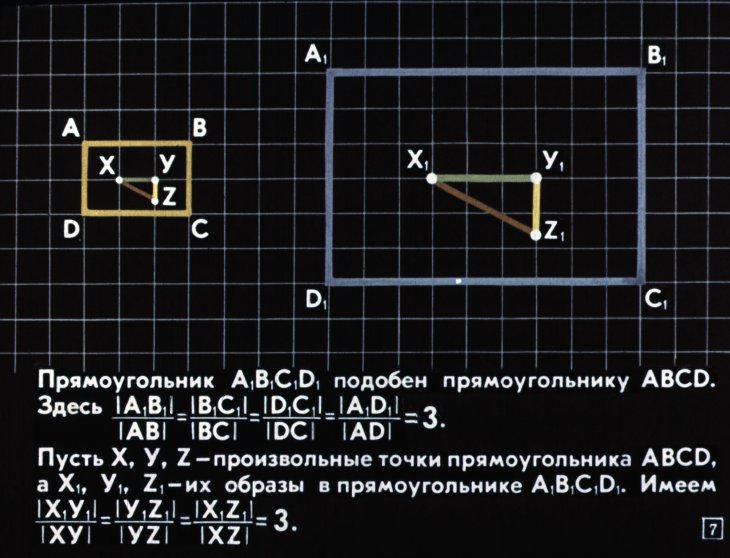 Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций.
Мы будем использовать эту информацию для отношений, чтобы вычислить размеры, которые дали бы второй прямоугольник, похожий из-за пропорций. Объяснение:
Объяснение: В любом случае вы получите 2,5.
В любом случае вы получите 2,5. Одной из наиболее часто встречающихся форм в геометрии являются многоугольники. Греческое слово «многоугольник» состоит из Poly , означающего «много», и gon , означающего «угол».
Одной из наиболее часто встречающихся форм в геометрии являются многоугольники. Греческое слово «многоугольник» состоит из Poly , означающего «много», и gon , означающего «угол». Конгруэнтные многоугольники имеют одинаковый размер, и они полностью совпадают, так как все соответствующие части конгруэнтны или равны.
Конгруэнтные многоугольники имеют одинаковый размер, и они полностью совпадают, так как все соответствующие части конгруэнтны или равны.
Соответствующие стороны имеют одинаковые соотношения.
\[\frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}\]
Подобные четырехугольники
Четырехугольники – это многоугольники, имеющие четыре стороны. Сумма внутренних углов четырехугольника равна 360 градусов. Два четырехугольника являются подобными четырехугольниками, когда три соответствующих угла одинаковы (четвертые углы автоматически становятся равными, так как сумма внутренних углов составляет 360 градусов), и две смежные стороны имеют равные отношения.
Все ли квадраты одинаковы?Обсудим подобие квадратов. Согласно подобию четырехугольников, соответствующие углы подобных четырехугольников должны быть равны. Мы знаем, что в квадрате все углы равны 90 градусов, поэтому все соответствующие углы любых двух квадратов будут одинаковыми.
Все стороны квадрата равны. Если, скажем, у квадрата1 длина стороны равна «а», а у квадрата2 длина стороны равна «b», то все отношения соответствующих сторон будут одинаковыми и эквивалентны a/b.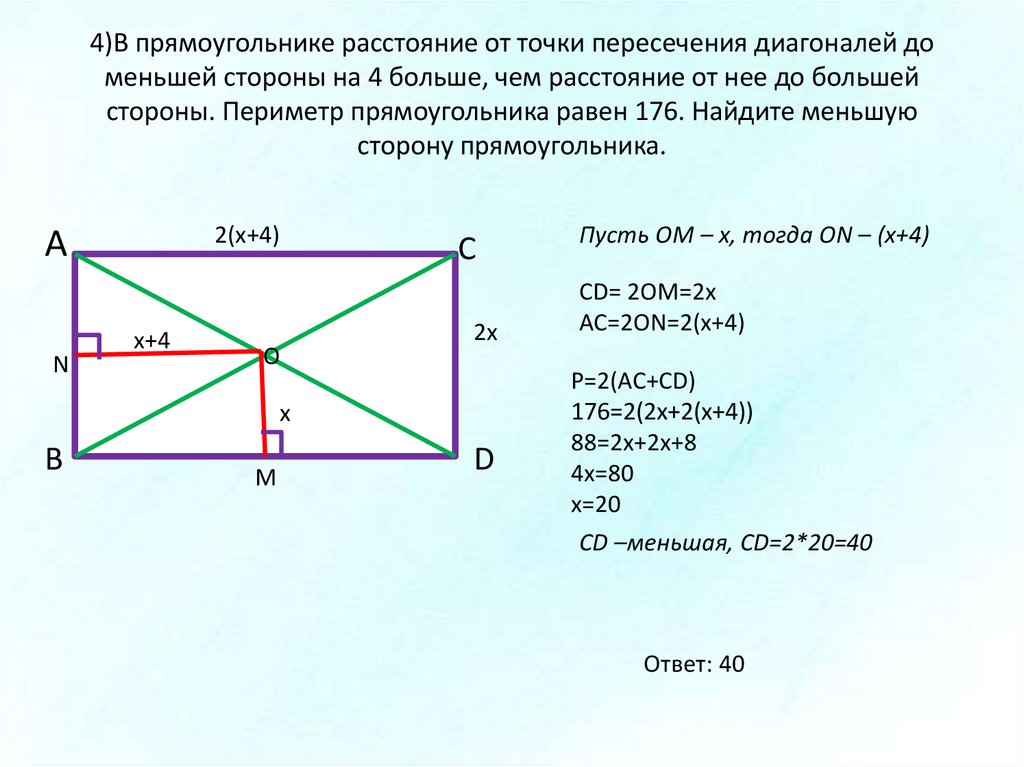
Следовательно, все квадраты подобны квадратам.
Все ли ромбы одинаковы?У ромба все стороны равны. Итак, как и квадраты, ромбы удовлетворяют условию равенства соответствующих сторон.
В ромбе противоположные стороны параллельны, а значит и противоположные углы равны. Но значение этих углов может быть любым. Итак, очень может случиться так, что два ромба имеют разные углы. Следовательно, не все ромбы подобны.
Подобные прямоугольники
Два прямоугольника подобны, если соответствующие смежные стороны имеют одинаковое отношение. Нам не нужно проверять углы, так как все углы в прямоугольнике равны 90 градусам.
На изображении выше отношения смежной стороны равны . Следовательно, это подобные прямоугольники.
Все ли прямоугольники подобны? Нет, все прямоугольники не являются подобными прямоугольниками. Соотношение соответствующих смежных сторон может быть различным. Например, возьмем прямоугольник 1 на 2 и возьмем другой прямоугольник размерами 1 на 4. Здесь соотношения не будут равными.
Например, возьмем прямоугольник 1 на 2 и возьмем другой прямоугольник размерами 1 на 4. Здесь соотношения не будут равными.
\[\frac{1}{1}\ne\frac{4}{2}\]
Конгруэнтные прямоугольникиДва прямоугольника называются конгруэнтными прямоугольниками, если соответствующие смежные стороны равны. Это значит, что они должны быть одного размера. Площадь и периметр равных прямоугольников также будут одинаковыми.
Резюме
Подобие и конгруэнтность — некоторые важные понятия геометрии. Твердое понимание этих тем помогает в создании хорошей основы в геометрии. В этой статье обсуждались концепции сходства многоугольников с учетом некоторых конкретных случаев подобных четырехугольников, таких как похожие квадраты, подобные прямоугольники и подобные ромбы.
Часто задаваемые вопросы (FAQ)
Что такое похожие полигоны?
Два многоугольника подобны, если соответствующие углы равны/конгруэнтны, а соответствующие стороны находятся в одинаковой пропорции.


 ,
,
 03.2006, 16:43
03.2006, 16:43  е PiPj= при ij.
е PiPj= при ij.  03.2006, 16:57
03.2006, 16:57  Если и существует, то вычислительные затраты не будут стоить результата. Но есть полезные эвристики подобия, которые можно использовать:
Если и существует, то вычислительные затраты не будут стоить результата. Но есть полезные эвристики подобия, которые можно использовать:  03.2006, 00:59
03.2006, 00:59  Введём в расмотрение функционал S=S(t1,t2,..,tn) ставящий в
Введём в расмотрение функционал S=S(t1,t2,..,tn) ставящий в  .,tn)<=h<4 такое , что для данного набора по этому числу
.,tn)<=h<4 такое , что для данного набора по этому числу  03.2006, 09:51
03.2006, 09:51  А, кстати, каков порядок их количества?
А, кстати, каков порядок их количества? А именно, перебрать все углы, образованные движением «вниз-влево». В каждый такой угол пытаемся пристроить новый прямоугольник, если он влезает.
А именно, перебрать все углы, образованные движением «вниз-влево». В каждый такой угол пытаемся пристроить новый прямоугольник, если он влезает.
 Дело в том , что не давно
Дело в том , что не давно  Естественно возникает вопрос:»Как укомплектовать заказы так и
Естественно возникает вопрос:»Как укомплектовать заказы так и  По этому я и решил обратится за помошью на Ваш форум.
По этому я и решил обратится за помошью на Ваш форум. 03.2006, 17:46
03.2006, 17:46  03.2006, 00:40
03.2006, 00:40 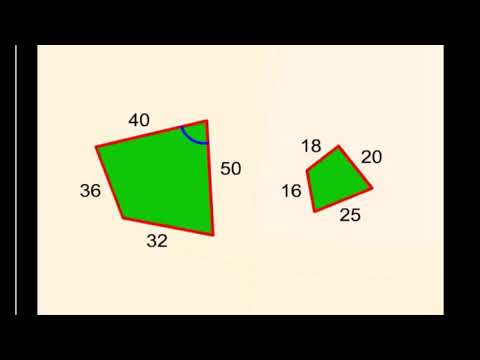 На практике при реализации она решалась симплекс – методом, а небольшие остатки раскидывались по хлыстам эвристическим алгоритмом (нет еще нормальных методов целочисленного программирования, чтобы их запрограммировать под 10000 уравнений и все их хорошо решить). Скажу, что составленная и проданная программа оказалась существенно эффективнее «дяди Васи» и всех других эвристических методов данного предприятия вместе взятых.
На практике при реализации она решалась симплекс – методом, а небольшие остатки раскидывались по хлыстам эвристическим алгоритмом (нет еще нормальных методов целочисленного программирования, чтобы их запрограммировать под 10000 уравнений и все их хорошо решить). Скажу, что составленная и проданная программа оказалась существенно эффективнее «дяди Васи» и всех других эвристических методов данного предприятия вместе взятых. 
 Н. писал(а):
Н. писал(а):