Координаты произведения вектора на число: Умножение вектора на число — урок. Геометрия, 9 класс.

Умножение вектора на число

Умножение вектора на число

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Онлайн калькулятор. Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; . .. ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2.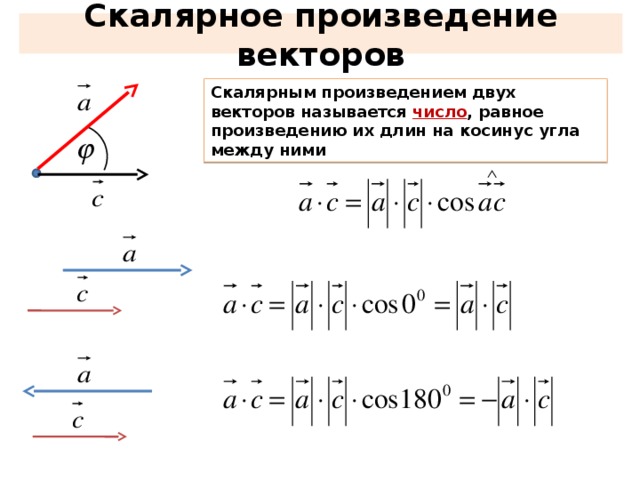 Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Умножение вектора на число.

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Онлайн калькулятор. Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x

; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; … ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

12.

4 Перекрестное произведение

Еще одна полезная операция: по двум векторам найти третий (ненулевой!) вектор перпендикулярно первым двум. Их конечно бесконечное множество таких векторов разной длины. Тем не менее, давайте найдем его. Предположим, что $\ds {\bf A}=\langle a_1,a_2,a_3\rangle$ и $\ds {\bf B}=\langle b_1,b_2,b_3\rangle$. Мы хотим найти вектор $\ds {\bf v} = \langle v_1,v_2,v_3\rangle$ с ${\bf v}\cdot{\bf A}={\bf v}\cdot{\bf B}=0$, или $$\выравнивание{ a_1v_1+a_2v_2+a_3v_3&=0,\кр b_1v_1+b_2v_2+b_3v_3&=0.\cr }$$ Умножьте первое уравнение на $\ds b_3$, а второе на $\ds a_3$ и вычесть, чтобы получить $$\выравнивание{ b_3a_1v_1+b_3a_2v_2+b_3a_3v_3&=0\кр a_3b_1v_1+a_3b_2v_2+a_3b_3v_3&=0\кр (a_1b_3-b_1a_3)v_1 + (a_2b_3-b_2a_3)v_2&=0\cr }$$ Конечно, это уравнение с двумя переменными имеет много решений; а особенно легко увидеть $\ds v_1=a_2b_3-b_2a_3$, $\ds ​​v_2=b_1a_3-a_1b_3$. Замена обратно на любой из исходных уравнения и решение для $\ds v_3$ дает $\ds v_3=a_1b_2-b_1a_2$.

Этот конкретный ответ на проблему, оказывается, имеет некоторые хорошие свойства, и он удостоился имени: перекрестное произведение : $$ {\bf A}\times{\bf B} = \langle a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle. $$ Хотя в этом векторе есть хороший шаблон, он может быть немного сложно запомнить; вот удобная мнемоника. Определитель матрицы два на два равен $$\left|\matrix{a&b\cr c&d\cr}\right|=ad-cb.$$ Это распространяется на определитель матрицы три на три: $$\выравнивание{ \left|\matrix{x&y&z\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\right|&=x\left|\matrix{a_2&a_3\cr b_2&b_3\cr}\right|-y\left|\matrix{a_1&a_3\cr b_1&b_3\cr}\right|+z\left|\matrix{a_1&a_2\cr b_1&b_2\cr}\право|\cr &=x(a_2b_3-b_2a_3)-y(a_1b_3-b_1a_3)+z(a_1b_2-b_1a_2)\cr &=x(a_2b_3-b_2a_3)+y(b_1a_3-a_1b_3)+z(a_1b_2-b_1a_2).\cr} $$ Каждая из матриц два на два формируется удалением верхней строки и один столбец матрицы три на три; вычитание середины термин также необходимо запомнить. Здесь не место превозносить использование определителя; достаточно сказать, что детерминанты необычайно полезно и важно.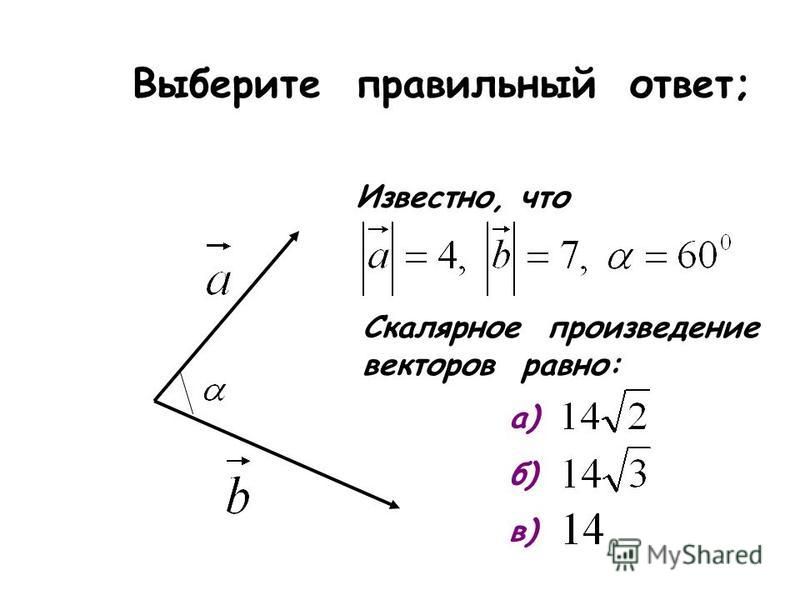

Здесь мы хотим использовать его просто как мнемонический прием. Вы могли заметить, что три выражения в круглые скобки в последней строке — это в точности три координаты перекрестный продукт; замена $x$, $y$, $z$ на $\bf i$, $\bf j$, $\bf k$ дает нам $$\выравнивание{ \left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\право| &=(a_2b_3-b_2a_3){\bf i}-(a_1b_3-b_1a_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=(a_2b_3-b_2a_3){\bf i}+(b_1a_3-a_1b_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=\лангл a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle\cr &={\bf A}\times{\bf B}.\cr} $$

Пример 12.4.1 Предположим, что ${\bf A}=\langle 1,2,3\rangle$, ${\bf B}=\langle 4,5,6\угол$. затем $$\выравнивание{ {\bf A}\times{\bf B}&=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr 1&2&3\кр 4&5&6\cr}\право|\cr &=(2\cdot 6-5\cdot 3){\bf i}+(4\cdot 3-1\cdot 6){\bf j}+ (1\cdot 5-4\cdot 2){\bf k}\cr &=-3{\bf i}+6{\bf j}-3{\bf k}\cr &=\langle -3, 6, -3\rangle\cr }$$ Немного потренировавшись, вы обнаружите, что избавляться от промежуточные шаги, переходя непосредственно от матрицы $3\times3$ к обычная векторная форма. 2\theta\cr |{\bf A}\times{\bf B}|&=|{\bf A}||{\bf B}|\sin\theta\cr }$$ Таким образом, величина ${\bf A}\times{\bf B}$ очень похожа на точку товар. В частности, обратите внимание, что если $\bf A$ параллелен $\bf B$, угол между ними равен нулю, поэтому $\sin\theta=0$, поэтому $|{\bf A}\times{\bf B}|=0$, и аналогично, если они антипараллельны, $\sin\theta=0$ и $|{\bf A}\times{\bf B}|=0$. Наоборот, если $|{\bf A}\times{\bf B}|=0$ и $|{\bf A}|$ и $|{\bf B}|$ не равны нулю, должно быть так, что $\sin\theta=0$, поэтому $\bf A$ параллелен или антипараллелен $\bf B$.

Вот любопытный факт по этому поводу количество, которое впоследствии оказывается весьма полезным: Даны два векторы, мы можем сложить их хвост к хвосту и сформировать параллелограмм, как на рисунке 12.4.1. высота параллелограмма $h$ равна $|{\bf A}|\sin\theta$, а основание равно $|{\bf B}|$, поэтому площадь параллелограмм $|{\bf A}||{\bf B}|\sin\theta$, в точности равно величине $|{\bf A}\times{\bf B}|$.

Рисунок 12. 4.1. Параллелограмм.

А как насчет направления перекрестного произведения? Примечательно, что существует простое правило, описывающее направление. Давайте посмотрим на простой пример: пусть ${\bf A}=\langle a,0,0\rangle$, ${\bf B}=\langle б, в, 0\угол$. Если векторы поставить хвостами в начале координат, $\bf A$ лежит вдоль оси $x$, а $\bf B$ лежит в плоскости $x$-$y$, поэтому мы знаем, что перекрестный продукт будет указывать либо вверх, либо вниз. Крест продукт $$\выравнивание{ {\bf A}\times {\bf B}=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а&0&0\кр b&c&0\cr}\right| &=\лангл 0,0,ac\угол.\cr} $$ Как и было предсказано, это вектор, направленный вверх или вниз, в зависимости от знак $ac$. Предположим, что $a>0$, поэтому знак зависит только от $c$: если $c>0$, $ac>0$ и вектор направлен вверх; если $c0$, то вектор указывает вниз, а если $a0$ и $c>0$ или $a

Хотя с вычислительной точки зрения довольно сложно увидеть, как это работает для любых двух начальных векторов, правило, по сути, такой же. Расположите $\bf A$ и $\bf B$ хвост к хвосту. Плоскость, в которой $\bf A$ и $\bf B$ можно рассматривать с двух сторон; посмотреть на это со стороны для которого $\bf A$ должен вращаться против часовой стрелки, чтобы достичь $\bf B$; тогда вектор ${\bf A}\times{\bf B}$ указывает на вас.

Это правило обычно называют правило правой руки . Представьте, что вы помещаете пятку правой руки в точку, где находятся решки. соединены так, чтобы ваши слегка согнутые пальцы указывали направление вращение из $\bf A$ в $\bf B$. Затем ваш большой палец указывает на направление векторного произведения ${\bf A}\times{\bf B}$.

Одним из непосредственных следствий этих фактов является то, что ${\bf A}\times{\bf B}\not={\bf B}\times{\bf A}$, потому что два перекрестные произведения указывают в противоположном направлении. С другой стороны, поскольку $$ |{\bf A}\times{\bf B}|=|{\bf A}||{\bf B}|\sin\theta =|{\bf B}||{\bf A}|\sin\theta=|{\bf B}\times{\bf A}|, $$ длины двух перекрестных произведений равны, поэтому мы знаем, что ${\bf A}\times{\bf B}=-({\bf B}\times{\bf A})$.

Перекрестное произведение имеет некоторые знакомые свойства, которые будут пригодится позже, поэтому мы перечислим их здесь. Как и в случае скалярного произведения, они могут быть доказано выполнением соответствующих вычислений по координатам, после чего мы можем иногда избежать таких вычислений, используя характеристики.

Теорема 12.4.2 Если ${\bf u}$, ${\bf v}$ и ${\bf w}$ — векторы, а $a$ — вещественное число, затем

1. ${\bf u}\times({\bf v}+{\bf w}) = {\bf u}\times{\bf v}+{\bf u}\times{\bf w}$

2. $({\bf v}+{\bf w})\times{\bf u} = {\bf v}\times{\bf u}+{\bf w}\times{\bf u}$

3. $(a{\bf u})\times{\bf v}=a({\bf u}\times{\bf v}) = {\ bf и} \ раз (a {\ bf v}) $

4. ${\bf u}\cdot({\bf v}\times{\bf w}) = ({\bf u}\times{\bf v})\cdot{\bf w}$

5. ${\bf u}\times({\bf v}\times{\bf w}) = ({\ bf u} \ cdot {\ bf w}) {\ bf v} — ({\ bf u} \ cdot {\ bf v}) {\ bf w} $ $\qed$

Вы можете использовать Sage для вычисления перекрестных произведений.

Пример 12.4.1 Найдите векторное произведение $\langle 1,1,1\rangle$ и $\лэнгл 1,2,3\рангл$. (отвечать)

Пример 12.4.2 Найдите векторное произведение $\langle 1,0,2\rangle$ и $\лангле -1,-2,4\рангл$. (отвечать)

Пример 12.4.3 Найдите векторное произведение $\langle -2,1,3\rangle$ и $\лэнгл 5,2,-1\рангл$. (отвечать)

Пример 12.4.4 Найдите векторное произведение $\langle 1,0,0\rangle$ и $\лэнгл 0,0,1\рангл$. (отвечать)

Пример 12.4.5 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/6$, а $|{\bf u}|=2$ и $|{\bf v}|=3$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 12.4.6 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/4$, а $|{\bf u}|=3$ и $|{\bf v}|=7$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 12.4.7 Найдите площадь параллелограмма с вершинами $(0,0)$, $(1,2)$, $(3,7)$ и $(2,5)$. (отвечать)

Пример 12.4.8 Найдите площадь параллелограмма с вершинами $(0,-1)$, $(3,4)$, $(1,6)$ и $(-2,1)$. (отвечать)

Пример 12.4.9 Найдите площадь треугольника с вершинами $(2,0,0)$, $(1,3,4)$, и $(-2,-1,1)$. (отвечать)

Пример 12.4.10 Найдите площадь треугольника с вершинами $(2,-2,1)$, $(-3,2,3)$, и $(3,3,-2)$. (отвечать)

Пример 12.4.11 Найдите и объясните значение $({\bf i} \times {\bf j}) \times {\bf k}$ и $({\bf i} + {\bf j}) \times ({\bf i} — {\bf j})$.

Пример 12.4.12 Докажите, что для всех векторов ${\bf u}$ и ${\bf v}$ $({\bf u}\times{\bf v})\cdot{\bf v}=0$.

Пример 12.4.13 Докажите теорему 12.4.2.

Пример 12.4.14 Определим тройное произведение трех векторов ${\bf x}$, ${\bf y}$ и ${\bf z}$, чтобы быть скаляром ${\bf x} \cdot ({\bf y} \times {\bf z})$. Докажите, что три вектора лежат в одной плоскости тогда и только тогда, когда их тройное произведение равно нулю. Убедитесь, что $\langle 1, 5, -2 \rangle$, $\langle 4, 3, 0 \rangle$ и $\langle 6, 13, -4 \rangle$ копланарный.

геометрия — Скалярное произведение в координатах

Спросил 12 лет, 2 месяца назад

Изменено 2 года, 8 месяцев назад

Просмотрено 14 тысяч раз

$\begingroup$

Скалярное произведение двух векторов на плоскости может быть определено как произведение длин этих векторов и косинус угла между ними.

В декартовых координатах скалярное произведение векторов с координатами $(x_1, y_1)$ и $(x_2, y_2)$ равно $x_1x_2 + y_1y_2$.

Как это доказать?

• геометрия
• линейная алгебра

$\endgroup$

1

$\begingroup$

Я полагаю, вы хотите доказать, что два ваших определения скалярного произведения совпадают. Начнем с определения скалярного произведения как $(\vec{u}, \vec{v}) = |\vec{u}| |\vec{v}| \cos\тета$. Начнем с определения скалярного произведения как $(\vec{u}, \vec{v}) = |\vec{u}| |\vec{v}| \cos \theta$ и докажите, что оно также удовлетворяет условию $(\vec{u}, \vec{v}) = x_1 x_2 + y_1 y_2$.

Сначала можно доказать линейность скалярного произведения: $(\vec{v_1}, \vec{v_2} + \alpha \vec{v_3}) = (\vec{v_1}, \vec{v_2}) + \альфа (\vec{v_1}, \vec{v_3})$. Это верно, потому что $(\vec{v_1}, \vec{v_2})$ равно произведению $|\vec{v_1}|$ и проекции $\vec{v_2}$ на $\vec{v_1 }$. Проекция суммы векторов равна сумме проекций. Следовательно, скалярное произведение линейно.

Пусть $\vec{e_1}$ и $\vec{e_2}$ — векторы с координатами $(1, 0)$ и $(0, 1)$.

После этого, если $\vec{v_1} = x_1 \vec{e_1} + y_1 \vec{e_2}$ и $\vec{v_2} = x_2 \vec{e_2} + y_2 \vec{e_2}$, то по линейность скалярного произведения у нас есть $(\vec{v_1}, \vec{v_2}) = x_1 x_2 (\vec{e_1}, \vec{e_1}) + x_1 y_2 (\vec{e_1}, \vec{e_2 }) + x_2 y_1 (\vec{e_2}, \vec{e_1}) + x_2 y_2 (\vec{e_2}, \vec{e_2})$.