Подобные треугольники определение: Подобные треугольники — урок. Геометрия, 8 класс.

Подобие треугольников — презентация онлайн

Похожие презентации:

Подобие в геометрии. Подобные треугольники

Первый признак подобия треугольников

Подобные треугольники. Подобные фигуры

Подобные треугольники

Открытый банк заданий ОГЭ на подобие треугольников

Подобные треугольники

Подобие фигур. 8 класс

Подобные треугольники

Материалы к урокам геометрии в 8 классе по теме: «Подобие треугольников. Признаки подобия треугольников»

Второй признак подобия треугольников

1. Определение подобных треугольников.

Цель урока:
Ввести определение
подобных треугольников
Доказать теорему об отношение
площадей
подобных
треугольников.
Закрепить полученные знания в
процессе решения задач. Развивать
логическое мышление.

3. Ход урока:

В окружающем нас мире часто встречаются
фигуры, имеющие различные размеры, но
одинаковую форму, например фотографии
одного и того же лица, изготовленные в
различных размерах, футбольный и теннисный
мячи и т. д.
В геометрии фигуры одинаковой формы принято
называть подобными. Подобными являются любые два
круга
два квадрата.
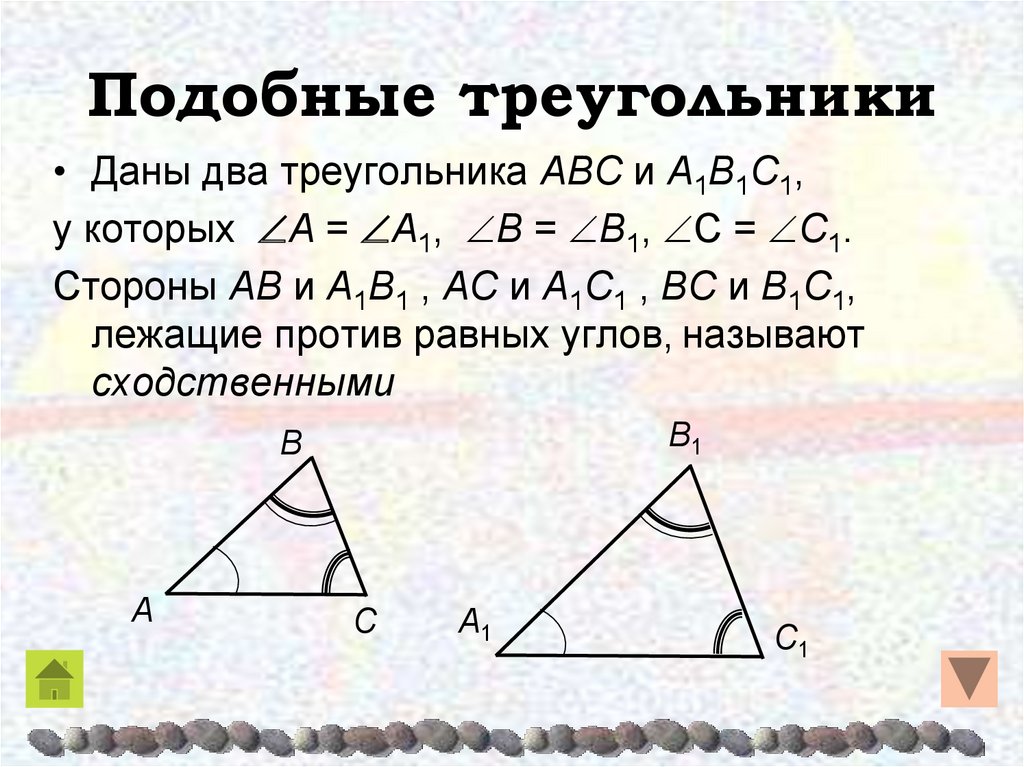
∟А=∟А1, ∟В=∟В1,
Введем В
понятие
∟С=∟С1.
этом подобных треугольников.
случае
стороны такие
АВ и треугольники, у которых углы
Рассмотрим
А1В1,
ВС исоответственно
В1С1, СА и равны углам другого. В
одного
1
С1А1 называются
В
сходственными.
А
С
А1
С1

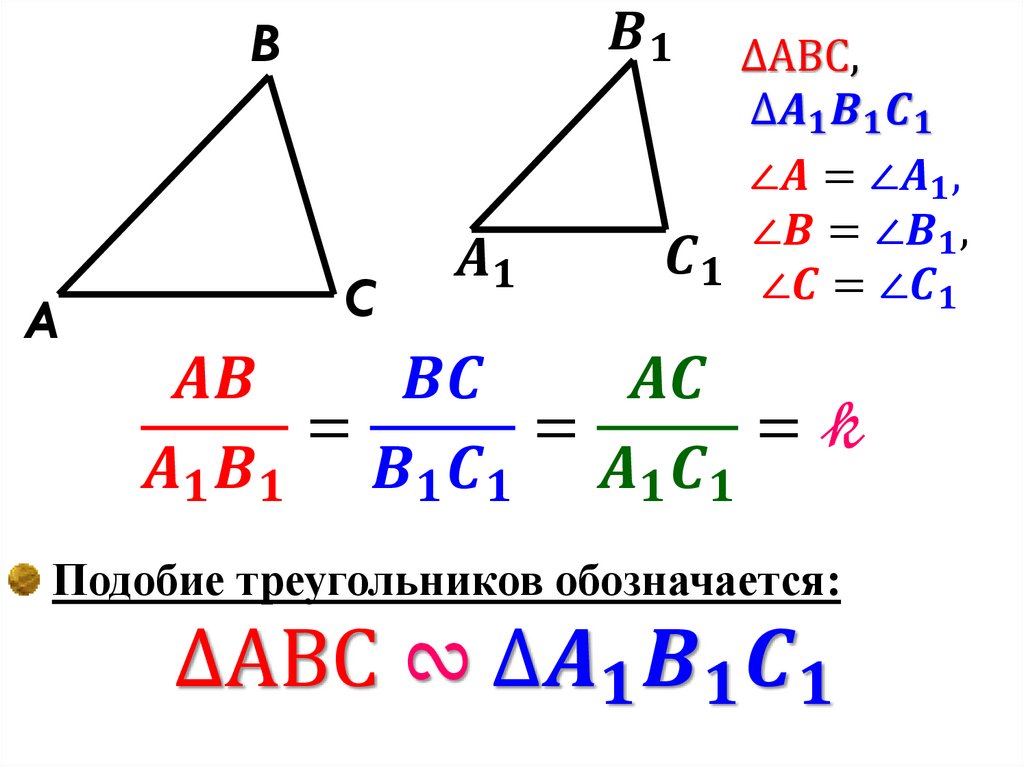
5. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны

сходственным сторонам другого
∆ABC ~ ∆A1B1C1 Если:
1)∟ A= ∟A1 ; ∟B=∟ B1 ; ∟ C= ∟ C1.
2)AB\A1B1=BC\B1C1=CA\C1A1=k, число k,
равное
отношению
сходственных
сторон
треугольников,
называется
коэффициентом
подобия.
В1
В
А
С
А1
С1

6. Задача: №

∟А = 1060, ∟В = 340, ∟Е = 1060, ∟F =
400, АС = 4,4 см, АВ = 5,2 см, ВС = 7,6 см,
DE = 15,6 см, DF = 22,8 см, EF = 13,2 см?
Подобны ли треугольники
АВС и DEF?
D
F
Е
1)∟А = ∟Е = 1060, ∟В = ∟ D =
340, ∟F = ∟C = 400.
2)DE/AB = DF/BC = EF/AC = k, k = 3
В
А
С

7. Отношение площадей подобных треугольников.

AN=BN, CM=5cм, MB=2см. Найдите площадь
треугольника ABC , если площадь
треугольника BMN равна 7см2.
Решение: ∆ АВС и ∆ NBM:
∟В – общий. По теореме об отношении
площадей треугольников, имеющих по
равному углу. S∆ АВС / S∆ NBM =
АВ∙ВС / NB∙BM.
S∆ АВС / 7 = 2x ∙ 7 / x ∙
S∆ АВС = 49 cм2
2.

8. Теорема:

Отношение площадей двух подобных треугольников
равно квадрату коэффициента подобия.
В1
Дано: S- площадь треугольника ABC, S1площадь треугольника A1B1C1.
∆ABC ~∆ A1B1C1, k – коэффициент
подобия.
Доказать: S\S1=k 2
А1
С1
Доказательство: ∟A= ∟A1, S\S1=
(AB∙AC)\(A1B1∙A1C1) (по теореме об
отношении
площадей
треугольников,
имеющих
по
равному
углу).
По
определению подобных треугольников
AB\A1B1=k , AC\A1C1=k , поэтому S\S1 =
(AB∙AC)\(A1B1∙A1C1) =k ∙ k= k 2
В
А
С
Задача
У подобных треугольников
Сходственные
стороны
равны 7 см и 35 см.
Площадь
первого
треугольника равна 37 см 2.
Найдите площадь второго
треугольника.
Т.к. треугольники подобны, то 35/7
= k = 5, по теореме х/37 = k 2 (х –
площадь второго треугольника). Х
= 37 ∙ 25 = 925 см2.
Задача
Площади
подобных
треугольников равны 17
см2 и 68 см2. Сторона
первого
треугольника
равна 8 см. Найдите
сходственную
сторону
второго треугольника.
Т.к. треугольники подобны,
то по теореме 68/17 = k 2 , k
= 2. х / 8 = k , х = 16. ( х –
сторона второго
треугольника)

10. Ответьте на вопросы:

1) Объясните какие фигуры приняты называть
подобными. Приведите примеры подобных
фигур.
2) Какие стороны треугольников называются
сходственными?
3) Объясните, что такое коэффициент подобия.
4) Сформулируйте определение подобных
треугольников.
5) Теорема об отношении площадей подобных
треугольников.

English     Русский Правила

8 класс.

Геометрия. Подобные треугольники. Практические приложения подобия треугольников. — Средняя линия треугольника.

Комментарии преподавателя

Сред­няя линия тре­уголь­ни­ка

По­вто­рим вто­рой при­знак по­до­бия тре­уголь­ни­ков.

Тео­ре­ма 1. Вто­рой при­знак по­до­бия тре­уголь­ни­ков (по двум сто­ро­нам и углу между ними). Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны двум сто­ро­нам дру­го­го тре­уголь­ни­ка и углы между этими сто­ро­на­ми равны, то такие тре­уголь­ни­ки по­доб­ны (см. Рис. 1).

.

Рис. 1

Опре­де­ле­ние. Два тре­уголь­ни­ка на­зы­ва­ют­ся по­доб­ны­ми, ес­ли­их углы по­пар­но равны, а сто­ро­ны, ле­жа­щие на­про­тив со­от­вет­ствен­ных углов, про­пор­ци­о­наль­ны.

.

Тео­ре­ма 2. Свой­ство и при­знак па­рал­лель­но­сти пря­мых. Если пря­мые па­рал­лель­ны, то их со­от­вет­ствен­ные углы равны; если со­от­вет­ствен­ные углы равны, то пря­мые па­рал­лель­ны (см.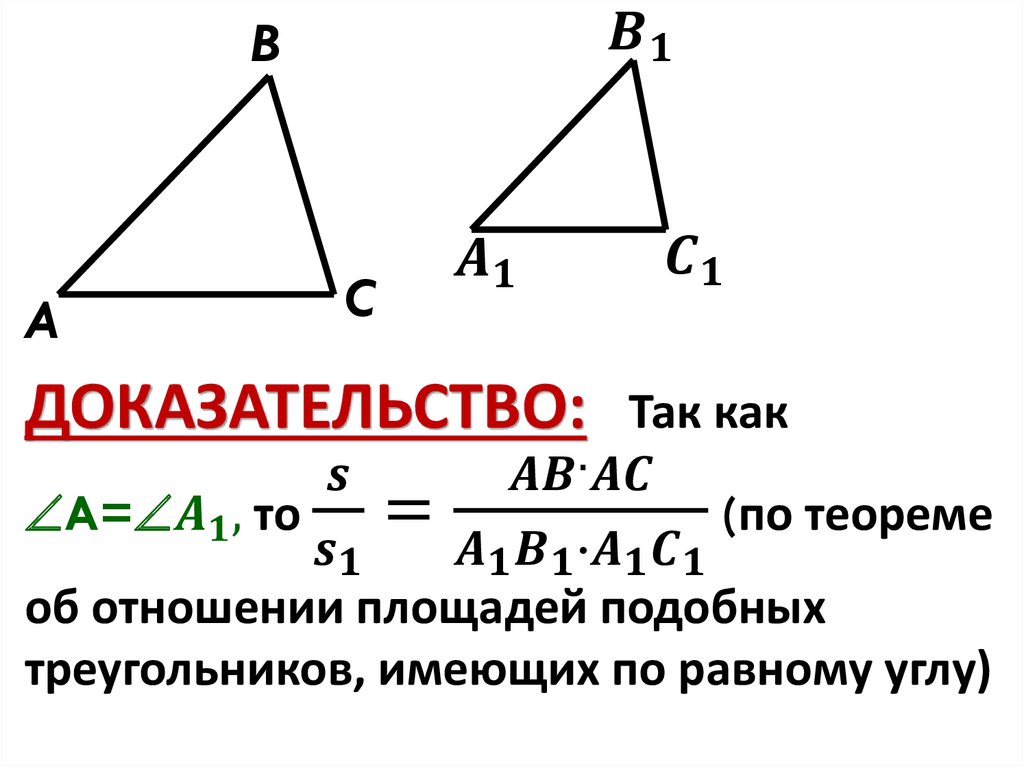 Рис. 2).

.

Рис. 2

Опре­де­ле­ние. Сред­няя линия тре­уголь­ни­ка – это от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны сто­рон тре­уголь­ни­ка. На Рис. 3  сред­няя линия тре­уголь­ни­ка ,  ос­но­ва­ние.

Тео­ре­ма 3. Тео­ре­ма о сред­ней линии тре­уголь­ни­ка. Сред­няя линия тре­уголь­ни­ка па­рал­лель­на ос­но­ва­нию и равна его по­ло­вине (Рис. 3).

.

До­ка­за­тель­ство.

По усло­вию из­вест­но, что .

Рис. 3

Рас­смот­рим  и :

 по вто­ро­му при­зна­ку по­до­бия тре­уголь­ни­ков. Сле­до­ва­тель­но,  как со­от­вет­ствен­ные, а по при­зна­ку па­рал­лель­но­сти пря­мых: . Па­рал­лель­ность сред­ней линии и со­от­вет­ству­ю­ще­го ей ос­но­ва­ния до­ка­за­на.

Кроме того, из по­до­бия тре­уголь­ни­ков  можно вы­пи­сать и от­но­ше­ние их тре­тьих сто­рон . То, что сред­няя линия равна по­ло­вине со­от­вет­ству­ю­ще­го ос­но­ва­ния, до­ка­за­но.

До­ка­за­но.

При­мер 1. В тре­уголь­ни­ке  се­ре­ди­ны сто­рон  . Найти пе­ри­метр  (см. Рис. 4).

Ре­ше­ние.

Рис. 4

Нач­нем с того, что про­ве­рим су­ще­ство­ва­ние ука­зан­но­го в усло­вии тре­уголь­ни­ка , для этого за­пи­шем нера­вен­ство тре­уголь­ни­ка для его наи­боль­шей сто­ро­ны: , нера­вен­ство вы­пол­не­но, сле­до­ва­тель­но, такой тре­уголь­ник су­ще­ству­ет.

Со­еди­ним се­ре­ди­ны сто­рон тре­уголь­ни­ка  и по­лу­чим его сред­ние линии, най­дем их длины по тео­ре­ме о сред­ней линии:

.

Ответ. 10.

Тео­ре­ма 4. Тео­ре­ма о пе­ре­се­че­нии ме­ди­ан тре­уголь­ни­ка. Ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке, ко­то­рой делят друг друга в от­но­ше­нии  счи­тая от вер­ши­ны (см. Рис. 5).

.

До­ка­за­тель­ство. Обо­зна­чим на ри­сун­ке точки  – се­ре­ди­ны сто­рон тре­уголь­ни­ка   со­от­вет­ствен­но.

Рас­смот­рим две ме­ди­а­ны  и , они пе­ре­се­ка­ют­ся в неко­то­рой точке  (см. Рис. 6).

Рис. 5, рис. 6

Сле­ду­ет до­ка­зать, что они пе­ре­се­ка­ют­ся, т.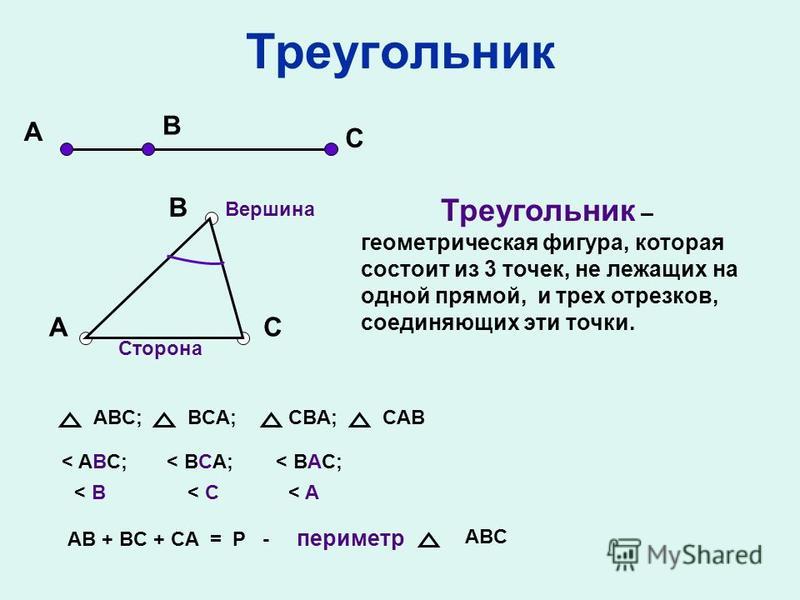 к. воз­мож­но, что ме­ди­а­ны могут быть па­рал­лель­ны. В таком слу­чае для них от­ре­зок  был бы се­ку­щей, а , но эти углы со­став­ля­ют неко­то­рую часть от углов тре­уголь­ни­ка , а сумма его углов равна , зна­чит, такое невоз­мож­но, и ме­ди­а­ны  и  пе­ре­се­ка­ют­ся.

Про­ве­дем от­ре­зок , он со­еди­ня­ет се­ре­ди­ны сто­рон тре­уголь­ни­ка, а сле­до­ва­тель­но, по опре­де­ле­нию яв­ля­ет­ся сред­ней ли­ни­ей, а по тео­ре­ме о сред­ней линии . Эти два па­рал­лель­ных от­рез­ка пе­ре­се­ка­ют­ся се­ку­щи­ми  и , а из этого сле­ду­ет, что  и  как на­крест ле­жа­щие. Из этого можно сде­лать вывод о том, что  по пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков. Ко­эф­фи­ци­ент по­до­бия этих тре­уголь­ни­ков по тео­ре­ме о сред­ней линии , а по опре­де­ле­нию по­доб­ных тре­уголь­ни­ков .

До­ка­за­но, что две ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют друг друга в от­но­ше­нии  2:1, счи­тая от вер­ши­ны, ана­ло­гич­но будем рас­суж­дать и о тре­тьей ме­ди­ане. По­сколь­ку в ка­че­стве пары ме­ди­ан можно вы­брать, на­при­мер, ме­ди­а­ны  и , то и они точ­кой пе­ре­се­че­ния будут рас­се­кать друг друга в от­но­ше­нии 2:1, счи­тая от вер­ши­ны. Од­на­ко не факт, что точки пе­ре­се­че­ния одной пары ме­ди­ан и вто­рой пары ме­ди­ан сов­па­дут. Пред­по­ло­жим, что это не так, и . Тогда  Рас­смот­рим до­пол­ни­тель­ный Рис. 7, на ко­то­ром изоб­ра­зим от­дель­но ме­ди­а­ну .

Рис. 7

По­сколь­ку из­вест­но, что от­ре­зок  и точ­кой , и точ­кой  де­лит­ся в от­но­ше­нии 2:1, счи­тая от вер­ши­ны , то эти точки сов­па­да­ют, т.к. у лю­бо­го от­рез­ка, оче­вид­но, такая точка толь­ко одна, т.е.  и все ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке .

Таким об­ра­зом, имеем, что , а из от­но­ше­ния от­рез­ков пер­вой пары рас­смот­рен­ных ме­ди­ан , из этого сле­ду­ет, что .

До­ка­за­но.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/podobnye-treugolniki/srednyaya-liniya-treugolnika

http://www.youtube.com/watch?v=Rd5j49nvJ6I

http://malay.ucoz.ru/_ld/2/285___14___.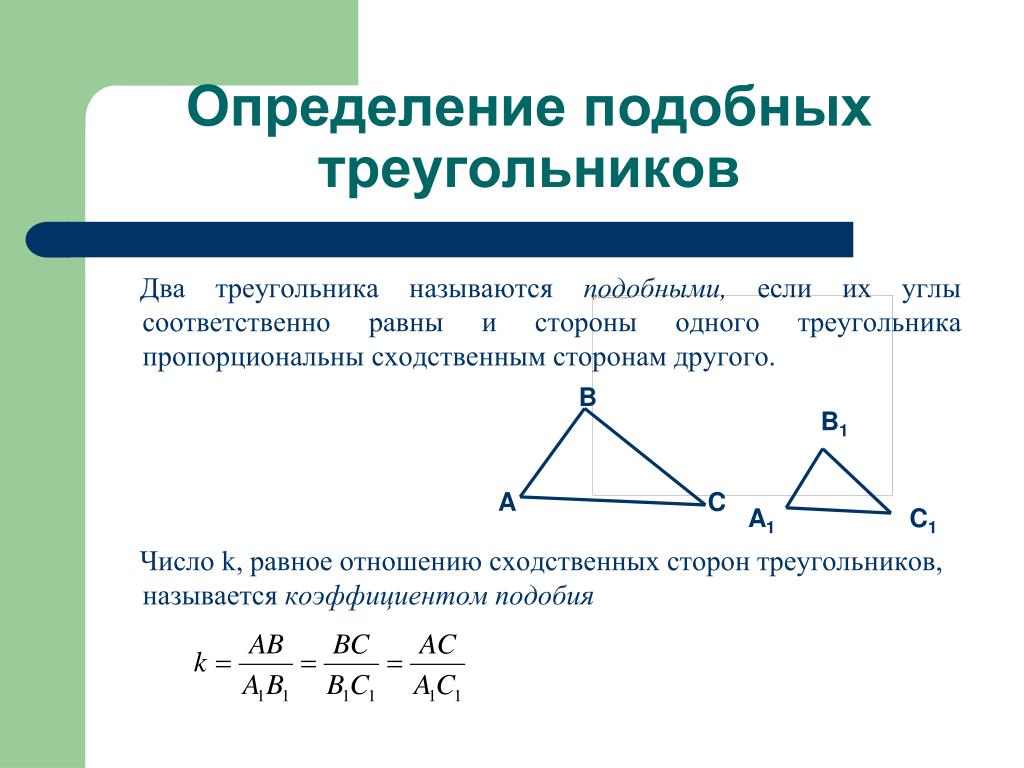 rar

http://ru.convdocs.org/docs/index-7888.html

Средняя линия треугольника

 

Определение, теорема, свойства и примеры.

Термин «сходство» происходит от латинского слова «similis», что означает «подобный, подобный или подобный ». В математике сходство требует, чтобы два объекта имели одинаковую форму, но не обязательно одинаковый размер. сходство не означает то же самое, что и в обычной жизни. Подобные треугольники — это треугольники, имеющие одинаковую форму, но разные длины сторон.

В этой статье по математике мы рассмотрим подобные треугольники: определение, формулы, теоремы, свойства и некоторые решенные примеры.

Подобные треугольники

Подобные треугольники в геометрии — это треугольники, которые имеют одинаковую форму, но могут быть разных размеров. К подобным треугольникам относятся все равносторонние треугольники.

Все эти треугольники одинаковы: равные углы указаны с одинаковым количеством дуг.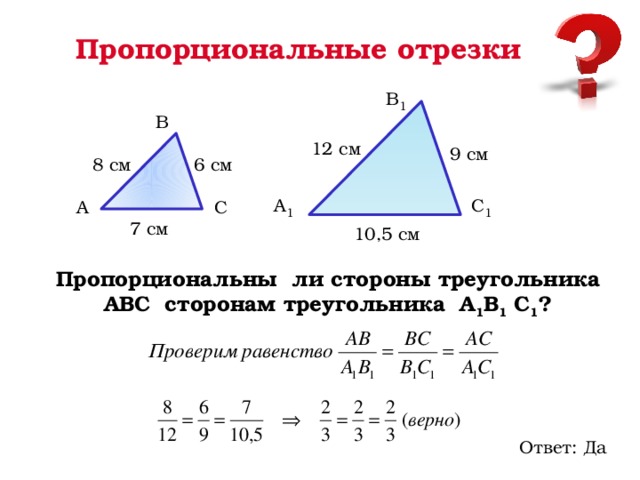 Некоторые из них имеют разные размеры, а некоторые были скручены или перевернуты.

Формулы подобных треугольников

Существуют два требования, которые можно использовать для определения того, является ли данный набор треугольников сравнимым или нет.

В соответствии с этими условиями два треугольника сравнимы, если их соответствующие углы равны или конгруэнтны, или если их соответствующие стороны пропорциональны.

В результате два треугольника ABC и EFG могут быть показаны сравнимыми (\(\left ( \bigtriangleup ABC\sim \bigtriangleup EFG \right )\)) с использованием любой из следующих формул для подобных треугольников,

Формула для Подобных треугольников

\( \угол A =\угол E,\угол B = \угол F \, и \, \угол C = \угол G\)

\( \frac{AB}{EF} = \frac{BC}{FG} = \frac{AC}{EG}\)

Примеры подобных треугольников

Выше приведены два подобных треугольника, ABC и PQR , которые математически представлены символом \( \sim\) .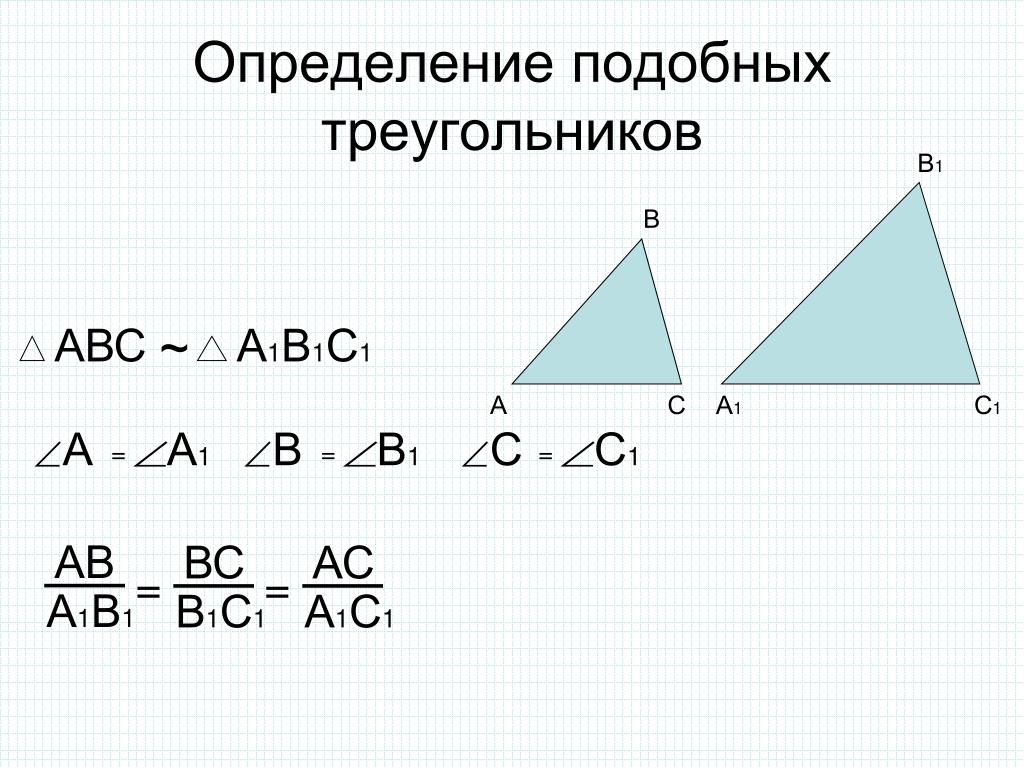

\( \bigtriangleup ABC\sim \bigtriangleup PQR\) используется здесь.

Теорема о подобных треугольниках

Используя теоремы подобия, мы можем определить или доказать, подобны ли два треугольника. Мы используем эти критерии подобия, когда у нас нет длин всех сторон треугольника или длин всех его углов.

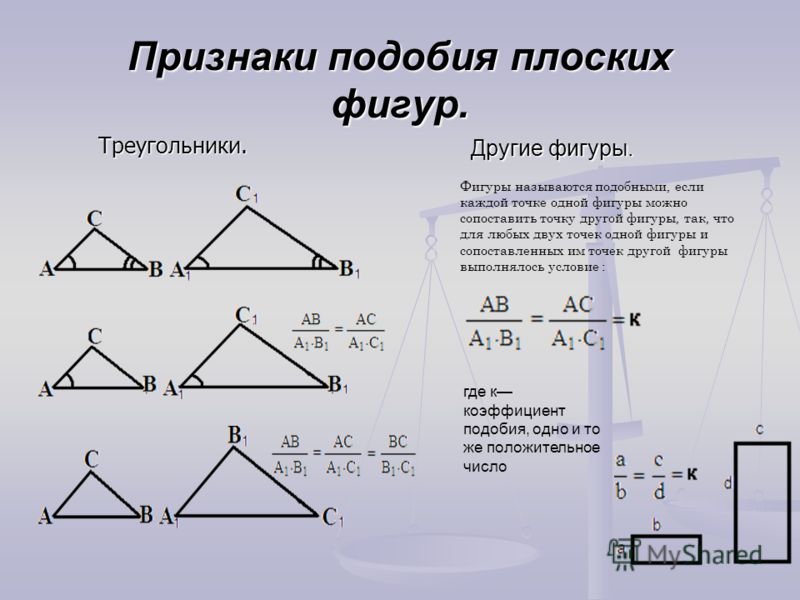
Существует 3 типа правил подобия

• AA (или AAA) или критерий подобия угол-угол
• SAS или критерий подобия сторона-угол-сторона
• SSS или критерий подобия сторона-сторона-сторона

905 ( или AAA) или Критерий подобия углов

Угол-угол (AA) говорит, что два треугольника сравнимы, если они имеют две пары конгруэнтных совпадающих углов. Два треугольника могут в конечном итоге стать более чем похожими; они могут быть даже идентичными. Все, что вам нужно сделать для AA, это сравнить две пары соответствующих углов.

SAS или Критерий сходства стороны-угла-стороны

Вторая теорема требует определенного порядка: сторона, за которой следует прилежащий угол, а затем следующая сторона.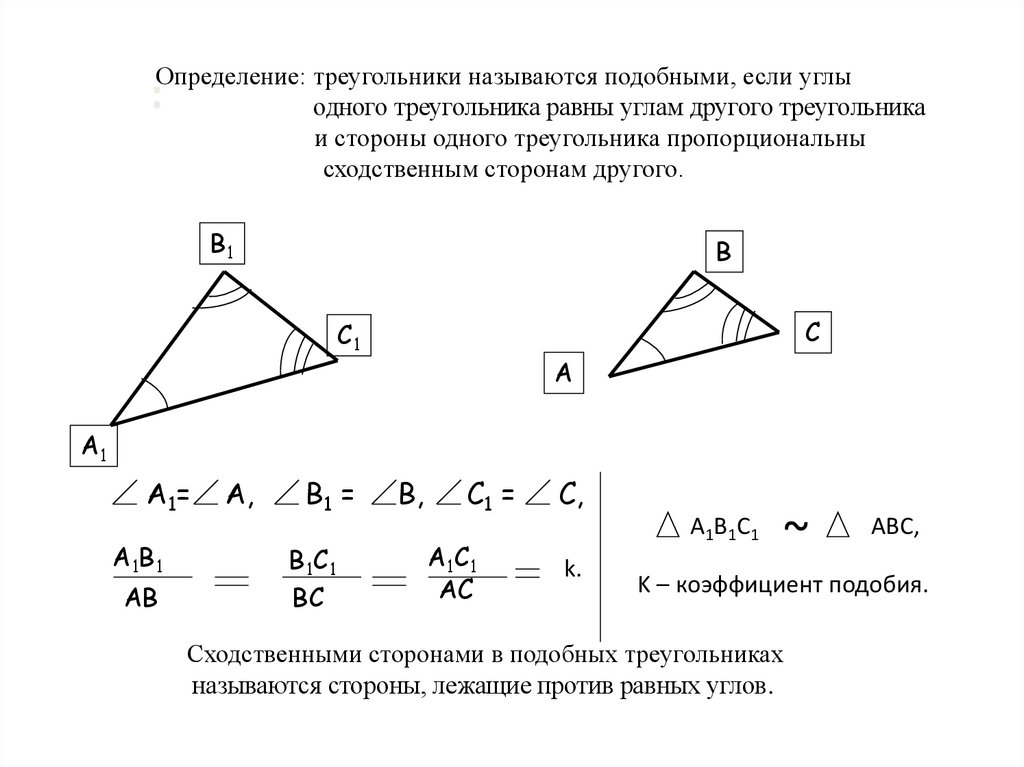 Согласно теореме «сторона-угол-сторона» (SAS), два треугольника сравнимы, если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, а соответствующие углы между ними конгруэнтны.

SSS или Критерий подобия Side-Side-Side

SSS, или Side-Side-Side, является окончательной теоремой. Согласно этой теореме, два треугольника с пропорциональными сторонами подобны. Это может показаться большим скачком, который упускает из виду их углы, но учтите следующее: единственный способ сделать треугольник со сторонами, пропорциональными сторонам другого треугольника, — это скопировать углы.

Свойства подобного треугольника

Свойства подобного треугольника:

• Они имеют похожую форму, но разные размеры.
• Каждая соответствующая пара углов равна.
• Любая пара соответствующих сторон имеет одинаковое отношение.

Шаги по поиску подобных треугольников

Определите длину s по указанным ниже треугольникам.

Шаг :1 Из-за правила RAR треугольники сравнимы.

Шаг : 2 Соотношение длины такое же.

\( \frac{4}{2} =\frac{6}{s}\)

4s = 12

s = 3

Разница между подобным треугольником и конгруэнтным треугольником

Различия между подобным треугольником и конгруэнтным треугольником Треугольники приведены в таблице ниже.

Подобные треугольники	Конгруэнтные треугольники
Подобные треугольники имеют одинаковую форму, но различаются по размеру.	Конгруэнтные треугольники одинаковы как по форме, так и по размеру.
Они обозначены знаком \( \sim \)	Они обозначены знаком \(\cong\)
Все соответствующие стороны имеют одинаковое отношение.	Отношение соответствующих сторон равно постоянному значению
Каждая соответствующая пара углов равна.	Все соответствующие углы равны.

Ключевые моменты, которые следует помнить

Некоторые ключевые моменты приведены ниже:

• Отношение площадей одинаковых треугольников равно квадрату соотношений их соответствующих сторон.
• Символ \( \sim \) используется для обозначения подобных треугольников.
• Все конгруэнтные треугольники подобны, но не все подобные треугольники конгруэнтны.

Примеры решения подобных треугольников

Задача: 1 Определите значение x на диаграмме ниже.

9{\circ}\)

\( \frac{AE}{EC} = \frac{BD}{CD}\)

\(\frac{x}{1.8} = \frac{24+12}{ 12}\)

\(\frac{x}{1.8} = \frac{36}{12}\)

Путем перекрестного умножения получаем,

\(12 x = 36\times 1.8\)

Когда мы разделим обе части, мы получим

\( x = \frac{\left ( 36\times 1,8 \right )}{12}\)

= 5,4

Значение x 5,4 мм

Задача: 2 Ниже показаны два треугольника.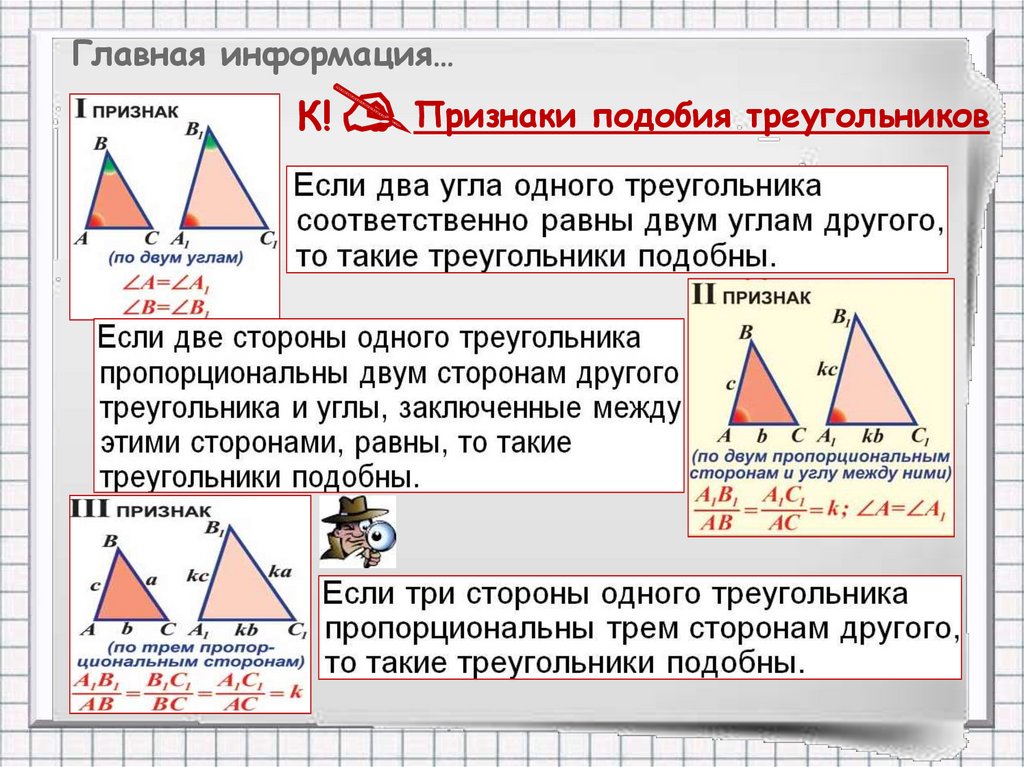 Они похожи?

9{\circ}\)

Согласно правилу АА

Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.

Ответы на часто задаваемые вопросы о подобных треугольниках

В.1 Каковы 3 способа доказать, что треугольники подобны?

Ответ 1 Три способа доказать, что треугольники подобны: Угол — Угол (AA), Сторона — Угол — Сторона (SAS) и Сторона — Сторона — Сторона (SSS),

Q.2 Что такое закон подобных треугольников?

Ответ 2 Если пропорция двух сторон одного треугольника равна пропорции двух сторон другого треугольника, и угол, вписанный между двумя сторонами обоих треугольников, равен, два треугольника говорят, что они похожи.

Q.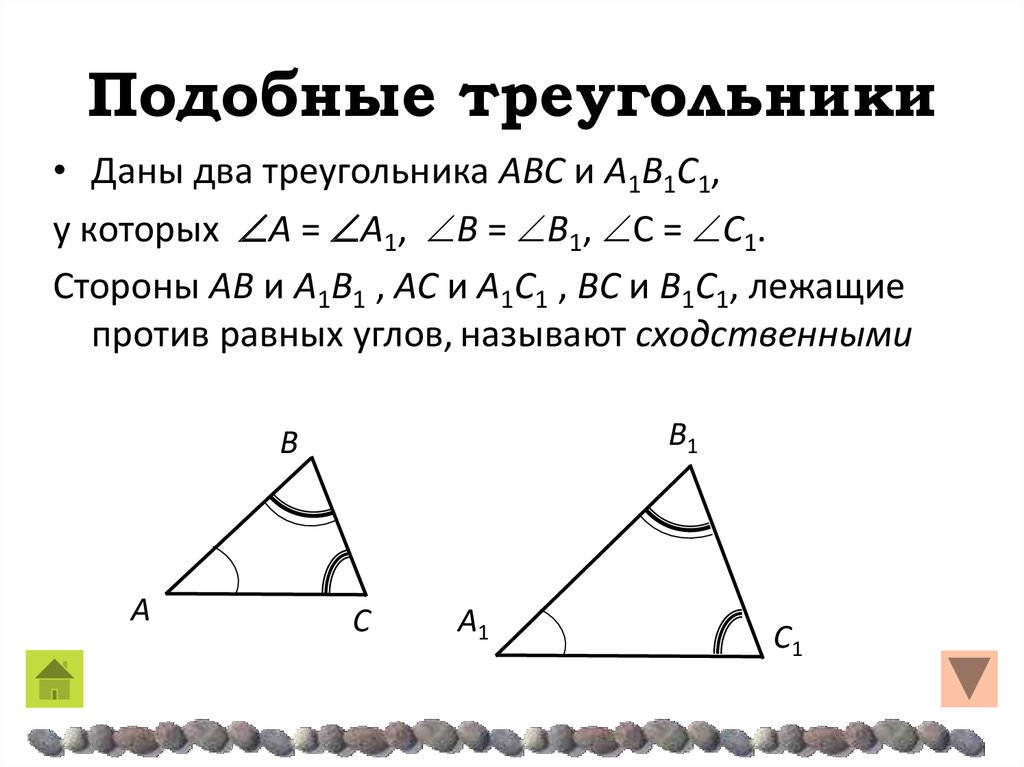 3 Как найти углы подобных треугольников?

Ответ 3 Следуя приведенным ниже шагам, мы найдем углы подобных треугольников. Признать эквивалентные углы в подобных треугольниках.
Найдите недостающие измерения конгруэнтных углов.
Используя тот факт, что сумма всех углов треугольника должна быть равна 180.


Найдите последний недостающий угол в одном из двух треугольников.
Из-за сходства треугольников последний недостающий угол также должен быть равен соответствующему угол. Определите окончательный недостающий угол.

В.4 Все ли подобные треугольники конгруэнтны?

Ответ 4 Да, все подобные треугольники конгруэнтны.

В.5 Как найти длины сторон подобных треугольников?

Ответ 5 Используя приведенные ниже шаги, мы можем найти длины сторон подобных треугольников. Сначала определите, какие стороны соответствуют друг другу.
Затем вычислите отношение совпадающих длин сторон, в котором одна из длин сторон содержит неизвестную, и сравните его с соотношением, найденным в шаге 1.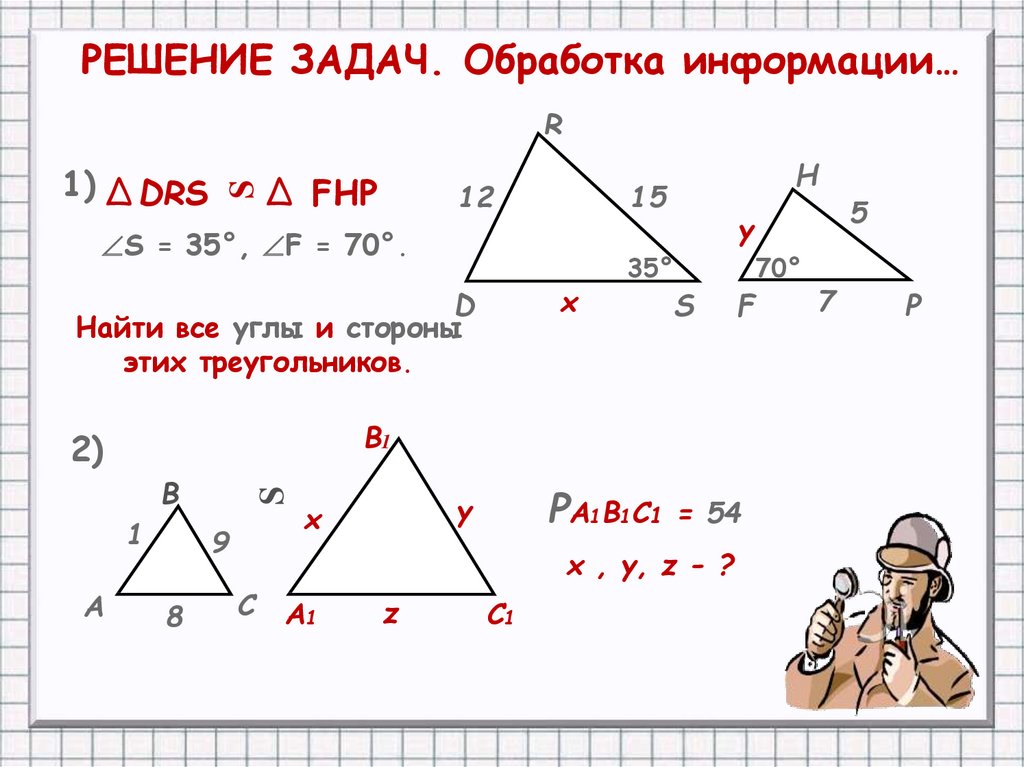
Умножьте крест-накрест, чтобы найти недостающую длину стороны.

В.6 Как найти отношение двух подобных треугольников?

Ответ 6 Мы начнем с вычисления площади двух сравнимых треугольников, а затем разделим их. Сходство двух треугольников затем используется для вычисления отношения их соответствующих сторон.

Скачать публикацию в формате PDF

Читать больше сообщений

Шаги по нахождению периметра полукруга с формулой и примерами0115
Volume of a Frustum: Formula, Method, and Solved Examples
Tan 60 Degrees Value, Formula with Derivation & Periodicity
Pentagonal Prism: Definition, Types, Formula with Examples

Article о похожих+треугольниках от The Free Dictionary

Похожие+треугольники | Статья о подобных+треугольниках от The Free Dictionary

Подобные+треугольники | Статья о подобных+треугольниках от The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

No related posts.