Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Подобные треугольники |
| Признаки подобия треугольников |
| Признаки подобия прямоугольных треугольников |
Подобные треугольники
Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.
Рис.1
Обозначим
a1 , b1 , c1
длины сторон треугольника KLM, расположенные в порядке возрастания.
Обозначим
a2 , b2 , c2
длины сторон треугольника TRP, расположенные в порядке возрастания.
Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2.
Рис.2
На рисунке 2 треугольник KLM обозначается как треугольник A1B1C1, а треугольник TRP обозначается как треугольник A2B2C2.
Определение 1. В треугольниках A1B1C1 и A2B2C2, изображённых на рисунке 2,
- вершины A1 и A2, B1 и B2, C1 и C2 называют сходственными вершинами,
- стороны A1B1 и A2B2, A1C1 и A2C2, B1C1 и B2C2 называют сходственными сторонами,
- углы A1 и A2, B1 и B2, C1 и C2 называют сходственными углами
Определение 2.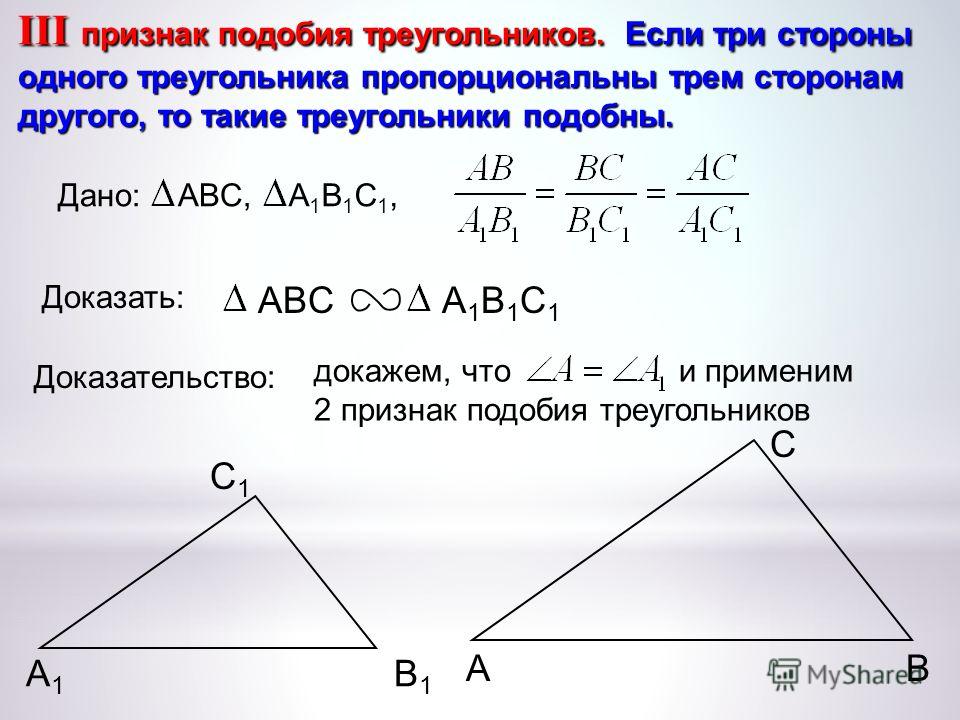 Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Треугольники A1B1C1 и A2B2C2 называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Другими словами, треугольники A1B1C1 и A2B2C2 подобны, если, во-первых,
а, во-вторых, существует положительное число k, такое, что справедливы равенства:
| a1 = k a2 , b1 = k b2 , c1 = k c2 . | (1) |
Определение 3. В случае, когда треугольники A1B1C1 и A2B2C2 подобны, число k, заданное формулами (1), называют коэффициентом подобия треугольников A1B1C1 и A2B2C2 .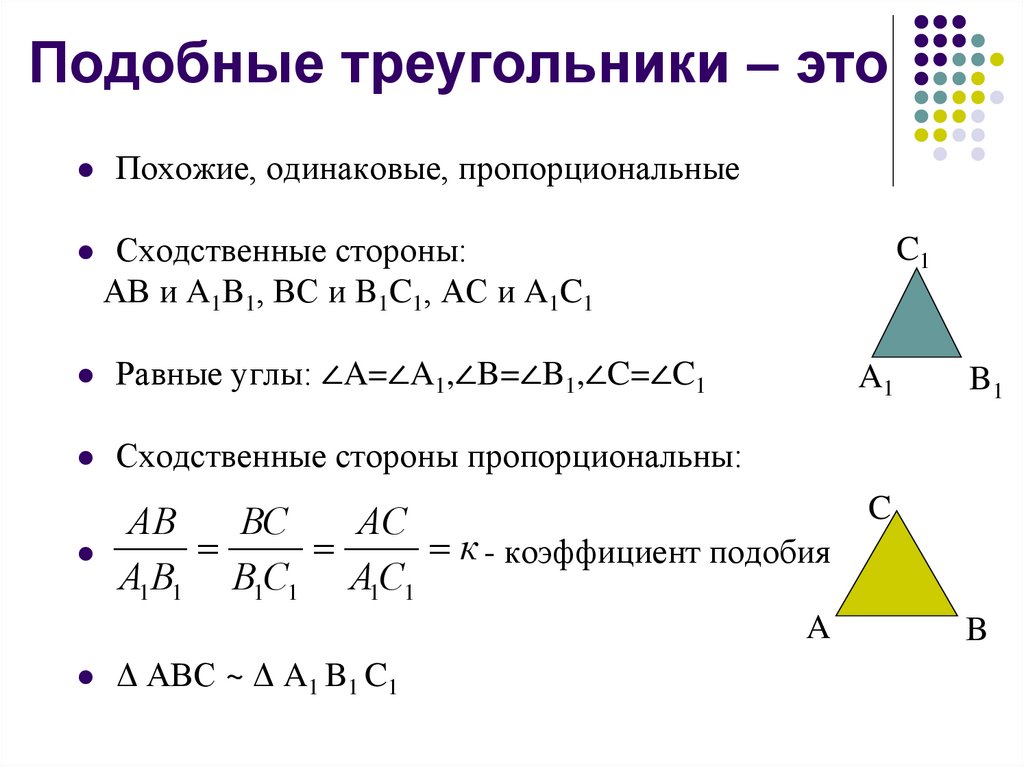
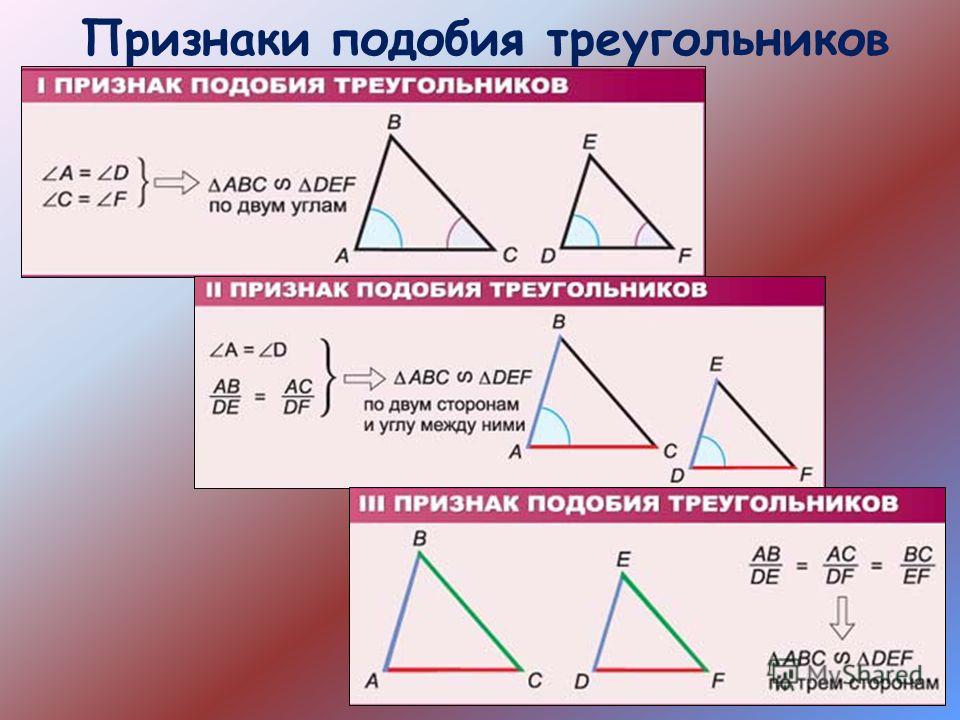
Признаки подобия треугольников
| Название признака | Рисунок | Формулировка признака |
Признак подобия треугольников по двум сторонам и углу между ними | Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. | |
Признак подобия треугольников по двум углам | Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. | |
Признак подобия треугольников по трём сторонам | Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны |
| Признак подобия треугольников по двум сторонам и углу между ними |
Формулировка признака подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. |
| Признак подобия треугольников по двум углам |
Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. |
| Признак подобия треугольников по трём сторонам |
Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны |
Признаки подобия прямоугольных треугольников
| Название признака | Рисунок | Формулировка признака |
Признак подобияпрямоугольных треугольников по двум катетам | Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. | |
Признак подобия прямоугольных треугольников по острому углу | Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. | |
Признак подобия прямоугольных треугольников по гипотенузе и катету | Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по двум катетам |
Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по острому углу |
Формулировка признака подобия прямоугольных треугольников: Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
| Признак подобия прямоугольных треугольников по гипотенузе и катету |
Формулировка признака подобия прямоугольных треугольников: Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны. |
Следствие 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).
Рис.3
Следствие 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)
Рис.4
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Подобные треугольники
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Определение подобных треугольников
Определение подобных треугольников
2. Соотношение площадей подобных треугольников
3. Признаки подобия треугольников
4. Примеры задач на понятие подобия треугольников
В этой статье мы рассмотрим понятие подобных треугольников и другие понятия и теоремы, связанные с этим определением.
Определение подобных треугольников
Будем рассматривать следующие два треугольника (Рис. 1).
Рисунок 1. Подобные треугольники
Определение 1
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]
Обозначение: $ABC\sim A_1B_1C_1$
Определение 2
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.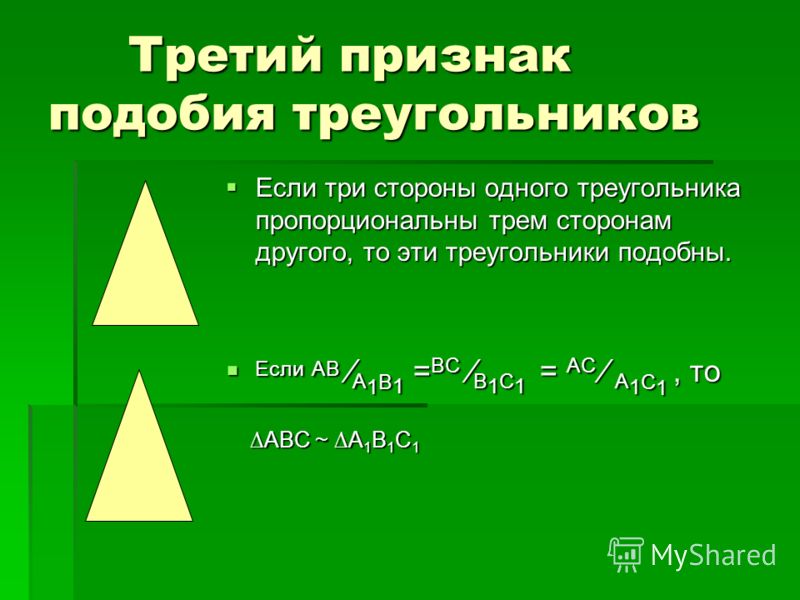 2\]
2\]
Признаки подобия треугольников
Приведем формулировки трех признаков подобия треугольников.
Теорема 2
Первый признак подобия треугольников: Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.
То есть, если $\angle A=\angle A_1,\ \angle B=\angle B_1$, то треугольники $ABC$ и $A_1B_1C_1$ подобны (рис. 2).
Рисунок 2. Первый признак подобия треугольников
Теорема 3
Второй признак равенства треугольников: Если две стороны одного треугольника пропорциональны соответствующим сторонам второго треугольника и углы между этими сторонами равны, то данные треугольники подобны.
То есть, если $\angle A=\angle A_1$ и $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}$, то треугольники $ABC$ и $A_1B_1C_1$ подобны (рис. 3).
Рисунок 3. Второй признак подобия треугольников
Теорема 4
Третий признак подобия треугольников: Если три стороны одного треугольника пропорциональны трем соответствующим сторонам второго треугольника, то такие треугольники подобны.
То есть, если $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$, то треугольники $ABC$ и $A_1B_1C_1$ подобны.
Примеры задач на понятие подобия треугольников
Пример 1
Подобны ли равнобедренные треугольники, если они имеют
По равному острому углу;
По равному тупому углу;
По равному прямому углу.
Решение.
Пусть даны равнобедренные треугольники $ABC$ и $A_1B_1C_1$ с $\angle A=\angle A_1.$
Пусть $\angle A=\angle A_1$ — острые углы треугольников. Тогда здесь возможны два случая:
а) $\angle A=\angle A_1$ — углы при вершине данных треугольников. Тогда, так как треугольник $ABC$ равнобедренный, то
\[\angle B=\angle C=\frac{180-\angle A}{2}\]Так как треугольник $A_1B_1C_1$ равнобедренный, то
\[\angle B_1=\angle C_1=\frac{180-A_1}{2}=\frac{180-\angle A}{2}=\angle B=\angle C\]То есть $\angle B=\angle B_1,\ \ \angle C=\angle C_1$. По первому признаку подобия, получаем, что треугольники $ABC$ и $A_1B_1C_1$ подобны.

б) $\angle A=\angle A_1$ — углы при основании данных треугольников. Так как треугольники подобны, то их углы при основании равны. Но тогда два соответствующих угла одного треугольника равны двум соответствующим углам второго треугольника. Значит, по первому признаку подобия треугольников, треугольники подобны.
Так как угол тупой, то он лежит при основании данных треугольников. Аналогично пункту 1,а) получим, что они подобны.
Так как угол прямой, то он лежит при основании данных треугольников. Аналогично пункту 1,а) получим, что они подобны.
Пример 2
Подобны ли треугольники $ABC$ и $A_1B_1C_1$, если $AB=17,\ BC=30,\ \ AC=42,\ {\ A}_1B_1=34,\ {\ B}_1C_1=60,\ \ A_1C_1=84$?
Решение.
Найдем коэффициент подобия каждой пары сторон треугольников:
\[\frac{AB}{A_1B_1}=\frac{17}{34}=\frac{1}{2}\] \[\frac{BC}{{B_1C}_1}=\frac{30}{60}=\frac{1}{2}\] \[\frac{AC}{A_1C_1}=\frac{42}{84}=\frac{1}{2}\]
Получаем
\[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}=\frac{1}{2}\]
Следовательно, по третьему признаку подобия треугольников получаем, что данные треугольники подобны.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 25.03.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Подобие треугольников | ЮКлэва
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.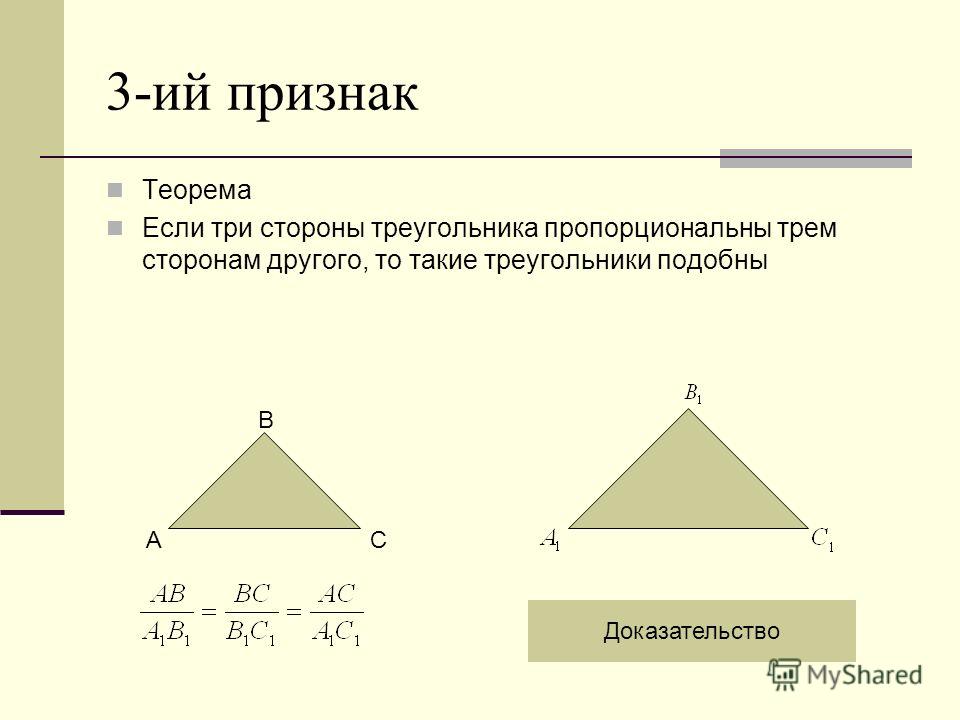
А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?
Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!
Читай эту статью, смотри вебинар по 16 задаче и все поймешь!
Подобие треугольников — коротко о главном
Подобные треугольники
– это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия \( \displaystyle k\).
Если \( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\) с коэффициентом подобия \( \displaystyle k\), то:
\( \angle A = \angle {A_1},\angle B = \angle {B_1},\angle C = \angle {C_1}\)
\( \displaystyle \frac{{AB}}{{{A_1}{B_1}}} = k,\frac{{AC}}{{{A_1}{C_1}}} = k,\frac{{BC}}{{{B_1}{C_1}}} = k \)
Отношение периметров подобных треугольников равно коэффициенту подобия: \( \displaystyle \frac{{{P}_{ABC}}}{{{P}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}=k\). {2}}\).
{2}}\).
Признаки подобия треугольников:
По двум углам:
\( \displaystyle \angle A=\angle {{A}_{1}}\), \( \displaystyle \angle C=\angle {{C}_{1}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
По одному углу и отношению заключающих его сторон:
\( \displaystyle \angle A=\angle {{A}_{1}}\), \( \displaystyle \frac{AB}{{{A}_{1}}{{B}_{1}}}=\frac{AC}{{{A}_{1}}{{C}_{1}}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
По отношению трех сторон:
\( \displaystyle \frac{AB}{{{A}_{1}}{{B}_{1}}}=\frac{AC}{{{A}_{1}}{{C}_{1}}}=\frac{BC}{{{B}_{1}}{{C}_{1}}}\) \( \displaystyle \Rightarrow \)\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\).
Подобные треугольники — подробнее
Мы разобрали подробно все, что касается треугольников в общем.
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Теорема косинусов
- Теорема синусов
- Медиана
- Биссектриса
- Высота
Но что такое подобные треугольники?
Вот, например, такой и такой:
Похожи эти треугольники? Ты скажешь, конечно же нет!
А такой и такой?
Похожи!
А вот такой и такой?
Посмотри внимательно, тоже похожи.
А теперь строго математически!
Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.
То есть все углы равны и все стороны одного треугольника в \( \displaystyle 5\), или, в \( \displaystyle 7\), или в \( \displaystyle 8,21\) (или и т.д.) больше сторон другого треугольника.
Записываются слова «треугольник \( \displaystyle ABC\) подобен треугольнику \( \displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}}\)» с помощью такого значка:
\( \displaystyle {} \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}} \)
То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы \( \displaystyle k\).
То есть, если
\( \displaystyle \Delta ABC\sim{\ }\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}\) с коэффициентом подобия \( \displaystyle k\), то это означает что
\(\angle A = \angle {A_1},\angle B = \angle {B_1},\angle C = \angle {C_1}\)
и \( \displaystyle \frac{{AB}}{{{A_1}{B_1}}} = k,\frac{{AC}}{{{A_1}{C_1}}} = k,\frac{{BC}}{{{B_1}{C_1}}} = k\)
Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон.
И они придумали признаки подобия треугольников.
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств.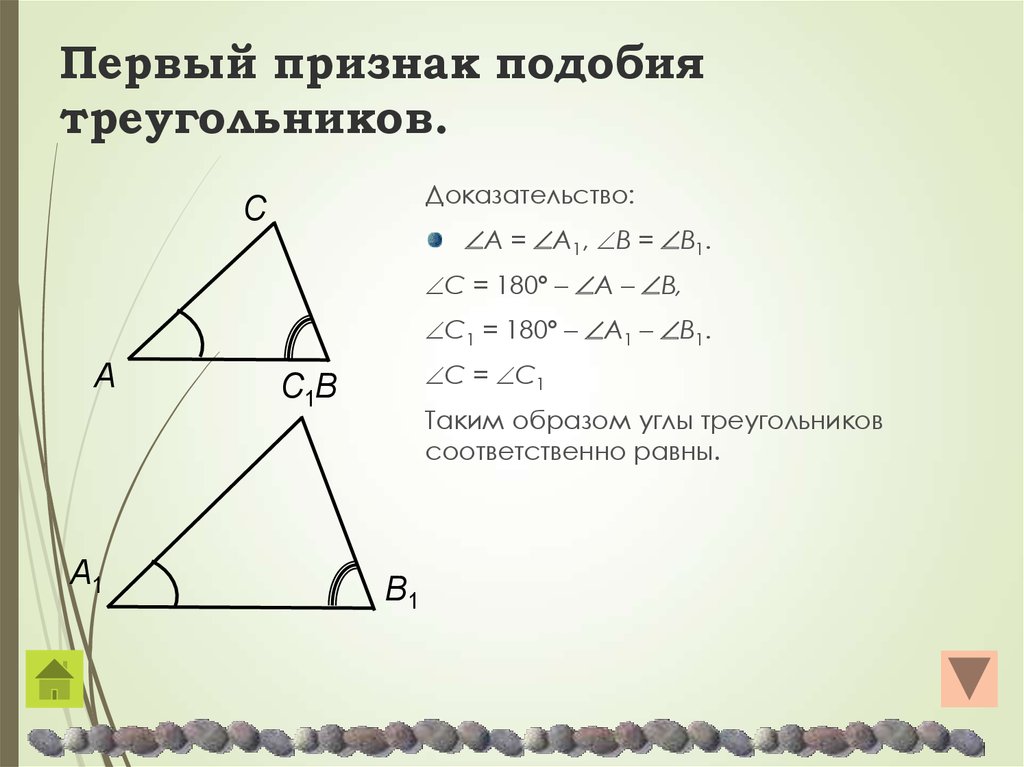 Баллы здесь снимают за любой пропущенный шаг доказательства.
Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).
Подобие. Признаки подобия треугольников презентация, доклад
Подобие. Признаки подобия треугольников.
Какие фигуры являются подобными?
1
4
5
3
5
2
6
II в.
I в.
1
2
3
4
6
1.
Ответ: 1 и 4; 2 и 3
Ответ: 1 и 5; 2 и 3; 4 и 6
Подобные фигуры — фигуры, одинаковые по форме, но разные по размерам.
Треугольники подобны, найдите сходственные стороны
I в.
II в.
K
B
N
A
D
C
M
F
S
A
P
X
2.
Ответ: KB и CD;
KN и AD;
BN и AC
Ответ: MF и AP;
SF и AX;
SM и PX
Сходственные стороны – стороны, лежащие против равных углов.
Найти коэффициент подобия, если сходственные стороны треугольников равны:
I в.
II в.
а). 5 и 25
в). 10 и 2
с). 20 и 21
3.
а). 3 и 6
в). 30 и 10
с). 5 и 7
Коэффициент подобия – равен отношению сходственных сторон подобных треугольников.
Ответ:
Ответ:
Найти коэффициент подобия, если периметры подобных треугольников равны:
4.
I в.
II в.
а). 1 и 4
в). 8 и 2
а). 2 и 4
в). 19 и 10
Найти коэффициент подобия, если площади подобных треугольников равны:
5.
а). 20 и 40
в). 9 и 10
а). 32 и 2
в). 18 и 3
Периметры подобных треугольников относятся как коэффициент подобия k.
Площади подобных треугольников относятся как коэффициент подобия в квадрате k2.
Могут ли быть подобны треугольники, у которых углы равны:
I в.
Δ A B C ~ Δ D E F
и почему?
Δ A B C ~ Δ D E F
и почему?
6.
Подобные треугольники – это треугольники, у которых
1). углы соответственно равны
2). сходственные стороны пропорциональны
Ответ: Да, так как
Ответ: Нет, так как
I I в.
Могут ли быть подобны треугольники, у которых стороны равны:
Δ A B C ~ Δ D E F
АB = 12 DF = 7
АС = 21 FE = 10
ВС = 30 ED = 4
и почему?
I в.
Δ A B C ~ Δ D E F
АB = 8 DF = 7
АС = 14 FE = 10
ВС = 20 ED = 4
и почему?
7.
Подобные треугольники – это треугольники, у которых
1). углы соответственно равны
2). сходственные стороны пропорциональны
II в.
Ответ: Да, так как
Ответ: Да, так как
Заданы площади подобных треугольников и одна сторон второго треугольника.
Найти сторону, сходственную ей.
8.
I в.
II в.
S 1 = 270
S 2 = 30
Сторона 2 Δ = 4 см
Найти сходственную сторону 1 Δ -?
S 1 = 144
S 2 = 36
Сторона 2 Δ = 10
Найти сходственную сторону 1 Δ -?
Площади подобных треугольников относятся как коэффициент подобия в квадрате k2.
Ответ: 12см
Ответ: 20
Сход. сторона 1Δ: 4 ∙ k = 4∙3 = 12
Сход. сторона 1Δ: 10∙k = 10 ∙2=20
Теория
Первый признак подобия треугольников
Второй признак подобия треугольников
I в.
II в.
Третий признак подобия треугольников
Коэффициент подобия – это…
9.
I признак подобия Δ:
(по равенству двух углов)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
II признак подобия Δ:
(по пропорциональности двух сторон и равенству угла между ними)
Если двe стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.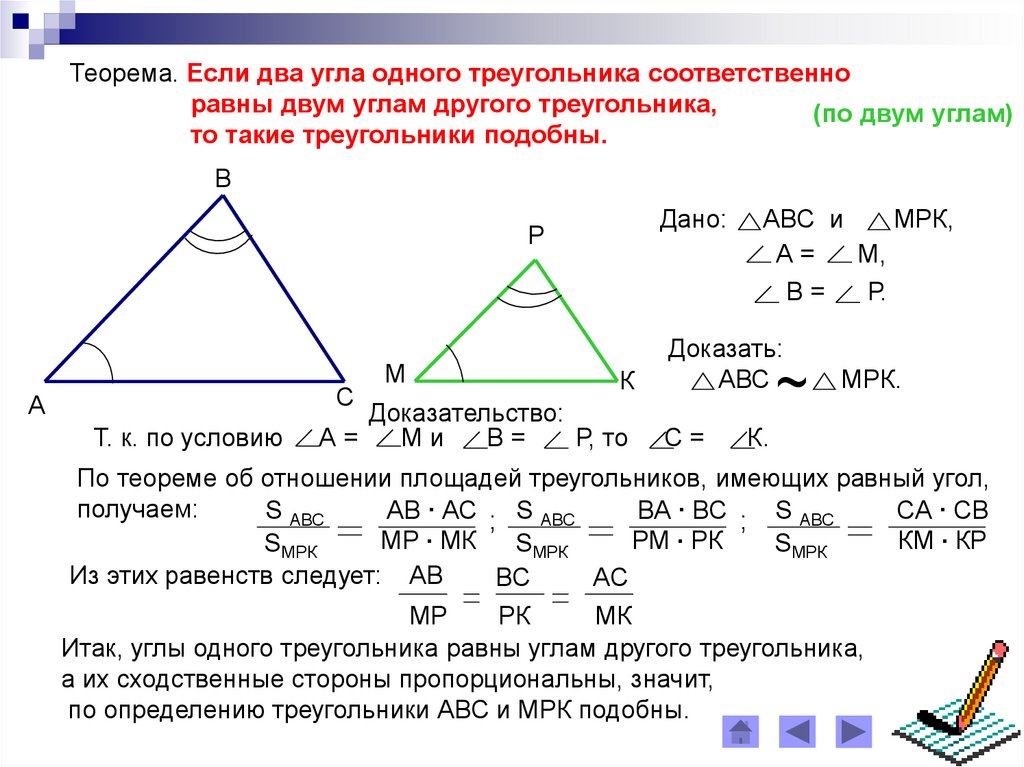
III признак подобия Δ:
(по пропорциональности трех сторон )
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Коэффициент подобия – это число, показывающее во сколько раз один треугольник больше (или меньше) другого, подобного ему.
Равен отношению сходственных сторон подобных Δ.
Скачать презентацию
2)Признаки подобия треугольников.
Подобные треугольники
— треугольники, у которых углы
соответственно равны, а стороны одного
пропорциональны сходственным сторонам
другого треугольника.Первый признак
:Если два угла одного треугольника
соответственно равны двум углам другого
треугольника, то треугольники подобны.
Второй признак:Если две стороны одного
треугольника пропорциональны двум
сторонам другого и углы между этими
сторонами равны, тогда эти треугольники
подобны. Третий признак:Если три стороны
одного треугольника пропорциональны
трём сходственным сторонам другого, то
треугольники подобны. Свойства подобных
треугольников :1)Отношение площадей
подобных треугольников равно квадрату
коэффициента подобия 2)Отношение объёма
подобных стереометрических фигур равно
кубу коэффициента подобия 3)Отношение
периметров и длин биссектрис, медиан,
высот и серединных перпендикуляров
равно коэффициенту подобия. Подобие в
прямоугольном треугольнике:Треугольники,
на которые высота, опущенная из прямого
угла, делит прямоугольный треугольник,
подобны всему треугольнику по первому
признаку, а значит:1)Высота прямоугольного
треугольника, опущенная на гипотенузу,
равна среднему геометрическому проекций
катетов на гипотенузу, 2)Катет равен
среднему геометрическому гипотенузы
и проекции этого катета на гипотенузу.
Свойства подобных
треугольников :1)Отношение площадей
подобных треугольников равно квадрату
коэффициента подобия 2)Отношение объёма
подобных стереометрических фигур равно
кубу коэффициента подобия 3)Отношение
периметров и длин биссектрис, медиан,
высот и серединных перпендикуляров
равно коэффициенту подобия. Подобие в
прямоугольном треугольнике:Треугольники,
на которые высота, опущенная из прямого
угла, делит прямоугольный треугольник,
подобны всему треугольнику по первому
признаку, а значит:1)Высота прямоугольного
треугольника, опущенная на гипотенузу,
равна среднему геометрическому проекций
катетов на гипотенузу, 2)Катет равен
среднему геометрическому гипотенузы
и проекции этого катета на гипотенузу.
Теорема о сумме углов треугольника утверждает что сумма углов треугольника равна 180°.
Доказательство:Пусть
ABC’ — произвольный треугольник. Проведем
через вершину B прямую, параллельную
прямой AC (такая прямая называется прямой
Евклида). Отметим на ней точку D так,
чтобы точки A и D лежали по разные стороны
прямой BC. Углы DBC и ACB равны как внутренние
накрест лежащие, образованные секущей
BC с параллельными прямыми AC и BD. Поэтому
сумма углов треугольника при вершинах
B и С равна углу ABD.Сумма всех трех углов
треугольника равна сумме углов ABD и BAC.
Так как эти углы внутренние односторонние
для параллельных AC и BD при секущей AB, то
их сумма равна 180°. Теорема доказана.
Следствия:Из теоремы следует, что у
любого треугольника два угла острые.
Действительно, применяя доказательство
от противного, допустим, что у треугольника
только один острый угол или вообще нет
острых углов. Тогда у этого треугольника
есть, по крайней мере, два угла, каждый
из которых не меньше 90°. Сумма этих углов
не меньше 180°. А это невозможно, так как
сумма всех углов треугольника равна
180°. Что и требовалось доказать.Выпуклым
многоугольником называется многоугольник,
обладающий тем свойством, что все его
точки лежат по одну сторону от любой
прямой, проходящей через две его соседние
вершины.Теорема о сумме внутренних
углов выпуклого многоугольника
Доказательство проводится для случая
выпуклого n-угольникаПусть A1A2.
Углы DBC и ACB равны как внутренние
накрест лежащие, образованные секущей
BC с параллельными прямыми AC и BD. Поэтому
сумма углов треугольника при вершинах
B и С равна углу ABD.Сумма всех трех углов
треугольника равна сумме углов ABD и BAC.
Так как эти углы внутренние односторонние
для параллельных AC и BD при секущей AB, то
их сумма равна 180°. Теорема доказана.
Следствия:Из теоремы следует, что у
любого треугольника два угла острые.
Действительно, применяя доказательство
от противного, допустим, что у треугольника
только один острый угол или вообще нет
острых углов. Тогда у этого треугольника
есть, по крайней мере, два угла, каждый
из которых не меньше 90°. Сумма этих углов
не меньше 180°. А это невозможно, так как
сумма всех углов треугольника равна
180°. Что и требовалось доказать.Выпуклым
многоугольником называется многоугольник,
обладающий тем свойством, что все его
точки лежат по одну сторону от любой
прямой, проходящей через две его соседние
вершины.Теорема о сумме внутренних
углов выпуклого многоугольника
Доказательство проводится для случая
выпуклого n-угольникаПусть A1A2. ..An —
данный выпуклый многоугольник и n > 3.
Тогда проведем из одной вершины к
противоположным вершинам n-3 диагонали:
A1A3,A1A4,A1A5…A1An − 1. Так как многоугольник
выпуклый, то эти диагонали разбивают
его на n — 2 треугольника:
ΔA1A2A3,ΔA1A3A4,…,ΔA1An − 1An. Сумма углов
многоугольника совпадает с суммой углов
всех этих треугольников. Сумма углов в
каждом треугольнике равна 180°, а число
этих треугольников есть n-2. Следовательно,
сумма углов n-угольника равна 180°(n-2).
Теорема доказана.
..An —
данный выпуклый многоугольник и n > 3.
Тогда проведем из одной вершины к
противоположным вершинам n-3 диагонали:
A1A3,A1A4,A1A5…A1An − 1. Так как многоугольник
выпуклый, то эти диагонали разбивают
его на n — 2 треугольника:
ΔA1A2A3,ΔA1A3A4,…,ΔA1An − 1An. Сумма углов
многоугольника совпадает с суммой углов
всех этих треугольников. Сумма углов в
каждом треугольнике равна 180°, а число
этих треугольников есть n-2. Следовательно,
сумма углов n-угольника равна 180°(n-2).
Теорема доказана.
4 . Теорема косинусов для треугольника. 5. Теорема синусов для треугольника.
м
6. Теорема о биссектрисе внутреннего угла треугольника.
Свойство биссектрис внутреннего и внешнего углов треугольника. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.Д о к а з а т е л ь с т в о. Пусть CD —биссектриса треугольника ABC (рис. ). Построим
BE || CD. Тогда угол ACD =
углу AEB и угол BCD = углу CBE, а так как угол
ACD= углу BCD, то угол AEB = углу CBE и поэтому
BC = CE.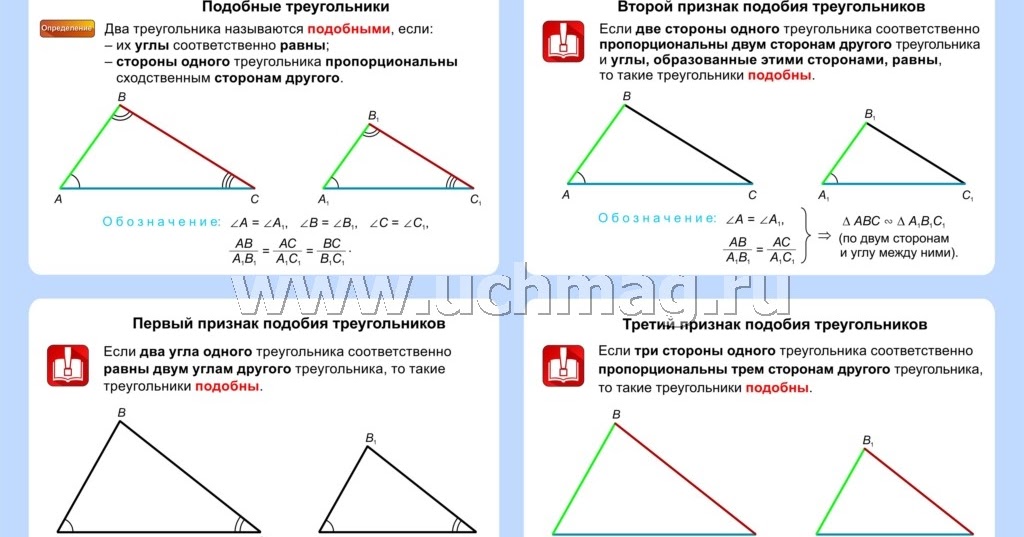 По теореме Фалеса AD/DB = AC/CE , т. е.AD/DB
= AC/BC , что и требовалось доказать.
По теореме Фалеса AD/DB = AC/CE , т. е.AD/DB
= AC/BC , что и требовалось доказать.
7. Определение касательной к окружности, ее свойство и признак.
Дано:Окружность с
центром в точке О радиуса r.Прямая,
которая не проходит через центр О.
Расстояние от центра окружности до
прямой обозначим буквой s.Возможны три
случая:1) s: Если расстояние от центра
окружности до прямой меньше радиуса
окружности, то прямая и окружность имеют
две общие точки. Прямая АВ называется
секущей по отношению к окружности. 2)
s=r: Если расстояние от центра окружности
до прямой равно радиусу окружности, то
прямая и окружность имеют только одну
общую точку.3) s>r: Если расстояние от
центра окружности до прямой больше
радиуса окружности, то прямая и окружность
не имеют общих точек. Определение:
Прямая, имеющая с окружностью только
одну общую точку, называется касательной
к окружности, а их общая точка называется
точкой касания прямой и окружности.
Свойства касательной: касательная к
окружности перпендикулярна к радиусу,
проведенному в точку касанияm –
касательная к окружности с центром О
. М – точка касания.OM – радиус.Признак
касательной: если прямая проходит через
конец радиуса, лешащей на окружности и
перпендикулярна радиусу, то она является
касательной.Свойство касательных
проходящих через одну точку:Отрезки
касательных к окружности, проведенные
из одной точки, равны и составляют равные
углы с прямой, проходящей через эту
точку и центр окружности.По свойству
касательной АВО, АСО–прямоугольные.АВО=АСО–по
гипотенузе и катету:ОА – общая,ОВ=ОС –
радиусы.АВ=АС.
М – точка касания.OM – радиус.Признак
касательной: если прямая проходит через
конец радиуса, лешащей на окружности и
перпендикулярна радиусу, то она является
касательной.Свойство касательных
проходящих через одну точку:Отрезки
касательных к окружности, проведенные
из одной точки, равны и составляют равные
углы с прямой, проходящей через эту
точку и центр окружности.По свойству
касательной АВО, АСО–прямоугольные.АВО=АСО–по
гипотенузе и катету:ОА – общая,ОВ=ОС –
радиусы.АВ=АС.
8. Теоремы об измерении вписанного угла; угла между касательной и хордой, проведенной из точки касания.
У гол, вершина которого находится на окружности, а стороны являются хордами, называется вписанным.Угол АВС — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (черт. 330).
2. Вписанный угол,
опирающийся на диаметр,—прямой, так
как он опирается на половину окружности.
Половина окружности содержит 180 дуговых
градусов, значит, угол, опирающийся на
диаметр, содержит 90 угловых градусов
(черт.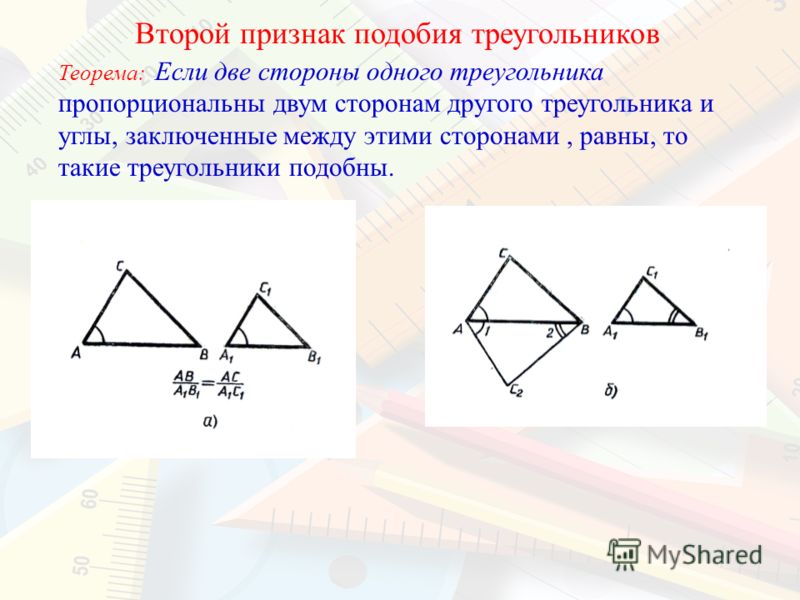 334, б).
334, б).
2. Угол, образованный касательной и хордой.
Теорема. Угол, образованный касательной и хордой, измеряется половиной дуги, заключённой между его сторонами.
9. Теорема о пересекающихся хордах окружности.
П ри пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
угол BAD = углу BCD = 1/2 BmD=> треуг. APD = треуг. CPD (по двум углам)PD/PB = AP/CP. доказано.
Хорда в планиметрии
— отрезок прямой линии, соединяющей
две точки данной кривой (например,
окружности, эллипса, параболы).Хорда
находится на секущей прямой — прямой
линии, пересекающей кривую в двух или
более точках. Плоская фигура, заключённая
между кривой и её хордой называется
сегмент, а отрезок кривой между крайними
точками хорды называется дугой. Хорда,
проходящая через центр окружности,
называется диаметр. Диаметр — это самая
длинная хорда в окружности.Свойства
хор:1)Хорды являются равноотстоящими
от центра окружности тогда и только
тогда, когда они равны по длине. 2)Перпендикуляр
с середины хорды окружности проходит
через центр этой окружности.3)Радиус,
перпендикулярный к хорде, делит эту
хорду пополам.4)Дуги, заключенные между
равными хордами, равны.5)При пересечении
двух хорд окружности, получаются отрезки,
произведение которых у одной хорды
равно произведению отрезков другой
хорды.
2)Перпендикуляр
с середины хорды окружности проходит
через центр этой окружности.3)Радиус,
перпендикулярный к хорде, делит эту
хорду пополам.4)Дуги, заключенные между
равными хордами, равны.5)При пересечении
двух хорд окружности, получаются отрезки,
произведение которых у одной хорды
равно произведению отрезков другой
хорды.
Подобие треугольников. Часть 1
Определение и свойства подобных треугольников
Числа a1, a2, a3, …, an называются пропорциональными числам b1, b2, b3, …, bn, если выполняется равенство: a1/b1 = а2/b2 = a3/b3 = … = an/bn = k, где k – некоторое число, которое называют коэффициентом пропорциональности.
Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку
6/-4 = -7,5/5 = 15/-10 = -1,5.
Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.
Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).
Рассмотрим на рис. 1 два треугольника АВС и А1В1С1 с равными попарно углами: A = A1, B = B1, C = C1.
Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными. Так, на рис. 1 стороны AB и A1B1, AC и A1C1, BC и B1C1, сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A1B1C1.
Дадим определение подобных треугольников:
Два треугольника называются подобными, если их углы попарно равны, а сходственные стороны пропорциональны.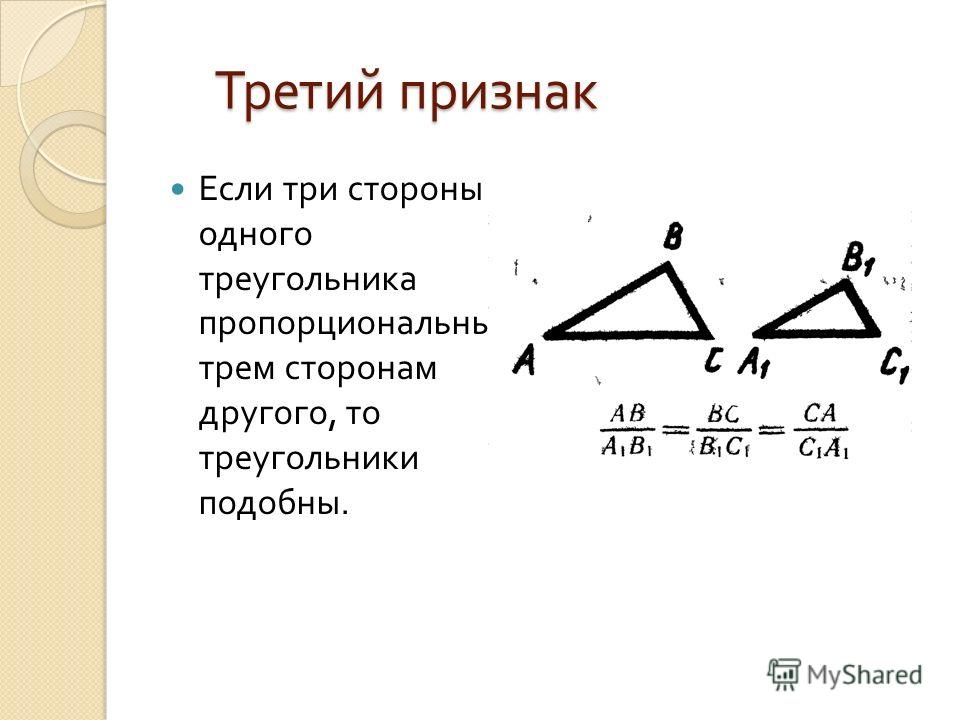
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия.
Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A1B1C1.
Итак, на рис. 2 имеем: Δ ABC ~ Δ A1B1C1
углы A = A1, B = B1, C = C1 и AB/A1B1 = ВC/В1C1 = АС/А1С1 = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.
Замечание 1: Равные треугольники подобны с коэффициентом 1.
Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B1C1A1 некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.
К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.
Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.
Сформулируем свойства подобных треугольников:
- Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.
- Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Пусть треугольники ABC и A1B1C1 подобны с коэффициентом k (рис. 2).
Докажем, что SABC/SA1B1C1 = k2.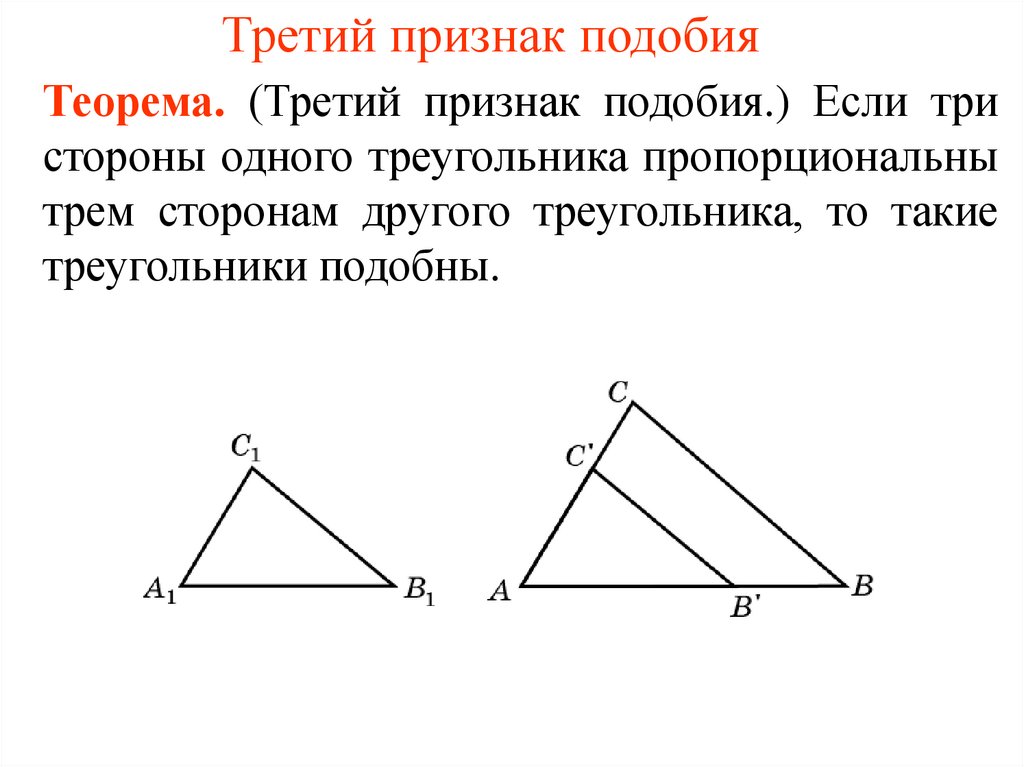
Поскольку углы подобных треугольников попарно равны, т.е A = A1, и по теореме об отношении площадей треугольников, имеющих по равному углу, имеем:
SABC/SA1B1C1 = (AB · AC) / (A1B1 · A1C1) = AB/A1B1 · AC/A1C1.
В силу подобия треугольников AB/A1B1 = k и AC/A1C1 = k,
поэтому SABC/SA1B1C1 = AB/A1B1 · AC/A1C1 = k · k = k2.
Замечание: Сформулированные выше свойства подобных треугольников справедливы и для произвольных фигур.
Признаки подобия треугольников
Требования, которые предъявляются к подобным треугольникам определением (это равенство углов и пропорциональность сторон) являются избыточными. Устанавливать подобие треугольников можно и по меньшему количеству элементов.
Так, при решении задач чаще всего используется первый признак подобия треугольников, утверждающий, что для подобия двух треугольников достаточно равенства их углов:
Первый признак подобия треугольников (по двум углам): Если два угла одного треугольника соответственно равны двум углам второго треугольника, то эти треугольники подобны (рис. 3).
Пусть даны треугольники Δ ABC, Δ A1B1C1, в которых углы A = A1, B = B1. Необходимо доказать, что Δ ABC ~ Δ A1B1C1.
Доказательство.
1) По теореме о сумме углов треугольника имеем:
угол C = 180° (угол A + угол B) = 180° (угол A1 + угол B1) = угол C1.
2) По теореме об отношении площадей треугольников, имеющих по равному углу,
SABC/SA1B1C1 = (AB · AC) / (A1B1 · A1C1) = (AB · ВC) / (A1B1 · В1C1) = (AС · ВC) / (A1С1 · В1C1).
3) Из равенства (AB · AC) / (A1B1 · A1C1) = (AB · ВC) / (A1B1 · В1C1) следует, что AC/A1C1 = BС/В1С1.
4) Из равенства (AB · ВC) / (A1B1 · В1C1) = (AС · ВC) / (A1С1 · В1C1) следует, что AВ/A1В1 = АС/А1С1.
Таким образом, у треугольников ABCи A1B1C1 DA = DA1, DB = DB1, DC = DC1, и AB/A1B1 = АС/А1С1.
5) AB/A1B1 = АС/А1С1 = ВC/В1C1, то есть сходственные стороны пропорциональны. А значит, Δ ABC ~ Δ A1B1C1 по определению.
Теорема о пропорциональных отрезках. Деление отрезка в заданном отношении
Теорема о пропорциональных отрезках является обобщением теоремы Фалеса.
Для использования теоремы Фалеса необходимо, чтобы параллельные прямые, пересекающие две данные прямые, отсекали на одной из них равные отрезки. Обобщенная же теорема Фалеса утверждает, что если параллельные прямые пересекают две данные прямые, то отрезки, отсекаемые ими на одной прямой, пропорциональны отрезкам, отсекаемым на второй прямой.
Теорема о пропорциональных отрезках доказывается аналогично теореме Фалеса (только вместо равенства треугольников здесь используется их подобие).
Теорема о пропорциональных отрезках (обобщенная теорема Фалеса): Параллельные прямые, пересекающие две данные прямые, отсекают на них пропорциональные отрезки.
Свойство медиан треугольника
Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:
Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, и делятся этой точкой в отношении 2 : 1, считая от вершины (рис. 4).
Точка пересечения медиан называется центроидом треугольника.
Пусть дан Δ ABC, у которого AA1, BB1, CC1 – медианы, кроме того, AA1∩CC1 = O. Необходимо доказать, что BB1 ∩ CC1 = O и АО/ОА1 = ВО/ОВ1 = СО/ОС1 = 2.
Доказательство.
1) Проведем среднюю линию A1C1. По теореме о средней линии треугольника A1C1 || AC, и A1C1 = AC/2.
2) Треугольники AOC и A1OC1 подобны по двум углам (угол AOC = углу A1OC1 как вертикальные, угол OAC = углу OA1C1 как внутренние накрест лежащие при A1C1 || AC и секущей AA1), следовательно, по определению подобных треугольников АО/А1О = ОС/ОС1 = АС/А1С1 = 2.
3) Пусть BB1∩CC1 = O1. Аналогично пунктам 1 и 2 можно доказать, что ВО/О1В1 = СО1/О1С = 2. Но поскольку на отрезке СС1 существует единственная точка О, делящая его в отношении СО : ОС1 = 2 : 1, то точки О и О1 совпадают. Значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2 : 1, считая от вершины.
Но поскольку на отрезке СС1 существует единственная точка О, делящая его в отношении СО : ОС1 = 2 : 1, то точки О и О1 совпадают. Значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2 : 1, считая от вершины.
В курсе геометрии в теме «площади многоугольников» доказывается тот факт, что медиана разбивает произвольный треугольник на две равновеликие части. Кроме того, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников.
Остались вопросы? Не знаете, как решать задачи на подобие треугольников?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Подобные треугольники – формулы, свойства, теоремы, доказательства
Подобные треугольники – это треугольники, у которых соответствующие стороны пропорциональны друг другу, а соответствующие углы равны друг другу. Подобные треугольники выглядят одинаково, но размеры могут быть разными. В общем, подобные треугольники отличаются от конгруэнтных треугольников. Существуют различные методы, с помощью которых мы можем определить, подобны два треугольника или нет. Давайте узнаем больше о подобных треугольниках и их свойствах вместе с несколькими решенными примерами.
Подобные треугольники выглядят одинаково, но размеры могут быть разными. В общем, подобные треугольники отличаются от конгруэнтных треугольников. Существуют различные методы, с помощью которых мы можем определить, подобны два треугольника или нет. Давайте узнаем больше о подобных треугольниках и их свойствах вместе с несколькими решенными примерами.
| 1. | Что такое подобные треугольники? |
| 2. | Формулы подобных треугольников |
| 3. | Теоремы о подобных треугольниках |
| 4. | Свойства подобных треугольников |
| 5. | Как найти подобные треугольники? |
| 6. | Разница между подобными треугольниками и конгруэнтными треугольниками |
| 7. | Часто задаваемые вопросы о подобных треугольниках |
Что такое подобные треугольники?
Подобные треугольники — это треугольники, которые выглядят похожими друг на друга, но их размеры могут не совпадать. Два объекта можно назвать похожими, если они имеют одинаковую форму, но могут различаться по размеру. Это означает, что похожие формы при увеличении или уменьшении накладываются друг на друга. Это свойство подобных фигур называется «сходством».
Два объекта можно назвать похожими, если они имеют одинаковую форму, но могут различаться по размеру. Это означает, что похожие формы при увеличении или уменьшении накладываются друг на друга. Это свойство подобных фигур называется «сходством».
Определение подобных треугольников
Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны находятся в одинаковом отношении или пропорции (соответствующие стороны). Подобные треугольники могут иметь разные индивидуальные длины сторон треугольников, но их углы должны быть равны, и их соответствующее отношение длин сторон должно быть одинаковым. Если два треугольника подобны, это означает, что
- Все соответствующие пары углов треугольников равны.
- Все соответствующие стороны треугольников пропорциональны.
Мы используем символ «∼» для обозначения сходства. Итак, если два треугольника подобны, мы показываем это как △QPR ∼ △XYZ
Примеры подобных треугольников
Подобные треугольники — это треугольники, у которых соответствующие пары углов равны. Это означает, что равноугольные треугольники подобны. Следовательно, все равносторонние треугольники являются примерами подобных треугольников. На следующем изображении показаны похожие треугольники, но мы должны заметить, что их размеры различаются.
Это означает, что равноугольные треугольники подобны. Следовательно, все равносторонние треугольники являются примерами подобных треугольников. На следующем изображении показаны похожие треугольники, но мы должны заметить, что их размеры различаются.
Формулы подобных треугольников
В предыдущем разделе мы видели, что есть два условия, с помощью которых мы можем проверить, подобны ли данный набор треугольников или нет. Эти условия гласят, что два треугольника можно назвать подобными, если их соответствующие углы равны или конгруэнтны, или если их соответствующие стороны пропорциональны. Следовательно, два треугольника △ABC и △EFG могут быть доказаны подобными (△ABC ∼ △EFG), используя любое условие из следующего набора формул подобных треугольников,
Формула для подобных треугольников в геометрии:
- ∠A = ∠E, ∠B = ∠F и ∠C = ∠G
- AB/EF = BC/FG = AC/EG
Теоремы о подобных треугольниках
Мы можем узнать или доказать, подобны ли два треугольника, используя теоремы подобия. Мы используем эти критерии подобия, когда у нас нет меры всех сторон треугольника или меры всех углов треугольника. Эти теоремы о подобных треугольниках помогают нам быстро выяснить, подобны два треугольника или нет. Существует три основных типа правил подобия, как указано ниже:
Мы используем эти критерии подобия, когда у нас нет меры всех сторон треугольника или меры всех углов треугольника. Эти теоремы о подобных треугольниках помогают нам быстро выяснить, подобны два треугольника или нет. Существует три основных типа правил подобия, как указано ниже:
- AA (или AAA) или Теорема подобия углов
- SAS или теорема о сходстве стороны-угла-стороны
- SSS или теорема о сходстве сторон
Давайте разберемся в этих теоремах о подобных треугольниках и их доказательствах.
AA (или AAA) или Критерий подобия углов
Критерий подобия AA утверждает, что если любые два угла в треугольнике соответственно равны любым двум углам другого треугольника, то они должны быть подобными треугольниками. Правило подобия AA легко применить, когда мы знаем только меру углов и не имеем никакого представления о длине сторон треугольника. На изображении, приведенном ниже, если известно, что ∠B = ∠G и ∠C = ∠F.
И мы можем сказать, что по критерию сходства АА △ABC и △EGF подобны или △ABC ∼ △EGF.
⇒AB/EG = BC/GF = AC/EF и ∠A = ∠E.
Нажмите здесь, чтобы подробно ознакомиться с критерием сходства AA — критерий сходства AA
SAS или критерий сходства стороны-угла-стороны
Согласно теореме подобия SAS, если любые две стороны первого треугольника находятся в точной пропорции к двум стороны второго треугольника вместе с углом, образованным этими двумя сторонами отдельных треугольников, равны, то они должны быть подобными треугольниками. Это правило обычно применяется, когда мы знаем только меру двух сторон и угол, образованный между этими двумя сторонами в обоих треугольниках соответственно.
На изображении ниже, если известно, что AB/DE = AC/DF и ∠A = ∠D
И мы можем сказать, что по критерию подобия SAS △ABC и △DEF подобны или △ABC ∼ △DEF.
SSS или Критерий подобия сторона-сторона-сторона
Согласно теореме подобия SSS два треугольника будут подобны друг другу, если соответствующие отношения всех сторон двух треугольников равны. Этот критерий обычно используется, когда у нас есть только мера сторон треугольника и меньше информации об углах треугольника.
Этот критерий обычно используется, когда у нас есть только мера сторон треугольника и меньше информации об углах треугольника.
На приведенном ниже изображении, если известно, что PQ/ED = PR/EF = QR/DF
И мы можем сказать, что по критерию подобия SSS △PQR и △EDF подобны или △PQR ∼ △EDF .
Свойства подобных треугольников
Если два треугольника подобны или доказаны подобными по любому из вышеприведенных критериев, то они обладают немногими свойствами подобных треугольников. Ниже приведены свойства подобных треугольников.
- Подобные треугольники имеют одинаковую форму, но разные размеры.
- В подобных треугольниках соответствующие углы равны.
- Соответствующие стороны подобных треугольников находятся в одинаковом отношении.
- Отношение площадей подобных треугольников равно отношению квадратов любой пары их соответствующих сторон.
Как найти подобные треугольники?
Два заданных треугольника можно доказать как подобные треугольники, используя вышеприведенные теоремы. Мы можем выполнить шаги, указанные ниже, чтобы проверить, подобны ли данные треугольники,
Мы можем выполнить шаги, указанные ниже, чтобы проверить, подобны ли данные треугольники,
- Шаг 1: Запишите заданные размеры треугольников (соответствующие стороны или соответствующие углы).
- Шаг 2: Проверьте, соответствуют ли эти размеры условиям теорем о подобных треугольниках (AA, SSS, SAS).
- Шаг 3: Данные треугольники, если они удовлетворяют любой из теорем подобия, могут быть представлены с использованием «∼» для обозначения подобия.
Давайте лучше разберем эти шаги на примере.
Пример: Проверить, являются ли △ABC и △PQR подобными треугольниками или нет, используя данные: ∠A = 65°, ∠B = 70º и ∠P = 70°, ∠R = 45°.
Решение:
Используя данное измерение углов, мы не можем сделать вывод, соответствуют ли данные треугольники критерию подобия AA или нет. Найдем меру третьего угла и оценим.
Мы знаем, используя свойство суммы углов треугольника, ∠C в △ABC = 180° — (∠A + ∠B) = 180° — 135° = 45°
Точно так же ∠Q в △PQR = 180° — (∠P + ∠R) = 180° — 115° = 65°
Следовательно, мы можем заключить, что в △ABC и △PQR ∠A = ∠Q, ∠B = ∠P и ∠C = R
⇒ △ABC ∼ △QPR
Разница между подобными треугольниками и конгруэнтными треугольниками
Подобие и конгруэнтность — два разных свойства треугольников. Следующая таблица помогает отличить подобные треугольники от конгруэнтных треугольников:
Следующая таблица помогает отличить подобные треугольники от конгруэнтных треугольников:
| Подобные треугольники | Конгруэнтные треугольники |
| Подобные треугольники имеют одинаковую форму, но могут быть разными по размеру. Они накладываются друг на друга при увеличении или уменьшении. | Конгруэнтные треугольники одинаковы по форме и размеру. Они накладываются друг на друга в своей первоначальной форме. |
| Они представлены с помощью символа «~». Например, подобные треугольники ABC и XYZ будут представлены как △ABC ∼ △XYZ | .Они представлены с помощью символа «9».0196 ≅’. Например, конгруэнтные треугольники ABC и XYZ будут представлены как △ABC ≅ △QPR |
| В подобных треугольниках отношение всех соответствующих сторон равно. Это общее отношение также называется «масштабным коэффициентом» в подобных треугольниках. | Отношение соответствующих сторон равно 1 для конгруэнтных треугольников. |
☛ Темы, относящиеся к подобным треугольникам:
- Что такое сходство
- ССС
- САС
- Треугольники
Важные замечания о подобных треугольниках:
- Отношение площадей подобных треугольников равно квадрату отношения их соответствующих сторон.
- Все конгруэнтные треугольники подобны, но не все подобные треугольники обязательно могут быть конгруэнтными.
- Подобные треугольники обозначаются символом «~».
Примеры подобных треугольников
Пример 1:
Рассмотрим два подобных треугольника, ΔABC и ΔDEF:
AP и DQ являются медианами в двух треугольниках соответственно. Покажите, что
AP/BC = DQ/EF
Решение:
Поскольку эти два треугольника подобны, они равноугольны.

Это означает, что
∠B=∠E
Также
AB/DE = BC/EF→ (1)
⇒AB/DE = [(BC/2)/(EF/2)] = BP/EQ
Следовательно, по критерию подобия SAS ,
ΔABP∼ΔDEQ
Таким образом, стороны этих двух треугольников будут соответственно пропорциональны, и поэтому:
AB/DE = AP/DQ
⇒AP/DQ = BC/EF . . . [Из (1)]
⇒AP/BC = DQ/EF
Отсюда доказано.
Пример 2: Джеймс ростом 140. Он стоит в 320 дюймах от фонарного столба. Его тень от света имеет длину 80 дюймов. Какая высота фонарного столба?
Решение:
Взяв △ABD и △ECD, мы можем видеть, что
∠B = ∠C = 90 o , а ∠Dcom угол = ∠mon угол △ABD похож на △ECD.
Следовательно,
AB/EC = BD/CD = AD/ED
Подставляя данные значения
AB/140 = (320+80)/80
AB/140 = 5
AB = 0700 Ответ: Высота столба 700 дюймов.
перейти к слайдуперейти к слайду
Разложите сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по подобным треугольникам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о подобных треугольниках
Что понимают под подобными треугольниками в геометрии?
Подобные треугольники в геометрии — это треугольники, имеющие одинаковую форму, но не равные по размеру. Все равносторонние треугольники являются примерами подобных треугольников.
Какой символ используется для подобных треугольников?
Подобные треугольники можно выразить с помощью символа «~». Этот символ означает, что данные две фигуры имеют одинаковую форму, но не обязательно одинаковый размер.
Что такое формула подобных треугольников?
Формула, используемая для проверки того, подобны ли два треугольника или нет, зависит от условия подобия. Для двух треугольников △PQR и △XYZ подобие можно доказать с помощью любого из следующих условий:
Для двух треугольников △PQR и △XYZ подобие можно доказать с помощью любого из следующих условий:
- ∠P = ∠X, ∠Q = ∠Y и ∠R = ∠Z
- PQ/XY = QR/YZ = PR/XZ
Каковы 3 теоремы о подобных треугольниках?
Три теоремы подобия, используемые для проверки подобия в треугольниках, приведены ниже:
- AA (или AAA) или теорема о сходстве углов
- SAS или теорема о сходстве стороны-угла-стороны
- SSS или теорема о сходстве сторон
Каковы свойства подобных треугольников?
Важные свойства двух подобных треугольников можно представить как.
- Форма двух подобных треугольников одинакова, но их размеры могут быть разными.
- В подобных треугольниках соответствующие углы равны.
- В подобных треугольниках соответствующие стороны находятся в одинаковом отношении.
Каковы правила для подобных треугольников?
Правила или условия, используемые для проверки того, подобны ли данный набор треугольников или нет, как указано,
- Все соответствующие пары углов треугольников должны быть одинаковыми.

- Все соответствующие стороны треугольников находятся в одной пропорции.
Как узнать, подобны ли два треугольника?
Два треугольника подобны, если их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.
Как найти долю подобных треугольников?
В подобных треугольниках пары соответствующих сторон пропорциональны. Это отношение / пропорциональность соответствующих сторон можно использовать для нахождения длины недостающей стороны фигуры, учитывая аналогичную фигуру, для которой известны соответствующие измерения.
Как найти недостающие стороны подобных треугольников?
Недостающие стороны подобного треугольника можно узнать, сравнив отношения последовательных соответствующих сторон треугольника. Сравниваем отношения и находим длину неизвестной стороны треугольника.
Могут ли два треугольника быть подобными и конгруэнтными?
Все конгруэнтные треугольники также являются подобными треугольниками, но не все подобные треугольники являются конгруэнтными треугольниками. Таким образом, два подобных треугольника могут быть равны, но не всегда. Чтобы два подобных треугольника были равны, они должны иметь одинаковый размер, одинаковую форму и одинаковую меру соответствующих углов.
Таким образом, два подобных треугольника могут быть равны, но не всегда. Чтобы два подобных треугольника были равны, они должны иметь одинаковый размер, одинаковую форму и одинаковую меру соответствующих углов.
Какой тип треугольников всегда похож?
Равносторонние треугольники всегда подобны. Любые два равносторонних треугольника всегда подобны независимо от длины сторон равностороннего треугольника. Два равнобедренных прямоугольных треугольника также всегда подобны.
Могут ли быть подобны два равнобедренных треугольника?
Два равнобедренных треугольника могут быть подобны тогда и только тогда, когда их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Следовательно, не всегда верно, что равнобедренные треугольники подобны.
Как вводить подобные треугольники?
Подобные треугольники могут быть представлены как треугольники одинаковой формы, но не обязательно одинакового размера. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.
Как найти отношение площадей двух подобных треугольников?
Если два треугольника подобны, то отношение площадей обоих треугольников пропорционально квадрату отношения их соответствующих сторон. Если два подобных треугольника имеют две соответствующие длины сторон, равные a и b, то отношение их площадей это а2:b2.
Подобные треугольники — как доказать, определение и теоремы (видео)
Подобные треугольники (определение, доказательство и теоремы)
Сходство в математике не означает то же, что и сходство в повседневной жизни. Подобные треугольники — это треугольники с одинаковой формой, но разными размерами сторон.
- Определение подобных треугольников
- Соответствующие углы
- Доля
- Включенный уголок
- Теорема AA
- Теорема SAS
- SSS Теорема
Определение похожих треугольников
Мятное мороженое с шоколадной крошкой и мороженое с шоколадной крошкой похожи, но не одно и то же. Это повседневное использование слова «подобный», но не так, как мы используем его в математике.
Это повседневное использование слова «подобный», но не так, как мы используем его в математике.
В геометрии две фигуры подобны , если они имеют одинаковую форму, но разные размеры. У вас может быть квадрат со стороной 21 см и квадрат со стороной 14 см; они были бы похожи. Равносторонний треугольник со стороной 21 см и квадрат со стороной 14 см не будут подобны, потому что это разные формы.
Подобные треугольники легко определить, поскольку к треугольникам можно применить три теоремы. Эти три теоремы, известные как Угол — Угол (AA) , Сторона — Угол — Сторона (SAS) и Сторона — Сторона — Сторона (SSS) , являются надежными методами определения подобия в треугольниках.
- Угол — Угол (AA)
- Сторона — Угол — Сторона (SAS)
- Сторона — Сторона — Сторона (SSS)
Соответствующие углы
В геометрии соответствие означает, что конкретная часть одного многоугольника точно относится к аналогично расположенной части другого. Даже если два треугольника ориентированы по-разному, если вы можете повернуть их, чтобы сориентировать одинаково, и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.
Даже если два треугольника ориентированы по-разному, если вы можете повернуть их, чтобы сориентировать одинаково, и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.
Три теоремы подобия треугольников зависят от соответствующих частей. Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом другого треугольника.
Пропорция
Сходство связано с пропорцией. Треугольники легко оценить по пропорциональным изменениям, которые делают их похожими. Их сравнительные стороны пропорциональны друг другу; их соответствующие углы равны.
Вы можете установить соотношения для сравнения длин сторон двух треугольников. Если отношения конгруэнтны, соответствующие стороны подобны друг другу.
Угол в комплекте
Угол в комплекте относится к углу между двумя парами соответствующих сторон. Вы не можете сравнить две стороны двух треугольников, а затем перепрыгнуть на угол, который не находится между этими двумя сторонами.
Доказательство подобных треугольников
Вот два конгруэнтных треугольника. Чтобы облегчить вам жизнь, мы сделали их равносторонними треугольниками.
△FOX сравнивается с △HEN. Обратите внимание, что ∠O на △FOX соответствует ∠E на △HEN. И ∠O, и ∠E являются 90 535 включенными углами 90 536 между сторонами FO и OX на △FOX и сторонами HE и EN на △HEN.
Сторона FO конгруэнтна стороне HE; сторона OX конгруэнтна стороне EN, а ∠O и ∠E — заключенные между ними конгруэнтные углы.
Два равносторонних треугольника одинаковы, за исключением их букв. Они одинакового размера, поэтому они представляют собой одинаковых треугольников . Если бы они оба были равносторонними треугольниками, но сторона EN была вдвое длиннее стороны HE, то они были бы подобных треугольников .
Теоремы подобия треугольников
Теорема об угле-угле (AA)
Угол-Угол (AA) говорит, что два треугольника подобны, если они имеют две пары соответствующих углов, которые конгруэнтны. Два треугольника могут быть на 90 535 больше, чем на 90 536; они могут быть идентичными. Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.
Два треугольника могут быть на 90 535 больше, чем на 90 536; они могут быть идентичными. Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.
Попытка Angle-Angle
Вот два разносторонних треугольника △JAM и △OUT. Мы уже отметили два внутренних угла каждого треугольника с помощью геометрического обозначения конгруэнтности: маленьких косых черт. Одинарная косая черта для внутренней части ∠A и такая же косая черта для внутренней части ∠U означают, что они конгруэнтны. Обратите внимание, что ∠M конгруэнтно ∠T, потому что у каждого из них есть две маленькие косые черты.
Поскольку ∠A конгруэнтна ∠U, а ∠M конгруэнтна ∠T, теперь у нас есть две пары конгруэнтных углов, поэтому теорема АА говорит, что эти два треугольника подобны.
Профессиональные хитрости
Следите за подвохами из учебников, онлайн-задач и учителей математики. Иногда треугольники не ориентированы одинаково, когда вы смотрите на них. Возможно, вам придется повернуть один треугольник, чтобы увидеть, сможете ли вы найти две пары соответствующих углов.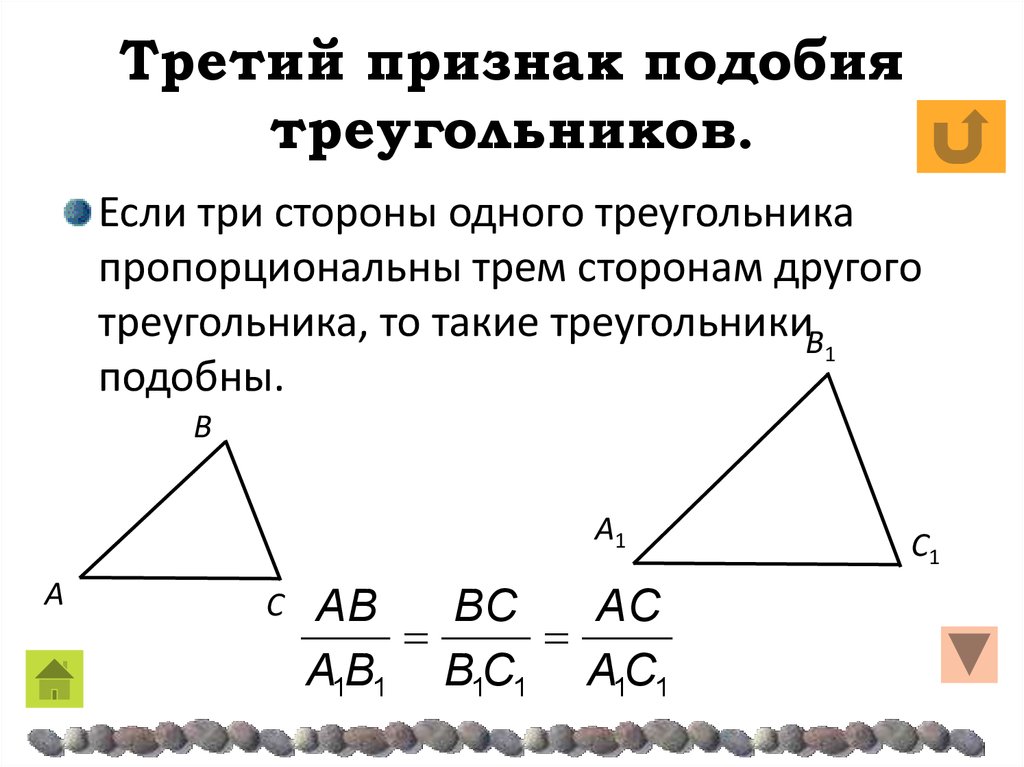
Еще одна задача: на одном треугольнике измеряются и идентифицируются два угла, а на другом измеряются и идентифицируются два разных угла.
Поскольку каждый треугольник имеет только три внутренних угла, каждый из идентифицированных углов должен быть конгруэнтным. Вычитая измеренные, идентифицированные углы каждого треугольника из 180°, вы можете узнать меру недостающего угла. Затем вы можете сравнить любые два соответствующих угла на конгруэнтность.
Сторона-угол-сторона (SAS) Теорема
Вторая теорема требует точного порядка: сторона, затем прилежащий угол, затем следующая сторона. Теорема 9019 «сторона-угол-сторона» (SAS) утверждает, что если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, а их соответствующие углы равны, то два треугольника подобны.
Пробуем Side-Angle-Side
Вот два треугольника, расположенных рядом и ориентированных одинаково. △RAP и △EMO идентифицировали стороны размером 37 дюймов на △RAP и 111 дюймов на △EMO, а также стороны 17 на △RAP и 51 дюйм на △EMO. Обратите внимание, что угол между идентифицированными и измеренными сторонами в обоих треугольниках одинаков: 47°.
Обратите внимание, что угол между идентифицированными и измеренными сторонами в обоих треугольниках одинаков: 47°.
Соотношение 37/111 такое же, как соотношение 17/51? Да; два отношения пропорциональны, поскольку каждое из них упрощается до 1/3. При одинаковом углу между ними эти два треугольника подобны.
Side-Side-Side (SSS) Теорема
Последняя теорема Side-Side-Side, или SSS . Эта теорема утверждает, что если два треугольника имеют пропорциональные стороны, то они подобны. Это может показаться большим скачком, который игнорирует их углы, но подумайте об этом: единственный способ построить треугольник со сторонами, пропорциональными сторонам другого треугольника, — это скопировать углы.
Попытка Side-Side-Side
Вот два треугольника, △FLO и △HIT. Обратите внимание, что мы не определили внутренние углы. Стороны △FLO имеют длину 15, 20 и 25 см. Стороны △HIT имеют длину 30, 40 и 50 см.
Вам необходимо установить отношения соответствующих сторон и оценить их:
1530 = 12
2040 = 12
2550 = 12
2550 = 12
9000, когда все они упрощены. Их всех 12. Таким образом, даже не зная внутренних углов, мы знаем, что эти два треугольника подобны, потому что их стороны пропорциональны друг другу.
Их всех 12. Таким образом, даже не зная внутренних углов, мы знаем, что эти два треугольника подобны, потому что их стороны пропорциональны друг другу.
Итоги урока
Теперь, когда вы изучили этот урок, вы можете определять и идентифицировать подобные фигуры, а также можете описать требования, чтобы треугольники были подобными (у них должны быть либо две конгруэнтные пары соответствующих углов, либо два пропорциональных соответствующих угла). стороны с включенным соответствующим углом конгруэнтны или все соответствующие стороны пропорциональны).
Вы также можете применить три теоремы подобия треугольников, известные как Угол — Угол (AA), Сторона — Угол — Сторона (SAS) или Сторона — Сторона — Сторона (SSS), чтобы определить, подобны ли два треугольника.
Следующий урок:
Постулаты о сходстве треугольников
Подобные треугольники — Дороти Мохан
ГЛАВНАЯ > w3.org/1999/xhtml» align=»left»> Подобные треугольники
| |||||||||||
Конгруэнтные треугольники
Треугольники, имеющие одинаковые размеры и форму, называются равных треугольников. Символ конгруэнтности ≅. Два треугольника равны, если три стороны и три угла одного треугольника имеют те же размеры, что и три стороны и три угла другого треугольника. Треугольники на рисунке 1 являются конгруэнтными треугольниками.
Рисунок 1 Конгруэнтные треугольники.
Соответствующие детали
Части двух треугольников, имеющие одинаковые размеры (конгруэнтные), называются соответствующие детали. Это означает, что соответствующих частей конгруэнтных треугольников конгруэнтны (CPCTC). Конгруэнтные треугольники называются путем перечисления их вершин в соответствующем порядке. На рисунке Δ BAT ≅ Δ ICE .
Пример 1: Если Δ PQR ≅ Δ STU , какие детали должны иметь одинаковые размеры?
Эти части равны, потому что соответствующие части конгруэнтных треугольников конгруэнтны.
Тесты на конгруэнтность
Чтобы показать, что два треугольника конгруэнтны, нет необходимости доказывать, что все шесть пар соответствующих частей равны. Следующие постулаты и теоремы являются наиболее распространенными методами доказательства конгруэнтности (или равенства) треугольников.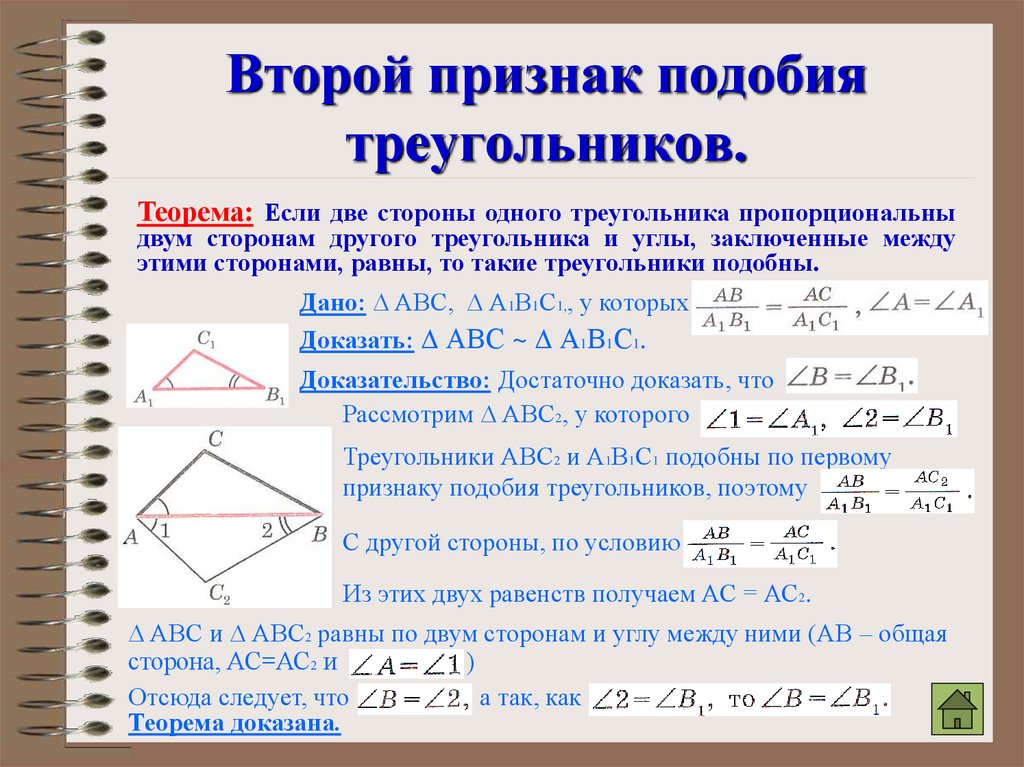
Постулат 13 (постулат SSS): Если каждая сторона одного треугольника конгруэнтна соответствующей стороне другого треугольника, то треугольники конгруэнтны (рис. 2).
Рисунок 2 Соответствующие стороны (SSS) двух треугольников конгруэнтны.
Постулат 14 (постулат SAS): Если две стороны и угол между ними в одном треугольнике конгруэнтны соответствующим частям другого треугольника, то эти треугольники конгруэнтны (рис. 3).
Рисунок 3 Две стороны и угол между ними (SAS) одного треугольника равны
соответствующих частей другого треугольника.
Постулат 15 (Постулат АСА): Если два угла и сторона между ними в одном треугольнике конгруэнтны соответствующим частям в другом треугольнике, то такие треугольники конгруэнтны (рис. 4).
Рисунок 4 Два угла и их общая сторона (ASA) в одном треугольнике равны
соответствующих частей другого треугольника.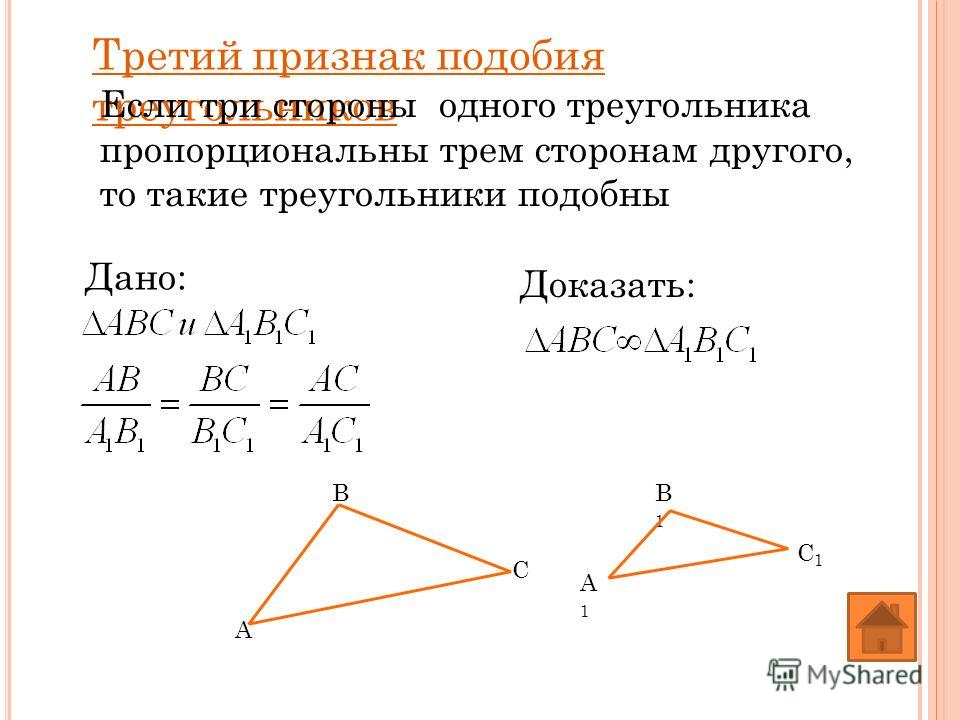
Теорема 28 (Теорема ААС): Если два угла и сторона, не заключенная между ними в одном треугольнике, конгруэнтны соответствующим частям в другом треугольнике, то такие треугольники конгруэнтны (рис. 5).
Рисунок 5 Два угла и сторона, противолежащая одному из этих углов (ААС) в одном треугольнике
равны соответствующим частям другого треугольника.
Постулат 16 (постулат HL): Если гипотенуза и катет одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 6).
Рисунок 6 Гипотенуза и катет (HL) первого прямоугольного треугольника равны
соответствующих частей второго прямоугольного треугольника.
Теорема 29 (Теорема HA): Если гипотенуза и острый угол одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то эти треугольники конгруэнтны (рис. 7).
7).
Рисунок 7 Гипотенуза и острый угол (HA) первого прямоугольного треугольника равны
к соответствующим частям второго прямоугольного треугольника.
Теорема 30 (Теорема LL): Если катеты одного прямоугольного треугольника конгруэнтны соответствующим частям другого прямоугольного треугольника, то треугольники конгруэнтны (рис. 8).
Рисунок 8 Катеты (LL) первого прямоугольного треугольника конгруэнтны соответствующим частям
второго прямоугольного треугольника.
Теорема 31 (теорема LA): Если один катет и острый угол одного прямоугольного треугольника равны соответствующим частям другого прямоугольного треугольника, то эти треугольники равны (рис. 9).
Рисунок 9 Один катет и острый угол (LA) первого прямоугольного треугольника равны
соответствующих частей второго прямоугольного треугольника.
Пример 2: Основываясь на маркировке на рисунке 10, заполните заявление о сравнении Δ ABC ≅Δ .
Рисунок 10 Конгруэнтные треугольники.
Δ YXZ , потому что A соответствует Y , B соответствует X , а C соответствует Z .
Пример 3: Каким методом будет доказана конгруэнтность каждого из треугольников на рисунках с 11 (а) по 11 (i)?
Рисунок 11 Методы доказательства конгруэнтности пар треугольников.
- (а) САС.
- (б) Нет. Метода AAA не существует.
- (с) HL.
- (г) ААС.
- (e) ССС. Третья пара конгруэнтных сторон — это сторона, общая для двух треугольников.
- (f) SAS или LL.
- (г) LL или SAS .

- (h) HA или AAS.
- (i) Нет. Метода SSA не существует.
Пример 4: Назовите дополнительные равные соответствующие части, необходимые для доказательства конгруэнтности треугольников на рисунках с 12 (a) по 12 (f) согласно указанному постулату или теореме.
Рисунок 12 Дополнительная информация, необходимая для доказательства конгруэнтности пар треугольников.
- (a) BC = EF или AB = DE (, но не AC = DF , потому что эти две стороны лежат между равными углами).
- (б) GI = JL.
- (c) MO = PO и NO = RO.
- (г) ТУ = ШХ и СУ = ВХ.
- (e) м ∠ T = м ∠ E и м ∠TOW = m ∠ EON.

- (f) IX = EN или SX = TN (но не IS = ET , поскольку они являются гипотенузами).
Подобные треугольники и тригонометрия
Подобные треугольники и тригонометрия Вернуться к оглавлениюОбзор урока
- Подобные треугольники
- Среднее геометрическое
- Особые треугольники, отношения длин сторон и тригонометрия
- Векторы, произведения векторов и векторные пространства
- Домашнее задание

Подобные треугольники
| Если три стороны треугольника пропорциональны трем сторонам другого треугольника, тогда треугольники подобны (теорема подобия SSS). | ВЫРАВНИВАНИЕ=ЦЕНТР>
| Если углы (два означает три) двух треугольников равны, тогда треугольники подобны (теорема о подобия АА). | ВЫРАВНИВАНИЕ=ЦЕНТР>
| Если две стороны треугольника пропорциональны двум сторонам другого
треугольник и углов равны, то треугольники подобны (теорема подобия SAS). | ВЫРАВНИВАНИЕ=ЦЕНТР>
Таким образом, остается случай SSA (ASS), который остается двусмысленный если не возникает HL или SsA.
| Прямые, параллельные стороне треугольника, пересекают две другие стороны в невершинах, тогда и только тогда, когда две стороны разделены на пропорциональные сегменты. 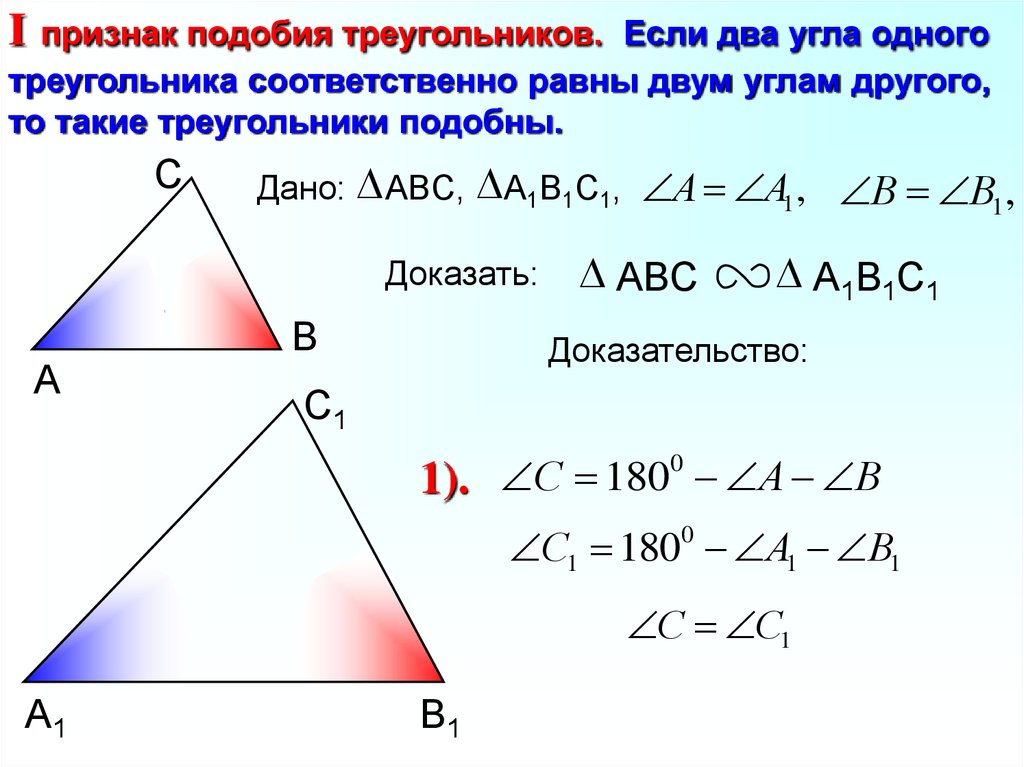 | ВЫРАВНИВАНИЕ=ЦЕНТР>
Поскольку эта теорема дается как тогда и только тогда, она работает в обоих направлениях. Таким образом, в учебнике есть и теорема, и ее обращение.
Среднее геометрическое
Мы ввели среднее геометрическое несколько в последняя глава и немного в статистике. Пожалуйста, ознакомьтесь с тем, что у нас есть. Обычно среднее геометрическое впервые встречается в пропорция когда средние равны, как в 8/ w 90 668 = 90 667 w 90 668 /4. Здесь w 2 =32 и квадратный корень с обеих сторон дает ответ. Однако, в целом, может быть n n th средние геометрические. Таким образом, мы не можем быть уверены в знаке w выше. Среднее геометрическое развито здесь из-за его применения к правому
треугольники и то, как высота гипотенузы делит треугольник
в подобные треугольники.
Предположим, у вас есть два из трех членов в геометрической последовательности,
например 2, ?, 50.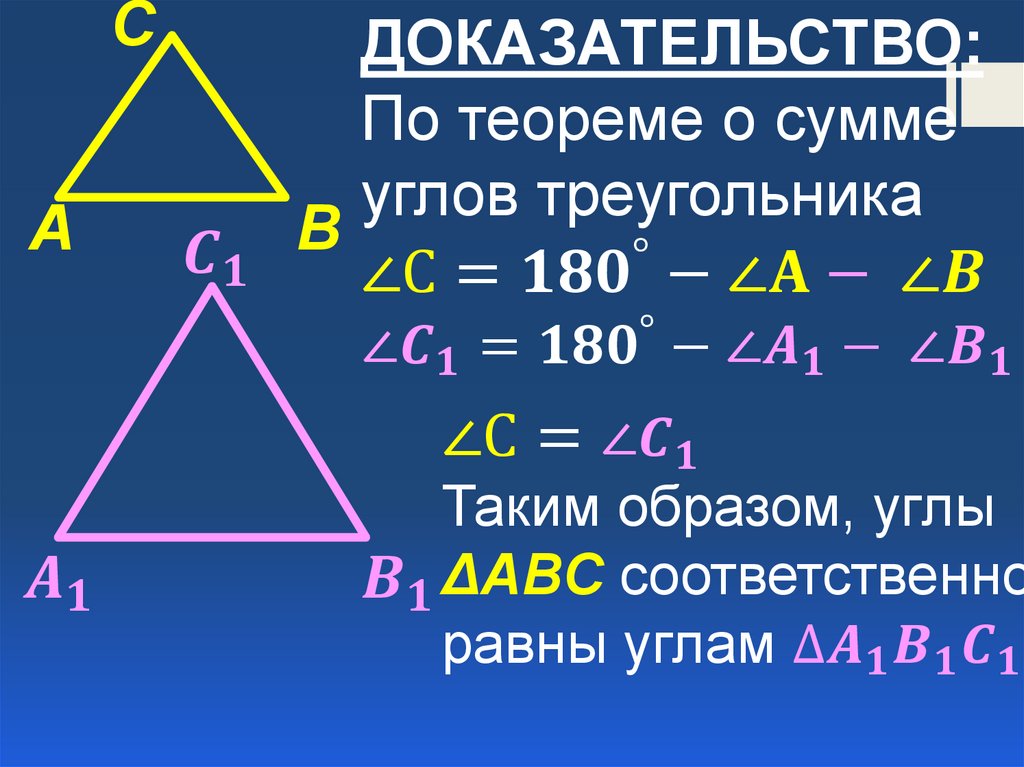 Другими словами, вам нужно число g ,
так что 2/ г = г /50, или 250=100= г 2 ,
поэтому очевидно, что г = 10 или, возможно, г = -10. Часто положительный
требуется среднее геометрическое, и оно будет указано таким образом.
Другими словами, вам нужно число g ,
так что 2/ г = г /50, или 250=100= г 2 ,
поэтому очевидно, что г = 10 или, возможно, г = -10. Часто положительный
требуется среднее геометрическое, и оно будет указано таким образом.
Использование строчных букв a , b и c для
Стороны треугольника — это общепринятое соглашение, восходящее к Эйлеру.
которых мы будем придерживаться. a относится либо к набору точек, составляющих сторону, либо к
длина стороны в зависимости от контекста. Угол против стороны и равен A , угол против b равен B , а угол
противоположная сторона c равна C . Если это прямоугольный треугольник, C будет правильно, поэтому c будет [длиной] гипотенузы.
Дан прямоугольный треугольник ABC высотой h (CD) до
гипотенуза, ч = ( х у ),
тогда как a = ( c x ),
и б =( с г ). Здесь х + у = с (BD + AD = AB),
и y катет подобного треугольника с гипотенузой b ,
а x — катет подобного треугольника с гипотенузой a .
Здесь х + у = с (BD + AD = AB),
и y катет подобного треугольника с гипотенузой b ,
а x — катет подобного треугольника с гипотенузой a .
| Высота треугольника – это среднее геометрическое отрезков
гипотенуза, которую она делит. Каждая сторона также была бы средним геометрическим гипотенуза и прилежащий к ней отрезок гипотенузы. | ALIGN=CENTER>
Специальные треугольники, отношения длин сторон и тригонометрия
Прямоугольный равнобедренный треугольник (45 ° 45 ° 90 ° ) очень необычный треугольник. Длины его сторон образуют совершенно особое соотношение, которое необходимо запомнить. В частности, если обе стороны имеют длину x , то гипотенуза имеет длину х по теорема Пифагора. Это соотношение 1/ = /2 или около 0,707 должны стать привычными. Аналогично, 30 ° 60 ° 90 ° треугольник нужно как-то запомнить. Один из способов — начать с
равносторонний треугольник, делит пополам один угол, который также делит пополам противоположную сторону,
и рассмотрим получившиеся конгруэнтные треугольники.
Очевидно, два конгруэнтных 30 ° 60 ° 90 ° образуются треугольники. Снова по теореме Пифагора длина стороны
соотношение может быть 1::2.
По теореме подобия AA любой треугольник с этими углами имеет эти
точное соотношение длин сторон.
Один из способов — начать с
равносторонний треугольник, делит пополам один угол, который также делит пополам противоположную сторону,
и рассмотрим получившиеся конгруэнтные треугольники.
Очевидно, два конгруэнтных 30 ° 60 ° 90 ° образуются треугольники. Снова по теореме Пифагора длина стороны
соотношение может быть 1::2.
По теореме подобия AA любой треугольник с этими углами имеет эти
точное соотношение длин сторон.
В прямоугольных треугольниках отношения длин шести сторон равны пропорциональны углам и называются следующим образом.
| sin A = противоположный катет ÷ гипотенуза
csc A = гипотенуза ÷ противолежащий катет cos A = соседний катет ÷ гипотенуза сек А = гипотенуза ÷ соседний катет tan A = противоположная ветвь ÷ соседняя ветвь кроватка A = соседняя ножка ÷ противоположная ножка |
Различные мнемоники обычно используются, чтобы помочь вспомнить эти отношения. SOH-CAH-TOA, с некоторой апокрифической ссылкой на так называемого индейского вождя,
общие: S = синус, O = противоположность, H = гипотенуза, C = косинус, A = смежная, T = касательная.
Oh Hech Another Hour Of Algebra — еще одна похожая мнемоника.
Совсем недавно мое внимание привлек еще один: OHAHOAAO, т.е.
сокращение от «Оскар однажды приложил руку к арке Алисы», что дает, по порядку,
отношения для синуса, косинуса, тангенса и котангенса.
Обратите внимание, как правая колонка взаимодействует с левой колонкой.
По этой причине левая колонка считается основной.
тригонометрические функции и вторичный правый столбец.
Большинство калькуляторов имеют только основные триггерные функции.
SOH-CAH-TOA, с некоторой апокрифической ссылкой на так называемого индейского вождя,
общие: S = синус, O = противоположность, H = гипотенуза, C = косинус, A = смежная, T = касательная.
Oh Hech Another Hour Of Algebra — еще одна похожая мнемоника.
Совсем недавно мое внимание привлек еще один: OHAHOAAO, т.е.
сокращение от «Оскар однажды приложил руку к арке Алисы», что дает, по порядку,
отношения для синуса, косинуса, тангенса и котангенса.
Обратите внимание, как правая колонка взаимодействует с левой колонкой.
По этой причине левая колонка считается основной.
тригонометрические функции и вторичный правый столбец.
Большинство калькуляторов имеют только основные триггерные функции.
Рассмотрим прямоугольный треугольник с c = 1, одна вершина в начале координат,
одна сторона вдоль оси x , и прямой угол, образованный
перпендикулярно оси x , таким образом, гипотенуза лежит в квадранте I.
В этом случае мы часто обозначаем одну ногу и , а другую
другая нога x .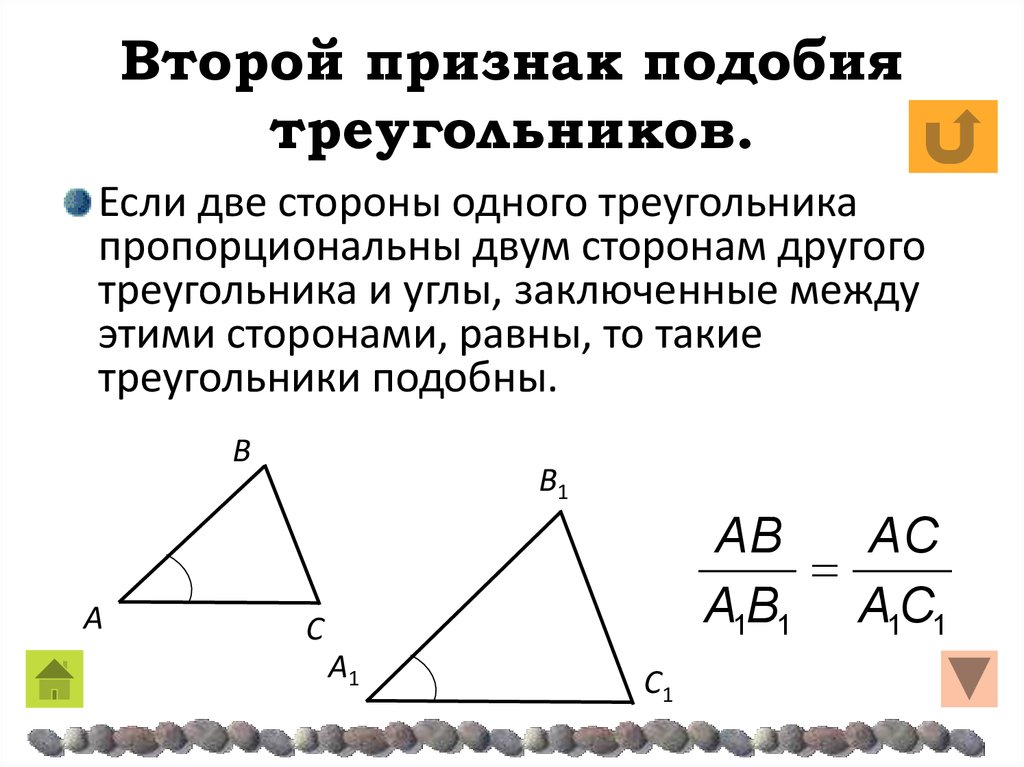 Рассмотрим, что произойдет, если мы позволим углу
при изменении происхождения. С увеличением угла противоположная сторона
увеличивается. Поскольку мы исправили c =1, эта вершина вычерчивает
часть единичного круга. Функция синуса описывает, как это
боковые изменения с углом, начиная с 0 для 0 ° и
монотонно возрастая до 1 за 90 ° (разумеется
при 0 ° и 90 ° это действительно не треугольник).
Точно так же функция косинуса, которая описывает, как соседняя сторона
варьируется, начинается с 1 для 0 ° и
всегда уменьшается до 0 для 90 ° .
Рассмотрим, что произойдет, если мы позволим углу
при изменении происхождения. С увеличением угла противоположная сторона
увеличивается. Поскольку мы исправили c =1, эта вершина вычерчивает
часть единичного круга. Функция синуса описывает, как это
боковые изменения с углом, начиная с 0 для 0 ° и
монотонно возрастая до 1 за 90 ° (разумеется
при 0 ° и 90 ° это действительно не треугольник).
Точно так же функция косинуса, которая описывает, как соседняя сторона
варьируется, начинается с 1 для 0 ° и
всегда уменьшается до 0 для 90 ° .
Тангенс – это не только отношение противолежащего катета к прилежащему.
стороны, но также может быть записано как синус над косинусом.
Если косинус равен 0, у нас есть проблема, деление на ноль,
поэтому тангенс 90 90 325 ° 90 326 не определен.
Большие таблицы триггерных функций были обычным явлением до появления калькуляторов.
стал повсеместным. Ниже небольшая таблица в 5 ° с шагом от 0 ° до 90 ° .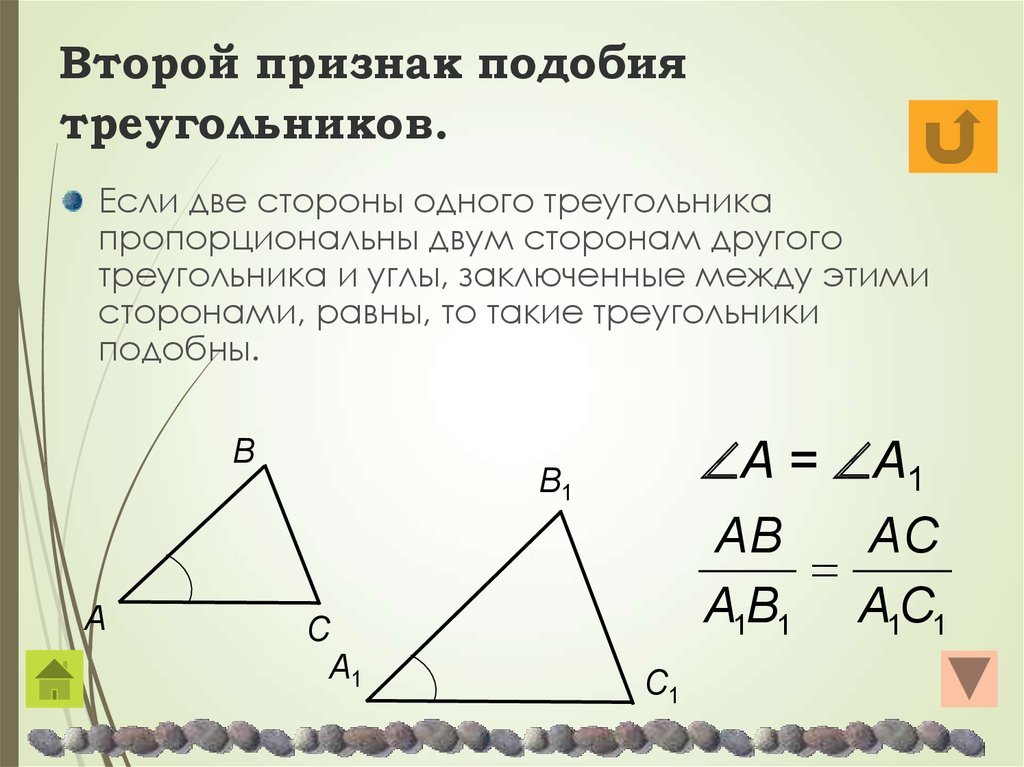 Обратите внимание, что значения косинуса совпадают со значениями синуса.
дополнительного угла. Тангенс и котангенс связаны аналогичным образом.
В следующем уроке эти триггерные функции будут расширены за пределы прямого угла,
на отрицательные углы, изобразите их на графике,
и снова ввести блок круг .
Обратите внимание, что значения косинуса совпадают со значениями синуса.
дополнительного угла. Тангенс и котангенс связаны аналогичным образом.
В следующем уроке эти триггерные функции будут расширены за пределы прямого угла,
на отрицательные углы, изобразите их на графике,
и снова ввести блок круг .
| Угол (градусы) | Угол (Радианы) | Синус | косицине | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | .0000 | 1.0000 | .0000 | NAN | 1.00088 1.00088|||||||||||||
| 5 | /36 | .0872 | .9962 | .0875 | 11.4301 | 1.0037 | 1.4738 8||||||||||||
| 10 | /18 | .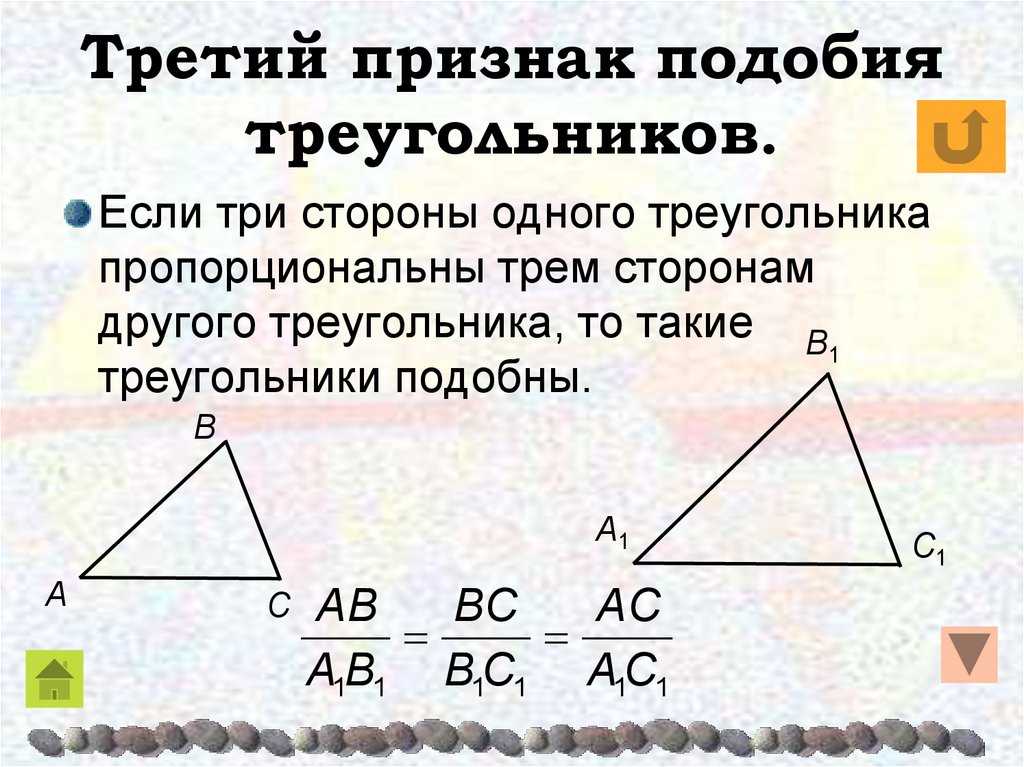 1736 1736 | .9848 | . | ||||||||||||||
| 15 | /12 | .2588 | .9659 | .2679 | 3.73218 10378 | 1278 3,8637 | ||||||||||||
| 20 | / | .3420 | .9397 | . | ||||||||||||||
| 25 | 5/36 | .4226 | .9063 | .4663 | 2,1445 | 1.1034 | 2,366298 | 1.1034 | 2,366298 | 1.1034 | 2,3662 | 1.1034 | 2,3662 | 1.1034 | 2.366298 | 1. 1034 1034 | 2,36278 | . |
| 30 | /6 | .5000 | .8660 | .5774 | 1,7321 | 1,1547 | 2,0000 | |||||||||||
| 35 | 7/36 | . | ||||||||||||||||
| 40 | 2/9 | .6428 | . | |||||||||||||||
| 45 | /4 | .7071 | .7071 | 1,0000 | 1,0000 | 1,4142 | 1,4142 | |||||||||||
| 50 | 5/18 | .7660 | .6428 | 1,1918 | .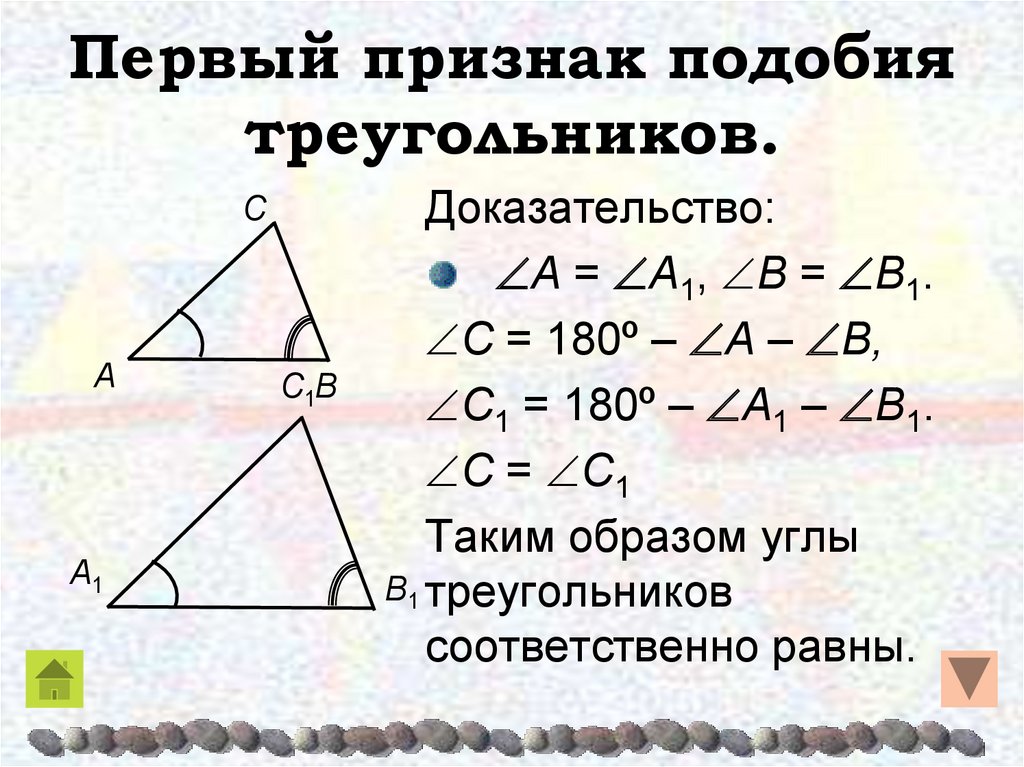 | |||||||||||||
| 55 | 11/36 | .8192 | .5736 | 1,4281 | . | |||||||||||||
| 60 | /3 | .8660 | .5000 | 1.7321 | .5774 | 2.0000 | 1.1547 | |||||||||||
| 65 | 13/36 | .9063 | .4226 | 2.1445 | . | |||||||||||||
| 70 | 7/18 | .9397 | .3420 | 2,7475 | . | |||||||||||||
| 75 | 5/12 | .9659 | .2588 | 3. 7321 7321 | . | |||||||||||||
| 80 | 4/9 | .9848 | .1736 | 5,6713 | . | |||||||||||||
| 85 | 17/36 | .9962 | .0872 | 11.4301 | .0875 | 11,4737 | 1,0038 | |||||||||||
| 90 | /2 | 1.0000 | .0000 | NAN | .00008 1078Бесконечно 9 | ВЫРАВНИВАНИЕ=ЦЕНТР>
Обратите особое внимание на NAN для tan 90 ° = cot 0 ° .
NAN — это F ORTRAN ese, что означает «не число».
Может показаться, что она приближается к положительной бесконечности, но поскольку она будет приближаться
отрицательный при приближении к 90 ° сверху, а так как
два предела не согласуются, мы говорим, что это не число или неопределенное.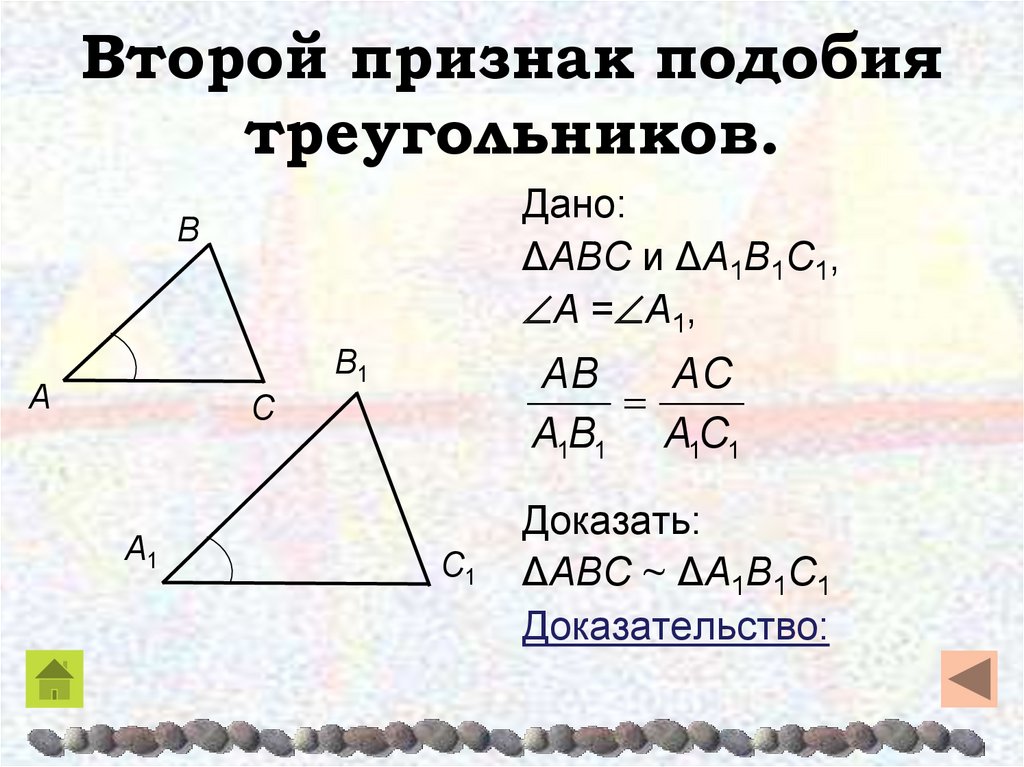
Пример: Рассмотрим флагшток, установленный точно перпендикулярно земле, который отбрасывает тень длиной 11,3355 м и углом от земли вверх на кончике тень к кончику полюса равна 34,5543 ° . Какова высота флагштока для правильного значения? Решение: Тангенс — это отношение стороны, противолежащей данному углу. в соседнюю сторону, таким образом, загар 34,5543 ° = ч /11,3355м. Решив для ч , получим ч =11,3355мtg 34,5543 ° =7,80650м. Если вы получили отрицательный ответ, переключите калькулятор в режим градусов!
Площадь любого треугольника можно найти, разделив его на два прямоугольных треугольника.
| Площадь треугольника = (1/2) a b sin C , где C угол между сторонами a и б . | ALIGN=CENTER>
Векторы, векторные произведения, векторные пространства
Математика и физика часто классифицируют объекты по размерности.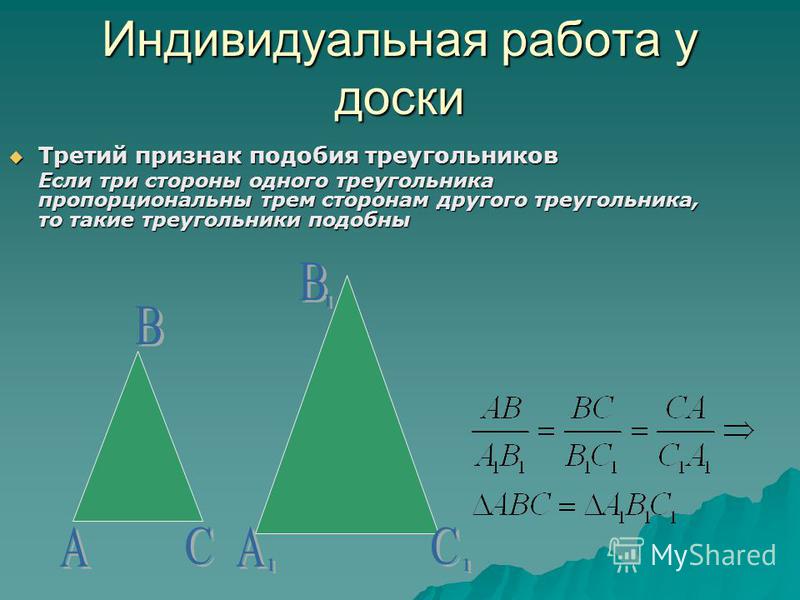 скаляров (только величина) и векторов (величина плюс направление)
занимают нижние ступени. Классический пример физики включает
скорость (скаляр) и скорость (вектор).
объект движется, но не в каком направлении.
скаляров (только величина) и векторов (величина плюс направление)
занимают нижние ступени. Классический пример физики включает
скорость (скаляр) и скорость (вектор).
объект движется, но не в каком направлении. Один из способов разработки векторов использует декартову систему координат.
и заказанные пары или тройки. Затем вектор определяется
направленный отрезок прямой из начала координат в заданную точку.
Конец в начале координат равен 9.0196 хвост, тогда как другой
конец — это головка и часто наконечник стрелы, который он туда кладет.
Это дает определенное направление между [0 ° ,360 ° )
и определенную величину или длину, которая может быть рассчитана с помощью
формула расстояния. Вектор, представленный направленным отрезком прямой
между (0,0) и (3,4) такое же, как и между (1,1) и (4,5),
однако, поскольку они имеют одинаковую величину и направление.
Мы часто говорим, что можем перемещать вектор до тех пор, пока не изменим его.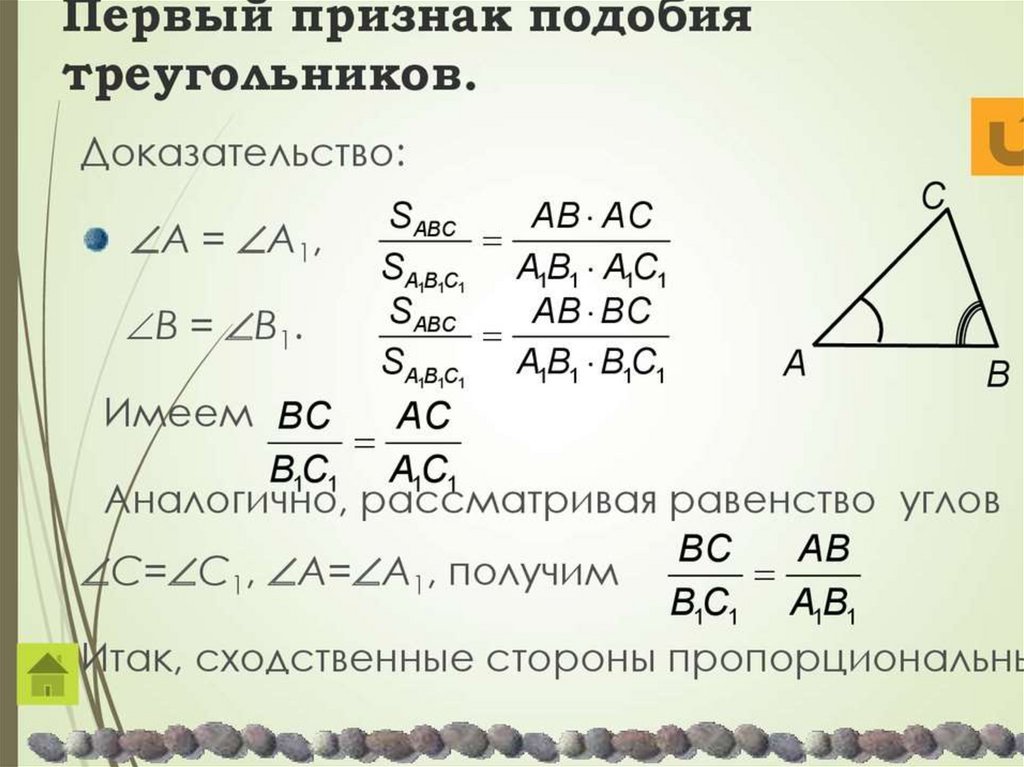 направление, которое он указывает, или его длина.
Мы часто разбиваем векторы на х , х и х Компоненты , , особенно с использованием синусов и косинусов для и и
Компоненты x . Единичные векторы , векторы длины 1,
особенно в направлениях x , y и z .
также используется. Для них есть специальные названия: i =(1,0,0), j =(0,1,0) и k =(0,0,1).
Единичный вектор в другом направлении, например v =(1,1,1) можно получить
путем деления этого вектора на его длину, обозначенную | против |:
(1,1,1)/, где подразумевается, что скаляр
относится ко всем компонентам упорядоченной тройки.
направление, которое он указывает, или его длина.
Мы часто разбиваем векторы на х , х и х Компоненты , , особенно с использованием синусов и косинусов для и и
Компоненты x . Единичные векторы , векторы длины 1,
особенно в направлениях x , y и z .
также используется. Для них есть специальные названия: i =(1,0,0), j =(0,1,0) и k =(0,0,1).
Единичный вектор в другом направлении, например v =(1,1,1) можно получить
путем деления этого вектора на его длину, обозначенную | против |:
(1,1,1)/, где подразумевается, что скаляр
относится ко всем компонентам упорядоченной тройки.
Говорят, что векторы добавляются голова к хвосту или, если они заданы
в компонентной форме, через компоненты. Таким образом, сумма векторов
( x 1 , y 1 , z 1 ) и
( x 2 , y 2 , z 2 )
вектор:
( x 1 + x 2 , y 1 + y 2 , z 1 + z 2 ). Графически сумма представляет собой диагональ параллелограмма, образованного
добавляя их в любом порядке. [сделать схему]
Графически сумма представляет собой диагональ параллелограмма, образованного
добавляя их в любом порядке. [сделать схему]
Направление двумерного вектора можно получить из его х и и составные части. В частности, тангенс угла относительно оси x равно х / х . В вашем калькуляторе есть специальный ключ тан -1 , более известный как атан , чтобы найти этот арктангенс или обратную функцию. НЕ путайте это с взаимным. (Из контекста вам должно быть ясно, что имеется в виду, арктангенс или котангенс.) Некоторая корректировка расчетного значения станет необходимой, поскольку предполагаются результаты для квадрантов I и IV. Так как наш учебник ограничивает углы между 0 ° и 180 ° , мы отложим это до другого урока.
Скаляр или скалярное произведение векторов
( x 1 , y 1 , z 1 ) и
( x 2 , y 2 , z 2 )
скалярная величина: x 1 x 2 + г 1 г 2 + z 1 z 2 . Вектор или векторное произведение двух векторов
является более сложной сущностью, которую мы оставим для более позднего урока.
Современная физика и математика прочно базируется на
алгебра векторных пространств.
Вектор или векторное произведение двух векторов
является более сложной сущностью, которую мы оставим для более позднего урока.
Современная физика и математика прочно базируется на
алгебра векторных пространств.
| ЗАДНЯЯ ЧАСТЬ | ДОМАШНЕЕ ЗАДАНИЕ | ДЕЯТЕЛЬНОСТЬ | ПРОДОЛЖИТЬ |
|---|
- электронная почта: [email protected]
- голос/почта: 269 471-6629; BCM&S Smith Hall 105; Университет Эндрюса;
- факс/аудитория: 269 471-6646; Смит Холл 100; Берриен Спрингс, Мичиган, 49104-0140
- домашний: 269 473-2572; 610 Н. Главная улица; Берриен Спрингс, Мичиган 49103-1013
- URL-адрес: http://www.andrews.edu/~calkins/math/webtexts/geom13.htm
- Copyright © 2004-05, Кит Г. Калкинс. Пересмотрено 8 мая 2005 г. или позднее.

Равные и подобные треугольники | Brilliant Math & Science Wiki
Содержание
- Определить конгруэнтные треугольники
- Определите подобные треугольники
- Сравните подобные треугольники
- Отношения площади и периметра
- Решение проблем — базовое
- Решение проблем — средний уровень
Два треугольника равны, если они имеют три одинаковые стороны и три одинаковых угла. У нас есть методы SSS (бок-бок-бок), SAS (бок-угол-бок) и ASA (угол-бок-угол). Обратите внимание, что для конгруэнтных треугольников стороны относятся к одинаковой длине.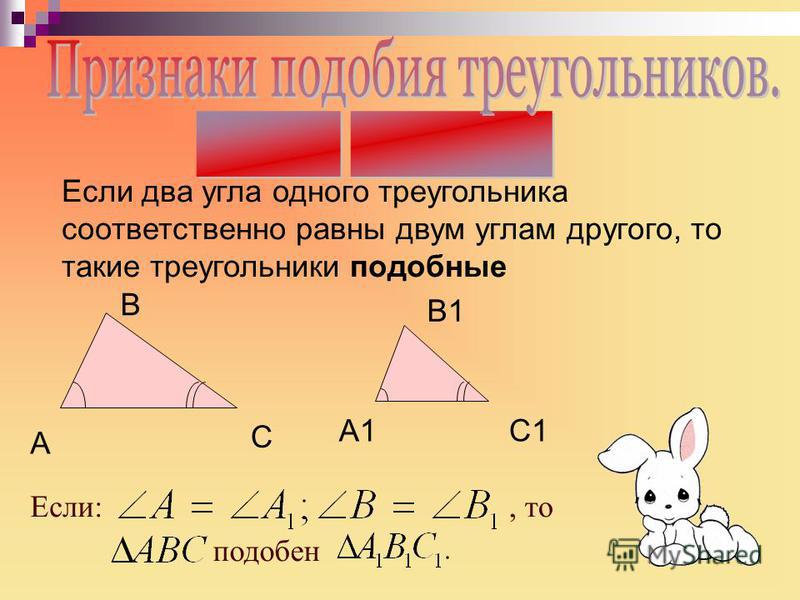 Символ LaTex для конгруэнтности ≅\cong≅ записывается как \cong.
Символ LaTex для конгруэнтности ≅\cong≅ записывается как \cong.
SSS: Поскольку мы работаем с треугольниками, если нам даны одинаковые три стороны, то мы знаем, что они имеют одинаковые три угла в процессе решения треугольников. Таким образом, два треугольника с одинаковыми сторонами будут равны.
(Примечание: если два треугольника имеют три равных угла, они не обязательно должны быть равными. Все, что мы знаем, это то, что эти треугольники подобны.)SAS: «Сторона, угол, сторона». Это особый сценарий решения треугольника, когда нам даны 2 стороны треугольника и угол между ними.
(Примечание: если вы попытаетесь использовать угол-сторона-сторона, это сделает из вас ASS. Эти треугольники не обязательно должны быть конгруэнтными или похожими. См. неоднозначный случай правила синусов для получения дополнительной информации.)ASA: «Угол, Сторона, Угол». Сторона не обязательно должна быть между углами, так как, зная два угла, мы знаем и третий.
 2R2.
2R2.Rdr\frac{R}{dr}drR rRd\frac{r}{R}dRrd Rdr\frac{R}{d}rdRr Rrd\frac{R}{r}drRd
Знаете ли вы, что вы можете приблизить диаметр луны с помощью монеты (((диаметра d)d)d), помещенной на расстоянии rrr перед вашим глазом?
Если расстояние между луной и вашим глазом равно R, R, R, каков диаметр луны?
а+абка+\фракция { аб }{ с } а+каб a+acaba+\frac { ac }{ ab } a+abac a+acba+\frac { ac }{ b } a+bac a+bcaa+\frac { bc }{ a } a+abc
Если отрезок длины aaa параллелен отрезку длины xxx На приведенной выше диаграмме, каково значение x?x?x?
Как показано выше, параллелограмм ABBCDABCDABCD разделен двумя прямыми AFAFAF и BEBEBE, так что площади красного △ABG=27\треугольника ABG = 27△ABG=27 и синего △EFG=12\треугольника EFG = 12 △EFG=12.





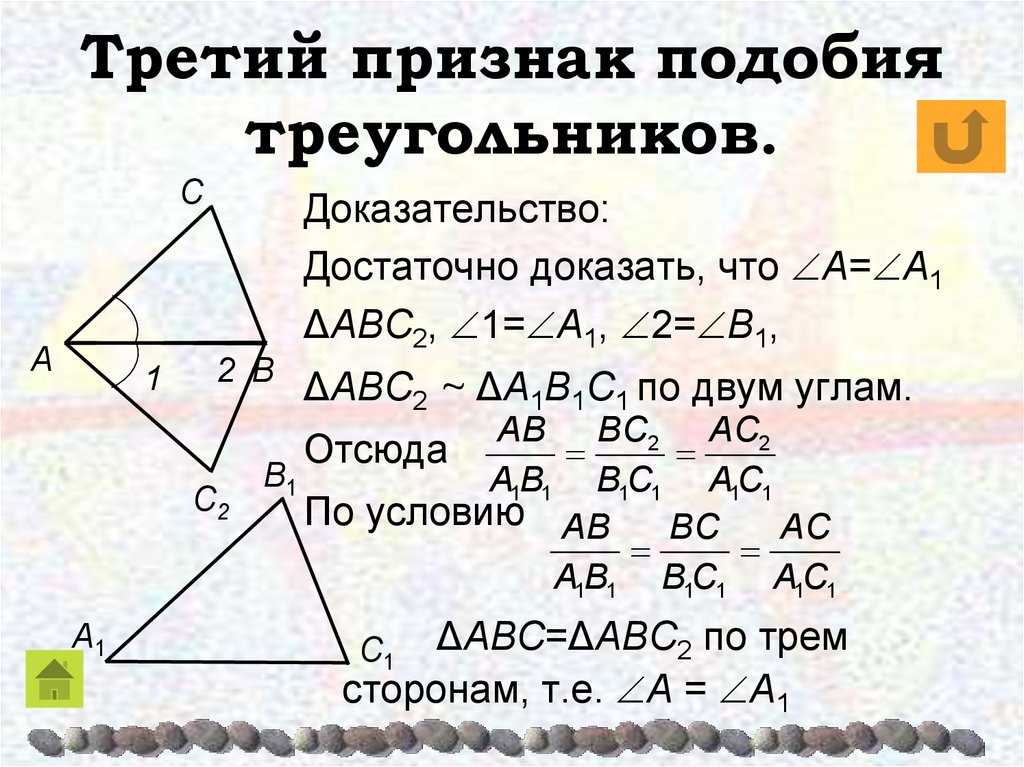


 Соответствующие стороны имеют длины в одном и том же отношении:
Соответствующие стороны имеют длины в одном и том же отношении: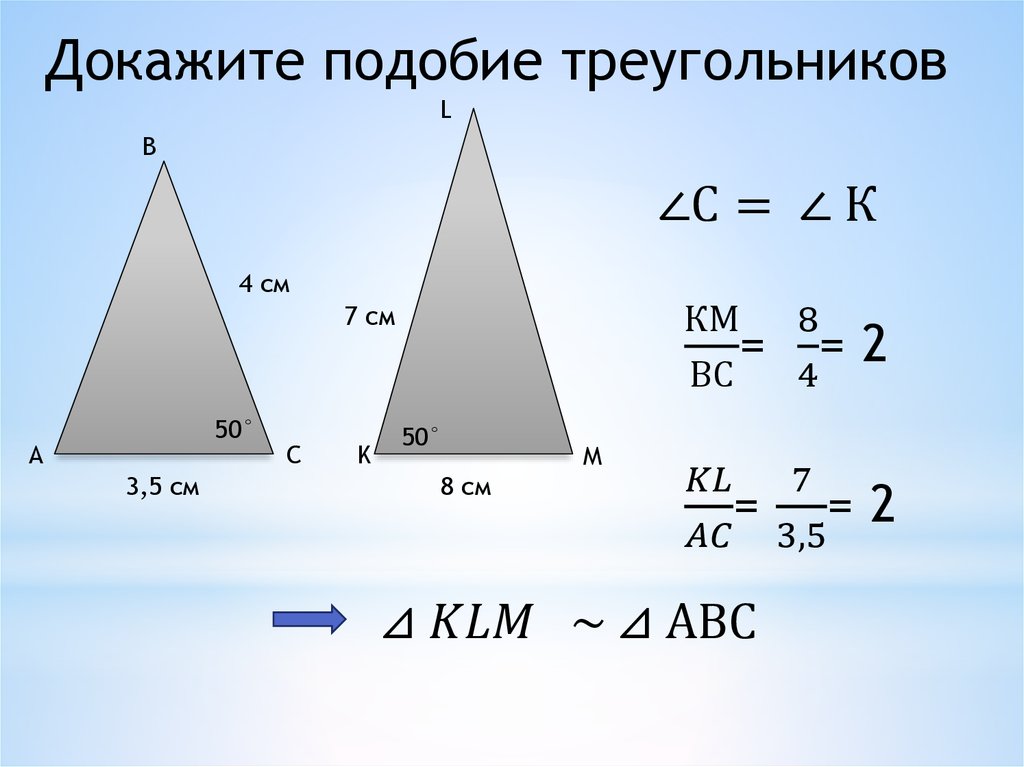 Этот критерий означает, что если
треугольник копируется для сохранения формы, затем копия масштабируется.
Этот критерий означает, что если
треугольник копируется для сохранения формы, затем копия масштабируется.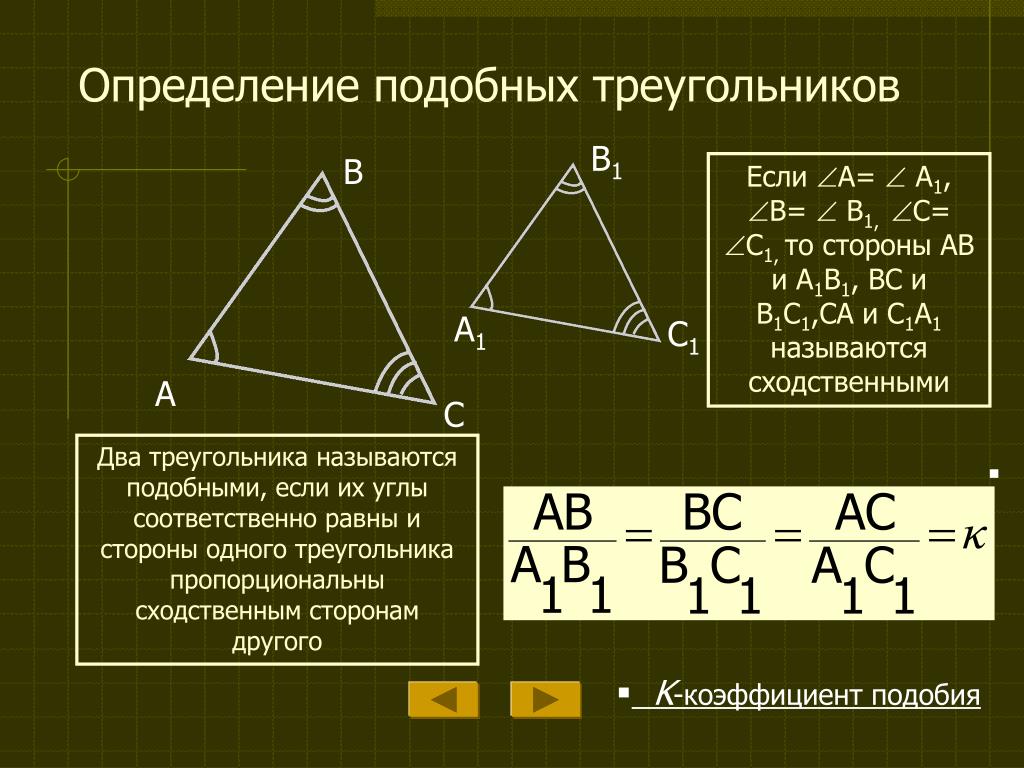 Это соотношение то, что вам нужно.
Это соотношение то, что вам нужно.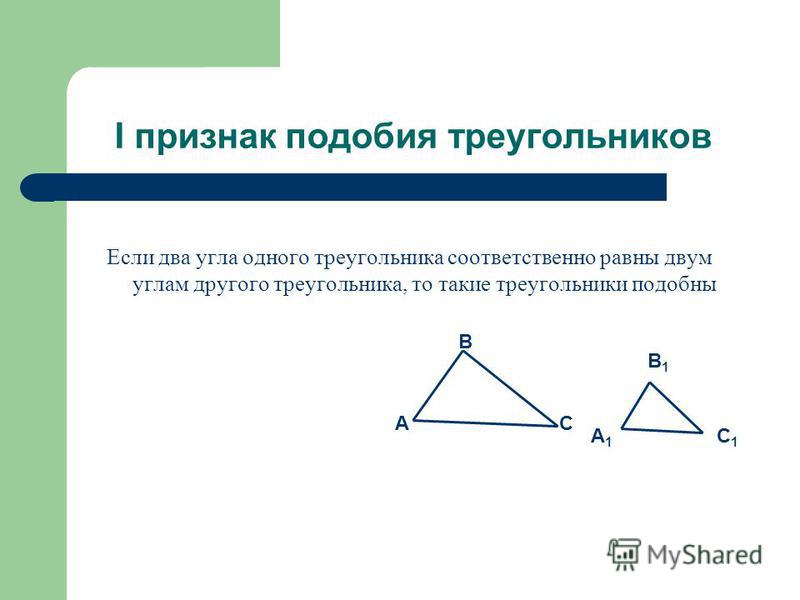

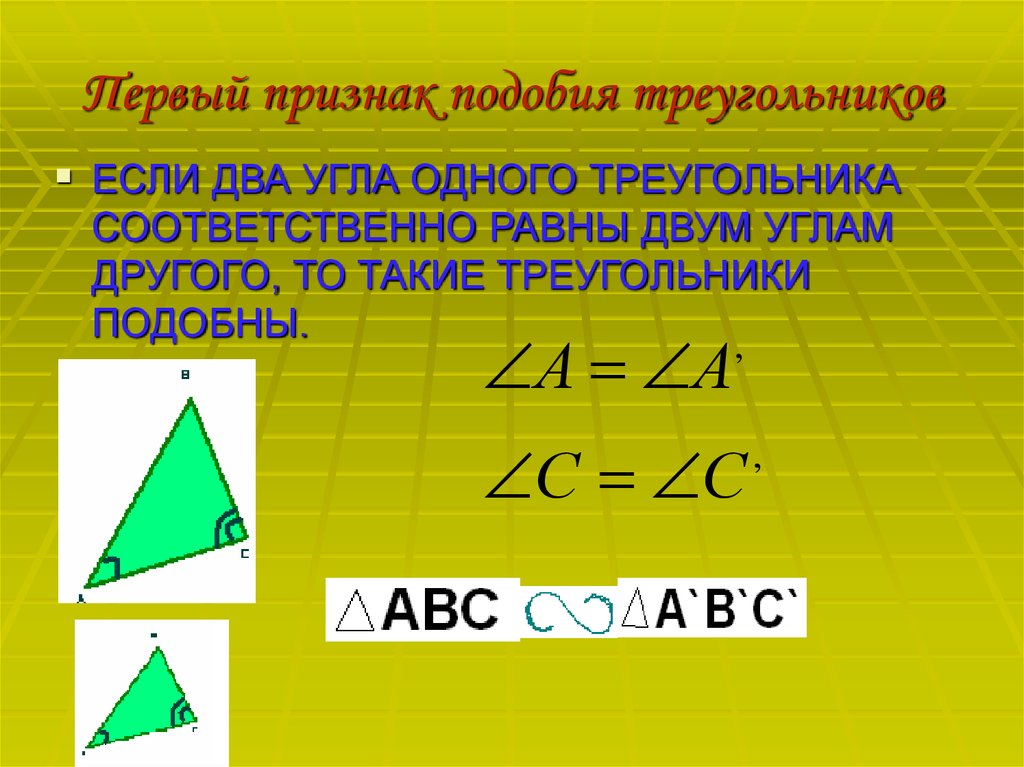



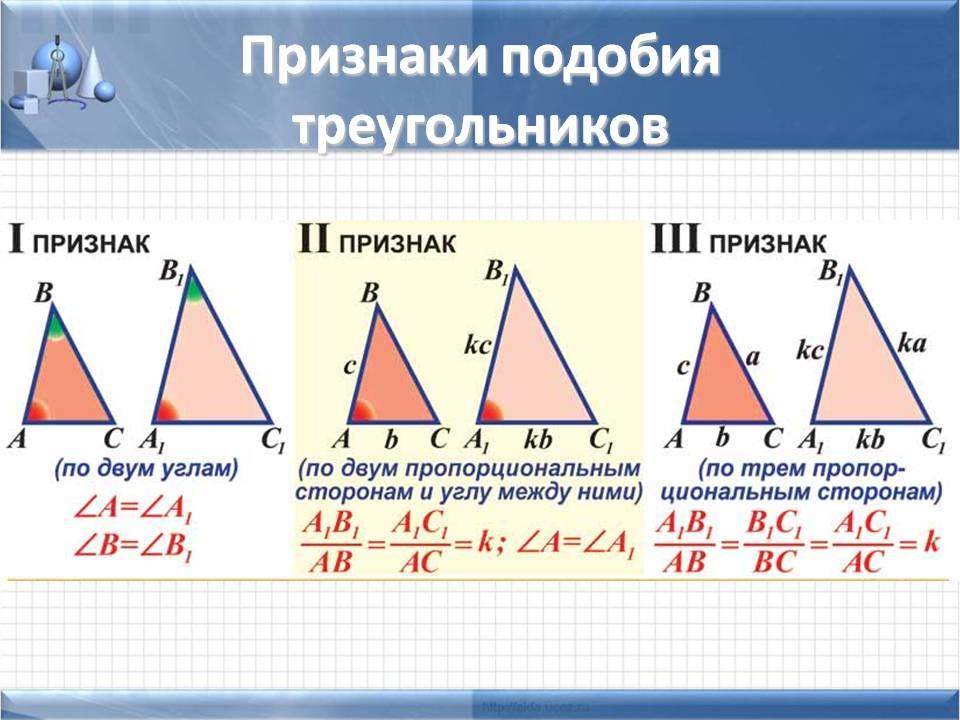 2R2.
2R2.