определения, обозначение, примеры, степень с отрицательным показателем
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a), а в качестве показателя – натуральное (обозначим буквой n).
Определение 1Степень числа a с натуральным показателем n – это произведение n-ного числа множителей, каждый из которых равен числу а. Записывается степень так: an, а в виде формулы ее состав можно представить следующим образом:
Например, если показатель степени равен 1, а основание – a, то первая степень числа a записывается как a1. Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a1=a.
Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a1=a.
В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8·8·8·8 можно сократить до 84. Примерно так же произведение помогает нам избежать записи большого числа слагаемых (8+8+8+8=8·4); мы это уже разбирали в статье, посвященной умножению натуральных чисел.
Как же верно прочесть запись степени? Общепринятый вариант – «a в степени n». Или можно сказать «n-ная степень a» либо «an-ной степени». Если, скажем, в примере встретилась запись 812, мы можем прочесть «8 в 12-й степени», «8 в степени 12» или «12-я степень 8-ми».
Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7(72), то мы можем сказать «7 в квадрате» или «квадрат числа 7». Аналогично третья степень читается так: 53 – это «куб числа 5» или «5 в кубе». (156). Но мы будем использовать обозначение anкак более употребительное.
(156). Но мы будем использовать обозначение anкак более употребительное.
О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n-ное число раз. Подробнее об этом мы писали в другой статье.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Определение 2Степень числа с целым положительным показателем можно отобразить в виде формулы: .
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Равенство am:an=am−n будет верно при условиях: m и n – натуральные числа, m <n, a≠0.
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: an:an=an−n=a0
Но при этом an:an=1 — частное равных чисел an и a. Выходит, что нулевая степень любого отличного от нуля числа равна единице.
Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: am·an=am+n .
Если n у нас равен 0, то am·a0=am (такое равенство также доказывает нам, что a0=1). Но если а также равно нулю, наше равенство приобретает вид 0m·00=0m, Оно будет верным при любом натуральном значении n, и неважно при этом, чему именно равно значение степени 00, то есть оно может быть равно любому числу, и на верность равенства это не повлияет.
При желании легко проверить, что a0=1 сходится со свойством степени (am)n=am·n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Пример 2Разберем пример с конкретными числами: Так, 50 — единица, (33,3)0=1, -4590=1, а значение 00не определено.
После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: am·an=am+n.
Введем условие: m=−n, тогда a не должно быть равно нулю. Из этого следует, что a−n·an=a−n+n=a0=1. Выходит, что an и
В итоге a в целой отрицательной степени есть не что иное, как дробь 1an.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Степень a с целым отрицательным показателем n можно представить в виде дроби 1an. Таким образом, a-n=1an при условии a≠0 и n – любое натуральное число.
Проиллюстрируем нашу мысль конкретными примерами:
Пример 43-2=132, (-4.2)-5=1(-4.2)5, 1137-1=111371
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Определение 4Степень числа a с натуральным показателем z – это: az=az, eсли z-целое положительное число1, z=0 и a≠0, (при z=0 и a=0 получается 00, значения выражения 00 не определяется) 1az, если z — целое отрицательное число и a≠0 (если z — целое отрицательное число и a=0 получается 0z, его значение не определяется)
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m/n, где n – натуральное число, а m – целое.
У нас есть некоторая степень с дробным показателем amn. Для того, чтобы свойство степени в степени выполнялось, равенство amnn=amn·n=am должно быть верным.
Учитывая определение корня n-ной степени и что amnn=am, мы можем принять условие amn=amn, если amn имеет смысл при данных значениях m, n и a.
Приведенные выше свойства степени с целым показателем будут верными при условии amn=amn.
Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m/n – это корень n-ой степени из числа a в степени m. Это справедливо в том случае, если при данных значениях m, n и a выражение amn сохраняет смысл.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
1. Мы можем ограничить значение основания степени: возьмем a, которое при положительных значениях m будет больше или равно 0, а для отрицательных – строго меньше (поскольку при m≤0 мы получаем 0m, а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:
Степень с дробным показателем m/n для некоторого положительного числа a есть корень n-ной степени из a, возведенного в степень m. В виде формулы это можно изобразить так:
amn=amn
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m/n можно выразить как
0mn=0mn=0 при условии целого положительного m и натурального n.
При отрицательном отношении mn<0 степень не определяется, т. е. такая запись смысла не имеет.
е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Выражение amn иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m. Так, верны записи (-5)23, (-1,2)57, -12-84, в которых основание отрицательно.
2. Второй подход – это рассмотреть отдельно корень amn с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a, в показателе которой стоит сократимая обыкновенная дробь, считается степенью a, в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись am·kn·k, то мы можем свести ее к amn и упростить расчеты.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то amn имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают.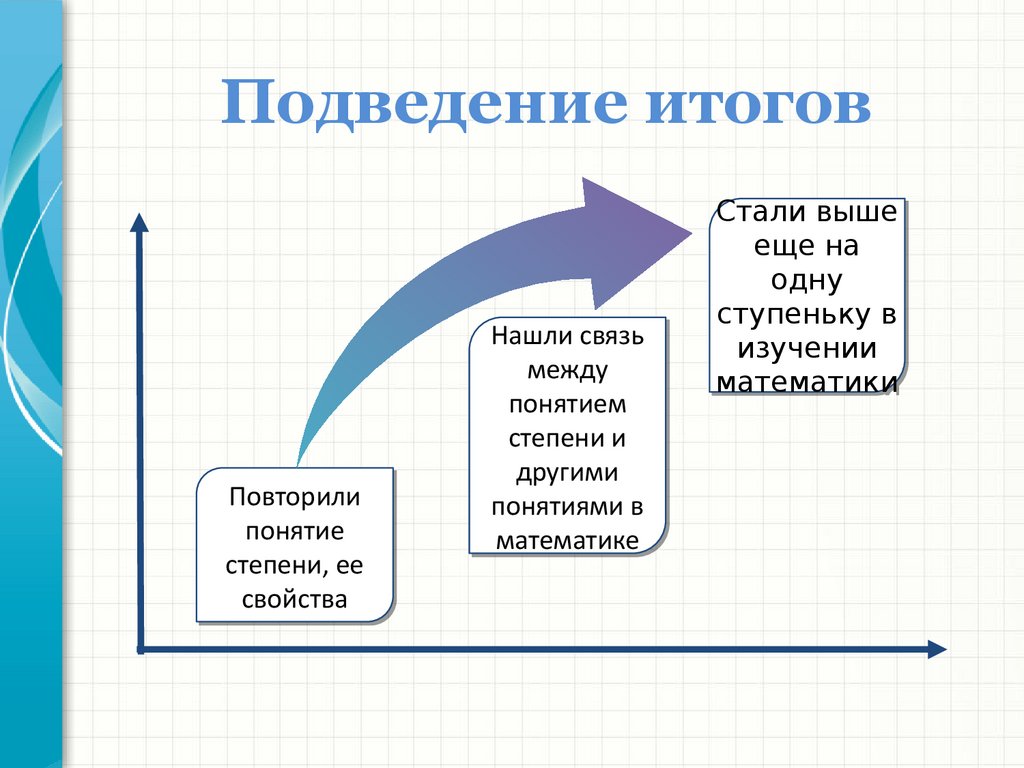 Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение 5Для любой обыкновенной сократимой дроби m·kn·k степень можно заменить на amn.
Степень числа a с несократимым дробным показателем m/n – можно выразить в виде amn в следующих случаях: — для любых действительных a, целых положительных значений m и нечетных натуральных значений n. Пример: 253=253, (-5,1)27=(-5,1)-27, 0519=0519.
— для любых отличных от нуля действительных a, целых отрицательных значений m и нечетных значений n, например, 2-53=2-53, (-5,1)-27=(-5,1)-27
— для любых неотрицательных a, целых положительных значений m и четных n, например, 214=214, (5,1)32=(5,1)3, 0718=0718.
— для любых положительных a, целых отрицательных m и четных n, например, 2-14=2-14, (5,1)-32=(5,1)-3, .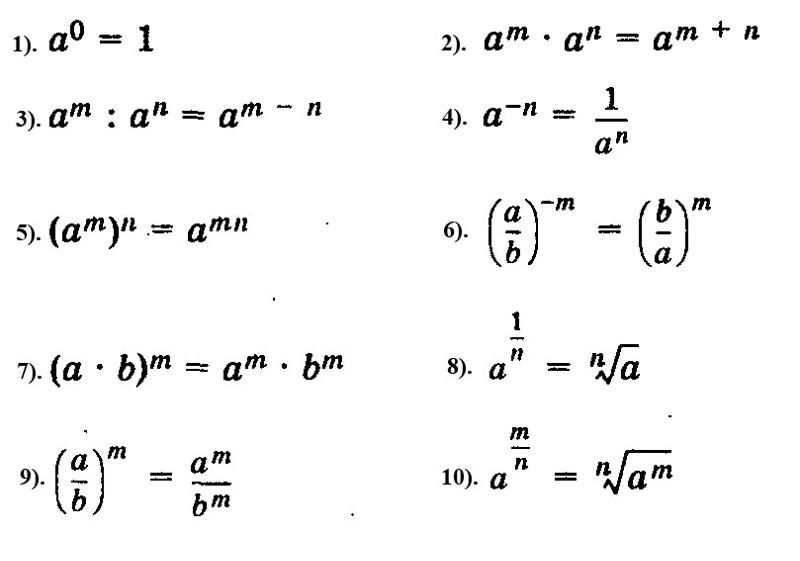
В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: -2116, -21232, 0-25.
Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6/10=3/5. Тогда должно быть верным (-1)610=-135, но -1610=(-1)610=110=11010=1, а (-1)35=(-1)35=-15=-155=-1.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
Определение 6Таким образом, степень положительного числа a с дробным показателем m/n определяется как 0mn=0mn=0. В случае отрицательных a запись amn не имеет смысла. Степень нуля для положительных дробных показателей m/n определяется как 0mn=0mn=0, для отрицательных дробных показателей мы степень нуля не определяем.
В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 51,7, 325-237.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
51,7=51710=5710325-237=325-177=325-177
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
Пример 5Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a0, a1, a2, …. Например, возьмем значение a=1,67175331…,тогда
a0=1,6, a1=1,67, a2=1,671, …,a0=1,67, a1=1,6717, a2=1,671753, …
и так далее (при этом сами приближения являются рациональными числами).
Последовательности приближений мы можем поставить в соответствие последовательность степеней aa0, aa1, aa2, . … Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.
… Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.
Возьмем для примера a=3, тогда aa0=31,67, aa1=31,6717, aa2=31,671753, … и т.д.
Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a. В итоге : степень с иррациональным показателем вида 31,67175331.. можно свести к числу 6,27.
Определение 7Степень положительного числа a с иррациональным показателем a записывается как aa. Его значение – это предел последовательности aa0, aa1, aa2, …, где a0, a1, a2, … являются последовательными десятичными приближениями иррационального числа a. Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0a=0 Так, 06=0,02133=0. А для отрицательных этого сделать нельзя, поскольку, например, значение 0-5, 0-2π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 12, 15в2 и 1-5 будут равны 1.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Степень с натуральным показателем
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Определение степени с натуральным показателем
2. Свойства степени с натуральным показателем
3. Примеры задач на использование свойств степени с натуральным показателем
Определение степени с натуральным показателем
Определение
Степенью действительного числа $a$ с натуральным показателем $n$ называется число, равное произведению $n$ множителей, каждый из которых равняется числу $a$.
$a$ — основание степени. 2\]
2\]
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 03.02.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
| История возникновения степени числа История возникновения степени числа Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. В своей знаменитой «Арифметике» Диофант Александрийский описывает первые натуральные степени чисел так: «Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя». Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михеля Штифеля «Полная арифметика» (1544 г. «Сумма знаний…» Луки Пачоли была одним из первых опубликованных сочинений. Но математики продолжали искать более простую систему обозначений так как его обозначения были не удобны. Француз, бакалавр медицины Никола Шюке (? — около 1500 г.) смело ввёл в свою символику не только нулевой, но и отрицательный показатель степени. Он писал его мелким шрифтом сверху и справа от коэффициента. В XVI в. итальянец Раффаэле Бомбелли в своей «Алгебре» использовал ту же идею. Он обозначал неизвестное специальным символом 1, а символами 2, 3,… — его степени. Обозначения Бомбелли также оказали влияние и на символику нидерландского математика Симона Стевина (1548—1620). Он обозначал неизвестную величину кружком О, внутри которого указывал показатели степени. Стевин предложил называть степени по их показателям — четвёртой, пятой и т. Д. и отверг Диофантовы составные выражения «квадрато-квадрат», «квадрато-куб». У Рене Декарта в его «Геометрии» (1637) мы находим современное обозначение степеней а2,а3,. Степень с натуральным показателем.Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a: an = В выражении an : — число а (повторяющийся множитель) называют основанием степени — число n (показывающее сколько раз повторяется множитель) – показателем степени Например: Отметим, что основание степени может быть любым числом. Вычисление значения степени называют действием возведения в степень. Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108 Каждое число больше 10 можно записать в виде: а · 10n , где 1 ≤ a Например: 4578 = 4,578 · 103 ; 103000 = 1,03 · 105. 1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются a m · a n = a m + n например: 71.7 · 7 — 0.9 = 71.7+( — 0.9) = 71.7 — 0.9 = 70.8 2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются a m / a n = a m — n , где, m > n, например: 133. | |||
| 1. Макеева Климанова «Русский язык» Ванюшкина, Юдовская, Баранов – «История Нового времени1800-1900. Всеобщая история» | «Свойства степени с целым показателем» … | ||
| Действительные числа. Квадратный корень из числа Модуль (абсолютная величина) числа. Сравнениерациональных чисел. Арифметические действия с рациональными числами. Степень с целым… | Тест алгебра. Степени. Многочлены. Алгебраические дроби Задание Верная запись произведения 7*7*7*7*х*х*х*х в виде степени указана под цифрой… | ||
| Конспект урока по алгебре в 7 классе по теме «Свойства степени с натуральным показателем» Сформировать умение применять свойства степени с натуральными показателями при решении задач | Задача «Квадратура круга» с. 14 Из истории вычислений числа π с. … …На уроках математики и физики мы часто используем число «пи» для конкретных вычислений. А что это за число, откуда оно появилось… | ||
| Рациональные и иррациональные числа Вспомним какие числа мы знаем натуральные, целые, рациональные, иррациональные.(опред, примеры) | Урок по теме: «Свойства степени с натуральным показателем» Обобщить и систематизировать знания обучающихся о свойствах степени с натуральным показателем | ||
| 1. История развития средств вычислительной техники | «Свойства степени с рациональным показателем» Цель урока: Повторить определение степени с рациональным показателем и свойства |
Степень числа: понятие, примеры, квадрат и куб числа
Содержание
На этом уроке мы изучим, что такое «степень числа», как правильно записать число в степени, как решать задачи с числами в степени, а также что такое квадрат и куб числа. {4}$$[[input-1]]»,»widgets»:{«input-1»:{«type»:»input»,»answer»:»27″}},»hints»:[«Сначала посчитай действия в скобках.»,»Затем вычисли степени чисел.»,»Дальше выполни действия второй ступени.»,»Потом посчитай действия первой ступени и запиши ответ.»]}]}
{4}$$[[input-1]]»,»widgets»:{«input-1»:{«type»:»input»,»answer»:»27″}},»hints»:[«Сначала посчитай действия в скобках.»,»Затем вычисли степени чисел.»,»Дальше выполни действия второй ступени.»,»Потом посчитай действия первой ступени и запиши ответ.»]}]}
Босов Андрей Витальевич — Что такое степень числа?
Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.
Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 46 и произносят «четыре в шестой степени».
4 · 4 · 4 · 4 · 4 · 4 = 46
Выражение 46 называют степенью числа, где:
- 4 — основание степени;
- 6 — показатель степени.

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:
Запомните!
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».
Запись «an» читается так: «а в степени n» или «n-ая степень числа a».
Исключение составляют записи:
- a2 — её можно произносить как «а в квадрате»;
- a3 — её можно произносить как «а в кубе».
Конечно, выражения выше можно читать и по определению степени:
- a2 — «а во второй степени»;
- a3 — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Запомните!
Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1
Выражение 00 (ноль в нулевой степени) считают лишённым смыслом.
- (−32)0 = 1
- 0253 = 0
- 14 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.
Пример. Возвести в степень.
53= 5 · 5 · 5 = 125
2,52= 2,5 · 2,5 = 6,25
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
Запомните!
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!
Отрицательное число, возведённое в чётную степень, есть числоположительное.
Отрицательное число, возведённое в нечётную степень, — числоотрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.
- 2 · (−3)2 = 2 · (−3) · (−3) = 2 · 9 = 18
- −5 · (−2)3 = −5 · (−8) = 40
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5)4 и −54 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (−5)4 означает найти значение четвёртой степени отрицательного числа.
(−5)4 = (−5) · (−5) · (−5) · (−5) = 625
В то время как найти «−54» означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число 5.
54 = 5 · 5 · 5 · 5 = 625 - Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).

−54 = −625
Пример. Вычислить: −62 − (−1)4
−62 − (−1)4 = −37
- 62 = 6 · 6 = 36
- −62 = −36
- (−1)4 = (−1) · (−1) · (−1) · (−1) = 1
- −(−1)4 = −1
- −36 − 1 = −37
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняютвовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».
Онлайн урок: Степень числа. Квадрат и куб числа по предмету Математика 5 класс
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
На данном уроке мы познакомимся с понятием степени числа.
Выясним, что называют «показателем степени» и «основанием степени».
Научимся вычислять квадрат и куб числа.
Составим таблицу степеней первых десяти натуральных чисел и рассмотрим ряд задач с использованием таких таблиц.
Определим, в каком порядке выполняют действия в выражениях, содержащих степень.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Известно, что сумму равных слагаемых можно заменить произведением.
Например, сумму пяти слагаемых, каждое из которых равняется четырем, можно записать короче:
4 + 4 + 4 + 4 + 4 = 5 ∙ 4
В произведении число 5 указывает на количество одинаковых слагаемых.
В свою очередь произведение одинаковых множителей тоже можно записать компактнее.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Произведение n одинаковых множителей можно представить в виде степени.
В буквенном виде произведение равных множителей можно представить следующим образом:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
аn— это произведение числа а на само себя n раз.
а— любое натуральное число.
Читают «а в n-ной степени» или «а в степени n».
Число а называют основанием (число, возводимое в степень).
n— это показатель степени (число, которое указывает сколько раз повторяется основание степени).
Степень числа представляют всегда так: записывают основание степени, а показатель ее записывают меньше размером в верхнем правом углу основания степени.
Операция умножения одинаковых множителей называется возведением в степень.
Например, произведение пяти множителей, каждое из которых равняется четырем, можно записать так:
4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 45
Читают данную запись следующим образом:
45— четыре в пятой степени.
Пример:
1)Вычислим значение степени 23, т.е. возведем число два в третью степень.
Данная степень равна произведению трех двоек.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
2— основание степени.
3— показатель степени.
2) Вычислим значение степени 54, т.е. возведем число пять в четвертую степень.
Данная степень равна произведению четырех пятерок.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
5— основание степени.
4— показатель степени.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Вторую степень числа называют квадратом числа.
Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а2(говорят и читают «а в квадрате»).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Например,
22 (два во второй степени) иначе говорят и читают «два в квадрате».
102 (десять во второй степени) иначе говорят и читают «десять в квадрате».
272 (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».
Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.
Один в квадрате равняется одному: 12 = 1 ∙ 1 = 1.
Два в квадрате равняется четырем: 22 = 2 ∙ 2 = 4.
Три в квадрате равняется девяти: 32 = 3 ∙ 3 = 9.
Четыре в квадрате равняется шестнадцати: 42 = 4 ∙ 4 = 16.
Пять в квадрате равняется двадцати пяти: 52 = 5 ∙ 5 = 25.
Шесть в квадрате равняется тридцати шести: 62 = 6 ∙ 6 = 36.
Семь в квадрате равняется сорока девяти: 72 = 7 ∙ 7 = 49.
Восемь в квадрате равняется шестидесяти четырем: 82 = 8 ∙ 8 = 64.
Девять в квадрате равняется восьмидесяти одному: 92 = 9 ∙ 9 = 81.
Десять в квадрате равняется сотне: 102 = 10 ∙ 10 = 100.
Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.
Таблица квадратов первых десяти натуральных чисел | ||||||||||
а | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
а2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
Пример.
Учитывая данные таблицы квадратов, решим уравнение.
Решим уравнение х2 = 49.
Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).
По таблице квадратов видно, что 49 = 72.
Следовательно, корень уравнения (х) равен семи.
х2 = 49
х = 7
Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х2 = 49, получим:
72 = 49
7 ∙ 7 = 49
49 = 49
Ответ: х = 7.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Третья степень числа тоже имеет свое название.
Число в третьей степени называют кубом числа.
Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а3 (говорят и читают «а в кубе»).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Например,
23 (два в третьей степени) иначе говорят и читают «два в кубе».
103 (десять в третьей степени) иначе говорят и читают «десять в кубе».
273 (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».
Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.
Один в кубе: 13 = 1 ∙ 1 ∙ 1 = 1.
Два в кубе: 23 = 2 ∙ 2 ∙ 2 = 8.
Три в кубе: 33 = 3 ∙ 3 ∙ 3 = 27.
Четыре в кубе: 43 = 4 ∙ 4 ∙ 4 = 64.
Пять в кубе: 53 = 5 ∙ 5 ∙ 5 = 125.
Шесть в кубе: 63 = 6 ∙ 6 ∙ 6 = 216.
Семь в кубе: 73 = 7 ∙ 7 ∙ 7 = 343.
Восемь в кубе: 83 = 8 ∙ 8 ∙ 8 = 512.
Девять в кубе: 93 = 9 ∙ 9 ∙ 9 = 729.
Десять в кубе: 103 = 10 ∙ 10 ∙ 10 = 1000.
Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.
Таблица кубов первых десяти натуральных чисел | ||||||||||
а | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
а3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.
Пример.
Представим в виде куба число 343.
По таблице кубов видим, что 343 = 73
Проверим: найдем произведение трех семерок:
73 = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343
Ответ: 343 = 73.
На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.
Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.
Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.
За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.
Рассмотрим поясняющие примеры.
При решении различных задач и примеров будем пользоваться составленными таблицами степеней.
Пример 1.
Найдите значение выражения 82 ÷ 4 — 10.
Определим порядок действий в выражении и найдем его значение.
Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).
82 ÷ 4 — 10 = 6
1) 82 = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).
2) 64 ÷ 4 = 16
3) 16 — 10 = 6
Пример 2.
Найдите значение выражения (21 — 11)2 ∙ 23.
Найдем значение данного выражения, определив порядок действий в нем.
(21 — 11)2 ∙ 23 = 800
Согласно порядка выполнения действий сначала выполняются действия в скобках.
Найдем разность 21 и 11.
1) 21 — 11 = 10
Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.
Найдем, чему равно 102по определению степени или по таблице квадратов.
2) 102 = 10 ∙ 10 = 100
Затем выполним действия, которые находятся в исходном выражении за скобками.
Определим третью степень двойки по таблице кубов или по определению степеней.
3) 23 = 2 ∙ 2 ∙ 2 = 8
Далее перемножим результаты, полученные в во втором и в третьем действии соответственно, т.е. найдем произведение 100 и 8.
4) 100 ∙ 8 = 800
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Степень обладает рядом свойств, которые подробно вы будете рассматривать и доказывать в старших классах.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сейчас мы познакомимся с некоторыми особенными свойствами степеней.
1. Любое число в первой степени равно этому же числу.
Первая степень числа а равна числу а.
В буквенном виде данное свойство запишем так:
а1 = а
Данная запись означает, что основание степени необходимо взять в качестве множителя один раз.
Например,
51 = 5, 1271 = 127, 10041 = 1004, 1234561 = 123456 и т.д.
Соответственно и единица в первой степени всегда равна единице: 11 = 1.
2. Любое натуральное число в нулевой степени равно единице.
а0 = 1
Например,
50 = 1, 1270 = 1, 100 = 1, 1234560 = 1 и т.д.
3. Ноль в любой степени равен нулю: 0n = 0.
На самом деле, по известному нам определению степени, 0 является основанием, n— показатель степени, указывающий сколько раз повторяется основание степени.
Таким образом получаем следующее равенство:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat.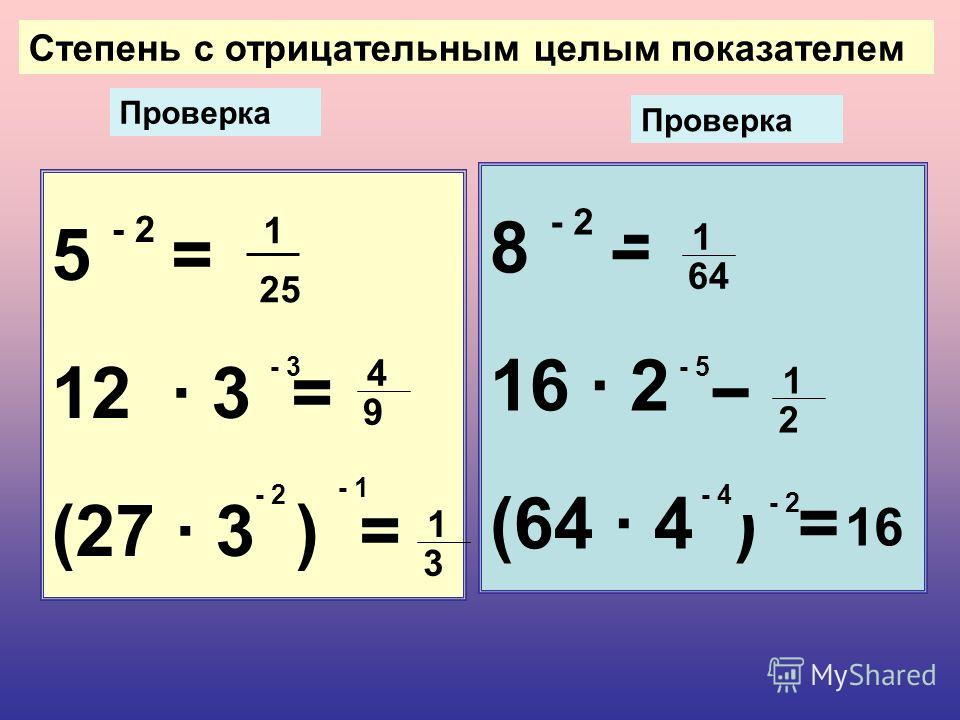 Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Например,
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
0128 = 0
015000 = 0
Слово «степень», порой, встречается в вашей повседневной жизни.
Степенные выражения используют в различных областях знаний, в науке и технике.
Часто приходится при расчетах и измерении встречаться с очень большими и очень маленькими числами.
С такими числами неудобно работать: выполнять различные действия и вычисления.
Иногда числа удобно представить в виде степени, записывая их, например, в стандартном виде.
Стандартный вид числа обобщенно можно записать так:
а ∙ 10n
В данной записи число (а), которое умножается на 10 в какой-либо степени, должно быть больше единицы или равно ей и быть меньше десяти.
Пример.
200000 = 2 ∙ 105
8000000000000 = 8 ∙ 1012
500 = 5 ∙ 102
Однозначное число, записанное в стандартном виде, будет равно самому себе, умноженному на десять в нулевой степени.
а = а ∙ 100 = а ∙ 1 = а
Пример.
2 = 2 ∙ 100 = 2 ∙ 1 = 2
5 = 5 ∙ 100 = 5 ∙ 1 = 5
8 = 8 ∙ 100 = 8 ∙ 1 = 8
Число десять представляют в стандартном виде, как произведение единицы и 10 в первой степени.
10 = 1 ∙ 101 = 1 ∙ 10 = 10
Изучая разряды и классы чисел, мы только лишь упоминали о больших и гигантских числах.
Известно, например, что один миллион записывается как единица и шесть нулей после нее.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В стандартном виде миллион запишем так:
1000000 = 1 ∙ 106.
Миллиард записывается следующим образом: единица и девять нулей после нее.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В стандартном виде миллиард запишем так:
1000000000 = 1 ∙ 109
Триллион представляет собой единицу и двенадцать нулей после нее.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В стандартном виде триллион запишем так:
1000000000000 = 1 ∙ 1012.
Самое большое число, которое называется «гугол», в десятичной системе исчисления изображается в виде единицы со ста нулями, записывают 10100(десять в степени сто).
Часто при решение различных задач удобно записывать числа сокращенно, с помощью степеней.
Пример.
24000 = 24 ∙ 103
350000 = 35 ∙ 104
24500000 = 245 ∙ 105
Однако, при этом эти числа не будут относится к числам, записанным в стандартном виде, так как 24 > 10, 35 > 10, 245 > 10.
Данные числа всего лишь имеют компактный вид, удобный при вычислениях.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Квадратом числа называют произведение двух одинаковых множителей.
Мы уже пробовали находить квадраты первого десятка натуральных чисел.
Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.
Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.
1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.
2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).
3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).
4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.
Рассмотрим поясняющий пример.
Найдем квадрат 65.
652 = 65 ∙ 65
Первая цифра в числе 65— это цифра 6, следовательно, нам необходимо найти произведение 6 и суммы 6 + 1.
6 ∙ (6 + 1) = 6 ∙ 7 = 42
Запишем число 42 и припишем к нему число 25.
652 = 4225
Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 652 = 65 ∙ 65, то
652 = 65 ∙ 65 = 4225
Получили все тот же ответ: 652 = 4225
Что такое степень по математике и почему это важно?
Математика изучает количество, структуру, пространство и изменения. Каким бы абстрактным это ни казалось, математика по своей сути является поиском абсолютов, окончательных решений и ответов. Мы можем думать о длинных числовых цепочках, море дробей или электронных таблицах, заполненных цифрами, но многие не осознают, что сложные математические уравнения на самом деле ведут к простоте. В результате тех, кто верит в лучшие, более быстрые и инновационные решения, часто привлекает математика.
В результате тех, кто верит в лучшие, более быстрые и инновационные решения, часто привлекает математика.
Нам нужна математика. Галилео Галилей использовал его для объяснения Вселенной. Математика разрешает истины и обнаруживает ошибки, делая нашу работу более достоверной. Отчеты, исследования и исследования почти обесцениваются без поддающихся количественной оценке фактов. Математика равна доказательству. Математика подтверждает.
Какая степень является математической степенью?
Те, кто поступает в колледж, чтобы получить степень по математике, в процессе обучения обнаруживают, что числа — это лишь малая часть привлекательности. Математика может научить нас искать решения дольше и усерднее — навык, применимый к любой карьере и жизни в целом. Кроме того, существует множество стратегий изучения математики , которые могут помочь в вашем образовательном путешествии.
Степень бакалавра в области математики способствует пониманию роли математики в обществе с давних времен до эпохи технологий. Когда вы получите степень бакалавра гуманитарных наук (BA) по математике онлайн, вы сможете развить передовые математические методы, навыки рассуждения и решения проблем. Онлайн-курсы по математике могут подготовить вас к разнообразной карьере, требующей высокой заработной платы и высокой степени удовлетворенности работой.
Когда вы получите степень бакалавра гуманитарных наук (BA) по математике онлайн, вы сможете развить передовые математические методы, навыки рассуждения и решения проблем. Онлайн-курсы по математике могут подготовить вас к разнообразной карьере, требующей высокой заработной платы и высокой степени удовлетворенности работой.
Роль математика вошла в число лучших профессий на 2021 год согласно отчету CareerCast на основе таких факторов, как окружающая среда, доход, перспективы и стресс. Другими ролями, которые может помочь вам получить степень по математике, являются статистик, занимающий третье место, и актуарий, занимающий девятое место.
Онлайн-курсы по математике могут дать вам хорошее представление о математике, связанной с бизнесом, естественными и социальными науками. Кроме того, они могут помочь вам научиться общаться по математике как устно, так и письменно. Наконец, вы можете узнать, как сложные и реальные проблемы могут быть решены с использованием математических концепций, добавив концентрацию прикладной математики.
Хотя Тим Макмиллан ’15 не решался вернуться в школу в 30 лет, он сделал это, чтобы продвинуться по карьерной лестнице в правоохранительных органах. «Я начал продвигаться по карьерной лестнице, становясь немного старше и взрослее, и я знал, какие возможности может открыть для меня степень по мере продвижения по карьерной лестнице», — сказал он.
Макмиллан решил изучать математику, потому что это бросало ему вызов, и он быстро понял, насколько ценной была курсовая работа. «Я начал понимать, как математика применима к моей работе», — сказал он. «Анализ данных, прикладная статистика и прикладная математика используются по всей стране и постепенно в правоохранительных органах, и я хотел быть в авангарде».
Студенты выбирают онлайн-программы по математике по разным причинам, и профессиональный успех — лишь одна из них. Многие студенты также используют программу, чтобы подготовиться к продолжению обучения в аспирантуре.
Программа бакалавриата является хорошей подготовкой к получению таких ученых степеней, как:
- Магистр делового администрирования
- Магистр прикладной экономики
- Магистр наук в области анализа данных
Любят ли работодатели математические специальности?
Любите ли вы математику или даже хорошо в ней разбираетесь, математика всегда рядом с нами. Когда вы находитесь в универмаге, подсчитываете свою чековую книжку или платите налоги, математика является необходимым навыком. Это может даже улучшить вашу спортивную игру.
Когда вы находитесь в универмаге, подсчитываете свою чековую книжку или платите налоги, математика является необходимым навыком. Это может даже улучшить вашу спортивную игру.
Многие профессии, такие как инженерное дело, медицина, физика, медсестры, информатика и актуарные науки, требуют математических знаний. Кроме того, практически все области извлекают пользу из аналитических навыков и навыков решения задач, которые учащиеся приобретают в математике. Поэтому ожидается, что любой, кто начинает карьеру в области науки, технологий, инженерии и математики (STEM), должен использовать базовые и продвинутые математические концепции.
Даже профессиональные повара и садовники используют математические основы при измерении и покупке расходных материалов. Если вы занимаетесь планированием мероприятий, математика поможет вам рассчитать затраты на человека и запасы. Швеи и декораторы ежедневно используют математику, как и все, кто работает с измерениями и графиками.
Я люблю математику.
 Что теперь?
Что теперь?Получение онлайн-степени по математике открывает перед вами целый мир возможностей. Например, Бюро статистики труда США (BLS) прогнозирует рост спроса на математиков и статистиков на 33% до 2030 года, а в 2020 году их средняя зарплата составит 93 290 долларов.
Согласно The Conversation, к 2025 году объем данных, создаваемых, собираемых, копируемых и потребляемых во всем мире, вырастет на 530%. Это означает, что все больше предприятий будут обращаться к математикам для анализа больших объемов собираемой информации. Эти данные помогут компаниям расти, совершенствоваться и разрабатывать новые продукты и процессы. Аналитика данных также используется, чтобы помочь компаниям размещать рекламу нужным потенциальным клиентам.
Также потребуются математики, чтобы помочь аналитикам по информационной безопасности создавать системы защиты данных для защиты конфиденциальности и личной информации всех, у кого есть доступ в Интернет.
Ожидайте конкуренции. Позиции для математиков желательны. Кандидаты с математическими степенями и опытом работы в этой области, несомненно, будут иметь преимущество. Что такое степень по математике на уровне выпускника? Добавлена страховка. Сильные навыки количественного анализа и анализа данных, а также опыт работы в смежных дисциплинах, таких как бизнес, информатика или статистика, являются определенным дополнением к вашему резюме.
Позиции для математиков желательны. Кандидаты с математическими степенями и опытом работы в этой области, несомненно, будут иметь преимущество. Что такое степень по математике на уровне выпускника? Добавлена страховка. Сильные навыки количественного анализа и анализа данных, а также опыт работы в смежных дисциплинах, таких как бизнес, информатика или статистика, являются определенным дополнением к вашему резюме.
Вам не обязательно быть математиком
Многие люди считают математический талант врожденным или унаследованным. Это не так, считают исследователи. Природные способности к математике далеко не уходят. Тяжелая работа и хорошие привычки в учебе гораздо ценнее. Студенты, поступающие на математические программы в колледжи, не являются гениями с математическим складом ума.
Многие дети не любят изучать математику, согласно статье Oxford Learning, в которой рассматриваются некоторые причины, по которым детям может не нравиться математика, и возможные решения. В отчете утверждается, что одна из причин, по которой детям может не нравиться этот предмет, заключается в том, что математика требует делать много ошибок, поэтому дети могут думать, что они плохо в ней разбираются. Тем не менее, Oxford Learning заверяет, что если дети разочаровываются, решение состоит в том, чтобы убедить их в том, что совершение ошибок — это всего лишь часть процесса обучения и что этот урок применим как в классе, так и в жизни.
В отчете утверждается, что одна из причин, по которой детям может не нравиться этот предмет, заключается в том, что математика требует делать много ошибок, поэтому дети могут думать, что они плохо в ней разбираются. Тем не менее, Oxford Learning заверяет, что если дети разочаровываются, решение состоит в том, чтобы убедить их в том, что совершение ошибок — это всего лишь часть процесса обучения и что этот урок применим как в классе, так и в жизни.
Имеют ли к этому какое-либо отношение хромосомы?
Мальчики лучше разбираются в математике, чем девочки? Статья в журнале Scientific American предполагает, что нет заметной разницы в математических способностях в дошкольных и начальных классах. Затем, начиная с подросткового возраста, появляются некоторые различия: мальчики часто получают более высокие баллы, чем девочки, по математической части SAT и другим экзаменам, не связанным напрямую с их учебной программой. Несмотря на то, что мальчики лучше девочек справляются с SAT, эти результаты не предсказывают успеваемость по математике в классе. Девочки опережают мальчиков в классе.
Девочки опережают мальчиков в классе.
Если вы считаете, что математика вам не по душе или вас беспокоит математика, но вы любите находить решения, пришло время пересмотреть степень по математике. Исследования доказывают, что стремление и желание, а не природные способности, являются наиболее важными факторами успеха.
Узнайте больше о программе бакалавриата SNHU по математике: узнайте, какие курсы вы будете посещать, навыки, которые вы приобретете, и как запросить информацию о программе.
Ребекка ЛеБёф, 18 лет, писатель из Университета Южного Нью-Гэмпшира. Свяжитесь с ней на LinkedIn.
Что такое степень по математике и почему она важна
Степень бакалавра по математике предлагает комплексную учебную программу, включающую углубленные темы по математике и статистике. Хотя он включает в себя курсы фундаментальной и теоретической математики, он также изучает прикладную математику.
Какая степень по математике может помочь трудолюбивым выпускникам? Достаточно много. Для любого студента, заинтересованного в карьере в области математики или статистики, получение такой степени, как онлайн-бакалавр наук в области математики Мэривилля, может предоставить важные квалификации, которые открывают дверь ко многим возможностям.
Для любого студента, заинтересованного в карьере в области математики или статистики, получение такой степени, как онлайн-бакалавр наук в области математики Мэривилля, может предоставить важные квалификации, которые открывают дверь ко многим возможностям.
Учебная программа бакалавриата по математике может варьироваться в зависимости от университета, но, как правило, включает, среди прочего, следующие темы:
- Основы математики. Вводные курсы математики для студентов бакалавриата гарантируют, что учащиеся усвоят все базовые знания, необходимые для изучения более сложных тем. Предметы, затрагиваемые во вводной курсовой работе, часто включают функции, теории и доказательства, логику, исчисление и свойства действительных чисел.
- Прикладная математика. Чтобы добиться успеха на работе, специалисты по математике должны понимать, как применять теоретическую математику в реальных условиях.
 Курсовая работа по прикладной математике может быть сосредоточена на прикладной теории чисел, дифференциальных уравнениях и линейной алгебре.
Курсовая работа по прикладной математике может быть сосредоточена на прикладной теории чисел, дифференциальных уравнениях и линейной алгебре. - Математические модели. Специалисты по математике узнают, как выбирать и создавать математические модели, такие как диаграммы и графики, для представления данных или информации в визуальном, простом для понимания формате.
Студенты также могут углубиться в такие темы, как машинное обучение и вероятность, что позволит им применять математику в современных методах анализа данных. Эти и другие курсы помогают учащимся развивать высоко востребованные на рынке навыки, применимые в самых разных отраслях и профессиях. Среди этих навыков:
- Аналитическое мышление. Специалисты по математике узнают, как выявлять тенденции в необработанной информации, чтобы определять вероятности и закономерности. По мере того, как они развивают аналитические навыки в ходе курсовой работы, они могут применять тот же образ мышления для решения проблем в других областях своей карьеры и жизни.

- Количественное мастерство. Учащиеся-математики развивают прочные количественные навыки, когда им становится комфортно работать с числами и наборами данных. Они понимают взаимосвязь между числами и знают, как использовать свои навыки для извлечения из них полезной информации.
Преимущества диплома по математике
Специалисты по математике используют данные для ответа на различные количественные вопросы, например, когда, как часто и сколько. По окончании учебы студенты часто обнаруживают, что они хорошо подготовлены для использования этих навыков, чтобы помогать организациям отвечать на вопросы и решать проблемы.
Потенциал заработка для математических специальностей может быть значительным. PayScale сообщает, что по состоянию на июль 2020 года средняя годовая зарплата специалистов, получивших степень бакалавра математических наук, составляет 76 000 долларов. Заработная плата варьируется в зависимости от ряда факторов, в том числе от места работы, многолетнего опыта сотрудника в этой области и выбранного карьерного пути.
Какое значение имеет диплом по математике для работодателей?
Работодатели ищут выпускников с большим опытом работы в области математики из-за множества аналитических и количественных навыков, которые они привносят на стол. Возможности для некоторых профессий, связанных с математикой, включая специалистов по обработке и анализу данных, математиков, статистиков, финансовых аналитиков и актуариев, быстро расширяются: по данным Бюро Лас-Вегаса, в период с 2018 по 2028 год прогнозируется рост рабочих мест на 30%. Сотрудники, имеющие математическое образование, высоко ценятся бизнесом по следующим причинам:
- Помощь предприятиям в принятии обоснованных решений. Чтобы быть высококонкурентными на насыщенных рынках и стать максимально эффективными, предприятия не могут полагаться на прошлые решения или интуицию. Вместо этого они должны обращаться к данным и статистике. Нанимая экспертов в области математики, предприятия могут принимать обоснованные решения, которые увеличивают прибыль, оптимизируют процессы и обеспечивают удовлетворенность клиентов.

- Разработка технологии хранения данных . Математики находятся на передовой, помогая предприятиям адаптироваться к новым технологиям хранения данных, включая облачные хранилища. С ростом объемов больших данных организации должны отслеживать и хранить необработанную информацию, которая затем используется для принятия решений, прогнозирования тенденций и повышения эффективности. Машинное обучение, то есть практика оснащения технологий интеллектуальными алгоритмами, которые адаптируются и обучаются, также может стать основной стратегией разработки новых процессов хранения данных.
- Анализ данных в здравоохранении. В то время как многие отрасли используют возможности анализа данных, одной из наиболее пострадавших от этой технологии является здравоохранение. Основное применение больших данных в здравоохранении — это записи пациентов, которые упорядочиваются для обеспечения более целостного представления о состоянии здоровья пациента.
 Кроме того, по мере распространения медицинских устройств и устройств Интернета вещей (IoT) и сбора данных о здоровье пациентов, а также по мере того, как пациенты начинают лучше понимать свое здоровье, привычки и генетику, все больше открывается путь для развития персонализированной медицины. Отрасли требуются талантливые специалисты по данным, математики и статистики, чтобы управлять потоком информации и использовать ее для улучшения жизни.
Кроме того, по мере распространения медицинских устройств и устройств Интернета вещей (IoT) и сбора данных о здоровье пациентов, а также по мере того, как пациенты начинают лучше понимать свое здоровье, привычки и генетику, все больше открывается путь для развития персонализированной медицины. Отрасли требуются талантливые специалисты по данным, математики и статистики, чтобы управлять потоком информации и использовать ее для улучшения жизни. - Смартфоны, умные дома и IoT. Согласно информационному бюллетеню Pew Research Center за 2019 год, 81% американцев владеют смартфоном, а Metova сообщает, что 90% приобрели хотя бы один продукт для умного дома. Согласно прогнозам Статистика. Из этих цифр становится ясно, что интеллектуальные потребительские и промышленные технологии находятся на подъеме, и эксперты по математике будут продолжать управлять этой массовой адаптацией.
Отрасли нанимают специалистов по математике
Математика — невероятно широкая и полезная область. Он поднимает большие вопросы с изученными практическими навыками. Области, которые стремятся добавить знания, опыт и навыки выпускников математических программ в свою рабочую силу, включают:
Он поднимает большие вопросы с изученными практическими навыками. Области, которые стремятся добавить знания, опыт и навыки выпускников математических программ в свою рабочую силу, включают:
- Финансы и банковское дело
- Машиностроение
- Страхование
- Исследование рынка
- Технология
- Разработка программного обеспечения
- Академия и исследования
- Бухгалтерия
- Путешествие
- Спорт
- Метеорология
- Образование
- Космология и воздухоплавание
- Наука о данных
- Здравоохранение
Общие профессии для математических специальностей
Степень в области математики дает студентам множество возможностей для карьерного роста. Общие математические карьеры включают финансового аналитика, математика и аналитика исследования операций.
- Финансовый аналитик: Финансовые аналитики консультируют частных лиц и предприятия по вопросам инвестирования.
 Данные BLS отмечают, что ожидается, что занятость в этой области вырастет на 6% в период с 2018 по 2028 год, что соответствует среднему темпу роста для всех профессий.
Данные BLS отмечают, что ожидается, что занятость в этой области вырастет на 6% в период с 2018 по 2028 год, что соответствует среднему темпу роста для всех профессий. - Математик: Математики определяют типы данных, которые можно использовать для решения конкретной задачи. Затем профессионалы в этой области используют свои навыки для разработки алгоритмических моделей, предназначенных для сбора, сортировки и анализа этих точек данных. BLS прогнозирует, что занятость математиков, как ожидается, вырастет на 30% в период с 2018 по 2028 год, что намного быстрее, чем средние темпы роста для всех профессий.
- Аналитик по исследованию операций: Профессионалы, выбравшие эту карьеру, используют математические методы, чтобы помочь предприятиям решать проблемы, например, как эффективно поставлять и распространять продукты. BLS сообщает, что занятость аналитиков по исследованию операций, по прогнозам, вырастет на 26% в период с 2018 по 2028 год, что намного быстрее, чем средний рост, прогнозируемый для всех профессий.

Что такое степень по математике? Дорога в будущее
С появлением больших данных и ростом стремления компаний принимать обоснованные решения, чтобы оставаться конкурентоспособными на современном глобальном рынке, работодатели все чаще ищут тех, кто может управлять и интерпретировать информацию и статистику. Записавшись на онлайн-программу бакалавриата по математике Университета Мэривилля, вы можете начать свой путь к полезной и эффективной карьере.
Рекомендуемое чтение
Привить любовь к числам: качества хорошего учителя математики
В чем разница между стандартами содержания и стандартами процессов по математике?
Бизнес-аналитик и специалист по данным
Источники
Dataversity, «Роль аналитики больших данных и искусственного интеллекта в будущем здравоохранения»
Forbes, «10 диаграмм, которые изменят ваше представление о росте Интернета вещей»
Интернет вещей для всех, «Что такое Интернет вещей? — Простое объяснение Интернета вещей»
Metova, инфографика: подключенный дом
PayScale, степень бакалавра наук (BS/BSc), степень математики
Pew Research Center, Mobile Fact Sheet
Sisense, что такое Healthcare Analytics?
Statista, Прогноз расходов конечных пользователей на решения IoT по всему миру с 2017 по 2025 год
Бюро статистики труда США, финансовые аналитики
Бюро статистики труда США, математики и статистики: перспективы работы Аналитики-исследователи
ZDNet, Хранение данных: «Все, что вам нужно знать о новых технологиях»
Путеводитель по различным математическим специальностям в колледже
Математические специальности — это разные группы. Специалисты по чистой математике борются с математическими теориями и концепциями, чтобы создать элегантные доказательства. Специалисты по прикладной математике используют концепции, изученные в классе, и применяют их к реальным ситуациям в самых разных отраслях.
Специалисты по чистой математике борются с математическими теориями и концепциями, чтобы создать элегантные доказательства. Специалисты по прикладной математике используют концепции, изученные в классе, и применяют их к реальным ситуациям в самых разных отраслях.
У потенциальных специалистов по математике есть несколько вариантов для их конкретной области обучения, поскольку «математика» может означать что угодно: от чистой математики до статистики и компьютерных наук.
Если вы заинтересованы в получении степени по математике, но не знаете, какую математическую специальность выбрать, продолжайте читать, чтобы узнать о различных специальностях и карьерных путях, на которые вас могут натолкнуть определенные степени.
Что вы можете делать со специальностью по математике в колледже?
Помимо очевидных навыков, которые развиваются при получении степени по математике, таких как понимание чисел, уравнений и методологии, изучение математики также способствует развитию других важных навыков, применимых в широком спектре областей. Критическое и аналитическое мышление возглавляет список навыков, которыми обладают специалисты по математике, равно как и решение задач и количественные рассуждения. В совокупности эти навыки позволяют специалистам по математике формировать сложные идеи и манипулировать ими, строить логические аргументы и разбирать нелогичные.
Критическое и аналитическое мышление возглавляет список навыков, которыми обладают специалисты по математике, равно как и решение задач и количественные рассуждения. В совокупности эти навыки позволяют специалистам по математике формировать сложные идеи и манипулировать ими, строить логические аргументы и разбирать нелогичные.
Кто должен изучать математику в колледже?
Учащиеся, которым нравились уроки математики в средней школе (и они были успешными), являются хорошими кандидатами на получение специальности по математике в колледже. Это особенно верно для студентов, которые посещали математические курсы высокого уровня и продвинутого уровня. Студенты-математики в колледже, как правило, склонны к решению проблем, и их не останавливает, когда ответы не появляются легко — готовность бороться с трудными вопросами является обязательным условием.
Специальности по математике изучают широкий спектр математических тем, так как в большинстве программ по математике студенты изучают все, от алгебры до исчисления и геометрии. Большая часть этой курсовой работы выполняется в рамках серии занятий в этих областях, причем каждое из них основано на предыдущем классе. Математика не является изолированной областью; самые успешные студенты — командные игроки, хорошие коммуникаторы и готовы работать в команде или с ассистентами и преподавателями для решения сложных проблем и концепций.
Большая часть этой курсовой работы выполняется в рамках серии занятий в этих областях, причем каждое из них основано на предыдущем классе. Математика не является изолированной областью; самые успешные студенты — командные игроки, хорошие коммуникаторы и готовы работать в команде или с ассистентами и преподавателями для решения сложных проблем и концепций.
Различные типы математических специальностей
Несмотря на то, что существует общая математическая специальность, есть несколько других типов специальностей, которые могут предлагаться на математическом факультете. Эти степени позволяют студентам следовать конкретным интересам и готовить их к уникальным потребностям областей, в которые они надеются войти.
Этот список включает некоторые из наиболее распространенных специальностей, предлагаемых на математических факультетах, включая прикладную математику, чистую математику, статистику и информатику. Мы не будем охватывать такие специальности, как финансы, физика или экономика, поскольку они часто предлагаются другими факультетами.
Прикладная математика
Степень в области прикладной математики является обычным курсом для студентов, которые хотят сделать карьеру в инженерии, естественных науках и компьютерах, поскольку она дает студентам функциональные знания, необходимые для применения математических идей и методов к задачам. . Многие программы по прикладной математике разработаны с учетом гибкости, что позволяет людям формировать свою курсовую работу в соответствии со своими интересами. Компьютерная смекалка требуется от специальностей прикладной математики, поскольку вычислительные методы и применение алгоритмов являются ключевыми компонентами курсовой работы.
Специалисты по прикладной математике могут посещать такие курсы, как:
- Численный анализ
- Теория оптимизации
- Дифференциальные уравнения
- Численный анализ
- Линейная алгебра
- Исчисление
- Физика
- Информатика
- Вычислительная математика
- Проектирование систем
Из-за гибкого характера прикладной математики степень в этой области может привести к карьере в самых разных отраслях, а также заложить основу для многих студентов, чтобы продолжить свое образование в программах магистратуры.
Общие профессии для обладателей степени по прикладной математике включают:
- Актуарий
- Аудитор
- Банкир
- Инженер
- Финансовый аналитик или консультант
- Исследователь
- Статистик
Чистая математика
Учащиеся, изучающие чистую математику, развивают понимание концепций и структур, лежащих в основе всей математики. В ходе обучения они будут работать в математических областях, таких как алгебра, анализ и геометрия, а также развивать основные компетенции, такие как решение проблем, критическое мышление и моделирование.
Изучающие чистую математику могут посещать такие предметы, как:
- Дискретная математика
- Дифференциальные уравнения
- Анализ (действительный и комплексный)
- Линейная алгебра
- Исчисление
- Многомерное исчисление
- Геометрия/топология
- Моделирование
Навыки решения задач и аналитические способности, которыми обладают обладатели степени в области чистой математики, открывают двери во многие отрасли. Общие области, в которых можно найти обладателей степени по чистой математике:
Общие области, в которых можно найти обладателей степени по чистой математике:
- Преподавание
- Финансы
- Вычислительная техника
- Страхование
- Медицинские и научные исследования
Компьютерные науки
Учащиеся, получившие степень в области компьютерных наук, могут решать сложные задачи с помощью компьютерных средств, таких как программное обеспечение и искусственный интеллект. Студенты, изучающие информатику, должны использовать прочную базу математических навыков для формирования вероятностей и создания статистических моделей. Информатика привлекает людей всех типов: одних волнует возможность провести долгие дни в лаборатории, разрабатывая новые алгоритмы, других привлекает идея совместной работы над такими проектами, как разработка автомобилей с автономным управлением.
Специалисты по компьютерным наукам могут посещать такие курсы, как:
- Исчисление
- Программирование
- Алгоритмы
- Структуры данных
- Логика
- Языки программирования
- Операционные системы
- Теория информатики
Информатика — это не только высокооплачиваемая специальность, но и одна из самых выгодных с финансовой точки зрения: в 2017 году CBS признала ее самой прибыльной специальностью в колледже. Некоторые вакансии, которые обычно заполняются специалистами в области компьютерных наук, включают:
Некоторые вакансии, которые обычно заполняются специалистами в области компьютерных наук, включают:
- Инженер-компьютерщик
- Специалист по информационным системам
- Специалист по взаимодействию человека с компьютером (HCI)
- Информационно-технический специалист
- Инженер-программист
- Ученый-компьютерщик
Статистика
В основе количественных рассуждений лежит статистика — студенты, изучающие статистику в колледже, учатся собирать, анализировать и интерпретировать данные. Кроме того, студенты учатся эффективно общаться и представлять аргументы и выводы, основанные на данных. Обладая востребованным набором навыков, студенты со степенью в области статистики найдут возможности во всех секторах, от правительства до бизнеса и промышленности, университетов и исследовательских лабораторий.
Общие курсы для специалистов по статистике включают такие классы, как:
- Исчисление
- Линейная алгебра
- Вероятность
- Анализ
- Прикладная статистика
- Теоретическая статика
- Статистические вычисления
Поскольку статистика имеет огромное количество практических применений, у обладателей степени в области статистики есть множество путей карьерного роста.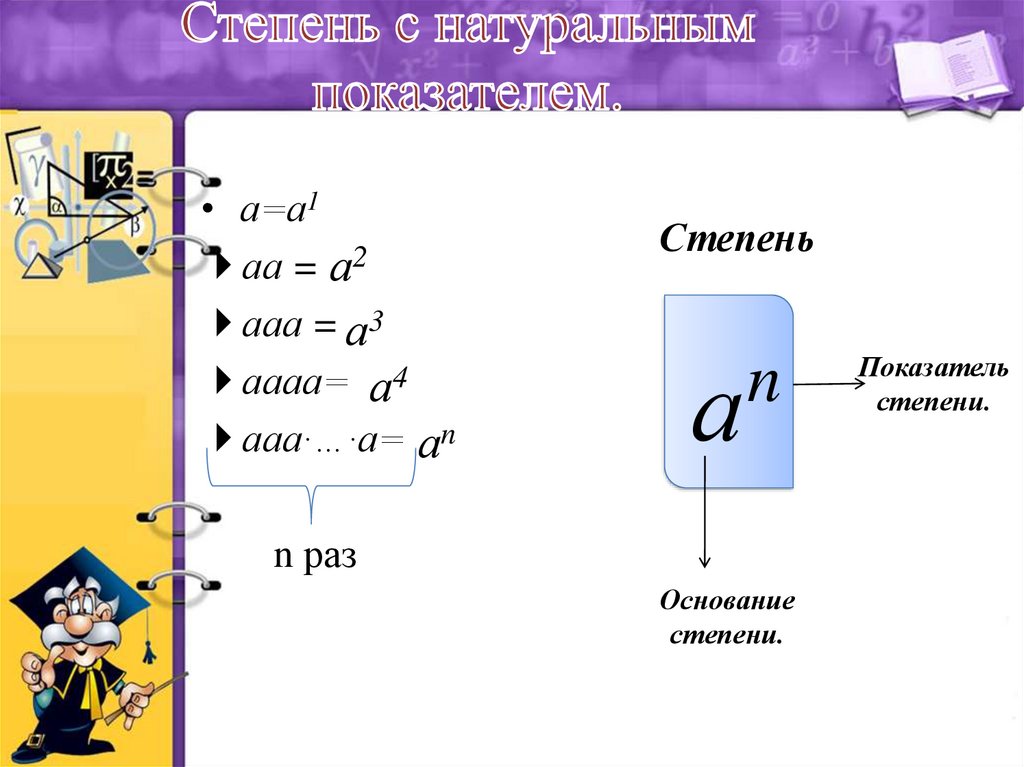 Общие карьеры включают в себя:
Общие карьеры включают в себя:
- Актуарий
- Бизнес-аналитик
- Оценщик стоимости
- Администратор базы данных
- Специалист по данным
- Экономист
- Финансовый аналитик
- Исследователь рынка
- Инженер-программист
- Статистик
Обязательно ознакомьтесь с этими сообщениями:
10 самых простых и 10 самых сложных специальностей
Самые простые и самые сложные инженерные специальности
Самые простые и самые сложные научные специальности
К счастью для старшеклассников, заинтересованных в том, чтобы изучать математику в колледже, вам не нужно иметь степень в области статистики, чтобы знать свои шансы на поступление в школу своей мечты. Наша бесплатная поисковая система расскажет вам о ваших шансах на поступление в более чем 500 колледжей. Зарегистрируйтесь в своей учетной записи CollegeVine сегодня, чтобы этот мощный инструмент работал на вас.
Куда меня приведет математика?
Специальность бакалавриата по математике предлагает основу для студентов, заинтересованных в понимании того, как подходить к проблемам с математическими решениями. Специальность «Математическая экономика» предлагает студентам программу, сочетающую математику, статистику и экономику.
Куда может привести меня математика?
Куда может привести меня математическая экономика?
Карьера в цифрах? You Do the Math
Математика — это сложно, полезно и весело. Это и логично, и креативно. Студенты, изучающие математику, имеют множество возможностей. Специальность по математике готовит студентов к традиционным занятиям, таким как аспирантура, преподавание и работа актуарием. Учащиеся, любящие математику, находят, что специализацию по математике можно сочетать с предпрофессиональной учебной программой или специализацией в области естественных или инженерных наук, чтобы обеспечить прочную основу для учебы в аспирантуре или работы в области, связанной с математикой.
Специальность «Математическая экономика» дает возможность студентам, интересующимся математикой и бизнесом или экономикой, объединить эти интересы. Департамент математики предлагает как степень бакалавра наук, так и степень бакалавра гуманитарных наук. Каждая степень может быть получена с помощью варианта A: математика или варианта B: математические науки. Вариант математики выбирают большинство учащихся. Вариант математических наук сочетает в себе изучение математики, статистики и информатики и готовит студентов к карьере, связанной с приложениями математики. Несовершеннолетний по математике доступен для студентов, которые хотели бы продолжить изучение математики, специализируясь в другой области. В дополнение к степеням бакалавра математический факультет предлагает программы, ведущие к получению степени магистра гуманитарных наук (MA), магистра наук (MS) и доктора философии (Ph.D).
Какие навыки развивает изучение математики?
- критическое мышление
- решение проблем
- аналитическое мышление
- количественные рассуждения
- способность манипулировать точными и сложными идеями
- создавать логические аргументы и выявлять нелогичные аргументы
- связь
- управление временем
- работа в команде
- независимость
- Высшее образование
- Высшее и докторское образование
Карьерные возможности
Карьерные возможности не ограничены для студентов, изучающих математику. Они могут получить последипломное образование, сделать карьеру в бизнесе, науке или технических областях или дисциплинах, таких как социальные услуги, образование и правительство. Некоторые из профессий, которые выбирают математики, включают:
Они могут получить последипломное образование, сделать карьеру в бизнесе, науке или технических областях или дисциплинах, таких как социальные услуги, образование и правительство. Некоторые из профессий, которые выбирают математики, включают:
- бухгалтер
- актуарий
- программист
- врач
- инженер
- инвестиционный менеджер
- юрист
- государственные исследования и лаборатории
- математик-теоретик
- математик
- численный аналитик
- статистик
- учитель
- исследователь рынка
- системный аналитик
- банковское дело
- правительство
- космическая/авиационная промышленность
Для получения дополнительной информации о карьере перейдите по следующему адресу:
- Математическая ассоциация Америки
- Американское математическое общество
- Общество актуариев
Для получения дополнительной информации о возможностях карьерного роста свяжитесь с консультантом по вопросам карьеры Джейми Джонсон по адресу jjjohn4@email. uky.edu или по телефону (859) 257-4023.
uky.edu или по телефону (859) 257-4023.
Сборник компетенций: степень по математической экономике
Специальность «Математическая экономика» предлагает студентам программу на получение степени, сочетающую математику, статистику и экономику. Во многих отношениях программа математической экономики параллельна инженерной философии. Он сочетает количественные методы математики с прикладными науками для решения реальных задач. В связи с постоянно растущим значением сектора услуг в нашей экономике степень математической экономики окажется ценным активом. Программа даст студенту возможность изучить увлекательную коллекцию идей, а также предоставит студенту очень востребованные на рынке навыки.
Какие навыки развивает изучение математической экономики?
- способность к математике и статистике
- способность решать проблемы
- умение общаться с публичными выступлениями и письменными заданиями
- способность сотрудничать с другими
- Высшее образование
Карьерные возможности
В сегодняшнем все более усложняющемся мире международного бизнеса серьезная подготовка в области экономики и математики имеет решающее значение для успеха. Эта программа на получение степени предназначена для подготовки студента к непосредственному погружению в мир бизнеса с навыками, которые пользуются большим спросом, или к продолжению обучения в аспирантуре по экономике или финансам. Степень в области математической экономики подготовит студента к началу карьеры в области исследования операций или актуарной науки. Другие занятия включают, но не ограничиваются следующим:
Эта программа на получение степени предназначена для подготовки студента к непосредственному погружению в мир бизнеса с навыками, которые пользуются большим спросом, или к продолжению обучения в аспирантуре по экономике или финансам. Степень в области математической экономики подготовит студента к началу карьеры в области исследования операций или актуарной науки. Другие занятия включают, но не ограничиваются следующим:
- экономист
- бухгалтер по управленческому учету
- актуарий
- банковский ревизор
- аналитик по маркетинговым исследованиям
- финансовый аналитик
- менеджер по маркетингу/продажам
- финансовый план
- эксперт по претензиям
- инвестиционный менеджер
- специалист по международной торговле
- инвестор в недвижимость
- статистик
- учитель
- профессор
Для получения дополнительной информации о карьере перейдите по следующему адресу:
- Общество промышленной и прикладной математики
- Институт операций и управленческих наук
- Общество актуариев
Для получения дополнительной информации о карьерных возможностях обращайтесь в UK Career Center.
Что я могу делать со степенью по математике?
Если вы уже увлекаетесь математикой, то, вероятно, уже знаете, что математика — это язык. И, как и языки, на которых говорят, язык чисел можно применять по-разному.
Как и любой другой язык, вы должны сначала изучить основные правила. С детского сада до 12-го класса грамматика и синтаксис чисел заполняют математические классы. Именно здесь многие теряют интерес к математике. Но не ты. Если вы заинтересованы в получении степени по математике на уровне бакалавриата или магистратуры, вы хотите научиться применять математику для решения действительно интересных задач.
Хорошей новостью является то, что в студенческие годы вы действительно начинаете учиться решать сложные, реальные задачи с помощью математики. От тонкой настройки самых сложных алгоритмов до проверки правильности статистического подхода к исследованию — математика находится в центре многих университетских и реальных дисциплин. Кроме того, в университетах есть преподаватели, которые помогут вам глубже погрузиться в теоретические проблемы математики.
Кроме того, в университетах есть преподаватели, которые помогут вам глубже погрузиться в теоретические проблемы математики.
Каким бы ни был ваш выбор, для тех, кто серьезно относится к совершенствованию своих математических знаний, высшее образование просто необходимо.
Здесь, в DegreeQuery, мы охватываем все типы программ высшего образования. И математика не исключение. Узнайте больше, чтобы узнать, что именно вы можете сделать со степенью в области математики!
Часто задаваемые вопросы о степени математики
- Как подготовиться к получению степени по математике в старшей школе?
- Как мне подготовиться к получению степени по математике в средней школе?
- Как мне подготовиться к получению степени по статистике в средней школе?
- Сколько времени нужно, чтобы получить степень по математике?
- Сколько времени нужно, чтобы получить степень в области математического образования?
- В чем преимущество степени математики по сравнению со степенью статистики?
- В чем преимущество степени математики по сравнению со степенью математического образования?
- В чем разница между степенью бакалавра математики и степенью магистра математики?
- Какова потенциальная заработная плата человека со степенью по математике?
- Какую работу можно получить со степенью по математике?
- Какая степень лучше для инженера-программиста?
- Куда мне пойти, чтобы получить степень STEM?
Что изучает математика?
Прежде чем мы перейдем к тому, что вы можете сделать со степенью в области математики, давайте рассмотрим, что такое изучение математики.
На самом общем уровне математика — это поиск и использование закономерностей в числах. Часто эти шаблоны имитируют или помогают представить некоторые явления в мире. Когда это происходит, возникают новые отрасли прикладной математики.
Итак, когда мы говорим о математике, мы имеем в виду как математиков-теоретиков, которые ищут закономерности, так и тех, кто использует математику для полезных приложений. Профессии, связанные с прикладной математикой, включают следующее:
- Математики
- Статистики
- Актуарии
- Бухгалтеры
- Финансовые аналитики
- Специалисты по данным
- Ученые-естествоиспытатели
- Социологи
- Экономисты
- Компьютерщики
- Педагоги
- И многие другие
.
На уровне бакалавриата курсы математики могут включать следующие предметы:
- Исчисление I-III
- Функции и моделирование
- Математика для инженеров
- Дифференциальные уравнения
- Дискретная математика
- Статистика
- Финансовая математика
- Продвинутая алгебра
- Математическая биология
- Несколько курсов по анализу
- Дифференциальная геометрия
- Теория чисел
- История математики
- и многое другое
В аспирантуре или при приеме на работу математики и связанные с ними профессии часто сосредотачиваются в основном на нескольких областях. Ниже приведены основные области, на которых можно сосредоточиться в изучении и применении математики.
Ниже приведены основные области, на которых можно сосредоточиться в изучении и применении математики.
Области чистой математики
- Фундаменты
- Арифметика
- Алгебра
- Анализ
- Комбинаторика
- Геометрия и топология
Области прикладной математики
- Вероятность и статистика
- Вычислительные науки
- Численный анализ
- Компьютерная алгебра
- Физические науки
- Механика
- Механика конструкций
- Механика деформируемых твердых тел
- Гидромеханика
- Механика частиц
- Исследование операций
- Математическое программирование
В каких областях обучения широко используется математика?
Первый шаг к ответу на вопрос «что вы можете делать» со степенью по математике — это посмотреть, в каких областях активно используется математика. После обсуждения этих областей мы рассмотрим, какие варианты степени могут помочь вам получить желаемую роль или направление.
После обсуждения этих областей мы рассмотрим, какие варианты степени могут помочь вам получить желаемую роль или направление.
Наука, технология, инженерия и математика (STEM) пользуются большим спросом во многих отраслях, и, хотя не так много должностей, которые на 100% состоят из математики, кандидаты с сильными количественными навыками действительно ценятся.
Некоторые из наиболее распространенных рабочих ролей, на которые в значительной степени полагаются, включают следующее:
- Математики и статистики работают с формулами и данными, помогая решать важные проблемы в государственных, академических и отраслевых учреждениях. Они пользуются большим спросом в сфере здравоохранения, инженерии, бизнеса и вычислительной техники.
- Актуарии анализируют — с финансовой точки зрения — неопределенность. Актуарии, обычно используемые в сфере финансов и страхования, используют финансовую теорию, статистику и другие инструменты математического моделирования для изучения и объяснения рисков, связанных с определенными событиями.

- Специалисты по обработке и анализу данных применяют статистику, анализ данных и машинное обучение для анализа данных. Из других областей STEM специалисты по данным наиболее тесно связаны со статистиками, которые полагаются на чисто цифровой набор инструментов и данных.
- Ученые-естествоиспытатели применяют ряд математических методов в зависимости от области их деятельности. Статистика и вероятность регулярно используются в научных дисциплинах. Ряд прикладных научных дисциплин был разработан в тандеме с учеными-естествоиспытателями, включая механику, механику жидкости и механику элементарных частиц. Эти дисциплины неразрывно связаны как с инженерией, так и с физикой.
- Инженеры используют математику в виде статистики, вероятности и изучения механики конструкций, жидкостей и частиц. Помимо математики и физики, инженерное дело часто рассматривается как наиболее «тяжелая по математике» дисциплина, изучаемая в университетах.

- Криптографы уже давно используются в различных условиях, от знаменитой машины Enigma времен Второй мировой войны до древних кодов для связи между римскими армиями. Сегодня криптографы наиболее активно работают в дисциплинах, связанных с кибербезопасностью и обеспечением информации. Криптография наиболее активно использует абстрактную геометрию и теорию чисел. (Узнайте больше о степени, необходимой для работы в области криптографии.)
Сколько зарабатывают специалисты по математике?
Математика является одной из самых востребованных специальностей в различных областях. Кроме того, математические специальности набирают самые высокие баллы по сравнению с любыми другими специальностями по стандартизированным тестам для аспирантуры (см. наш раздел о том, как математика готовит вас к поступлению в аспирантуру ниже).
Заработная плата математических специальностей зависит от ряда факторов, но мы можем посмотреть на среднюю заработную плату для обычных должностей, которые математические специальности занимают после окончания учебы.
Из четырех профессий, наиболее тесно связанных с математикой, средняя заработная плата высока:
Средняя заработная плата для профессий, связанных с математикой
- Математик: $103 010
- Актуарии: $101 560
- Статистики: $84 760
- Аналитики исследования операций: $81 390
Конечно, существует множество профессий, которыми могут заниматься специалисты по математике или обладатели ученых степеней. Из ролей, которые ценятся математиками с небольшой дополнительной подготовкой, вот обычные зарплаты:
Средняя заработная плата по профессиям, в которых могут работать математики
- Физики: $117 220
- Специалисты по компьютерным и информационным исследованиям: $114 520
- Финансовые аналитики: $84 300
- Учителя математики средней школы: $59 170
- Data Scientist: $118 709
- Криптограф: $112 560
- Преподаватель математики в университете: $74 460
Дополнительные специальности по математике, пользующиеся большим спросом у рабочей силы, включают выпускников, специализирующихся на биологической математике, финансовой математике и преподавании математики.
Как математика готовит вас к поступлению в аспирантуру
Количественное мышление, которому учат на курсах математики, ценится в самых разных областях. Это также важный навык для успешной сдачи стандартизированных тестов для аспирантов. По специальностям математика в среднем набираются более высокие баллы, чем по любой другой специальности на тестах LSAT и GMAT. Это преобладающие тесты для поступления в аспирантуру в юридических школах, а также в бизнесе.
В приведенном ниже маркированном списке указано, на сколько баллов выше или ниже среднего балла GMAT и LSAT набирают отдельные специальности.
Три основных направления по результатам LSAT и разница со средним баллом
- Математика: +12,8%
- Экономика: +9,6%
- Философия: +8,7%
Три последних предмета по результатам LSAT и разница со средним баллом
- Образование: -8,7%
- Бизнес: -4,5%
- Политология: -1,6%
Три основных направления по результатам GMAT и разницам со средним баллом
- Математика: +13,3%
- Философия: +11%
- Химия: +7,5%
Три худшие специальности по результатам GMAT и разницам со средним баллом
- Социология: -5%
- Образование: -4,2%
- Бизнес: -0,8%
Математические методы могут быть применены ко многим дисциплинам, включая те, которые просто нуждаются в прочной основе для решения логических задач. Это делает математику отличной специализацией бакалавриата, которую можно взять в аспирантуру по другой дисциплине.
Это делает математику отличной специализацией бакалавриата, которую можно взять в аспирантуру по другой дисциплине.
Некоторые распространенные программы магистратуры по математике включают:
- Математика
- Статистика
- Бухгалтерия
- Финансы
- Деловое администрирование
- Информатика
- Машиностроение
- Физика
- Закон
- Образование
Чтобы получить представление о том, насколько хорошо степень по математике готовит вас к поступлению в аспирантуру различных типов, давайте углубимся в средние баллы GMAT по специальностям.
ТестыGMAT оцениваются по шкале от 200 до 800 со средним баллом около 500. Средний балл по математике, сдающий GMAT, на 13,3% выше среднего. Это означает, что средний балл по математике, сдающий GMAT, составляет около 580, что на 80 баллов выше среднего.
Имейте в виду, что есть много частей заявления выпускника бизнес-школы. Однако стандартизированные тесты, такие как GMAT, обычно являются одним из самых больших компонентов.
Многие ведущие бизнес-школы, занимающие в настоящее время между 60-м и 100-м местами в стране, имеют средний балл GMAT чуть более 600 баллов. Это означает, что балл GMAT по специальности математика достаточно высок, чтобы получить допуск во многие 100 лучших бизнес-программ для выпускников. Кроме того, помимо философии или экономики — только двух других специальностей, которые могут похвастаться такими же высокими баллами по GMAT, — это единственная специальность, которая может похвастаться такими высокими результатами.
Каковы карьерные перспективы для тех, кто имеет математическое образование?
Если мы еще не пояснили, обладатели степени по математике пользуются большим спросом во многих дисциплинах. От школьного образования до «квантов» в сфере финансов — математики обеспечивают «секретный соус» успеха многих организаций. Математиков тоже не много. Это делает тех, кто имеет математическое образование, еще более желанными.
Ниже мы рассмотрим перспективы карьерного роста для тех, кто имеет математическое образование, с двух точек зрения: выпускники математических факультетов, которые работают математиками или статистиками, и те, кто работает в более прикладных областях или в областях, связанных с математикой.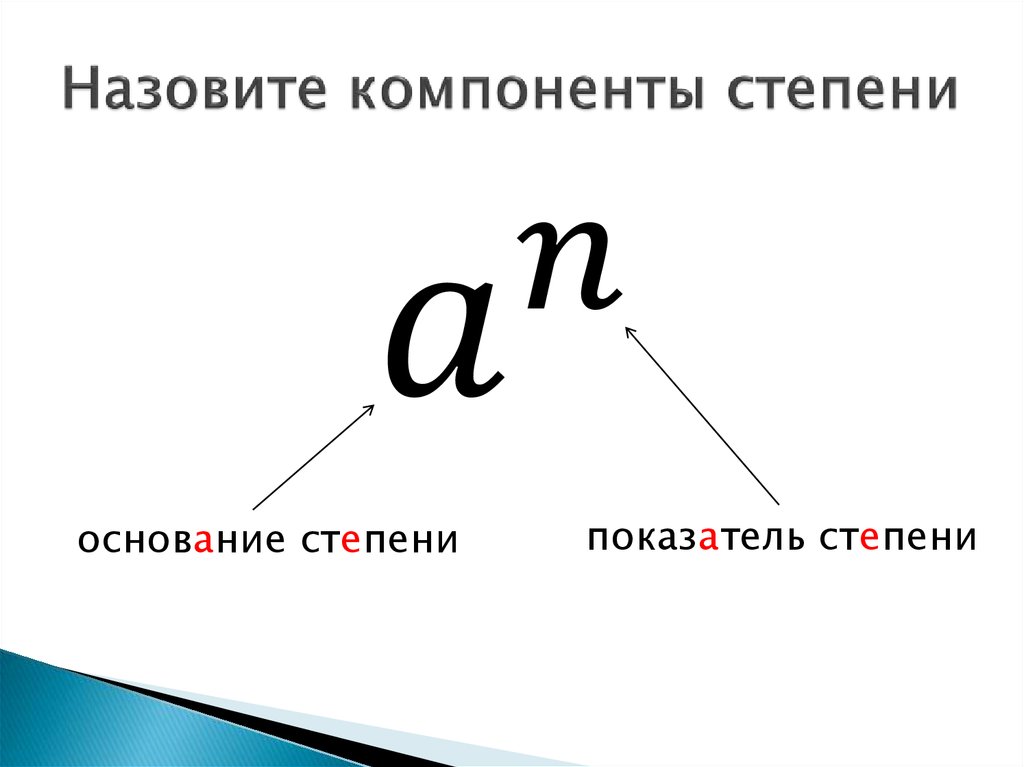
Перспективы карьерного роста для математиков и статистиков
В 2016 году в Америке насчитывалось немногим более 40 000 работников, занимающих должности математиков и статистиков. Ожидается, что в период с 2016 по 2026 год в этих областях появится еще около 13 500 рабочих мест. Таким образом, за десятилетие количество рабочих мест для математиков и статистиков увеличится на треть (33%).
Средняя зарплата на этих должностях по состоянию на 2016 год составляет 84 760 долларов США. С наибольшим количеством рабочих мест для тех, кто работает математиком или статистиком в следующих местах:
Места работы для математиков
- Федеральное правительство
- Исследования и разработки в области физических наук, техники и наук о жизни
- Колледжи и университеты
- Финансы и страхование
- А Менеджмент, научно-технический консалтинг
Места работы статистиков
- Федеральное правительство
- Исследования и разработки в области физических наук, техники и наук о жизни
- Страхование
- Здравоохранение и социальная помощь
- Колледжи и университеты
Перспективы карьерного роста для математиков-тяжелых должностей
Возможно, самая большая должность, связанная с математикой, по количеству должностей — учитель математики. За этим следует широкий спектр ролей, связанных с математикой, включая актуария, специалиста по данным, определенные инженерные роли и аналитиков по исследованию операций. Карьерные перспективы этих типов карьеры можно увидеть ниже:
За этим следует широкий спектр ролей, связанных с математикой, включая актуария, специалиста по данным, определенные инженерные роли и аналитиков по исследованию операций. Карьерные перспективы этих типов карьеры можно увидеть ниже:
Рост числа вакансий к 2026 году
- Актуарий: +22%
- Специалисты по данным: +19%
- Инженеры-электрики: +9%
- Аналитики исследования операций:+27%
- Учитель математики: +12%
Заработная плата математиков-тяжелых должностей
- Актуарий: $101 560
- Наука о данных: $114 520
- Инженеры-электрики: $97 970
- Аналитики исследования операций: $81 390
- Преподаватель математики: $55 035
Заинтересованы в советах по прохождению собеседования? Ознакомьтесь с освещением DegreeQuery о том, как пройти собеседование на некоторые из наиболее распространенных математических вакансий ниже:
- Что нужно знать при прохождении собеседования на работу со степенью в области актуарных наук?
- Что нужно знать при собеседовании на работу со степенью в области математического образования?
- Что нужно знать при приеме на работу со степенью по математике?
Удовлетворенность работой для математиков
Заработок — это только одна составляющая любви к своей работе (хотя и важная). Ряд детальных опросов оценил удовлетворенность работой математиков и смежных профессий как одну из самых высоких среди всех профессий. В опросе 200 типов карьеры в 2017 году CareerCast оценил ряд профессий, связанных с математикой, как одни из самых высоких по удовлетворенности работой. Некоторые из основных моментов включают следующие роли.
Ряд детальных опросов оценил удовлетворенность работой математиков и смежных профессий как одну из самых высоких среди всех профессий. В опросе 200 типов карьеры в 2017 году CareerCast оценил ряд профессий, связанных с математикой, как одни из самых высоких по удовлетворенности работой. Некоторые из основных моментов включают следующие роли.
- Статистик: первое место по удовлетворенности работой
- Аналитик по исследованию операций: 3-е место по удовлетворенности работой
- Data Scientist: 5-е место по удовлетворенности работой
- Профессор университета: №6 по удовлетворенности работой
- Математик: 7-е место по удовлетворенности работой
- Инженер-программист: 8-е место по удовлетворенности работой
Учитывая, что 6 из 10 лучших профессий оцениваются как наиболее удовлетворенные работой, трудно ошибиться со степенью по математике!
Типы математических степеней
Математика и связанные с ней степени доступны на уровнях от младшего до докторского. Ваш выбор степени, которую вы хотите получить, поможет определить, на какую работу вы можете претендовать, и зависит от вашего текущего уровня образования, стоимости обучения и времени, которое вы можете выделить для продолжения образования. Ниже мы рассмотрим описания общих программ получения степени по математике.
Ваш выбор степени, которую вы хотите получить, поможет определить, на какую работу вы можете претендовать, и зависит от вашего текущего уровня образования, стоимости обучения и времени, которое вы можете выделить для продолжения образования. Ниже мы рассмотрим описания общих программ получения степени по математике.
Ассоциированная степень по математике
Степени младшего специалиста по математике обычно представляют собой программы перевода, по которым учащиеся переходят на четырехлетнюю программу по бухгалтерскому учету, математике, актуарным наукам или инженерии после того, как они закончили свою степень младшего специалиста.
Как и в случае со степенью младшего специалиста по другим дисциплинам, для получения степени младшего специалиста по математике обычно требуется 60 кредитных часов обучения, что часто требует 1,5-2 лет обучения. Учащиеся в первую очередь стараются выполнить общеобразовательные требования. Требования к общему образованию помогают гарантировать, что выпускники будут всесторонними и аналитически мыслящими. Курсы, необходимые для этой части вашего обучения, могут включать курсы по гуманитарным наукам, социальным наукам, искусству, точным наукам и письму.
Курсы, необходимые для этой части вашего обучения, могут включать курсы по гуманитарным наукам, социальным наукам, искусству, точным наукам и письму.
Наряду с прохождением общеобразовательных курсов, специалисты по математике в программах младшего специалиста часто проходят следующие курсы:
Образец учебной программы по математике на уровне младшего специалиста
- Предварительный расчет
- Исчисление I, II и III
- Линейная алгебра
- Дискретная математика
- Статистика
- Несколько факультативов по математике
Как видите, математика на уровне младшего специалиста обычно только начинает вас на пути к высшему образованию. Степени бакалавра в области математики, статистики, актуарных наук, бухгалтерского учета или инженерии изучают математику гораздо более подробно.
Степени бакалавра по математике
Степень бакалавра математики или смежных дисциплин является стандартной степенью для должностей начального уровня в области инженерии, бухгалтерского учета, актуарных наук, статистики или математики. Для получения степени бакалавра обычно требуется около 120 семестровых кредитных часов. Для получения этих степеней обычно требуется 4 года, хотя получение степени бакалавра за 3-6 лет является обычным явлением без предшествующей степени младшего специалиста.
Для получения степени бакалавра обычно требуется около 120 семестровых кредитных часов. Для получения этих степеней обычно требуется 4 года, хотя получение степени бакалавра за 3-6 лет является обычным явлением без предшествующей степени младшего специалиста.
Как и в случае со степенью младшего специалиста по математике, требования к общему образованию помогают гарантировать, что специалисты по математике будут всесторонними и аналитически мыслящими. Курсы общего образования могут включать курсы гуманитарных наук, искусства, социальных наук, точных наук и письма. После выполнения общих требований к образованию вы перейдете к основным требованиям. Мы подробно изложили основные требования для математических степеней ниже:
Учебная программа бакалавриата по математике
- Вероятность и статистика
- Предварительный расчет
- Исчисление I, II и III
- Реальный анализ I и II
- Линейная алгебра
- Абстрактная алгебра
- Дифференциальные уравнения
- Геометрия
- Случайные процессы
- Математическое программирование
Степени бакалавра математики обычно предлагаются в бакалавриате. и Б.С. формат. Кроме того, некоторые школы могут предлагать степени как по математике, так и по прикладной математике. Степени по математике подталкивают к глубине понимания, углубляясь в более продвинутую чистую математику. Степени по прикладной математике подталкивают студентов к пониманию приложений математики, в том числе уделяют больше внимания науке о данных, статистике, анализу и математическому программированию.
и Б.С. формат. Кроме того, некоторые школы могут предлагать степени как по математике, так и по прикладной математике. Степени по математике подталкивают к глубине понимания, углубляясь в более продвинутую чистую математику. Степени по прикладной математике подталкивают студентов к пониманию приложений математики, в том числе уделяют больше внимания науке о данных, статистике, анализу и математическому программированию.
Некоторые школы предлагают специализацию по математике на уровне бакалавриата. Общие специализации включают в себя:
- Биологическая математика
- Финансовая математика
- Математика и информатика
Учебная программа для получения степени бакалавра актуарных наук
Актуарная наука помогает подготовить будущих актуариев. Актуарий собирает и анализирует статистику, чтобы помочь оценить риск. Актуарии обычно работают в страховых компаниях, в финансовых учреждениях и в правительстве.
Как мы отмечали выше в разделе о карьере, у актуариев одни из самых высоких показателей удовлетворенности работой среди всех профессий. И наиболее распространенной степенью для начала актуарной карьеры является степень бакалавра актуарных наук. Общую учебную программу по специальности актуарная наука можно увидеть ниже.
И наиболее распространенной степенью для начала актуарной карьеры является степень бакалавра актуарных наук. Общую учебную программу по специальности актуарная наука можно увидеть ниже.
- Исчисление I-V
- Введение в актуарную науку
- Микроэкономика
- Макроэкономика
- Линейная алгебра
- Статистика и вероятность для актуарной науки
- Финансы
- Дифференциальные уравнения
- Математические вычисления
- Теория графов
- Линейное программирование
- Факультативы
Учебная программа для получения степени бакалавра по статистике
Статистики могут похвастаться одним из самых высоких показателей удовлетворенности работой среди всех профессий. И степень, необходимая для должностей начального уровня в роли статистика, — это степень бакалавра в области математики или статистики. Ниже мы подробно описали общую учебную программу для специальности статистики на уровне бакалавра.
- Исчисление I, II и III
- Линейная алгебра
- Статистика I и II
- Экспериментальный дизайн
- Регрессионный анализ
- Информатика I и II
- Управление данными
- И факультативы
Степени, связанные с математикой
Несколько других степеней связаны с большим количеством математики и часто сочетаются как второстепенные или двойные специальности со степенью математики из-за совпадения и приобретения ценных навыков. Связанные степени включают:
- Физика
- Машиностроение
- Информатика
- Бухгалтерия
- Финансы
Если вам интересно, сколько математики присутствует в некоторых из вышеперечисленных степеней, обязательно ознакомьтесь с нашими часто задаваемыми вопросами о связи между математикой и смежными предметами:
- Сколько математики требуется для получения степени в области бухгалтерского учета?
- Сколько математики требуется для получения степени в области аудита?
- Сколько математики требуется для получения степени инженера?
- Сколько математики требуется для получения степени магистра бухгалтерского учета?
- Требуется ли математика для получения степени медсестры?
Степени магистра математики
Для тех, кто хочет по-настоящему выделиться в своей области, очень востребованы степени магистра математики, статистики и актуарных наук.
Степени магистра математики позволяют учащимся больше специализироваться в одной области прикладной математики. Студенты, желающие продолжить исследования в области чистой математики, обычно получают докторскую степень после степени бакалавра. Студенты докторских программ получают степень магистра в процессе обучения.
Общие специализации на уровне магистра математики включают:
- Общая математика
- Математическое образование
- Вычислительные науки и инженерия
- Вычислительные финансы
- Вычислительная биология
- Статистика
- Актуарная наука
Для получения степени магистра обычно требуется 1,5–2 года обучения и от 30 до 54 кредитных часов для завершения. Кроме того, от студентов на уровне магистра обычно требуется создать завершающий проект или выполнить магистерскую диссертацию. Диссертация, как правило, представляет собой обзор современной литературы объемом более ста страниц в области, в которой вы изучаете. В отличие от диссертации, которая является оригинальным исследованием, магистерская диссертация показывает, что вы в курсе текущих исследований в своей области и что вы можете критически относиться к проблемам в своей области.
В отличие от диссертации, которая является оригинальным исследованием, магистерская диссертация показывает, что вы в курсе текущих исследований в своей области и что вы можете критически относиться к проблемам в своей области.
Общие учебные программы для магистерских степеней, связанных с математикой, указаны ниже. Хотя студенты обычно могут адаптировать свой курс обучения больше, чем на уровне бакалавриата.
Магистерские курсы математики
Распространен некоторый выбор следующих курсов:
- Два курса анализа для выпускников
- Дискретная математика и алгебра
- Геометрия и топология
- Дифференциальные уравнения
- Вероятность и статистика
- Численный анализ
- Диссертация
Магистерские курсы по статистике
Распространены некоторые из следующих вариантов:
- Статистика выпускников I и II
- Планирование и анализ экспериментов
- Моделирование и регрессионный анализ
- Анализ
- Статистическая оценка
- Проверка гипотез
- Многомерный статистический анализ
- Анализ временных рядов
- Случайные процессы
- Байесовская статистика
- Биологическая статистика
- Финансовая статистика
- Интеллектуальный анализ данных
- Теория надежности
- Среди прочих
Магистерские курсы по актуарным наукам
Распространены некоторые из следующих вариантов:
- Теория вероятностей
- Статистический вывод
- Теория процента
- Актуарные методы
- Актуарные модели
- Финансово-экономические модели
- Линейная регрессия и временные ряды
- Байесовская статистика
- Случайные процессы
- Отраслевые курсы
Магистр математического образования
Одним из распространенных способов получения степени бакалавра в области образования является получение должности преподавателя математики в начальной или средней школе. Многие магистерские программы по математике помогают получить лицензию по этим предметам для целей преподавания в государственных школах. Ниже приведены некоторые из наиболее распространенных курсов в этом типе степени:
Многие магистерские программы по математике помогают получить лицензию по этим предметам для целей преподавания в государственных школах. Ниже приведены некоторые из наиболее распространенных курсов в этом типе степени:
- Исчисление I и II
- Статистика I и II
- Линейная алгебра
- Абстрактная алгебра
- Тригонометрия
- Преподавание математики
- Преподавание алгебры
- Преподавание геометрии
- Обучение исчислению
- Статистика обучения
- История математики и технологий
Докторские степени по математике
Доктора философии (Ph.D.) по математике являются вершиной как прикладной, так и чистой математики. Кандидаты наук — это исследовательские докторские степени, а это означает, что главной целью этих программ является подготовка студентов к продвижению исследований в своей области. В рамках этой цели к.т.н. кандидаты по математике должны представить диссертацию или публикацию оригинального исследования на нескольких сотнях страниц, чтобы получить докторскую степень.
Докторские программы по математике обычно принимают кандидатов со степенью бакалавра по математике, хотя некоторые допускают поступление для лиц со степенью магистра. Как правило, докторанты получают степень магистра математики на полпути к докторантуре.
Программы докторантуры по математике обычно занимают 4-6 лет. Типичная курсовая работа включает в себя следующее, хотя большая часть программы также будет связана с вашим первоначальным исследованием:
- Аналитическая теория чисел
- Алгебраическая теория чисел
- Комбинаторика
- Дифференцируемые коллекторы
- Уравнения в частных производных
- Логика
Как правило, докторские степени позволяют студентам специализироваться гораздо больше, чем другие степени. Докторские степени по математике обычно требуют от студентов выбора между направлениями прикладной и чистой математики и часто предлагают междисциплинарные курсы в области естественных наук, инженерии, бизнеса или вычислительной техники.
Для дополнительной информации:
Каковы 5 лучших профессий в науке об окружающей среде?
Общая математика | Математика и статистика
Комплексная математика | Математика и статистика | Университет Небраски в КирниПерейти к основному содержанию
Главная » Академики » Математика и статистика » Общеобразовательный курс математики
О программе комплексного обучения математике
В кампусе
Выполнив требования комплексной программы по математике в Университете штата Небраска в Кирни, вы получите глубокие знания по математике. Вы также выбираете акцент в области информатики, прикладной математики или общей математики. Темы занятий варьируются от прикладных курсов по дифференциальным уравнениям и численному анализу до рефератов, включая углубленное исчисление, теорию чисел и современную алгебру.
Вы также выбираете акцент в области информатики, прикладной математики или общей математики. Темы занятий варьируются от прикладных курсов по дифференциальным уравнениям и численному анализу до рефератов, включая углубленное исчисление, теорию чисел и современную алгебру.
Некоторые выпускники получают ученые степени в области математики, статистики, делового администрирования или естественных наук. Другие выпускники работают в финансовой сфере или в области актуарных наук. Как студент-математик, консультант факультета проведет вас через вашу курсовую работу и поможет вам достичь ваших личных целей. В UNK классы небольшие, и вы можете познакомиться со своими инструкторами, попросить о помощи или получить совет в комфортной обстановке.
Математика и статистика
Краткий обзор комплексной программы по математике
120
Кредит-часы
Общие требования к обучению снижены до 30 кредит-часов, что дает больше свободы и облегчает перевод в UNK.
Просмотреть полный учебный план
Полученная степень
Всесторонняя математика, бакалавр наук
Подать заявку
$209
За кредитный час0003
Посмотреть стоимость
Посмотреть полную программу обучения
Подать заявку
Посмотреть стоимость
Четырехгодичное расписание занятий:
Новый общеобразовательный учебный план UNK требует меньше часов, упрощает перевод и дает студентам большую гибкость в получении степени. Это сократило требования к общему обучению с 45 часов до 30 часов. Приведенное ниже четырехлетнее расписание занятий представляет собой примерный график продвижения к получению степени по математике в Университете Небраски в Кирни. Проконсультируйтесь с вашим научным руководителем.
Это сократило требования к общему обучению с 45 часов до 30 часов. Приведенное ниже четырехлетнее расписание занятий представляет собой примерный график продвижения к получению степени по математике в Университете Небраски в Кирни. Проконсультируйтесь с вашим научным руководителем.
Семестр 1 (14 кредитов)
- МАТЕМАТИКА 115 Исчисление I с аналитической геометрией
- РУС 101 или курс GS Distribution Area
- Курс устного общения GS
- Портал GS
Семестр 2 (17 кредитов)
- MATH 202 Исчисление II с аналитической геометрией
- МАТЕМАТИКА 250 Основы математики
- Гуманитарный курс GS
- Курс демократии GS
- RUS 102 Академическое письмо и исследования
Семестр 3 (14 кредитов)
- МАТЕМАТИКА 260 Исчисление III
- МАТЕМАТИКА 413 Дискретная математика
- Гуманитарный курс GS
- Курс GS по социальным наукам
Семестр 4 (15 кредитов)
- MATH 350 Абстрактная алгебра
- МАТЕМАТИКА 305 Дифференциальные уравнения
- КИБР 101, КИБР 102, ИЛИ КИБР 103
- Курс GS по естественным наукам
- Курс GS по социальным наукам
Семестр 5 (14 кредитов)
- PHYS 275/PHYS 275L Общая физика I (Исчисление)
- MATH 460 Расширенное исчисление I
- Курс GS Capstone
- Курс области акцента
Семестр 6 (15 кредитов)
- МАТЕМАТИКА 365 Комплексный анализ
- MATH 440 Линейная алгебра
- Курс области акцента
- Неограниченные факультативы
Семестр 7 (15 кредитов)
- Курс области акцента
- Курс области акцента
- Неограниченные факультативы
Семестр 8 (16 кредитов)
- MATH 420 Численный анализ
- МАТЕМАТИКА 404 Теория чисел
- STAT 441 Вероятность и статистика
- Курс с особыми акцентами или неограниченный факультативный курс
- Курс эстетики GS
«Когда я стал изучать математику в UNK, я впервые в жизни почувствовал себя окруженным единомышленниками. Я встретил группу людей, которые ценили математику больше, чем просто средство для достижения цели.» «Я действительно мало что знал о выборе колледжа. Оглядываясь назад, если бы я знал, я бы все равно выбрал UNK из-за небольшого соотношения студентов и преподавателей, большого количества возможностей для студентов и того факта, что Кирни — небольшой город, но достаточно большой, чтобы в нем кипела активная ночная жизнь».
Я встретил группу людей, которые ценили математику больше, чем просто средство для достижения цели.» «Я действительно мало что знал о выборе колледжа. Оглядываясь назад, если бы я знал, я бы все равно выбрал UNK из-за небольшого соотношения студентов и преподавателей, большого количества возможностей для студентов и того факта, что Кирни — небольшой город, но достаточно большой, чтобы в нем кипела активная ночная жизнь».
Natalie Hansich
Что вы можете делать со степенью бакалавра по математике
Узнайте больше о типах профессий и общих работодателях, на которых работают выпускники факультета математики.
Карьера
- Компьютерное программирование
- Актуарная наука
- Паевые инвестиционные фонды и финансовые отрасли
- Аналитик компьютерных систем
- Администрация
- Высшее образование
- Криптография
- Биоматематика
- Исследование операций
- Статистика
Связанные программы
Математика B.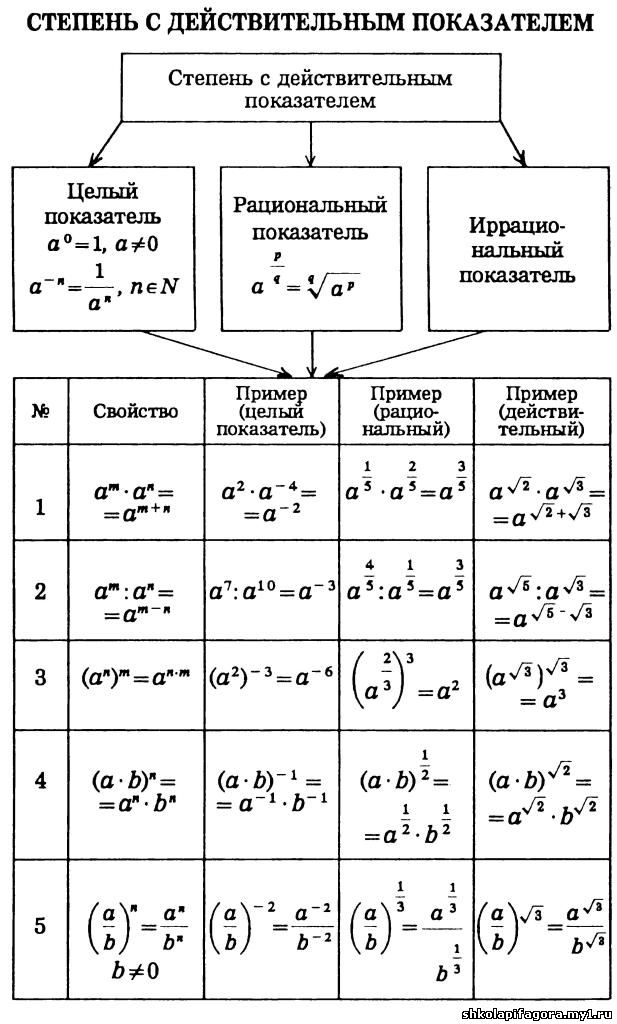 A./B.S.
Языковые искусства 7-12 Преподавание и практическая поддержка
A./B.S.
Языковые искусства 7-12 Преподавание и практическая поддержка
Самый доступный университет Небраски — еще более ценный благодаря смелым наградам.


 У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.
У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней. ) сыграла в этом значительную роль.
) сыграла в этом значительную роль. .. Любопытно, что Декарт считал, что а*а не занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей. Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а2.
.. Любопытно, что Декарт считал, что а*а не занимает больше места, чем а2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей. Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а2. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание). 8 / 13 -0.2 = 13(3.8 -0.2) = 133.6
8 / 13 -0.2 = 13(3.8 -0.2) = 133.6

 Курсовая работа по прикладной математике может быть сосредоточена на прикладной теории чисел, дифференциальных уравнениях и линейной алгебре.
Курсовая работа по прикладной математике может быть сосредоточена на прикладной теории чисел, дифференциальных уравнениях и линейной алгебре.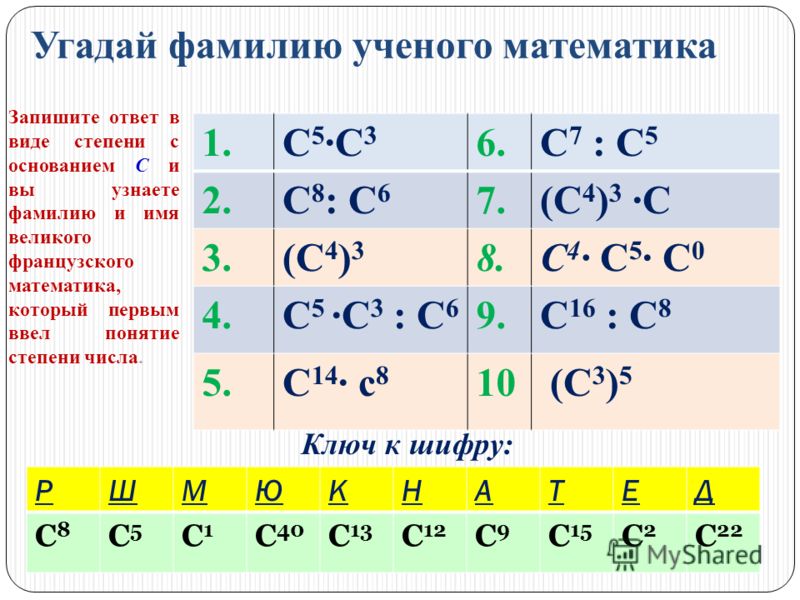

 Кроме того, по мере распространения медицинских устройств и устройств Интернета вещей (IoT) и сбора данных о здоровье пациентов, а также по мере того, как пациенты начинают лучше понимать свое здоровье, привычки и генетику, все больше открывается путь для развития персонализированной медицины. Отрасли требуются талантливые специалисты по данным, математики и статистики, чтобы управлять потоком информации и использовать ее для улучшения жизни.
Кроме того, по мере распространения медицинских устройств и устройств Интернета вещей (IoT) и сбора данных о здоровье пациентов, а также по мере того, как пациенты начинают лучше понимать свое здоровье, привычки и генетику, все больше открывается путь для развития персонализированной медицины. Отрасли требуются талантливые специалисты по данным, математики и статистики, чтобы управлять потоком информации и использовать ее для улучшения жизни. Данные BLS отмечают, что ожидается, что занятость в этой области вырастет на 6% в период с 2018 по 2028 год, что соответствует среднему темпу роста для всех профессий.
Данные BLS отмечают, что ожидается, что занятость в этой области вырастет на 6% в период с 2018 по 2028 год, что соответствует среднему темпу роста для всех профессий.

