Свойства степеней при сложении. Основные свойства степеней. Примеры на умножение степеней с одинаковыми показателями
Каждая арифметическая операция порою становится слишком громоздкой для записи и её стараются упростить. Когда-то так было и с операцией сложения. Людям было необходимо проводить многократное однотипное сложение, например, посчитать стоимость ста персидских ковров, стоимость которого составляет 3 золотые монеты за каждый. 3+3+3+…+3 = 300. Из-за громоздкости было придумано сократить запись до 3 * 100 = 300. Фактически, запись «три умножить на сто» означает, что нужно взять сто троек и сложить между собой. Умножение прижилось, обрело общую популярность. Но мир не стоит на месте, и в средних веках возникла необходимость проводить многократное однотипное умножение. Вспоминается старая индийская загадка о мудреце, попросившем в награду за выполненную работу пшеничные зёрна в следующем количестве: за первую клетку шахматной доски он просил одно зерно, за вторую – два, третью – четыре, пятую – восемь и так далее. 3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.
3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n
.
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Операции со степенями и корнями. Степень с отрицательным
,нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются :
a m · a n = a m + n .
2. При делении степеней с
одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc … ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
(a m )
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень
из отношения равен отношению корней делимого и делителя:
Корень
из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т
еперь
формула a
m : a
n = a
m
—
n может быть использована не
только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :
О выражениях, не имеющих смысла. Есть несколько таких выражений. любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно
определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
Случай 3.
0 0 — любое число.
Действительно,
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
(Почему?).
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
Нашем случае x > 0 , ответом является x > 0 ;
3) при x x / x = 1, т. e . –1 = 1, следовательно,
В этом случае нет решения.
Таким образом, x > 0.
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.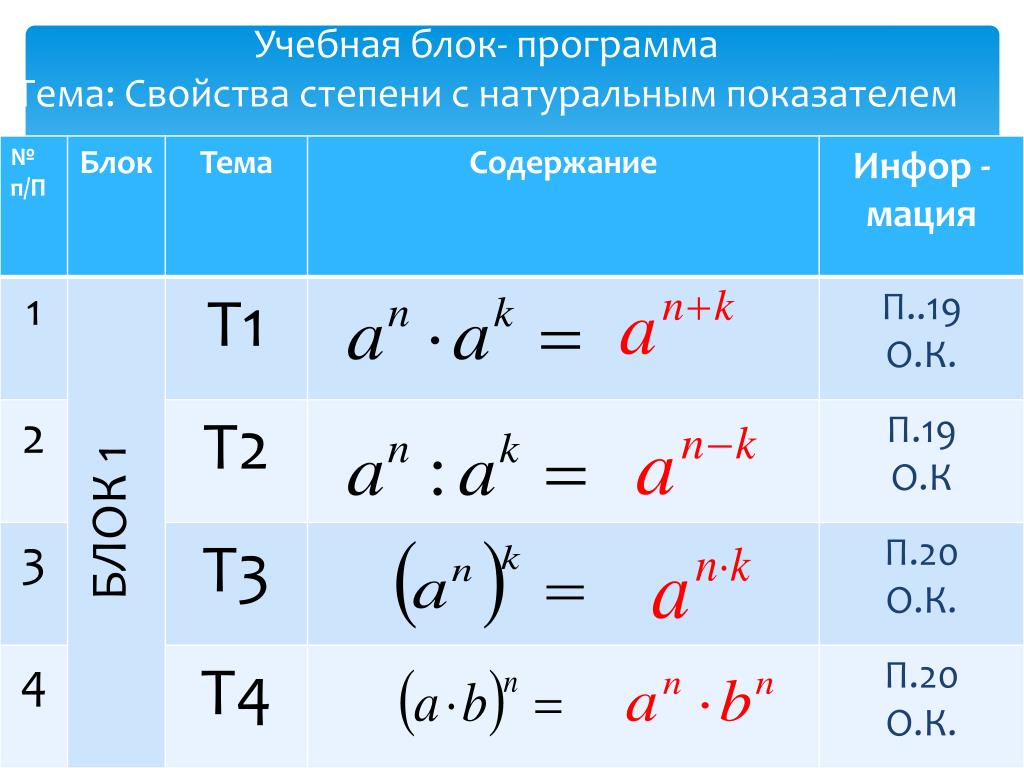
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
www.algebraclass.ru
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Правила умножения степеней с разным основанием
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 69. Умножение и деление степеней с одинаковыми основаниями
Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть
Доказательство. По определению степени
По определению степени
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.
Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п
(a =/= 0)
Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу
Если т > п , то число т — п будет натуральным; следовательно, по теореме 1
Теорема 2 доказана.
Следует обратить внимание на то, что формула
доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:
Поэтому из доказанного пока нельзя делать, например, таких выводов:
К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .
Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть
Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:
что и требовалось доказать.
Например, (2 3) 2 = 2 6 = 64;
518 (Устно.) Определить х из уравнений:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (У с т н о.) Упростить:
520. (У с т н о.) Упростить:
521. Данные выражения представить в виде степеней с одинаковыми основаниями:
1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;
2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .
Сложение переменных с разными степенями. Действия с одночленами. Применение степеней и их свойств
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
a n = a * a * a * …a n .
Например:
- 2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
- 4 2 = 4 в степ. два = 4 * 4 = 16;
- 5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
- 10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- a n * a m = (a) (n+m) ;
- a n: a m = (a) (n-m) ;
- (a b) m =(a) (b*m) .
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается :
A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.
И наоборот:
1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.
А если дробь?
(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.
Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;
- 0˂А˂1.
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r 1 – в этом случае равно 3;
r 2 – будет равно 4.
Тогда, при А = 1, 1 π = 1.
А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.
А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Статьи по естественным наукам и математике
Свойства степеней с одинаковыми основаниями
Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это
- Произведение сумма
- Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей.
- Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.
Будьте внимательны! Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует .
Запишем эти свойства-правила в виде формул:
- a m ? a n = a m+n
- a m ? a n = a m–n
- (a m) n = a mn
Теперь рассмотрим их на конкретных примерах и попробуем доказать.
5 2 ? 5 3 = 5 5 — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:
5 2 ? 5 3 = 5 ? 5 ? 5 ? 5 ? 5 = 5 5 — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5 5 .
3 9 ? 3 5 = 3 9–5 = 3 4 . Запишем деление в виде дроби:
Ее можно сократить:
В результате получим:
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.
Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку мы рассматриваем степени только с натуральными показателями, то не можем в результате вычитания показателей получить число меньше, чем 1. Поэтому на формулу a m ? a n = a m–n накладываются ограничения: a ? 0 и m > n.
Перейдем к третьему свойству:
(2 2) 4 = 2 2?4 = 2 8
Запишем в развернутом виде:
(2 2) 4 = (2 ? 2) 4 = (2 ? 2) ? (2 ? 2) ? (2 ? 2) ? (2 ? 2) = 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 = 2 8
Можно прийти к такому выводу и логически рассуждая. Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.
Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.
scienceland.info
Правила сложения и вычитания.
1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения)
13+25=38, можно записать как: 25+13=38
2. Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).
10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т.д.
3. Единицы складываются с единицами, десятки с десятками и т.д.
34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица).
4. Единицы вычитаются из единиц, десятки из десятков и т.д.
53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток)
примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого.
41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29).
5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое.
Это значит, что сложение можно проверить с помощью вычитания.
Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7
Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка.
6. Если к разности прибавить вычитаемое, то получится уменьшаемое.
Это значит, что вычитание можно проверить сложением.
Для проверки к разности прибавим вычитаемое: 19+50=69.
Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка.
Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби, где a – это числитель дроби, b – знаменатель дроби. Причем b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа .
Навигация по уроку:
Пример 1. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении является знаком операции и не относится к дроби. У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа. Поэтому мы из вычли . Получили ответ. Затем сократив эту дробь на 2, получили окончательный ответ .
При желании некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который дан в выражении является знаком операции и не относится к дроби.
Дробь в данном случае является положительным рациональным числом, имеющим знак плюса, который невидим. Но мы запишем его для наглядности:
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Пример 3. Найти значение выражения
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к одинаковому (общему) знаменателю. Не будем подробно останавливаться на этом. Если испытываете трудности, обязательно вернитесь к уроку действия с дробями и повторите его.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший и перед полученным ответом ставим тот знак, модуль которого больше:
Пример 4. Найти значение выражения
Получили сумму из трёх слагаемых. Сначала найдём значение выражения, затем к полученному ответу прибавим
Первое действие:
Второе действие:
Таким образом, значение выражения равно.
Решение для данного примера можно записать покороче
Пример 5 . Найти значение выражения
Найти значение выражения
Заключим каждое число в скобки вместе со своими знаками. Для этого смешанное число временно развернём
Вычислим целые части:
В главном выражении вместо запишем полученную единицу:
Полученное выражение свернём. Для этого опустим скобки и запишем единицу и дробь вместе
Решение для данного примера можно записать покороче:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальную часть перепишем как есть:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Сложим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно .
Решение для данного примера можно записать покороче:
Пример 7. Найти значение выражение
Запишем смешанное число в развёрнутом виде. Остальное перепишем как есть:
Заключим каждое рациональное число в скобки вместе своими знаками
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо запишем полученное число?7
Выражение является развёрнутой формой записи смешанного числа . Можно сразу записать ответ, записав вместе числа?7 и дробь (спрятав минус этой дроби)
Можно сразу записать ответ, записав вместе числа?7 и дробь (спрятав минус этой дроби)
Таким образом, значение выражения равно
Решение для данного примера можно записать значительно короче. Если пропустить некоторые подробности, то его можно записать следующим образом:
Пример 8. Найти значение выражения
Данное выражение можно вычислить двумя способами. Рассмотрим каждый из них.
Первый способ. Целые и дробные части выражения вычисляются по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Заключим каждое число в скобки вместе со своими знаками:
Заменим вычитание сложением там, где это можно:
Получили сумму из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение содержит несколько слагаемых, то сумма не будет зависеть от порядка действий. Это позволит нам сгруппировать целые и дробные части по отдельности:
Вычислим целые части:
В главном выражении вместо запишем полученное число?3
Вычислим дробные части:
В главном выражении вместо запишем полученное смешанное число
Чтобы вычислить получившееся выражение, смешанное число нужно временно развернуть, затем заключить в скобки каждое число и заменить вычитание сложением. Делать это нужно очень аккуратно, чтобы не перепутать знаки слагаемых.
Делать это нужно очень аккуратно, чтобы не перепутать знаки слагаемых.
После преобразования выражения мы получили новое выражение , которое легко вычисляется. Похожее выражение было в примере 7. Напомним, что мы отдельно сложили целые части, а дробную оставили как есть:
Значит значение выражения равно
Решение для данного примера можно записать покороче
В коротком решении пропускаются этапы заключения чисел в скобки, замена вычитания сложением, проставление модулей. Если вы учитесь в школе или в другом учебном заведении, то от вас будут требовать пропускать эти примитивные действия, чтобы сэкономить время и место. Приведённое выше короткое решение можно записать ещё короче. Выглядеть оно будет так:
Поэтому, находясь в школе или в ином учебном заведении, будьте готовы к тому, что некоторые действия придётся выполнять в уме.
Второй способ. Смешанные числа выражения переводят в неправильные дроби и вычисляют, как обычные дроби.
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением:
Теперь смешанные числа и переведём в неправильные дроби:
Получили сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим минус:
Сложим их модули и перед полученным ответом поставим минус:
Получили ответ как и в прошлый раз.
Подробное решение вторым способом выглядит следующим образом:
Пример 9. Найти выражения выражения
Первый способ. Сложим целые и дробные части по отдельности.
В этот раз попробуем пропустить некоторые примитивные действия, такие как запись выражения в развёрнутом виде, заключение чисел в скобки, замена вычитания сложением, проставление модулей:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Второй способ. Переведём смешанные числа в неправильные дроби и вычислим, как обычные дроби.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки. Тогда получим простейшее выражение, которое вычисляется легко:
В данном примере целые и дробные части были вычислены по отдельности.
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед полученными числом поставим тот знак, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких параметров. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение , затем выражение Полученные ответы сложим.
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Пример 13. Найти значение выражения
Заменим вычитание сложением:
Получили сложением рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше. Но мы имеем дело со смешанными числами. Чтобы понять какой модуль больше, а какой меньше, нужно сравнить модули этих смешанных чисел. А чтобы сравнить модули смешанных чисел, нужно перевести их в неправильные дроби и сравнить, как обычные дроби.
А чтобы сравнить модули смешанных чисел, нужно перевести их в неправильные дроби и сравнить, как обычные дроби.
На следующем рисунке показаны все этапы сравнения модулей смешанных чисел
Узнав какой модуль больше, а какой меньше, мы можем продолжить вычисление нашего примера:
Таким образом, значение выражения равно
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть, как положительными, так и отрицательными.
Пример 14. Найти значение выражения?3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
Модуль числа 4,3 больше, чем модуль числа?3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку в ответе должен стоять знак большего модуля, то есть модуля |+4,3|.
Таким образом, значение выражения?3,2 + (+4,3) равно 1,1
Пример 15. Найти значение выражения 3,5 + (?8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим тот знак, модуль которого больше
3,5 + (?8,3) = ?(|?8,3| ? |3,5|) = ?(8,3 ? 3,5) = ?(4,8) = ?4,8
Таким образом, значение выражения 3,5 + (?8,3) равно?4,8
Этот пример можно записать покороче:
Пример 16. Найти значение выражения?7,2 + (?3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Запись с модулями можно пропустить, чтобы не загромождать выражение:
7,2 + (?3,11) = ?7,20 + (?3,11) = ?(7,20 + 3,11) = ?(10,31) = ?10,31
Таким образом, значение выражения?7,2 + (?3,11) равно?10,31
Этот пример можно записать покороче:
Пример 17. Найти значение выражения?0,48 + (?2,7)
Это сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим знак минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
0,48 + (?2,7) = (?0,48) + (?2,70) = ?(0,48 + 2,70) = ?(3,18) = ?3,18
Пример 18. Найти значение выражения?4,9 ? 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который дан в выражении, является знаком операции и не относится к десятичной дроби 5,9. У этой десятичной дроби свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Сложить их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Сложить их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
(?4,9) + (?5,9) = ?(4,9 + 5,9) = ?(10,8) = ?10,8
Таким образом, значение выражения?4,9 ? 5,9 равно?10,8
= ?(4,9 + 5,9) = ?(10,8) = ?10,8
Пример 19. Найти значение выражения 7 ? 9,3
Заключим в скобки каждое число вместе со своим знаками
Заменим вычитание сложением
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше. Запись с модулями можно пропустить, чтобы не загромождать выражение:
(+7) + (?9,3) = ?(9,3 ? 7) = ?(2,3) = ?2,3
Таким образом, значение выражения 7 ? 9,3 равно?2,3
Подробное решение данного примера записывается следующим образом:
7 ? 9,3 = (+7) ? (+9,3) = (+7) + (?9,3) = ?(|?9,3| ? |+7|) =
Короткое решение будет выглядеть так:
Пример 20. Найти значение выражения?0,25 ? (?1,2)
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше:
Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше:
0,25 + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
Подробное решение данного примера записывается следующим образом:
0,25 ? (?1,2) = (?0,25) + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
Короткое решение будет выглядеть так:
Пример 21. Найти значение выражения?3,5 + (4,1 ? 7,1)
В первую очередь выполним действия в скобках, затем сложим полученный ответ с числом?3,5. Запись с модулями пропустим, чтобы не загромождать выражения.
Первое действие:
4,1 ? 7,1 = (+4,1) ? (+7,1) = (+4,1) + (?7,1) = ?(7,1 ? 4,1) = ?(3,0) = ?3,0
Второе действие:
3,5 + (?3,0) = ?(3,5 + 3,0) = ?(6,5) = ?6,5
Ответ: значение выражения?3,5 + (4,1 ? 7,1) равно?6,5.
3,5 + (4,1 ? 7,1) = ?3,5 + (?3,0) = ?6,5
Пример 22. Найти значение выражения (3,5 ? 2,9) ? (3,7 ? 9,1)
Выполним действия в скобках, затем из числа которое получилось в результате выполнения первых скобок вычтем число, которое получилось в результате выполнения вторых скобок. Запись с модулями пропустим, чтобы не загромождать выражения.
Запись с модулями пропустим, чтобы не загромождать выражения.
Первое действие:
3,5 ? 2,9 = (+3,5) ? (+2,9) = (+3,5) + (?2,9) = 3,5 ? 2,9 = 0,6
Второе действие:
3,7 ? 9,1 = (+3,7) ? (+9,1) = (+3,7) + (?9,1) = ?(9,1 ? 3,7) = ?(5,4) = ?5,4
Третье действие
0,6 ? (?5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 ? 2,9) ? (3,7 ? 9,1) равно 6.
Короткое решение данного примера можно записать следующим образом:
(3,5 ? 2,9) ? (3,7 ? 9,1) = 0,6 ? (?5,4) = 6,0 = 6
Пример 23. Найти значение выражения?3,8 + 17,15 ? 6,2 ? 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением там, где это можно
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а сложим все слагаемые слева направо в порядке их следования:
Первое действие:
(?3,8) + (+17,15) = 17,15 ? 3,80 = 13,35
Второе действие:
13,35 + (?6,2) = 13,35 ? ?6,20 = 7,15
Третье действие:
7,15 + (?6,15) = 7,15 ? 6,15 = 1,00 = 1
Ответ: значение выражения?3,8 + 17,15 ? 6,2 ? 6,15 равно 1.
Короткое решение данного примера можно записать следующим образом:
3,8 + 17,15 ? 6,2 ? 6,15 = 13,35 + (?6,2) ? 6,15 = 7,15 ? 6,15 = 1,00 = 1
Короткие решения создают меньше проблем и путаниц, поэтому желательно привыкнуть к ним.
Пример 24. Найти значение выражения
Переведём десятичную дробь?1,8 в смешанное число. Остальное перепишем, как есть. Если испытываете затруднения с переводом десятичной дроби в смешанное число, обязательно повторите урок десятичные дроби.
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (?4,4) в неправильную дробь
Попутно переведём десятичную дробь (?4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и опустить скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число в неправильную дробь, а десятичную дробь?0,85 в обыкновенную дробь. Получим следующее выражение:
Получили сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим знак минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками.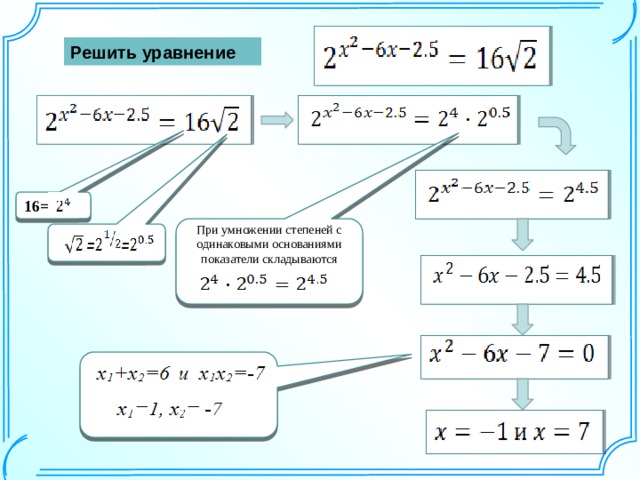 Вычтем из большего модуля меньший и перед полученным ответом поставим тот знак, модуль которого больше:
Вычтем из большего модуля меньший и перед полученным ответом поставим тот знак, модуль которого больше:
Пример 28. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь в обыкновенную дробь
Пример 29. Найти значение выражения
Переведём десятичные дроби?0,25 и?1,25 в обыкновенные дроби, остальное оставим как есть. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим. Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного числа вычесть рациональное число . Этим вариантом и воспользуемся.
Первое действие:
Второе действие:
Ответ: значение выражения равно?2.
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное оставим как есть
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас
Второе действие:
Ну и сложим полученное число?7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, то есть их сумма будет равна нулю, поскольку сумма противоположных чисел равна нулю
Третье действие:
Ответ: значение выражения равно
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Сложение и вычитание целых чисел
В этом уроке мы изучим сложение и вычитание целых чисел , а также правила для их сложения и вычитания.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, а где положительные.
Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате, мы окажемся в точке, где располагается число 4. На рисунке можно увидеть как это происходит:
На рисунке можно увидеть как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 ? 3.
Значение данного выражения равно?2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число?2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 ? 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения?2 + 4
Значение данного выражения равно 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.
В результате мы окажемся в точке, где располагается положительное число 2.
Видно, что мы сдвинулись из точки где располагается отрицательное число?2 в правую сторону на четыре шага и оказались в точке, где располагается положительное число 2.
Знак плюса в выражении?2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 4. Найти значение выражения?1 ? 3
Значение данного выражения равно?4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число?4
Видно, что мы сдвинулись из точки где располагается отрицательное число?1 в левую сторону на три шага и оказались в точке, где располагается отрицательное число?4.
Знак минуса в выражении?1 ? 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Пример 5. Найти значение выражения?2 + 2
Значение данного выражения равно 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число?2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Знак плюса в выражении?2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Правила сложения и вычитания целых чисел
Чтобы вычислить то или иное выражение, необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения?2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. ?2 это отрицательное число, а 5 — положительное. Для таких случаев предусмотрено следующее правило:
Для таких случаев предусмотрено следующее правило:
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа?2. Правило требует из большего модуля вычесть меньший. Поэтому, мы должны из 5 вычесть 2, и перед полученным ответом поставить тот знак, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть, ответ будет положительным:
Обычно записывают покороче?2 + 5 = 3
Пример 2. Найти значение выражения 3 + (?2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 — это положительное число, а?2 — отрицательное. Обратите внимание, что число?2 заключено в скобки, чтобы сделать выражение понятнее и красивее. Это выражение намного проще для восприятия, чем выражение 3+?2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим тот знак, модуль которого больше:
3 + (?2) = |3| ? |?2| = 3 ? 2 = 1
Модуль числа 3 больше, чем модуль числа?2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили тот знак модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
Обычно записывают покороче 3 + (?2) = 1
Пример 3. Найти значение выражения 3 ? 7
В этом выражении из меньшего числа вычитается большее. Для такого случая предусмотрено следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 ? 7 как мы узнали равно?4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны?4
Но мы видим, что на втором этапе располагается выражение 7 ? 3, которое не равно?4.
Чтобы исправить эту ситуацию, выражение 7 ? 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 ? 7 = ? (7 ? 3) = ? (4) = ?4
В этом случае равенство будет соблюдаться на каждом этапе:
После того как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 ? 7 = ? (7 ? 3) = ? (4) = ? 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a ? b = ? (b ? a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 ? 7 = ? 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Что это означает? Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 ? 3. На начальных этапах изучения математики мы просто ставили знак равенства и записывали ответ:
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5?3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число?3. Записываем новое выражение:
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели выше. Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше:
5 + (?3) = |5| ? |?3| = 5 ? 3 = 2
Модуль числа 5 больше, чем модуль числа?3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без своего знака плюс.
Это связано с тем, что положительные числа записываются без своего знака плюс.
Например, в выражении 3 ? 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами по традиции не записывают.
А стало быть для наглядности данное выражение можно записать следующим образом:
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще. Вычитаемое в данном случае это число (+1), а противоположное ему число (?1). Заменим операцию вычитания сложением и вместо вычитаемого (+1) записываем противоположное ему число (?1)
(+3) ? (+1) = (+3) + (?1) = |+3| ? |?1| = 3 ? 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 ? 7, используя правило вычитания. Сначала приведём выражение к нормальному виду, расставив каждому числу свои знаки. У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она также является положительным числом:
Заменим вычитание сложением:
Дальнейшее вычисление не составляет труда:
Пример 7. Найти значение выражения?4 ? 5
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (?4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (?5).
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев предусмотрено следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило и поставим перед полученным ответом минус:
(?4) ? (+5) = (?4) + (?5) = |?4| + |?5| = 4 + 5 = ?9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
Так мы обеспечим минус, который должен стоять перед ответом:
(?4) ? (+5) = (?4) + (?5) = ?(|?4| + |?5|) = ?(4 + 5) = ?(9) = ?9
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения?3 ? 5 ? 7 ? 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа?3 являются положительными, поэтому у них будут знаки плюса:
Заменим операции вычитания операциями сложения. Все минусы (кроме минуса, который перед тройкой) поменяются на плюсы и все положительные числа поменяются на противоположные:
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
= ?(|?3| + |?5| + |?7| + |?9|) = ?(3 + 5 + 7 + 9) = ?(24) = ?24
Решение для данного примера можно записать покороче:
3 ? 5 ? 7 ? 9 = ?(3 + 5 + 7 + 9) = ?24
Пример 9. Найти значение выражения?10 + 6 ? 15 + 11 ? 7
Приведём выражение к понятному виду:
Здесь сразу две операции: сложение и вычитание. Сложение оставляем как есть, а вычитание заменяем сложением:
Сложение оставляем как есть, а вычитание заменяем сложением:
(?10) + (+6) ? (+15) + (+11) ? (+7) = (?10) + (+6) + (?15) + (+11) + (?7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(?10) + (+6) = ? (10 ? 6) = ? (4) = ? 4
Второе действие:
(?4) + (?15) = ? (4 + 15) = ? (19) = ? 19
Третье действие:
(?19) + (+11) = ? (19 ? 11) = ? (8) = ?8
Четвёртое действие:
(?8) + (?7) = ? (8 + 7) = ? (15) = ? 15
Таким образом, значение выражения?10 + 6 ? 15 + 11 ? 7 равно?15
Примечание . Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить тот знак, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить знак минуса.
Вычесть одно число из другого означает, прибавить к уменьшаемому число противоположное вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить знак минус.
- Хоккей без правил В Контакте Игра была выпущена в сентябре 2012 года, и набрала уже почти 700 000 пользователей. Предусмотрено два режима игры и множество возможностей для комплектования команды. Течение матча в Хоккее без правил В Контакте напоминает ранние игры серии NHL от Electronic Arts. 3 игрока на […]
- Правила покера Омаха Холдем
Омаха Хай-Лоу и пятикарточная Омаха
Омаха Холдем (Omaha Hold»Em) является небольшим видоизменением Техасского Холдема. Если вы плохо знакомы с этой самой популярной разновидностью покера, изучайте правила Техасского Холдема по ссылке; их знание необходимо для понимания правил Омахи.
 Все […]
Все […] - Решение задач по генетике с использованием 1 и 2 законов Менделя Лекция 8 Julia Kjahrenova 1. — презентация Презентация была опубликована 3 года назад пользователемАлина Артемьева Похожие презентации Презентация на тему: » Решение задач по генетике с использованием 1 и 2 законов Менделя Лекция 8 Julia Kjahrenova 1.» […]
- 5-7 алгебра правила Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом d, называют арифметической прогрессией. Число d называют разностью арифметической прогрессии. В арифметической прогрессии, т. е. в […]
- Определяем ставку транспортного налога для фургонов и других нетипичных автомобилей с категорией «B» Вылавливаем нужную информацию из ПТС Сразу скажем, что данные, указанные в строке 4 «Категория ТС (A, B, C, D, прицеп)» паспорта транспортного средства (ПТС), учитывать не нужно. Ведь категория «B» вовсе не означает, […]
- Рейтинг страховых компаний ОСАГО
ОСАГО относится к обязательному страхованию, оно действует не только на территории России, но и в других странах ближнего зарубежья.
 Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]
Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […] - Проживание гостиница уфа Мини-отель в Уфе 5 Five Rooms Приглашаем гостей столицы в уютный комфортабельный отель, расположенный в центре города Уфа по улице Комсомольская 159/1. В непосредственной близости от отеля расположены кинокомплекс «Искра IMAX», цирк, ресторан-клуб А кафе, ресторан Beer Berry, ТРЦ […]
- Правила использования Present Simple Tense в английском языке Present Simple Tense – это грамматическое время, которое считается одним из самых простых в понимании, поскольку, настоящее простое время существует во всех языках. В славянских языках так точно. Если вы читаете эту статью, это значит, что вы только […]
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
www.algebraclass.ru
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2.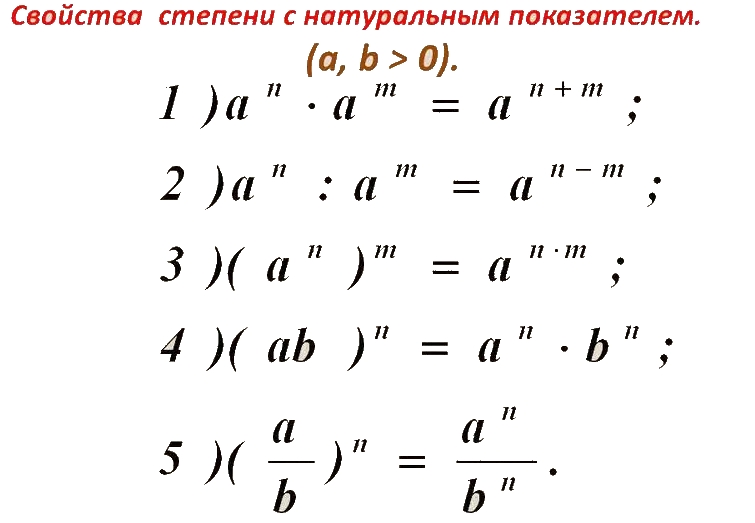 Корень из отношения равен отношению корней делимого и делителя:
Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Правила умножения степеней с разным основанием
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 69. Умножение и деление степеней с одинаковыми основаниями
Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть
Доказательство. По определению степени
По определению степени
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.
Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п
(a =/= 0)
Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу
Если т > п , то число т — п будет натуральным; следовательно, по теореме 1
Теорема 2 доказана.
Следует обратить внимание на то, что формула
доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:
Поэтому из доказанного пока нельзя делать, например, таких выводов:
К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .
Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть
Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:
что и требовалось доказать.
Например, (2 3) 2 = 2 6 = 64;
518 (Устно.) Определить х из уравнений:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (У с т н о.) Упростить:
520. (У с т н о.) Упростить:
521. Данные выражения представить в виде степеней с одинаковыми основаниями:
1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;
2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где «a » — любое число, а «m », «n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями . Оно не относится к их сложению.
Оно не относится к их сложению.
Нельзя
заменять сумму
(3 3 + 3 2)
на 3 5
. Это понятно, если
посчитать
(3 3 + 3 2) = (27 + 9) = 36
, а
3 5 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5 - Пример. Найти значение выражения, используя свойства степени.
= = =
=2 9 + 2 2 5
= 2 11 − 5 = 2 6 = 642 11 2 5 Важно!
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степеньЗапомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где «a » — любое число, а «m », «n » — любые натуральные числа.
Свойства 4
Степень произведенияЗапомните!
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где «a », «b » — любые рациональные числа; «n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4Свойства 5
Степень частного (дроби)Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где «a », «b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

- Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
- Пример 1.
В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.
Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.
Правила сложения и вычитания одночленов
Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).
Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.
Пример 1
Условие: выполните сложение одночленов − 3 · x и 2 , 72 · x 3 · y 5 · z .
Решение
Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:
(− 3 · x) + (2 , 72 · x 3 · y 5 · z)
Когда мы выполним раскрытие скобок, получится — 3 · x + 2 , 72 · x 3 · y 5 · z . Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.
Ответ: (− 3 · x) + (2 , 72 · x 3 · y 5 · z) = − 3 · x + 2 , 72 · x 3 · y 5 · z .
Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.
Пример 2
Условие: проведите в правильном порядке указанные действия с многочленами
3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Решение
Начнем с раскрытия скобок.
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = = (3 · a 2 + a 2 — 7 · a 2) + 4 · a · c — 2 2 3 · a · c + 4 9 = = — 3 · a 2 + 1 1 3 · a · c + 4 9
У нас получился многочлен, который и будет результатом данного действия.
Ответ: 3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = — 3 · a 2 + 1 1 3 · a · c + 4 9
В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.
О том, как это делается, мы расскажем в отдельной статье.
Правила умножения одночленов
Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.
Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:
- Правильно записать произведение.
- Раскрыть скобки в полученном выражении.
- Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
- Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.
Посмотрим, как это делается на практике.
Пример 3
Условие: выполните умножение одночленов 2 · x 4 · y · z и — 7 16 · t 2 · x 2 · z 11 .
Решение
Начнем с составления произведения.
Раскрываем в нем скобки и получаем следующее:
2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11
Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:
В итоге получим следующее:
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11 = — 7 8 · t 2 · x 4 + 2 · y · z 3 + 11 = = — 7 8 · t 2 · x 6 · y · z 14
Ответ: 2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11 = — 7 8 · t 2 · x 6 · y · z 14 .
Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.
Правила возведения одночлена в степень
Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.
Пример 4
Условие: выполните возведение одночлена − 2 · a · b 4 в степень 3 .
Решение
Мы можем заменить возведение в степень на умножение 3 -х одночленов − 2 · a · b 4 . Запишем и получим нужный ответ:
Запишем и получим нужный ответ:
(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12
Ответ: (− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .
А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.
Решим задачу, которую мы привели выше, указанным способом.
Пример 5
Условие: выполните возведение − 2 · a · b 4 в третью степень.
Решение
Зная свойство степени в степени, мы можем перейти к выражению следующего вида:
(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .
После этого мы возводим в степень — 2 и применяем свойство степени в степени:
(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .
Ответ: − 2 · a · b 4 = − 8 · a 3 · b 12 .
Возведению одночлена в степень мы также посвятили отдельную статью.
Правила деления одночленов
Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.
Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.
Пример 6
Условие: выполните деление одночлена − 9 · x 4 · y 3 · z 7 на − 6 · p 3 · t 5 · x 2 · y 2 .
Решение
Начнем с записи одночленов в форме дроби.
9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2
Эту дробь можно сократить. После выполнения этого действия получим:
3 · x 2 · y · z 7 2 · p 3 · t 5
Ответ: — 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2 = 3 · x 2 · y · z 7 2 · p 3 · t 5 .
Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как решать выражения со степенями и дробями. Сложение, вычитание, умножение, и деление степеней
Разделы: Математика
Тип урока: урок обобщения и систематизации знаний
Цели:
Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация “Степени” для устного счета, карточки с заданиями, раздаточный материал.
План урока:

Ход урока
I. Организационный момент
Сообщение темы и целей урока.
На предыдущих уроках вы открыли для себя удивительный мир степеней, научились умножать и делить степени, возводить их в степень. Сегодня мы должны закрепить полученные знания при решении примеров.
II. Повторение правил (устно)
- Дайте определение степени с натуральным показателем? (Степенью числа а с натуральным показателем, большим 1, называется произведение n множителей, каждый из которых равен а .)
- Как умножить две степени? (Чтобы умножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели сложить.)
- Как разделить степень на степень? (Чтобы разделить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели вычесть.
 )
) - Как возвести произведение в степень? (Чтобы возвести произведение в степень, надо каждый множитель возвести в эту степень)
- Как возвести степень в степень? (Чтобы возвести степень в степень, надо основание оставить тем же, а показатели перемножить)
- для глаз
- для шеи
- для рук
- для туловища
- для ног
III. Устный счет (по мультимедиа)
IV. Историческая справка
Все задачи из папируса Ахмеса, который записан около 1650 года до н. э. связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, здесь присутствует и возведение в разные степени, решение уравнений первой и второй степени с одним неизвестным.
Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления.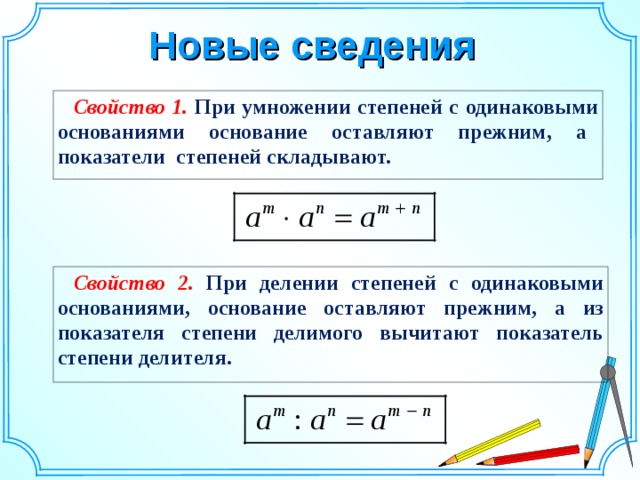 Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
V. Работа у доски
Найдите значение выражения рациональным способом:
Вычислите значение выражения:
VI. Физкультминутка
VII. Решение задач (с показом на интерактивной доске)
Является ли корень уравнения положительным числом?
xn--i1abbnckbmcl9fb.xn--p1ai
Формулы степеней и корней.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
5. Возводя степень в степень, показатели степеней перемножают:
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n –ой степени из m -ой степени этого числа а :
Формулы степеней.
6. a — n = — деление степеней;
7. — деление степеней;
— деление степеней;
8. a 1/n = ;
Степени правила действия со степенями
1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):
(abc…) n = a n b n c n …
Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3
Практически более важно обратное преобразование:
a n b n c n … = (abc…) n
т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.
Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 =[(a +b)(a 2 – ab +b 2)] 2 =(a 3 +b 3) 2
2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:
Пример 5. Пример 6.
Обратное преобразование:. Пример 7.. Пример 8..
3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
Пример 9. 2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого
Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.
5. При возведении степени в степень показатели степеней перемножаются:
Пример 13. (2 3) 2 =2 6 =64. Пример 14.
www.maths.yfa1.ru
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.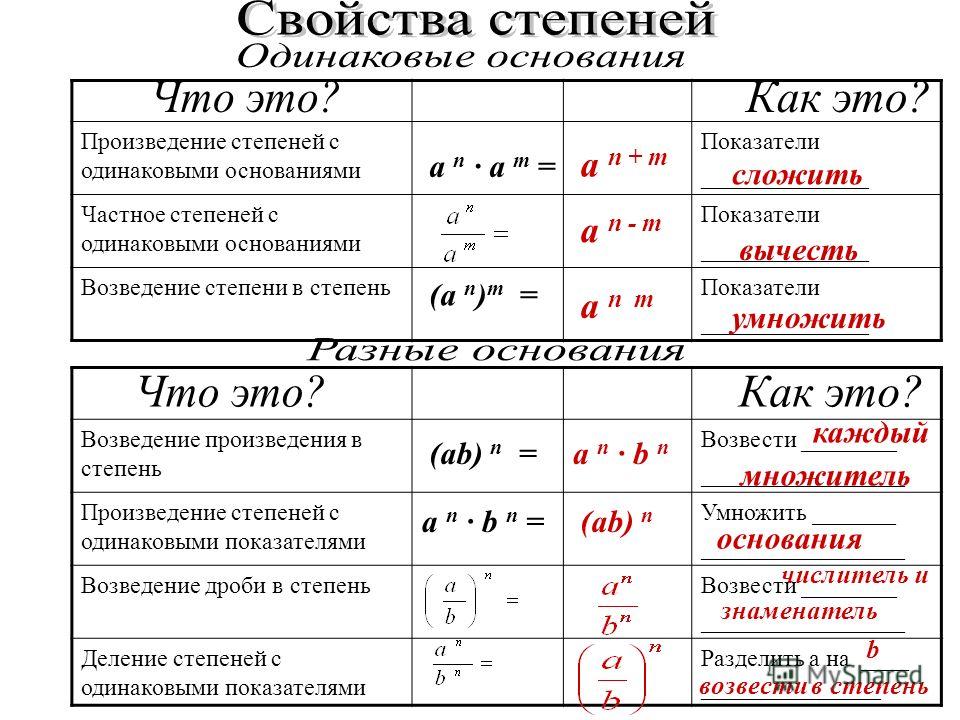
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .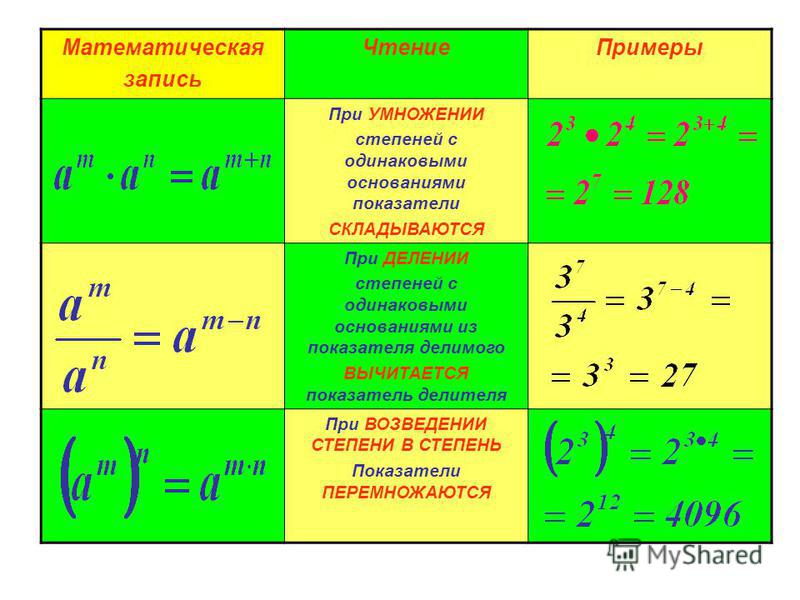
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Вычислить.

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
(a 4) 6 = a 4 · 6 = a 24
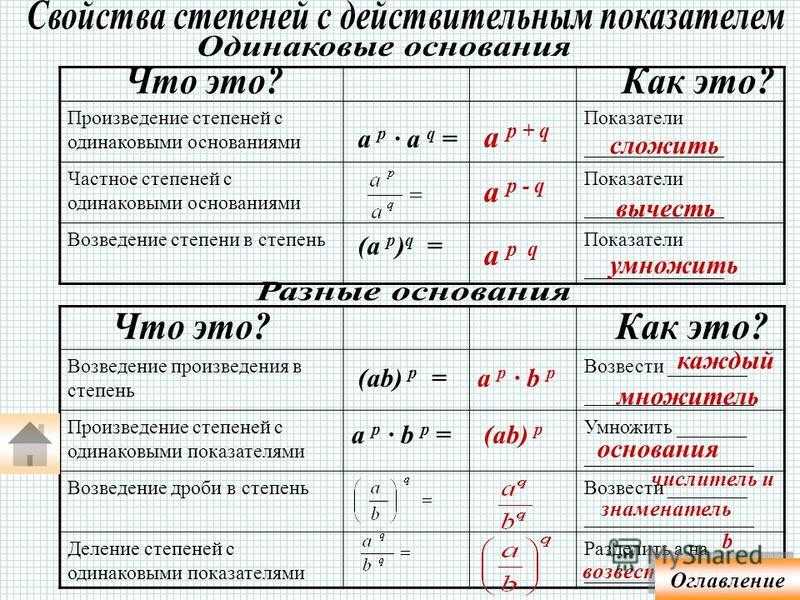 Представить 3 20 в виде степени с основанием 3 2 .
Представить 3 20 в виде степени с основанием 3 2 .По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
Свойства 4
Степень произведения
При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.
(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6 - Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример.
 Вычислить.
Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1 - Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Yandex.RTB R-A-339285-1
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , (2 + 1) 5 , (− 0 , 1) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , (a 2) 3 . А также степени с нулевым показателем: 5 0 , (a + 1) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: (0 , 5) 2 + (0 , 5) — 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1
Вычислите значение степенного выражения 2 3 · (4 2 − 12) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · (4 2 − 12) = 2 3 · (16 − 12) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · (4 2 − 12) = 32 .
Пример 2
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Пример 3
Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1
Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2 + 0 , 3 · 7) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a · (a + 1) − a 2) 2 · (x + 1) и получить степенное выражение более простого вида a 2 · (x + 1) .
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
Определение 2
- a r · a s = a r + s ;
- a r: a s = a r − s ;
- (a · b) r = a r · b r ;
- (a: b) r = a r: b r ;
- (a r) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Пример 4
Представьте выражение a 2 , 5 · (a 2) − 3: a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a 2) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6: a − 5 , 5 = a 2 , 5 − 6: a − 5 , 5 = a − 3 , 5: a − 5 , 5 = a − 3 , 5 − (− 5 , 5) = a 2 .
Ответ: a 2 , 5 · (a 2) − 3: a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство (a · b) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · (3 · 7) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Пример 6
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени (a r) s = a r · s справа налево и получим (a 0 , 5) 3: a 1 , 5 − a 0 , 5 − 6 = (a 0 , 5) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Пример 8
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Пример 9
Сократите дробь: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
Получаем:
30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1)
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10
Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 — 1 · x 1 2 + 1
Вычтем числители:
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .
Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1
Пример 11
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на (x 2 , 7 + 1) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .
Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 (1 — log 3 5) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Тип урока: урок обобщения и систематизации знаний
Цели:
- обучающие – повторить определение степени, правила умножения и деления степеней, возведения степени в степень, закрепить умения решения примеров, содержащих степени,
- развивающие – развитие логического мышления учащихся, интереса к изучаемому материалу,
- воспитывающие – воспитание ответственного отношения к учебе, культуры общения, чувства коллективизма.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация “Степени” для устного счета, карточки с заданиями, раздаточный материал.
План урока:
- Организационный момент.
- Повторение правил
- Устный счет.
- Историческая справка.
- Работа у доски.
- Физкультминутка.
- Работа на интерактивной доске.
- Самостоятельная работа.
- Домашнее задание.
- Подведение итогов урока.
Ход урока
I. Организационный момент
Сообщение темы и целей урока.
На предыдущих уроках вы открыли для себя удивительный мир степеней, научились умножать и делить степени, возводить их в степень. Сегодня мы должны закрепить полученные знания при решении примеров.
II. Повторение правил (устно)
- Дайте определение степени с натуральным показателем? (Степенью числа а с натуральным показателем, большим 1, называется произведениеn множителей, каждый из которых равен а .
 )
) - Как умножить две степени? (Чтобы умножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели сложить.)
- Как разделить степень на степень? (Чтобы разделить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели вычесть.)
- Как возвести произведение в степень? (Чтобы возвести произведение в степень, надо каждый множитель возвести в эту степень)
- Как возвести степень в степень? (Чтобы возвести степень в степень, надо основание оставить тем же, а показатели перемножить)
III. Устный счет (по мультимедиа)
IV. Историческая справка
Все задачи из папируса Ахмеса, который записан около 1650 года до н. э. связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, здесь присутствует и возведение в разные степени, решение уравнений первой и второй степени с одним неизвестным.
Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
V. Работа у доски
Найдите значение выражения рациональным способом:
Вычислите значение выражения:
VI. Физкультминутка
- для глаз
- для шеи
- для рук
- для туловища
- для ног
VII. Решение задач (с показом на интерактивной доске)
Является ли корень уравнения положительным числом?
а) 3x + (-0,1) 7 = (-0,496) 4 (x > 0)
б) (10,381) 5 = (-0,012) 3 — 2x (x
VIII. Самостоятельная работа
Самостоятельная работа
IX. Домашнее задание
Х. Подведение итогов урока
Анализ результатов, объявление оценок.
Полученные знания о степенях мы будем применять при решении уравнений, задач в старших классах, также они часто встречаются в ЕГЭ.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n
.
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Что делать со степенями при сложении чисел?
Что делать со степенями при сложении чисел?
Как складывать числа с одинаковыми степенями Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень. Сначала возводим каждое число в степень и затем выполняем сложение. В уравнениях это будет происходить немного иначе.
Что происходит с показателями степени при сложении?
Свойство № 1 При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются. am · an = am + n, где «a» — любое число, а «m», «n» — любые натуральные числа. Данное свойство степеней также действует на произведение трёх и более степеней. Примеры.
am · an = am + n, где «a» — любое число, а «m», «n» — любые натуральные числа. Данное свойство степеней также действует на произведение трёх и более степеней. Примеры.
Как разделить степени с одинаковыми основаниями?
Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Что нужно делать со степенями при делении?
При делении степеней с одинаковым основанием их показатели вычитаются. … Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
Как умножать и делить числа с разными основаниями и степенями?
Как перемножить степени с разными основаниями в виде чисел?
- Если надо умножить два числа с одинаковыми основаниями, но разными показателями степеней, то общее основание возводится в сумму степеней.
 …
… - Если основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.
Как решить число в степени?
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.
Как считается степень числа?
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a». Запись «an» читается так: «а в степени n» или «n-ая степень числа a».
Когда умножаются степени?
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Как разделить число в отрицательной степени?
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя. Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью: a 5 : a 8 = a5 — 8 = a -3. = x -2.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью: a 5 : a 8 = a5 — 8 = a -3. = x -2.
Как умножить число на степень?
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто: 23 = 2·2·2, где
Почему любое число в нулевой степени равно единице?
Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя. …
Почему число в нулевой степени равно единице?
Известно, что абсолютно любое число в нулевой степени равно единице. Почему 0 в степени 0 равно 1? Доказать это просто, при умножении степеней с одинаковым основанием их показатели складываются, а при делении – вычитаются. … Но ведь мы делим число на себя, это всегда будет равно единице!
… Но ведь мы делим число на себя, это всегда будет равно единице!
Чему равно число е в первой степени?
Возведение числа е в степень означает возведение в степень числа Эйлера e x = exp (x). Число е в 1-й степени, как и любое число в этой степени, будет равно самому себе, т. е. 2.
Как посчитать е в минусовой степени?
При возведении экспоненты в отрицательную степень нужно 1 делить на число е в заданной степени, но со знаком плюс.
Чему будет равно число в минус первой степени?
Степень с отрицательным показателем К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1). Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины.
Что такое е в математике?
Само число e — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приблизительно оно равно 2,718. … Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.
Приблизительно оно равно 2,718. … Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.
Что значит 1е 5?
1e5 — это 100000. 5 обозначает количество нулей, которые вы добавляете за этим числом. Например, предположим, что у меня есть 1e7. Я бы поставил 7 нулей за 1, так что он станет
Что значит 1е 9?
e (или e ) означает «times 10-to-the», поэтому 1e9 «один раз десять до девятой мощности», а 1e-9 означает «один раз десять до отрицательного девятой власти». В математических научных обозначениях это обычно обозначается надстрочным индексом: 1 × 10 —9 или —1 × 10 9 .
Что значит 1 е7?
В большинстве случаев код ошибки 1Е / 1C / E7 прямо указывает на поломку прессостата, однако, в некоторых случаях, исправить возникшую неполадку можно своими силами.
Как на калькуляторе посчитать экспоненту?
В виндовом калькуляторе есть неприметная галочка Inv, выставив которую, пользователь информирует калькулятор, что хочет применить функцию, обратную вызываемой. Функцией, обратной экспоненте, является натуральный логарифм — следовательно, чтобы вычислить экспоненту числа, нужно нажать сначала Inv, потом ln.
Функцией, обратной экспоненте, является натуральный логарифм — следовательно, чтобы вычислить экспоненту числа, нужно нажать сначала Inv, потом ln.
Свойства степеней, которые пригодятся в жизни и школьникам, и их родителям / Бери и делай
В жизни нередко возникают ситуации, когда полезно уметь правильно возводить число в степень, а также решать задачи, опираясь на особенности и свойства степеней. К примеру, без математических операций над числами в степени вы не сможете рассчитать, сколько плитки вам нужно приобрести, чтобы выложить пол и стены в ванной комнате.
«Бери и Делай» кратко объясняет, какими свойствами обладают степени и какие ошибки мы чаще всего допускаем, решая даже простые выражения с подобными числами. Сохраните эту статью, чтобы всегда иметь под рукой в нужный момент.
Что такое степень числа
Когда мы умножаем число само на себя, мы называем этот процесс возведением числа в степень. Так, если умножить число 3 само на себя, то мы запишем это как 32,или «три во второй степени».
Для 2-й и 3-й степеней часто используют специальные названия:
- возведение в квадрат (или возведение во 2-ю степень), например a2
- возведение в куб (или возведение в 3-ю степень), например a3
Если по известным значениям степени и показателя определяют неизвестное основание, это называется извлечением корня.
Свойства степеней
У степени есть основание и показатель. Посмотрите на картинку выше. Основание степени — это a, то есть повторяющийся множитель, а показатель степени — это b, то есть число, указывающее число повторений множителя. Читается это как «a в степени b».
Если показатель степени является натуральным числом, то его называют натуральным показателем. Из определения натуральных чисел следует, что натуральный показатель степени не может являться нулем, отрицательным или нецелым числом.
У степени с натуральным показателем есть несколько свойств, благодаря которым процесс вычислений можно упростить. Они перечислены выше. Давайте разберемся с каждым из них отдельно.
Свойство № 1: В 1-ю степень можно возвести любое число. И тогда число в 1-й степени будет равняться самому числу.
Например, 11 = 1, а 31 = 3. В алгебре 1-я степень обычно не записывается, но при действиях со степенями учитывается. Например, a4 × a = a4 × a1 = a4 + 1 = a5.
Свойство № 2: Степень произведения. Если нужно возвести в степень произведение множителей, то каждый из множителей возводят в степень, а затем результаты перемножают. При этом для вышеуказанной формулы важно, что a и b — это основания степеней (не равные нулю), а n — это показатель степени, натуральное число.
Пример использования: (3a)2 = (3 × a)2 = 32 × a2 = 32a2.
Свойство № 3: Степень частного. Если нужно возвести в степень результат деления делимого на делитель, то можно возвести в эту степень отдельно делимое и делитель, а затем первый результат разделить на второй. При этом для вышеуказанной формулы важно, что a и b — это основания степеней (не равные нулю) и любые рациональные числа, но b ≠ 0. А n — это натуральный показатель степени.
Пример использования: (5/8)2 = 52 ÷ 82.
Свойство № 4: Произведение степеней. Если нужно умножить степени с одинаковыми основаниями, то основание оставляют без изменений, а показатели степеней складывают. При этом для вышеуказанной формулы важно, что n, m — это натуральные показатели степени.
Пример использования: 3435 = 34 × 35 = 34 + 5 = 39.
Свойство № 5: Частное степеней. Если нужно разделить степени с одинаковыми основаниями, то основание оставляют без изменений, а из показателя степени делимого вычитают показатель степени делителя. При этом для вышеуказанной формулы важно, что a — любое число, не равное нулю, a n, m — это любые натуральные числа, но такие, что n > m.
При этом для вышеуказанной формулы важно, что a — любое число, не равное нулю, a n, m — это любые натуральные числа, но такие, что n > m.
Пример использования: 48 ÷ 45 = 48 − 5 = 43.
Свойство № 6: Возведение степени в квадрат. Если нужно возвести степень в степень, то основание степени оставляют без изменений, а показатели степеней умножают друг на друга. При этом для вышеуказанной формулы важно, что a — основание степени (не равное нулю), a n, m — натуральные показатели степени.
Пример использования: (42)3 = 42 × 3 = 46.
Другие свойства степеней
Число с дробным показателем степени равняется корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю. Получается, что операцию извлечения корня всегда можно заменить возведением в степень. Это хорошо использовать для упрощения записи выражения.
Это хорошо использовать для упрощения записи выражения.
Пример использования: 3√a6 = a6 ÷ 3 = a2.
Любое число, возведенное в нулевую степень, будет равно единице (за исключением нуля). Нуль в нулевой степени не определен, поэтому подобное выражение не имеет смысла.
Пример использования: 74 × 7−4 = 74 + (−4) = 70 = 1.
Любое число, возведенное в отрицательную степень, равно единице, разделенной на это же число, но в положительной степени. В частности:
- a−1 = 1/a,
- (a/b)−n = (b/a)n
Пример использования: 6−2 = 1/62 = 1/36.
Степень с отрицательным основанием и четным показателем равна степени с основанием, противоположным данному, но с тем же показателем. Чтобы возвести в нечетную степень отрицательное число, нужно поставить знак «минус» и возвести в эту степень число, противоположное данному.
Пример использования: (−8)4 = 84 = 8 × 8 × 8 × 8 = 4 096. Или (−8)3 = −83 = −512.
Какие ошибки часто допускают, когда речь идет о свойствах степеней
- Неправильно возводят число в нулевую, 1-ю и −1-ю степени, путая их между собой. Исходя из вышеуказанных свойств степеней, мы помним, что a0 = 1, a1 = a, a−1 = 1/a.
- Неправильно умножают и складывают степени. Чаще всего это происходит тогда, когда в выражении степени с одинаковыми основаниями. Посмотрите на картинку выше: в первом случае основания не перемножаются, то есть должно быть 33 × 33 = 33 + 3 = 36. А во втором случае при сложении мы не можем складывать показатели степени, даже если бы они были одинаковыми: нужно сначала возвести в степень каждое число, а затем произвести сложение, то есть 53 + 54 = 125 + 625 = 750.
- Неправильно возводят дробное число в отрицательную степень.
 На картинке выше только нижний вариант ответа соответствует правилу (a/b)−n = (b/a)n.
На картинке выше только нижний вариант ответа соответствует правилу (a/b)−n = (b/a)n.
Бонус: проверьте себя, решив простой пример
Этот пример выглядит настолько простым, что кажется, будто бы с ним мог бы справиться даже ребенок. Но на самом деле он легко поставит в тупик большинство взрослых. Главное здесь — это не попасть в ловушку и выполнить все действия в правильном порядке. Начнем с левой стороны и воспользуемся свойством частного степеней. Тогда 23/22 = 23 − 2 = 21. Далее подставим это число в выражение и получим 21 + 21 + 20. На этом шаге кому-то захочется просто сложить показатели степеней. Но мы помним, что это неверный путь, и, воспользовавшись правилами возведения чисел в 1-ю и нулевую степени, получим 21 + 21 + 20 = 2 + 2 + 1 = 5.
Ответ: 5.
Бери и делай/Культура/Свойства степеней, которые пригодятся в жизни и школьникам, и их родителям
Показатели в математике (целые, дробные + функция) с примерами и образцами
Оглавление:
Показатель — это число, показывающее, в какую именно степень возводится основание.
Показатель — в большинстве случаев, обобщённая характеристика какого-либо объекта, процесса или его результата, понятия или их свойств, обычно, выраженная в числовой форме.
Целые показателиСвойства целых положительных показателей: Показатели степени до сего времени предполагались нами целыми и положительными, причём мы им придавали смысл, выражаемый в следующем определении:
Возвысить число а в степень с целым и положительным показателем n — значит найти произведение n одинаковых сомножителей aaa…a.
Перечислим свойства этих показателей, известные нам из предыдущих глав алгебры:
- 1) при умножении степеней одного и того же числа показатели их складываются;
- 2) при делении степеней одного и того же числа показатель делителя вычитается из показателя делимого, если показатель делителя не больше показателя делимого;
- 3) при возвышении отрицательного числа в степень с чётным показателем получается положительное число, а с нечётным показателем — отрицательное;
- 4) чтобы возвысить в степень произведение, достаточно возвысить в эту степень каждый сомножитель отдельно;
- 5) чтобы возвысить степень в степень, достаточно перемножить показатели этих степеней;
- 6) чтобы возвысить в степень дробь, достаточно возвысить в эту степень отдельно числитель и знаменатель;
- 7) чтобы возвысить радикал в степень, достаточно возвысить в эту степень подкоренное выражение;
- 8) чтобы извлечь корень из степени, достаточно разделить показатель степени на показатель корня, если такое деление выполняется нацело.

Теперь мы расширим понятие о показателях, введя показатели отрицательные и дробные, которых до сего времени мы не употребляли. Мы увидим при этом, что все свойства целых положительных показателей сохраняются и для показателей отрицательных и дробных.
Нулевой показательПри делении степеней одного и того же числа показатель делимого может оказаться равным показателю делителя.
Пусть нужно разделить аⁿ на аⁿ.
Применяя правило (2), получаем:
aⁿ : aⁿ =aⁿ⁻ⁿ = α⁰.
Но нуль, как показатель степени, не имеет того значения, которое придаётся показателям целым и положительным, так как нельзя повторить число сомножителем нуль раз. Чтобы придать смысл выражению α⁰, подойдём к вопросу о делении аⁿ на аⁿ с другой стороны. Мы знаем, что при делении любого (отличного от нуля) числа на равное ему число частное равно единице.
Поэтому условились считать α⁰=l.
Таким образом, по определению:
Всякое число (за исключением нуля) в нулевой степени равно единице.
Легко убедиться в том, что перечисленные выше свойства целых положительных показателей применимы и к нулевому показателю. Так:
Условимся при делении степеней одного и того же числа вычитать показатель делителя из показателя делимого и в том случае, если показатель делителя больше показателя делимого. Тогда мы получим в частном букву с отрицательным показателем, например: α² : α⁵= α⁻³. Таким образом, число с отрицательным показателем мы условимся употреблять для обозначения частного от деления степеней этого числа в том случае, когда показатель делителя превосходит показатель делимого на столько единиц, сколько их находится в абсолютной величине отрицательного показателя. Так, α⁻² означает частное α : α³, или α² : α⁵, или α³ : α⁵, вообще частное α ͫ : α ͫ ⁺².
Применяемое в этом смысле число с отрицательным показателем равно дроби, у которой числитель 1, а знаменатель — то же число, но с положительным показателем, равным абсолютной величине отрицательного показателя.
Действительно, согласно нашему условию, мы должны иметь:
Сократив две первые дроби на ат и третью дробь на хт (т. е. в обоих случаях сократив дроби на числитель), получим:
Вообще:
Заметим, что отрицательные показатели дают возможность представить всякое дробное алгебраическое выражение под видом целого; для этого стоит только все множители знаменателя перенести множителями в числитель, взяв их с отрицательными показателями. Например:
Убедимся теперь, что все действия над степенями с отрицательными показателями можно производить по тем же правилам, какие были прежде выведены для показателей положительных. Достаточно обнаружить это только для умножения и возвышения в степень, так как правила обратных действий — деления и извлечения корня — являются следствиями правил прямых действий.
Предстоит показать, что при умножении степеней показатели одинаковых букв складываются и в том случае, когда эти показатели отрицательные. Убедимся, что , где m и n — целые положительные числа.
Действительно, заменив степени с отрицательными показателями дробями и произведя действие умножения по правилам, относящимся к дробям, получим:
Подобно этому:
так как
Надо показать, что при возвышении в степень показатели этих степеней перемножаются и в том случае, когда они отрицательные. Убедимся, что .
Действительно:
Подобно этому:
, потому что
Примеры:
1) (3α⁻ ²b²c⁻ ³) (0,8ab⁻ ³ c⁴)=2,4α⁻ ¹b⁻ ¹ c.
2) (x⁻ ¹ y³ z²) : (5x²y⁻ ² z³ ) = x⁻ ³y⁵z⁻ ¹ .
3) (2αx⁻ ³ )⁻ ² =2⁻ ² α⁻ ² x⁶.
4) (х⁻ ² — у⁻ ¹ )² =(x⁻ ² ) ² — 2x⁻ ² y⁻ ¹ +(y⁻ ¹ ) ² =x⁻ ⁴ — 2x⁻ ² y⁻ ¹ +y⁻ ² .
5) (a⁻ ² + b⁻ ³ ) (а⁻ ² — b⁻ ³ )=a⁻ ⁴ — b⁻ ⁶.
6) =3p⁻ ³ q⁻ ¹.
В каком смысле употребляются дробные показатели: Мы знаем, что при извлечении корня из степени делят показатель степени на показатель корня, если такое деление выполняется нацело; например: и т. д. Условимся теперь распространять это правило и на те случаи, когда показатель степени не делится нацело на показатель корня. Например, мы условимся принимать, что:
Вообще мы условимся, что:
Выражение означает корень, показатель которого равен знаменателю, а показатель степени подкоренного числа равен числителю показателя
Условимся употреблять отрицательные дробные показатели в том же смысле, в каком мы употребляли отрицательные целые показатели; например, условимся, что
Величина степени с дробным показателем не изменится, если мы умножим или разделим на одно и то же число (отличное от нуля) числитель и знаменатель дробного показателя.
Так:
Вообще:
Действительно, знаменатель дробного показателя означает показатель корня, а числитель его означает показатель степени подкоренного выражения, а такие показатели, как мы видели, можно умножать и делить на одно и то же число.
Основываясь на этом свойстве, мы можем преобразовывать дробный показатель совершенно так же, как и обыкновенную дробь; например, мы можем сокращать дробный показатель или приводить несколько дробных показателей к одному знаменателю.
Действия над степенями с дробными показателямиПредстоит доказать, что к дробным показателям применимы правила, выведенные раньше для целых показателей. Это достаточно обнаружить только для умножения и возвышения в степень, так как правила деления и извлечения корня являются следствиями правил умножения и возвышения в степень.
УмножениеДокажем, что при умножении показатели степеней одинаковых букв складываются и тогда, когда эти показатели дробные. Например, убедимся, что
Например, убедимся, что
Для этого изобразим степени с дробными показателями в виде радикалов и произведём умножение по правилу умножения радикалов:
Результат получился тот же самый, какой мы получили после сложения показателей; значит, правило о сложении показателей (при умножении) можно применять и для дробных показателей.
Таким образом:
Возвышение в степень
Докажем, что при возвышении степени в степень показатели степеней можно перемножать и тогда, когда эти показатели дробные. Например, убедимся, что
Действительно, заменив радикалами степени с дробными показателями и произведя действия над радикалами, получим:
Если показатели не только дробные числа, но и отрицательные, то и тогда к ним можно применять правила, доказанные раньше для положительных показателей. Например:
Смысл степени с иррациональным показателем:
Рассмотрим степени , в которых α — какое-нибудь иррациональное число, когда основание степени α есть какое-нибудь положительное число, не равное 1. При этом могут представиться следующие три случая:
При этом могут представиться следующие три случая:
a) α > 1 и α — положительное иррациональное число; например, .
Обозначим через α₁ любое рациональное приближённое значение числа α, взятое с недостатком, и через α₂ — любое приближённое рациональное значение числа а, взятое с избытком. Тогда степень , означает таксе число, которое больше всякой степени , но меньше всякой степени . Можно доказать, что такое число существует, и единственно. Например, означает такое число, которое больше каждого из чисел ряда:
в котором показатели — десятичные приближённые значения , взятые с недостатком, но меньше каждого из чисел ряда:
в котором показатели — десятичные приближения V 2, взятые с избытком.
б) a < 1 и α — по-прежнему положительное иррациональное число, например, .
Тогда под степенью разумеют такое число, которое меньше всякой степени , но больше всякой степени . Так, есть число, меньшее каждого из чисел ряда:
но большее каждого из чисел ряда:
Таким образом, если иррациональное число а заключено между двумя рациональными числами α₁ и α₂, то степень заключена между степенями и и тогда, когда α > 1, и тогда, когда α < l.
в) и α — отрицательное иррациональное число; например:
Тогда выражению придают тот же смысл, какой имеют степени с отрицательными рациональными показателями. Так:
При подробном рассмотрении теории иррациональных показателей обнаруживается, что все свойства показателей рациональных применимы и к показателям иррациональным; так:
Определение:
Показательной функцией называется функция, представляющая собой степень, у которой основание а есть какое-нибудь постоянное положительное число, не равное 1, а показатель х — независимое переменное, могущее принимать всевозможные значения, положительные и отрицательные, целые и дробные, рациональные и иррациональные. При этом предполагается, что в том случае, когда показатель х равен дроби и, следовательно, когда означает радикал некоторой степени, то из всех значений радикала берётся только одно арифметическое, т. е. положительное.
е. положительное.
Из того, что мы знаем о показателях степени, следует, что функция при всяком значении х имеет единственное значение (благодаря условию брать для радикалов только арифметическое значение).
Свойства показательной функцииРассмотрим некоторые свойства показательной функции, помня, что а мы считаем положительным числом.
1. При всяком положительном основании функция положительна, т. е. > 0.
При х целом положительном >0, каково бы ни было положительное число а; следовательно, высказанное нами положение в этом случае справедливо.
Пусть теперь х равно некоторой положительной дроби, например
Тогда:
Но > 0, следовательно, и > 0, так как мы условились брать лишь арифметическое значение корня.
Пусть х — положительное иррациональное число. Обозначим через α₁ и a₂ приближённые рациональные значения х по недостатку и избытку. Эти приближённые значения можно выбрать положительными. Тогда значение , будучи заключённым между двумя положительными числами и , является положительным числом.
Тогда значение , будучи заключённым между двумя положительными числами и , является положительным числом.
Пусть, наконец, х равно некоторому отрицательному числу, например x=—р. Тогда:
Каково бы ни было положительное число р, согласно предыдущему > 0, но тогда и .
Таким образом, высказанное нами положение справедливо для всякого х.
2. При a > 1 функция >l, если х>0, и < l, если x < 0 (при a < l знаки неравенства для противоположны).
Пусть х — целое положительнее число. Тогда:
Пусть х — положительная дробь, например . Тогда:
Если х — положительное иррациональное число, то > 1, где a₁ — приближённое рациональное значение х по недостатку, а поэтому и . Таким образом, при всяком положительном х
Пусть теперь х есть какое-либо отрицательное число, например x = —р. Тогда:
Тогда:
Но согласно предыдущему > 1. Следовательно:
При a>1 функция возрастает при возрастании х.
Если x₁ и x₂ — два целых положительных числа и x₂ > x₁, то очевидно, что при 1 будем иметь:
Пусть теперь x₁ и x₂ — положительные дроби, например x₁= и x₂ =. Пусть также . Тогда:
Или по приведении дробей к одному знаменателю:
Из двух неравных дробей с одинаковыми знаменателями та больше, у которой числитель больше. Следовательно:
Так как рn и mq — целые числа, то к ним можно применить предыдущие рассуждения и мы получим:
Извлечём из и корень степени qn. Мы знаем, что из двух корней одинаковой степени тот больше, у которого больше подкоренное число. Следовательно:
Сокращая показатели, получим:
Пусть x₁ и x₂ — два вещественных числа, из которых одно или оба иррациональны.
Обозначим через β приближённое рациональное значение x₁ по избытку, а через а приближённое значение x₂ по недостатку. Если x₁ < x₂, то можно выбрать а и β при условии β < α. Тогда будем иметь Но так как , то .
График показательной функции. Построим график следующих трёх показательных функций:
Для построения графиков первых двух функций мы дадим переменному числу х ряд целых значений:
-3; -2; -1; 0; 1; 2; 3.
При x=—3 мы получим:
Подобно этому вычислим значения у и для всех остальных значений x.
Для функции неудобно брать указанные значения числа х, так как мы получили бы тогда для у такие большие числа, которые на чертеже 29 не умещаются (например, при х = 3 мы получили бы y= 10³ = 1000). Для этой функции мы возьмём такие дробные значения (заключающиеся между —1 и +1):
Соответствующие значения у вычислим в такой последовательности:
Далее простым умножением и делением находим:
Выпишем все найденные значения в следующие три таблицы:
| x = | возрастает | -3 | -2 | -1 | 0 | 1 | 2 | 3 | возрастает |
| y = | возрастает | 1 | 2 | 4 | 8 | возрастает |
| x = | возрастает | -3 | -2 | -1 | 0 | 1 | 2 | 3 | возрастает |
| y = | возрастает | 8 | 4 | 2 | 1 | возрастает |
| x = | возрастает | -1 | 0 | 1 | возрастает | ||||||
| y = | возрастает | 0,1 | 0,17 | 0,32 | 0,56 | 1 | 1,78 | 3,16 | 5,62 | 10 | возрастает |
(в последней таблице числа округлены).
Нанеся эти значения на чертёж и соединяя полученные точки кривыми, мы получим (черт. 29) три графика взятых функций (удобно чертёж выполнить на миллиметровой бумаге, беря за единицу длины сантиметр).
Рассматривая графики показательных функций, мы видим на них в наглядном изображении следующие свойства:
- При всяком положительном основании функция положительна (все кривые расположены выше оси х-ов).
- При α > 1 функция > 1, если х > 0, и < 1, если х < 0 (при а < 1 знаки неравенств для противоположны).
- При возрастании х функция ах возрастает, если а > 1 (и убывает, если a < l).
- Если х=0, то =1 при всяком а (все кривые проходят через одну и ту же точку, лежащую на оси у-ов и отстоящую от точки 0 на +1).
- При a > 1 функция при возрастании х возрастает тем быстрее, чем больше а (кривая при a = 10 поднимается вверх значительно больше, чем при a=2).

Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Сложение и вычитание с показателями (видео и практика)
vimeo.com/video/364362144?app_id=122963″ frameborder=»0″ allow=»autoplay; fullscreen» allowfullscreen=»»>TranscriptPractice
Привет, ребята! Добро пожаловать в это видео о сложении и вычитании с показателями степени.
Для начала, чтобы мы все были на одной странице, я собираюсь определить экспоненты , а также несколько других вещей, чтобы в дальнейшем, надеюсь, не было такой путаницы.
Итак, я начну с базы (или переменной базы в данном случае). база — это число, которое возводится в степень чего-то, и это число, на которое оно возводится, называется показателем степени . Теперь показатель степени представляет собой то, сколько раз это основание умножается само на себя. Итак, в этом случае \(x\), наша база, умножается сама на себя дважды (\(x \cdot x\)). Число перед основанием или переменной называется коэффициентом . Надеюсь, теперь, продвигаясь вперед, вы сможете лучше понять, о чем я говорю, когда я ссылаюсь на эти термины. 93\)
93\)
Итак, чтобы упростить это, мы должны искать две вещи. Во-первых, наши базы (или переменные) одинаковы; и два, наши показатели одинаковы? Обе вещи должны быть истинными, чтобы мы могли сложить эти два термина вместе. Этот же процесс сложения и вычитания с показателями также называется объединением одинаковых терминов, что может показаться вам более знакомым. Ну, это одно и то же.
Итак, оглядываясь назад на нашу задачу, мы видим, что наши основания одинаковы, и наши показатели одинаковы. Это означает, что у нас есть два одинаковых термина, которые можно объединить вместе. Итак, чтобы на самом деле объединить их, вот что вам нужно сделать: 92+15\), который является периметром треугольника.
Скрыть ответ
Вернуться к видео по алгебре I
875756
Сложение показателей степени — определение, шаги, метод, примеры
Другими словами, добавление основания и показателей степени — это добавление показателей степени. Показатель степени также называется степенью числа и показывает, сколько раз число умножается само на себя. В общем х n означает, что x умножается сам на себя n раз. Добавление показателей выполняется в разных типах, давайте посмотрим, что это за типы, и решим несколько примеров, чтобы лучше понять эту концепцию.
Показатель степени также называется степенью числа и показывает, сколько раз число умножается само на себя. В общем х n означает, что x умножается сам на себя n раз. Добавление показателей выполняется в разных типах, давайте посмотрим, что это за типы, и решим несколько примеров, чтобы лучше понять эту концепцию.
| 1. | Что такое добавление показателей? |
| 2. | Шаги добавления показателей |
| 3. | Добавление методов экспоненты |
| 4. | Часто задаваемые вопросы о добавлении экспонентов |
Что такое добавление показателей?
Сложение показателей степени — это процесс сложения показателей степени или степени числа независимо от того, совпадает ли основание. Показатель степени также можно назвать степенью числа, поскольку он представляет собой количество раз, когда число умножается само на себя. Например, 3 2 = 3 × 3, где 3 — основание, а 2 — показатель степени.
Например, 3 2 = 3 × 3, где 3 — основание, а 2 — показатель степени.
Здесь в члене х n ,
- x называется базой
- n называется показателем степени или степенью
- x n читается как x в степени n (или) x в степени n
При сложении показателей следует помнить одно главное правило: основание и показатель степени должны совпадать, а сложение выполняется с коэффициентом. Переменные, которые объединяются, имеют одно и то же основание и одинаковую мощность. Это правило применимо и ко всем другим формам показателей степени, то есть к вычитанию, умножению и делению.
Шаги добавления экспоненты
Добавление показателей степени может быть выполнено, когда основание и степень совпадают. Бывают случаи, когда основание и показатели степени различаются, но мы все равно можем выполнять сложение для этих выражений. Давайте посмотрим на шаги добавления показателей.
- Шаг 1: Проверьте члены в выражении, имеют ли они одинаковое основание и одинаковые показатели степени.
 Например, 2 2 + 2 2 . Как мы видим, и основание, и показатель степени равны 2,9.0281
Например, 2 2 + 2 2 . Как мы видим, и основание, и показатель степени равны 2,9.0281 - Шаг 2: Если основание и показатели различны, вычислите выражение с отдельными членами. Например, 5 3 + 4 2 . База и показатели разные.
- Шаг 3. Сложите результаты.
Добавление методов экспоненты
Сложение показателей может выполняться различными способами. Основное правило при добавлении показателей степени состоит в том, что основание и степень должны быть одинаковыми. Однако иногда основание и показатели могут не совпадать, поэтому нам нужно вычислять члены по отдельности, чтобы вычислить выражение. Давайте посмотрим на различные методы.
Метод 1: Сложение показателей степени с одинаковыми основанием и показателями
Сложение показателей степени, когда основание и показатели совпадают, выполняется очень простым методом. Общая форма сложения показателей с одинаковым основанием и показателями такова: n + n = 2a n . Давайте посмотрим на пример, чтобы понять это лучше. Например: 4 3 + 4 3 = 2(4 3 ) = 2 × 4 × 4 × 4 = 128.
Давайте посмотрим на пример, чтобы понять это лучше. Например: 4 3 + 4 3 = 2(4 3 ) = 2 × 4 × 4 × 4 = 128.
Метод 2. Сложение показателей степени с разным основанием и степенью
Если основание и показатель степени имеют разные значения, мы сначала добавляем каждый показатель степени, а затем вычисляем все выражение. Общая форма вычисления различных оснований и показателей степени такова: a n + b m . Давайте посмотрим на пример, чтобы понять это лучше. Например: 3 3 + 5 2 = 3 × 3 × 3 + 5 × 5 = 27 + 25 = 52.
Метод 3: сложение отрицательных степеней с разными основаниями
срок по отдельности, а затем добавить общее количество. Термины записываются в дробной форме, а затем добавляются. Общая форма вычисления отрицательных показателей с разными основаниями — это -н + б -м = 1/а н + 1/б м . Давайте применим общую форму в примере, чтобы понять это лучше. Например: 6 -2 + 3 -3 = 1/6 2 + 1/3 3 = 1/36 + 1/27 = 0,0648.
Например: 6 -2 + 3 -3 = 1/6 2 + 1/3 3 = 1/36 + 1/27 = 0,0648.
Метод 4: добавление дробных показателей степени с одинаковым основанием и показателями степени
Показатели степени также могут быть выражены в форме дроби. Таким образом, сложение этих дробей в виде показателей степени может быть выполнено с использованием этой общей формы, н/м + a н/м = 2a н/м . Для дробей мы можем преобразовать дробные показатели в форму корня, то есть либо квадратный корень, либо кубический корень, в зависимости от дроби. Давайте применим эту общую форму в примере для лучшего понимания. Например: 4 1/2 + 4 1/2 = 2(4 1/2 ) = 2 × √4 = 2 × 2 = 4.
Метод 5. Сложение дробных показателей с разным основанием и Показатель степени
Показатель степени, записанный в дробной форме с разным основанием и разными показателями степени, выражается в общей форме как н/м + б д/к . Здесь сначала вычисляется каждый член, а затем вычисляется весь результат. Дробная форма преобразуется в ее корень, а затем вычисляется. Давайте рассмотрим пример: 27 1/3 + 4 1/2 = 3 √27 + √4 = 3 + 2 = 5. аналогично методу сложения показателей степени с одинаковым основанием и одинаковыми показателями степени. Общая форма х н + х н = 2x n . Давайте посмотрим на пример, 7 2 + 7 2 = 2(7 2 ) = 2 × 7 × 7 = 98.
Здесь сначала вычисляется каждый член, а затем вычисляется весь результат. Дробная форма преобразуется в ее корень, а затем вычисляется. Давайте рассмотрим пример: 27 1/3 + 4 1/2 = 3 √27 + √4 = 3 + 2 = 5. аналогично методу сложения показателей степени с одинаковым основанием и одинаковыми показателями степени. Общая форма х н + х н = 2x n . Давайте посмотрим на пример, 7 2 + 7 2 = 2(7 2 ) = 2 × 7 × 7 = 98.
Метод 7: Добавление переменной с разными показателями степени
Общая форма для вычисления переменных с разными показателями составляет x n + x m . Давайте рассмотрим пример: 4 2 + 4 3 = 4 2 × 3 = 4 6 = 4096. Взглянем.
- Как определить степени и степени
- Экспоненциальные функции
- Иррациональные Показатели
Часто задаваемые вопросы о добавлении экспонентов
Что означает добавление показателей?
Добавление показателей степени — это процесс добавления терминов, имеющих одно и то же основание и показатель степени. Сложение возможно только в том случае, если основание и показатель степени совпадают. Есть случаи, когда это не так, это можно решить, увидев, одинаковы ли показатели двух терминов или одинаковое основание двух терминов. В противном случае добавление показателей степени невозможно.
Сложение возможно только в том случае, если основание и показатель степени совпадают. Есть случаи, когда это не так, это можно решить, увидев, одинаковы ли показатели двух терминов или одинаковое основание двух терминов. В противном случае добавление показателей степени невозможно.
Каковы шаги по добавлению показателей?
Добавление показателей степени выполняется в 3 простых шага, а именно:
- Проверьте члены в выражении, имеют ли они одно и то же основание и одинаковые степени.
- Если основание и показатели различны, вычислите выражение с отдельными членами.
- Сложите результаты вместе.
Каково правило добавления показателей?
Наиболее важным правилом сложения показателей степени является то, что основание и степень членов, которые помещаются для сложения, должны быть одинаковыми. Если они одинаковые, коэффициенты будут складываться вместе, при этом основание и показатель степени одинаковы.
Можно ли складывать числа с разными показателями степени?
Нет, сложение чисел с разными показателями степени применимо, поскольку правило сложения показателей степени состоит в том, что основание и показатель степени должны быть одинаковыми. В то время как что-то основание и показатель степени могут быть разными, но только одно отличие не применимо.
В то время как что-то основание и показатель степени могут быть разными, но только одно отличие не применимо.
Добавляете ли вы показатели при добавлении?
Для добавления показателей степени основание и показатель степени должны совпадать. Коэффициент переменной добавляется, оставляя показатель степени неизменным. В выражение добавляются члены с одинаковыми переменными и степенями. Это правило применимо как к умножению, так и к делению.
Как складывать одночлены с показателями степени?
Складывая два или более подобных одночлена, мы сначала складываем коэффициенты, пока переменные и показатели степени переменной одинаковы. Мы можем получить результат, добавляя подобные одночлены.
Добавление показателей – методы и примеры
Алгебра — один из основных курсов математики. Чтобы понять алгебру, важно знать, как использовать экспоненты и радикалы. Добавление показателей является частью программы по алгебре, и по этой причине для учащихся важно иметь более прочную основу в математике.
Многие ученики часто путают сложение показателей степени с сложением чисел , и, следовательно, делают ошибки. Эти недоразумения обычно влекут за собой разницу в значении таких терминов, как возведение в степень и показатель степени.
Прежде чем углубляться в советы о том, как добавлять показатели степени, давайте начнем с определения терминов для показателей степени. Начнем с того, что показатель степени — это просто многократное умножение числа само на себя. В математике эта операция называется возведением в степень. Таким образом, возведение в степень — это операция с числами в форме b n , где b называется основанием, а число n — показателем степени, индексом или степенью . Например, x 4 содержат 4 в качестве показателя степени, а x называются основанием.
Экспоненты иногда называют степенями чисел. Показатель степени представляет количество раз, которое число должно быть умножено само на себя. Например, x 4 = x × x × x × x.
Например, x 4 = x × x × x × x.
Чтобы добавить показатели степени, и показатели степени, и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и степенями. Это правило также согласуется с умножением и делением показателей.
Ниже приведены шаги для добавления степеней:
- Проверьте члены, если они имеют одинаковые основания и степени
Например, 4 2 +4 2 , эти члены имеют одинаковое основание 4 и показатель степени 2.
- Вычислите каждый член отдельно, если они имеют разное основание или показатель степени
Например, 3 2 + 4 3 , эти члены имеют разные показатели степени и основания.
- Сложите результаты вместе.
Сложение показателей степени с разными показателями степени и основаниями
Сложение показателей степени выполняется путем вычисления сначала каждой степени, а затем добавления: Общая форма таких показателей степени: a n + b m .
Пример 1
- 4 2 + 2 5 = 4–4 + 2=2 ОТ 2-2 = 16 + 32 = 48
- 8 3 3 3 39. 2 = (8)(8)(8) + (9)(9) = 512 + 81 = 593
- 3 2 + 5 3 = (3)(3) + (5)(5)(5) = 9 + 125 = 134
- 6 2 + 6 3 9 252.
- 3 4 + 3 6 = 81 + 729 = 810.
Добавление экспонентов с теми же основаниями и экспонентами
. n
Пример 2
- 4 2 + 4 2 = 2⋅4 2 = 2 % 4 = 32
- 8 3 + 8 3 + 8 3 = 3 (8 3 ) = 3 * 512 = 1536
- 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 ) = 2 = 2(3 2 ) = 2 * 9 = 18
- 5 2 + 5 2 = 2(5 2 ) = 2 * 25 = 50.
 с разными базами?
с разными базами?Добавление отрицательных показателей выполняется путем вычисления каждого показателя отдельно, а затем добавления:
a -n + b -m = 1/a n + 1/b m
Example 3
4 -2 + 2 -5 = 1/4 2 + 1/2 5 = 1/(4⋅4)+1/(2⋅2⋅2⋅2⋅2) = 1/16+1/32 = 0,09375
Как сложить дробь с разными основаниями и показателями?
Добавление дробных показателей степени выполняется путем вычисления каждого показателя степени отдельно, а затем добавления:
a n/m + b k/j .
Пример 4
3 3/2 + 2 5/2 = √ (3 3 ) + √ (2 5 ) = √ (27) + √ (32). = 5,196 + 5,657 = 10,853
Как сложить дробные показатели с одинаковыми основаниями и одинаковыми дробными показателями?
b n/m + b n/m = 2b n/m
Example 5
4 2/3 + 4 2/3 = 2⋅4 2/3 = 2 ⋅ 3 √ (4 2 ) = 5,04
Как сложить переменные с разными показателями степени?
Добавление показателей выполняется путем вычисления каждого показателя отдельно, а затем сложения:
x n + x m
Как сложить переменные с одинаковыми показателями?
x N +x N = 2x N
Пример 6
x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2
10. 0096 x 2
0096 x 2 Пример 7
(4 -1 + 8 -1 ) ÷ (2/3) -1 1 900÷1 9000
0 (3/2)
= (2 + 1)/8 ÷ 3/2
= (3/8 ÷ 3/2)
= (3/8 ÷ 2/3)
= ¼
Пример 8
Упрощение: (1/2) -2 + (1/3) -2 + (1/4) -2
Решение:
(1/2) -2 + (1/3) -2 + (1/4) -2
= (2/1) 2 + (3/1) 2 + (4/1) 2
= (2 2 + 3 2 + 4 5) 90 90 + 9 + 16)
= 29сложение, вычитание, умножение и деление
Возведение в степень — математическая операция с двумя числами: — основание $x$ и — показатель степени $a$ . Когда $a$ является положительным целым числом, возведение в степень соответствует -кратному умножению основания . 93$. Это означает, что мы трижды умножили число $2$ само на себя или: $2\cdot{2}\cdot{2}$, что равняется $8$.

По определению каждое число, имеющее в качестве показателя степени 0, равно 1. Это означает, что независимо от того, насколько велико основание, если их показатель степени равен 0, это число всегда равно 1.
Каждое число, к которому не присоединен показатель степени, на самом деле имеет число 1 в качестве показателя степени. Число 1 является показателем степени каждого числа по умолчанию, поэтому его не обязательно записывать, но в некоторых задачах это может быть полезно. 94 $
РАБОТЫ ДЕЙСТВИТЕЛЬНЫЕ ПЕРЕДАЧИ
СВОЙСТВА ЭКСПОНЕРС. (166,4 КиБ, 1976 совпадений)
Экспоненциальное представление — запись в стандартной нотации (187,0 КиБ, 1740 совпадений)
Операции с показателями степени
Умножение (195,3 киб, 2281 хиты)
Дивизион (197,0 киб, 1993 хиты)
Повышенные до власти (174,1 киб, 2123 Хиты)
Экспоненты.
 Умножение
УмножениеОбновлено 14 декабря 2020 г.
Ли Джонсон
Выполнение вычислений и работа с показателями степени являются важной частью математики высокого уровня. Хотя выражения, включающие несколько степеней, отрицательные степени и т. д., могут показаться очень запутанными, все, что вам нужно сделать для работы с ними, можно суммировать с помощью нескольких простых правил. Узнайте, как складывать, вычитать, умножать и делить числа с показателями степени и как упростить любые выражения, в которых они используются, и вы почувствуете себя намного более комфортно, решая задачи с показателями степени.
TL;DR (слишком длинный; не читал)
Умножьте два числа с показателями степени путем сложения показателей степени: + N
Разделите два числа с показателями, вычитая один показатель из остальных: x M ÷ x N = ÷ x N = x x N = x M N = x M N = X M N .
 − п
− п Когда экспонент повышается на мощность, умножьте экспоненты вместе: ( x Y ) Z = x Y ×
6969649634 × 9696969634 ×
69696969997 × 9696969997 × 969696999797 ×
696969
. z Любое число, возведенное в нулевую степень, равно единице: x 0 = 1
Что такое экспонента?
Показатель степени относится к числу, в степень которого что-то возводится. Например, 94 = x × x × x × x
Показатели также могут быть переменными; например, 4 x представляет четыре, умноженные на себя x раз.
Правила для показателей степени
Выполнение вычислений с показателями степени требует понимания основных правил, регулирующих их использование.
 Вам нужно подумать о четырех основных вещах: сложении, вычитании, умножении и делении.
Вам нужно подумать о четырех основных вещах: сложении, вычитании, умножении и делении.Сложение и вычитание степеней
Сложение показателей степени и вычитание показателей степени на самом деле не требует правила. Если число возведено в степень, добавьте его к другому числу, возведенному в степень (либо с другим основанием, либо с другим показателем степени), вычислив результат члена степени, а затем напрямую добавив его к другому. Когда вы вычитаете степени, применяется тот же вывод: просто вычислите результат, если можете, а затем выполните вычитание как обычно. Если и показатели степени, и основания совпадают, вы можете складывать и вычитать их, как любые другие совпадающие символы в алгебре. Например: 9{10} \end{aligned}
Сложение и вычитание показателей степени — GeeksforGeeks
В математике показатели степени используются для представления большего числа с точки зрения мощности. Он показывает, во сколько раз основание умножается само на себя.
 Где основанием является любое число или любое математическое выражение. Например, A 3 здесь основание равно A, а степень равна 3, что означает, что A умножится само на себя три раза, то есть A 3 = A x A x A. Общий член показателя степени равен
Где основанием является любое число или любое математическое выражение. Например, A 3 здесь основание равно A, а степень равна 3, что означает, что A умножится само на себя три раза, то есть A 3 = A x A x A. Общий член показателя степени равенY n = Y × Y × Y ×………n раз
Здесь y называется основанием, а n — степенью или показателем степени. Типы показателей степени:
- Отрицательная степень: Отрицательные степени — это те степени, которые показывают, во сколько раз обратная величина основания умножается сама на себя. Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .
- Дробный показатель степени: Когда показатель степени представлен в виде дроби, такие типы показателей называются дробными показателями. Он представлен как 1/н . Например, 3 1/2 , 4 1/3 .
- Десятичный показатель степени: Когда показатель степени представлен десятичными цифрами, такие типы показателей называются десятичными показателями степени.
 Он представлен как 1.3 . Например, 3 1,5 , 4 12,3 .
Он представлен как 1.3 . Например, 3 1,5 , 4 12,3 .
Сложение и вычитание показателей степени
Сложение и вычитание — две основные математические операции. Сложение означает нахождение суммы двух цифр, а вычитание — нахождение разницы между двумя цифрами. Но мы не можем напрямую складывать или вычитать показатели степени, мы можем выполнять сложение или вычитание только с коэффициентами или переменными, имеющими одинаковое основание и одинаковую мощность. Мы можем только складывать показатели степени при умножении и вычитать степени степени при делении.
Шаги для сложения или вычитания между показателями степени в алгебре:
Чтобы выполнить сложение или вычитание, мы будем следовать тем же шагам:
Шаг 1: основание и показатели совпадают или нет.
Шаг 2: Расположите похожие переменные/члены вместе.
Шаг 3: Теперь при необходимости выполните сложение или вычитание между коэффициентами членов.

Пример 1: решить 6x 3 + 12x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
6x 3 + 12x 3 = (6 + 12) x 3
= 18x 3
. Пример 2: Сорев 3 -135.13x 3.
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем вычесть коэффициенты двух слагаемых, чтобы получить результат.
9x 3 -13x 3 = (9 -13) x 3
= -4x 3
Шаги для выполнения или субтракции между эксплу сложение или вычитание мы будем следовать тем же шагам:
Шаг 1: Перед выполнением любого сложения или вычитания между показателями степени мы должны наблюдать, совпадают ли основание и показатели степени.

Шаг 2: Расположите одинаковые члены основания и степени вместе. Если члены имеют разные основание и показатель степени, то решите их по отдельности.
Шаг 3: Теперь выполните сложение или вычитание по мере необходимости между базой терминов.
Пример 1: решить 6 3 + 6 3 .
Решение:
Здесь основание одинаковое, т. е. 6 и показатели степени двух членов тоже одинаковые, т. е. 3
. 2(6) 3
= 2 x 6 x 6 x 6
= 432
Пример 2: решить 9 2 – 13 3 .
Решение:
Здесь основание и показатели разные
Итак, мы решаем их по отдельности.
9 2 -13 3 = 9 x 9 -13 x 13 x 13
= 81 -2197
= -2116
Аналогичные вопросы
Вопрос 1: Solve 5x 3
53535353 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x 3x
.
 3 .
3 . Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
5x 3 + 3x 3 = (5 + 3)x 3
= 8x 3
So, 5x 3 + 3x 3 = 8x 3
Question 2: Что является результатом выражения -11a 2 + 4a 2 .
Решение:
+ 4a 2 = -7a 2Здесь основание одинаковое, т. е. a и показатели степени двух слагаемых также одинаковы, т. е. 2
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
-11a 2 + 4A 2 = (-11 + 4) A 2
= (4 -11) A 2
= -7a 2
SO, -1134.
 2
2 Question 3: Solve the expression 4x 3 + 4x 2 – 2x 3 + x 2 – x + 1
Решение:
Здесь у нас разные термины (x 3 , x 2 , х), т. е. основания одинаковые, но разные показатели.
Итак, идентифицируйте похожие переменные, сгруппируйте их и выполните сложение/вычитание на основе знаков и расположите в полиномиальном порядке, т. е. основания с большей экспонентой сначала и меньшей в конце.
4x 3 + 4x 2 — 2x 3 + x 2 — x + 1 = (4x 3 — 2x 3 ) + (4x 2 3535353353333333333333333333333334 333533333333333333333333 333533333333333333333333333333334) + (4x 2 353533533333333333333333333333334). х + 1
= (4 – 2)х 3 + (4 + 1)х 2 – х + 1
= 2 х 3 + 5 х 2 – х + 1
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и степени x, y в двух терминах одинаковы, т.
 е. 3,1 соответственно.
е. 3,1 соответственно.Таким образом, мы можем считать, что эти 2 термина имеют совпадающие переменные, и мы можем добавлять/вычитать коэффициент 2 терминов в зависимости от требований.
x 3 Y + 4x 3 Y = (1 + 4) x 3 y
= 5x 3 Y
Вопрос 5: Соревто y 2 + 4x – x + 1
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и показатель степени x в 2 терминах одинаковы, т. е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
Но есть еще два члена с той же базовой переменной x и показателем степени, что и 1. Поэтому мы группируем их и выполняем вычисления с их коэффициентами.
x 3 Y + 4x 3 Y 2 + 4x — x + 1 = 4x 3 y 2 + x 3 Y + (4x — x) + 1
= 40234 x 3 3 .



 Все […]
Все […] Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]
Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]


 )
)
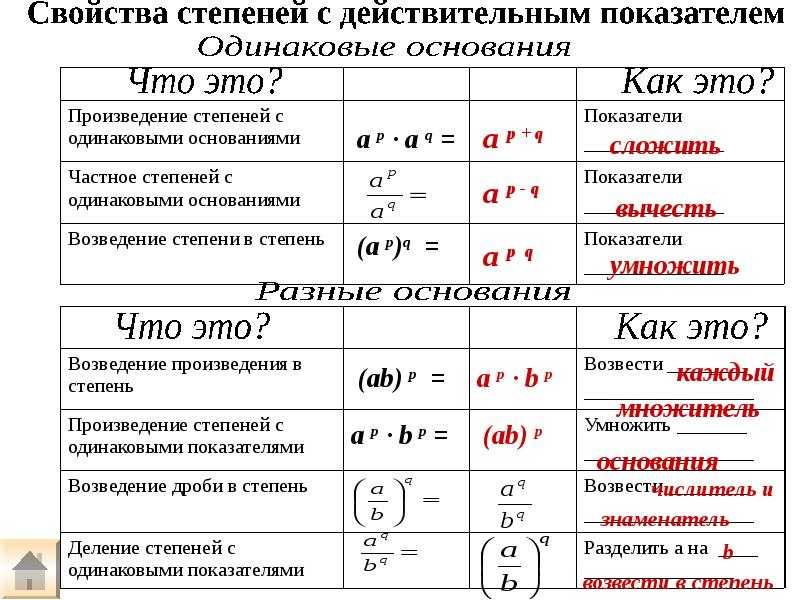 Вычислить.
Вычислить. 