Показательные уравнения решение: Как решать показательные уравнения. Методы и способы решения

П.3.4.Простейшие показательные уравнения .

Определение. Показательными называются уравнения, у которых переменная стоит в показателе степени.

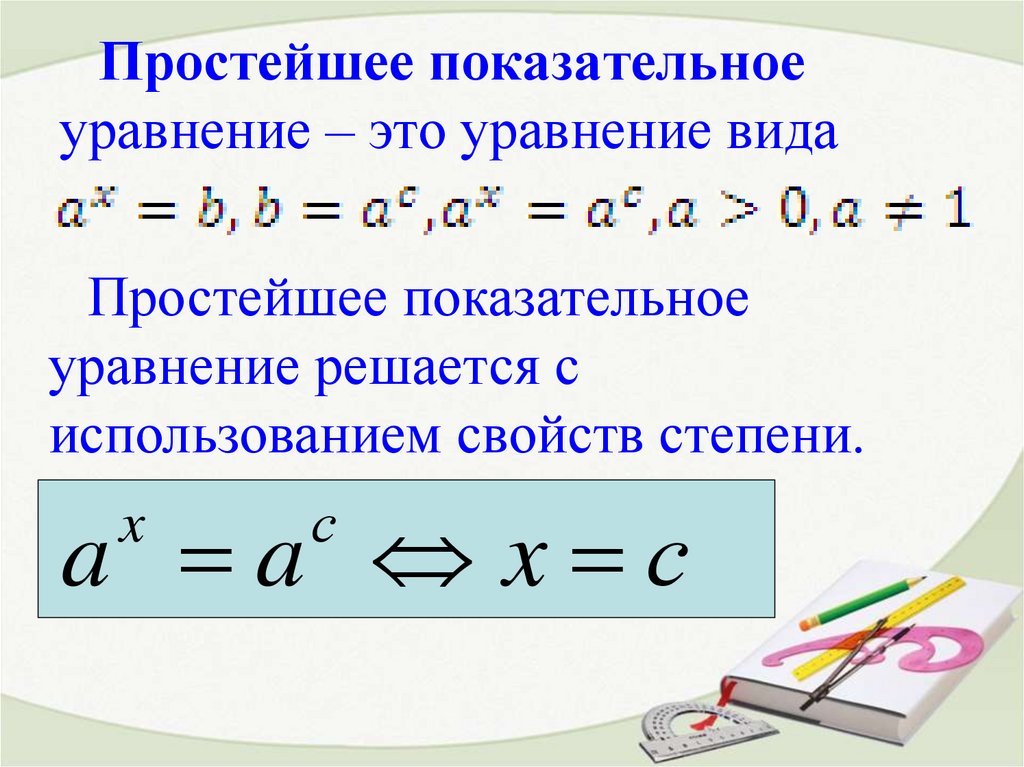
Рассмотрим простейшее показательное уравнение а^х=b, где и

Область значений функции — множество положительных чисел. Поэтому, в случае или уравнение a^x=b не имеет решений.

При уравнение a^x=b имеет единственный корень.

Если, вместо в показателе степени стоит некоторая функция , то уравнение имеет вид:

Общего метода решения показательных уравнений нет. Выделим несколько видов показательных уравнений и приведем способы их решений. Самым распространенным есть способ

I. Приведение обеих частей показательного уравнения к общему основанию.

а) чтобы решить уравнение , представляют в виде . Получают:

Например.

Решить уравнения:

б)

Например.

в) решение уравнения с помощью основного логарифмического тождества:

Например. Решить уравнения:

II. Решение уравнения вида по определению логарифма .

Например: Решить уравнения:1) 2)

III. Приведениe показательных уравнений к квадратным.

Уравнение вида решается путем замены .

Тогда . Находим , и подставляя их в замену имеем: и .

Находим и .

Например. Решить уравнение:

Учитывая замену, имеем: и

Ответ: 0 ; 2

IV. Способ вынесения общего множителя за скобку.

Например. Решить уравнение:

Ответ: 2

V. Способ приведения к общему показателю.

Например. Решить уравнение:

Ответ: 3

VI. Решение показательных уравнений путем логарифмирования обеих частей.

Например. Решить уравнения:

П.3.5. Показательные неравенства.

Показательные неравенства имеют вид:

или

Например. Решить неравенство: 1) 0,5 < 4

1 способ : 2 способ :

Решим неравенство методом интервалов:

+ — +

─── ────── ────

9

< y < 9

Учитывая замену, имеем:

Вопросы для повторения по теме

Показательная функция.

1) Дать определение показательной функции y = a^x. Почему в нем вводится

ограничение а > 0 и а ≠ 1?

2) Назвать область определения и множество значений показательной функции.

3) Какие из функций y = x^1,3; y = 2,75^x; y = ; y = x⁻³; y = являются показательными?

4) Какие свойства имеет функция y = a^x , если а > 1? Построить эскиз графика этой функции? Привести пример такой функции.

5) Какие свойства имеет функция y = a^x , если 0 < а < 1? Объяснить, используя экскиз графика этой функции. Привести пример такой функции.

6) Сравнить и , если > и 0 < а < 1? Привести пример.

7) Сравнить и , если < , а > 1? Привести пример.

8) Сравнить и , если > ; < 0,5 .

9) Какие из функций: y = 0,26^x; y = ( )^x; y = ; y = 3^x; y = ; y = возрастают, а какие убывают?

10) Сравнить число а с единицей в каждом из неравенств:

а) а^1,27 > а^0,419; б) > ; в) > ; г) < .

11) Как расположены графики функций y = a^x и y = (а > 0; а ≠ 1) относительно

друг друга?

12)

Какие процессы в области техники и естествознания описываются с помощью

показательной функции?

13) Какие уравнения называются показательными? Привести пример.

14) Сколько решений имеет показательное уравнение a^x = b, если b > 0; b = 0; b < 0?

Показать графически.

15) Что называется логарифмом числа по данному основанию?

16) По определению логарифма определить, какие из трех утверждений верны:

а) логарифм − степень;

б) логарифм − показатель степени;

в) логарифм − основание степени.

17) Найти: log₂(− 8) = ; 4 = ; log₃27=

18) Какие свойства логарифмов вы знаете?

19) Дать определение десятичного логарифма и натурального логарифма.

20) Записать основное логарифмическое тождество.

21) Записать формулу перехода к новому основанию.

22) Что значит прологарифмировать выражение? Например, прологарифмировать выражение х = 8ас².

23) В чем заключается способ решения показательных уравнений путем приведения

обеих его частей к общему основанию. Записать схему его решения. Например.

24)Как решаются уравнения вида а^f(x)=b по определению логарифма?

25) Решить уравнения:

а) 5^х = 5³; б) 17^х = 1; в) 4^х = ; г) (0,1)^х = 1000; д) = 81; е) 3^х = 5; ж) 3

26) Решить показательные уравнения способом вынесения общего множителя за скобки: а) 2^х+2 − 2^х = 96 б) 7^х − 7^х-1 = 6.

27)Как решаются показательные уравнения вида Аа^2х + Ва^х + С = 0? Записать схему их решения. Например, решить уравнения: а) 4

х + 2^х = 72 б) 7^2х − 6 ∙ 7^х + 5 = 0.

28) Решить уравнение способом приведения к общему показателю: 2^х · 5^х = 0,01

29) Решить показательные уравнения логарифмированием: а) 3^x = 8^x; б) 5^2x−1 = 7^−x.

30) Записать в аналитической форме показательное неравенство простейшего вида.

31) Какое свойство показательной функции y = a^x используется при решении показательных неравенств? Рассмотреть случаи а > 1 и 0 < а < 1.

32) Решить неравенства: а) 3^2-х > 27 б) 0,5^5-2х < 2 в) 2^5х+6 > ; г) > 6³.

Показательные уравнения — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Показательные уравнения

Эта тема не так сложна, как кажется, стоит лишь по-хорошему
разобраться в ней, в чем я постараюсь помочь.

2. Что же такое показательные уравнения ?

Показательные уравнения – это уравнения, в которых
неизвестное число находится в показателе степени.
Например: 2x=4
или
4x-1=1
Чаще всего решение показательных уравнений сводится к решению
уравнения аx=ab где а – заданное число, а>0, а 1, х – неизвестное.
,
Разобрался>

3. Как решать?

Напомню: чаще всего решение показательных уравнений сводится к решению
x
b
уравнения а =a , где а – заданное число, а>0, а 1, х – неизвестное.
Это уравнение можно решить очень просто с помощью свойства
степени с одинаковым основанием а>0, а 1 равны только
когда, когда их показатели равны. (напомнить свойства степени)
Попробуем решить уравнение:
4*2х =1
запишем уравнение в другом виде
22*2х=1 ;
теперь, пользуясь свойством степени
22+х=1
любое число нулевой степени = 1, значит
22+х=20
теперь приравниваем показатели
2+х=0
видим, что
х=-2
Ответ: х=-2
Перейти к практическим
заданиям
<Назад
Разобрался>

4. Свойства степени

Решим уравнение
9х- 4*3х- 45=0
Это уравнение можно решить при помощи замены переменных
Заменим 3х=t
Получаем
t2-4t-45=0
Решаем простое квадратное уравнение, получаем корни
t1=9, t2=-5
теперь подставим в уравнение 3х=t получившиеся значения
3х=9
3х=32
х=2
и
3х=-5
нет корней.
(показательная функция не
может принимать
отрицательные значения)
Ответ: х=2
<Назад
Разобрался>

5. Еще пример

Решаем уравнение
2х+1+2х-1+2х=28
Вынесем общий множитель 2х за скобку (пользуясь свойствами степени)
2х(21+2-1+1)=28
Подсчитаем действие в скобках
2х * 3,5= 28
Теперь можно разделить обе части уравнения на одно и то же число
2х * 3,5= 28 / : 3,5
2х=8
8 представим как 23
2х=23
Основания равны. Теперь можно прировнять показатели.
х=3
Ответ: х=3
<Назад
Разобрался>

6. Еще пример

Задание: 3х+1 – 2*3х-2=25
Решение: (Некоторые строчки пропущены. Допиши решение.)
3х+1 – 2*3х-2=25
3х-2(33-2)=25
____________
3х-2=1
____________
х=2
Разобрался>

7. Решаем вместе

Теперь, думаю, мы в состоянии сами решить некоторые уравнения. Вот
несколько заданий. Реши их и проверь себя сам.
Задание 1:
0,33х-2=1
Задание 2:
2 * 4х=64
Задание 3:
16х -17 * 4х +16=0
Посмотреть
ответы и решения
Как решать?
Разобрался>

8. Реши сам

Задание 4
32х+6=2х+3
Задание 5
16*9х-25*12х+9*16х=0
Задание 6
=
Посмотреть
ответы
Разобрался>

9. Сложные задания

Мы научились решать показательные уравнения.
Думаю, не стоит напоминать, что теорию надо выучить.
С практикой же поступим так: просто возьми свой учебник и
порешай задания, либо подойди к учителю и возьми задание.
Я все понял. Знаю теорию. Умею решать
показательные уранения.
Ни чего не понял.

English     Русский Правила

Видео-урок: графическое решение показательных уравнений

Стенограмма видео

Решение показательных уравнений Графически

В этом видео мы научимся определить количество решений показательного уравнения, заданного графически, и мы также увидим, как применить это для решения экспоненциальных уравнений с использованием графического методы. Прежде чем мы начнем с попытки решить экспоненциальные уравнения графически, давайте начнем с того, что вспомним, что мы подразумеваем под экспоненциальная функция.

Напомним, что показательная функция является одной из форм 𝑓 из 𝑥 равна 𝑎, умноженной на 𝑏 в степени 𝑥, где 𝑏 положителен, а 𝑏 не может быть равен единице. Что ж, стоит отметить, что это не единственный пример показательных функций.

Например, мы могли бы умножить наше значение 𝑥 константой, или мы могли бы добавить константу к этому значению 𝑥, и это все равно будет экспоненциальной функцией. Однако пока мы просто сосредоточимся на этот тип экспоненциальной функции. Тогда это означает, что экспоненциальный уравнение — это уравнение, включающее показательную функцию. Итак, это одна из форм 𝑎 раз 𝑏 в степени 𝑥 равно некоторой функции 𝑔 от 𝑥. Решение этого уравнения будет быть значением 𝑥, которое делает обе части уравнения равными.

Иногда мы можем решать уравнения с помощью с помощью алгебраических манипуляций. Однако для показательных уравнений это часто очень трудно. Это потому, что 𝑥, наша переменная, появляется в экспоненте. Поэтому вместо этого мы сосредоточимся на поиске эти решения графически. Чтобы увидеть, как мы могли бы решить показательное уравнение графически, начнем с примера.

Допустим, нам дали график показательной функции 𝑦 равен четырем в степени 𝑥, и пусть скажем, нас попросили решить уравнение четыре в степени 𝑥 равно единице. Это означает, что нам нужно найти значение 𝑥 мы подставляем в нашу экспоненциальную функцию, чтобы вывести значение один. Мы можем сделать это с помощью нашего график. Помните, 𝑦-координата каждая точка на нашей кривой сообщает нам выходное значение для нашей функции при этом значении 𝑥.

Мы хотим знать, когда наша функция выводит значение один, оно выводит значение один, когда его 𝑦-координата равен единице. Итак, рисуем линию 𝑦 равно к одному на наши оси. Затем мы можем увидеть, когда наша кривая 𝑦-значение единицы. Он имеет 𝑦-значение, равное единице, когда его 𝑥-значение равно нулю. Другими словами, мы показали, что одна точка пересечения прямой 𝑦 равна единице, а кривая 𝑦 равна равно четырем в степени 𝑥. Это точка с координатами ноль, один. При этом значении 𝑥 оба наших функция четыре в степени 𝑥 и функция один выводят одно и то же значение. Они выводят значение единицы. Следовательно, это должно быть решение к нашему уравнению. 𝑥 равно нулю решает уравнение четыре в степени 𝑥 равно единице.

Есть еще несколько вещей, которые мы можем уведомление. Например, это единственная точка точки пересечения нашей линии и кривой. И каждое решение нашего уравнения будет точкой пересечения прямой и кривой. Итак, потому что есть только один момент пересечения линии и кривой, мы можем заключить, что существует только один решение этого уравнения. Также стоит отметить, что мы можем проверить то, что 𝑥 равно нулю, является решением нашего уравнения путем замены 𝑥 равно обнулить обе части уравнения и убедиться, что они равны. Начнем с замены 𝑥 на равным нулю в левую часть уравнения.

Замена 𝑥 равна нулю в левую часть нашего уравнения, мы получаем четыре в степени нуля. И мы можем оценить это, используя наши законы показателей. Мы знаем любое ненулевое число, поднятое в нулевой степени всегда равен единице. Затем мы можем сделать то же самое с правая часть нашего уравнения. Однако правая сторона это уравнение представляет собой просто постоянное значение единицы, поэтому значение 𝑥 не влияет это значение. Следовательно, когда 𝑥 равно нулю, то и левая, и правая части нашего уравнения равны. Это подтверждает, что 𝑥 равно ноль является решением нашего уравнения.

Мы можем использовать точно такой же метод решать другие показательные уравнения. Например, давайте решим уравнение четыре в степени 𝑥 равно пяти минус 𝑥. Еще раз, поскольку решение нашей уравнение — это значение 𝑥 такое, что обе части нашего уравнения равны, мы можем найти решения нашего уравнения, ища точки пересечения между кривая 𝑦 равна четырем в степени 𝑥, а линия 𝑦 равна пяти минус 𝑥 потому что точки пересечения будут иметь одинаковый выход для обоих наших функции, другими словами, они будут решениями нашего уравнения.

У нас уже есть график 𝑦 равно четырем в степени 𝑥. Итак, на одной оси мы должны нарисуйте линию 𝑦 равно пяти минус 𝑥. Во-первых, мы знаем, что его 𝑦-перехват равен пяти. Мы также можем найти 𝑥-перехват этой линии. Подставляем 𝑦 равно нулю и найдите наше значение 𝑥. Мы видим, что 𝑥-перехват эта строка, когда 𝑥 равно пяти. Мы можем использовать это, чтобы построить линия. Мы знаем, что его 𝑦-перехват в пять и его 𝑥-перехват также равен пяти. Затем прямая, соединяющая эти две точки — линия 𝑦 равна пяти минус 𝑥.

Наконец, мы видим, что есть одна точка пересечения между нашей кривой и нашей линией, и это будет точка где выходы обеих этих функций равны. Мы видим, что 𝑥-координата этой точки пересечения является одной. Итак, мы имеем, что 𝑥 равно единице является решением нашего уравнения. И на самом деле, поскольку это единственный точка пересечения линии и кривой, это единственное решение наше уравнение. Однако нам нужно быть осторожный. Нарисуем линию 𝑦 равно пять минус 𝑥, и мы используем это, чтобы оценить точку пересечения между линия и кривая. Таким образом, мы не можем быть уверены, что 𝑥 равным единице, является точным решением нашего уравнения, поскольку мы приближаемся к используя наш эскиз.

Чтобы показать, что 𝑥 равно единице, решение этого уравнения, которое нам нужно заменить 𝑥 равно единице как в левую, так и в правую часть нашего уравнения и проверьте, совпадают ли они равный. Мы можем начать с левой руки сторону нашего уравнения. Подставляя 𝑥 равно единице, мы получить четыре в первой степени. И, используя наши законы показателей, мы знаем, что любое число, возведенное в первую степень, равно самому себе. Итак, четыре в первой степени равно равно четырем. Затем мы можем сделать то же самое с правая часть нашего уравнения. Подставляя 𝑥 равно единице, мы получаем пять минус один, который мы можем оценить равным четырем. Поэтому, поскольку и лево-, и правые части нашего уравнения равны, когда 𝑥 равно единице, мы можем сделать вывод то, что 𝑥 равно единице, является решением нашего показательного уравнения.

До сих пор все наши уравнения имели были решения. Однако также возможно, что уравнение не имеет решений. Например, мы можем видеть, что линия 𝑦 равна минус двум, а кривая 𝑦 равна четырем в степени 𝑥 не имеют точек пересечения. Это означает, что если бы нас попросили решить уравнение четыре в степени 𝑥 равно минус два с помощью данной диаграммы, мы могли бы заключить, что нет решений для этой уравнение, потому что любое решение этого уравнения было бы точкой пересечения между кривой 𝑦 равна четырем в степени 𝑥, а линия 𝑦 равна минус два. И вместо того, чтобы сказать, что нет решений этого уравнения, мы можем ввести понятие множества решений.

Набор решений уравнения множество всех решений этого уравнения. Таким образом, вместо того, чтобы говорить уравнение четыре в степени 𝑥 равно минус два не имеет решений, мы можем сказать, что его множество решений — это пустое множество. Давайте теперь рассмотрим пример где нам дан график экспоненциальной функции, и нам нужно использовать его, чтобы определить множество решений показательного уравнения.

Использовать заданный график функции 𝑓 of 𝑥 равно двум в степени пять минус 𝑥, чтобы найти множество решений уравнение два в степени пять минус 𝑥 равно двум.

В этом вопросе нам дается график экспоненциальной функции и эта экспоненциальная функция появляется в заданном показательное уравнение. Нам нужно использовать это, чтобы определить множество решений уравнения. Сначала напомним множество решений уравнения – это множество всех решений этого уравнения. Поэтому мы ищем набор всех значений 𝑥, которые уравновешивают обе части уравнения. Другой способ думать об этом поскольку два в степени пять минус 𝑥 равно функции 𝑓 от 𝑥, мы можем подставьте 𝑓 из 𝑥 в наше уравнение. Это дает нам уравнение 𝑓 из 𝑥 равен двум. Мы ищем набор всех значения 𝑥 такие, что 𝑓 из 𝑥 равно двум.

Чтобы найти эти значения 𝑥, мы можем напомним, что каждая точка на кривой 𝑦 равна 𝑓 из 𝑥 будет иметь координаты вида 𝑥, 𝑓 из 𝑥. Другими словами, 𝑦-координаты точек на кривой говорят нам о результатах нашей функции для данного значения из 𝑥. Мы хотим определить значения 𝑥 где наша функция выводит два. Это будут точки на нашем кривая с 𝑦-координатой, равной двум. Итак, мы можем найти их, зарисовав линия 𝑦 равна двум на той же системе осей. Мы видим, что есть только одна точка на нашей кривой 𝑦-координата равна двум. Это будет точка пересечение прямой 𝑦 равно двум и кривой 𝑦 равно двум сила пяти минус 𝑥. 𝑦-координата этой точки равна два, а его 𝑥-координата равна четырем. Другими словами, когда 𝑥 равно четыре, наша функция выводит два. 𝑓 оценка четыре равна двум.

Следовательно, 𝑥 равно четырем решение нашего уравнения. На самом деле, поскольку это единственный точка пересечения линии и кривой, это единственное решение наше уравнение. Это означает, что решение, установленное для нашего уравнение — это просто набор, содержащий четыре.

Так же стоит отметить можем проверить наш ответ путем подстановки 𝑥 равен четырем в наше уравнение или в наше функция. Замена 𝑥 равно четырем в нашу функцию 𝑓 от 𝑥, мы получаем 𝑓, оцениваемое как четыре, равно двум в степени пять минус четыре. Пять минус четыре равно один. Итак, это упрощает, чтобы дать нам два в первую степень. И любое число возведенное в первое сила просто равна самой себе. Итак, 𝑓, оцененное в четыре, равно к двум, что в точности совпадает с правой частью нашего уравнения, подтверждая то, что 𝑥 равно четырем, является решением нашего уравнения. Таким образом, мы смогли показать множество решений уравнения два в степени пять минус 𝑥 равно двум только набор, содержащий четыре.

Давайте теперь перейдем к другому примеру где нам дан график экспоненциальной функции, и нам нужно использовать его, чтобы решить показательное уравнение.

На схеме изображен график 𝑓 𝑥 равно двум в степени двойки 𝑥. Используйте этот график, чтобы найти решение множество уравнения два в степени два 𝑥 равно четырем.

В этом вопросе нам дается график экспоненциальной функции, и нас просят решить показательное уравнение где появляется эта функция. Для этого начнем с того, что вспомним множество решений уравнения — это множество всех решений этого уравнения. Это означает, что мы ищем все значения 𝑥, которые решают уравнение два в степени двойки 𝑥, равны четыре. Чтобы помочь нам в этом, давайте начнем с заменив два в степени двойки 𝑥 в нашем уравнении на 𝑓 из 𝑥. Это означает, что уравнение, которое нам задают для решения можно переписать как 𝑓 of 𝑥 равно четырем.

Другими словами, мы просто ищем для значений 𝑥 таких, что наша функция 𝑓 выводит значение четыре. И мы можем вспомнить, что 𝑦-координата точки на нашей кривой сообщает нам выходное значение функции для это значение 𝑥. Итак, мы можем найти все значения где наша функция выводит четыре, нарисовав линию 𝑦 равно четырем на наш диаграмма. И тогда мы можем видеть на нашей диаграмме на нашей кривой есть только одна точка с 𝑦-координатой, равной четырем. Это точка координат один, четыре.

И это стоит повторить говорит нам, что 𝑓, оцененное в единицу, равно четырем. И, следовательно, одно из решений наше уравнение. По сути, все решения нашей уравнение будет точкой пересечения прямой 𝑦 равной четырем и кривая 𝑦 равна двум в степени двойки 𝑥. Итак, поскольку мы видим, что есть только одна точка пересечения, мы знаем, что есть только одно решение. Таким образом, множество решений уравнение два в степени двойки 𝑥 — это просто множество, содержащее единицу.

Давайте теперь посмотрим на пример, где мы сначала нужно изменить экспоненциальное уравнение, которое нам дано.

На схеме изображен график 𝑓 𝑥 равно двум в степени 𝑥 над двумя. Используйте этот график, чтобы найти решение набор уравнения два в степени 𝑥 два плюс пять равен девяти.

В этом вопросе нам дается график показательной функции 𝑓 от 𝑥. И нас просят использовать это для определить множество решений уравнения, которое содержит нашу функцию 𝑓 от 𝑥. Для этого начнем с того, что вспомним множество решений уравнения — это множество всех решений этого уравнения. В данном случае это будет совокупность все значения 𝑥, такие что два в степени 𝑥 больше двух плюс пять равно девять. Чтобы ответить на этот вопрос, можно помогите нам переписать наше показательное уравнение в терминах функции 𝑓 от 𝑥. Подставляем два в степень 𝑥 больше двух равно 𝑓 из 𝑥 в наше уравнение, мы получаем 𝑓 из 𝑥 плюс пять равно до девяти. Мы можем упростить это уравнение далее, вычитая пять с обеих сторон. Получаем 𝑓 из 𝑥 равно девяти минус пять, что упрощает получение 𝑓 из 𝑥 равно четырем. Итак, мы хотим найти значения 𝑥 таким образом, что наша функция выводит значение четыре.

Помните, что 𝑦-координата любая точка на нашей кривой сообщает нам выходное значение нашей функции при этом значении 𝑥. Итак, мы хотим найти все точек на нашей кривой с 𝑦-координатой четыре. Мы делаем это, набрасывая линию 𝑦 на нашей диаграмме равно четырем. Мы видим, что есть только одна точка точки пересечения нашей линии и нашей кривой. И мы видим, что эта точка имеет 𝑥-координата четыре. Поэтому, когда мы вводим значение 𝑥 равно четырем в нашу функцию, выходное значение равно четырем. 𝑓 из четырех равно четырем. И на самом деле, поскольку это единственный точка пересечения между нашей линией и нашей кривой, это единственное решение наше уравнение. Поэтому множество решений этой уравнение представляет собой набор, содержащий четыре.

Мы можем проверить, что 𝑥 равно четыре является решением нашего уравнения путем подстановки 𝑥 равно четырем в левая часть нашего уравнения. Замена 𝑥 равно четырем в левую часть нашего уравнения, мы получаем два в степени четыре над двумя плюс пять, которые мы можем упростить четыре вместо двух, равно двум. Значит, это равно двум в квадрате плюс пять. И тогда мы сможем это оценить. Два в квадрате равно четырем. Таким образом, мы получаем четыре плюс пять, что равно равный девяти, который, как мы видим, в точности равен правой части этого уравнение. Таким образом, четыре является решением для наше уравнение, и мы знаем, что это единственное решение. Таким образом, множество решений уравнение два в степени 𝑥 над двумя плюс пять равно девяти это множество содержащий четыре.

Давайте теперь посмотрим на пример, где наш показательное уравнение включает линейную функцию.

Используйте приведенные ниже графики, чтобы ответить на вопрос следующий вопрос. Правда или ложь: уравнение два к степень 𝑥 равна отрицательной 𝑥 не имеет решения.

В этом вопросе нам дается график двух функций. Начнем с определения того, какой две функции это графики. Во-первых, мы видим, что наш прямой прямая проходит через начало координат, поэтому ее 𝑦-перехват равен нулю. Далее мы можем увидеть для каждой единицы мы переходим, мы путешествуем на одну единицу вниз. Значит, его наклон отрицательный. В форме пересечения наклона это строка 𝑦 равна отрицательной единице 𝑥 плюс ноль, то есть просто 𝑦 равна отрицательной 𝑥. Другая наша кривая имеет форму экспоненциальная функция, и мы видим, что она проходит через точку с координатами один два. Если мы подставим 𝑥 равно единице в функцию два в степени 𝑥, мы можем видеть, что это выводит значение два. Мы могли бы сделать это с другими точками на нашей кривой, чтобы сделать вывод, что это действительно набросок кривой 𝑦 равен два в степени 𝑥.

Нам нужно использовать эти графики для определить, равно ли уравнение два в степени 𝑥 отрицательному 𝑥 имеет решение. У нас может возникнуть соблазн попробовать и решить это с помощью манипуляции. Однако это будет очень сложно, потому что 𝑥 появляется в показателе степени, а не в показателе степени. Вместо этого вспомните, что решение это уравнение представляет собой значение 𝑥 такое, что обе части уравнения равны. Другими словами, нам нужно ввести значение 𝑥 в функции два в степени 𝑥, а затем поместить то же значение в отрицательную функцию 𝑥, чтобы получить тот же результат. Мы можем сделать это прямо из нашего график. Для выходов этих двух функции равны с одним и тем же 𝑥-входом, они должны иметь точку пересечение. Это потому, что 𝑦-координата сообщает нам выходные данные этой функции для данного входа.

Следовательно, поскольку есть одна точка пересечение линии и кривой, мы можем заключить, что два в степени 𝑥 равно отрицательному 𝑥 имеет одно решение. На самом деле, мы можем даже приблизительно это значение, пытаясь считать его 𝑥-координату с графика. Делая это, мы получим, что 𝑥 есть примерно равно отрицательному 0,6. Поэтому мы смогли показать что неверно, что уравнение два в степени 𝑥 равно отрицательному 𝑥 не имеет решений.

В нашем последнем примере мы решим показательное уравнение графически, также рисуя линейную функцию на той же заданный граф.

Следующий график показывает функция 𝑓 под одной из 𝑥 равна двум в степени отрицательного 𝑥. Используйте этот график и постройте функция 𝑓 sub two of 𝑥 равна 𝑥 плюс три, чтобы найти набор решений уравнение два в отрицательной степени 𝑥 равно 𝑥 плюс три.

В этом вопросе нам дано два функции 𝑓 под одной из 𝑥 и 𝑓 под одной из 𝑥, и нам дан график функция 𝑦 равна 𝑓 под одной из 𝑥. Нас просят найти решение набор уравнений. А так как 𝑓 под одной из 𝑥 равно в левой части этого уравнения, а 𝑓 меньше двух из 𝑥 равно правая часть этого уравнения, уравнение 𝑓 меньше одного из 𝑥 равно 𝑓 меньше двух из 𝑥. Мы можем решить это уравнение графически. Любое решение этого уравнения будет точка пересечения кривой 𝑦 равна 𝑓 под одной из 𝑥 и строка 𝑦 равна 𝑓 меньше двух из 𝑥. Потому что точка пересечения будет иметь ту же 𝑦-координату, а 𝑦-координата является выходом функция для данного координатора 𝑥, что означает, что выходы функции будут будут одинаковыми, поэтому наше уравнение будет решено.

Нам нужно нарисовать кривую 𝑦 равно 𝑥 плюс три. Во-первых, отметим, что его 𝑦-перехват будет в три. Мы также можем найти его 𝑥-перехват подстановкой 𝑦 равно нулю. Решая это, мы получаем, что 𝑥 есть равно минус трем. Затем мы можем построить нашу линию. Его 𝑦-перехват равен трем, и его 𝑥-перехват находится на отрицательном уровне три. Затем это позволяет нам построить наш линия. Мы просто соединяем 𝑦- и 𝑥-пересечение с прямой. Тогда единственная точка пересечение между нашей линией и нашей кривой будет единственным решением нашей уравнение. Мы можем прочитать его 𝑥-координату; его 𝑥-координата отрицательна.

Тогда, поскольку вопрос задают нам запишите это как набор решений, мы напишем это как набор, содержащий отрицательные один. Таким образом, мы смогли показать множество решений уравнения два в отрицательной степени 𝑥 равно 𝑥 плюс три — это просто набор, содержащий отрицательную единицу.

Давайте теперь рассмотрим некоторые ключевые моменты этого видео. Во-первых, набор решений уравнение — это множество всех решений этого уравнения, другими словами, это множество все значения, которые удовлетворяют уравнению. И, в частности, если уравнение не имеет решений, можно сказать, что множество решений — это пустое множество. Далее мы увидели, что можем решить уравнение 𝑓 из 𝑥 равно 𝑔 из 𝑥 путем нахождения 𝑥-координат всех точек пересечения графиков 𝑦 равно 𝑓 из 𝑥, а 𝑦 равно 𝑔 из 𝑥.

Каждая точка пересечения является решение уравнения. А если точек нет пересечение, то решений уравнения нет. Наконец, мы увидели графику. решения уравнений могут быть приближениями. Это особенно верно, если мы нужно нарисовать одну из функций самостоятельно. В этих случаях мы должны использовать линии сетки, чтобы попытаться сделать нашу аппроксимацию максимально точной.

Формула экспоненциального уравнения — GeeksforGeeks

Экспоненты используются в экспоненциальных уравнениях, как следует из названия. Показатель степени числа (основания) показывает, сколько раз число (основание) было умножено. Показательное уравнение — это уравнение, в котором степень является переменной и является частью уравнения.

Показательные уравнения

Переменная — это показатель степени (или часть показателя степени) в показательном уравнении. Например,

• 3 ^x = 243
• 5 ^{x – 3} = 125
• 6 ^{y – 7} = 216

Приведенные выше примеры изображают экспоненциальные уравнения. Обратите внимание, как переменные x и y формируют либо весь показатель степени в уравнении, либо только его часть. Экспоненциальные уравнения чаще всего используются для решения задач, связанных со сложными процентами, экспоненциальным ростом, распадом и т. д.

Типы экспоненциальных уравнений

Экспоненциальные уравнения подразделяются на три категории. Вот их имена:

• Уравнения с обеих сторон имеют одну и ту же основу. Эти типы уравнений могут быть решены путем приравнивания их показателей. Пример:

12 ^x = 12 ²

• Уравнения с разными основаниями можно изменить, чтобы получить одно и то же решение. Затем, когда основания приравнены, их показатели степени можно приравнять, чтобы найти переменную. Пример:

12 ^x = 144 можно представить как 12 ^x = 12 ²

• Уравнения, которые не могут быть построены с одной и той же основой. Эти уравнения можно решить, применяя логарифмирование к обеим частям. Пример:

2 ^x = 9 может быть решено как log ₂ 9 = x

Проблемы

Вопрос 1. Решение. 10 .

Решение:

Ясно, что основания в обеих частях данного уравнения равны, то должны быть равны и их показатели.

Таким образом, x = 10.

Вопрос 2. Решение: 6 ^{z — 7} = 216.

Решение:

Мы знаем, что 216 = 6 ³ .

⇒ 6 ^{z – 7} = 6 ³

Ясно, что основания в обеих частях данного уравнения равны, значит, и их показатели должны быть равны.

⇒ z — 7 = 3

⇒ z = 3 + 7

⇒ z = 10

Вопрос 3. Решение: (—5) ^x = 625.

: .

Мы знаем: 625 = 5 ⁴ = (−5) ⁴

⇒ (−5) ^x = (−5) ⁴

по обеим сторонам основания. уравнения равны, то и их показатели должны быть равны.

⇒ х = 4

Вопрос 4. Решите: 5 ^x = 4.

Решение:

.

⇒ log 5 ^x = log 4

Согласно свойству log a ^m = m log a, мы имеем:

⇒ x log 5 = log 4

Разделим левую и правую стороны на log 5.

⇒ x = log 4/log 5.

Вопрос 5. Решение: 7 ^{3x + 7} = 490.

Решение:

Применить журнал на обеих сторонах данного уравнения,

Log 7 ^{3x + 7} = log 490 490 490.

По свойству log a ^m = m log a имеем:

(3x + 7) log 7 = log 490 … (1)

x = -5/3 + (1/(3 log 7))

Вопрос 6. Решить: 5 ^{x – 4} = 125.

Решение:

Мы знаем: 125 = 5 ³

⇒ (5) ^x-4 = (5) ³

Ясно, что обе части данного уравнения равны. то их показатели также должны быть равны.

⇒ x — 4 = 3

⇒ x = 7

Вопрос 7.