МатАнализКР-2, 1 вариант
1 вариант
Понятие производной. Производная функции хп.
Пусть функция y=f(x) определена в некоторой точки х0. Зададим аргументу приращение такое, что значение находится в указанной окрестности точки х0. Тогда приращение функции y=f(x) в точке х0, соответствующее приращению аргумента равно
Производной функции y=f(x) в точке х0 называется конечный предел (если он существует) при отношения приращения функции в этой точке к соответствующему приращению аргумента.
Производную функции y=f(x) в точке х0 будем обозначать символом или .
По определению производной
Если функция y=f(x) определена на некотором интервале (a,b), то в любой фиксированной точке х этого интервала аналогичным образом определяются приращение и производная в точке х:
Нахождение
производной функции называется
дифференцированием этой функции.
Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке.
Функция, дифференцируемая в каждой точке промежутка Х, называется дифференцируемой на этом промежутке.
Пользуясь определением производной, получим формулы для вычисления производной :
, где n – натуральное число.
Воспользовавшись формулой бинома Ньютона получим:
10.Производные обратных тригонометрических функций.
Если функция y=f(x) определена, непрерывна и строго монотонна в некоторой окрестности точки х0 и в этой точке существует производная то и обратная функция имеет производную в точке причём
С помощью этого можно получить производную функции y=arcsin x, где -1<x<1 и обратную для x=siny.
Аналогично для остальных обратных тригонометрических функций:
Задание №1. Найти производные следующих функций.
Найти производные следующих функций.
Решение:
Задание №2. Найти пределы функции, применяя правило Лопиталя.
Решение:
Задание №3. Методами дифференциального исчисления исследовать функцию y = f(x) и по результатам исследования построить ее график. Найти наименьшее и наибольшее значения функции на отрезке [a; b].
Решение:
Область определения:
Функция нечётная:
Пересечение с осями координат: x=0,y=0;
Асимптоты функции: y=kx+b – наклонная асимптота, где
Тогда y=0 – наклонная асимптота.
Возрастание, убывание функции:
x1=2; x2=-2;
— функция убывает
— функция возрастает
y(-2)=-1 – min
y(2)=1 – max
Вогнутость, выпуклость функции:
— точки перегиба функции;
— функция выпуклая;
— функция вогнутая;
График:
б) I=[-3;3]
Из рисунка видно,
что максимум достигается в точке 2, а
минимум в точке -2.
Наибольшее и наименьшее значения равны:
y(2)=1 и y(-2)=-1.
Это глобальный максимум и глобальный минимум.
Задание №4. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
Решение:
Точки x1=-1, x2=1- подозрительные на разрыв, т.к. меняется аналитическое значение функции.
Для x1=-1
Значит, функция в т. x1=-1 – непрерывна.
Для x2=1
Значит, функция в т. x2=1 имеет разрыв 1-го рода (функция терпит скачок).
Рисунок:
404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| jpg»> |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Как найти производную от $\\arcsin x+\\arccos x$?
Последняя обновленная дата: 12 февраля 2023
•
Общее представление: 221,1K
•
Просмотры сегодня: 5.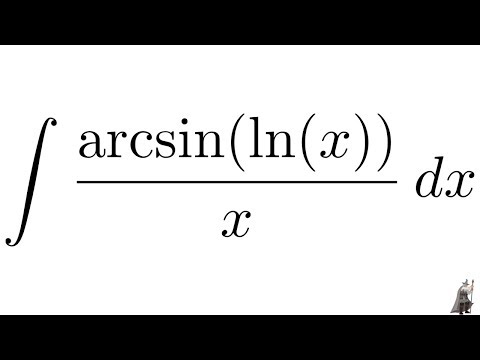 {-1}}x=\dfrac{\pi }{2}$, а затем продифференцировать функция.
{-1}}x=\dfrac{\pi }{2}$, а затем продифференцировать функция.
Недавно обновленные страницы
Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main
Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main
Вычислить значение intlimits0 cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно0002 KCN легко реагирует с образованием цианида с A. Этиловый спирт класс 12 химический состав JEE_Main
Если ab и c единичные векторы, то левый ab2 правый+bc2+ca2 класс 12 математический JEE_Main
Стержень AB длиной 4 единицы движется горизонтально при выполнении класса 11 maths JEE_Main
Оцените значение intlimits0pi cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно 1 nleft S cup T right class 10 maths JEE_Main
Какова площадь треугольника с вершинами Aleft 11 класс математика JEE_Main
KCN легко реагирует с образованием цианида с этиловым спиртом класса 12 по химическому составу JEE_Main
Возникающие сомнения
Производное арксина: формула, доказательство, примеры, решение формула.
 Также поймите, как доказать производную от arcsin по первому принципу и неявному дифференцированию.
Также поймите, как доказать производную от arcsin по первому принципу и неявному дифференцированию.от Алана Уокера — Опубликовано на 04 ноября 2022 г.
Введение в производную от arcsin
Производные находят широкое применение практически во всех областях техники и науки. Производную от sin, обратную x, можно вычислить, следуя правилам дифференцирования.
Или мы можем напрямую найти производную арксинуса, применив первый принцип дифференцирования. В этой статье вы узнаете, что такое производная обратного синуса x и как вычислить производную обратного синуса, используя различные подходы.
Какая производная от sin
-1 х?Производная от cos x по переменной ‘x’ равна -sin x. Обозначается d/dx (sin -1 x). Это обратная скорость изменения тригонометрической функции sin x. В треугольнике это отношение противоположной стороны к гипотенузе. Пишется как;
sin x = противолежащее/ гипотенуза
Формула производной arcsin
Формула производной arcsin равна отрицательной производной обратного cos, т. е.
е.
d / dx(sin -1 x) = 1/√1-x 2
Как доказать производную sin
-1 x?Существует множество способов получения производной арксинуса. Следовательно, мы можем доказать производную от sin x, используя;
Первый принцип
Неявное дифференцирование
Дифференцирование производной sin, обратной x, по первому принципу
Обратная производная sin по первому принципу относится к нахождению общего выражения для наклона кривой с помощью алгебры. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна
f'(x)=lim f(x+h)-f(x)/h
Доказательство производной обратного синуса по первому принципу
Чтобы доказать дифференцирование по арксинусу с использованием первого принципа, замените f(x) по греху х. f(x)=lim h→0 f(x+h)-f(x)/h
Итак,
f(x)=lim h→0 sin -1 (x+h )-sin -1 x /h
Предположим, что
sin -1 (x+h) = A и sin -1 x = B
Кроме того, h = x+h-h = sin B — sin A, следовательно, по мере приближения h к нулю A будет приближаться к B.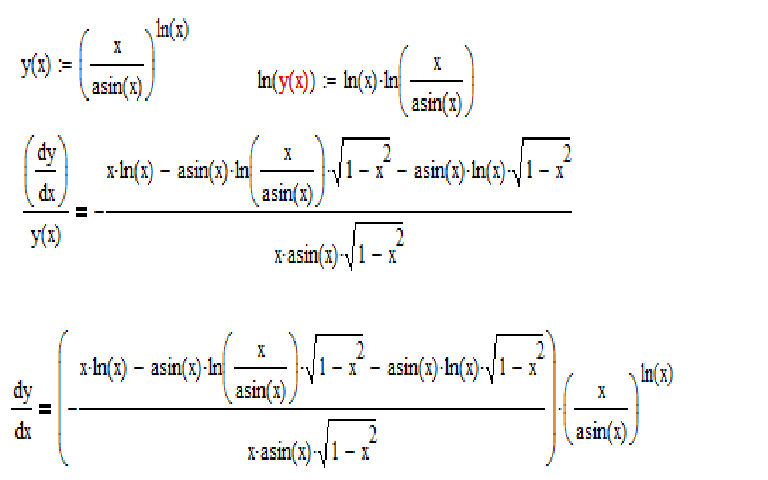
f(x)=lim A→B A-B /sin A — sin B
Используя формулу sin A — sin B = 2cos(A+B)/2sin(A-B)/2
f(x) =lim A→B A-B /2cos(A+B)/2sin(A-B)/2
Или,
f(x)=lim A→B (A-B)/2 /cos(A+B) )/2sin(A-B)/2
Пусть A-B/2 = t, тогда
f(x)=lim A→B 1 /cos(A+B)/2 * )=lim t→0 t /sin t
Когда A приближается к B, а t приближается к нулю,
f'(x) = 1/cos B = 1/√1-x 2
Дифференцирование по арксинусу с использованием неявного дифференцирования
Поскольку при неявном дифференцировании мы дифференцируем функцию с двумя переменными. Здесь мы докажем дифференцирование sin по обратному x неявным дифференцированием.
Доказательство производной арксинуса неявным дифференцированием
Чтобы доказать производную арксинуса, предположим, что
y = sin -1 x.
Тогда мы можем записать приведенное выше уравнение как;
sin у= х
Поскольку дифференцирование уравнения двух независимых переменных известно как неявное дифференцирование, поэтому из приведенного выше уравнения
(cos y) dy/dx = 1
Используя тригонометрические тождества,
sin2y + cos2y = 1
→ cos2y + x 2 = 1
→ cos2y = 1 — x 2
Извлечение квадратного корня с обеих сторон,
→ cos y = √(1 — x 2 )
9000 i), получаем√(1 — x 2 ) dy/dx = 1
Путем перестановки получаем,
dy/dx = 1/√(1 — x 2 ),
Следовательно, мы доказали обратную производную синуса, используя неявное дифференцирование.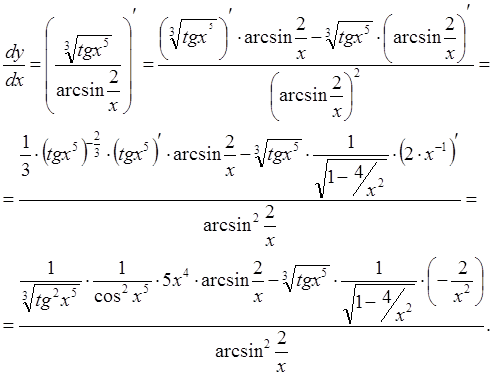 Также рассчитать
Также рассчитать
Как найти производную арксинуса с помощью калькулятора?
Самый простой способ вычислить производную обратного синуса — использовать онлайн-инструмент дифференцирования. Для этого вы можете воспользоваться нашим калькулятором производных. Здесь мы предлагаем вам пошаговый способ расчета производных с помощью этого инструмента.
Запишите функцию как sin -1 x в поле ввода функции. На этом шаге вам нужно ввести входное значение в виде функции, так как вы должны вычислить производную от sin -1 x.
Теперь выберите переменную, по которой вы хотите дифференцировать sin -1 x. Здесь вы должны выбрать «x».
Выберите, сколько раз вы хотите дифференцировать синус, обратный x. На этом шаге вы можете выбрать 2 для второй производной, 3 для третьей производной и так далее.
Нажмите кнопку расчета. После этого шага вы получите производную синуса, обратную х, в течение нескольких секунд.


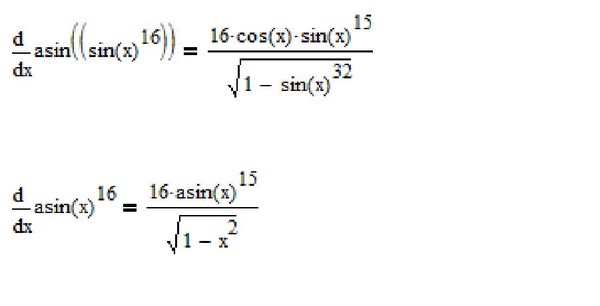 11.16
11.16 