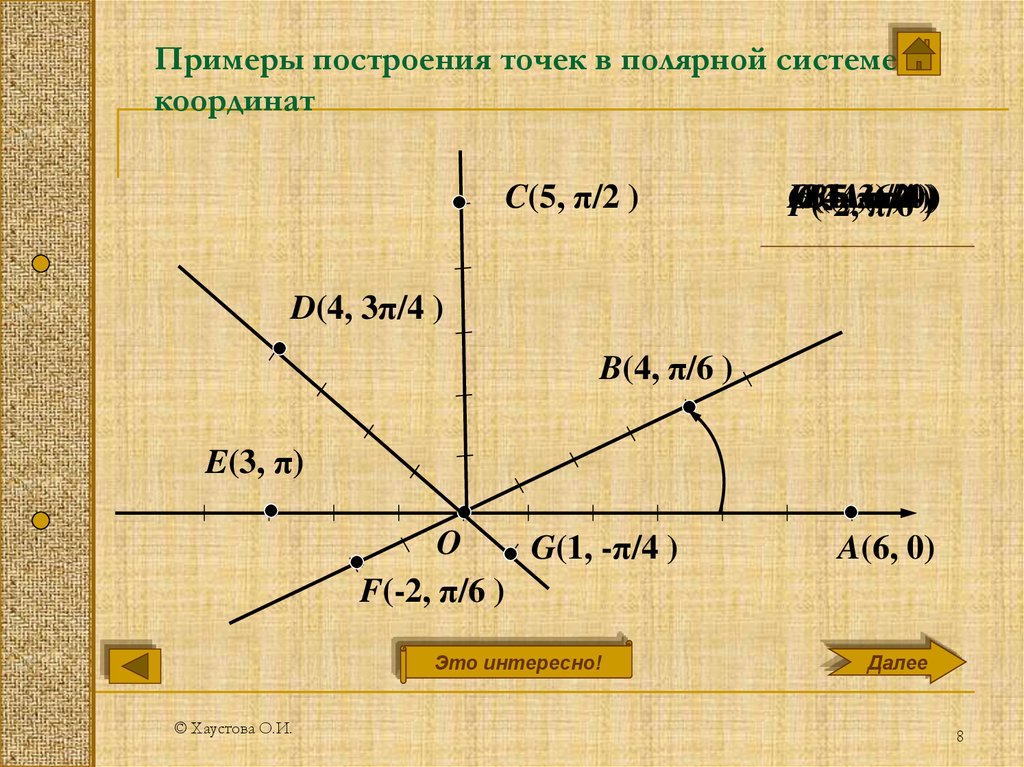
Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. 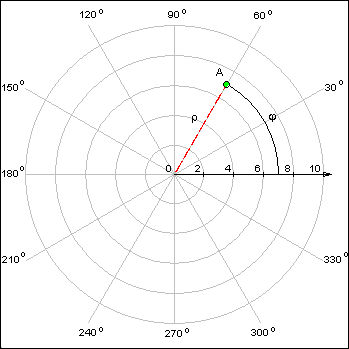 § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры.  § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. 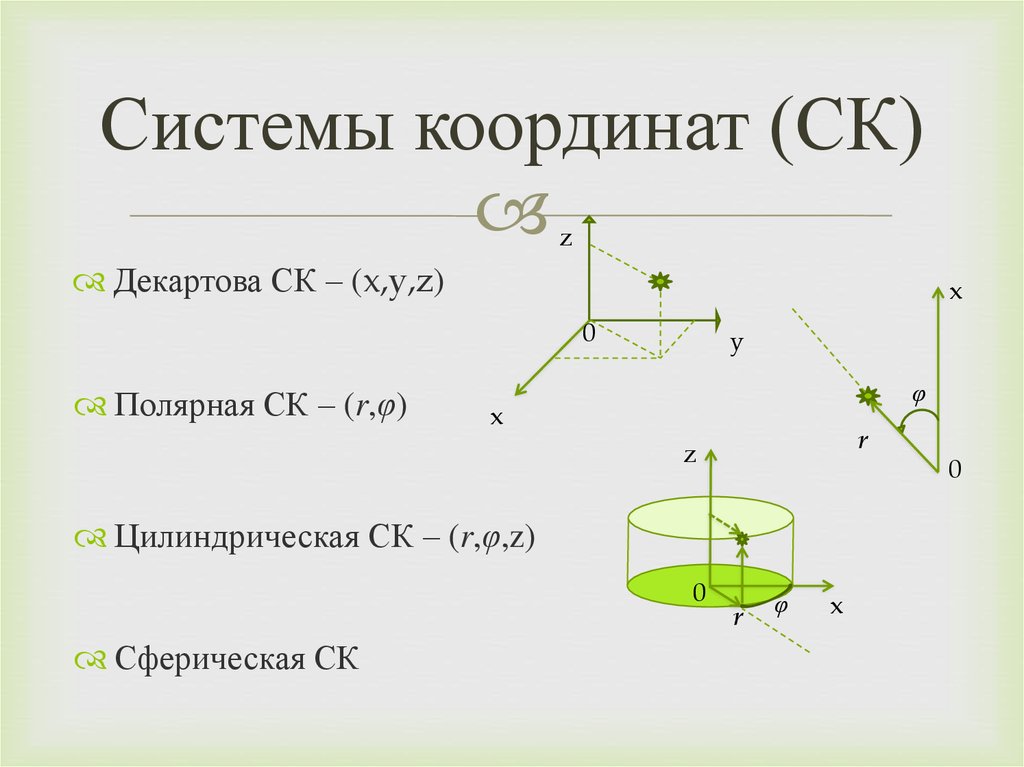 Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III.  ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. 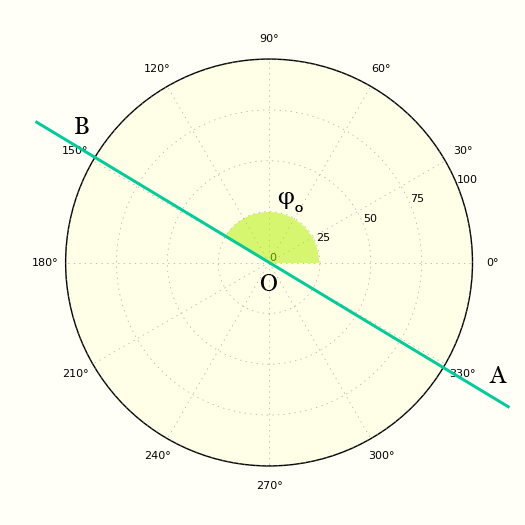 Общие уравнения прямой. Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка.  Конструкции В. Г. Шухова. Конструкции В. Г. Шухова.Упражнения Ответы |
Координатная плоскость 6 класс онлайн-подготовка на Ростелеком Лицей
Основные сведения о координатной плоскости
Как известно, на каждом доме указаны его номер и название улицы – это адрес дома. На билете в любой зрительный зал написаны номер ряда и номер места – это адрес кресла. Для определения положения точки на глобусе надо знать долготу и широту – это адрес географической точки (географические координаты). Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх» (см. Рис. 1). На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают и называют осью ординат.
Рис. 1). На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают и называют осью ординат.
Две перпендикулярные оси и с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал.
Рис. 1. Координатная плоскость
Координаты точки
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке 2 показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки , пересечение другой прямой с осью ординат – это координата точки . Сначала указывают координату , потом . Точка имеет координаты . Аналогично находим координаты точки , она имеет координаты (см. Рис. 2).
Сначала указывают координату , потом . Точка имеет координаты . Аналогично находим координаты точки , она имеет координаты (см. Рис. 2).
Рис. 2. Определение координат точек на координатной плоскости
Можно сделать все и в обратном порядке. То есть изобразить точку на плоскости по известным координатам.
Пример
1. Построить точки по заданным координатам ,
Для построения точки необходимо отложить число 2 на оси и провести перпендикулярную прямую; на оси откладываем число 5 и проводим перпендикулярную оси прямую (см. Рис. 3). На пересечении перпендикуляров получим точку с координатами .
Для построения точки необходимо отложить на оси число 3 и провести перпендикулярную оси прямую; на оси откладываем число (–1) и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами . (см. Рис. 3).
3).
Рис. 3. Построение точек на координатной плоскости по заданным координатам
2. Построить точки по заданным координатам ,
Для построения точки необходимо отложить число 3 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).
Для построения точки необходимо отложить число 2 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).
Рис. 4. Построение точек на координатной плоскости по заданным координатам
Таким образом, если нулю равна координата , то точка лежит на оси , а если нулю равна координата , то точка лежит на оси .
Задача
1. Выписать координаты точек , , , (см. Рис. 5).
2. Изобразить точки , , , , .
Рис.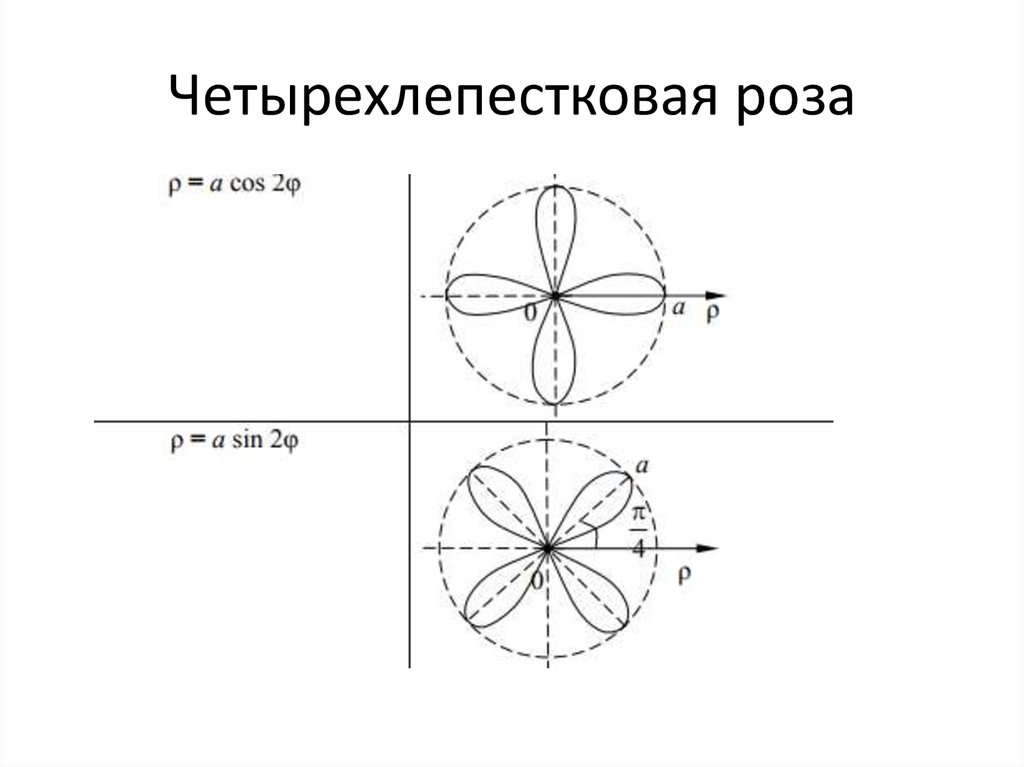 5. Иллюстрация к задаче
5. Иллюстрация к задаче
Решение
1. Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты (см. Рис. 6).
Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты .
Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна (–2). Следовательно, точка имеет координаты .
Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна –5. Следовательно, точка имеет координаты .
Рис. 6. Иллюстрация к задаче
Иллюстрация к задаче
2. Для построения точки откладываем число (–3) на оси и проводим перпендикулярную прямую; на оси откладываем число (–2) и проводим перпендикулярную оси прямую (см. Рис. 7). На пересечении перпендикуляров получим точку с координатами .
Координата точки равна нулю, поэтому эта точка лежит на оси . Отложим на оси число 5 и получим точку с координатами .
Для построения точки откладываем число 3 на оси и проводим перпендикулярную оси прямую; на оси откладываем число 4 и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами .
Координата точки равна нулю, поэтому эта точка лежит на оси . Отложим на оси число (–4) и получим точку с координатами .
Две координаты точки равны нулю, следовательно, эта точка лежит на оси и на оси , то есть является точкой пересечения двух осей (начало координат).
Рис. 7. Иллюстрация к задаче
Координатные четверти
Координатные оси разбивают координатную плоскость на четыре части – четверти. Порядковые номера четвертей принято считать против часовой стрелки (см. Рис. 8).
Рис. 8. Нумерация четвертей координатной плоскости
Если точка имеет положительную координату и положительную координату , то она лежит в первой четверти.
Если точка имеет отрицательную координату и положительную координату , то она лежит во второй четверти.
Если точка имеет отрицательную координату и отрицательную координату , то она лежит в третьей четверти.
Если точка имеет положительную координату и отрицательную координату , то она лежит в четвертой четверти.
Например, у точки координата положительная, а координата отрицательная, следовательно, эта точка находится в четвертой четверти.
Другие системы координат
Чтобы присвоить точке числовой «адрес» (координаты), используются и другие системы координат.
Причины использования различных систем координат:
1. Размерность.
На этом уроке мы рассматривали прямоугольную систему координат на плоскости. Размерность такого пространства равна 2, то есть точка задавалась двумя координатами. Однако пространство может иметь другую размерность, например равную единице, когда точка может менять свое положение только в одном направлении (двигаться вперед-назад или вверх-вниз). В качестве примера можно привести движение автомобиля по ровной дороге или движение лифта. Для указания местоположения точки нужна только одна координата. Эта координата будет означать то расстояние, которое проехал автомобиль (см. Рис. 9), или этаж, на котором находится лифт (см. Рис. 10).
Рис. 9. Координата в данном случае – это расстояние, на которое отъехал автомобиль
9. Координата в данном случае – это расстояние, на которое отъехал автомобиль
Рис. 10. Координата в данном случае – этаж, на котором находится лифт
В математике такая система координат представлена числовой или координатной осью. Чтобы из любой прямой получить координатную ось, необходимо отметить на прямой начало отсчета, масштаб и направление отсчета (см. Рис. 11). По одной координате можно однозначно понять, где находится точка.
Рис. 11. Координатная ось
Размерность пространства может быть равной трем (пространство, в котором мы живем, имеет три измерения). Для указания места положения точки в этом случае нужны три координаты. Например, если в высотном здании на каждом этаже находится кинотеатр, то для указания места в билете должны быть указаны три координаты – этаж, ряд, номер кресла. В математике такая система координат строится точно так же, как на плоскости, только добавляется третья ось (см.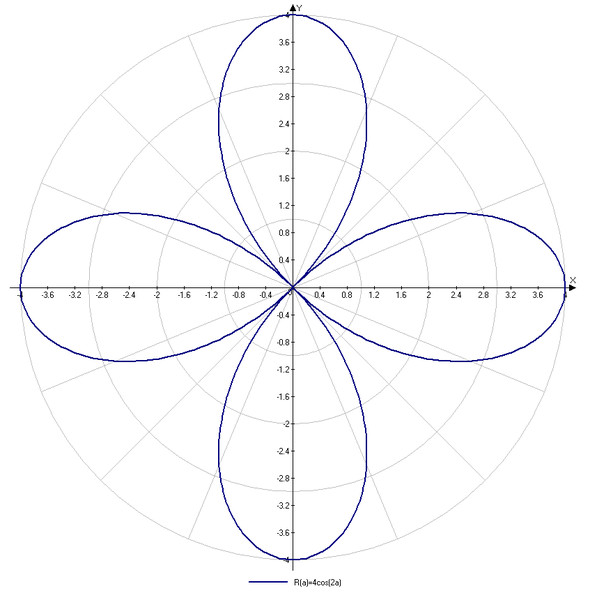 Рис. 12).
Рис. 12).
Рис. 12 Декартова система координат в пространстве
2. Другой метод задания координат точки (использование полярной системы координат на плоскости).
Проводится ось , а для точки указывается расстояние от нуля до нее и угол, который образует отрезок с осью . Эти два числа и будут являться координатами точки (см. Рис. 13).
Рис. 13. Полярная система координат на плоскости
В трехмерном пространстве строятся аналогичные системы, например сферическая или цилиндрическая система координат.
Таким образом, прямоугольная система координат широко применяется в математике, но не является единственной.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В. В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт mathematics-repetition.com (Источник)
2. Интернет-сайт youtube.com (Источник)
3. Интернет-сайт exponenta.ru (Источник)
Домашнее задание
1. Вопросы в конце раздела 45 (§9), задание 1393, 1394, 1396, 1398 (стр. 245-246) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 (Источник)
Вопросы в конце раздела 45 (§9), задание 1393, 1394, 1396, 1398 (стр. 245-246) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 (Источник)
2. Выберите точки расположенные выше оси абсцисс: , , , , .
3. В координатной плоскости построить следующие точки, соединяющие их последовательно с предыдущей точкой отрезком (получите определенный рисунок): , , , , , , , , , , , , , , , , , , , , , , , , , , , .
Что такое полярный график? Построение полярного графика с примером
Определение : График, представляющий передаточную функцию системы G(jω) на комплексной плоскости, построенный в полярных координатах, известен как полярный график.
Представление графика в полярных координатах показывает график амплитуды в зависимости от фазового угла в полярных координатах при изменении ω от 0 до ∞. Он используется для анализа стабильности.
Построение полярного графика
Нам известно, что построение частотной характеристики означает набросок изменений амплитуды и фазового угла относительно входной частоты.
На графике Боде частотная характеристика изображена в логарифмическом масштабе.
Итак, на полярной диаграмме формируется скетч между величиной и фазовым углом передаточной функции G(jω) для различных значений ω.
Предположим, что M представляет величину, а φ обозначает фазовый угол, тогда для передаточной функции системы он задается как:
Таким образом, при изменении ω от 0 до ∞ можно определить значения M и φ .
Как мы уже обсуждали в начале, полярный график представляет собой график амплитуды в зависимости от фазового угла, построенный для различных значений ω.
Итак, для построения полярного графика различные значения амплитуды и фазового угла заносятся в таблицу и далее формируется эскиз. Таблица приведена ниже:
| Частота | Величина | Фазовый угол |
| 0 | М 0 | φ 0 |
| ω 1 | M 1 | φ 1 |
| ω 2 | M 2 | φ 2 |
| | | | | | |
| | | | | | |
| ∞ | М ∞ | φ ∞ |
В принципе, здесь каждая точка на полярной диаграмме значимо построена для каждого конкретного значения амплитуды и фазового угла для конкретной частоты ω.
Как и в таблице выше, для ω = ω 1 , M = M 1 и φ = φ 1 определяется точка в полярной системе координат, представляющая M 1 ∠φ 1 , следовательно, точка на графике соответствует вершине вектор магнитуды M 1 , построенный под углом φ 1 .
Итак, используя табличные данные, можно построить полярный график. Таким образом, таким образом можно построить график зависимости амплитуды от фазового угла для различных значений частоты.
Здесь следует отметить, что преобразование величины в децибелы или логарифмические значения не требуется. Кроме того, направление против часовой стрелки представляет положительные фазовые углы, тогда как направление по часовой стрелке показывает отрицательные фазовые углы.
На рисунке ниже представлена полярная диаграмма для ω в диапазоне от 0 до ∞ :
Таким образом, из приведенного выше обсуждения мы можем заключить, что полярная диаграмма начинается с точки, определяющей величину и угол для ω = 0, и заканчивается в точке точка, определяющая величину и угол для ω = ∞.
- Другой метод используется для грубого наброска полярного графика, в котором не вычисляются величина и углы для различных значений ω.
Предположим, в полярной системе координат у нас есть две точки n 1 ∠φ 1 и n 2 ∠φ 2 как указано ниже:
Здесь из приведенного выше рисунка видно, что перемещение точки X из Y вызывает угловой поворот, φ 2 – φ 1 . А если разница отрицательна, то вращение будет по часовой стрелке. В то время как, если разница положительна, вращение будет в направлении против часовой стрелки.
Аналогичным образом можно рассмотреть изменение ω от 0 до ∞ в двух точках. Один при ω = 0 с магнитудой M 0 и угол φ 0 , а другой при ω = ∞ с величиной M ∞ и углом φ ∞ . Затем произойдет поворот от φ ∞ к φ 0 .
Более просто,
ω = 0 дает M 0 ▲ 0 является отправной точкой,
ω = ∞ дает M ∞ ∞ ∞ 9000 9000 9000 9000 9000 9000 эй конечной точки и
φ ∞ – φ 0 соответствует вращению
Следовательно, таким образом можно построить полярный график.
До сих пор мы обсуждали, что в основном представляет собой полярный график и как он строится. Давайте теперь рассмотрим пример, чтобы лучше понять построение полярного графика.
Предположим, у нас есть система Типа 0, передаточная функция которой задана как:
Мы должны нарисовать для нее полярный график.
Первым шагом является преобразование заданной передаточной функции в частотную область. Таким образом, это будет записано как:
Теперь, дальнейшее вычисление магнитуды,
Кроме того, условие фазового угла,
Теперь мы должны вычислить магнитуду и угол, подставляя различные значения ω между 0 и ∞.
Таким образом, табличное представление будет:
| Частота | Магнитуда | Фазовый угол |
| 0 | 1 | 0° |
| 1 | -45° | |
| 10 | -84,2° | |
| | | | | | |
| | | | | | |
| ∞ | 0 | -90° |
Следовательно, табличные данные показывают, что начальная точка 1 ∠0°, а конечная точка 0 ∠-90°. Таким образом, график завершится в начале координат по касательной к оси под углом -90°.
Таким образом, график завершится в начале координат по касательной к оси под углом -90°.
Таким образом, график представляется как:
Теперь применим альтернативный метод для построения полярного графика.
Как мы уже говорили ранее, в этом методе основное значение имеют только начальная и конечная точки. Таким образом, частота необходима для 0 и ∞.
Из приведенного выше табличного представления видно, что
Для ω = 0 величина и угол = 1 ∠0°
Для ω = ∞ величина и угол = -9 0 °
Следовательно,
φ ∞ – φ 0 = -90° – 0° = – 90°
Поскольку разница между ними отрицательна, то вращение от начальной до конечной точки будет происходить по часовой стрелке.
Таким образом, начальная точка 1 ∠0° поворачивается на 90° по часовой стрелке, чтобы закончиться на 0 ∠-90°. Таким образом, грубый набросок полярного графика приведен ниже:
Здесь следует отметить, что в основном этот приблизительный метод используется для построения полярного графика.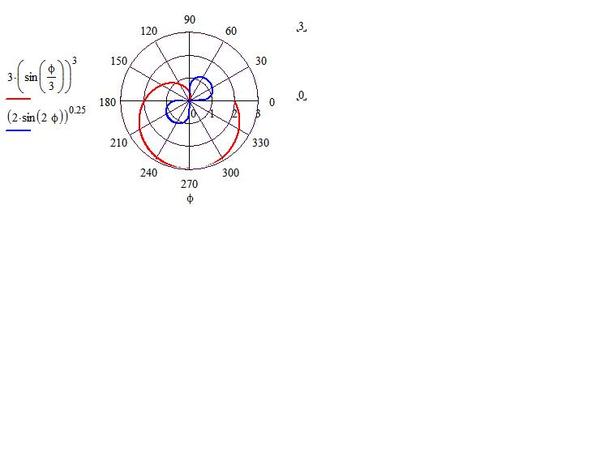
Полярная система координат | безграничная алгебра |
Введение в полярную систему координат
Полярная система координат — это альтернативная система координат, в которой две переменные:
rrr
и
θ\thetaθ
вместо
xxx
и
90 902 0 y05.Цели обучения
Обсудите характеристики полярной системы координат
Ключевые выводы
Ключевые точки
- Полярная система координат представляет собой двумерную систему координат, в которой каждая точка на плоскости определяется расстоянием от исходной точки и углом от нее. опорное направление.
Ключевые термины
- радиус : Расстояние, измеренное от полюса.
- угловая координата : Угол, измеряемый от полярной оси, обычно против часовой стрелки.

- полюс : Опорная точка полярного графика.
- полярная ось : Луч от полюса в опорном направлении.
Введение полярных координат
В математике полярная система координат представляет собой двумерную систему координат, в которой каждая точка на плоскости определяется расстоянием от исходной точки и углом от исходного направления.
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах
(x,y)(x,y)(x,y)
в декартовой координатной плоскости. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. Полярные координаты — это точки, обозначенные
(r, θ) (r, θ) (r, θ)
и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.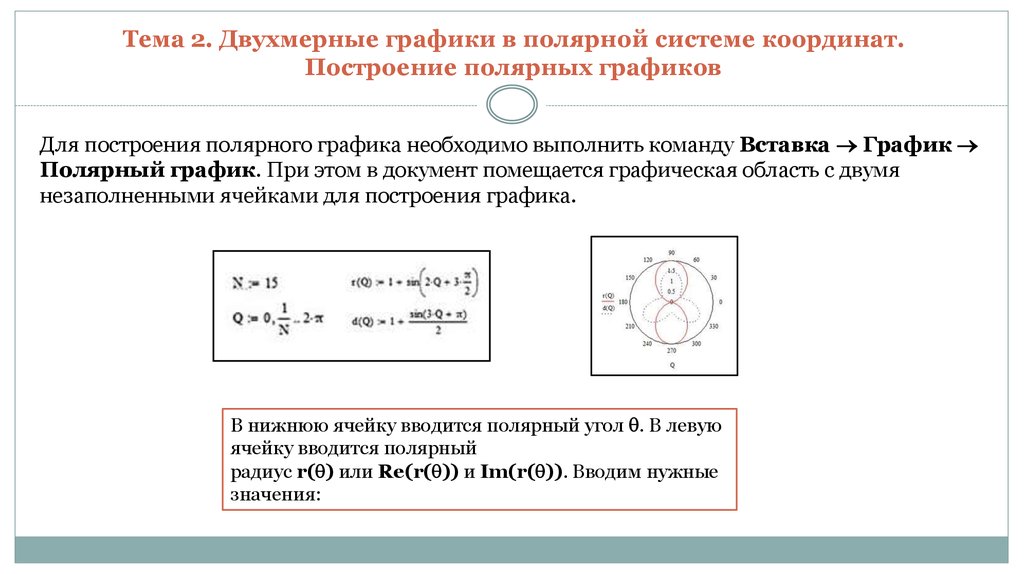
Исходная точка (аналог начала декартовой системы) называется полюсом, а луч от полюса в исходном направлении — полярной осью. Расстояние от полюса называется радиальной координатой или радиусом, а угол называется угловой координатой, полярным углом или азимутом. Радиальную координату часто обозначают
rrr
или
ρρρ
, а угловую координату
ϕϕϕ
,
θθθ 9{\ circ} 360∘
). Градусы традиционно используются в навигации, геодезии и многих прикладных дисциплинах, тогда как радианы чаще используются в математике и математической физике. Во многих контекстах положительная угловая координата означает, что угол
ϕϕϕ
измеряется против часовой стрелки от оси. В математической литературе полярная ось часто изображается горизонтальной и направленной вправо.
Нанесение точек с использованием полярных координат
Полярная сетка масштабируется как единичный круг с положительным
xxx
— ось теперь рассматривается как полярная ось, а начало координат — как полюс.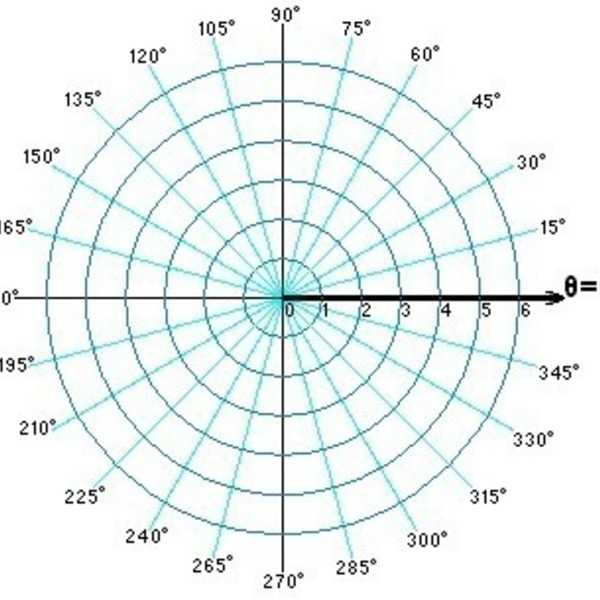 Первая координата
Первая координата
rrr
радиус или длина направленного отрезка прямой от полюса. Угол
θθθ
, измеренный в радианах, указывает направление
rrr
. Сдвинемся против часовой стрелки от полярной оси на угол
θθθ
и отмерим направленный отрезок длиной
ррр
в направлении
θθθ
. Несмотря на то, что мы измеряем
θθθ
сначала, а затем
rrr
, полярная точка сначала записывается с координатой
rrr
-координата. Например, чтобы нанести точку
(2,π4)(2,\frac{\pi }{4})(2,4π)
, мы должны переместить
π4\frac{\pi }{4 }4π
единиц в направлении против часовой стрелки, а затем длина
222
9{\circ} 360∘или
2π2\pi2π
радиан) на угловую координату не меняет соответствующего направления.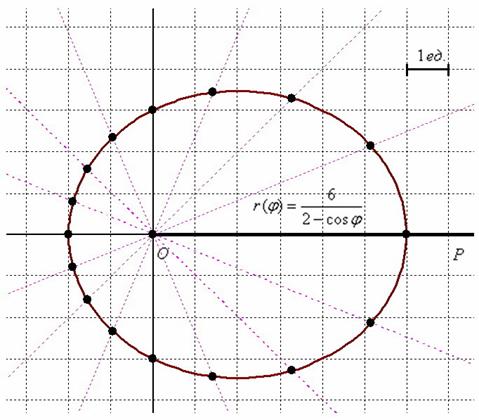 Кроме того, отрицательную радиальную координату лучше всего интерпретировать как соответствующее положительное расстояние, измеренное в противоположном направлении. Следовательно, одна и та же точка может быть выражена бесконечным числом различных полярных координат (
Кроме того, отрицательную радиальную координату лучше всего интерпретировать как соответствующее положительное расстояние, измеренное в противоположном направлении. Следовательно, одна и та же точка может быть выражена бесконечным числом различных полярных координат (
r,ϕ±n⋅360°r, \phi \pm n\cdot 360°r,ϕ±n⋅360°
) или (
−r,ϕ±(2n+1)⋅180°-r, \phi \pm (2n + 1)\cdot 180°−r,ϕ±(2n+1)⋅180°
), где
nnn
— любое целое число. Более того, сам полюс может быть выражен как (
0,ϕ0, ϕ0,ϕ
) для любого угла
ϕϕϕ
.
Преобразование полярных и декартовых координат
Полярные и декартовы координаты можно преобразовать друг в друга с помощью теоремы Пифагора и тригонометрии.
Цели обучения
Получите и используйте формулы для преобразования полярных и декартовых координат 92\\\tan\theta=\frac{y}{x}cosθ=rx→x=rcosθsinθ=ry→y=rsinθr2=x2+y2tanθ=xy
Преобразование полярных координат в прямоугольные (декартовы) координаты
Когда задан набор полярных координат, нам может потребоваться преобразовать их в прямоугольные координаты.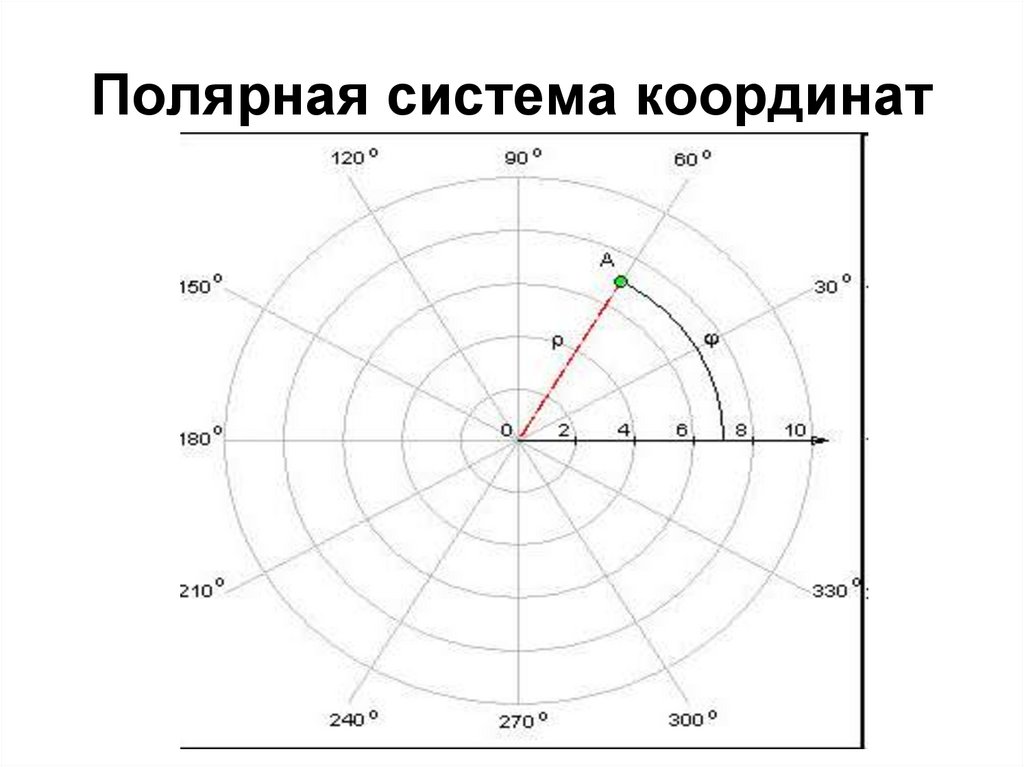 Для этого мы можем вспомнить отношения, которые существуют среди переменных
Для этого мы можем вспомнить отношения, которые существуют среди переменных
XXX
,
YYY
,
RRR
и
θθ
, из определений
θθ
, из определений
θθ
, из определений
0005
cosθ\cos \thetacosθ
и
sinθ\sin \thetasinθ
. Решение для переменных
xxx
и
yyy
дает следующие формулы:
cosθ=xr⇒x=rcosθ\displaystyle \cos \theta =\frac{x}{r}\quad\Rightarrow\quad x=r\cos \theta cosθ=rx⇒x=rcosθ
sinθ=yr⇒y=rsinθ\displaystyle \sin \theta =\frac{y}{r}\quad\Rightarrow\quad y=r\sin \theta sinθ=ry⇒y=rsinθ
Простой способ запомнить приведенные выше уравнения – подумать о
cosθ\cos\thetacosθ
как прилежащая сторона к гипотенузе и
sinθ\sin\thetasinθ
как противолежащая сторона к гипотенузе.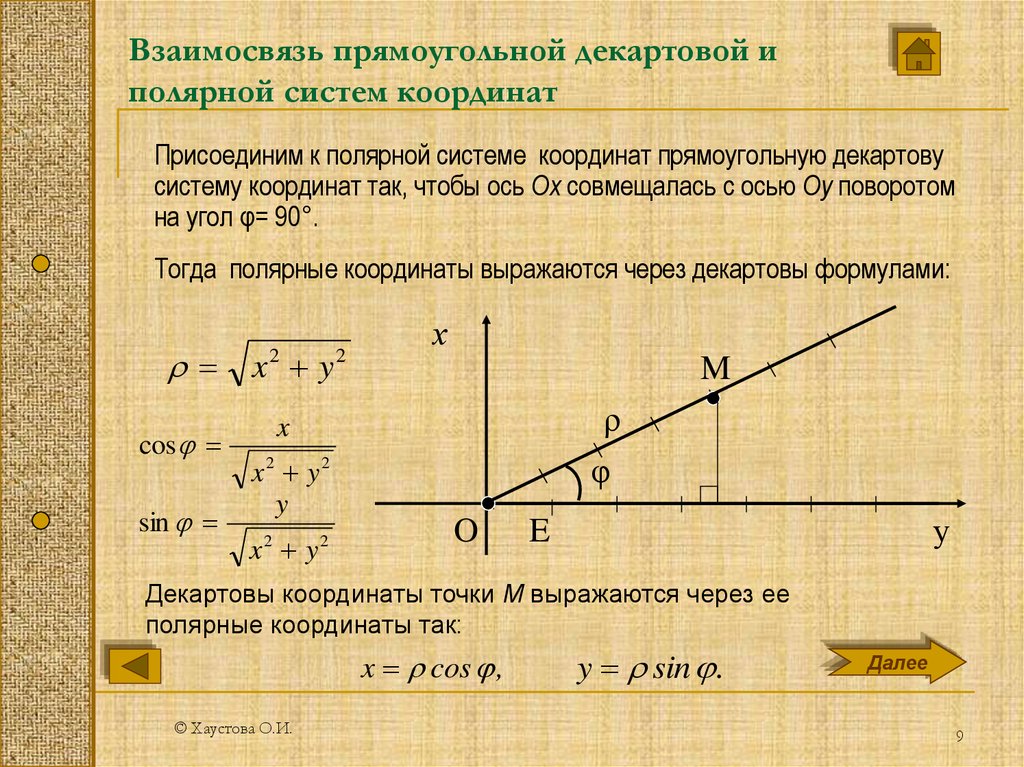 Если опустить перпендикуляр из точки плоскости на ось
Если опустить перпендикуляр из точки плоскости на ось
xxx
— , получится прямоугольный треугольник, как показано на рисунке ниже.
Тригонометрия Прямоугольный треугольник: Прямоугольный треугольник с прямоугольными (декартовыми) координатами и эквивалентными полярными координатами.
Чтобы преобразовать полярные координаты
(r,θ)(r,θ)(r,θ)
в прямоугольные координаты
(x,y)(x,y)(x,y)
, выполните следующие действия:
1) Напишите
cosθ=xr⇒x=rcosθ\cos \theta =\frac{x}{r}\Rightarrow x=r\cos \theta cosθ=rx⇒x=rcosθ
и
sinθ=yr⇒y=rsinθ\sin \theta =\frac{y}{r}\Rightarrow y=r\sin \theta sinθ=ry⇒y=rsinθ
.
2) Оценить
cosθ\cos\thetacosθ
и
sinθ\sin\thetasinθ
.
3) Умножьте
cosθ\cos\thetacosθ
на
rrr
, чтобы найти
xxx
-координату.
4) Умножить
sinθ\sin\thetasinθ
на
rrr
, чтобы найти
yy -координату прямоугольной формы 5.
Пример: Запишите полярные координаты
(3,π2)(3,\frac {\pi}{2})(3,2π)
в виде прямоугольных координат.х=rcosθ=3cosπ2=0\displaystyle \начать{выравнивать} х &= г \ соз \ тета \\ &= 3cos \ гидроразрыва {\ pi} {2} \\ &= 0 \end{align}x=rcosθ=3cos2π=0
y=rsinθ=3sinπ2=3\displaystyle \начать{выравнивать} y&=r\sin\theta\\&=3\sin\frac{\pi}{2}\\&=3 \end{align}y=rsinθ=3sin2π=3
Прямоугольные координаты:
(0,3)(0,3)(0,3)
.
Полярная и координатная сетка эквивалентных точек: Прямоугольная координата
(0,3)(0,3)(0,3)
то же, что и полярная координата
(3,π2)(3,\frac {\pi}{2})(3,2π )
, как показано на двух сетках выше.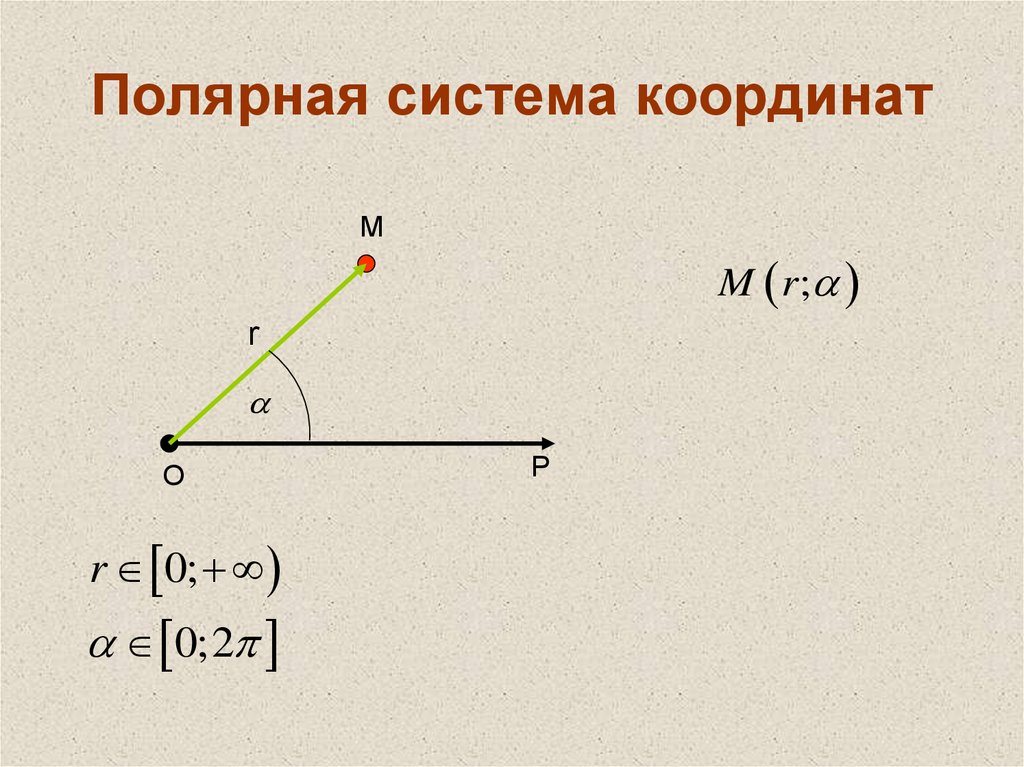
Прямоугольные (декартовы) координаты в полярные координаты
Чтобы преобразовать прямоугольные координаты в полярные координаты, мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки.
Преобразование прямоугольных координат в полярные требует использования одного или нескольких соотношений, показанных ниже. Напомним: 92\\\тангенс\тета&=\фракция {у} {х} \end{align}cosθsinθr2tanθ=rx⇒x=rcosθ=ry⇒y=rsinθ=x2+y2=xy
Тригонометрия Прямоугольный треугольник: Прямоугольный треугольник с прямоугольными (декартовыми) координатами и эквивалентной полярной координаты.
Пример:
Преобразование прямоугольных координат
(3,3)(3,3)(3,3)
в полярные координаты. Нам даны значения
xxx
и
yyy
и нужно решить для
9{-1}\left( 1 \right)tan−1(1) есть много ответов.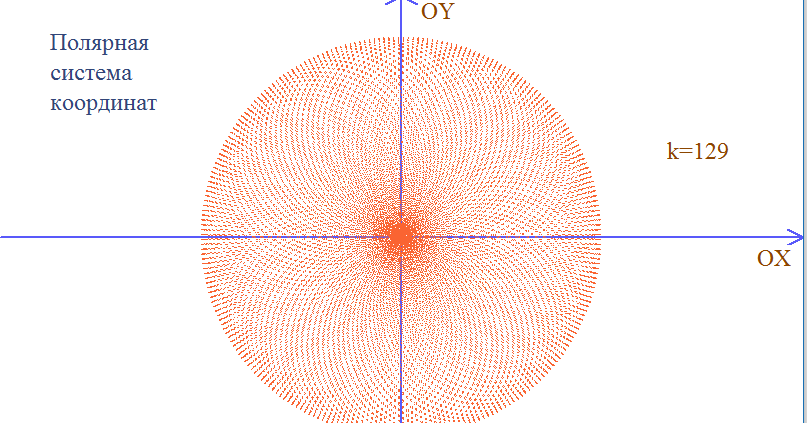 Это соответствует неоднозначности полярных координат. Несколько наборов полярных координат могут иметь то же местоположение, что и наше первое решение. Например, точки
Это соответствует неоднозначности полярных координат. Несколько наборов полярных координат могут иметь то же местоположение, что и наше первое решение. Например, точки
(−32,5π4)(-3\sqrt2,\frac{5\pi}{4})(−32
,45π)
и
(32,−7π2 )(3\sqrt2,-\frac{7\pi}{2})(32
,−27π)
совпадет с исходным решением
(32,π4)(3\sqrt2,\ frac{\pi}{4})(32
,4π)
.
Коники в полярных координатах
Полярные координаты позволяют элегантно выразить конические сечения.
Цели обучения
Опишите уравнения для различных конических сечений в полярных координатах
Ключевые выводы
Ключевые точки
- Конические сечения имеют несколько ключевых особенностей, которые определяют их полярное уравнение; фокусы, эксцентриситет и директриса.

- Все конические сечения имеют одно и то же основное уравнение в полярных координатах, что демонстрирует связь между ними всеми. 92x=2+y2
. Любая коника может быть определена тремя характеристиками: одним фокусом, фиксированной линией, называемой направляющей, и отношением расстояний каждой из них до точки на графике.
Мы можем определить любую конику в полярной системе координат через фиксированную точку, фокус
P(r,θ)P(r,θ)P(r,θ)
на полюсе и прямую , директриса, перпендикулярная полярной оси.
Для конуса с эксцентриситетом
eee
,
- Если
0≤e<10≤e<10≤e<1
, то коника является эллипсом. - Если
e=1e=1e=1
, то коника является параболой. - Если
e>1e>1e>1
, то коника является гиперболой .
Используя это определение, теперь мы можем определить конику в терминах направляющей:
.
 Таким образом, каждая коника может быть записана как полярное уравнение в терминах
Таким образом, каждая коника может быть записана как полярное уравнение в терминах ррр
и
θ\тетаθ
.
Для коники с фокусом в начале координат, если направляющая
x=±px=±px=±p
, где
ppp
— положительное действительное число, а эксцентриситет — положительное действительное число число
eee
, коника имеет полярное уравнение:
r=e⋅p1 ± e⋅cosθ\displaystyle r=\frac{e\cdot p}{1\: \pm\: e\cdot\cos\theta}r=1±e⋅cosθe⋅p
Для коники с фокусом в начале координат, если директриса
y=±py=±py=±p
, где
ppp
положительное действительное число, а эксцентриситет является положительным действительным числом
eee
, коника имеет 0 уравнение 0 поляры r = e⋅p1 ± e⋅sinθ\displaystyle r=\frac{e\cdot p}{1\: \pm\: e\cdot\sin\theta}r=1±e⋅sinθe⋅p
Другие кривые в полярных координатах
Некоторые кривые имеют простое выражение в полярных координатах, тогда как их было бы очень сложно представить в декартовых координатах.

Цели обучения
Описать уравнения для спиралей и роз в полярных координатах
Основные выводы
Ключевые моменты
- Формулы, по которым строится график кривой розы , задаются следующим образом:
r=a cosnθr=a\:\cos n\ thetar=acosnθ
andr=a sinnθr=a\:\sin n\thetar=asinnθ
гдеa≠0a \ne 0a=0
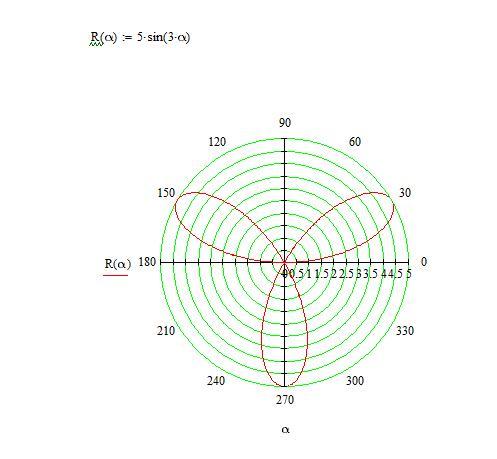
. Еслиnnn
четно, то кривая имеет2n2n2n
лепестков. Еслиnnn
нечетно, кривая имеетnnn
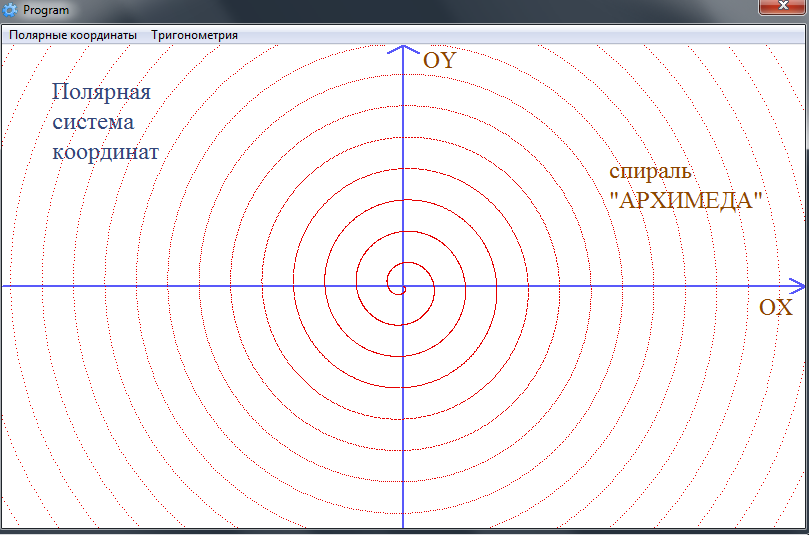
лепестков. - Формула, по которой построен график спирали Архимеда , имеет следующий вид: По мере того, как
θ\thetaθ
увеличивается,rrr
увеличивается с постоянной скоростью по постоянно расширяющейся, бесконечной, спиральной траектории.
Ключевые термины
- Спираль Архимеда : кривая, заданная уравнением вида
r=a+bθr=a + b\thetar=a+bθ
- кривая розы : Кривая, заданная уравнением вида
r=acosnθr = a\cos n\thetar=acosnθ
илиr=asinnθr=a\sin n\thetar=asinnθ
Для построения графика в прямоугольной системе координат построим таблицу значений
xxx
и
yyy
.
 Для построения графика в полярной системе координат построим таблицу значений
Для построения графика в полярной системе координат построим таблицу значений rrr
и
θ\thetaθ
. Мы вводим значения
θ\thetaθ
в полярное уравнение и вычислить
ррр
. Однако использование свойств симметрии и нахождение ключевых значений
θ\thetaθ
и
rrr
означает, что потребуется меньше вычислений.
Исследование кривых розы
Полярные уравнения можно использовать для создания уникальных графиков. Следующий тип полярного уравнения дает форму лепестка, называемую кривой розы. Хотя графики выглядят сложными, простое полярное уравнение создает закономерность. Формулы, которые генерируют график кривой розы, задаются следующим образом:
r=a⋅cos(nθ) и dr=a⋅sin(nθ), где a≠0\displaystyle r=a\cdot\cos\left(n\theta\right) \qquad\text{and} \qquad r=a\cdot\sin \left( n\theta \right) \qquad \text{где} \qquad a\ne 0r=a⋅cos(nθ)andr=a⋅sin(nθ), где a=0
Если
nnn
четно, то кривая имеет
2n2n2n
6 3 лепестков.
 Если
Еслиnnn
нечетно, то кривая имеет
nnn
лепестков.
Кривые розы: Сложные графики, созданные с помощью простых полярных формул, которые генерируют кривые розы: 9, 0a=0
.
Исследование спирали Архимеда
Спираль Архимеда названа в честь ее первооткрывателя, греческого математика Архимеда (
c.287BCE-c.212BCEc. 287 BCE — c.212 BCEc.287BCE-c.212BCE
), которому приписывают многочисленные открытия в области по геометрии и механике.
Формула, которая генерирует график спирали Архимеда , задается следующим образом:
r=a+bθforθ≥0\displaystyle r=a + b\theta \qquad \text{for} \qquad \theta\geq 0r=a +bθforθ≥0
As
θ\thetaθ
увеличивается,
rrr
увеличивается с постоянной скоростью по постоянно расширяющейся, бесконечной, спиральной траектории.

Спираль Архимеда: Формула для построения графика спирали:
r=θr=θr=θ
для
θ≥0θ≥0θ≥0
.
Лицензии и атрибуты
Контент под лицензией CC, совместно используемый ранее
- Курирование и пересмотр. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Полярные координаты. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- Система полярных координат. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- 250px-Polar_graph_paper.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Examples_of_Polar_Coordinates.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Полярная система координат. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Полярные координаты. Предоставлено : ОпенСтакс. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- 250px-Polar_graph_paper.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Examples_of_Polar_Coordinates.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_08_03_010new.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_08_03_007.
 jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_008.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Полярные координаты: Графики. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-4-polar-coordinates-graphs. Лицензия : CC BY-SA: Attribution-ShareAlike
- Конические сечения в полярных координатах. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-5-conic-sections-in-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- Система полярных координат.
 Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- 250px-Polar_graph_paper.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Examples_of_Polar_Coordinates.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_08_03_010new.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.
 org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_007.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_08_03_008.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_10_05_001.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-5-conic-sections-in-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- Полярная система координат. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Полярные координаты: Графики.
 Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-4-polar-coordinates-graphs. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-4-polar-coordinates-graphs. Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_08_03_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
- 250px-Polar_graph_paper.svg.png. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system. Лицензия : CC BY-SA: Attribution-ShareAlike
- Examples_of_Polar_Coordinates.svg.png. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_08_03_010new.jpg. Предоставлено : OpenStax.

- Если


 Таким образом, каждая коника может быть записана как полярное уравнение в терминах
Таким образом, каждая коника может быть записана как полярное уравнение в терминах 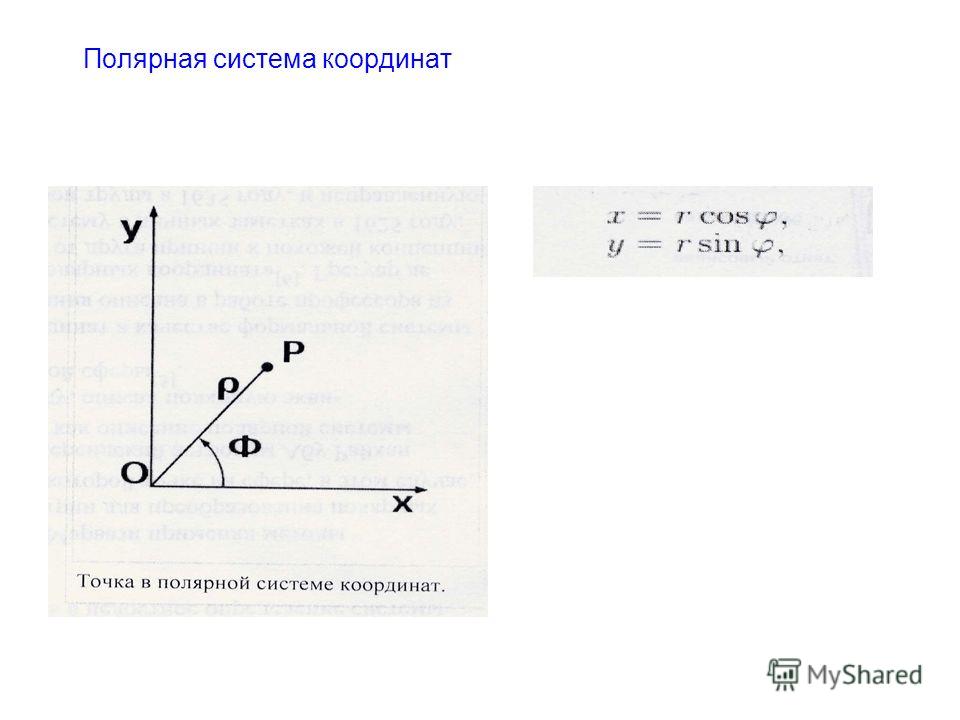
 Для построения графика в полярной системе координат построим таблицу значений
Для построения графика в полярной системе координат построим таблицу значений 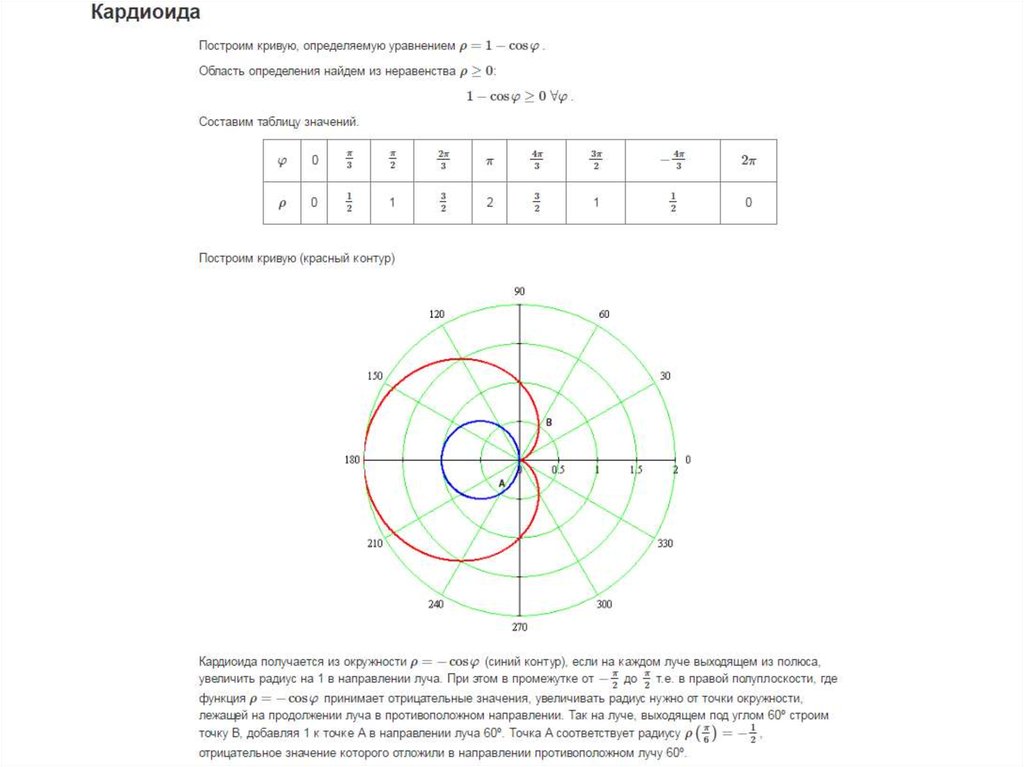 Если
Если
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 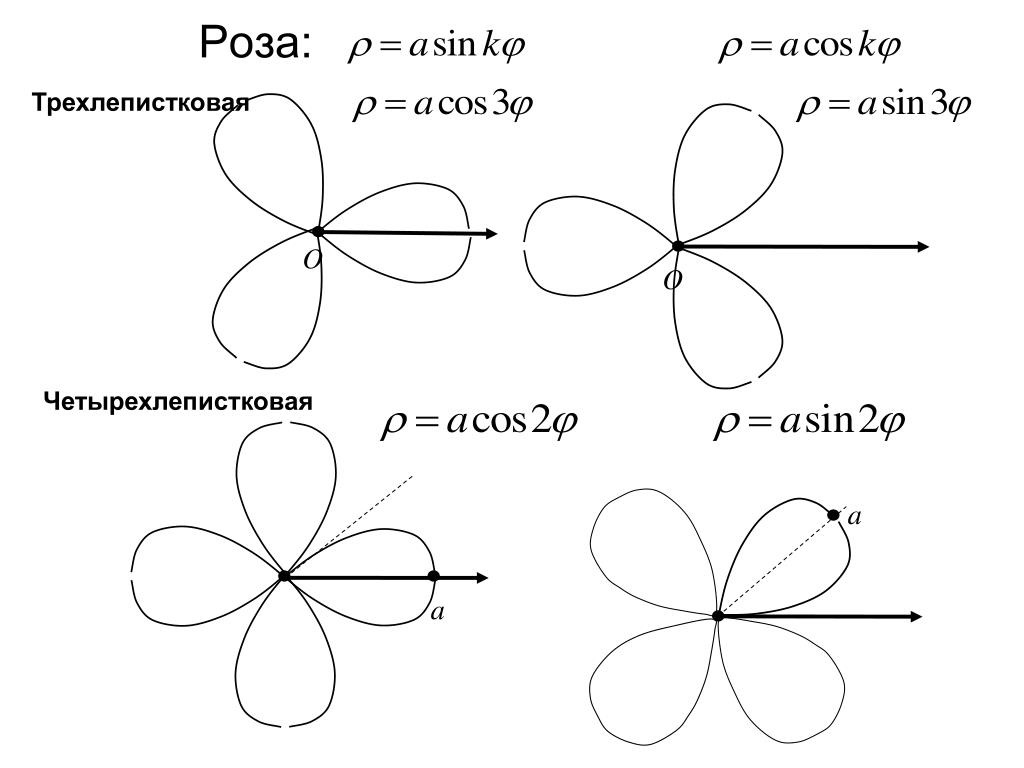 jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]/Polar-Coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike 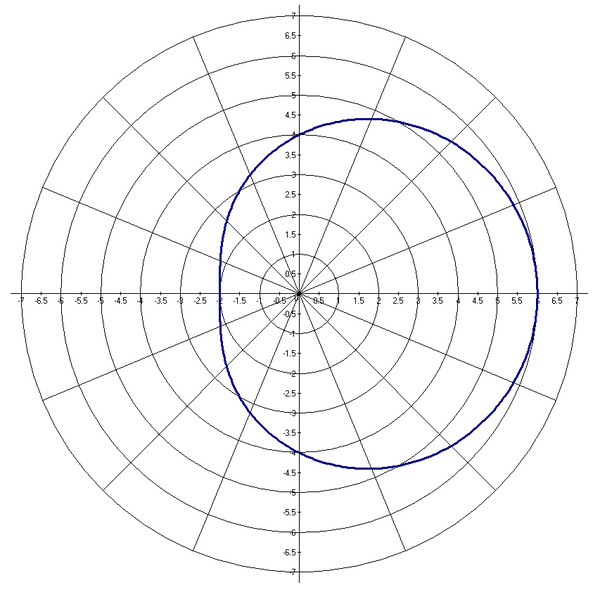 Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike 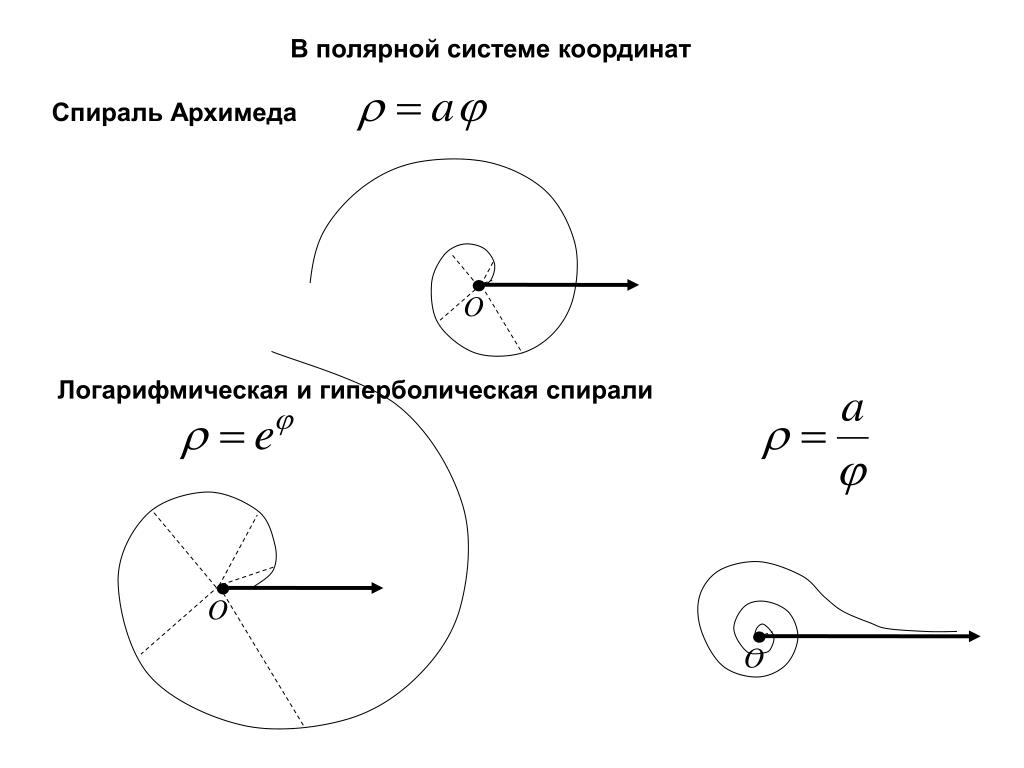 org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike
org/books/алгебра-и-тригонометрия/pages/10-3-polar-coordinates. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-4-polar-coordinates-graphs. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/10-4-polar-coordinates-graphs. Лицензия : CC BY-SA: Attribution-ShareAlike