Исследовательский проект «Как помогают круги Эйлера решать задачи из повседневной жизни» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательский проект «Как помогают круги Эйлера решать задачи из повседневной жизни»
Автор: Мурзакаева Малика Руслановна
Место работы/учебы (аффилиация): МОУ «СОШ №11 г. Зеленокумска», Ставропольский край, 4 класс
Научный руководитель: Кузьменко Ольга Григорьевна, учитель начальных классов
Цель проекта: выявить задачи, которые можно решать с помощью кругов Эйлера и научиться их решать.
Задачи проекта:
- Провести социологический опрос среди одноклассников «Кто такой Эйлер? Что они знают о кругах Эйлера?»
- Изучить материалы разных источников по данному вопросу.
- Поделиться опытом решения задач с другими учениками
- Создать мини-сборник «Задачи из повседневной жизни, которые можно решить с помощью кругов Эйлера.
Это просто?»
Это просто?»Гипотеза: с помощью кругов Эйлера можно легко решать задачи из повседневной жизни, которые обычным путём можно решить только при составлении системы нескольких уравнений с несколькими неизвестными (это сложно).
Проблемный вопрос: Возможно ли решение практических задач из повседневной жизни геометрическим способом с помощью кругов Эйлера?
Учебный предмет, в рамках которого выполнен проект: математика, окружающий мир, кружок «Вектор перемен».
Методы, использованные в работе над проектом:
- Теоретический: изучение исторической и научно-популярной литературы.
- Эмпирический: опросы, анкетирование, анализ, синтез, сравнение и обобщение.
Сроки реализации: 15 ноября — 10 декабря 2022 г.
Исследовательский проект «Дом развития Тамбовщины в искусстве»
Цель: сделать макет здания.
Формулировка задач, которые необходимо решить для достижения цели: Для реализации необходимо первым делом представить или же нарисовать здание, которое мы будем переносить в blender. Далее мы переносим здание в программу b…
Посмотреть работу
Презентация к исследовательской работе «Математика и профессии моей семьи»
Когда я выбирала тему проекта, мне было интересно, где в жизни можно столкнуться с математикой, кроме уроков в школе. Мне хотелось понять необходимость изучения математики для овладения знаниями при выборе профессии, исследовать, какие математические…
Посмотреть работу
Исследовательская работа «Математика в архитектуре»
Математика — это уникальное средство познания красоты, а не только стройная система законов, теорем и задач. Математика играет ведущую роль в архитектуре, её действия необходимы для реализации проектов в строительстве.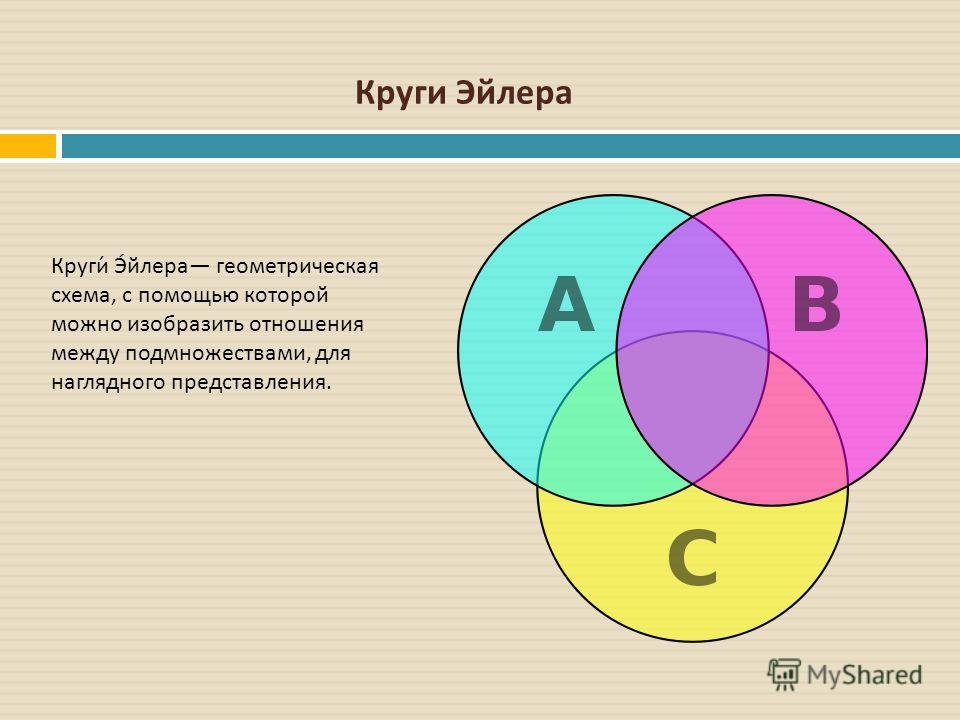
Путешествуя по территориям наше…
Посмотреть работу
Научно-исследовательская работ «Загадочный мир калейлоскопа»
Узорник – это устаревшее слово. Сейчас – это калейдоскоп. Незатейливая трубка с зеркалами и кусочками стекла, которая нравилась детям и в XIX веке, и в XXвеке, и в XXI веке. Калейдоскоп – это прибор, в котором разноцветные кусочки стекла, многократно…
Посмотреть работу
Что такое диаграмма Венна? | Miro
Диаграмма Венна — это простой, но эффективный способ визуальной организации отношений между множествами, независимо от их сложности. Эти логические диаграммы удобно использовать для поиска сходств и отличий, сравнения идей и принятия обоснованных решений.
45M пользователей по всему миру доверяют Miro
Расположив свои мысли на диаграмме Венна, вы сможете обнаружить взаимосвязи и закономерности, которые помогут вам принимать решения или лучше понимать сложные концепции.
Используйте предлагаемый Miroконструктор диаграмм Венна для построения собственной диаграммы и наглядно продемонстрируйте, как перекрываются, сопоставляются и чем отличаются друг от друга концепции.
Что такое диаграмма Венна?
Диаграмма Венна — это графическая диаграмма, построенная с использованием перекрывающихся кругов. Каждый круг представляет собой отдельную концепцию или группу данных, а перекрывающиеся области отображают общие свойства. Это делает диаграммы Венна отличным инструментом для сравнения данных и определения степени вероятности.
На диаграмме Венна хорошо видны отличия и подобия между концепциями в группе, поэтому они так популярны в сфере бизнеса и образования. Они также широко используются в математике, статистике и социальной антропологии.
Диаграмму Венна изобрел примерно в 1800 году Джон Венн (John Venn), британский ученый-логик. Но свидетельства об использовании подобных диаграмм датируются 1200-ми годами, за столетия до их изобретения Джоном Венном (John Venn).
Типы диаграмм Венна
Диаграмму Венна может выглядеть по-разному. Скорее всего, вам чаще всего встречалась диаграмма Венна, состоящая из трех кругов, но существует несколько типов диаграмм Венна, каждый из которых используется для разных целей.
Диаграмма Венна, состоящая из двух кругов
Два круга перекрываются в центре.
Диаграмма Венна из трех кругов
Три круга в виде триады перекрываются в центре.
Диаграмма Венна из четырех кругов
Четыре круга формируют перекрывающуюся область в виде ромба в центре.
Диаграмма Эдвардса-Венна
Четвертый вариант диаграммы Венна предложил в середине 1800-х годов британский биолог Энтони Эдвардс (Anthony Edwards). Он назвал ее диаграммой Эдвардса-Венна.
Вместо 2-4 кругов, диаграмма Эдвардса-Венна состоит из фигур, подобных шву теннисного мяча.
Диаграмма Венна этого типа помогает определить и классифицировать схожие характеристики между гораздо большим количеством групп или концепций. Если традиционные диаграммы Венна из 2, 3 и 4 кругов лучше всего использовать для небольших групп данных, то диаграмма Эдвардса-Венна может использоваться для анализа значительно большего числа различных характеристик рассматриваемого предмета. Однако диаграммы Венна любых типов предназначены для демонстрации сходства и отличия наборов данных.
В каких случаях лучше использовать диаграмму Венна
Прелесть диаграммы Венна заключается в ее простоте и в то же время универсальности. Диаграмма Венна является ценным инструментом во многих сферах: от маркетинга до математики. Вот некоторые ситуации, в которых удобно использовать диаграмму Венна.
1. Для проведения мозгового штурма
Если планируется провести мозговой штурм в команде и быстро добраться до сути проблемы, диаграмма Венна — это то, что нужно. Представив потенциальные идеи в виде кругов, на перекрывающихся областях можно увидеть, что дает наилучшие результаты и что в наибольшей степени способствует реализации стратегии.
2. Возможность увидеть взаимосвязи между двумя элементами
Когда два круга на диаграмме Венна пересекаются, область пересечения представляет собой место связи между двумя различными наборами данных. Такой подход может быть крайне полезен для выявления взаимоотношений между различными элементами и понимания выгоды от их взаимодействия.
3. Сравнение вариантов
Диаграмма Венна для сравнения и сопоставления вариантов — одна из самых популярных диаграмм, которые встречаются в работе. Эта высшей степени наглядная диаграмма позволяет командам проводить сравнения совершенно различных наборов данных, и дает возможность принимать более информированные решения.
4. Наглядная организация и представление информации
Визуальная диаграмма — отличный способ стимулировать интуитивное понимание предмета у группы разных людей. При проведении встречи или конференции использование диаграммы Венна может помочь докладчикам донести до слушателей и организовать свои идеи в простой форме.
5. Решение сложных математических задач
Диаграмма Венна уже тысячи лет используется в математике и науке. В математике диаграммы Венна позволяют визуально сравнивать числа и делать вероятностные заключения, а не просто сравнивать концепции или идеи.
В каких областях используется диаграмма Венна
В профессиональной деятельности на диаграммы Венна полагаются как на источник понимания для измерения и анализа взаимосвязей между элементами. Диаграммы Венна можно встретить в самых разных сферах деятельности:
Преподавание
Диаграмма Венна так популярна во многих сферах из-за того, что ее можно упростить до такой степени, что даже ребенок сможет легко интерпретировать изображенные на ней символы.
Образование — идеальная сфера для использования диаграммы Венна, поскольку она знакомит учащихся с понятиями вероятности и взаимосвязи между несколькими объектами. Она также помогает заложить основу для изучения математики в средней школе.
Принятие решений
Диаграммы Венна — отличный инструмент для принятия решений. Если для принятия решения необходимо учесть несколько перекрывающихся факторов, диаграмма Венна поможет проанализировать различные варианты и выбрать из них лучший. Например, имеется список бизнес-идей и необходимо решить, какую из идей лучше всего реализовать. Диаграмма Венна поможет выбрать лучший вариант, определив, какой из них приносит прибыль, пользуется спросом и действительно интересен.
Математика
В математике диаграмма Венна может иллюстрировать логические связи между числами и определять вероятные исходы. Например, математик может использовать диаграмму Венна, чтобы показать взаимосвязь между различными группами подмножеств или чисел. Поскольку диаграмма Венна помогает измерять, сравнивать и объединять наборы данных, логично, что эту уникальную диаграмму можно использовать для анализа числовых значений.
Статистика
При оценке или прогнозировании результатов того или иного события необходимы инструменты, которые помогут наглядно иллюстрировать все возможные варианты.
Поэтому диаграмма Венна играет важную роль в области статистики и теории вероятности.
Логика
В диаграмме Венна есть нечто очень простое и логичное. Разделение различных концепций или элементов на равные круги облегчает визуализацию и понимание взаимосвязей между различными группами идей.
Информатика
В современной информатике диаграммы Венна часто используются для визуализации отношений между наборами данных. Они помогают понять, как различные классы, множества и объекты соотносятся друг с другом в отдельной взятой вычислительной системе, и могут использоваться для выражения схожих элементов между различными языками кода с целью создания более эффективных систем. Диаграммы Венна можно использовать для демонстрации подобных элементов в различных языках программирования при создании более эффективных систем.
Бизнес
Чаще всего диаграмма Венна встречается в корпоративной сфере. Для выполнения бизнес-операций требуется постоянное сопоставление данных.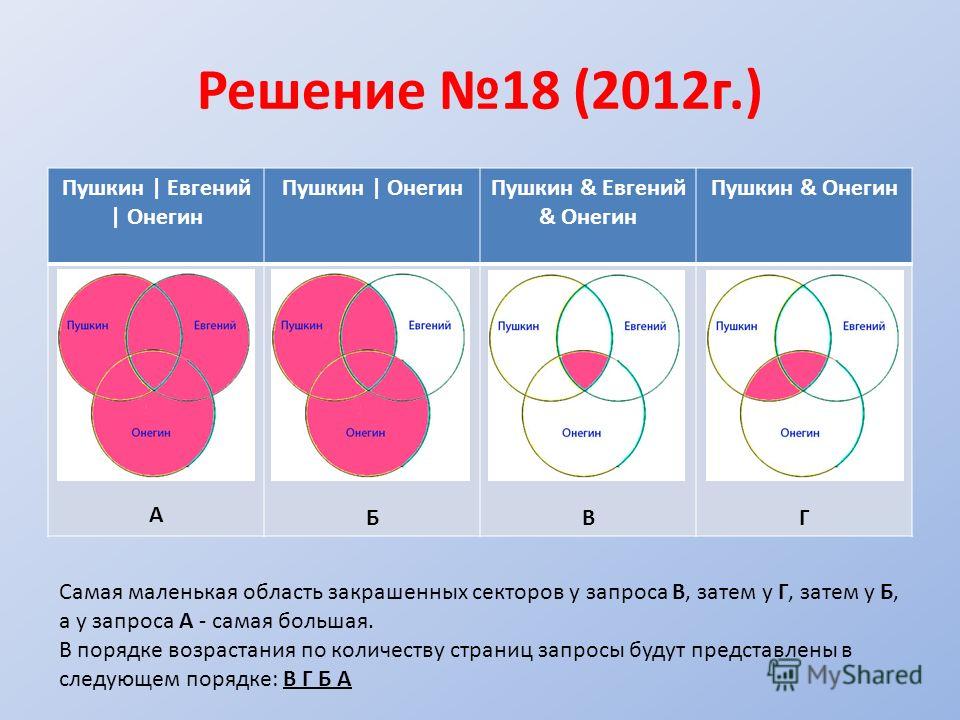
Это помогает специалистам разрабатывать успешные бизнес-стратегии и кампании.
Лингвистика
Лингвистика во всем мире полна взаимосвязанных направлений и иерархий. Диаграмма Венна пригодится тем, кто изучает сложные взаимосвязи между различными языками и диалектами. Эта диаграмма позволяет людям легко визуализировать такие связи.
Понятия и символы диаграммы Венна
Существует множество символов диаграммы Венна, которые стоит изучить, и которые позволят использовать все возможности этого типа диаграмм. Вот наиболее известные:
Множество
Совокупность объектов или элементов.
Объединение
Две фигуры (представляющие отдельные идеи) соединяются между собой.
Пересечение
Центральная точка диаграммы Венна, где пересекаются все фигуры.
Универсальное множество
Множество, содержащее всю необходимую информацию на диаграмме Венна.
Пустое множество
Множество, не содержащее элементов.
Дополнение
Множество, состоящее из элементов, присутствующих в универсальном множестве.
Символ объединения (∪)
Используется для обозначения объединения в математическом контексте (например, на диаграмме Венна A U B).
Символ пересечения (∩)
Используется для обозначения пересечения в математическом контексте.
Символ дополнения
Используется для обозначения дополнения в диаграмме Венна.
Как построить диаграмму Венна
Существует множество различных способов построения диаграммы Венна. Правильно подобранный шаблон может помочь форматировать и структурировать любой сравнительный или сопоставительный анализ. Для построения диаграммы Венна можно использовать интуитивно понятный шаблон диаграммы Венна в Miro:
Шаг 1
Для начала запишите все объекты, элементы и идеи, которые планируется изобразить. Такой набор данных является универсальным множеством.
Шаг 2
Затем решите, какой тип диаграммы Венна будет удобнее всего использовать.
Например, для поиска подобий и отличий между тремя множествами, следует использовать диаграмму Венна из трех кругов.
Шаг 3
Нарисуйте круг для каждого набора данных. В шаблоне уже есть три круга для каждого множества, при необходимости можно добавлять и удалять круги.
Шаг 4
Добавляйте элементы на диаграмму в зависимости от того, имеют ли они сходства или различия с другими множествами. Элементы, не имеющие сходства, необходимо поместить в один из кругов для каждого множества: A, B или C. Если между элементами из A и B есть сходство, этот элемент необходимо поместить в область пересечения этих двух кругов. Он войдет в объединение множеств создаваемой диаграммы Венна. Если характеристика элемента является общей для A, B и C, данный элемент необходимо поместить в центр диаграммы, где пересекаются все круги. Это и будет пересечением диаграммы.
Шаг 5
После добавления всех множества на диаграмму, персонализируйте диаграмму Венна с помощью цветов, меток и заметок.
Поделитесь диаграммой Венна со своей командой и отметьте членов своей команды, чтобы они составили свое мнение и оставили отзыв.
Диаграммы Венна и теория множеств
Ранее мы обсуждали применение диаграмм Венна в различных сферах. Давайте рассмотрим, как диаграммы Венна используются в разделе математики, называемом теорией множеств.
Теория множеств — это раздел математики, изучающий общие и индивидуальные свойства объектов. В этом разделе математики используется диаграмма Венна из 2, 3 и 4 кругов. Процесс, лежащий в основе теории множеств, соответствует структуре диаграммы Венна, поскольку они оба связаны с одновременным сравнением нескольких объектов (или чисел). Например, диаграмма Венна может помочь проиллюстрировать уравнение теории множеств, чтобы определить общие свойства для группы чисел.
«Множество» — это совокупность объектов, каждый из которых представляет собой отдельный элемент целого. Допустим, у нас имеется диаграмма Венна из двух кругов. Один круг красный, а другой синий.
Вычисление вероятности с помощью диаграммы Венна
Еще одно направление, где широко используются диаграммы Венна — это вычисление вероятности. Вычисление вероятности с помощью диаграммы Венна — это продукт математики, используемый для прогнозирования исхода того или иного сценария.
Например, можно использовать диаграмму Венна из двух кругов для расчета вероятности наступления события. Для этого в круги вставляются числа, а не концепции или идеи.
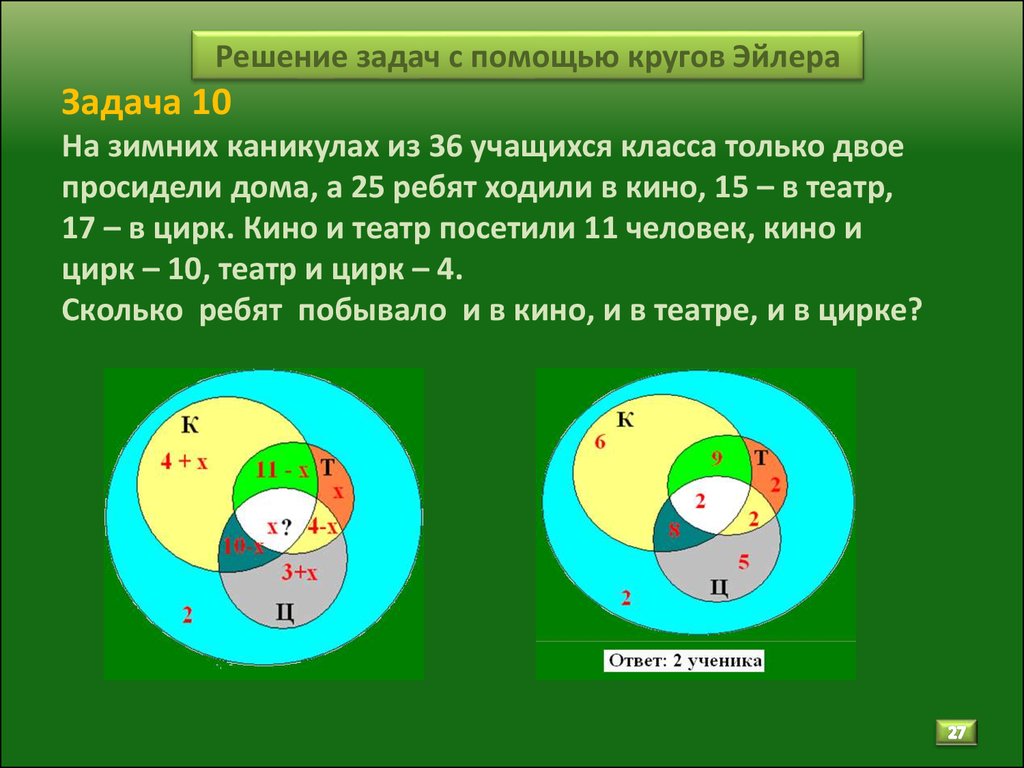
Рассмотрим на примере колоды игральных карт, как диаграммы Венна используются для расчета вероятности различных событий. В колоде 52 карты без джокеров.
В колоде карты четырех мастей, каждая масть содержит 13 карт.
необходимо узнать вероятность того, что выпадет дама или черви. Прямоугольник представляет все исходы, то есть все 52 карты. Поскольку в колоде четыре дамы, вероятность того, что выпадет дама составляет 4/52. Вероятность того, что выпадет черви — 13/52. Но одна из этих карт — это червовая дама. Круги пересекаются, показывая, что дама присутствует в обоих множествах.
Визуализация результатов с помощью диаграммы Венна позволяет не учитывать червовую даму дважды. Основываясь на диаграмме Венна, следует использовать следующий расчет: 4+13-1 = 16. Вероятность того, что выпадет дама или черви, составляет 16/52.
Подобный расчет может помочь определить вероятность самых разных событий или ситуаций, например, успех проекта, количество ожидаемых клиентов или результат маркетинговой кампании. Вероятность в большей степени определяет то, как организации отслеживают и измеряют успех.
Использование диаграмм Венна для сравнения и сопоставления
Одним из наиболее популярных применений диаграммы Венна является мозговой штурм путем сравнения идей и сопоставления их друг с другом.
Диаграммы Венна и диаграммы Эйлера
Еще один тип диаграмм, который очень похож на диаграмму Венна — это диаграмма Эйлера. Диаграммы Эйлера и Венна основаны на теории множеств и состоят из кругов, демонстрирующих взаимоотношения между множествами. Однако это разные вещи.
Диаграмма Венна показывает все возможные взаимосвязи между различными множествами. Сюда входят гипотетически возможные взаимосвязи. Диаграммы Венна включают все возможные сочетания пересечений между элементами.
Диаграмма Эйлера показывает только те сочетания пересечений или взаимосвязей, которые уже существуют. Она состоит из кругов, которые содержат или не содержат другие круги, либо пересекаются друг с другом.
Чтобы определить, является ли диаграмма диаграммой Венна или диаграммой Эйлера необходимо проверить наличие пустого пересечения. На диаграммах Венна необходимо изображать каждое пересечение множеств, даже если пересечение является пустым. Но на диаграмме Эйлера изображаются только те пересечения, которые не являются пустыми.
Диаграммы Эйлера, как правило, сложнее диаграмм Венна. Они используются для пояснения сложных иерархий, изображения пересекающихся концепций и определения достоверности логического доказательства.
Пример диаграммы Венна
Ниже приведен практический пример использования диаграммы Венна в сфере бизнеса.
Допустим, необходимо сравнить роли или обязанности различных команд в организации с целью оптимизации рабочего процесса. Необходимо изобразить взаимосвязи между командами маркетологов и веб-разработчиков.
Команды маркетологов занимаются анализом данных, юридическими вопросами, исследованием потребительского спроса, публикацией информации в социальных сетях и управлением брендом.
Команды веб-разработчиков занимаются UX и UI дизайном, управлением брендом, тестированием качества, SEO-анализом, управлением проектами, исследованием потребительского спроса и анализом данных.
В данном примере диаграммы Венна точка пересечения включает все пересекающиеся области ответственности — аналитику данных, управление брендом и исследования потребительского спроса.
Это области, в которых могут сотрудничать команды маркетологов и веб-разработчиков.
Примеры диаграмм Венна могут проиллюстрировать взаимосвязи и различия между любыми объектами или элементами. В процессе работы диаграмма Венна может быть использована для анализа данных, мозгового штурма, разработки стратегий, сравнения или сопоставления идей.
Начните работу с диаграммой Венна прямо сейчас
Конструктор диаграмм Венна Miro идеально подходит для команд специалистов, которым требуется наглядное сопровождение для объединения, выявления сходства и отличия, а также сравнения наборов данных, связанных с проектом. Этот простой в использовании инструмент идеально подходит для команд, которым требуется простое визуальное представление сложных сравнений данных. Шаблон диаграммы Венна в Miro, который содержит пересекающиеся круги для демонстрации отдельных наборов данных и их сходств, станет полезным ресурсом для любой команды.
eulerr
Связывайте комбинации, соединяя их
с амперсандом (&).
Тип отношений
Непересекающиеся комбинации Союзы
Форма
Круг Эллипс
Случайное семя
стресс
ошибка диагностики
- Сюжет
- Соответствовать
Цвета Список разделенных запятыми
х11
или
шестнадцатеричные цвета.
Легенда
справа слева вверху внизу
Шрифт
Простой Смелый Курсив Жирный курсив
Границы
Твердый Варьируется Никто
Точечный размер
Показать количества
Непрозрачность
Ширина (дюймы)
Высота (дюймы)
Сохранить сюжет
пдф png
Диаграммы, пропорциональные площади, с Эйлером
Этот
блестящий
приложение основано на
р
пакет, который я разработал, называется eulerr.
Он генерирует диаграммы Эйлера, пропорциональные площади, используя числовые значения.
процедуры оптимизации.
Диаграммы Эйлера
являются обобщенными диаграммами Венна, для которых выполняется требование
все пересечения присутствуют расслаблены. Они построены
из спецификации установленных отношений, но иногда может
не отображать их должным образом. Например, попробуйте дать
приложение спецификация А = 5, В = 3, С = 1, А и В = 2, АВ и С = 2 чтобы увидеть, что я имею в виду.
Когда это происходит, Эйлер пытается указать на
насколько плохо диаграмма соответствует данным по метрикам стресс и ошибка диагностики. Последние из них показывают наибольшую разницу в процентах.
точки между спецификацией любой комбинации набора
и его результирующая подгонка. Это максимальное значение ошибка региона, который дается за каждую комбинацию. Этот показатель был
заимствовано из
статья Микаллефа и Питера Роджерса.
Стресс объяснить сложнее, но я советую
заинтересованному читателю читать
Отличная статья Леланда Уилкинсона.
для надлежащего резюме.
Наконец, я многим обязан вышеупомянутый Уилкинсон, а также Бен Фредериксон чьими работами вдохновлялся Эйлер.
Йохан Ларссон
Ограничения в приложении Shiny
Размещенное здесь приложение Shiny не полностью охватывает
все функции, которые предлагает пакет R.
Например, здесь количество наборов ограничено пятью.
но такого ограничения в упаковке нет.
Если вы хотите установить пакет R, вам нужно сначала
установить Р.
После этого вы можете просто установить пакет, вызвав install.packages("eulerr") .
Чтобы узнать больше о пакете R, посетите страницу пакета в CRAN.
Пожертвовать
eulerr — это проект с открытым исходным кодом, который приветствует вклад от всех, кто готов скинуться. См. страница разработки для пакета R если вы заинтересованы в участии или просто хотите сообщить проблема с пакетом. Если вы обнаружите какие-либо проблемы с этим сайтом, пожалуйста, посетите страница разработки приложения Shiny и задайте вопрос там.
Чтобы цитировать eulerr в публикациях, используйте
Запись BibTeX для пользователей LaTeX:
В математике есть нечто большее, чем соревнования.
Вы старшеклассник, который любит математику? Вы находите традиционную учебную программу по математике слишком простой? Вы хотите изучать увлекательную и сложную математику? Вы хотите работать над задачами и подружиться с математически мыслящими сверстниками? Если это так, вы пришли в нужное место!
ЧтоEuler Circle — математический институт для продвинутых студентов, любящих математику. Мы предлагаем ряд занятий по математике на уровне колледжа, специально адаптированных к потребностям старшеклассников, многие из которых исчерпали учебную программу по математике в своих школах и хотят узнать больше. Каждый предлагаемый нами курс эквивалентен уроку математики в колледже. На каждом занятии учащиеся решают множество задач, чтобы ознакомиться с новым материалом, а на продвинутых занятиях каждый учащийся пишет пояснительную работу по теме, связанной с материалом занятия.
Классы устроены таким образом, чтобы обеспечить путь к независимым исследованиям.
Многие из наших наборов задач в продвинутых классах включают нерешенные проблемы, которые учащиеся могут исследовать после того, как освоят материал, представленный в классе. Мы предлагаем встречи в небольших группах для студентов, заинтересованных в работе над исследовательскими проблемами, после того, как они продемонстрировали способность усердно работать над сложными задачами. Подробнее об исследованиях см. в круге Эйлера.
Математика — это больше, чем соревнования. Тем не менее, у старшеклассников мало ресурсов, чтобы узнать об остальном чудесном мире математики. Мы считаем, что многие студенты хотели бы увидеть, что еще есть, и мы хотим поделиться тем, что знаем.
Когда/гдеОткрыт прием заявок на весенние и летние курсы. Весенние занятия можно будет посещать онлайн или лично в Пало-Альто. Все летние занятия пройдут онлайн. Таким образом, студенты со всего мира могут подать заявку.
Весной у нас будет промежуточный курс по переходу к доказательствам в анализе, класс между средним и продвинутым уровнем по основам высшей математики с упором на точечно-множественную топологию и продвинутый класс по дифференциальной топологии.
Занятия будут проходить в гибридном очном и онлайн-формате, поэтому подавать заявки могут студенты со всего мира.
Летом у нас будет два продвинутых класса. На первой летней сессии у нас будет независимый класс по исследованию и написанию статей, а на второй летней сессии у нас будет класс по математике Эйлера. Летние занятия будут проходить полностью онлайн.
Вот даты и время весенних занятий:
| Класс | Дата начала | Дата окончания | Все | Онлайн | Лично |
|---|---|---|---|---|---|
| Переход к корректуре | 3 апреля | 7 июня | Понедельник 17:00–18:00 | Вторник 17:00–19:00 | Среда 18:30–20:30 |
| Основы высшей математики | 3 9 апреля0151 | 7 июня | Понедельник 17:00–18:30 | Среда 17:00–19:00 | Среда 18:30–20:30 |
| Дифференциальная топология | 3 апреля | 7 июня | Понедельник 18:30–20:30 | Вторник 17:00–19:00 | Среда 18:30–20:30 |
Заявки на весенние занятия принимаются до 19 февраля .