Построение графиков функций в полярной системе координат — МегаЛекции
Рисунок 19
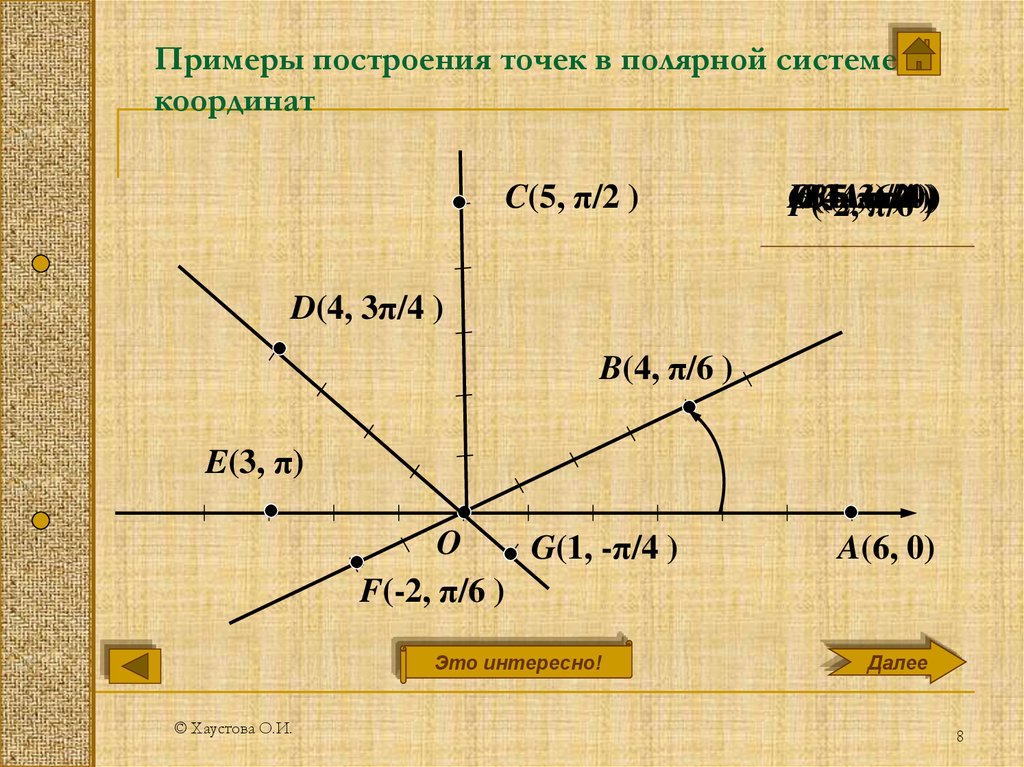
Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой , называемой полярной осью.
Положение точки M в полярной системе координат определяется расстоянием r (полярным радиусом) от точки M до полюса и углом j (полярным углом) между полярной осью и вектором . (рисунок 19).
Полярный радиус и полярный угол составляют полярные координаты точки M , что записывается в виде M(r,j). Полярный угол измеряется в радианах и отсчитывается от полярной оси:
— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Связь между декартовыми и полярными координатами
Пару полярных координат r и j можно перевести в Декартовы координаты x и y по следующим фомулам:
Обратно, полярный радиус r можно найти, зная декартовы координаты x и y , по теореме Пифагора (см. Рис. ??):
,
а полярный угол j в диапазоне [0, 2p), находится при помощи обратной (к тангенсу) тригонометрической функции арктангенс:
Пример № 2. Построить график функции r(j) = 2.
1. Задаём значения j в градусах в диапазоне [0, 2p] с шагом в 5 градусов с использованием автозаполнения (см. Приложение 1).
2. Перевести j из градусов в радианы с использованием функции РАДИАНЫ (см. Приложение 2).
3. Рассчитать значения r(jрад).
4. По значениям jрад и r(jрад) рассчитать декартовы координаты x и y.
5. По рассчитанным значениям x и y построить график, выбрав тип диаграммы Точечная.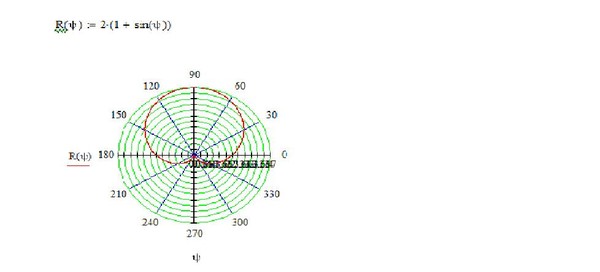
Рисунок 20. Результаты расчёта
Рисунок 21. График функции r(j) = 2
Задание № 4
С помощью пакета Microsoft Excel построить график функций, приведенные в Приложении 5 соответственно варианту. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести расчётные формулы и результаты расчёта,
d. График построенной функции,
e. Указать полярные координаты точки графика, заданной преподавателем.
Построение графиков функций с использованием логарифмической шкалы.
|
Шкала называетсялогарифмической,если метками шкалы являются числа, а расстояния между метками –пропорциональны логарифму отношения величин отмеченных на концах этого отрезка (в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах ). Ни нуль, ни отрицательные числа не могут быть показаны на логарифмической шкале (см. рисунок 22)
Ни нуль, ни отрицательные числа не могут быть показаны на логарифмической шкале (см. рисунок 22)
Рисунок 22
Логарифмическая шкала исключительно удобна для отображения очень больших диапазонов значений величин.
Пример № 3. Построить график функции . в диапазоне значений [-5, 5] и определить по графику значение функции для х = -3.6 и х = 4.
1. Задаём значения х в диапазоне [-5, 5] с шагом 0.5 с использованием автозаполнения (см. Приложение 1).
2. По заданным х рассчитываем значения функции у.
3. Строим график функции, используя тип диаграммы «точечная» и замечаем, например,что значение функции при отрицательных х очень близко к 0, так что определить его из графика не представляется возможным
Рисунок 23
4. Выделяем ось у.
5. Делаем щелчок правой кнопкой мыши и в раскрывшемся контекстном меню выбираем «формат оси» (см. рисунок 12)
рисунок 12)
6. В окне «формат оси» помечаем галочкой логарифмическую шкалу.
7. Добавить основные и промежуточные линии сетки.
Результаты представлены на Рисунке 24
Рисунок 24
Из рисунка определяем, что для х = -3.6 значение примерно равно 0.02, а для х = 4 .
6.1.Задание № 5.Построить график функций в диапазоне значений [-10, 10] с шагом 0.5 . Уметь из графика определять значение функции для указанного (преподавателем) аргумента. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести графики без использования логарифмической шкалы,
d. Привести графики с использованием логарифмической шкалы,
e. Сравнить результаты.
Воспользуйтесь поиском по сайту:
Построение графиков полярных кривых в Visual Basic
Образовательные цели урока.
Сформировать понятие полярной системы
координат
Изучение данной темы рекомендуется проводить после знакомства с графическими возможностями Visual Basic, изучения построения графиков функций в прямоугольной системе координат. Изложение материала сопровождается показом презентации (Презентация).
1. Понятие полярной системы координат. (Слайд 1)
Суть задания какой-либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. Например, в декартовой прямоугольной системе это координаты точки (x, y).
Любая точка на плоскости может быть однозначно
определена в различных системах координат. Выбор
системы координат зависит от нескольких
факторов, например, от способа задания начальных
значений при решении задачи, от наглядности
представления результата.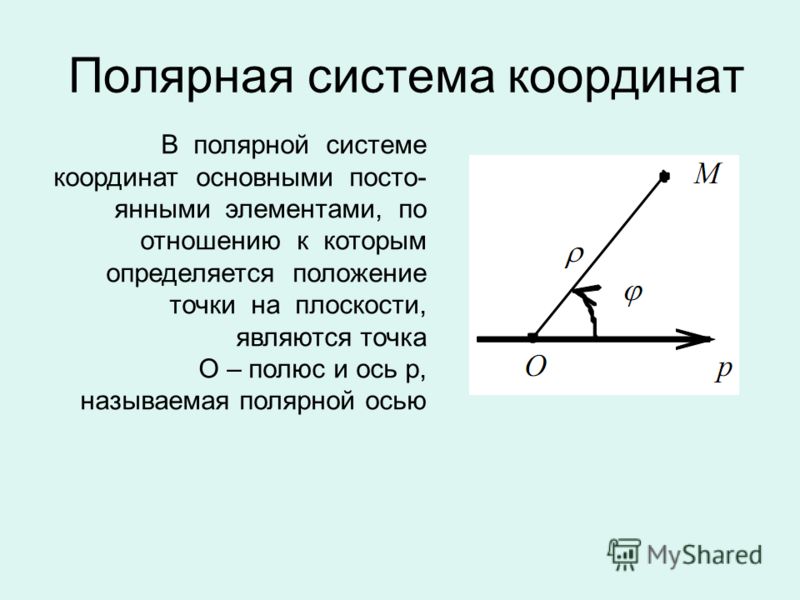
Одной из наиболее часто используемых наряду с декартовой является полярная система координат.
Полярная система координат образуется полярным полюсом О и полярной осью, которая представляет луч, проведённый из полюса в направлении слева направо (Рис. 1).
В полярной системе координат любой точке (например, т. А) соответствует единственная пара полярных координат А(r, f), где r – полярный радиус, f – полярный угол. Таким образом, по заданной паре полярных координат можно однозначно определить положение точки на плоскости.
Полярный радиус r – отрезок, соединяющий
полюс с заданной точкой А.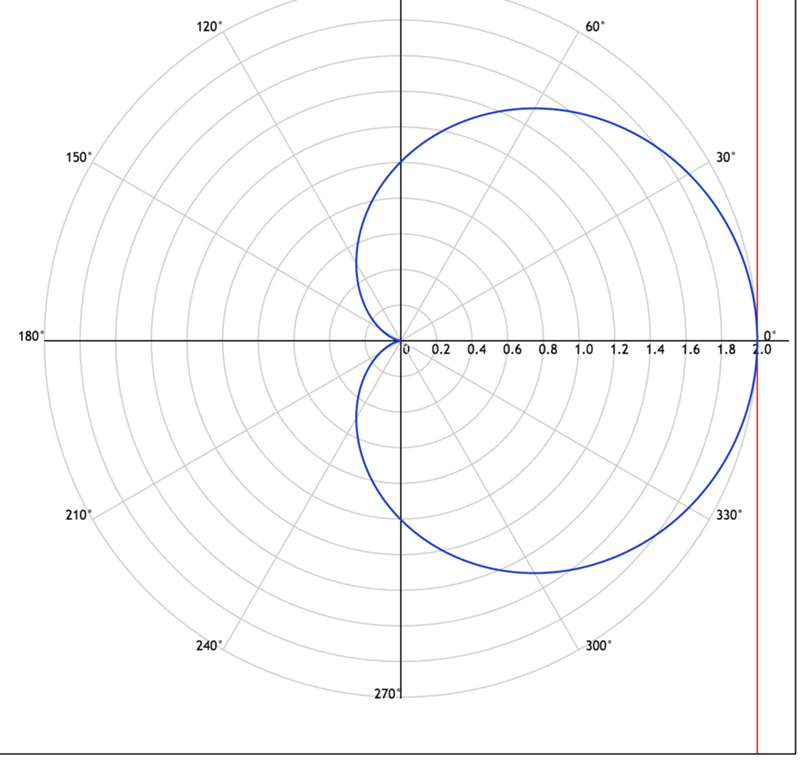
Полярный угол f — угол между полярной осью и полярным радиусом. За положительное направление полярного угла f примем направление против часовой стрелки.
Для перехода от полярных координат к декартовым (слайд 2) нужно совместить полярную и декартову прямоугольную сиcтемы таким образом, чтобы начала их координат совпадали, а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы координат. (Рис. 2).
Тогда получим формулы перехода от полярных координат (r, а) к декартовым (х, у):
x = r*cos f
у = r*sin f
Эти уравнения называются параметрическими.
Формулы обратного перехода от декартовых координат к полярным:
r =
f = arctg (y/x)
2. Практическая работа. Построение графиков полярных кривых по параметрическим уравнениям
Задание.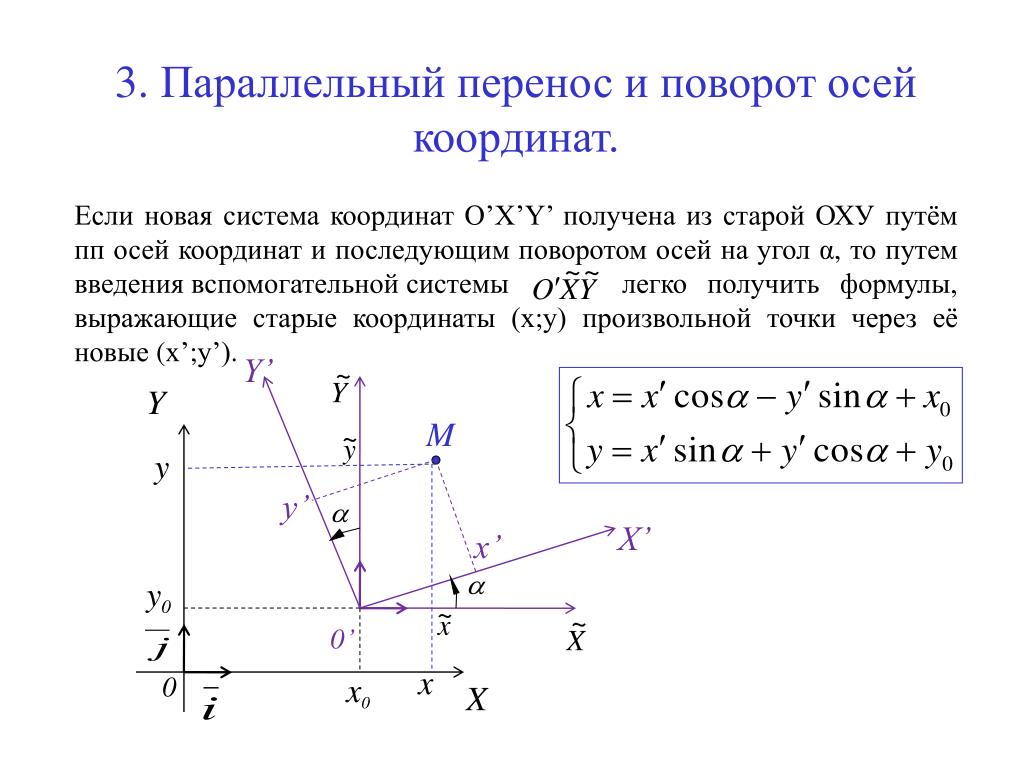 3)
3)
x = r * Cos(f)
y = r * Sin(f)
f I [0, 2*p ]
4) Фигура Лиссажу
r = 5
x = r * Cos(3 * f)
y = r * Sin(2 * f)
f I [-p , p ]
5) k-лепестковая роза
При чётных значениях k получается 2*k-лепестковая роза, а при нечётных значениях – k-лепестковая роза.
r = Sin(k * f)
x = 10 * r * Cos(f)
y = 10 * r * Sin(f)
f I [-p ,p ]
6) Эпициклоида
x = (a + b) * Cos(f) — a * Cos((a + b) * f / a)
y = (a + b) * Sin(f) — a * Sin((a + b) * f / a)
f I [0, 2*p ]
Значение b вводится с клавиатуры. Значение a примем равным a = b / 3.
Решение.
1. Разработка интерфейса проекта (Рис. 3). (Слайд 4)
Для выбора типа полярной кривой создадим
массив переключателей Option1, который разместим в
контейнере Frame1. Для построения графика разместим
на форме графическое окно Picture1. Для вывода
названия графика и параметрических уравнений
создадим метку Label2 и текстовое поле Text1. Для
управления проектом создадим 3 командные кнопки
Command1, Command2, Command3 (Пуск, Сброс, Выход).
Для вывода
названия графика и параметрических уравнений
создадим метку Label2 и текстовое поле Text1. Для
управления проектом создадим 3 командные кнопки
Command1, Command2, Command3 (Пуск, Сброс, Выход).
Интерфейс проекта представлен на рис. 3.
Рис.3. Интерфейс проекта
2. Для созданных элементов управления установим свойства, приведенные в таблице. (Слайды 5, 6)
Свойства элементов управления
| Элемент управления | Свойство | Значение |
| Frame1 | Caption | Выбор типа полярной кривой |
| Option1(0) | Caption | кардиоида |
| Option1(1) | Caption | логарифмическая спираль |
| Option1(2) | Caption | декартов лист |
| Option1(3) | Caption | k-лепестковая роза |
| Option1(4) | Caption | фигура Лиссажу |
| Option1(5) | Caption | эпициклоида |
| Label3 | Caption | Построение полярных кривых |
| Label1 | Caption | График |
| Label2 | Caption | |
| Label1, Label2, Label3 | Alignment | 2 — center |
| Text1 | Text | |
| Text1 | Alignment | 0 — left |
| Picture1 | FillStyle | 0 — solid |
| Command1 | Caption | Пуск |
| Command2 | Caption | Выход |
| Command3 | Caption | Сброс |
3. Описание переменных. (Слайд 7)
Описание переменных. (Слайд 7)
x, y – координаты точки, f — угол, r – радиус, a, b, k, q — коэффициенты уравнений, z — переменная для хранения индекса выбранного переключателя, i – параметр цикла для задержки изображения, pi – число Пи.
В разделе описаний опишем типы выбранных переменных.
Dim z, k As Integer, f, pi, a, r, b, q As Single, i As Long, x, y As Single
4. Разработка программного кода. (Слайды 8-13)
Программный код проекта полностью приведён в Приложении 1.
Создадим процедуру переключателя Option1_Click для выбора типа полярной кривой. Для этого нужно проанализировать значение свойства Value. У включенного переключателя Value=True. В переменной z запоминаем индекс выбранного переключателя.
Фрагмент 1
По кнопке Пуск в зависимости от значения z
строим графики полярных кривых. Рассмотрим
построение графиков на примере кардиоиды, фигуры
Лиссажу и эпициклоиды. Графики остальных кривых
вы построите самостоятельно.
Графики остальных кривых
вы построите самостоятельно.
Фрагмент 2
Графики полярных кривых и параметрические уравнения приведены на слайдах 14-18.
Задания для самостоятельной работы. (Слайды 19-22)
Фрагмент 3
Литература
- Глушаков С.В., Мельников В.В., Сурядный А.С. Программирование в среде Windows. Visual Basic 6.0. М.: ООО “Издательство АСТ”, 2001.
- Браун С. Visual Basic. Учебный курс. – Спб.: Питер, 2002.
- Есипов А.С., Паныгина Н.Н., Громада М.И. Информатика. Задачник. – СПб: Наука и техника, 2001.
- Журнал “Информатика и образование”, № 2/2005.
Построение графика функции, заданной в полярной системе координат. — Информатика, информационные технологии
Создайте в новом проекте форму «График функции в полярной системе координат»
1.Условие:
Построить график функции, заданной в полярной системе координат.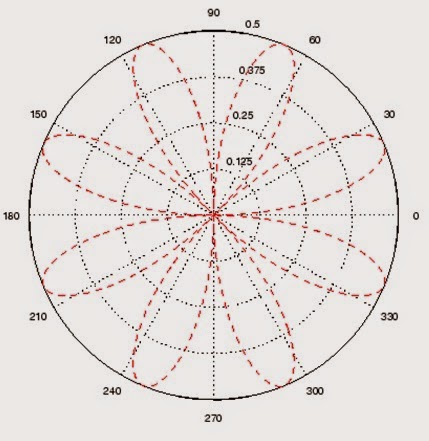
R=10*(1+cos(t)), где t € [0; 2?] шаг изменения t h=0.01
2.Программа:
Результат;
Сохранитепроект в папкеЛабораторная работа 11/Задание 3.
Задание 4
Построение графиков функций
Создайте в новом проекте форму «Построение графиков функций»
Создаваемое приложение должно состоять из таблицы для задания списка точек графика функции и графического поля для рисования графика. При этом любое изменение данных в таблице должно вызывать обновление графика.
Описание работы
Программа будет состоять из одной формы, на которой необходимо разместить:
| Элемент | Caption | Name | Другие свойства |
| Форма | Построение графика функции | ChartForm | |
| Таблица для ввода координат точек | StringGrid | Options – qoEditing – True ColCount.RowCount – 3 | |
| Панель для расположения диаграммы | отсутствует | PanelChart | |
| Компонент TPaintBox для отображенияграфика функции | PaintBox | ||
| Метка | График функции | Label1 | |
| Метка | Исходные точки | Label2 | |
| Панель для отображения ошибок ввода данных | отсутствует | PanelStatus | |
| Кнопка | Выход | ButtonExit | Можно добавить свойство ModalResult — mrOk |
Таблица для ввода координат точек должна автоматически изменять размер в соответствии с количеством уже введенных точек функции. Как это сделать, описано в предыдущих лабораторных работах.
Как это сделать, описано в предыдущих лабораторных работах.
После ввода данных необходимо сформировать два массива введенных координат X и Y, отсортировать их по оси X, после чего необходимо перерисовать окно с графиком.
Замечание
При необходимости перерисовки компонента в ответ на какое-то событие, например, нажатие кнопки, сразу не рисуйте, а вызовите метод Invalidate и создайте обработчик события OnPaint визуального компонента, например, формы или TPaintBox.
Рассмотрим, как Windows отображает все свои окна.
Окнами в общем случае являются кнопки, строки ввода, списки и т.д. Они могут находиться друг в друге, например, кнопки в диалоговом окне или окна внутри многодокументного интерфейса. Каждое окно при этом имеет специальную главную управляющую процедуру, которая обрабатывает поступающие от системы сообщения. Некоторые из этих сообщений Delphi преобразует в события, которые можно затем обрабатывать в программе.
Windows сама никогда не хранит изображения окон, поэтому одним из сообщений является команда о необходимости отображения содержимого окна на экране.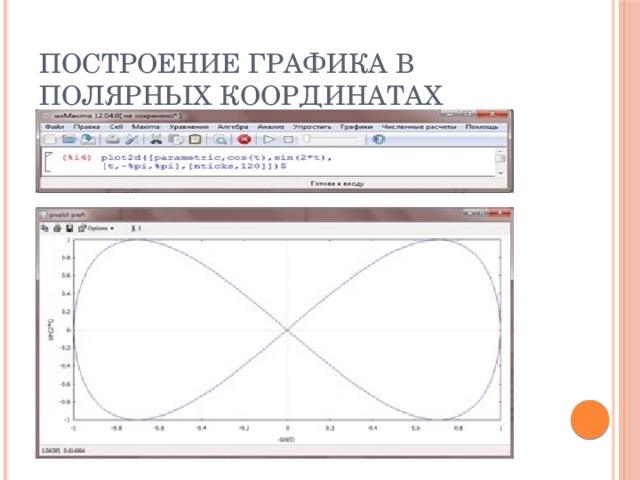
В нашей программе сразу же после ввода координат точек мы не должны вызывать процедуру рисования. При этом мы должны указать Windows, что как только появится свободное процессорное время, система должна послать сообщение о необходимости реального отображения окна. При таком подходе, если окно приложения будет временно закрыто другим окном и опять станет видимым, система автоматически пошлет сообщение о необходимости восстановления графического изображения в окне.
В Delphi для указания, что необходимо перерисовать любой элемент управления, нужно вызвать его метод Invalidate.
Для изображения произвольной графики в Delphi обычно используется компонент TPaintBox, находящийся на закладке System палитры компонентов. Этот компонент имеет событие OnPaint, для которого мы и должны создать обработчик для рисования графика.
Для прорисовки произвольных изображения используется класс TCanvas(холст), а также методы, позволяющие рисовать графические примитивы (краткое описание свойств и методов объектов для рисования графики приведено выше).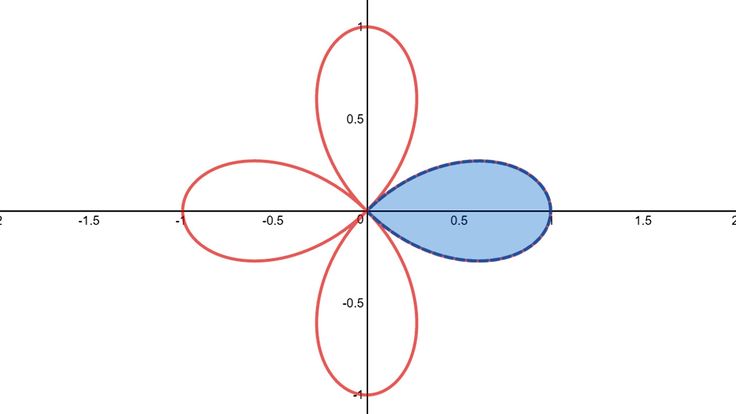
Для упрощения алгоритма рисования графика будем считать, что обе координаты всех точек попадают в интервал
[-10, 10]’. Процедура рисования графика при этом распадается на две части:
-рисование осей координат с засечками и подписями
-и собственно изображение графика.
Теперь рассмотрим вопрос автоматического изменения положения и размеров визуальных компонентов при изменении формы. Для этого у компонентов имеются такие свойства, как Align и Anchors. Собственно, свойство Align является подмножеством возможностей свойства Anchors. Свойство Anchors имеет 4 логических подсвойства:
-akLefn,
-akTop,
-akRight,
-akBotton
Например, если свойство akRight установлено в True, то правая сторона элемента будет находиться на одинаковом расстоянии от правой стороны содержащей его формы при изменении пользователем ее размера, иначе правая сторона элемента будет находиться на одинаковом расстоянии от левой стороны. При изменении свойства Align на самом деле изменяется свойство Anchors, которое впоследствии и учитывается при изменении размеров.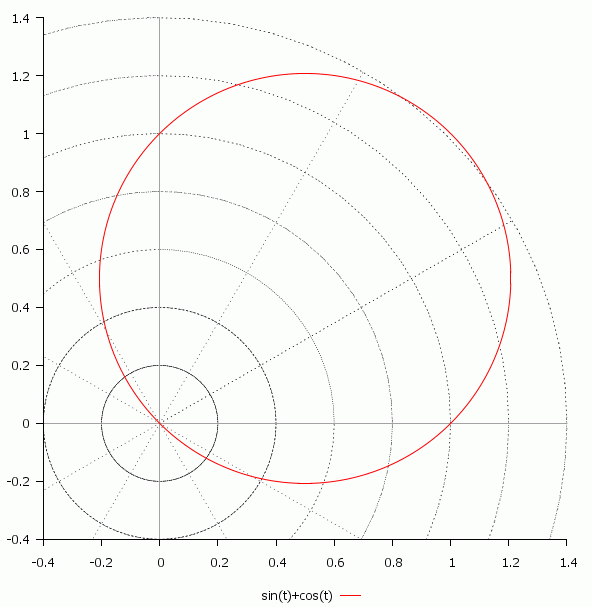
Замечание
По возможности делайте любое окно растягиваемым, но при этом не забывайте отслеживать, чтобы внутренности окна изменялись при изменении его размеров. Для этого используйте свойства Аlign и Anchors.
Поэкспериментируйте приведенными свойствами и добейтесь, чтобы в нашем приложении график растягивался в размерах при увеличении размеров формы, но в то же время таблица оставалась с правой стороны формы, a кнопка выхода в правом нижнем.Обратите внимание, что процедура рисования графика должна учитывать изменяющийся размер элемента TPaintBox.
Программа:
Результат
На рис. приведен внешний вид запущенного приложения после того, как окно растянуто.
Сохранитепроект в папкеЛабораторная работа 11/Задание 4.
Вопросы и задания для самостоятельной работы
1. Как Windows перерисовывает свои окна?
2. Как заставить Windows перерисовать какое-то окно?
3. Для чего используются свойства визуальных компонентов Align и Anchors?
4. Поместите на форму компоненты для выбора стиля изображения на графике введенных точек (кружочки, квадратики или «не изображать»), толщины и цвета линий. При этом график должен автоматически перерисовываться при изменении этих параметров.
Поместите на форму компоненты для выбора стиля изображения на графике введенных точек (кружочки, квадратики или «не изображать»), толщины и цвета линий. При этом график должен автоматически перерисовываться при изменении этих параметров.
5. Добавьте кнопку для генерации случайного набора точек.
Статьи к прочтению:
- Построение графиков и диаграмм
- Построение и работа импульсного кольца.
14 вопросов которые нужно задать до свадьбы? Сатья дас. Карпаты. 3.08.2017
Похожие статьи:
Построение графика функции с двумя и более условиями. 3 страница
2. Найти с помощью инструмента Подбор параметра корни кубического уравнения с одной переменной согласно своему варианту. Вариант 1. Вариант 2. Вариант 3….
Построение графика функции с двумя и более условиями. 4 страница
б) Дважды щелкнув имя поля в верхней части окна.
 в) Щелкнув в столбце в конце строки Поле и из раскрывающегося списка выберать нужное поле. В строке…
в) Щелкнув в столбце в конце строки Поле и из раскрывающегося списка выберать нужное поле. В строке…
ПОСТРОЕНИЕ НЕКОТОРЫХ КРИВЫХ ВТОРОГО ПОРЯДКА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ, ЗАВИСИМОСТЬ КРИВЫХ ОТ КОЭФФИЦИЕНТОВ
ПОСТРОЕНИЕ НЕКОТОРЫХ КРИВЫХ ВТОРОГО ПОРЯДКА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ, ЗАВИСИМОСТЬ КРИВЫХ ОТ КОЭФФИЦИЕНТОВ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Сучков Р.В. 1
1
Веретенникова А.Л. 1
1
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Конечно же, каждый из нас слышал о таких понятиях как график функции, система координат, гипербола и т. п. Всё это является составляющими темы «Функции», с которой знакомимся мы в школе ещё в среднем звене.
п. Всё это является составляющими темы «Функции», с которой знакомимся мы в школе ещё в среднем звене.
Функция — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Этот закон определяется уравнением , и на основе него строится график в плоской системе координат, задаваемой двумя осями X и Y. Двигаясь от 6 до 10 класса, мы усложняли уравнения и графики, вводили новые понятия, но никогда не выходили за рамки основного определения функции и принципа построения графиков. То есть нами не рассматривалась возможность построения, например, такой кривой как трехлепестковая полярная роза. Единственным, наверное, примером кривой (не функции) была окружность, которая встречалась нам как тригонометрии, так и при решении задания №18 с параметром в ЕГЭ. В 10-м классе на уроке информатики в рамках работы в табличном процессоре я столкнулся с построением графиков функций, и чтобы расширить область преподаваемого нам материала, заглянул за рамки заданных ограничений. В этом и заключается одна из целей, поставленных в данной работе — расширить знания по теме графики, попрактиковаться в области их построения. Таким образом, объектом моего исследования стали кривые II порядка — графики, в уравнениях которых нет такой строгой зависимости Y от X, как в функциях. Другим предметом моего исследования являются системы координат прямоугольная и полярная, а именно связь между декартовыми и полярными координатами.
В этом и заключается одна из целей, поставленных в данной работе — расширить знания по теме графики, попрактиковаться в области их построения. Таким образом, объектом моего исследования стали кривые II порядка — графики, в уравнениях которых нет такой строгой зависимости Y от X, как в функциях. Другим предметом моего исследования являются системы координат прямоугольная и полярная, а именно связь между декартовыми и полярными координатами.
Вот главная цель работы: построить графики кривых II порядка в полярной системе координат, а также выяснить, как различаются их графики в зависимости от варьирования коэффициентов и параметров функций. Для достижения целей работы было поставлено несколько задач:
-
пополнить знания о стандартных (невырожденных) кривых II порядка: эллипс, параболу, гиперболу;
-
рассмотреть нестандартные кривые II порядка;
-
познакомиться с полярной системой координат и сопоставить с декартовой, уже изучавшейся в школе.

Процесс решения каждой из задач был разбит на 2 этапа:
-
изучение и разбор теоретического материала, знакомство с новыми понятиями;
-
применение полученных знаний на практике, построение графиков.
Историческая справка: впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур. Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической.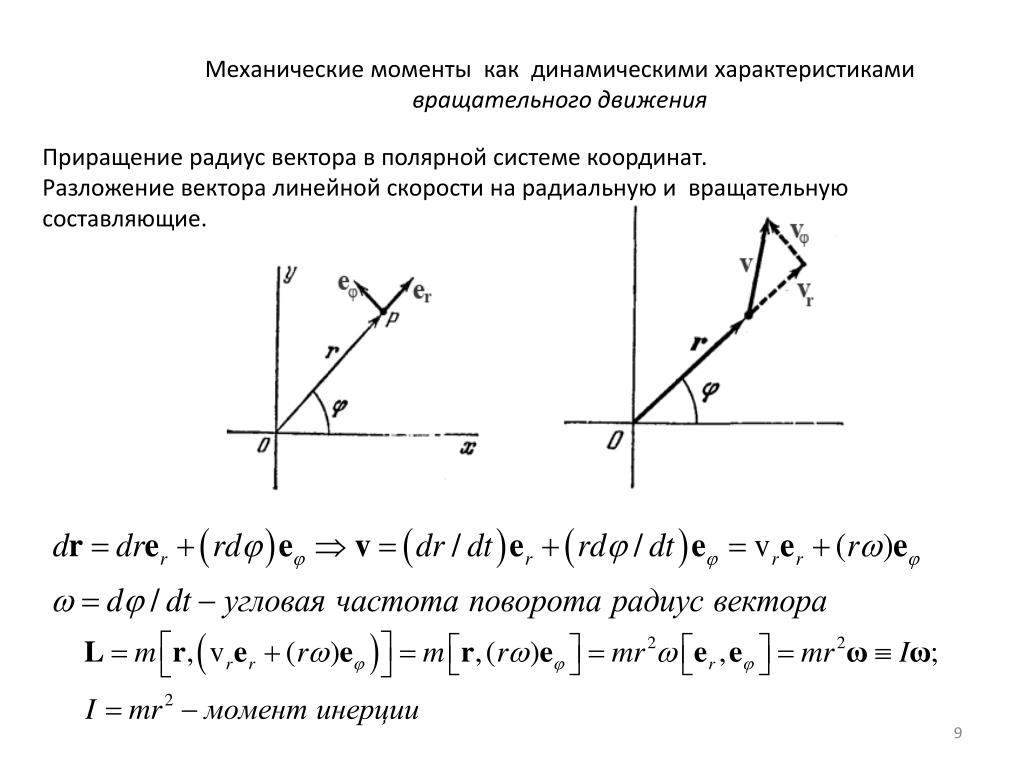 Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а при достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а при достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Алгебраической кривой второго порядка называется кривая , уравнение которой в декартовой системе координат имеет вид , где не все коэффициенты А, В и С равны одновременно нулю (иначе — прямая, т.е. алгебраическая кривая первого порядка). Кривые второго порядка делятся на вырожденные и невырожденные. Вырожденные кривые второго порядка это прямые и точки, которые задаются уравнением второй степени. Если уравнению второго порядка не удовлетворяет ни одна точка плоскости, то тоже говорят, что уравнение определяет вырожденную кривую (мнимую кривую второго порядка). Если же кривая невырожденная, то для неё найдётся такая декартова прямоугольная система координат, в которой уравнение этой кривой имеет один из следующих трёх видов:
Эллипс, гипербола, парабола
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через . Фокусы эллипса обозначают буквами и , расстояние между ними — через . По определению эллипса .
Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через . Фокусы эллипса обозначают буквами и , расстояние между ними — через . По определению эллипса .
Гиперболой называется геометрическое место точек на плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек, называемых фокусам, одинаково и равно
Параболой называется множество точек на плоскости, расстояния от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны. С гиперболой мы часто сталкиваемся в повседневной жизни. По параболистической траектории летит брошенный вверх камень, отскакивает мяч от пола, движутся планеты вокруг Солнца.
1.2. Системы координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Знания обычного человека в большинстве случаев ограничиваются одной-двумя системами координат. На самом же деле их существует великое множество: прямоугольная, полярная, аффинная, сферическая, цилиндрическая и т.д. На одном из уроков алгебры мы затрагивали кое-какие из них, а в этом исследовании я решил сопоставить две: прямоугольную (ёще называющуюся декартовой) и полярную (как хорошо знакомую и в корне отличающуюся).
Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Знания обычного человека в большинстве случаев ограничиваются одной-двумя системами координат. На самом же деле их существует великое множество: прямоугольная, полярная, аффинная, сферическая, цилиндрическая и т.д. На одном из уроков алгебры мы затрагивали кое-какие из них, а в этом исследовании я решил сопоставить две: прямоугольную (ёще называющуюся декартовой) и полярную (как хорошо знакомую и в корне отличающуюся).
Прямоугольная, или Декартова, система координат — прямолинейная система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям. Названа по имени Р Декарта. Это наиболее простая и поэтому часто используемая система координат как на плоскости, так и в пространстве.
Историческая справка: Декарт впервые ввел координатную систему в своей работе «Рассуждение о методе» в 1637 году.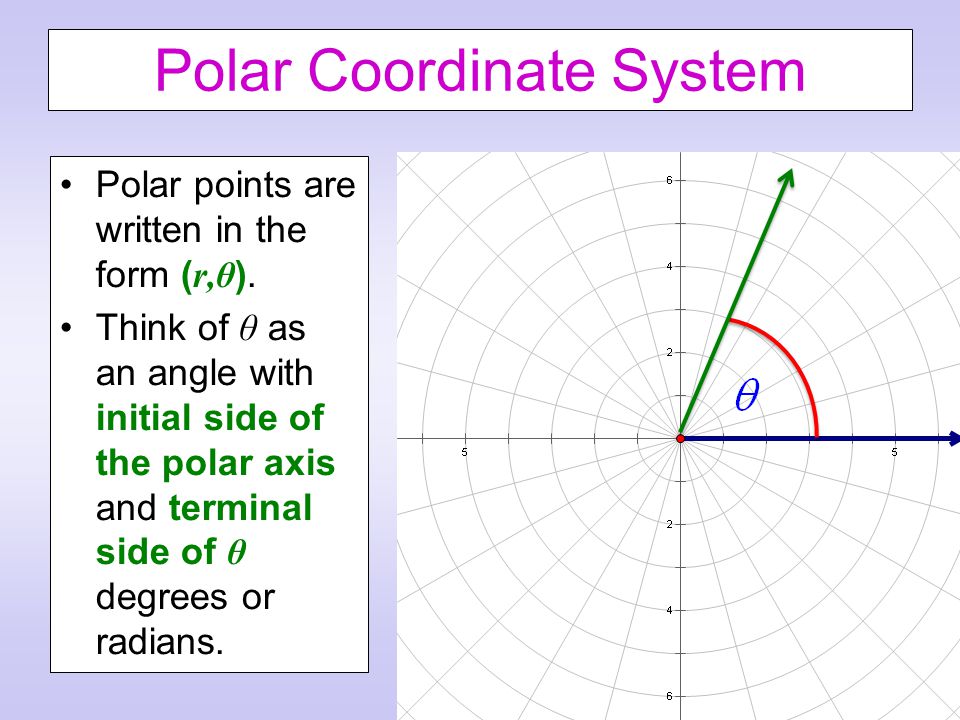 Она существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта.
Она существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта.
Данная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Эти оси пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей. Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY.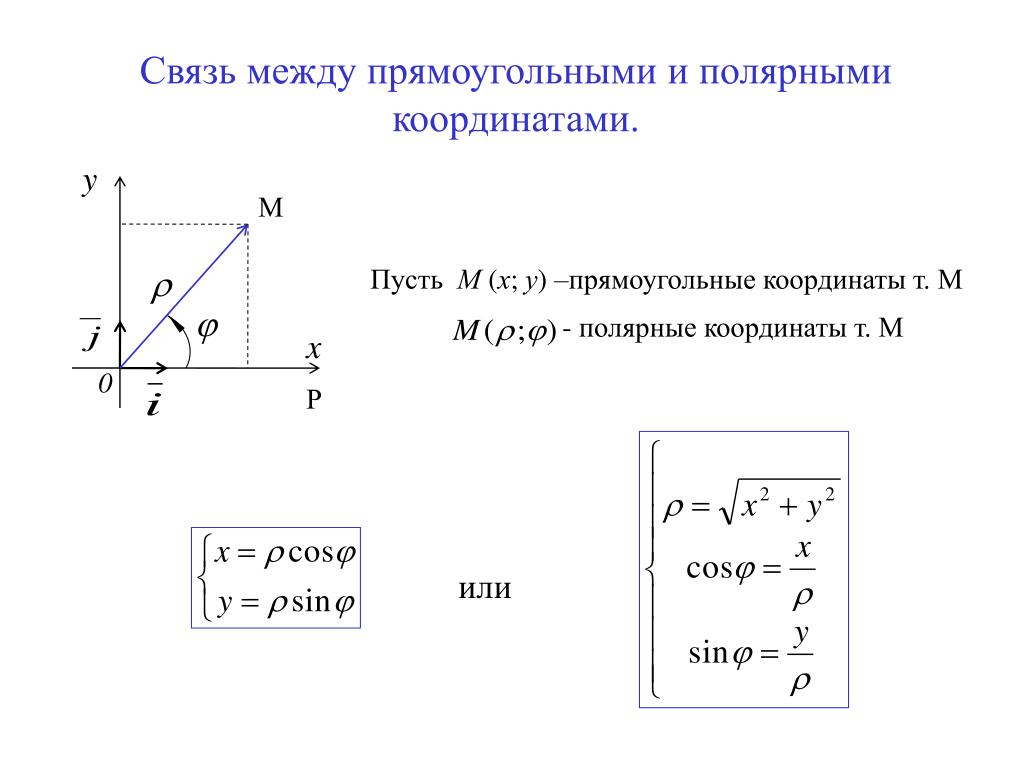 Четыре угла — четверти (I, II, III, IV) — образованные осями координат OX и OY, называются координатными углами.
Четыре угла — четверти (I, II, III, IV) — образованные осями координат OX и OY, называются координатными углами.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат.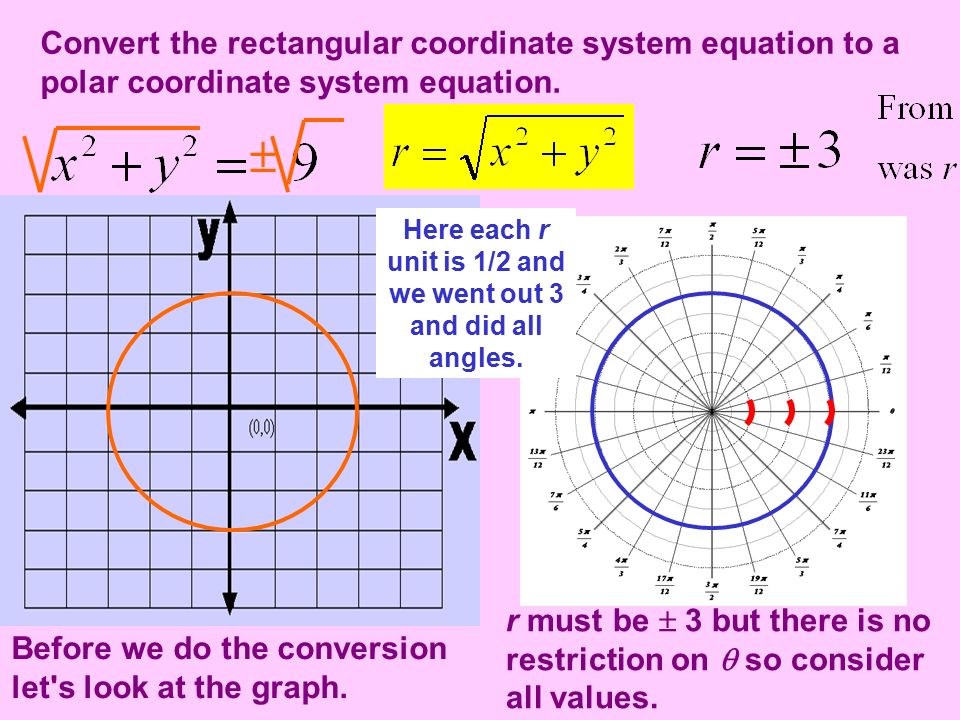 Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
1.2.3. Связь между декартовыми и полярными координатамиПару полярных координат и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
в то время как две декартовы координаты x и y могут быть переведены в полярную координату :
(по теореме Пифагора).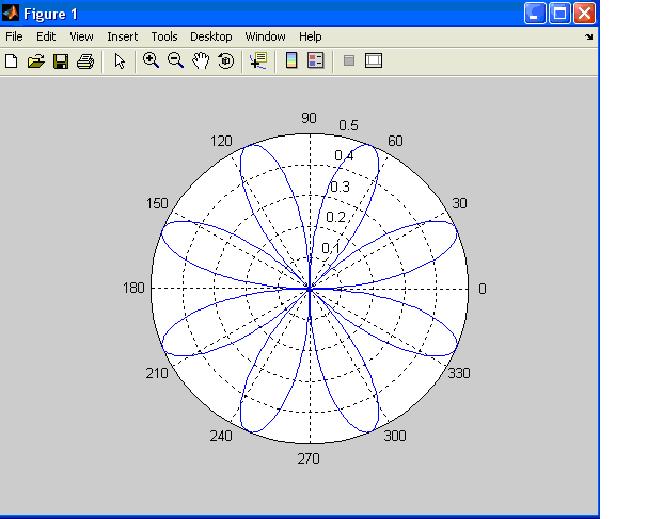
Просмотрев этот раздел, неосведомлённый человек может подумать, что часть нестандартных кривых второго порядка можно спокойно отнести к стандартным, другая же часть не имеет с ними ничего общего. Некоторые из них действительно представляют собой красивые витиеватые узоры, но некоторые выглядят как-то слишком просто, без изысков. Конечно, такое мнение имеет место существовать. Но ведь дело в степени и области применения кривых: одни встречаются постоянно, другие — только в узких специализированных целях — и в сложности уравнения. Хотелось бы в этом разделе рассмотреть наиболее интересные кривые: спираль Архимеда, улитка Паскаля, Розы Гранди. В разделе «Кривые II порядка в полярной системе координат» я перевел графики в другую полярную систему координат и построил их с помощью табличного процессора.
Кривые второго порядка в полярной системе координат
Эта часть является самой главной в моей работе, так как в ней описывается построение графиков в полярной системе координат в табличном процессоре MSExcel 2007.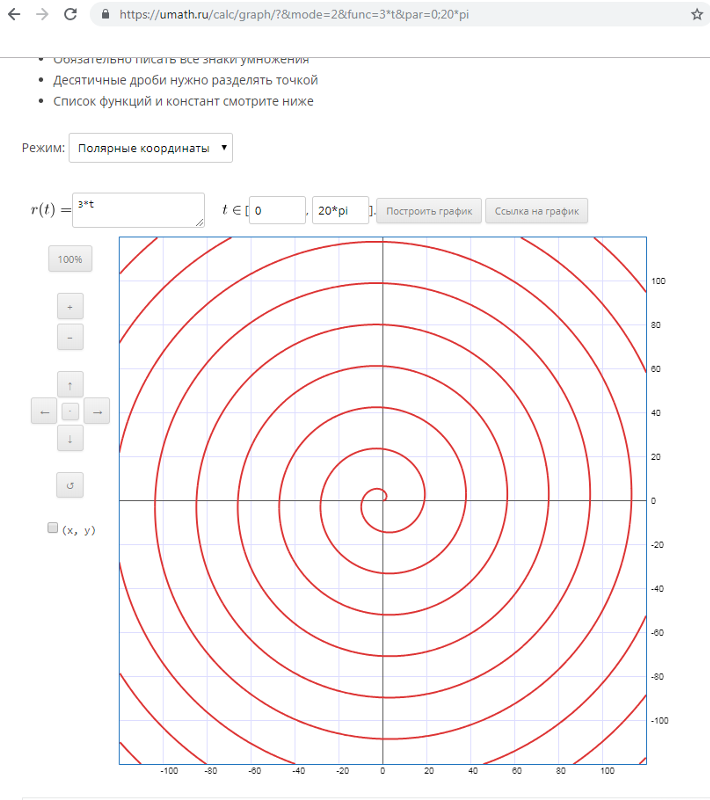 Выполняя построения мы старались акцентировать внимание на красоте математики, на том насколько все гениальное просто, ведь математика это предметная область, в которой все для жизни.
Выполняя построения мы старались акцентировать внимание на красоте математики, на том насколько все гениальное просто, ведь математика это предметная область, в которой все для жизни.
Полярная роза (Розы Гранди)
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах: ,
для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных, либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.
Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
|
— трехлепестковая роза |
— клевер |
|
|
— космея |
Два графика в одной системе |
|
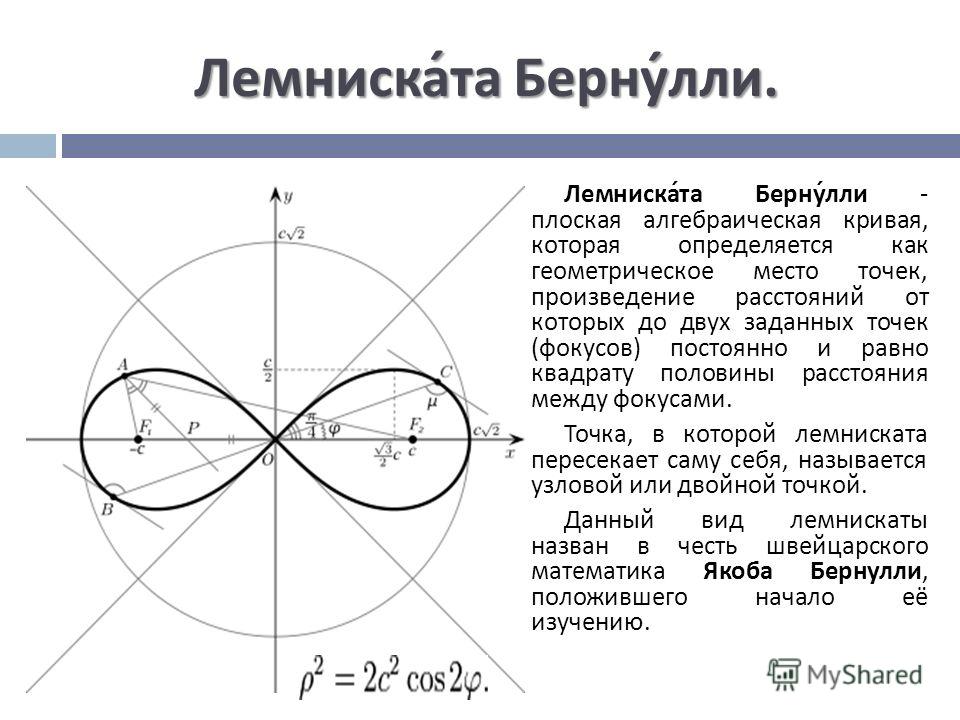
Улитка Паскаля
Улитка Паскаля ― плоская алгебраическая кривая 4-го порядка.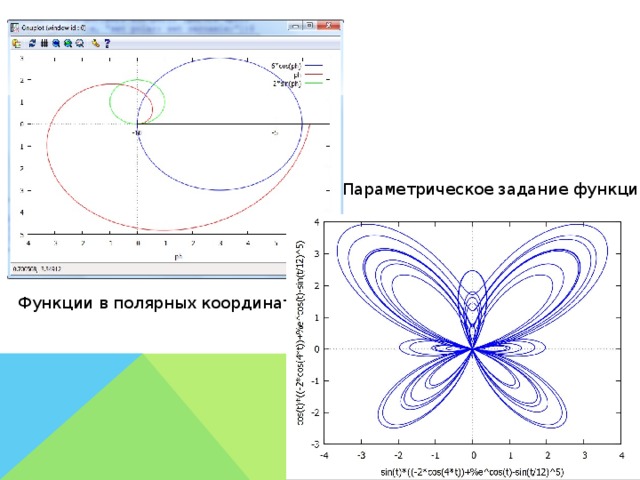 Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнение в полярных координатах:
Здесь — диаметр исходной окружности, а — расстояние, на которое смещается точка вдоль радиус-вектора.
|
В зависимости от диапазона получаются следующие графики |
||
Спираль Архимеда
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для >0, а другую для
Спираль Архимеда имеет две ветви, одну для >0, а другую для
Просмотров работы: 635
Построение графиков и эпюр в MathCad 13, 14, 15 на примерах. Декартовая и полярная системма координат
В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:
- График по заданным точкам
- График функции
- Построение эпюры (распределение физической величины)
- График функции в полярных координатах
Построение графика по точкам
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши.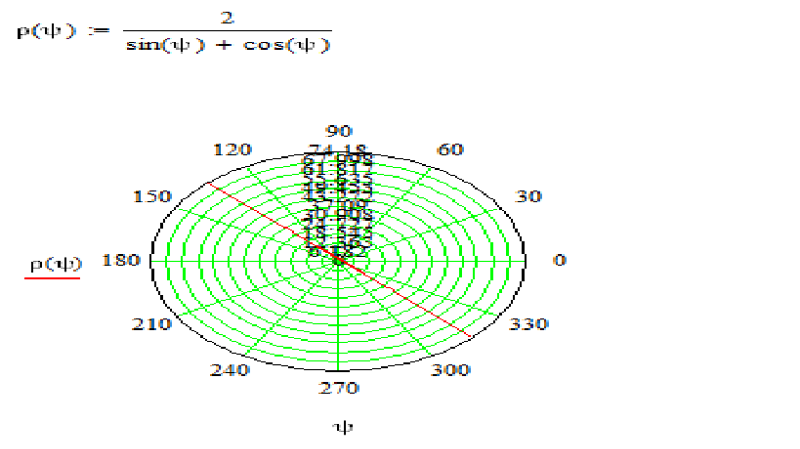 У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
Построение графика функции f(x)
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой
Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=.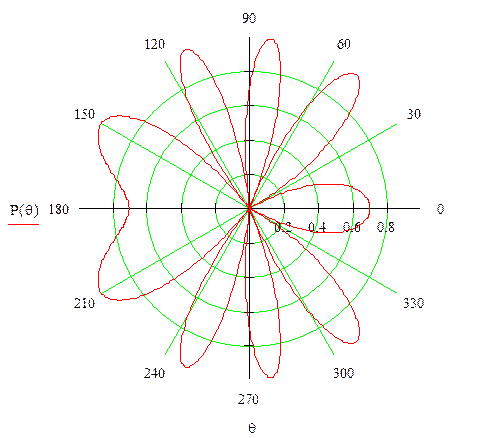 …, поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7
…, поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7
Построение эпюры в mathcad
Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:
— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании
Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. 2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.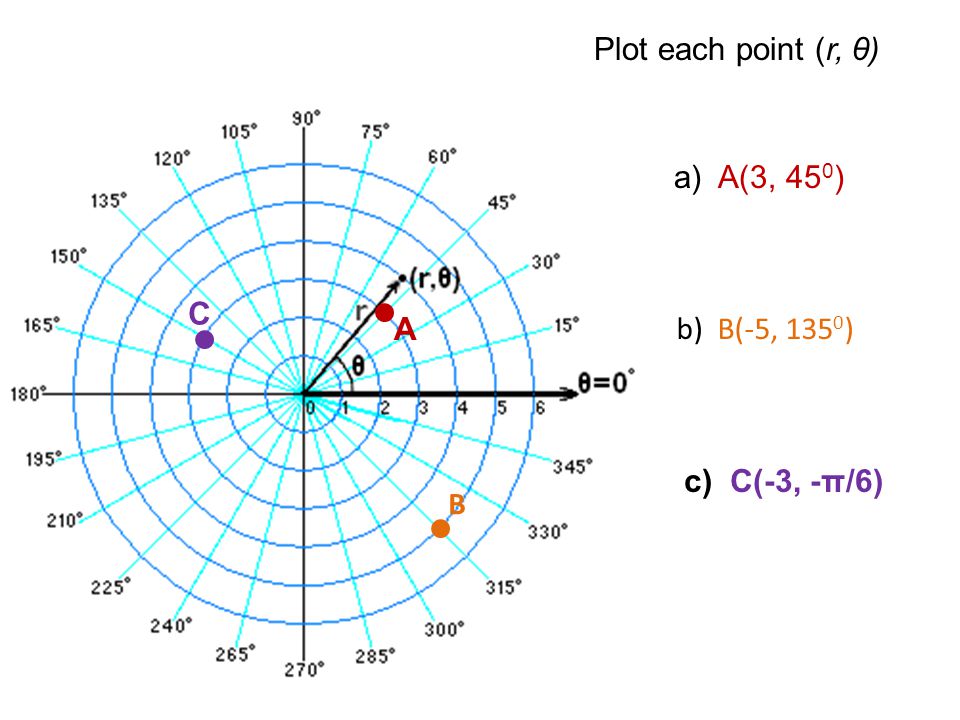
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)
Построение графика в полярных координатах в mathcad
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)
Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph
Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter.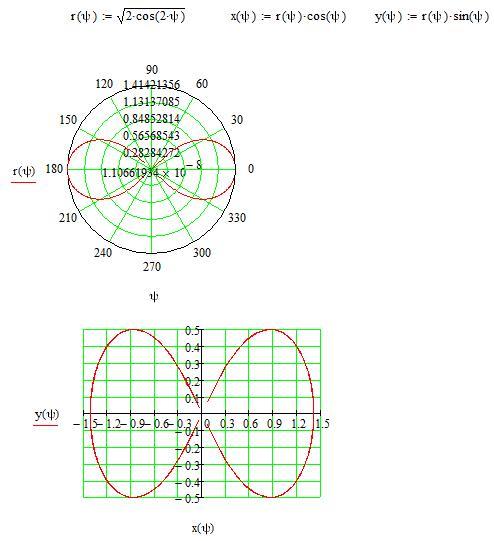 Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Построение графиков функций онлайн
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн.
| Оператор | Значение |
|---|---|
-
|
вычитание |
*
|
умножение |
/
|
деление |
^n
|
возведение в степень: x^n — x в степени n |
^(1/n)
|
корень степени n: x^(1/n) |
()
|
скобки |
| |
|
скобки модуля: |x| |
Список функций
| Имя | Описание | |
|---|---|---|
log2(x)
|
логарифм по основанию 2 от x | |
lg(x) или log10(x)
|
логарифм по основанию 10 от x | |
log(x;b)
|
логарифм x по основанию b log(x;3) | |
ln(x)
|
натуральный логарифм (логарифм по основанию e (2.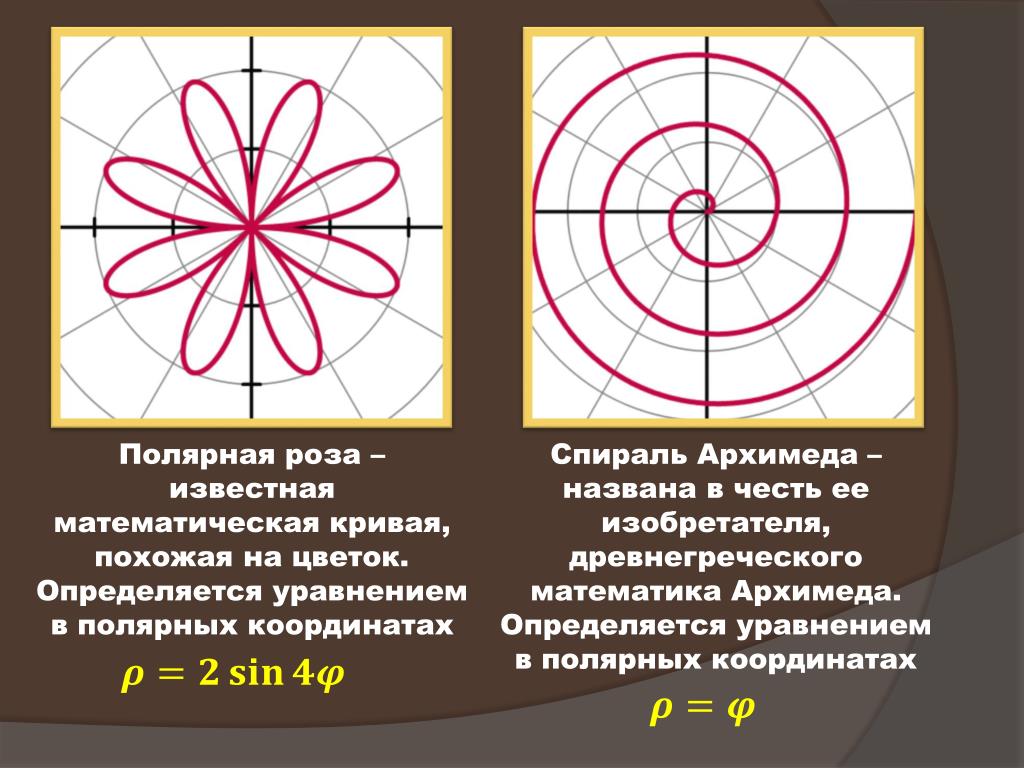 x x
|
экспонента от х (e в степени x) |
sqrt(x)
|
квадратный корень из x | |
sign(x)
|
функция знака: -1 если x<0, 1 если x>0 и 0 если x=0 | |
| Тригонометрические функции | ||
sin(x)
|
синус х | |
cos(x)
|
косинус х | |
tg(x) или
tan(x)
|
тангенс х | |
ctg(x) или
cot(x)
|
котангенс х | |
arcsin(x) или
asin(x)
|
арксинус х | |
arccos(x) или
acos(x)
|
арккосинус х | |
arctg(x) или
atan(x)
|
арктангенс х | |
arcctg(x) или
acot(x)
|
арккотангенс х | |
sinh(x) или
sh(x)
|
гиперболический синус х | |
cosh(x) или
ch(x)
|
гиперболический косинус х | |
tanh(x) или
th(x)
|
гиперболический тангенс х | |
coth(x) или
cth(x)
|
гиперболический котангенс х | |
asinh(x)
|
гиперболический арксинус х | |
acosh(x)
|
гиперболический арккосинус х | |
atanh(x)
|
гиперболический арктангенс х | |
acoth(x)
|
гиперболический арккотангенс х | |
Встроенные константы
| Имя | Описание |
|---|---|
pi
|
Пи = 3,14. .. ..
|
e
|
e = 2,71828… число Эйлера |
Полярные координаты | Алгебра и тригонометрия
Цели обучения
В этом разделе вы будете:
- Наносить точки с помощью полярных координат.
- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
На расстоянии более 12 км от порта парусник попадает в непогоду и сбивается с курса ветром силой 16 узлов (см. (рисунок)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Рисунок 1.
Построение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах[латекс]\,\влево(х,у\вправо)\,[/ латекс] в декартовой плоскости координат. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные [латекс]\,\левый(r,\тета\правый)\,[/латекс] и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью x-, которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата[latex]\,r\,[/latex] — это радиус или длина направленного отрезка прямой от полюса. Угол[латекс]\,\тета,[/латекс], измеренный в радианах, указывает направление[латекс]\,r.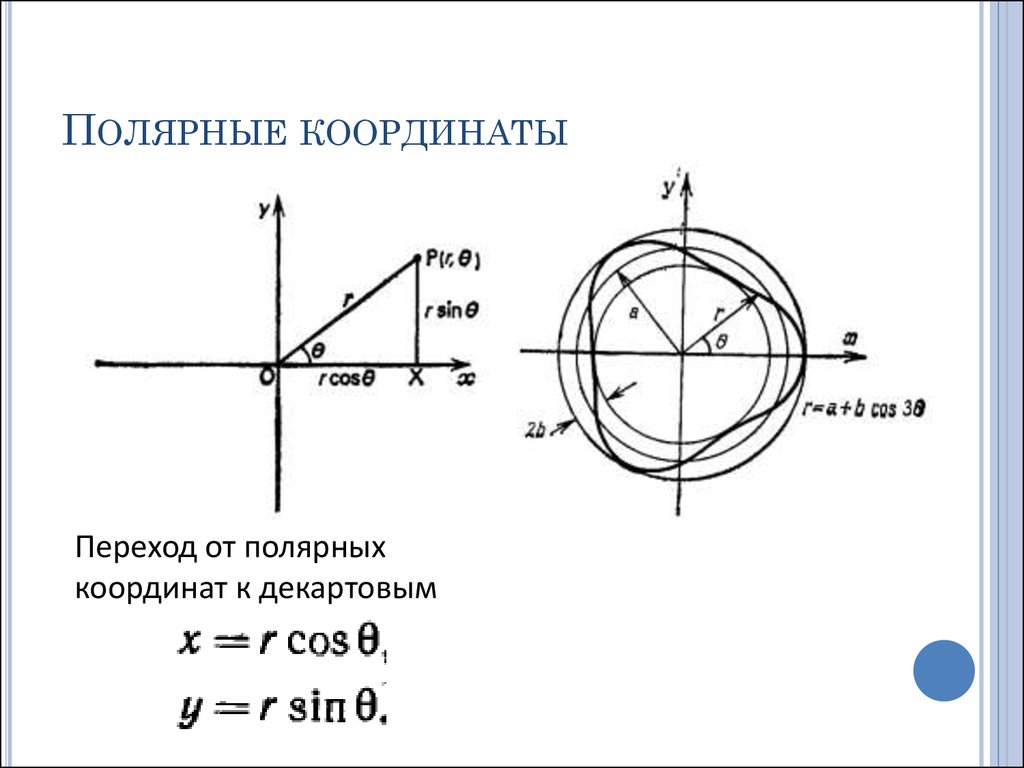 \,[/латекс]Мы двигаемся против часовой стрелки от полярной оси на угол[латекс]\ ,\theta ,[/latex]и измерьте направленный отрезок длины[latex]\,r\,[/latex]в направлении[latex]\,\theta .\,[/latex]Хотя мы сначала измерьте [латекс]\,\тета \,[/латекс], а затем [латекс]\,r,[/латекс] полярная точка записывается с помощью r -координата первая. Например, чтобы построить точку [латекс]\,\влево(2,\фракция{\пи} {4}\вправо),[/латекс] мы должны переместить[латекс]\,\фракция{\пи} {4 }\,[/latex]единицы в направлении против часовой стрелки, а затем длину 2 от полюса. Эта точка нанесена на сетку (рисунок).
\,[/латекс]Мы двигаемся против часовой стрелки от полярной оси на угол[латекс]\ ,\theta ,[/latex]и измерьте направленный отрезок длины[latex]\,r\,[/latex]в направлении[latex]\,\theta .\,[/latex]Хотя мы сначала измерьте [латекс]\,\тета \,[/латекс], а затем [латекс]\,r,[/латекс] полярная точка записывается с помощью r -координата первая. Например, чтобы построить точку [латекс]\,\влево(2,\фракция{\пи} {4}\вправо),[/латекс] мы должны переместить[латекс]\,\фракция{\пи} {4 }\,[/latex]единицы в направлении против часовой стрелки, а затем длину 2 от полюса. Эта точка нанесена на сетку (рисунок).
Рис. 2.
Построение точки на полярной сетке полярная сетка.
Показать решение
Попробуй
Нанесите точку[латекс]\,\влево(2,\,\frac{\pi }{3}\вправо)\,[/латекс]в полярную сетку.
Показать решение
Нанесение точки в полярной системе координат с отрицательной составляющей на полярной сетке.
Показать решение
Попробуйте
Нанесите точки [латекс]\,\влево(3,-\frac{\pi }{6}\right)[/латекс]и[латекс]\,\влево(2,\frac{ 9\pi }{4}\right)\,[/latex]на той же полярной сетке.
Показать решение
Преобразование полярных координат в прямоугольные
Когда задан набор полярных координат, нам может понадобиться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными [latex]\,x,\,y,\,r,\,[/latex] и [latex]\,\theta .[/latex]
[латекс]\begin{array}{l}\begin{array}{l}\\ \mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\ ,\theta \end{массив}\hfill \\ \mathrm{sin}\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta \hfill \end{массив }[/латекс]
При опускании перпендикуляра из точки плоскости на ось x- образуется прямоугольный треугольник, как показано на (Рисунок). Простой способ запомнить приведенные выше уравнения — представить [латекс]\,\mathrm{cos}\,\тета \,[/латекс] как примыкающую сторону к гипотенузе и [латекс]\,\mathrm{sin} \,\theta\,[/latex] как противоположная сторона гипотенузы.
Рисунок 5.
Преобразование полярных координат в прямоугольные
Преобразование полярных координат [латекс]\,\left(r,\,\theta \right)\,[/latex]в прямоугольные координаты[латекс ]\,\left(x,\,y\right),[/latex] пусть
[латекс]\mathrm{cos}\,\theta =\frac{x}{r}\to x=r\mathrm{cos}\,\theta [/latex]
[латекс]\mathrm{sin }\,\theta =\frac{y}{r}\to y=r\mathrm{sin}\,\theta [/latex]
How To
Учитывая полярные координаты, преобразовать в прямоугольные координаты.
- Учитывая полярную координату [латекс]\,\влево(г,\тета \вправо),[/латекс] напишите[латекс]\,х=г\mathrm{cos}\,\тета \,[ /латекс] и [латекс]\,y=r\mathrm{sin}\,\тета .[/латекс]
- Оценить [латекс]\,\mathrm{cos}\,\theta \,[/latex]и[латекс]\,\mathrm{sin}\,\theta .[/latex]
- Умножьте [латекс]\,\mathrm{cos}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату x- прямоугольной формы.

- Умножьте [латекс]\,\mathrm{sin}\,\theta \,[/латекс] на [латекс]\,r\,[/латекс], чтобы найти координату y- прямоугольной формы.
Запись полярных координат в виде прямоугольных координат
Запись полярных координат [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] в виде прямоугольных координат.
Показать решение
Запись полярных координат в виде прямоугольных координат
Запись полярных координат[латекс]\,\влево(-2,0\вправо)\,[/латекс]в виде прямоугольных координат.
Показать решение
Попробуйте
Запишите полярные координаты[латекс]\,\влево(-1,\фракция{2\пи }{3}\вправо)\,[/латекс]в виде прямоугольных координат.
Показать решение
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 9{2}\hfill \\ \mathrm{tan}\,\theta =\frac{y}{x}\,\hfill \end{array}[/latex]
Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 9{2}\hfill \\ \mathrm{tan}\,\theta =\frac{y}{x}\,\hfill \end{array}[/latex]
Рис. 8.
Запись прямоугольных координат as Полярные координаты
Преобразовать прямоугольные координаты[латекс]\,\влево(3,3\вправо)\,[/латекс]в полярные координаты.
Показать решение
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки[латекс]\,\влево(-3\sqrt{2},\,\frac{5\pi }{4}\right)\,[/latex]и[латекс]\,\влево (3\sqrt{2},-\frac{7\pi }{4}\right)\,[/latex] совпадет с исходным решением [latex]\,\left(3\sqrt{2}, \,\frac{\pi }{4}\right).\,[/latex]Точка[латекс]\,\left(-3\sqrt{2},\,\frac{5\pi }{4 }\right)\,[/latex]обозначает движение против часовой стрелки на [latex]\,\pi ,\,[/latex], которое прямо противоположно [latex]\,\frac{\pi }{4}. \ ,[/latex]Радиус выражается как [латекс]\,-3\sqrt{2}.\,[/latex]Однако угол[латекс]\,\frac{5\pi }{4}\, [/latex] находится в третьем квадранте, и, поскольку [latex]\,r\,[/latex]отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и [латекс]\,\left(3\sqrt{2},\,\,\frac{\pi }{4}\right).\,[/latex]Точка [латекс]\ ,\left(3\sqrt{2},\,-\frac{7\pi }{4}\right)\,[/latex] — ход дальше по часовой стрелке на [latex]\,-\frac{7\ pi }{4},\,[/latex]из [латекса]\,\frac{\pi }{4}.\,[/latex]Радиус,[латекс]\,3\sqrt{2},\ ,[/латекс]то же самое.
\ ,[/latex]Радиус выражается как [латекс]\,-3\sqrt{2}.\,[/latex]Однако угол[латекс]\,\frac{5\pi }{4}\, [/latex] находится в третьем квадранте, и, поскольку [latex]\,r\,[/latex]отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и [латекс]\,\left(3\sqrt{2},\,\,\frac{\pi }{4}\right).\,[/latex]Точка [латекс]\ ,\left(3\sqrt{2},\,-\frac{7\pi }{4}\right)\,[/latex] — ход дальше по часовой стрелке на [latex]\,-\frac{7\ pi }{4},\,[/latex]из [латекса]\,\frac{\pi }{4}.\,[/latex]Радиус,[латекс]\,3\sqrt{2},\ ,[/латекс]то же самое.
Преобразование уравнений между полярной и прямоугольной формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
How To
Имея уравнение в полярной форме, постройте его график с помощью графического калькулятора.
- Измените MODE на POL , представляя полярную форму.
- Нажмите кнопку Y= , чтобы открыть экран, позволяющий ввести шесть уравнений: [латекс]\,{r}_{1},\,\,{r}_{2},\,\,. \,\,.\,\,.\,\,\,\,{r}_{6}.[/латекс]
- Введите полярное уравнение, установите его равным [латекс]\,r.[/латекс]
- Пресс ДИАГРАММА 9{2}\,[/latex] в полярной форме.
Показать решение
Идентификация и построение полярных уравнений путем преобразования в прямоугольные уравнения
Мы узнали, как преобразовывать прямоугольные координаты в полярные координаты, и мы увидели, что точки действительно совпадают.
 Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.Построение графика полярного уравнения путем преобразования в прямоугольное уравнение
Преобразуйте полярное уравнение[латекс]\,r=2\mathrm{sec}\,\theta \,[/латекс] в прямоугольное уравнение и нарисуйте соответствующий график.
Показать решение
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение[latex]\,r=\frac{3}{1-2\mathrm{cos}\,\theta }\,[/latex]в виде декартова уравнение.
Показать решение
Анализ
В этом примере правая часть уравнения может быть расширена, а уравнение еще больше упрощено, как показано выше. Однако уравнение нельзя записать в виде одной функции в декартовой форме. Мы можем захотеть записать прямоугольное уравнение в стандартной форме гиперболы.
 Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]
Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]Попробуйте
Перепишите полярное уравнение[latex]\,r=2\mathrm{sin}\,\theta \,[/latex] в декартовой форме.
Показать решение
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение[латекс]\,r=\mathrm{sin}\left(2\theta \right)\,[/latex]в декартовой форме.
Показать решение
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными координатами. 9{2}\hfill \\ \hfill & \mathrm{tan}\,\theta =\frac{y}{x}\hfill \end{массив}[/latex]
Ключевые понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или исходной точки.
- Чтобы нанести точку в виде [латекс]\,\влево(r,\тета\вправо),\,\тета >0,\,[/латекс] переместите против часовой стрелки от полярной оси на угол [латекс]\,\theta ,\,[/латекс], а затем продлите направленный отрезок от полюса на длину [латекс]\,r\,[/латекс] в направлении [латекс]\,\тета .
 {2}}.\,[/latex] См. (рисунок).
{2}}.\,[/latex] См. (рисунок). - Преобразование уравнений между полярной и прямоугольной формой означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. (Рисунок), (Рисунок) и (Рисунок).
- Использование соответствующих замен позволяет переписать полярное уравнение как уравнение прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. (Рисунок), (Рисунок) и (Рисунок).
Упражнения по разделам
Вербальные
Чем полярные координаты отличаются от прямоугольных координат?
Показать решение
Чем полярные оси отличаются от осей x и y декартовой плоскости?
Объясните, как изображаются полярные координаты.
Показать решение
Как расположены точки [латекс]\,\left(3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(-3,\frac{\ pi }{2}\right)\,[/latex]связаны?
Объясните, почему точки [латекс]\,\left(-3,\frac{\pi }{2}\right)\,[/latex] и [латекс]\,\left(3,-\frac{ \pi }{2}\right)\,[/latex] одинаковы.

Показать решение
Алгебраический
Для следующих упражнений преобразуйте заданные полярные координаты в декартовы координаты с помощью [латекс]\,r>0\,[/латекс]и[латекс]\,0\le \theta \le 2\pi . \,[/latex]Не забывайте учитывать квадрант, в котором находится данная точка, при определении[latex]\,\theta \,[/latex]для точки.
[латекс]\влево(7,\фракция{7\пи }{6}\вправо)[/латекс]
[латекс]\влево(5,\пи \вправо)[/латекс]
Показать решение
[латекс]\влево(6,-\frac{\pi }{4}\вправо)[/латекс]
[латекс]\влево(-3,\frac{\pi }{6}\вправо)[/латекс]
Показать решение
[латекс]\left(4,\frac{7\pi }{4}\right)[/latex]
В следующих упражнениях преобразуйте заданные декартовы координаты в полярные координаты с помощью [латекс]\,r> 0,\,\,0\le \theta <2\pi .\,[/latex]Не забудьте рассмотреть квадрант, в котором находится данная точка.

[латекс]\влево(4,2\вправо)[/латекс]
Показать решение
[латекс]\влево(-4,6\вправо)[/латекс]
9{2}=9x[/latex][latex]9xy=1[/latex]
Показать решение
Для следующих упражнений преобразуйте данное полярное уравнение в декартово уравнение. Если возможно, напишите в стандартной форме коники и определите представленное коническое сечение.
[латекс]r=3\mathrm{sin}\,\theta [/latex]
[латекс]r=4\mathrm{cos}\,\theta [/latex]
Показать решение
[латекс]r=\frac{4}{\mathrm{sin}\,\theta +7\mathrm{cos}\,\theta}[/latex]
[латекс]r=\frac{6} {\ mathrm {cos} \, \ theta +3 \ mathrm {sin} \, \ theta} [/ латекс] 9{2}=4[/latex]
Показать решение
[латекс]r=\frac{1}{4\mathrm{cos}\,\theta -3\mathrm{sin}\,\theta}[/latex]
[латекс]r=\frac{3 }{\mathrm{cos}\,\theta -5\mathrm{sin}\,\theta }[/latex]
Показать решение
Графический
Для следующих упражнений найдите полярные координаты точки.

Показать решение
Показать решение
Для следующих упражнений отметьте точки.
[латекс]\влево(-2,\frac{\pi }{3}\вправо)[/латекс]
Показать решение
[латекс]\влево(-1,-\frac{\pi }{2}\right)[/latex]
[латекс]\left(3.5,\frac{7\pi }{4}\right )[/latex]
Показать решение
[латекс]\влево(-4,\frac{\pi} {3}\вправо)[/латекс]
[латекс]\влево(5,\frac{\pi} {2}\вправо)[ /латекс]
Показать решение
[латекс]\left(4,\frac{-5\pi }{4}\right)[/latex]
[латекс]\left(3,\frac{5\pi }{6}\right )[/latex]
Показать решение
[латекс]\влево(-1,5,\фракция{7\пи }{6}\вправо)[/латекс] 9{2}=3x[/latex]
Показать решение
Для следующих упражнений преобразуйте уравнение из полярной формы в прямоугольную и постройте график на прямоугольной плоскости.

[латекс]r=6[/латекс]
[латекс]r=-4[/латекс]
Показать решение
[латекс]\theta =-\frac{2\pi }{3}[/latex]
[латекс]\theta =\frac{\pi }{4}[/latex]
Показать решение
[латекс]r=\mathrm{sec}\,\theta [/latex]
[латекс]r=-10\mathrm{sin}\,\theta [/latex]
Показать решение
[латекс]r=3\mathrm{cos}\,\theta [/латекс]
Технология
С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(2,-\frac{ \pi }{5}\right).\,[/latex]Округлите до тысячных.
Показать решение
С помощью графического калькулятора найдите прямоугольные координаты [латекса]\,\left(-3,\frac{3\pi }{7}\right).\,[/latex]Округлите до тысячных.
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(-7,8\вправо)\,[/латекс]в градусах.
 Округлить до тысячных.
Округлить до тысячных.Показать решение
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\влево(3,-4\вправо)\,[/латекс]в градусах. Округлить до сотых.
Используйте графический калькулятор, чтобы найти полярные координаты [латекс]\,\левый(-2,0\правый)\,[/латекс]в радианах. Округлить до сотых.
Показать решение
Расширения
Описать график [латекс]\,r=a\mathrm{sec}\,\theta ;a>0.[/latex]
Описать график [латекс]\,r=a\ mathrm{sec}\,\theta ;a<0.[/latex]
Показать решение
Описать график [латекс]\,r=a\mathrm{csc}\,\theta ;a>0.[/latex]
Описать график [латекс]\,r=a\mathrm{csc }\,\theta ;a<0.[/latex]
Показать решение
Какие полярные уравнения дадут косую линию?
Для следующего упражнения постройте график полярного неравенства.
[латекс]r<4[/латекс]
Показать решение
[латекс]0\le \theta \le \frac{\pi }{4}[/latex]
[латекс]\theta =\frac{\pi }{4},\,r\,\ge \,2[/латекс]
Показать решение
[латекс]\theta =\frac{\pi }{4},\,r\,\ge -3[/latex]
[латекс]0\le \theta \le \frac{\pi }{ 3},\,r\,<\,2[/latex]
Показать решение
[латекс]\frac{-\pi }{6}<\theta \le \frac{\pi }{3},-3
Глоссарий
- полярная ось
- на полярной сетке, эквивалент положительной оси x- на прямоугольной сетке
- полярные координаты
- на полярной сетке координаты точки, помеченной угол поворота от полярной оси и [латекс]\,r\,[/латекс] представляет собой радиус или расстояние точки от полюса в направлении [латекс]\,\тета [/латекс]
- полюс
- происхождение полярной сетки
10.
 3: Полярные координаты — Математика LibreTexts
3: Полярные координаты — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50235
- ОпенСтакс
- ОпенСтакс
Цели обучения
- Нанесение точек с использованием полярных координат.
- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
На расстоянии более \(12\) километров от порта парусник попадает в непогоду и сбивается с курса ветром силой \(16\) узлов (см.
 рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.Рисунок \(\PageIndex{1}\)
Нанесение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольные координаты \((x,y)\) в декартовой координатной плоскости . Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные \((r,\theta)\) и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительным \(x\) 9Ось 0029 — теперь рассматривается как полярная ось, а начало координат — как полюс.
 Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).
Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).Рисунок \(\PageIndex{2}\)
Пример \(\PageIndex{1}\): Нанесение точки на полярную сетку
Нанесение точки \(\left(3, \dfrac{\pi}{2}\right)\) на полярной сетке.
Решение
Угол \(\dfrac{\pi}{2}\) находится путем протягивания против часовой стрелки \(90°\) от полярной оси.
 Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).
Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).Рисунок \(\PageIndex{3}\)
Упражнение \(\PageIndex{1}\)
Постройте точку \(\left(2, \dfrac{\pi}{3 }\right)\) в полярной сетке.
- Ответить
Рисунок \(\PageIndex{4}\)
Пример \(\PageIndex{2}\): построение точки в полярной системе координат с отрицательной составляющей
Нанесение точки \(\left(−2, \dfrac{\pi}{6}\right) \) на полярной сетке.
Решение
Мы знаем, что \(\dfrac{\pi}{6}\) находится в первом квадранте. Однако \(r=−2\). Мы можем построить точку с отрицательным значением \(r\) двумя способами:
- dfrac{\pi}{6}\) в направлении против часовой стрелки и продолжение направленного отрезка \(2\) единиц в первый квадрант. Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;
- Переместите \(\dfrac{\pi}{6}\) в направлении против часовой стрелки и нарисуйте направленный отрезок от полюса \(2\) единиц в отрицательном направлении в третий квадрант.

См. рисунок \(\PageIndex{5a}\). Сравните это с графиком полярной координаты \((2,π6)\), показанным на рисунке \(\PageIndex{5b}\).
Рисунок \(\PageIndex{5}\)
Упражнение \(\PageIndex{2}\)
Постройте точки \(\left(3,−\dfrac{\pi}{ 6}\справа)\) и \(\слева(2,\dfrac{9\pi}{4}\right)\) на той же полярной сетке.
- Ответить
Рисунок \(\PageIndex{6}\)
Преобразование полярных координат в прямоугольные
Когда задан набор полярных координат , нам может потребоваться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \ sin \theta\)
Если опустить перпендикуляр из точки плоскости на ось x-, получится прямоугольный треугольник, как показано на рисунке \(\PageIndex{7}\).
 Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.Рисунок \(\PageIndex{7}\)
ПРЕОБРАЗОВАНИЕ ПОЛЯРНЫХ КООРДИНАТ В ПРЯМОУГОЛЬНЫЕ
Преобразование полярных координат \((r, \theta)\) в прямоугольные координаты \((x, y)\) , пусть
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y =r \sin\тета\]
Как выполнить преобразование заданных полярных координат в прямоугольные.
- Учитывая полярную координату \((r,\theta)\, запишите \(x=r \cos \theta\) и \(y=r \sin \theta\).
- Оценить \(\cos\theta\) и \(\sin\theta\).
- Умножьте \(\cos \theta\) на \(r\), чтобы найти \(x\) — координату прямоугольной формы.
- Умножьте \(\sin\theta\) на \(r\), чтобы найти координату \(y\) — прямоугольной формы.

Пример \(\PageIndex{3A}\): запись полярных координат в виде прямоугольных координат
Запись полярных координат \(\left(3,\dfrac{\pi}{2}\right)\) в виде прямоугольных координат.
Решение
Используйте эквивалентные соотношения.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y& = 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
Прямоугольные координаты \((0,3)\). См. рисунок \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\)
Пример \(\PageIndex{3B}\): запись полярных координат в виде прямоугольных координат
Запишите полярные координаты \((−2,0)\) в виде прямоугольных координат.
Решение
См. рисунок \(\PageIndex{9}\). Записав полярные координаты в виде прямоугольника, мы имеем
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
Прямоугольные координаты также равны \((−2,0)\).

Рисунок \(\PageIndex{9}\)
Упражнение \(\PageIndex{3}\)
Запишите полярные координаты \(\left(−1,\dfrac{2\pi}{3}\right)\) в виде прямоугольных координат.
- Ответить
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 92\)
\(\tan \theta=\dfrac{y}{x}\)
Рисунок \(\PageIndex{10}\)
Пример \(\PageIndex{4} \): запись прямоугольных координат в виде полярных координат
Преобразование прямоугольных координат \((3,3)\) в полярные координаты.
Решение
Мы видим, что исходная точка \((3,3)\) находится в первом квадранте.
92}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\] Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает
Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это даетИтак, \(r=3\ sqrt{2}\) и \(\theta=\dfrac{\pi}{4}\), что дает нам полярную точку \((3\sqrt{2},\dfrac{\pi}{4})\ ). См. рисунок \(\PageIndex{11}\).
Рисунок \(\PageIndex{11}\)
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как и наше первое решение. Например, точки \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) и \(\left(3\sqrt{2},−\dfrac{ 7\pi}{4}\right)\) будет совпадать с исходным решением \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) указывает на движение против часовой стрелки на \(\pi\), что прямо противоположно \(\ dfrac{\pi}{4}\). Радиус выражается как \(−3\sqrt{2}\). Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант .
 Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.Преобразование уравнений между полярной и прямоугольной формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
Как: Имея уравнение в полярной форме, начертите его с помощью графического калькулятора
- Измените MODE на POL , представляя полярную форму.

- Нажмите кнопку Y= , чтобы вызвать экран, позволяющий ввести шесть уравнений: \(r_1\), \(r_2\),…, \(r_6\).
- Введите полярное уравнение, установите его равным \(r\).
- Нажмите ГРАФИК .
Пример \(\PageIndex{5A}\): запись декартова уравнения в полярной форме 92=6y\) (b) полярная форма \(r=6 \sin \theta\)
Декартово или прямоугольное уравнение наносится на прямоугольную сетку, а полярное уравнение наносится на полярную сетку. Ясно, что графики идентичны.
Упражнение \(\PageIndex{4A}\):
Переписывание декартова уравнения в полярной форме
Перепишите декартово уравнение \(y=3x+2\) как полярное уравнение.
- Ответить
Мы будем использовать соотношения \(x=r \cos \theta\) и \(y=r \sin \theta\). 92\) в полярной форме.
- Ответить
\(r=\sqrt{3}\)
Определение и построение полярных уравнений путем преобразования в уравнения прямоугольной формы
Мы научились преобразовывать прямоугольные координаты в полярные координаты и увидели, что точки действительно совпадают.
 Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.Пример \(\PageIndex{6A}\): построение графика полярного уравнения путем преобразования в прямоугольное уравнение
Преобразование полярного уравнения \(r=2 \sec \theta\) в прямоугольное уравнение и построение соответствующего ему графика .
Решение
Преобразование
\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \ theta &=2 \\ x &=2 \end{align*}\]
Обратите внимание, что уравнение \(r=2 \sec \theta\), нарисованное на полярной сетке, явно совпадает с вертикальной линией \( x=2\), нарисованный на прямоугольной сетке (см. рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.

Рисунок \(\PageIndex{14}\): (a) Полярная сетка (b) Прямоугольная система координат
Аналогичное обсуждение показало бы, что график функции \(r=2 \csc \theta\) будет горизонтальной линией \(y=2\). На самом деле \(r=c\csc\theta\) является стандартной формой горизонтальной линии в полярной форме, соответствующей прямоугольной форме \(y=c\).
Пример \(\PageIndex{6B}\): переписывание полярного уравнения в декартовой форме 92 \end{align*}\]
Когда все наше уравнение было изменено с \(r\) и \(\theta\) на \(x\) и \(y\), мы можем остановиться, если нас не попросят решить для \(y\) или упростить. См. рисунок \(\PageIndex{15}\).
Рисунок \(\PageIndex{15}\)
График в форме песочных часов называется гиперболой . Гиперболы имеют много интересных геометрических свойств и приложений, которые мы будем исследовать далее в разделе «Аналитическая геометрия».
 2}. \конец{массив}\) 9{\frac{2}{3}}\)
2}. \конец{массив}\) 9{\frac{2}{3}}\)СМИ
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с полярными координатами.
- Введение в полярные координаты
- Сравнение полярных и прямоугольных координат
Ключевые уравнения
Формулы преобразования \(\cos\theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\)
\(\sin\theta=\dfrac{y}{r} \rightarrow y=r \sin\theta\) 92\)
\(\тангенс\тета=\dfrac{y}{x}\)
Основные понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или источника.
- Чтобы нанести точку в виде \((r,\theta)\), \(\theta>0\), переместитесь против часовой стрелки от полярной оси на угол \(\theta\), а затем продлите направленный отрезок от полюса на длину \(r\) в направлении \(\theta\).
 2}\). См. пример \(\PageIndex{5}\).
2}\). См. пример \(\PageIndex{5}\). - Преобразование уравнений между полярной и прямоугольной формой означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. Пример \(\PageIndex{6}\), Пример \(\PageIndex{7}\) и Пример \(\PageIndex{8}\).
- Использование соответствующих замен позволяет переписать полярное уравнение как уравнение прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. Пример \(\PageIndex{9}\), Пример \(\PageIndex{10}\) и Пример \(\PageIndex{11}\).
Эта страница под названием 10.3: Polar Coordinates распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- полярные координаты
- полярная сетка
- прямоугольные координаты
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus - источник[1]-math-2682
Интерактивировать: Полярные координаты
Наставник: Вы, вероятно, знакомы с декартовой системой координат, которая позволяет вам строить графики. точки и функции на координатной плоскости. Если вам дан набор точек в виде (x, y), вы сможете отобразить их на осях x и y графика.
Студент: Да. Если бы мне дали точку (2,3), я бы начал с начала координат и прошел две единицы до прямо по оси x, а затем переместитесь вверх на 3 единицы в направлении y.
Наставник: Это верно. И если бы вам дали функцию, скажем, y=2x+3, вы, вероятно, могли бы построить ее график. слишком.
Ученик: Конечно, я бы выбрал значения x, которые я бы ввел в функцию, чтобы получить значения у для этой функции. Затем я нарисовал точки на графике.
Наставник: Да! Знаете ли вы, что вы также можете наносить точки на график другого типа на основе полярной диаграммы? Система координат.

Ученик: Что такое полярная система координат?
Наставник: Полярная система координат — это круговая, а не прямоугольная система координат. Ты точки графика, заданные значением r, которое представляет собой расстояние от центра; и угол мера, которая дается в градусах или, чаще, в радианах. Вы помните, что такое радианы?
Ученик: Конечно, это еще одна единица измерения углов. Круг содержит 360 градусов что совпадает с 2π радиан. Но для чего бы вы использовали эту систему?
Ментор: Ну, иногда правильнее описать локацию круговым движением. а не по прямой. Эта система хорошо подходит для тригонометрических функций и используется в навигации, потому что значения могут быть нанесены на график с точки зрения расстояния (r) и направления (угол, также упоминается как греческая буква тета, показанная как символ θ).
Ученик: Как бы вы нанесли точки на полярный график?
Наставник: Полярная система координат имеет оси, подобные декартовой системе, и точку, подобную происхождения, за исключением того, что он называется столб.
 Он также имеет луч, который проходит горизонтально через полюс, называемый
полярная ось. Вместо квадратной сетки есть концентрические круги с центром на полюсе, которые получают
равномерно больше и расходятся от полюса. Полярная координатная плоскость выглядит так:
Он также имеет луч, который проходит горизонтально через полюс, называемый
полярная ось. Вместо квадратной сетки есть концентрические круги с центром на полюсе, которые получают
равномерно больше и расходятся от полюса. Полярная координатная плоскость выглядит так:Наставник: Как и прямоугольные координаты, полярные координаты также называются упорядоченной парой, но значение каждого из чисел разное. Первое число в паре координат, r, представляет собой расстояние от полюса и походит на измерение радиуса круга. Секунда номер пары, θ, представляет угол, измеренный от горизонтальной оси. Полярная ось представляет угловую меру 0 радиан или 0 градусов. Движение против часовой стрелки от этой оси представляет собой положительную меру угла, а по часовой стрелке — отрицательную.
Ученик: Думаю, я понял. Углы определяются в полярной системе координат так, как они единичный круг, обычно в радианах.
 Итак, если вам дана полярная координата (3, π/4),
точка находится в трех единицах от центра под углом π/4 радиан, измеренным
против часовой стрелки от полярной оси:
Итак, если вам дана полярная координата (3, π/4),
точка находится в трех единицах от центра под углом π/4 радиан, измеренным
против часовой стрелки от полярной оси:Ученик: Получается, что заданные координаты тоже могут быть отрицательными?
Ментор: Это отличный вопрос, и ответ положительный. Как и на единичном круге, отрицательное углы идут по часовой стрелке от полярной оси. Вы помните -3π/4 это то же самое как 5π/4?
Ученик: Да, а -4π/3 — это то же самое, что 2π/3?
Наставник: Это верно. И, поскольку вы можете добавить столько вращений в виде кратных 2Ï, сколько вам нужно хотите, любой угол может иметь бесконечное количество отрицательных и положительных значений. Кроме того, р может быть отрицательным. Отрицательный r указывает, что точка находится в противоположном квадрант от угла, заданного в паре координат. Например, π/4 находится в 1-м квадрант, поэтому положительные значения r нанесены на r единиц от полюса в 1-м квадранте и отрицательные значения нанесены в противоположном квадранте, 3-м квадранте, на угол идентифицируется как 5π/4.
 Как вы думаете, где находится точка (-2, π/3)?
Как вы думаете, где находится точка (-2, π/3)?Ученик: Ну, так как (2, π/4) было измерено на 2 единицы вправо вдоль полярной оси, то -2 будет указывают, что точка измеряется на 2 единицы левее вдоль полярной оси, а затем на π/4 градусов против часовой стрелки. Поскольку угол π/3 лежит в первой четверти, затем, чтобы нанести точку (-2, π/3), вы должны нанести точку в двух единицах от полюса вдоль угол 4π/3. Верно?
Наставник: Это верно. Это будет выглядеть так:
Ученик: Значит, одна точка может иметь много разных значений?
Наставник: Правильно! Значения для r могут быть заданы как положительные и отрицательные значения, а θ может быть не только в положительных и отрицательных значениях, но и в виде любого значения θ + любого кратного из 2π. Таким образом, в отличие от декартовой системы, где каждая точка имеет уникальный набор координат, в В полярной системе любая точка может иметь бесконечное количество координат!
Ученик: Это означает, что точка, заданная как (2,π/4), также может быть задана как (2,-7π/4) или (2, 9π/4) или (-2,5π/4)!
Ментор: Точно.
 Попробуйте нанести эти точки на график с помощью действия «Полярные координаты» и убедитесь, что они
тот самый момент!
Попробуйте нанести эти точки на график с помощью действия «Полярные координаты» и убедитесь, что они
тот самый момент!исчисление — Пытаюсь изобразить эти точки в полярной системе координат
Я не решаюсь написать хотя бы частичный ответ, так как без картинок он будет безнадежно неадекватным. Возможно, кто-то с навыками рисования даст ответ и сделает этот устаревшим.
Вам действительно нужен живой человек, чтобы показать вам, что происходит. Или как слабое второе место, погуглите «Полярные координаты». Несколькими записями ниже есть пара видео. Не слишком впечатляюще, но лучше, чем ничего.
Но вот частичный ответ на ваш вопрос.
Знакомая вам прямоугольная система координат представляет собой «схему адресации» для точек на плоскости. Полярная система координат — это совершенно другая схема адресации.
Пусть $O$ будет источником. Нарисуйте обычные оси, но сконцентрируйтесь на 9.0021 положительный

Пример: Пусть $P$ имеет полярные координаты $(4, \pi/6)$. Итак, нам нужно повернуть положительную ось $x$ на $30$ градусов и выйти наружу на расстояние $4$ от начала координат. Я надеюсь, что вы сможете вычислить, используя базовые элементы прямоугольного треугольника, и увидите, что $P$ имеет прямоугольные координаты $(2\sqrt{3},2)$.
Вам следует немного потренироваться, переходя от полярных координат к прямоугольным и наоборот. В вашем тексте будет много упражнений.
Рисунок $r=2+\sin\theta$: Точками на этой кривой являются все точки с полярным адресом $(r,\theta)$ и такие, что $r=2+\sin\theta$ .
Читая далее, рисуйте.
Начнем с $\theta=0$. Таким образом, мы вообще не отвернулись от положительной оси $x$. И мы хотим, чтобы расстояние от начала координат было $2+\sin(0)$. Таким образом, мы получаем точку с прямоугольными координатами $(2,0)$.
Теперь возьмите $\theta=\pi/6$. Итак, $2+\sin\theta=2,5$.
 Теперь наша точка $P$ находится на расстоянии $2,5$ от начала координат, а $PO$ составляет угол $30$ градусов с положительной осью $x$.
Теперь наша точка $P$ находится на расстоянии $2,5$ от начала координат, а $PO$ составляет угол $30$ градусов с положительной осью $x$.Продолжайте в том же духе, нанося точки. Но это , а не , как мне кажется. Я бы представил, что $\theta$ растет, то есть угол с положительной осью $x$ растет, поэтому мой карандаш движется против часовой стрелки. Тогда $2+\sin\theta$, расстояние от начала координат, по крайней мере, некоторое время увеличивается. Он растет до тех пор, пока $\theta$ не достигнет $\pi/2$, когда $r=3$. Таким образом, точка с прямоугольными координатами $(0,3)$ находится на кривой. Чтобы перейти от $\theta=0$ к $\theta=\pi/2$, нарисуйте кривую, которая начинается на расстоянии $2$ от начала координат и, двигаясь против часовой стрелки, продвигается все дальше и дальше от начала координат, пока расстояние достигает $3$, когда вы достигаете положительной оси $y$.
Продолжим за $\pi/2$. Теперь $\sin\theta$ уменьшается и достигает $0$ при $\theta=pi$.
 Таким образом, по мере того, как вы продолжаете движение против часовой стрелки, $r$ уменьшается, пока не достигнет $2$ в точке $\theta=\pi$. Мы оказываемся в точке с прямоугольными координатами (-2,0)$.
Таким образом, по мере того, как вы продолжаете движение против часовой стрелки, $r$ уменьшается, пока не достигнет $2$ в точке $\theta=\pi$. Мы оказываемся в точке с прямоугольными координатами (-2,0)$.Продолжить после $\pi$. Теперь $\sin\theta$ отрицательное и становится еще более отрицательным. Таким образом, $r$ падает ниже $2$ и достигает $1$ при $\theta=3\pi/2$. Мы достигли точки с прямоугольными координатами $(0,-1)$.
Теперь продолжайте от $\theta=3\pi/2$ до $\theta=2\pi$. Вы должны быть в состоянии соединиться с первой точкой, которую мы нарисовали на кривой.
После всего этого у нас получается что-то похожее на перевернутое валентиночное сердце или, для менее романтичных настроений, на сидящего толстого остроголового мужчину.
Рисунок $r=5\sin\theta$: К сожалению, здесь есть одна сложность. Есть два соглашения о том, как обращаться с отрицательным значением $r$. Соглашение $1$ гласит, что отрицательное значение $r$ не имеет смысла.
 Соглашение $2$ гласит, что, например, чтобы нанести точку с полярными координатами $(-8,\theta)$, вы представляете построение $(8,\theta)$ и отражаете результат через начало координат или, что то же самое, поворачиваете на $180 $ градусов. Я не знаю, какое соглашение использует ваш курс/книга.
Соглашение $2$ гласит, что, например, чтобы нанести точку с полярными координатами $(-8,\theta)$, вы представляете построение $(8,\theta)$ и отражаете результат через начало координат или, что то же самое, поворачиваете на $180 $ градусов. Я не знаю, какое соглашение использует ваш курс/книга.Представьте, что вы рисуете $r=5\sin\theta$, используя соглашение $1$. Начните с $\тета=0$. Тогда $r=0$, значит, мы в начале координат. Теперь пусть $\theta$ растет в сторону $\theta=\pi/2$. По мере роста $\theta$ растет $\sin\theta$, поэтому по мере увеличения нашего угла с положительной осью $x$ наше расстояние от начала координат увеличивается, пока при $\theta=\pi/2$ расстояние не достигнет $5 $, и мы получаем $(0,5)$. Теперь пусть $\theta$ увеличивается от $\pi/2$ до $\pi$. Наше расстояние от начала координат уменьшается и достигает $0$ при $\theta=\pi$, поэтому мы соединяемся с нашей начальной точкой. По мере того, как мы идем дальше $\pi$, $\sin\theta$ становится отрицательным, и по соглашению $1$ мы не получаем никакой кривой.

Если вместо этого мы воспользуемся соглашением $2$, то по мере перехода от $\pi$ к $2\pi$ мы снова проведем кривую (вспомните про отражение через начало координат). Таким образом, визуально два разных соглашения дают кривые, которые выглядят одинаково. Что , а не всегда будет правдой.
Район: Я не буду этого делать. Но при тщательном рисовании вы сможете определить область, о которой идет речь. И вы были правы, считая точки пересечения важными. Вы правильно нашли соответствующий $\theta$.
Как создать полярный график в Excel
В этом руководстве показано, как создать полярный график во всех версиях Excel: 2007, 2010, 2013, 2016 и 2019.
Полярный график — скачать бесплатный шаблон
Загрузите наш бесплатный шаблон полярного графика для Excel.
Загрузить сейчас
В этой статье
- Полярный график — загрузка бесплатного шаблона
- Начало работы
- Шаг № 1: Настройте вспомогательную таблицу.

- Шаг № 2. Вычислите значения угла (тета).
- Шаг №3: Вычислите значения радиуса.
- Шаг №4: Скопируйте последние значения радиуса во вспомогательную строку.
- Шаг №5: Рассчитайте значения по осям x и y для каждой компании.
- Шаг № 6: Настройте вторую вспомогательную таблицу для сетки полярного графика.
- Шаг № 7: Создайте набор кольцевых диаграмм.
- Шаг №8: Уменьшите размер отверстия бублика.
- Шаг №9: Настройте сетку диаграммы.
- Шаг 10. Добавьте данные диаграммы.
- Шаг №11: Измените тип диаграммы для вставленного ряда данных.
- Шаг №12: Измените масштаб горизонтальной и вертикальной осей.
- Шаг №13: Удалите линии сетки, оси и ненужные элементы легенды.
- Шаг 14: Добавьте метки данных.
- Шаг 15. Настройте метки данных.
- Шаг №16: Переместите этикетки.
- Загрузить шаблон графика в полярных координатах
График в полярных координатах используется для определения точки в пространстве в так называемой полярной системе координат, где вместо использования стандартных координат x и y выражается каждая точка на полярной плоскости.
 используя эти два значения:
используя эти два значения:- Радиус ( r ) – Расстояние от центра участка
- Тета (θ) – Угол от опорного угла
Сама плоскость состоит из концентрических окружностей, расширяющихся наружу от начала координат или полюса — отсюда и название. Полярный график пригодится, когда анализируемые данные имеют циклический характер.
В качестве примера на приведенной ниже диаграмме сравниваются оценки удовлетворенности клиентов (CSAT), показатель, который иллюстрирует удовлетворенность клиентов брендом или продуктом, двух организаций за 2019 год.: Simpson Ltd и Griffin Ltd.
График позволяет быстро оценить хорошие и плохие месяцы для каждой компании, что облегчает принятие более эффективных решений.
Однако вот в чем загвоздка:
Excel не поддерживает этот тип диаграммы — фактически, он даже не может считывать полярные координаты — это означает, что вам придется создавать его с нуля.
 Кроме того, не забудьте проверить надстройку Chart Creator, мощный инструмент для создания умопомрачительных расширенных диаграмм и графиков Excel всего за несколько кликов.
Кроме того, не забудьте проверить надстройку Chart Creator, мощный инструмент для создания умопомрачительных расширенных диаграмм и графиков Excel всего за несколько кликов. В этом подробном пошаговом руководстве вы узнаете, как преобразовать необработанные данные в полярный график в Excel с нуля. Напомним, что эта статья основана на руководстве, созданном Джоном Пельтье.
Приступая к работе
Поскольку баллы CSAT обычно выражаются в виде процентной шкалы, рассмотрите следующую таблицу:
Шаг № 1: Настройте вспомогательную таблицу.
Сразу набросайте вспомогательную таблицу, в которой будут выполняться все расчеты для вашей диаграммы. Чтобы построить график, вам нужно сначала вычислить полярные координаты, а затем преобразовать их в значения осей x и y, используемые Excel для создания диаграммы.
Настройте отдельную фиктивную таблицу следующим образом:
Обратите внимание, что вспомогательная таблица начинается с фиктивной строки ( E2:h3 ) — она определяет опорный угол. Давайте поговорим о каждом элементе таблицы немного подробнее:
Давайте поговорим о каждом элементе таблицы немного подробнее:- Месяц — этот столбец содержит качественные категории, полученные из ваших исходных данных. Введите «Начало» в первой ячейке ( E2 ) и скопируйте категории (в нашем случае месяцы) прямо под ней ( E3:E14 9).0022).
- Угол (тета) — этот столбец содержит тета-значения, отвечающие за рисование спиц, где будут размещены фактические значения. Вы всегда должны вводить «0» в первую ячейку ( F2 ) этого столбца.
- CSAT Simpson LTD (Radius) и CSAT Griffin LTD (Radius) — эти столбцы содержат значения радиуса, иллюстрирующие производительность каждой компании в течение года.
Шаг 2. Вычислите значения угла (тета).
Если вы уже вычислили значения r и тета, пропустите эту часть и прокрутите вниз до . Шаг #4 .
На этом этапе наша цель состоит в том, чтобы равномерно наметить спицы на основе количества категорий в наборе данных.
 Поскольку один полный круговой оборот равен 360 градусам, чтобы выполнить задачу, вам нужно разделить 360 на количество категорий в вашем наборе данных (в нашем случае двенадцать месяцев).
Поскольку один полный круговой оборот равен 360 градусам, чтобы выполнить задачу, вам нужно разделить 360 на количество категорий в вашем наборе данных (в нашем случае двенадцать месяцев).Затем сложите это число по мере продвижения от нуля до 360. И здесь в игру вступает функция СЧЕТЧИК. По сути, он подсчитывает количество непустых ячеек в указанном диапазоне.
Скопируйте эту формулу в ячейку F3 :
=360/COUNTA($A$3:$A$14)
С этой формулой в ячейке F3 используйте эту другую формулу в ячейке F4 , чтобы добавить до заданного значения угла до суммы всех тета-значений, которые идут перед ним в столбце:
=F3+360/COUNTA($A$3:$A$14)
Важно заблокировать диапазон ячеек ( A3:A14 ), чтобы легко скопировать формулу в оставшиеся ячейки.
Теперь выполните формулу для остальных ячеек в столбце ( F5:F14 ), выбрав F4 и перетащив маркер заполнения вниз.

Шаг №3: Вычислите значения радиуса.
Полярный график будет состоять из 10 колец данных, каждая радиальная точка (расстояние между внутренним и внешним краями кольца) представляет собой десятипроцентное приращение по шкале от 0 до 100.
Поскольку баллы CSAT также измеряется по процентной шкале, просто разделите каждую таблицу баллов CSAT на 10.
Вот как это сделать быстро и легко. Чтобы найти значения радиуса для первой компании ( Simpson Ltd ), введите эту крошечную формулу в ячейку G3 и скопируйте ее в остальные ячейки ( G4:G14 ):
=B3/10
Теперь по тому же принципу рассчитайте радиусы для второй компании ( Griffin Ltd ):
=C3/10
В этот момент вы можете подумать про себя: «А что, если мой тип данных отличается? Как вы корректируете, сравнивая, например, доход, полученный компаниями, с показателями CSAT?»
Проще говоря, вы должны проанализировать свои фактические данные, определить эквивалент одной радиальной точки (скажем, 50 000 долларов США) и разделить все значения в вашем наборе данных на это число.
 Предположим, что какая-то компания заработала 250 000 долларов в мае. Чтобы найти свой радиус, разделите 250 000 долларов на 50 000. Так просто, как, что.
Предположим, что какая-то компания заработала 250 000 долларов в мае. Чтобы найти свой радиус, разделите 250 000 долларов на 50 000. Так просто, как, что.Шаг №4: Скопируйте последние значения радиуса во вспомогательную строку.
Заполните таблицу, скопировав значения r в самом низу ( G14:h24 ) каждого столбца в соответствующие пустые ячейки ( G2:h3 ).
Шаг № 5: Рассчитайте значения по осям x и y для каждой компании.
Пришло время перейти к преобразованию полярных координат в соответствующие значения осей X и Y. Благодаря тригонометрии вы можете осуществить переход, используя две специальные формулы, которые вы собираетесь выучить за несколько секунд.
Сначала начнем со значений по оси X. В ячейку рядом с вспомогательной таблицей ( I2 ) введите следующую формулу:
=G2*SIN(F2/180*PI())
Скопируйте эту формулу в остальные ячейки под ней ( I3:I14 ).

Таким же образом вставьте эту формулу в ячейку J2 , чтобы найти значения по оси Y, и выполните ее также для остальных ячеек ( J3:J14 ):
=G2*COS (F2/180*PI())
Важное примечание . Имейте в виду, что ячейка строки заголовка (J1) столбца со значениями по оси Y (столбец J) будет действовать как имя ряда, то есть значение в эта ячейка перейдет в легенду диаграммы.
Повторите точно такой же процесс для вычисления значений X и Y для второй компании, изменив формулу для использования данных в столбце Griffin Ltd:
=h3*SIN(F2/180*PI() )
=h3*COS(F2/180*PI())
Шаг № 6: Настройте вторую вспомогательную таблицу для сетки полярного графика.
Да, вы не ослышались. Вам нужна еще одна вспомогательная таблица. К счастью, худшее уже позади, так как для составления таблицы не требуется единой формулы.

Взгляните на нее:
По сути, таблица состоит из трех элементов:
- Качественная шкала (желтая область или N2:N11) данные. Заполните ячейки процентами, как показано на скриншоте. В качестве примера альтернативных данных, если бы мы анализировали доход, упомянутый ранее, этот столбец увеличился бы с 50 000 до 500 000 долларов.
- Строка заголовка (красная область или O1:Z1) — содержит все имена категорий, полученные из исходной таблицы данных, просто расположенные вертикально.
- Значения сетки (зеленая область или O2:Z11) — Эти значения разделят будущие кольца данных на равные части, очерчивая сетку графика. Просто выберите число из воздуха и скопируйте его во все ячейки в пределах диапазона.
Шаг 7. Создайте набор кольцевых диаграмм.
Наконец-то вы собрали все необходимые графические данные — это было довольно напряженно. Попрощайтесь с функциями и формулами, потому что теперь вы можете начать строить сам полярный график.

Начните с настройки полярной плоскости, создав 10 кольцевых диаграмм, расположенных друг над другом:
- Выделите все значения сетки из второй вспомогательной таблицы ( O2:Z11 ).
- Перейдите на вкладку Вставка .
- Нажмите кнопку « Вставить круговую или кольцевую диаграмму ».
- Выберите « Пончик ».
В результате Excel должен выдать набор из 10 колец.
Иногда Excel не может правильно прочитать ваши данные. Чтобы обойти проблему, если это произойдет с вами, следуйте нескольким простым инструкциям, чтобы сложить диаграммы вручную. Для наглядности предположим, что вместо этого вы решили проанализировать данные за восемь месяцев.
Сначала выберите любую пустую ячейку и постройте пустую кольцевую диаграмму, следуя описанным выше шагам.
Затем щелкните правой кнопкой мыши график и выберите « Select Data. »
После этого в диалоговом окне Select Data Source нажмите кнопку « Add ».

В поле Edit Series выберите все значения сетки в первой строке ( O2:V2 ) и нажмите « OK ».
Как вы уже догадались, промойте и повторите для каждого ряда, чтобы получить те же самые 10 колец, нанесенных на график.
Шаг 8: Уменьшите размер отверстия бублика.
Как видите, все кольца сжаты вместе вдали от центра. Давайте изменим это, уменьшив размер отверстия для пончика.
- Щелкните правой кнопкой мыши любое кольцо данных.
- Выберите « Формат серии данных. »
В появившейся панели задач измените значение размера отверстия пончика по умолчанию, чтобы произошло волшебство:
- Перейдите на вкладку Опции серии .
- Установите размер отверстия пончика на « 10%. »
Шаг 9: Настройте сетку диаграммы.
В той же панели задач преобразуйте кольца в сетку, выполнив следующие простые шаги:
- Перейдите на вкладку Заливка и линия .

- В разделе « Заполнить, » выберите « Без заполнения». »
- В разделе «Граница , » выберите « Сплошная линия. »
- Щелкните значок « Цвет контура », чтобы открыть цветовую палитру и выбрать светло-серый.
- Установите ширину на « 5 pt. »
Промойте и повторите для остальных колец.
Шаг 10: Добавьте данные диаграммы.
Теперь, когда основа заложена, добавьте на диаграмму значения x и y из первой вспомогательной таблицы.
- Выделите все значения по осям X и Y, иллюстрирующие баллы CSAT первой компании (Simpson Ltd), а также ячейки строки заголовка ( I1:J14 ) и скопируйте данные (щелкните правой кнопкой мыши и выберите Копировать ).
- Выберите область диаграммы.
- Перейдите на вкладку Главная .
- Нажмите кнопку « Вставить ».

- Выберите « Специальная вставка. »
В появившемся крошечном диалоговом окне Специальная вставка выполните следующие действия:
- В разделе « Добавить ячейки как, » выберите « Новая серия». »
- Под « Значения (Y) в, ” выберите “ Столбцы. »
- Установите флажки «Названия серий в первой строке » и «Категории (метки X) в первом столбце ».
- Нажмите « ОК. »
Повторите процесс, чтобы добавить данные диаграммы, связанные со второй компанией (Griffin Ltd).
Шаг № 11: Измените тип диаграммы для вставленного ряда данных.
Теперь измените тип диаграммы обоих недавно добавленных рядов, представляющих фактические значения.
- Щелкните правой кнопкой мыши любой ряд, представляющий фактические значения (либо Series «Simpson Ltd» , либо Series «Griffin Ltd» ).

- Выберите « Изменить тип диаграммы серии. »
После этого измените тип диаграммы для серии «Simpson Ltd» и серии «Griffin Ltd» на «Scatter with Smooth Lines and Markers».
Шаг 12: Измените масштаб горизонтальной и вертикальной осей.
Когда оси диаграммы отобразятся, измените диапазоны шкал горизонтальной и вертикальной осей для диаграммы, чтобы точно отражать нанесенные на нее данные.
- Щелкните правой кнопкой мыши по вертикальной оси.
- Выберите « Формат оси. »
Когда появится панель задач, определите новые диапазоны масштаба оси:
- Перейдите на вкладку Параметры оси.
- Установите для параметра Минимальные границы значение «-10».
- Измените значение параметра Максимальные границы на «10».

После этого прыгайте на горизонтальную ось и делайте то же самое.
Шаг 13: Удалите линии сетки, оси и ненужные элементы легенды.
Очистите график, удалив элементы диаграммы, которые не имеют никакого практического значения: линии сетки, оси, а также все элементы легенды — за исключением двух, которые вам действительно нужны (отметка информации о компании).
Для этого дважды щелкните каждый элемент, затем снова щелкните его правой кнопкой мыши и выберите « Удалить». ”
Шаг 14: Добавьте метки данных.
По мере того, как мы постепенно приближаемся к концу нашего грандиозного приключения с Excel, пришло время добавить метки данных, представляющие каждую качественную категорию в вашем наборе данных.
Щелкните правой кнопкой мыши внешнее кольцо ( Серия «10» ) и выберите « Добавить метки данных». ”
Шаг 15: Настройте метки данных.

По сути, все, что вам нужно сделать здесь, это заменить метки данных по умолчанию именами категорий из таблицы, содержащей ваши фактические данные.
Щелкните правой кнопкой мыши любую метку данных и выберите « Формат меток данных». »
Когда откроется панель задач, замените значения, выполнив следующие действия:
- Перейдите на вкладку Параметры метки .
- Установите флажок « Значение из ячеек ».
- Выделите значения категории из исходной таблицы данных ( А3:А14 ).
- Нажмите « ОК. »
- Снимите флажок « Значение ».
- Снимите флажок « Показать линии выноски ».
Шаг 16: Переместите этикетки.
Теперь немного сдвиньте метки, разместив их вдоль края внешнего кольца в порядке, показанном на скриншоте ниже. Это нужно будет сделать вручную, перетащив каждый заголовок в нужное положение.

Наконец, измените название диаграммы, и все готово!
Загрузить шаблон полярного графика
Загрузите наш бесплатный шаблон полярного графика для Excel.
Загрузить сейчас
Система построения полярных графиков ценна, но имеет недостатки
Столбцы
Полярные координаты должны записывать входные данные перед выходными
, где точки изображаются на основе их координат «x» и «y», но есть еще одна важная система построения графиков для изучения математики: полярная система координат. Декартова система координат была создана в 1637 году математиком Рене Декартом, а полярная система координат была изобретена несколько десятилетий спустя физиком Исааком Ньютоном, которую затем использовал математик Якоб Бернулли для решения математических задач.
Для тех, кто не знаком с полярной системой координат, первый шаг в построении графика — нарисовать ось, которая представляет собой любую точку — теперь начало координат — а затем луч, проведенный вправо.
 Похоже на правую половину оси x. Затем точки наносятся на график на основе значения r, которое представляет расстояние от начала координат до этой точки, и значения θ, или тета, которое представляет собой меру в градусах или радианах угла, образованного исходным полюсом и линией, соединяющей сказал указать на происхождение. Как и в декартовой системе, точки записываются как упорядоченные пары, но на этот раз в виде (r, θ), а не (x, y).
Похоже на правую половину оси x. Затем точки наносятся на график на основе значения r, которое представляет расстояние от начала координат до этой точки, и значения θ, или тета, которое представляет собой меру в градусах или радианах угла, образованного исходным полюсом и линией, соединяющей сказал указать на происхождение. Как и в декартовой системе, точки записываются как упорядоченные пары, но на этот раз в виде (r, θ), а не (x, y).Примером полярной системы координат в действии является точка (2, π). В этом случае, поскольку r равно двум, точка будет находиться на расстоянии двух от начала координат, а угол между этой точкой и осью будет равен π радианам, или 180 градусам. При построении этого графика вы должны поместить точку, которая находится на две единицы непосредственно слева от начала координат, потому что это образует прямую линию между осью и точкой, которая имеет угол 180 градусов.
Полярная система координат полезна не только для построения графиков точек, но и для графических функций.
 2, которая принимает входные данные x и производит выходные данные y. Точно так же существуют полярные координаты, которые обычно записываются как r, равное некоторому действию с θ, например, r = sin(θ). График этой функции в полярной системе координат представляет собой круг, а полярная система построения графиков ценна тем, что позволяет математикам отображать важные кривые, такие как кардиоиды и розы, которые не могут быть легко построены с помощью функций в декартовой системе.
2, которая принимает входные данные x и производит выходные данные y. Точно так же существуют полярные координаты, которые обычно записываются как r, равное некоторому действию с θ, например, r = sin(θ). График этой функции в полярной системе координат представляет собой круг, а полярная система построения графиков ценна тем, что позволяет математикам отображать важные кривые, такие как кардиоиды и розы, которые не могут быть легко построены с помощью функций в декартовой системе.Однако есть проблема с полярной системой координат — принято записывать точки как (r, θ). Я считаю, что было бы более разумно записывать полярные точки как (θ, r), потому что это более логично согласуется с декартовыми точками (x, y). Суть моего аргумента заключается в том, что θ больше похоже на x, а r больше похоже на y. Следовательно, полярные точки следует записывать как (θ, r), чтобы они естественным образом сливались с декартовыми точками (x, y), что делало их менее запутанными.
92. Координата x — это вход, потому что с ней что-то делается путем возведения в квадрат, а y — это выход. С другой стороны, полярная функция, которую я дал, была r = sin(θ), которая помещает θ в качестве входа и r в качестве выхода. Поскольку x и θ обычно являются входными данными функций соответствующего типа, а y и r обычно являются выходными данными, логично, что они должны находиться в одних и тех же местах своих упорядоченных пар.
С другой стороны, полярная функция, которую я дал, была r = sin(θ), которая помещает θ в качестве входа и r в качестве выхода. Поскольку x и θ обычно являются входными данными функций соответствующего типа, а y и r обычно являются выходными данными, логично, что они должны находиться в одних и тех же местах своих упорядоченных пар.Кроме того, чтобы построить сходство ввода и вывода между декартовыми и полярными координатами, имеет смысл записать ввод перед выводом в упорядоченных парах. Допустим, перед вами стоит задача найти точку, лежащую на функции r = sin(θ). Чтобы решить эту проблему, вы можете выбрать значение r, а затем решить для θ, но было бы намного проще сначала выбрать значение θ, потому что вам не нужно брать арксинус обеих частей уравнения, что делает проблема намного сложнее, чем она должна быть. Поскольку значение θ определяется первым, оно должно быть записано первым, потому что оно использовалось для нахождения значения r, а не наоборот.
Наконец, мое последнее замечание состоит в том, что использование условного обозначения (θ, r) более полезно при графическом отображении полярных точек, чем условное обозначение (r, θ).


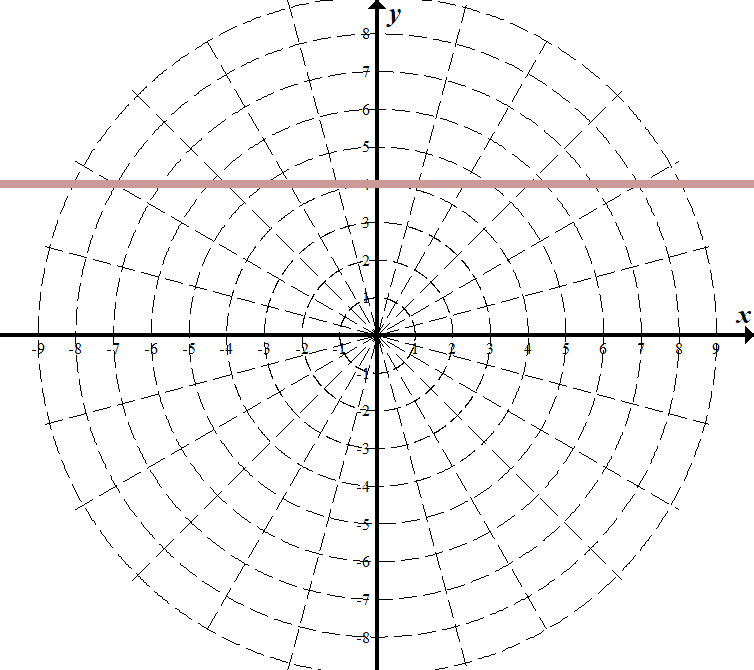 в) Щелкнув в столбце в конце строки Поле и из раскрывающегося списка выберать нужное поле. В строке…
в) Щелкнув в столбце в конце строки Поле и из раскрывающегося списка выберать нужное поле. В строке…
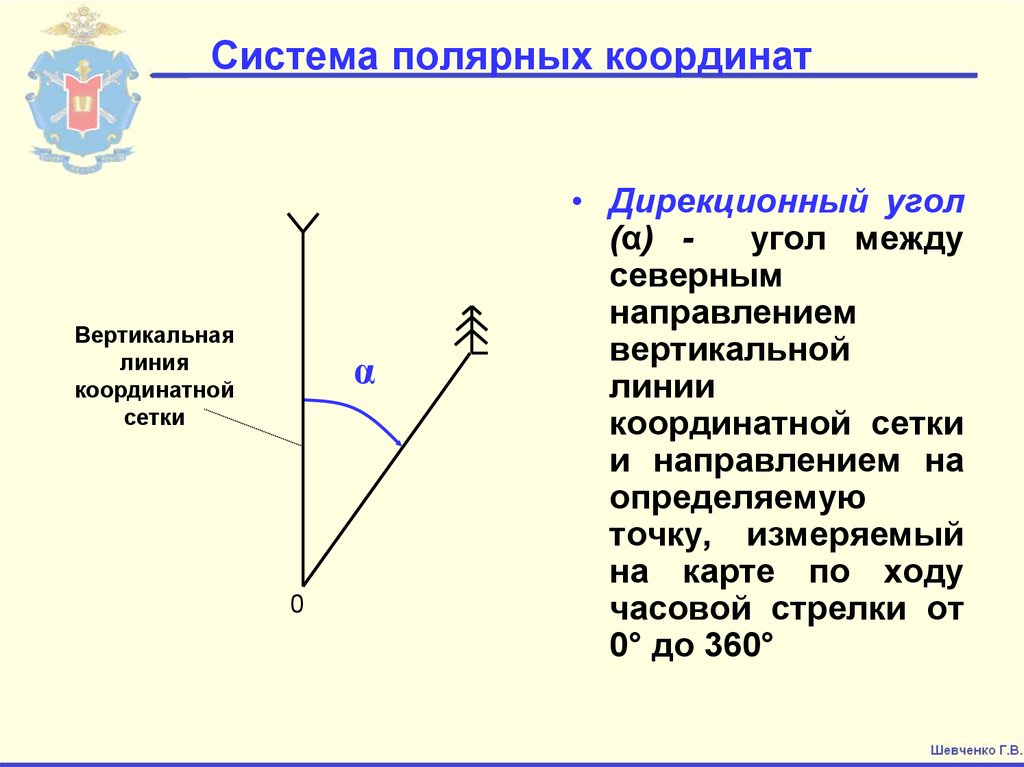
 Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.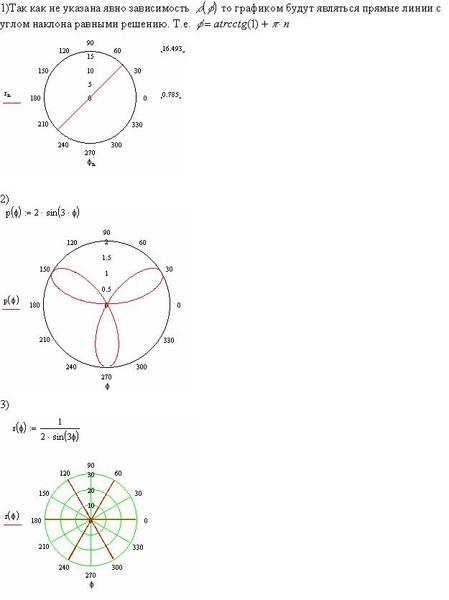 Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]
Для этого мы можем начать с исходного уравнения. 9{2}}{3}=1\hfill & \hfill \end{array}[/latex]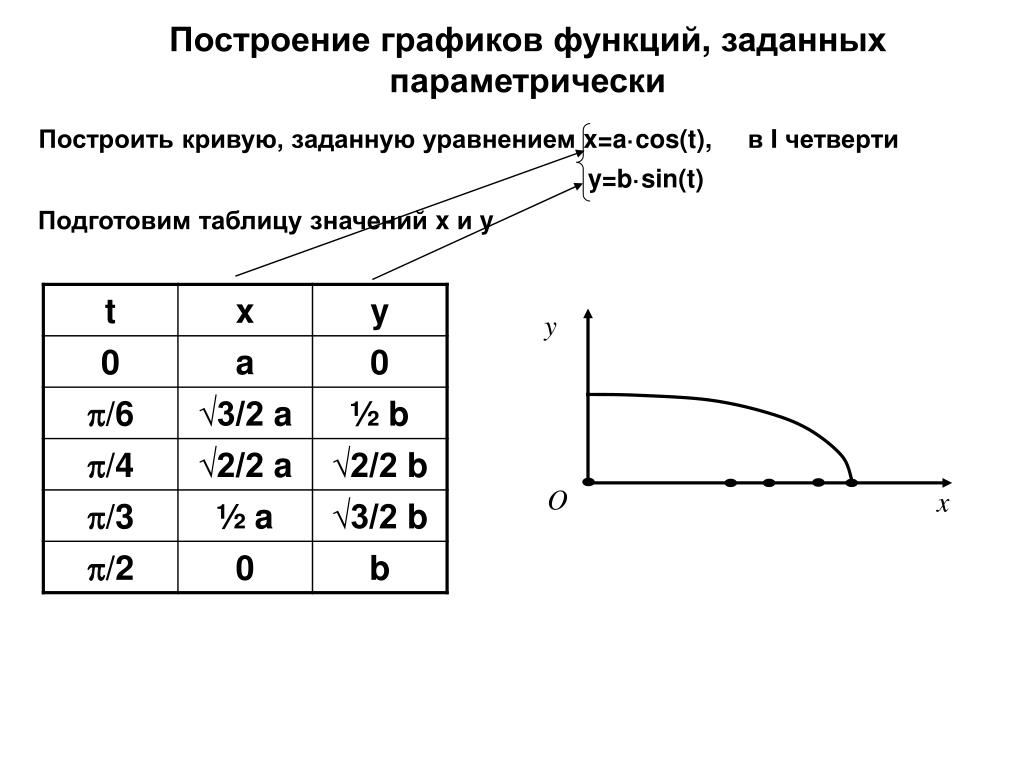 {2}}.\,[/latex] См. (рисунок).
{2}}.\,[/latex] См. (рисунок).
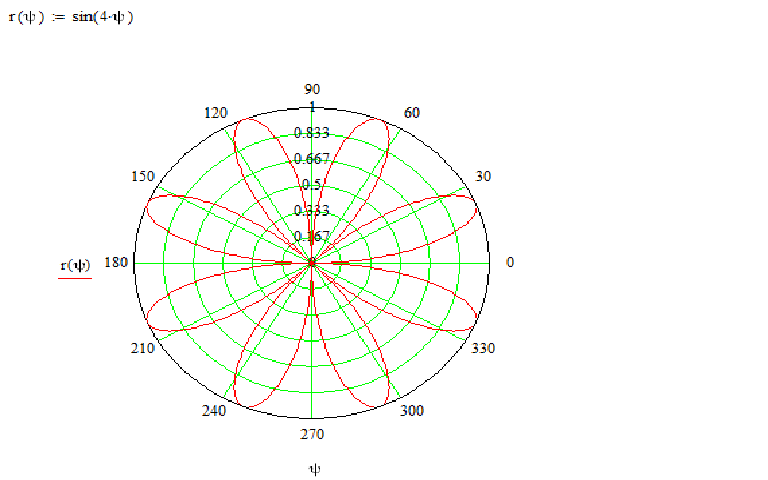
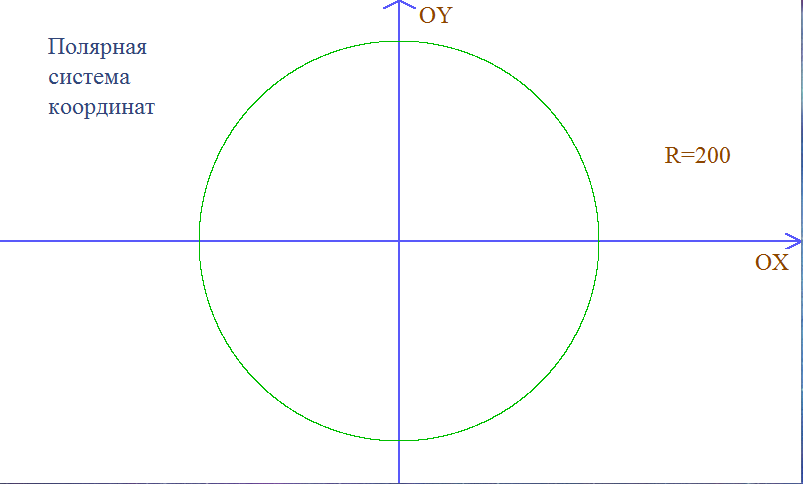

 Округлить до тысячных.
Округлить до тысячных.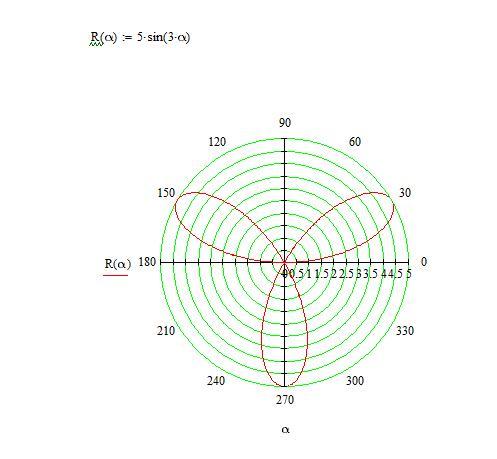 3: Полярные координаты — Математика LibreTexts
3: Полярные координаты — Математика LibreTexts рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат. Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).
Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\). Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).
Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).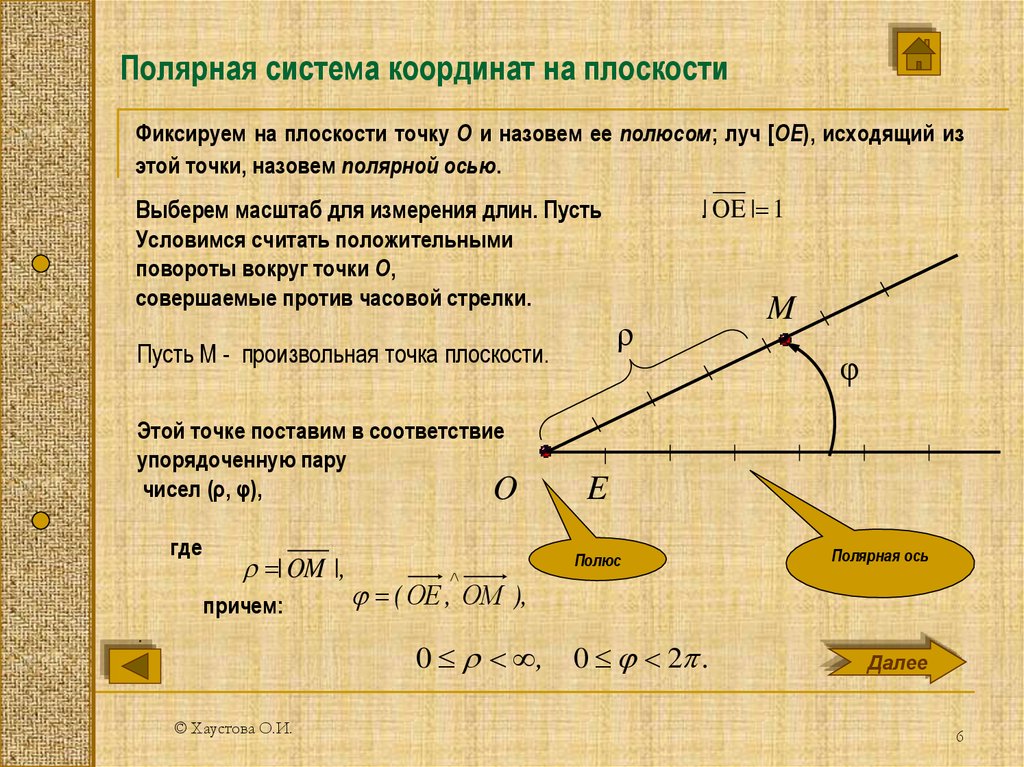
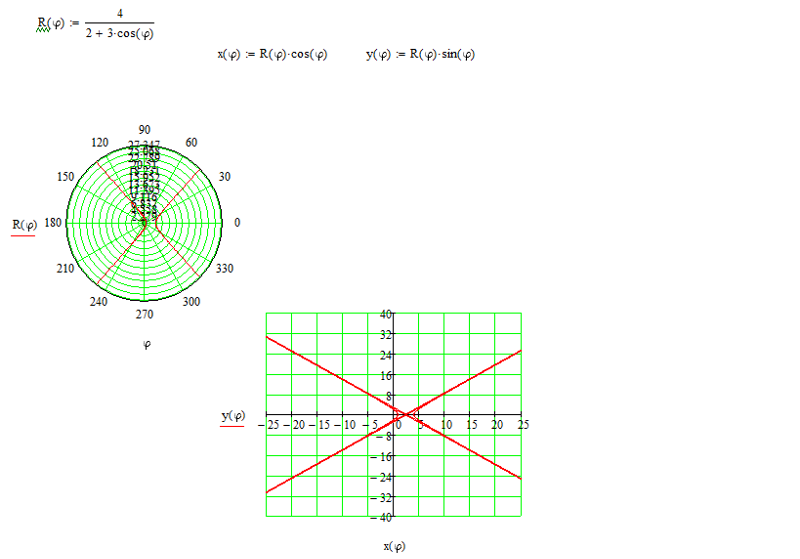 Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
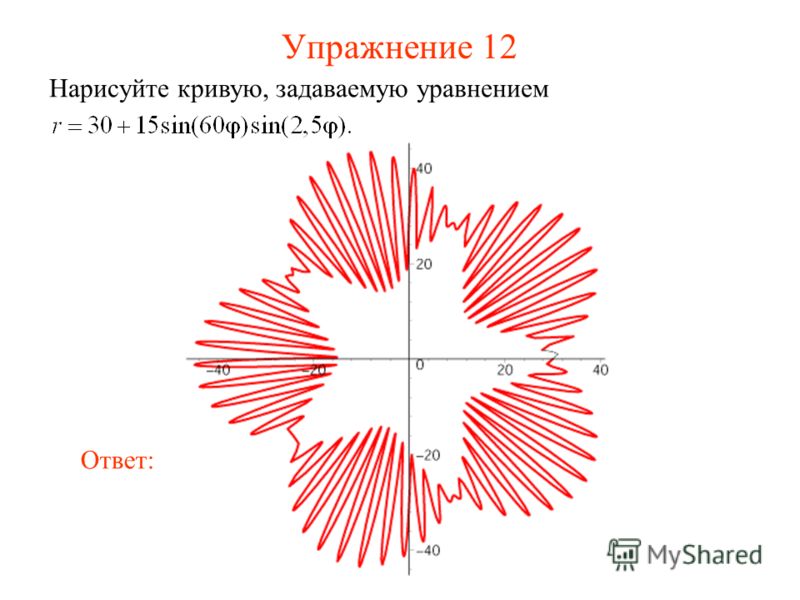
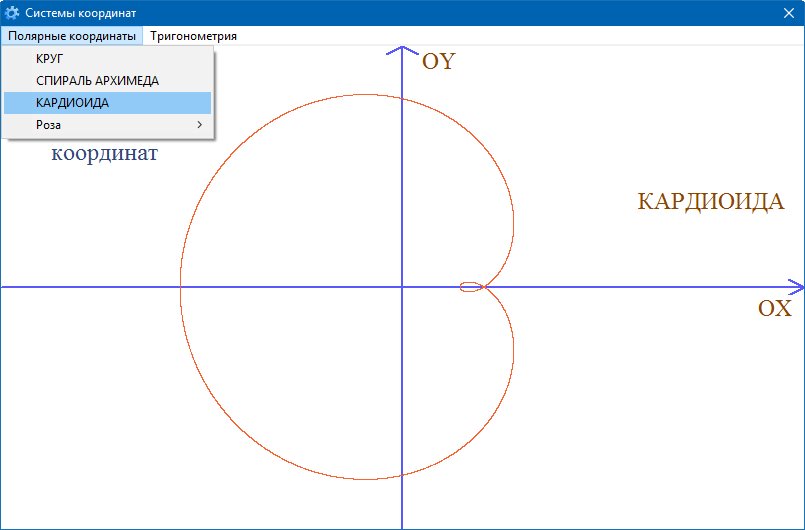 Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает
Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает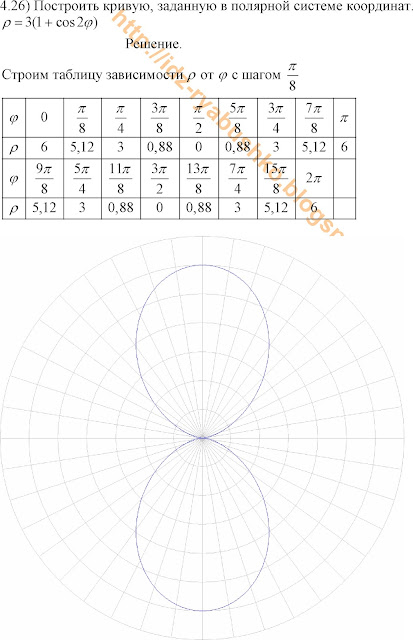 Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.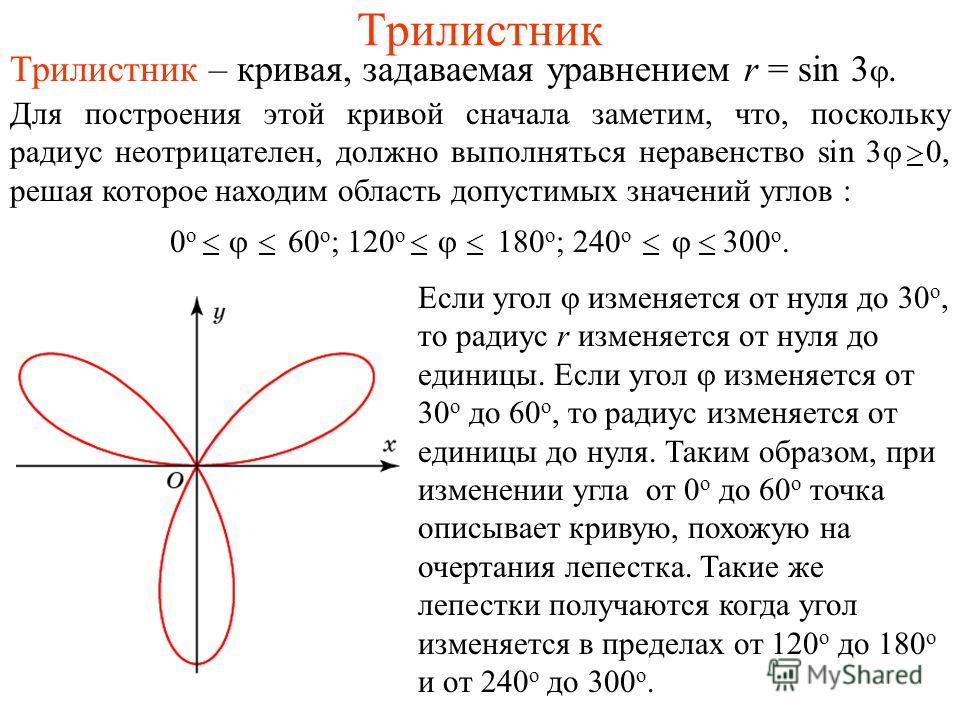
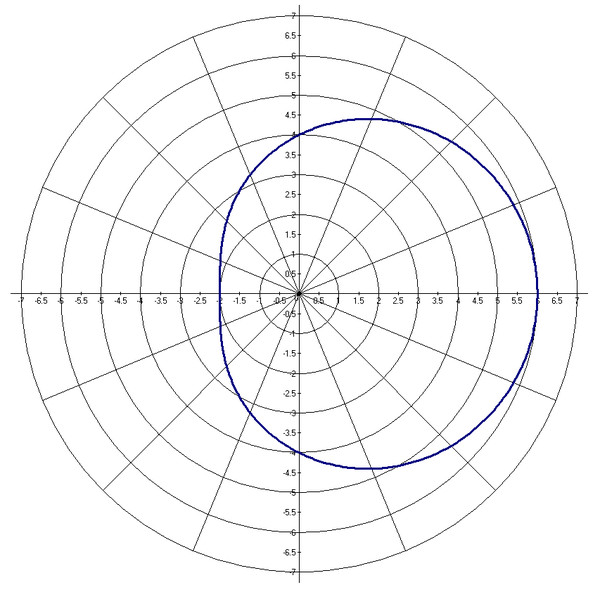 Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.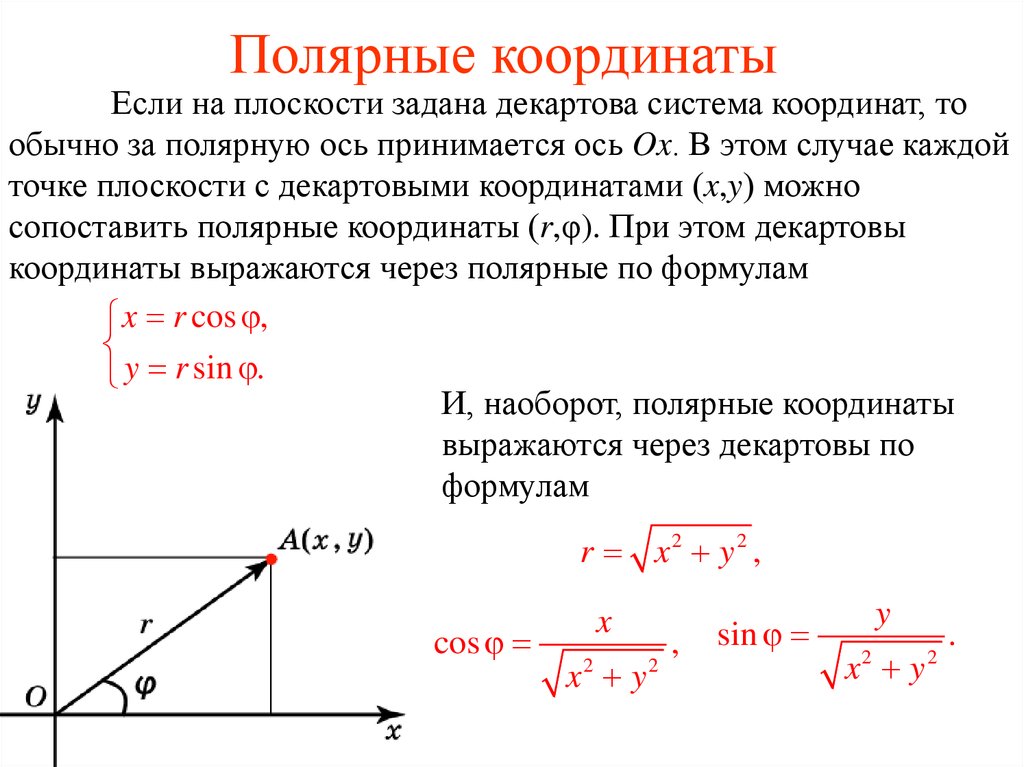
 2}. \конец{массив}\) 9{\frac{2}{3}}\)
2}. \конец{массив}\) 9{\frac{2}{3}}\)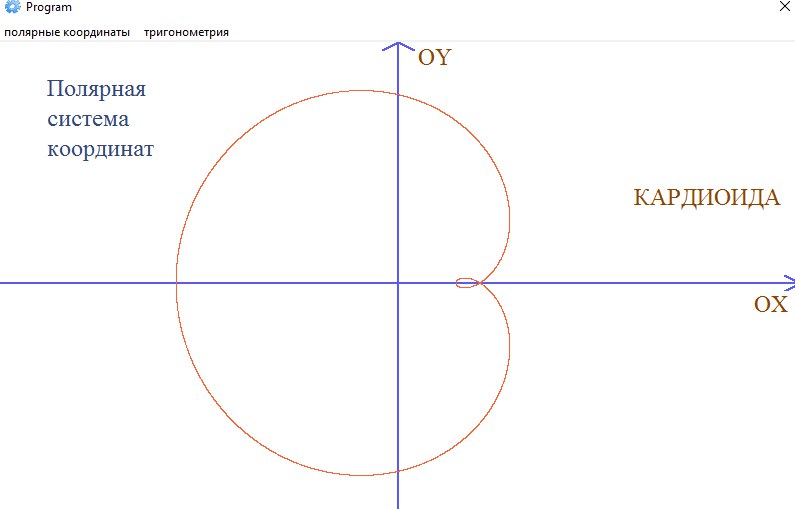 2}\). См. пример \(\PageIndex{5}\).
2}\). См. пример \(\PageIndex{5}\).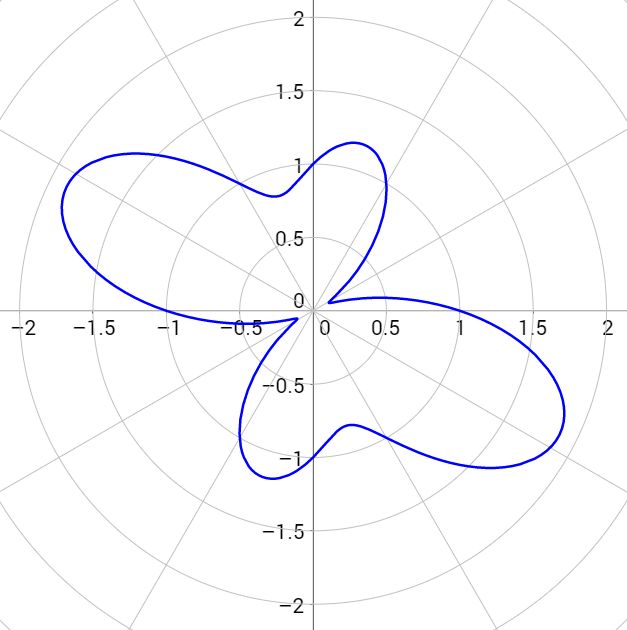 org/details/books/precalculus
org/details/books/precalculus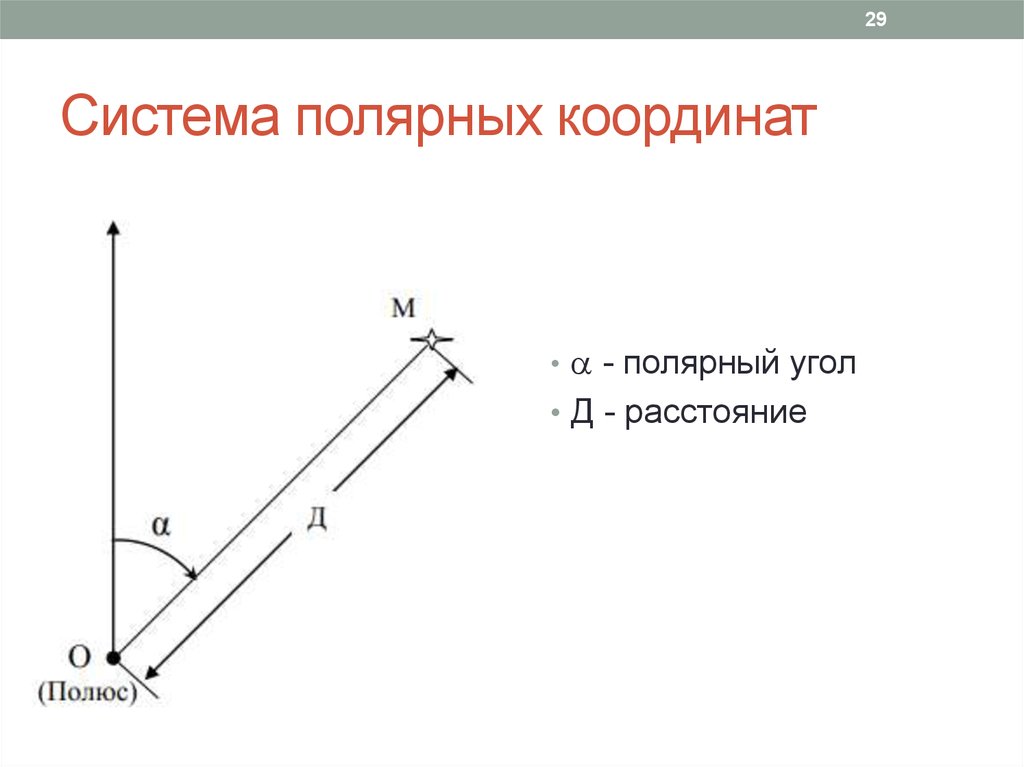
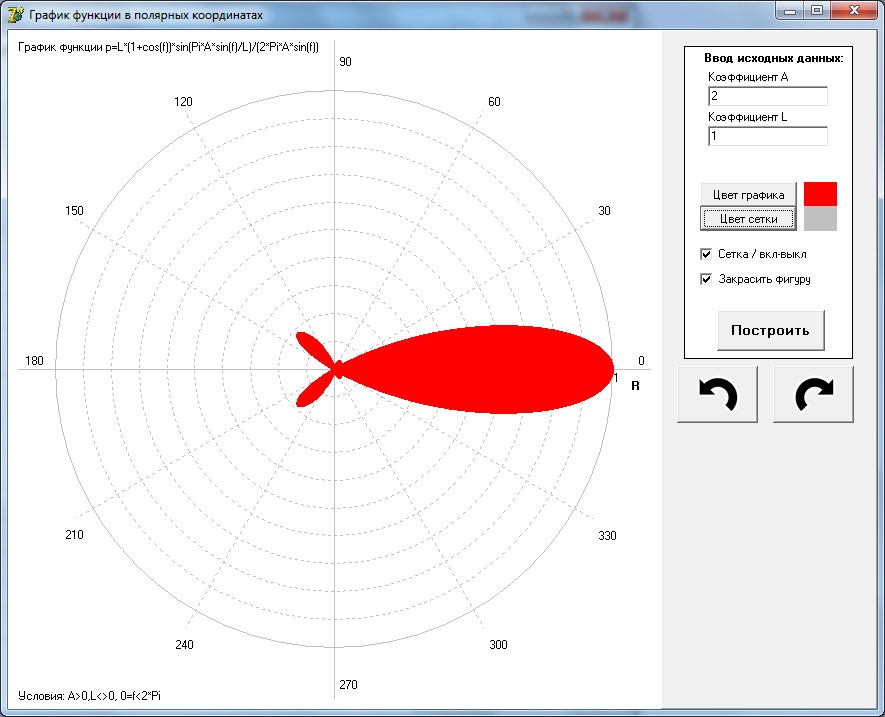 Он также имеет луч, который проходит горизонтально через полюс, называемый
полярная ось. Вместо квадратной сетки есть концентрические круги с центром на полюсе, которые получают
равномерно больше и расходятся от полюса. Полярная координатная плоскость выглядит так:
Он также имеет луч, который проходит горизонтально через полюс, называемый
полярная ось. Вместо квадратной сетки есть концентрические круги с центром на полюсе, которые получают
равномерно больше и расходятся от полюса. Полярная координатная плоскость выглядит так: Итак, если вам дана полярная координата (3, π/4),
точка находится в трех единицах от центра под углом π/4 радиан, измеренным
против часовой стрелки от полярной оси:
Итак, если вам дана полярная координата (3, π/4),
точка находится в трех единицах от центра под углом π/4 радиан, измеренным
против часовой стрелки от полярной оси: Как вы думаете, где находится точка (-2, π/3)?
Как вы думаете, где находится точка (-2, π/3)? Попробуйте нанести эти точки на график с помощью действия «Полярные координаты» и убедитесь, что они
тот самый момент!
Попробуйте нанести эти точки на график с помощью действия «Полярные координаты» и убедитесь, что они
тот самый момент!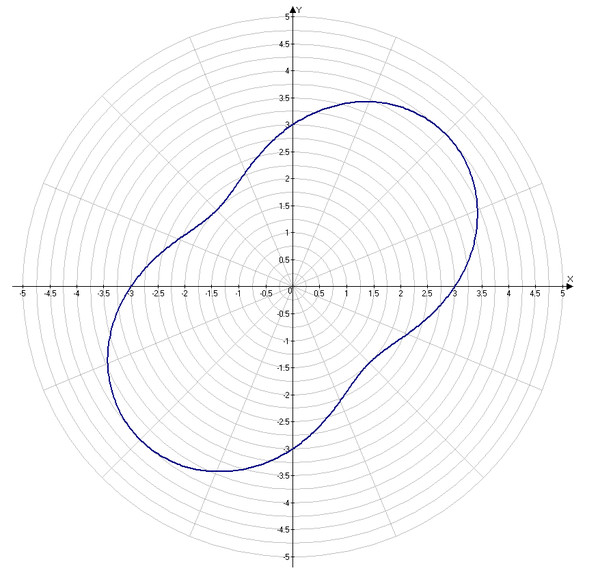
 Теперь наша точка $P$ находится на расстоянии $2,5$ от начала координат, а $PO$ составляет угол $30$ градусов с положительной осью $x$.
Теперь наша точка $P$ находится на расстоянии $2,5$ от начала координат, а $PO$ составляет угол $30$ градусов с положительной осью $x$.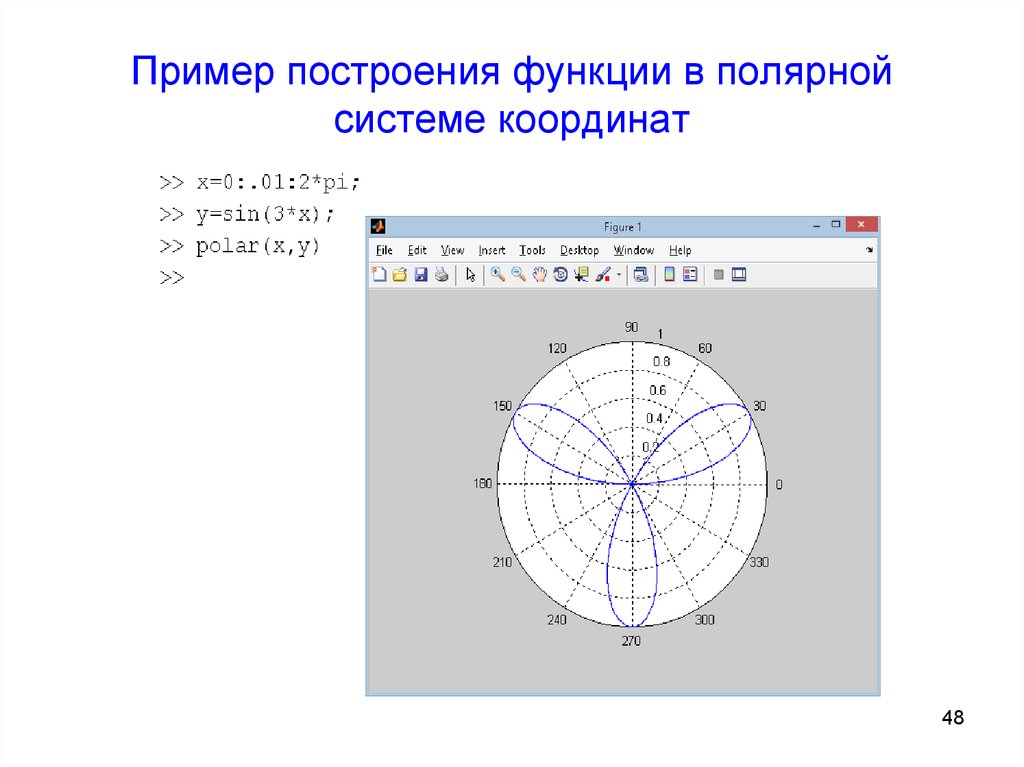 Таким образом, по мере того, как вы продолжаете движение против часовой стрелки, $r$ уменьшается, пока не достигнет $2$ в точке $\theta=\pi$. Мы оказываемся в точке с прямоугольными координатами (-2,0)$.
Таким образом, по мере того, как вы продолжаете движение против часовой стрелки, $r$ уменьшается, пока не достигнет $2$ в точке $\theta=\pi$. Мы оказываемся в точке с прямоугольными координатами (-2,0)$.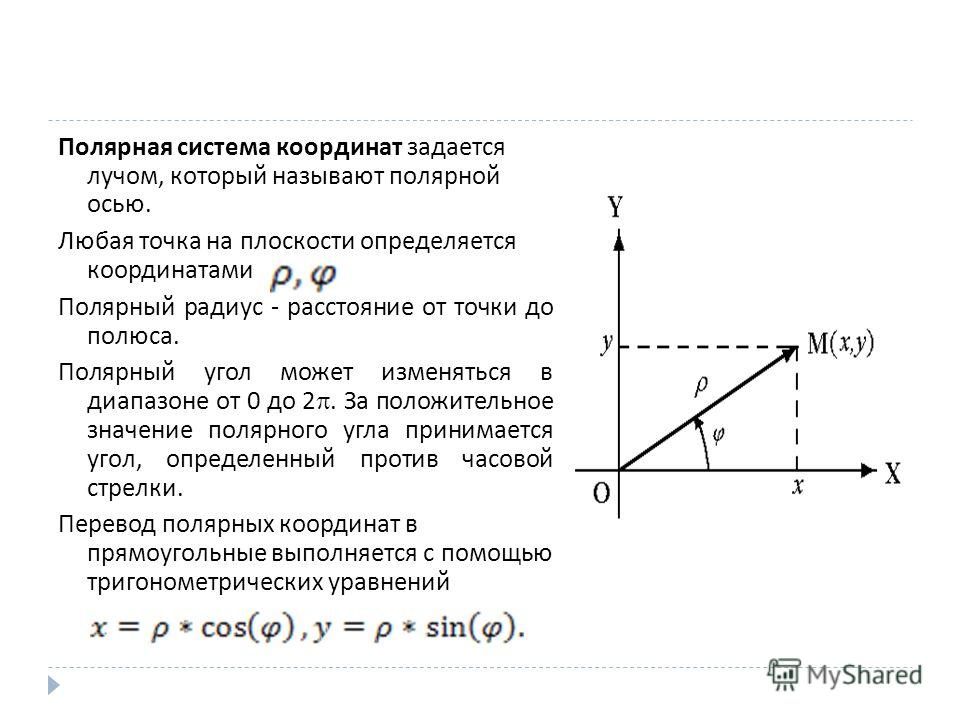 Соглашение $2$ гласит, что, например, чтобы нанести точку с полярными координатами $(-8,\theta)$, вы представляете построение $(8,\theta)$ и отражаете результат через начало координат или, что то же самое, поворачиваете на $180 $ градусов. Я не знаю, какое соглашение использует ваш курс/книга.
Соглашение $2$ гласит, что, например, чтобы нанести точку с полярными координатами $(-8,\theta)$, вы представляете построение $(8,\theta)$ и отражаете результат через начало координат или, что то же самое, поворачиваете на $180 $ градусов. Я не знаю, какое соглашение использует ваш курс/книга.
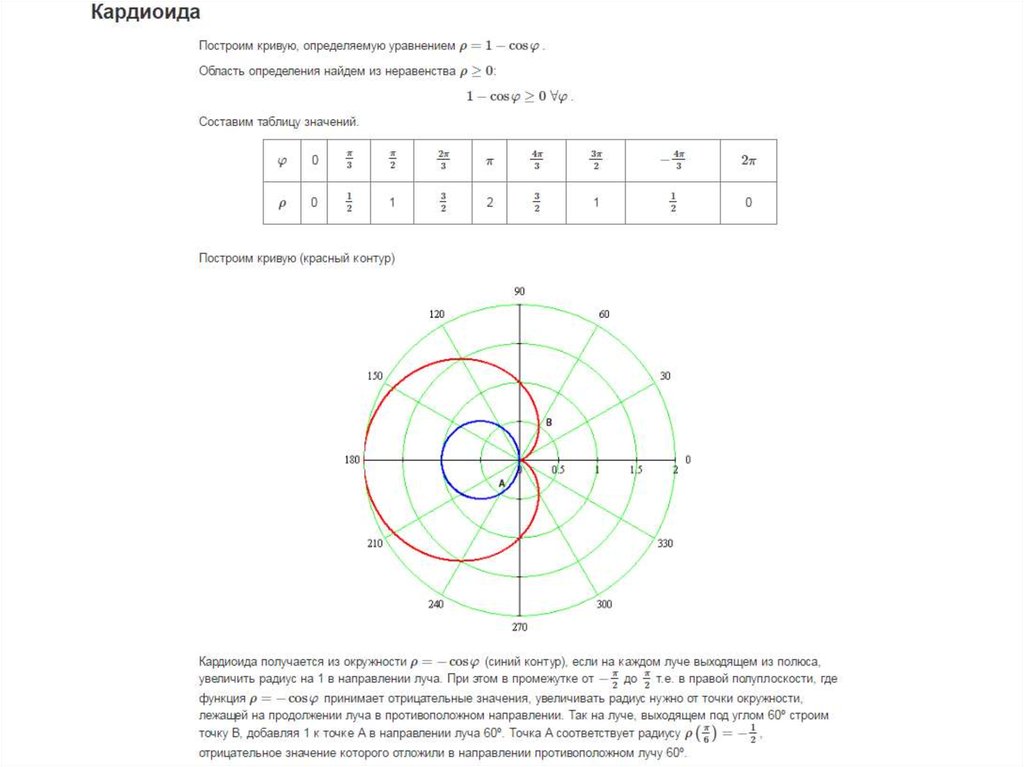
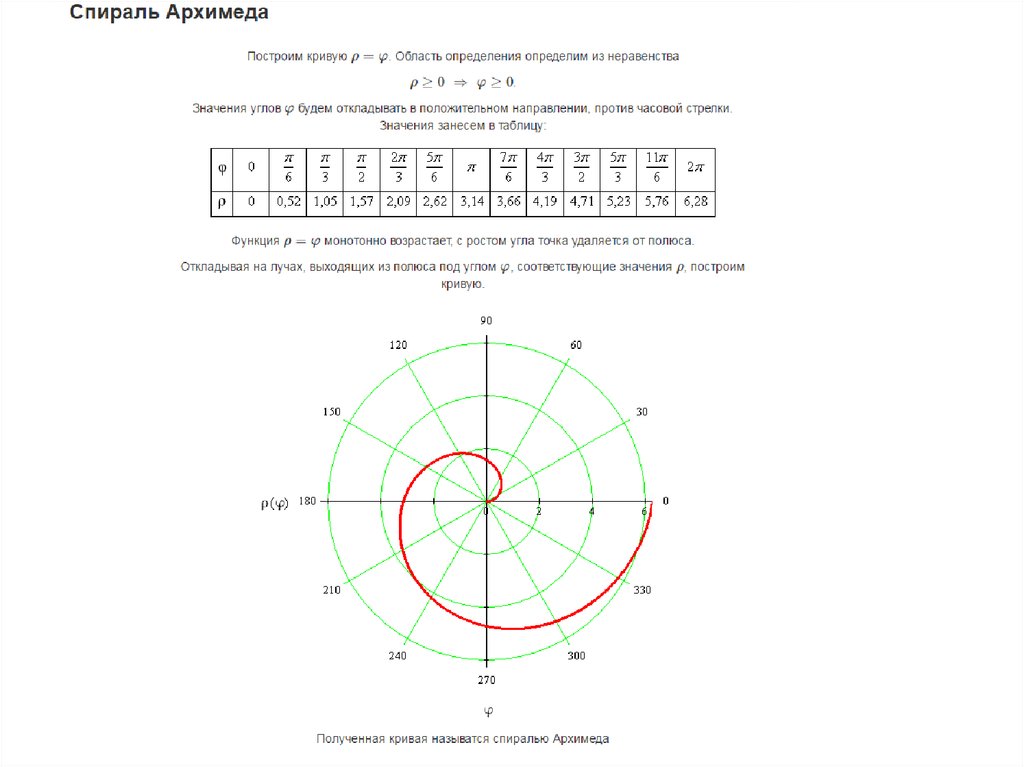 используя эти два значения:
используя эти два значения: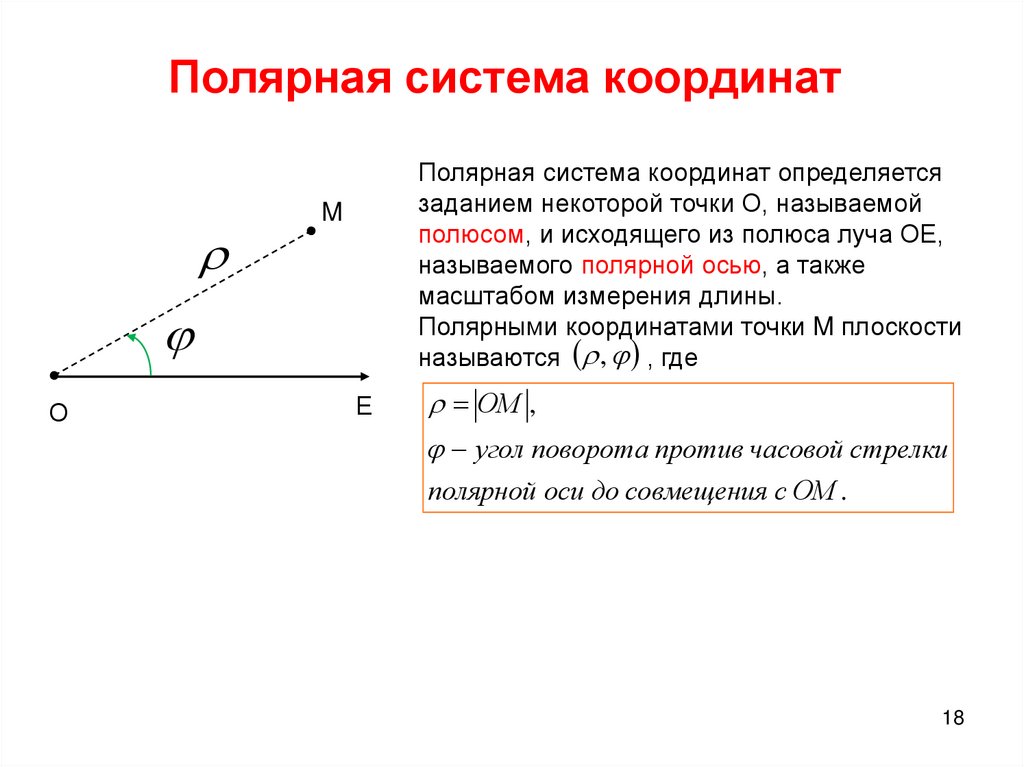 Кроме того, не забудьте проверить надстройку Chart Creator, мощный инструмент для создания умопомрачительных расширенных диаграмм и графиков Excel всего за несколько кликов.
Кроме того, не забудьте проверить надстройку Chart Creator, мощный инструмент для создания умопомрачительных расширенных диаграмм и графиков Excel всего за несколько кликов. 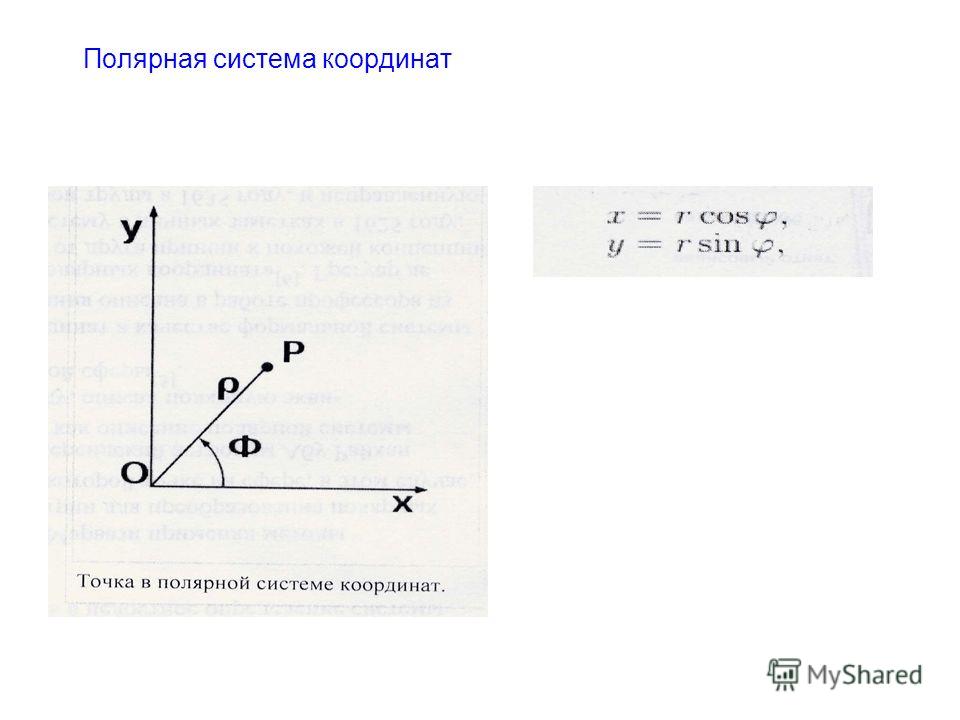 Давайте поговорим о каждом элементе таблицы немного подробнее:
Давайте поговорим о каждом элементе таблицы немного подробнее: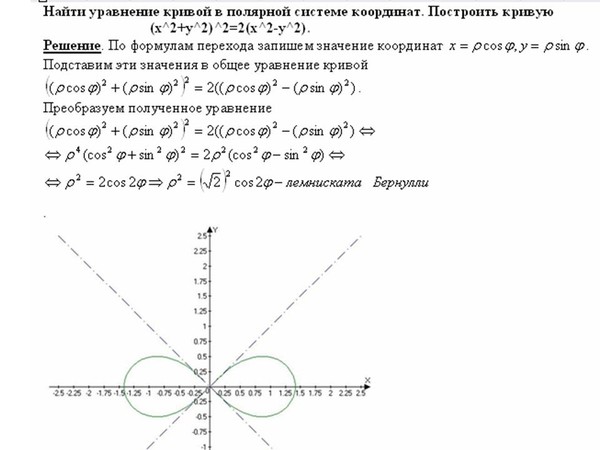 Поскольку один полный круговой оборот равен 360 градусам, чтобы выполнить задачу, вам нужно разделить 360 на количество категорий в вашем наборе данных (в нашем случае двенадцать месяцев).
Поскольку один полный круговой оборот равен 360 градусам, чтобы выполнить задачу, вам нужно разделить 360 на количество категорий в вашем наборе данных (в нашем случае двенадцать месяцев).
 Предположим, что какая-то компания заработала 250 000 долларов в мае. Чтобы найти свой радиус, разделите 250 000 долларов на 50 000. Так просто, как, что.
Предположим, что какая-то компания заработала 250 000 долларов в мае. Чтобы найти свой радиус, разделите 250 000 долларов на 50 000. Так просто, как, что.
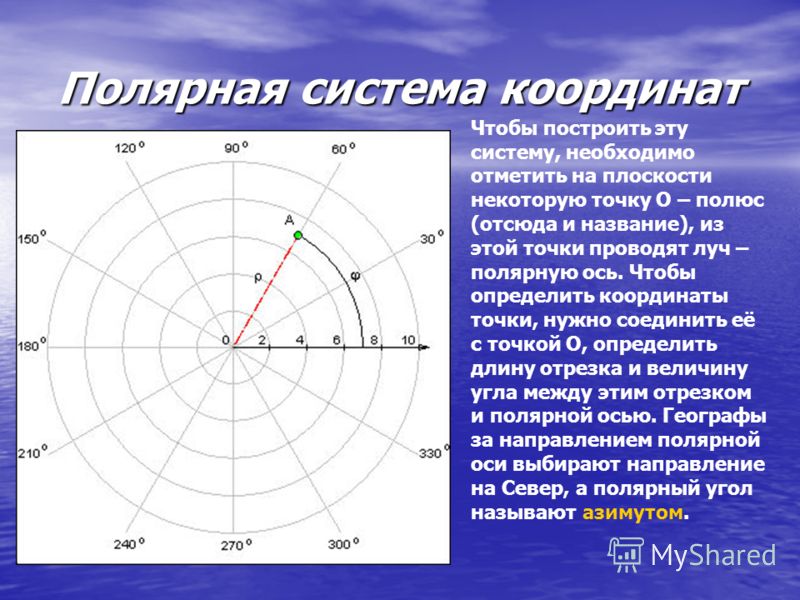
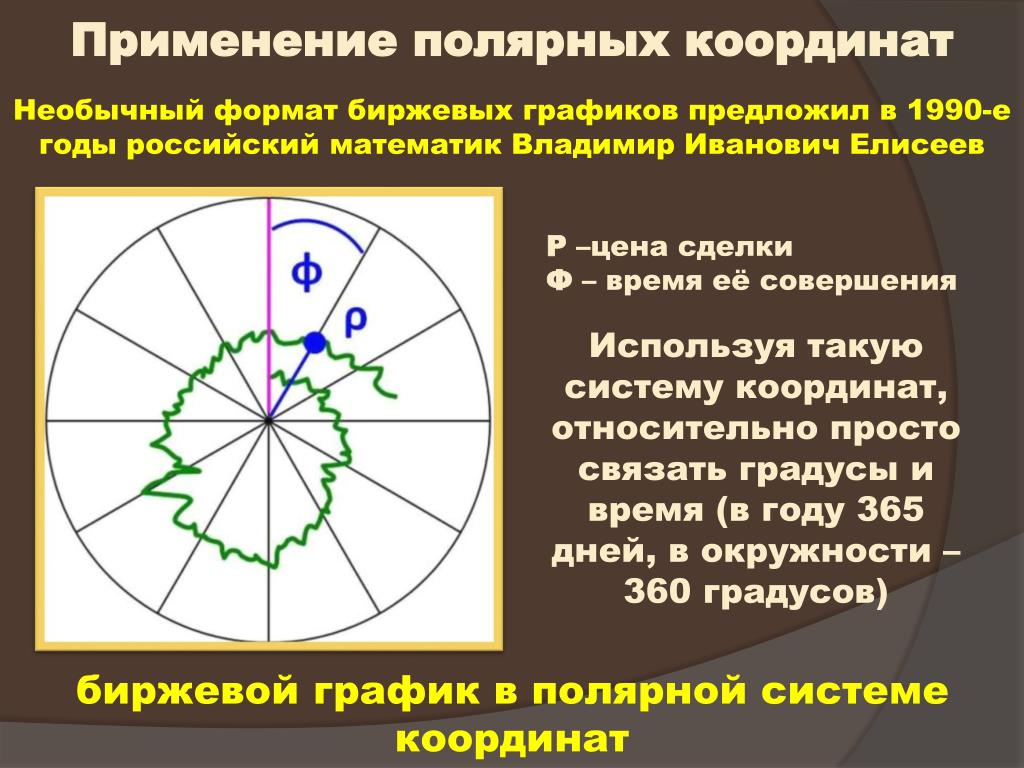
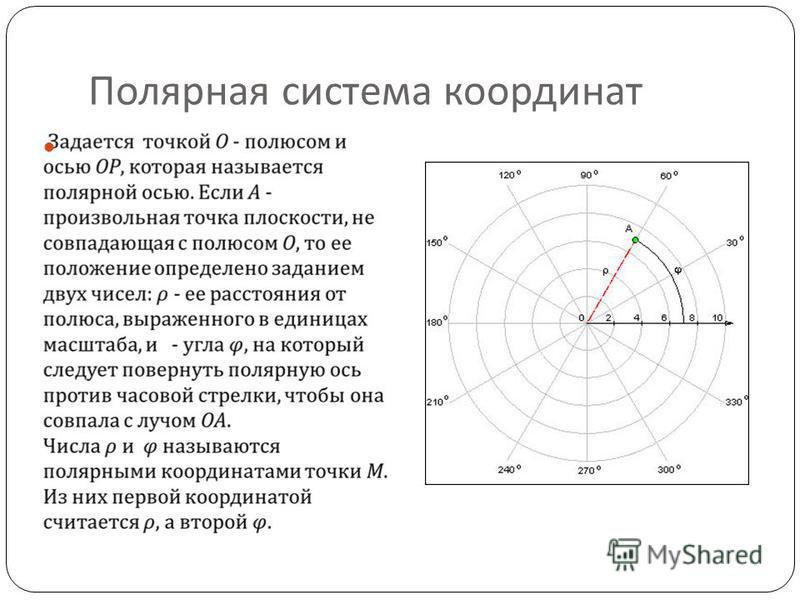

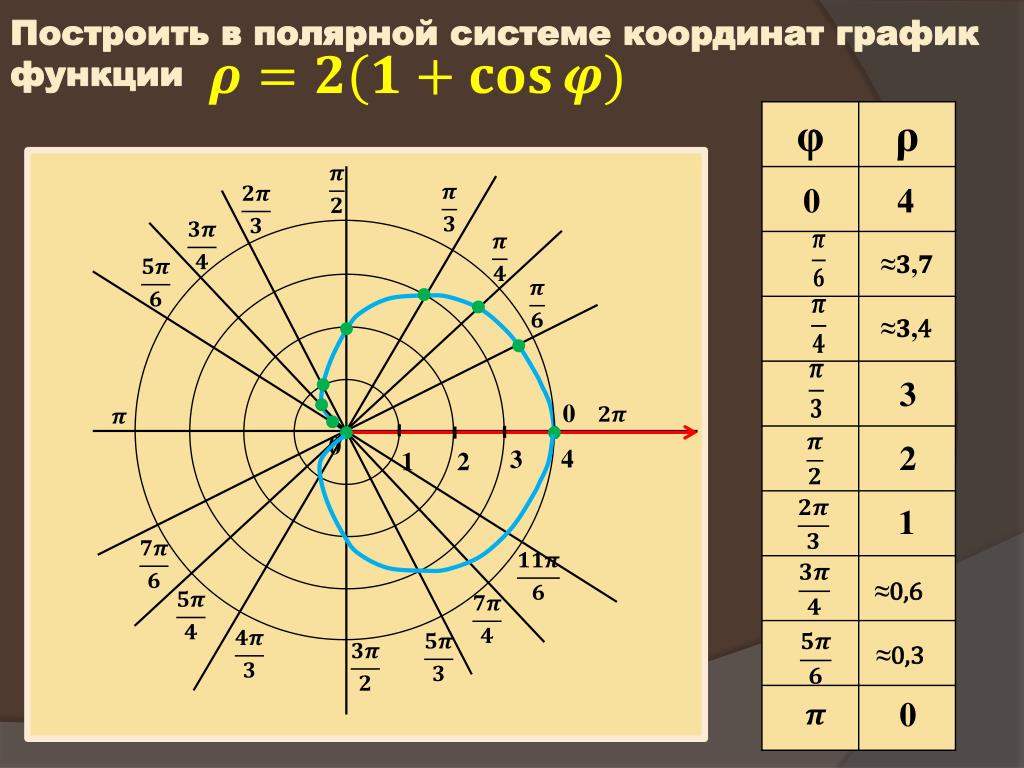
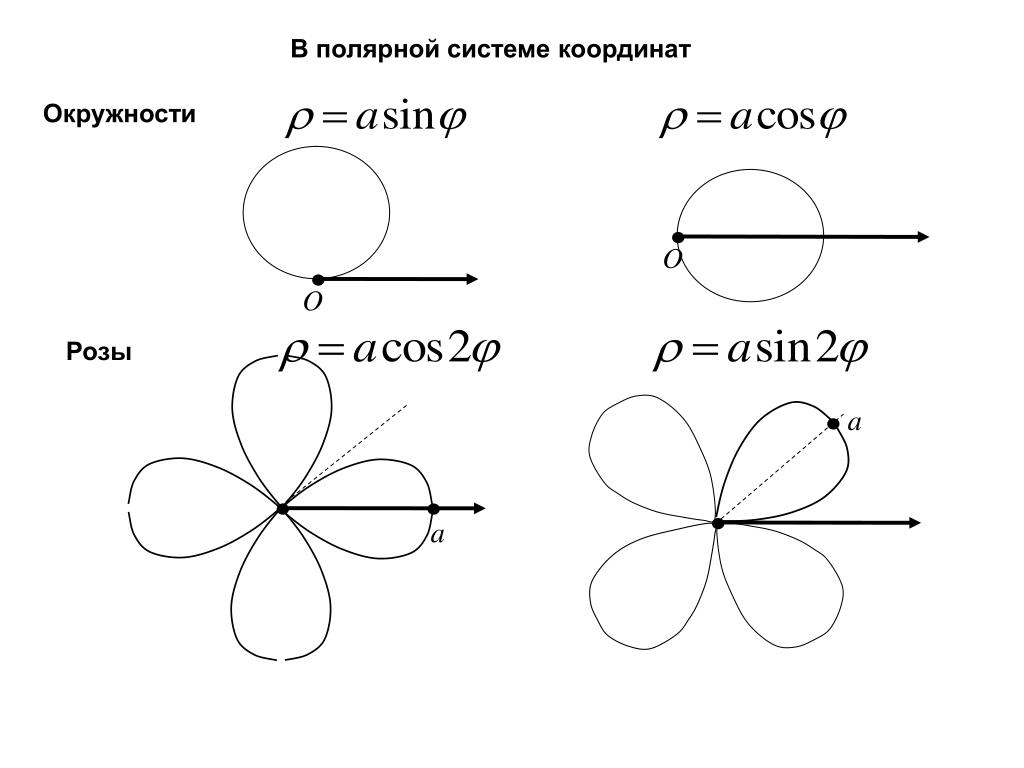
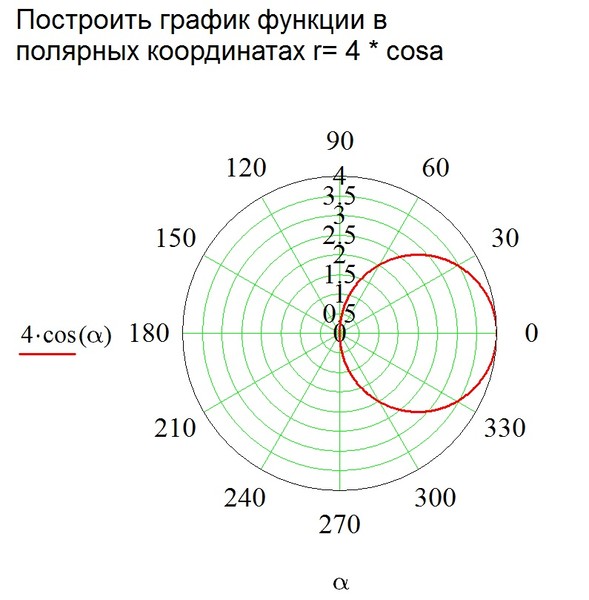

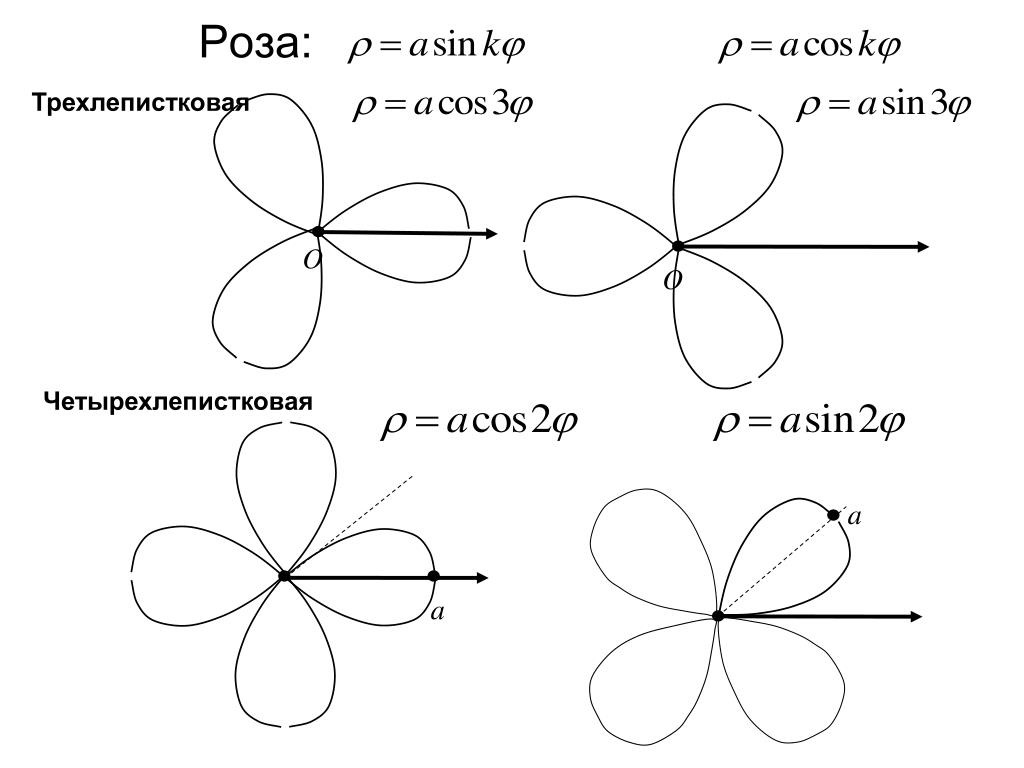
 Похоже на правую половину оси x. Затем точки наносятся на график на основе значения r, которое представляет расстояние от начала координат до этой точки, и значения θ, или тета, которое представляет собой меру в градусах или радианах угла, образованного исходным полюсом и линией, соединяющей сказал указать на происхождение. Как и в декартовой системе, точки записываются как упорядоченные пары, но на этот раз в виде (r, θ), а не (x, y).
Похоже на правую половину оси x. Затем точки наносятся на график на основе значения r, которое представляет расстояние от начала координат до этой точки, и значения θ, или тета, которое представляет собой меру в градусах или радианах угла, образованного исходным полюсом и линией, соединяющей сказал указать на происхождение. Как и в декартовой системе, точки записываются как упорядоченные пары, но на этот раз в виде (r, θ), а не (x, y). 2, которая принимает входные данные x и производит выходные данные y. Точно так же существуют полярные координаты, которые обычно записываются как r, равное некоторому действию с θ, например, r = sin(θ). График этой функции в полярной системе координат представляет собой круг, а полярная система построения графиков ценна тем, что позволяет математикам отображать важные кривые, такие как кардиоиды и розы, которые не могут быть легко построены с помощью функций в декартовой системе.
2, которая принимает входные данные x и производит выходные данные y. Точно так же существуют полярные координаты, которые обычно записываются как r, равное некоторому действию с θ, например, r = sin(θ). График этой функции в полярной системе координат представляет собой круг, а полярная система построения графиков ценна тем, что позволяет математикам отображать важные кривые, такие как кардиоиды и розы, которые не могут быть легко построены с помощью функций в декартовой системе. С другой стороны, полярная функция, которую я дал, была r = sin(θ), которая помещает θ в качестве входа и r в качестве выхода. Поскольку x и θ обычно являются входными данными функций соответствующего типа, а y и r обычно являются выходными данными, логично, что они должны находиться в одних и тех же местах своих упорядоченных пар.
С другой стороны, полярная функция, которую я дал, была r = sin(θ), которая помещает θ в качестве входа и r в качестве выхода. Поскольку x и θ обычно являются входными данными функций соответствующего типа, а y и r обычно являются выходными данными, логично, что они должны находиться в одних и тех же местах своих упорядоченных пар.