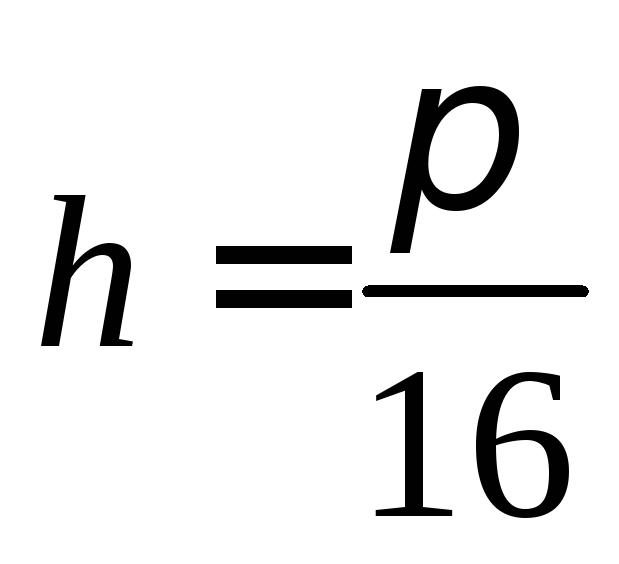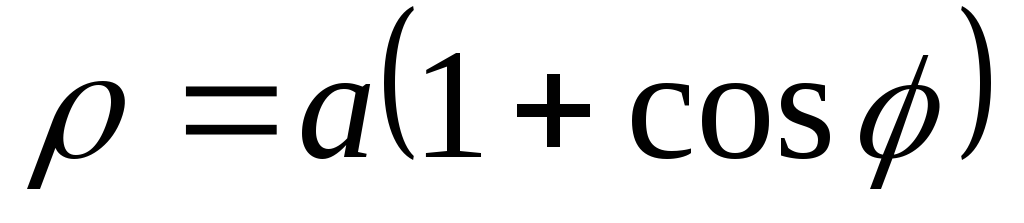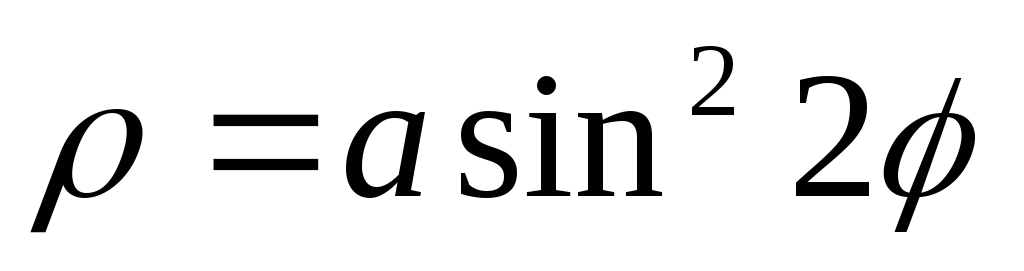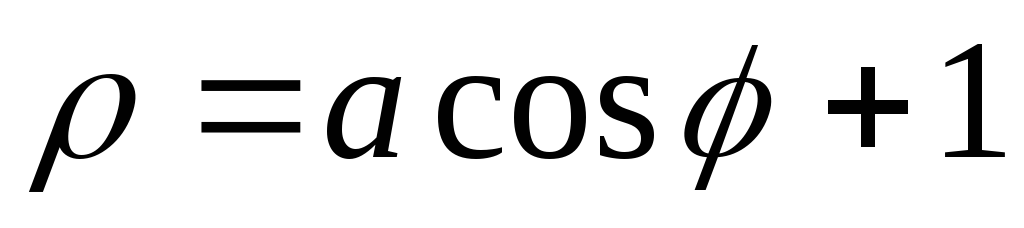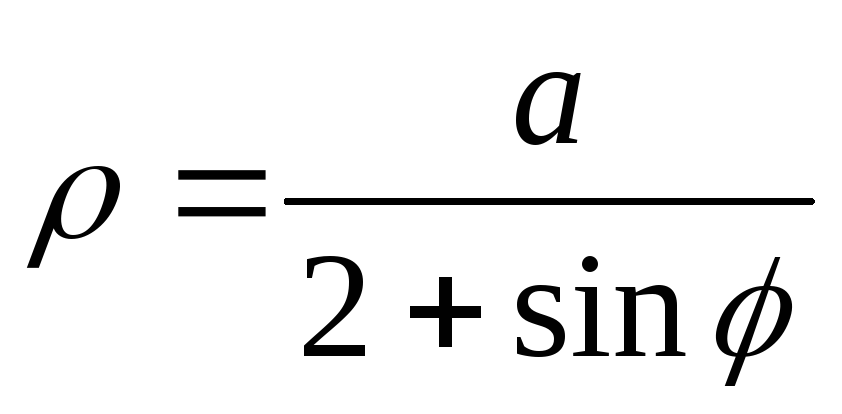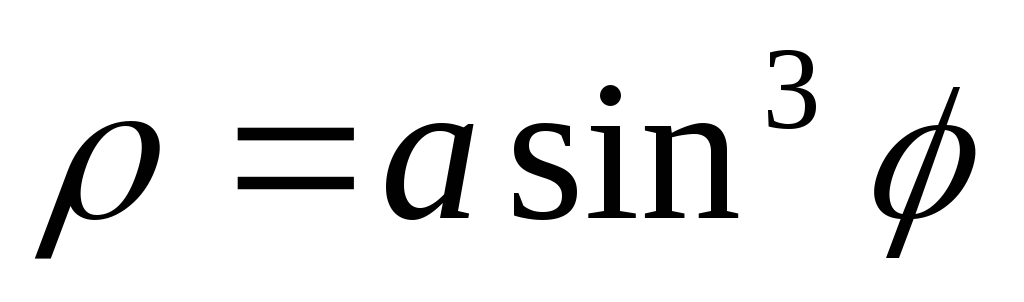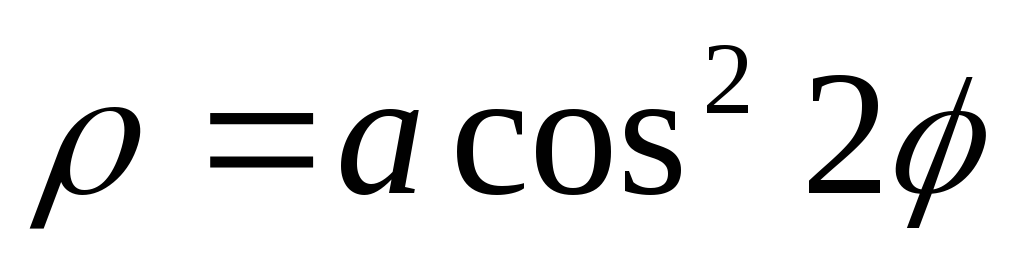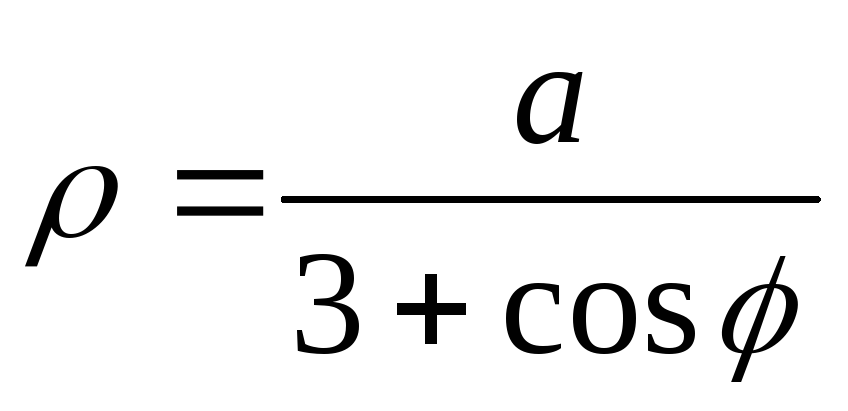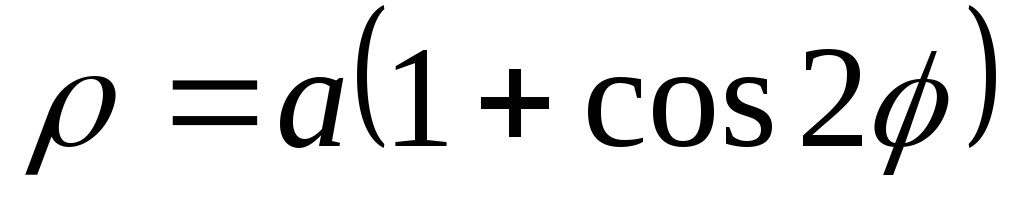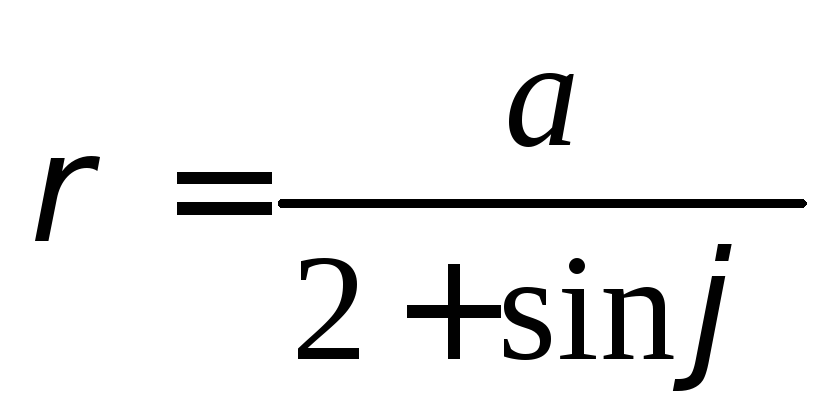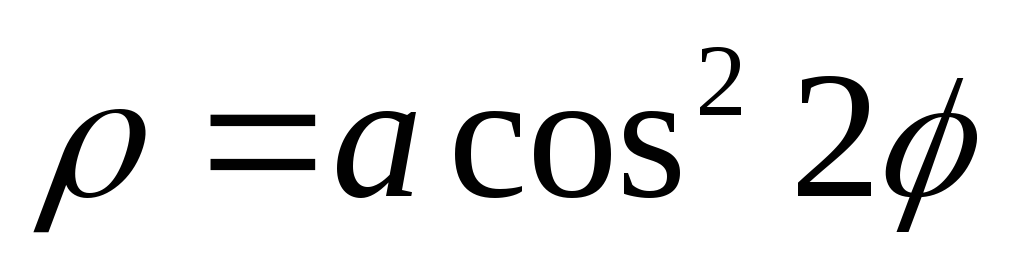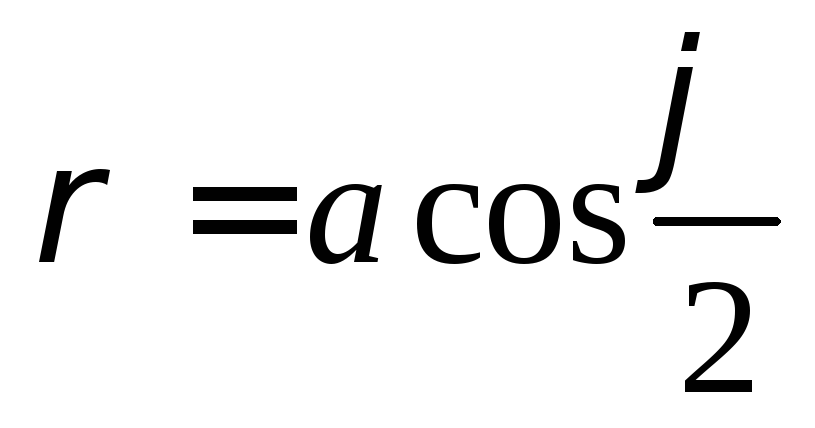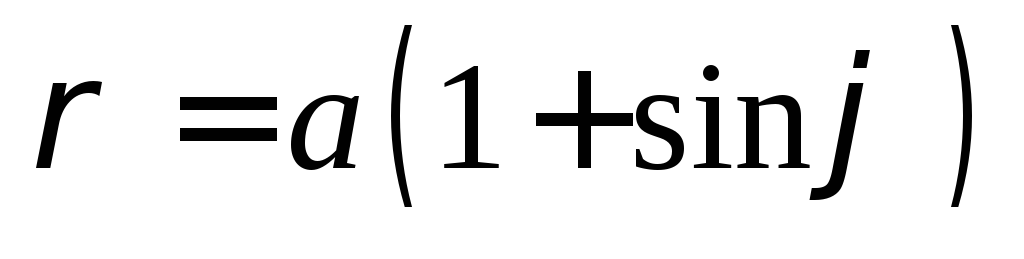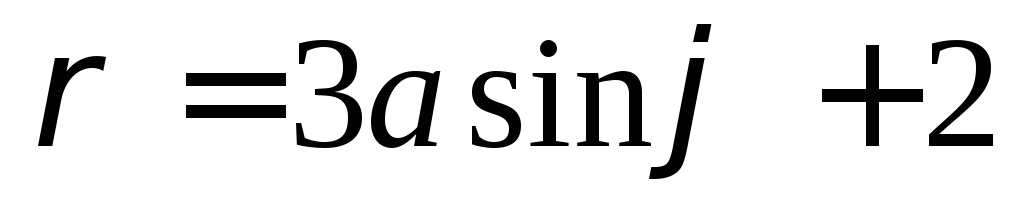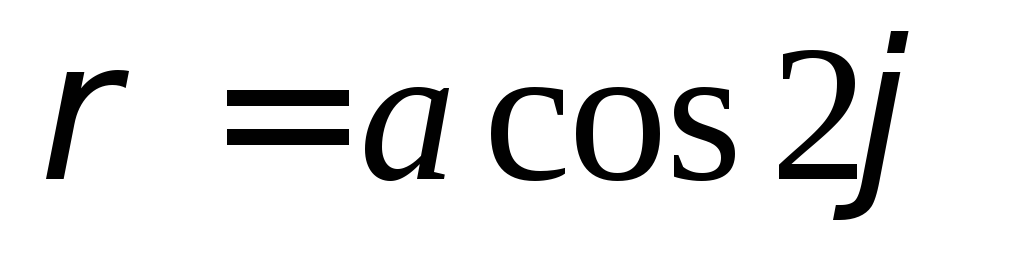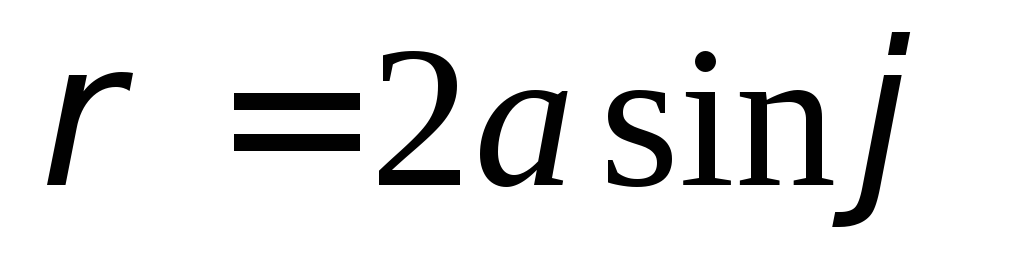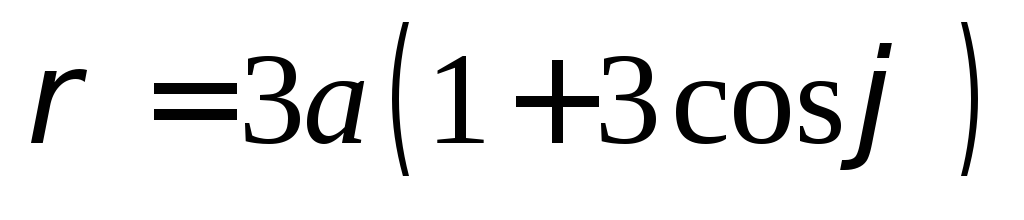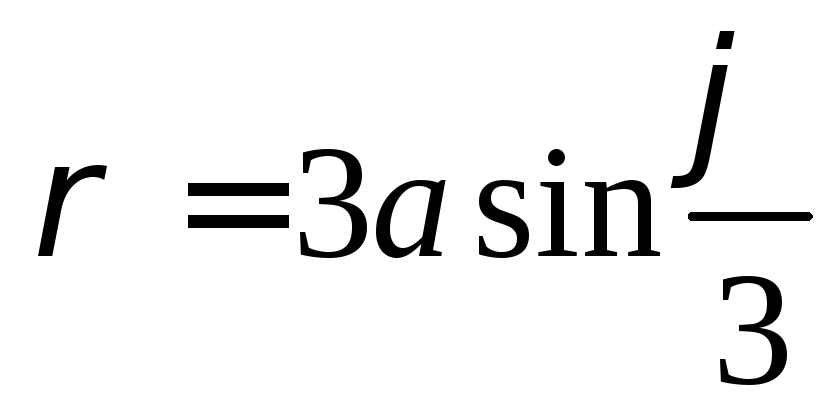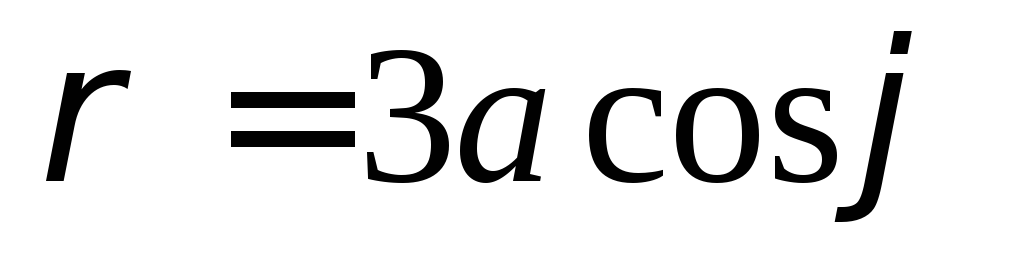Полярная система координат построение графиков: Построить график в полярных координатах на плоскости

Полярная система координат: основные понятия и примеры

Если уж речь зашла о полярной системе координат, то вообразите себя полярниками, стоящими на Северном полюсе. Или на Южном (это не так важно). Пусть в точке полюса находится начало линейки. В точку полюса также положим начало карандаша, а весь карандаш полностью прилегает к линейке. Теперь повернём карандаш так, чтобы его начало оставалось там же, на полюсе, а между ним и линейкой образовался некоторый угол поворота. Конец карандаша оказался в некоторой точке, назовём её M. Вот мы и получили полярные координаты точки M: длина карандаша и угол, на который был повёрнут карандаш. А теперь об этом же в более строгих и точных определениях.

Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки

O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

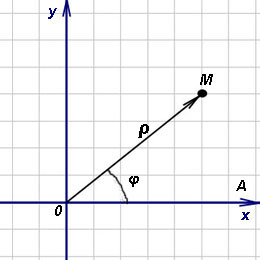
Итак, выберем на плоскости (рисунок выше) некоторую точку O (полюс) и некоторый выходящий из неё луч Ox. Кроме того, укажем единицу масштаба. Полярными координатами точки M называются два числа ρ и φ, первое из которых (полярный радиус ρ) равно расстоянию точки M от полюса O, а второе (полярный угол φ, который называют также амплитудой) — угол, на который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом OM.

Точку M с полярными координатами ρ и φ обозначают символом

M(ρ, φ).

Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда

x = ρ cos φ)

и

y = ρ sin φ).

Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

.

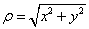Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка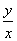

M, и, кроме того, воспользоваться тем, что тангенс угла φ равен .

Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.

Пример 1. В полярной системе координат на плоскости даны точки

A(3; π/4);

B(2; —π/2);

C(3; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полярной оси точки будет как и у данной точки. Как видно из рисунка в начале урока, при построении симметричной относительно полярной оси точки данную точку нужно повернуть вокруг полярной оси на тот же угол φ. Следовательно, в полярной системе координат второй координатой симметричной точки будет угол для исходной точки, взятый с противоположным знаком, то есть -φ. Итак, полярные координаты точки, симметричной данной относительно полярной оси будут отличаться лишь второй координатой, и эта координата будет с противоположным знаком. Полярные координаты искомых симметричных точек будут следующими:

A’(3; —π/4);

B’(2; π/2);

C’(3; π/3).

Пример 2. В полярной системе координат на плоскости даны точки

A(1; π/4);

B(5; π/2);

C(2; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полюса.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полюса точки будет как и у данной точки. Симметричная относительно полюса точка получается вращением исходной точки на 180 градусов против часовой стрелки, то есть на угол π. Следовательно, вторая координата точки, симметричной данной относительно полюса рассчитывается как φ + π (если в результате получится числитель больше знаменателя, то вычтем из полученного числа один полный оборот, то есть 2π). Получаем следующие координаты точек, симметричных данным относительно полюса:

A’(1; 3π/4);

B’(5; —π/2);

C’(2; 2π/3).

Пример 3.

Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки

A(6; π/2);

B(5; 0);

C(2; π/4).

Найти декартовы координаты этих точек.

Решение. Используем формулы перехода от полярных координат к декартовым:

x = ρ cos φ)

и

y = ρ sin φ).

Получаем следующие декартовы координаты данных точек:

A(0; 6);

B(5; 0);

C’(√2; √2).

Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки

A(0; 5);

B(-3; 0);

C(√3; 1).

Найти полярные координаты этих точек.

Решение. Определяем первую из полярных координат по формуле 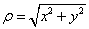, а тангенс угла φ — второй из полярных координат как 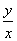. Получаем следующие полярные координаты данных точек:

A(5; π/2);

B(3; π);

C(2; π/6).

Поделиться с друзьями

Весь блок «Аналитическая геометрия»

• Векторы
• Плоскость
• Прямая на плоскости

Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel» — К уроку — Информатика

Практическая работа «Красивые графики функций»

1. Построить спираль Архимеда по следующим данным:
   — в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
   — в столбце В – значения r = 0,5*t
   — в столбце С – значения х = r*cos(t)
   — в столбце D – значения y = r*sin(t)
   — выделить значения в столбцах С и D

   и построить диаграмму
   (тип: точечная с гладкими кривыми)

2. Построить астроиду по следующим данным:
   — в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
   — в столбце В – значения х = 2*(cos (t))³
   — в столбце С – значения y = 2*(sin (t))³
   — выделить значения в столбцах B и С и построить диаграмму
   (тип: точечная с гладкими кривыми)

3. П остроить улитку Паскаля по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения p = cos

   (t)–0,5
   — в столбце D – значения x = p*cos(t)
   — в столбце Е – значения у = p*sin(t)
   — выделить значения в столбцах D и E и построить диаграмму
   (тип: точечная с гладкими кривыми)
   
   

4. Построить лемнискату Бернулли по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения r = 2*sin(2*t)²
   — в столбце D – значения x = r*cos(t)
   — в столбце E – значения y = r*sin(t

   )
   — выделить значения в столбцах D и E и построить диаграмму
   (тип: точечная с гладкими кривыми)

5. П остроить график в форме сердца по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения x = 16*(sin(t))³
   — в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
   — выделить значения в столбцах C и D и построить диаграмму
   (тип: точечная с гладкими кривыми)

5.2. Построение графиков в полярной системе координат при помощи MathCad

Для того чтобы построить график в полярной системе координат при помощи MathCAD, необходимо:

1. Определить  как дискретную переменную (в пределах области определения).

2. Задать функцию () .

3. Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» PolarPlot (Полярный график).

4. В появившемся шаблоне напечатать  в нижнем поле, напечатать () в левом поле.

5. Щелкнуть мышью вне графика.

Пример 2. Построим график функции 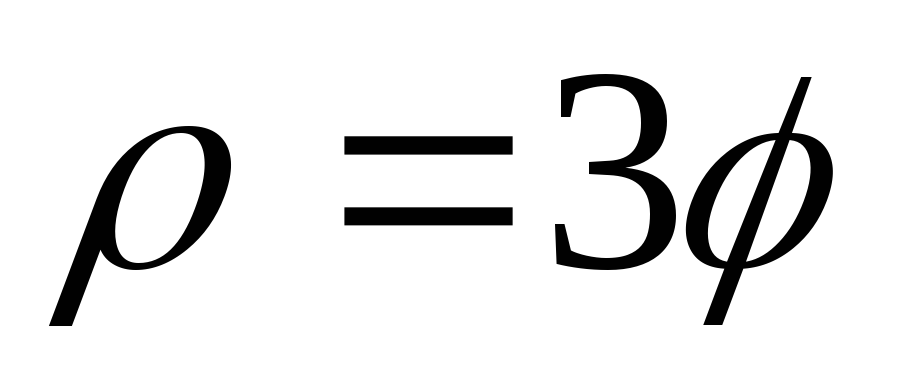(спираль Архимеда) при помощиMathCAD.

Решение.

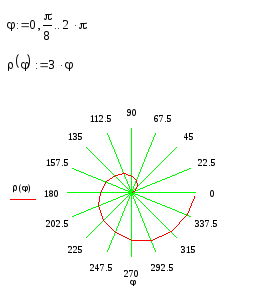
График в полярных координатах можно форматировать.

Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.

5.3. Задания для самостоятельного решения

1. Построить (в тетради) в полярной системе координат линию по точкам, придавая  значения от 0 до с шагом (для вычисления значений  можно использовать возможности MathCAD):

1.	,,	11.	, ,
2.	, ,	12.	, ,
3.	, ,	13.	, ,
4.	, ,	14.	, ,
5.	, ,	15.	,,
6.	, ,	16.	, ,
7.	, ,	17.	, ,
8.	, ,	18.	, ,
9.	, ,	19.	, ,
10.	, ,	20.	, ,

2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:

1.		11.
2.		12.
3.		13.
4.		14.
5.		15.
6.		16.
7.		17.
8.		18.
9.		19.
10.		20.

Лабораторная работа № 6 Тема: Символьные вычисления

Цель работы: Научиться производить символьные вычисления: преобразовывать выражения, вычислять пределы.

MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.

Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).

Знак символьного равенства представляет собой стрелку вправо () и набирается сочетанием клавиш [Ctrl] и [.], либо с палитры «Преобразования».

Чтобы произвести символьные вычисления, необходимо:

1. Ввести выражение, которое надо вычислить или преобразовать.

2. Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.

3. Щелкнуть мышью вне выражения.

Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим 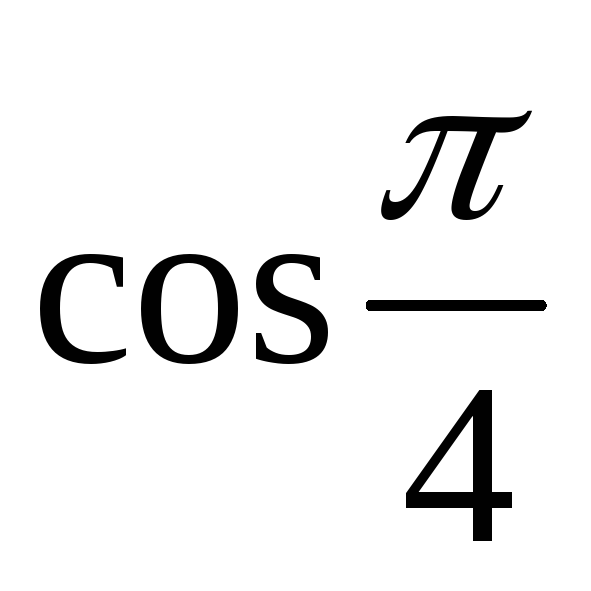двумя способами:

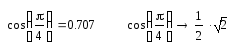
Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.

При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.

Полярная система координат — Википедия с видео // WIKI 2

Полярная сетка, на которой отложено несколько углов с пометками в градусах

Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью. Точка, из которой выходит этот луч, называется началом координат, или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r {\displaystyle r} ) соответствует расстоянию от точки до начала координат. Угловая координата также называется полярным углом или азимутом и обозначается φ {\displaystyle \varphi } , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку^[1].

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Энциклопедичный YouTube

• 1/5

  Просмотров:

  23 757

  2 363

  7 982

  1 686

  19 544

• ✪ Видеоурок «Полярная система координат»

• ✪ Полярная система координат

• ✪ Полярные координаты. Тема

• ✪ Полярная система координат. Часть 1.

• ✪ Двойной интеграл в полярных координатах — теория (от bezbotvy)

Содержание

История

Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческий астроном Гиппарх (190—120 до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел^[2]. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.

В IX веке персидский математик Хаббаш аль-Хасиб (аль-Марвази́) применял методы картографических проекций и сферической тригонометрии для преобразования полярных координат в другую систему координат с центром в некоторой точке на сфере, в этом случае, для определения Киблы — направления на Мекку^[3]. Персидский астроном Абу Райхан Бируни (973—1048) выдвинул идеи, которые выглядят как описание полярной системы координат. Он был первым, кто, примерно в 1025 году, описал полярную экви-азимутальную равнопромежуточную проекцию небесной сферы^[4].

Существуют разные версии о введении полярных координат в качестве формальной системы координат. Полная история возникновения и исследования описана в работе профессора из Гарварда Джулиан Лоувел Кулидж «Происхождение полярных координат»^[5]. Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635 году, и исправленную версию в 1653 году. Кавальери применял полярные координаты для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль впоследствии использовал полярные координаты для вычисления длин параболических дуг.

В книге «Метод флюксий» (англ. Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак Ньютон исследовал преобразование между полярными координатами, которые он обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For Spirals»), и девятью другими системами координат^[6]. В статье, опубликованной в 1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой системе координат.

Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов. В английский язык термин попал через перевод трактата Сильвестра Лакруа «Дифференциальное и интегральное исчисление», выполненного в 1816 году Джорджем Пикоком^[7][8] Для трёхмерного пространства полярные координаты впервые предложил Алекси Клеро, а Леонард Эйлер был первым, кто разработал соответствующую систему^[5].

Графическое представление

Точка в полярной системе координат

Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются r {\displaystyle r} (радиальная координата, встречается вариант обозначения ρ {\displaystyle \rho } ) и φ {\displaystyle \varphi } (угловая координата, полярный угол, фазовый угол, азимут, позиционный угол, иногда пишут θ {\displaystyle \theta } или t {\displaystyle t} ). Координата r {\displaystyle r} соответствует расстоянию от точки до центра, или полюса системы координат, а координата φ {\displaystyle \varphi } равна углу, отсчитываемого в направлении против часовой стрелки от луча через 0° (иногда называемому полярной осью системы координат)^[1].

Полярный радиус определен для любой точки плоскости и всегда принимает неотрицательные значения r ⩾ 0 {\displaystyle r\geqslant 0} . Полярный угол φ {\displaystyle \varphi } определен для любой точки плоскости, за исключением полюса O {\displaystyle O} , и принимает значения − π < φ ⩽ π {\displaystyle -\pi <\varphi \leqslant \pi } . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

• в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
• в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Например, точка с координатами ( 3 , 60 ∘ ) {\displaystyle (3,\;60^{\circ })} будет выглядеть на графике как точка на луче, который лежит под углом 60° к полярной оси, на расстоянии 3 единиц от полюса. Точка с координатами ( 3 , − 300 ∘ ) {\displaystyle (3,\;-300^{\circ })} будет нарисована на том же месте.

Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. В общем случае точка ( r , φ ) {\displaystyle (r,\;\varphi )} может быть представлена в виде ( r , φ ± n × 360 ∘ ) {\displaystyle (r,\;\varphi \pm n\times 360^{\circ })} или ( − r , φ ± ( 2 n + 1 ) × 180 ∘ ) {\displaystyle (-r,\;\varphi \pm (2n+1)\times 180^{\circ })} , где n {\displaystyle n}  — произвольное целое число^[9].

Для обозначения полюса используют координаты ( 0 , φ ) {\displaystyle (0,\;\varphi )} . Независимо от координаты φ {\displaystyle \varphi } точка с нулевым расстоянием от полюса всегда находится на нём^[10]. Для получения однозначных координат точки, обычно следует ограничить значение расстояния до неотрицательных значений r ⩾ 0 {\displaystyle r\geqslant 0} , а угол φ {\displaystyle \varphi } к интервалу [ 0 , 360 ∘ ) {\displaystyle [0,\;360^{\circ })} или ( − 180 ∘ , 180 ∘ ] {\displaystyle (-180^{\circ },\;180^{\circ }]} (в радианах [ 0 , 2 π ) {\displaystyle [0,\;2\pi )} или ( − π , π ] {\displaystyle (-\pi ,\;\pi ]} )^[11].

Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом 2 π R A D = 360 ∘ {\displaystyle 2\pi \;\mathrm {RAD} =360^{\circ }} . Выбор, как правило, зависит от области применения. В навигации традиционно используют градусы, в то время как в некоторых разделах физики и почти во всех разделах математики используют радианы^[12].

Связь между декартовыми и полярными координатами

Пару полярных координат r {\displaystyle r} и φ {\displaystyle \varphi } можно перевести в Декартовы координаты x {\displaystyle x} и y {\displaystyle y} путём применения тригонометрических функций синуса и косинуса (при этом предполагается. что нулевой луч полярной системы координат совпадает с осью x {\displaystyle x} декартовой системы):

x = r cos ⁡ φ , {\displaystyle x=r\cos \varphi ,}

y = r sin ⁡ φ , {\displaystyle y=r\sin \varphi ,}

в то время как две декартовы координаты x {\displaystyle x} и y {\displaystyle y} могут быть переведены в полярную координату r {\displaystyle r} :

r 2 = y 2 + x 2 {\displaystyle r^{2}=y^{2}+x^{2}} (по теореме Пифагора).

Для определения угловой координаты φ {\displaystyle \varphi } следует принять во внимание два следующих соображения:

Для вычисления φ {\displaystyle \varphi } в интервале [ 0 , 2 π ) {\displaystyle [0,\;2\pi )} , можно воспользоваться такими уравнениями ( a r c t g {\displaystyle \mathrm {arctg} } обозначает обратную функцию к тангенсу):

θ = { arctg ⁡ ( y x ) , x > 0 , y ≥ 0 arctg ⁡ ( y x ) + 2 π , x > 0 , y < 0 arctg ⁡ ( y x ) + π , x < 0 π 2 , x = 0 , y > 0 3 π 2 , x = 0 , y < 0 − x = 0 , y = 0 {\displaystyle \theta ={\begin{cases}\operatorname {arctg} ({\frac {y}{x}}),&x>0,y\geq 0\\\operatorname {arctg} ({\frac {y}{x}})+2\pi ,&x>0,y<0\\\operatorname {arctg} ({\frac {y}{x}})+\pi ,&x<0\\{\frac {\pi }{2}},&x=0,y>0\\{\frac {3\pi }{2}},&x=0,y<0\\-&x=0,y=0\end{cases}}} .

Для вычисления φ {\displaystyle \varphi } в интервале ( − π , π ] {\displaystyle (-\pi ,\;\pi ]} , можно воспользоваться такими уравнениями:^[13]

θ = { arctg ⁡ ( y x ) , x > 0 arctg ⁡ ( y x ) + π , x < 0 , y ≥ 0 arctg ⁡ ( y x ) − π , x < 0 , y < 0 π 2 , x = 0 , y > 0 − π 2 , x = 0 , y < 0 − x = 0 , y = 0 {\displaystyle \theta ={\begin{cases}\operatorname {arctg} ({\frac {y}{x}}),&x>0\\\operatorname {arctg} ({\frac {y}{x}})+\pi ,&x<0,y\geq 0\\\operatorname {arctg} ({\frac {y}{x}})-\pi ,&x<0,y<0\\{\frac {\pi }{2}},&x=0,y>0\\-{\frac {\pi }{2}},&x=0,y<0\\-&x=0,y=0\end{cases}}} .

Учитывая, что для вычисления полярного угла недостаточно знать отношение y {\displaystyle y} к x {\displaystyle x} , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты x {\displaystyle x} .

Уравнение кривых в полярных координатах

Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.

Окружность

Окружность, заданная уравнением r ( φ ) = 1 {\displaystyle \scriptstyle {r(\varphi )=1}}

Общее уравнение окружности с центром в ( r 0 , θ {\displaystyle r_{0},\;\theta } ) и радиусом a {\displaystyle a} имеет вид:

r 2 − 2 r r 0 cos ⁡ ( φ − θ ) + r 0 2 = a 2 . {\displaystyle r^{2}-2rr_{0}\cos(\varphi -\theta )+r_{0}^{2}=a^{2}.}

Это уравнение может быть упрощено для частных случаев, например

r ( φ ) = a {\displaystyle r(\varphi )=a}

является уравнением, определяющим окружность с центром в полюсе и радиусом a {\displaystyle a} ^[14].

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

φ = θ {\displaystyle \varphi =\theta } ,

где θ {\displaystyle \theta }  — угол, на который прямая отклоняется от полярной оси, то есть, θ = a r c t g m {\displaystyle \theta =\mathrm {arctg} \,m} , где m {\displaystyle m}  — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую φ = θ {\displaystyle \varphi =\theta } в точке ( r 0 , θ ) {\displaystyle (r_{0},\;\theta )} определяется уравнением

r ( φ ) = r 0 sec ⁡ ( φ − θ ) . {\displaystyle r(\varphi )=r_{0}\sec(\varphi -\theta ).}

Полярная роза

Полярная роза задана уравнением r ( φ ) = 2 sin ⁡ 4 φ {\displaystyle \scriptstyle {r(\varphi )=2\sin 4\varphi }}

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:

r ( φ ) = a cos ⁡ ( k φ + θ 0 ) {\displaystyle r(\varphi )=a\cos(k\varphi +\theta _{0})}

для произвольной постоянной θ 0 {\displaystyle \theta _{0}} (включая 0). Если k {\displaystyle k}  — целое число, то это уравнение будет определять розу с k {\displaystyle k} лепестками для нечётных k {\displaystyle k} , либо с 2 k {\displaystyle 2k} лепестками для чётных k {\displaystyle k} . Если k {\displaystyle k}  — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если k {\displaystyle k}  — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная a {\displaystyle a} определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном k {\displaystyle k} мы будем иметь k {\displaystyle k} -лепестковую розу. Таким образом, уравнение r ( φ ) = cos ⁡ ( 2 φ ) {\displaystyle r(\varphi )=\cos(2\varphi )} будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением r ( φ ) = φ {\displaystyle \scriptstyle {r(\varphi )=\varphi }} для 0 < θ < 6 π {\displaystyle \scriptstyle {0<\theta <6\pi }}

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

r ( φ ) = a + b φ . {\displaystyle r(\varphi )=a+b\varphi .}

Изменения параметра a {\displaystyle a} приводят к повороту спирали, а параметра b {\displaystyle b}  — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ > 0 {\displaystyle \varphi >0} а другую для φ < 0

Окружность в полярных координатах | Формулы и расчеты онлайн

Уравнение окружности в полярных координатах выглядит очень просто

\[ ρ = R = \const \]

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Построение окружности по простому уравнению в полярной системе координат

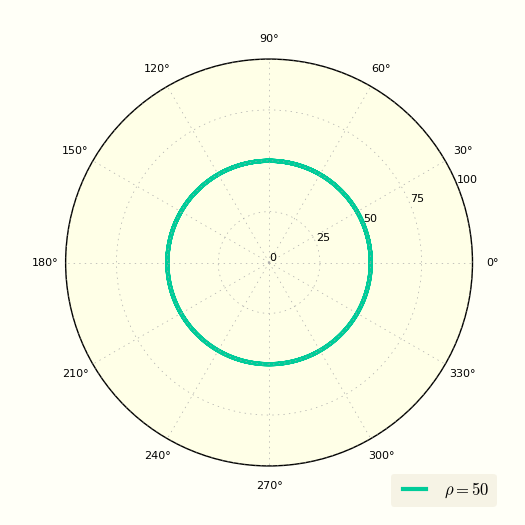
Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

\[ (x-R)^2 + y^2 = R^2 \]

Также известны формулы перевода декартовых координат в полярные

Используя эти формулы и подставив их в (1) мы получим:

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

\[ ρ^2-2Rρ\cos(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\cos(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\cos(φ) \]

Построение окружности в полярной системе координат

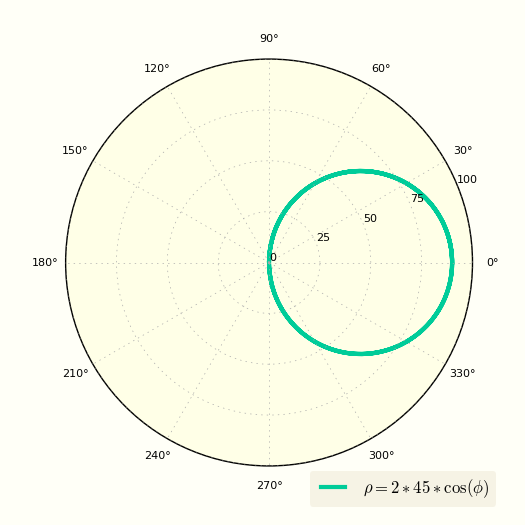
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

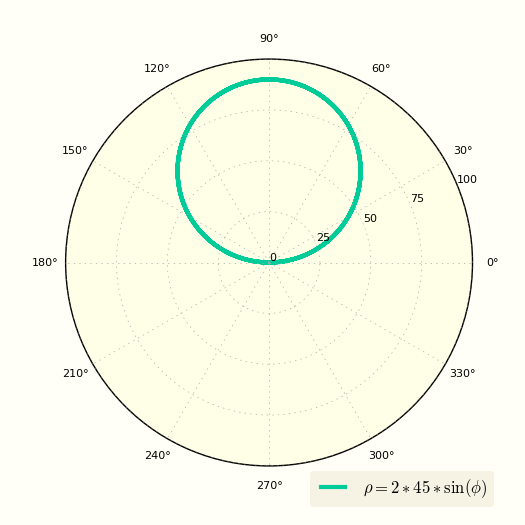
В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

\[ x^2 + (y-R)^2 = R^2 \]

Снова используем формулы перевода декартовых координат в полярные

получаем:

\[ ρ^2-2Rρ\sin(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\sin(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\sin(φ) \]

Построение окружности в полярной системе координат смещенной вверх относительно полюса

Прямоугольная и полярная система координат на плоскости

Прямоугольная система координат на плоскости вводится следующим образом. Возьмем на плоскости две взаимно перпендикулярные числовые оси 0х и 0у, имеющие общее начало точку 0 и общую единицу масштаба.
Оси 0х и 0у образуют прямоугольную (декартовую) систему координат на плоскости.
Проекции точки на плоскости на оси координат, а точнее, их числовые значения, называются прямоугольными или декартовыми прямоугольными координатами точки на плоскости.

Кроме прямоугольных декартовых координат на плоскости существуют другие системы координат, позволяющие определить положение каждой точки плоскости с помощью двух действительных чисел. Наиболее употребительной после декартовой системы координат является полярная система координат.

Возьмем на плоскости точку 0, которую назовем полюсом. Проведем из полюса луч 0р, называемый полярной осью.
Полюс и полярная ось образуют полярную систему координат на плоскости.

Расстояние r от точки до полюса называют полярным радиусом точки . Угол между полярной осью и радиусом называют полярным углом точки.
Полярный радиус и полярный угол называют полярными координатами точки на плоскости.

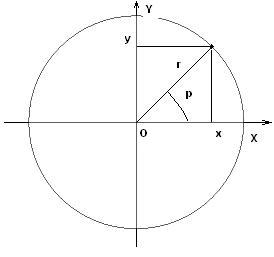
Два калькулятора ниже используются для перехода от прямоугольных координат точки на плоскости к полярным и обратно.
(В предположении, что начала координат у обоих систем совпадают, а полярная ось направлена вдоль положительного направления оси Х)

Переход от прямоугольной к полярной системе координат на плоскости

Точность вычисления

Знаков после запятой: 2

Полярный радиус

 

Полярный угол (радианы)

 

Полярный угол (градусы)

 

save Сохранить extension Виджет

Переход от полярной к прямоугольной системе координат на плоскости

Точность вычисления

Знаков после запятой: 2

Координата по оси X

 

Координата по оси Y

 

save Сохранить extension Виджет

Полярные и декартовы координаты

… и как между ними конвертировать.

Спешите? Прочтите резюме. Но сначала прочтите почему:

Чтобы точно определить, где мы находимся на карте или графике, есть две основные системы:

Декартовы координаты

Используя декартовы координаты, мы отмечаем точку по , насколько далеко вдоль и , насколько она выше :

Полярные координаты

Используя полярные координаты, мы отмечаем точку , как далеко , и , под каким углом это:

Преобразование

Для преобразования одного в другой мы будем использовать этот треугольник:

для преобразования из декартовой системы координат в полярную

Когда мы знаем точку в декартовых координатах (x, y) и хотим, чтобы она была в полярных координатах (r, θ ), мы решаем прямоугольный треугольник с двумя известными сторонами .

Пример: что такое (12,5) в полярных координатах?

Используйте теорему Пифагора, чтобы найти длинную сторону (гипотенузу):

r ² = 12 ² + 5 ²

г = √ (12 ² + 5 ² )

г = √ (144 + 25)

г = √ (169) = 13

Используйте функцию касания, чтобы найти угол:

тангенс ( θ ) = 5/12

θ = tan ^-1 (5/12) = 22.6 ° (с точностью до одного знака после запятой)

Ответ : точка (12,5) равна (13, 22,6 °) в полярных координатах.

Что такое загар ^-1 ?

Это функция обратной касательной:

• Касательная принимает угол и дает нам отношение,
• Обратный тангенс принимает соотношение (например, «5/12») и дает нам угол.

Сводка : для преобразования декартовых координат (x, y) в полярные координаты (r, θ):

Примечание. Калькуляторы могут дать неправильное значение tan ^-1 () , если x или y отрицательны… Подробнее см. ниже.

Преобразовать из полярной в декартову

Когда мы знаем точку в полярных координатах (r, θ ) и хотим, чтобы она была в декартовых координатах (x, y), мы решаем прямоугольный треугольник с известной длинной стороной и углом :

Пример: Что такое (13, 22,6 °) в декартовых координатах?

Используйте функцию косинуса для x:		cos (22,6 °) = x / 13
Перестановка и решение:		x = 13 × cos (22.6 °)
		х = 13 × 0,923
		х = 12,002 …
Используйте функцию синуса для y:		sin (22,6 °) = y / 13
Перестановка и решение:		y = 13 × sin (22.6 °)
		y = 13 × 0,391
		г = 4,996 …

Ответ: точка (13, 22,6 °) равна почти точно (12, 5) в декартовых координатах.

Сводка : преобразовать из полярных координат (r, θ ) в декартовы координаты (x, y):

Как помнить?

(x, y) по алфавиту,
(cos, sin) также по алфавиту

Также «y and sine rhyme» (попробуйте сказать это!)

Но как насчет отрицательных значений X и Y?

Четыре квадранта

Когда мы включаем отрицательные значения, оси x и y делят пространство
на 4 части:

Квадранты I, II, III и IV

(пронумерованы против часовой стрелки)

При преобразовании полярных координат в декартовы все получается отлично:

Пример: Что такое (12, 195 °) в декартовых координатах?

r = 12 и θ = 195 °

• x = 12 × cos (195 °)
  x = 12 × −0.9659 …
  x = −11,59 до 2 десятичные разряды
• y = 12 × sin (195 °)
  y = 12 × −0,2588 …
  y = −3,11 до 2 десятичные разряды

Итак, точка находится в (-11,59, -3,11) , что в квадранте III

.

Но при преобразовании из декартовых координат в полярные …

… калькулятор может дать неправильное значение tan ^-1

Все зависит от того, в каком квадранте находится точка! Используйте это, чтобы исправить ситуацию:

Квадрант	Значение тангенса -1
I	Использование значение калькулятора
II	Добавить 180 ° к значению калькулятора
III	Добавить 180 ° к значению калькулятора
IV	Добавить 360 ° к значению калькулятора

Пример: P = (−3, 10)

P находится в квадранте II

• r = √ ((- 3) ² + 10 ² )
  r = √109 = 10.4 до 1 знака после запятой
• θ = tan ^-1 (10 / −3)
  θ = tan ^-1 (−3,33 …)

Значение tan ^-1 (-3,33 …) калькулятора равно -73,3 °

Правило для квадранта II: Добавить 180 ° к значению калькулятора

θ = -73,3 ° + 180 ° = 106,7 °

Итак, полярные координаты для точки (−3, 10) равны (10,4, 106,7 °)

Пример: Q = (5, −8)

Q находится в квадранте IV

• г = √ (5 ² + (−8) ² )
  г = √89 = 9.4 до 1 знака после запятой
• θ = tan ^-1 (-8/5)
  θ = tan ^-1 (−1,6)

Значение tan ^-1 (-1,6) калькулятора равно -58,0 °

Правило для квадранта IV: Добавить 360 ° к калькулятору значение

θ = -58,0 ° + 360 ° = 302,0 °

Таким образом, полярные координаты точки (5, −8) равны (9,4, 302,0 °)

Сводка

Для преобразования полярных координат (r, θ ) в декартовы координаты (x, y):

• x = r × cos ( θ )
• y = r × sin ( θ )

Для преобразования декартовых координат (x, y) в полярные координаты (r, θ):

• r = √ (x ² + y ² )
• θ = tan ^-1 (y / x)

Значение тангенса ^-1 (y / x) может потребоваться корректировка:

• Квадрант Я использую значение калькулятора
• Квадрант II: Добавить 180 °
• Квадрант III: Добавить 180 °
• Квадрант IV: Добавить 360 °

.

Полярная система координат — Precalculus

Precalculus

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

• Алгебра
• Исчисление
• Геометрия
• Предалгебра
• Precalculus
• Статистика
• Тригонометрия

Гуманитарные науки

.

новейших вопросов о полярных координатах — Stack overflow на русском

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

2. Авторизоваться зарегистрироваться

3. текущее сообщество

   • Переполнение стека Помогите болтать
   • Переполнение мета-стека

   ваши сообщества

   Зарегистрируйтесь или

.2D полярный график

gnuplot с тепловой картой из набора данных 3D — возможно?

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

.
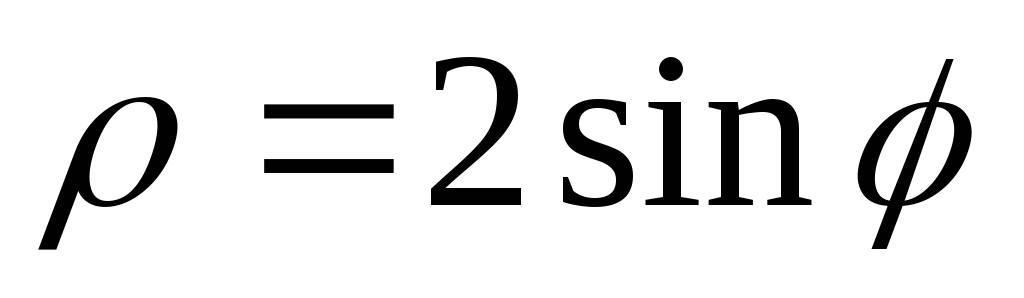
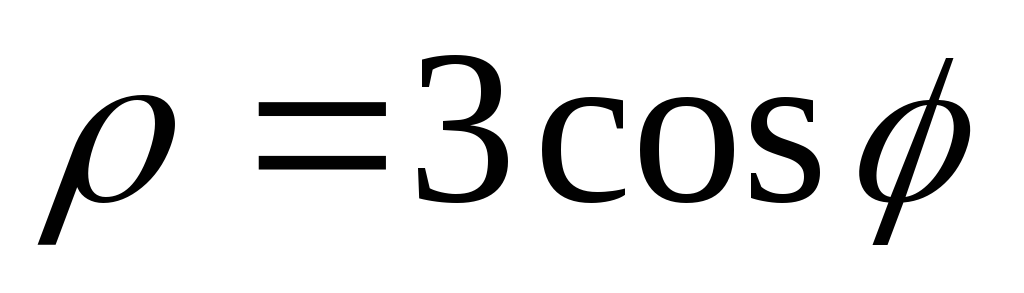
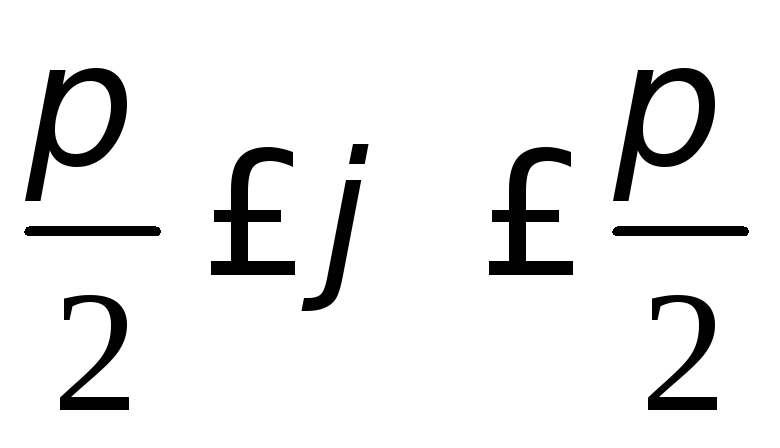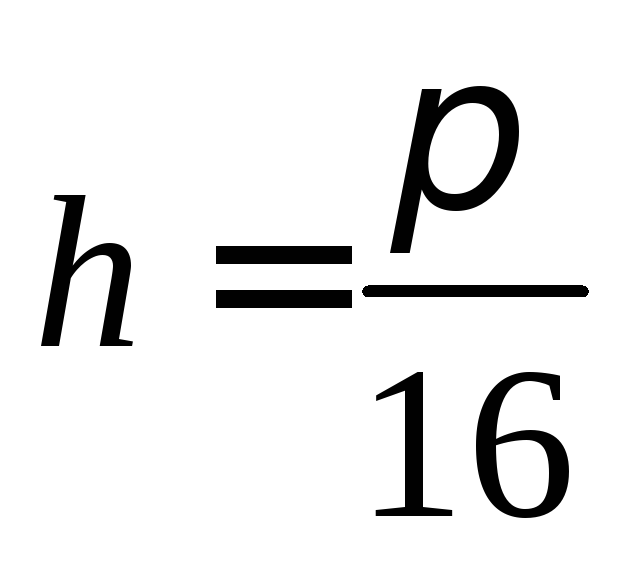
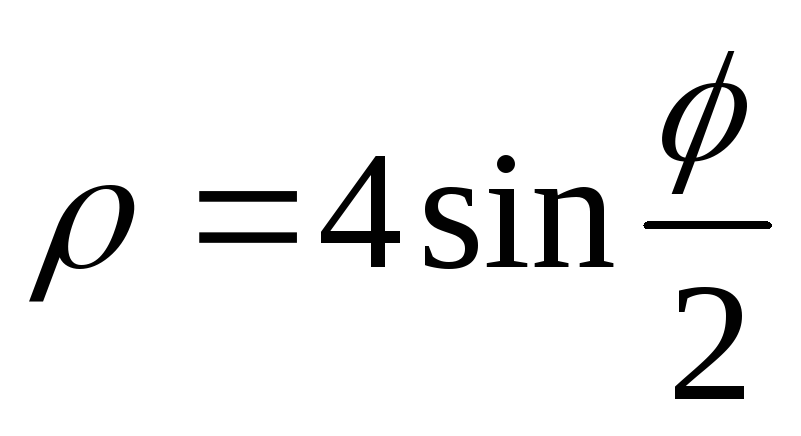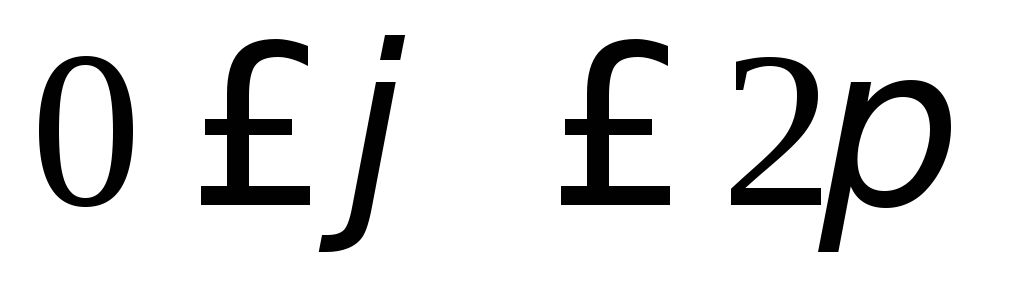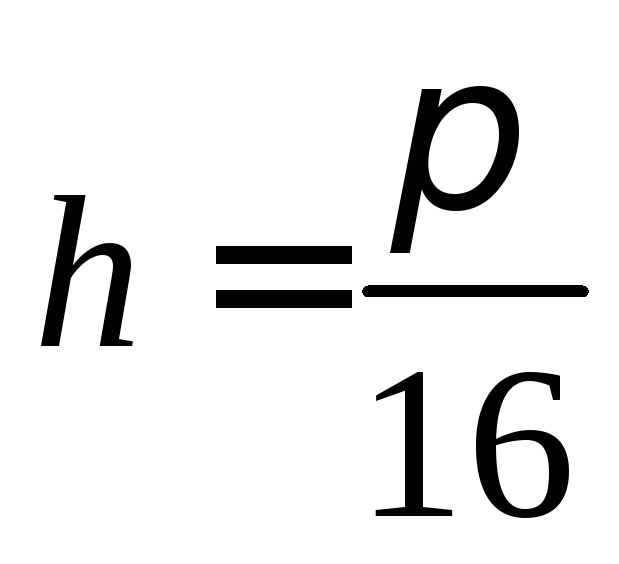
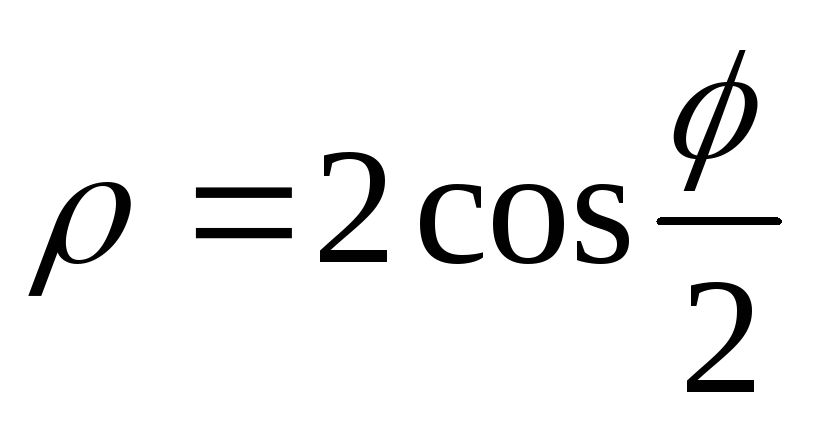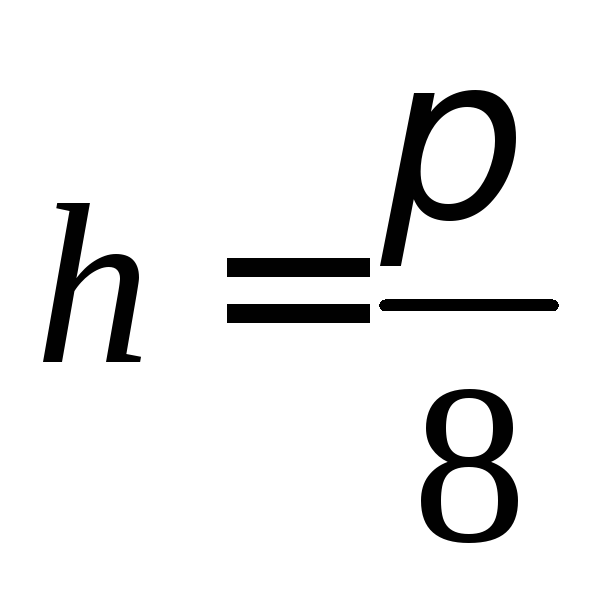
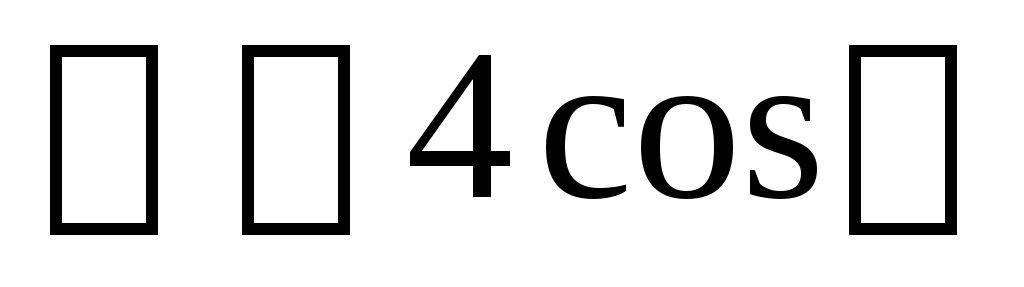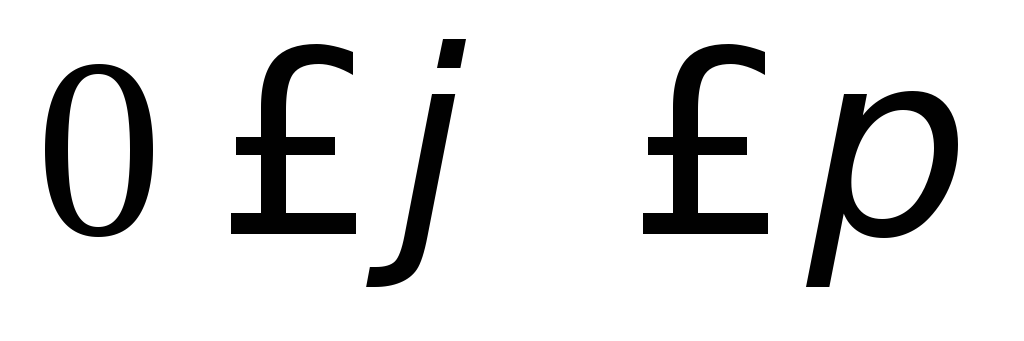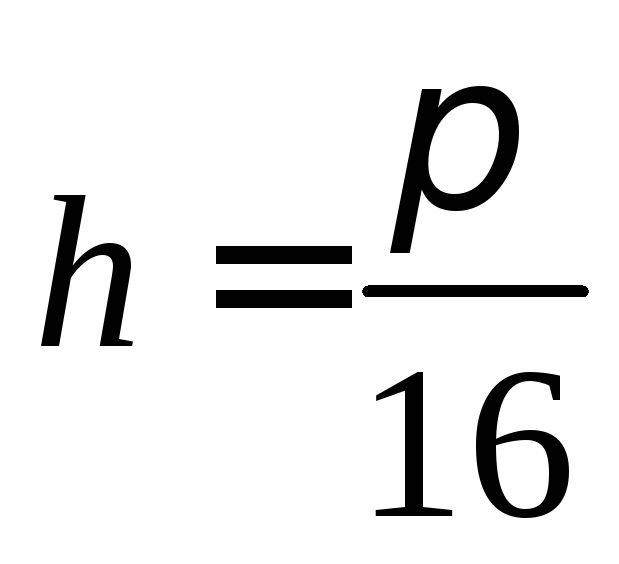
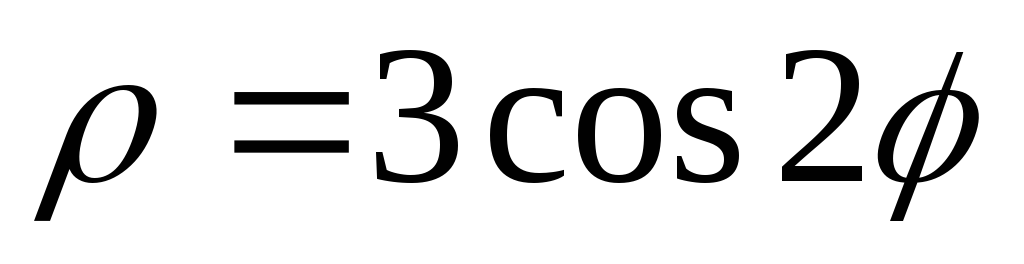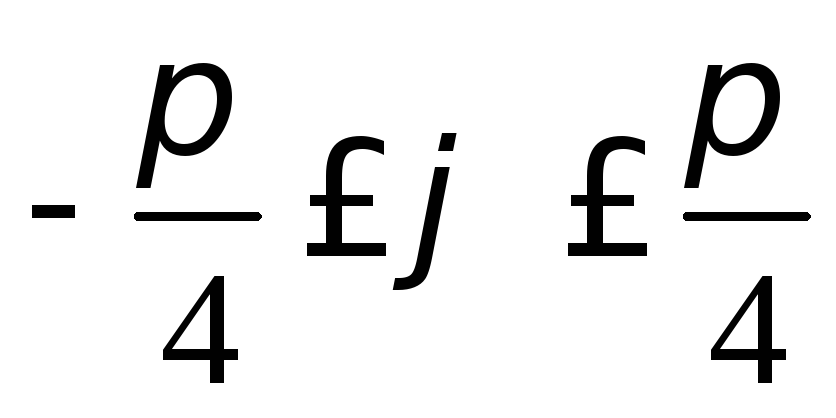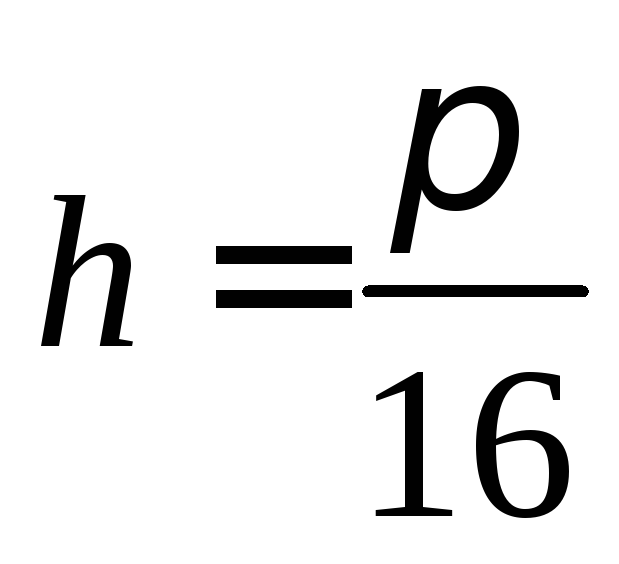
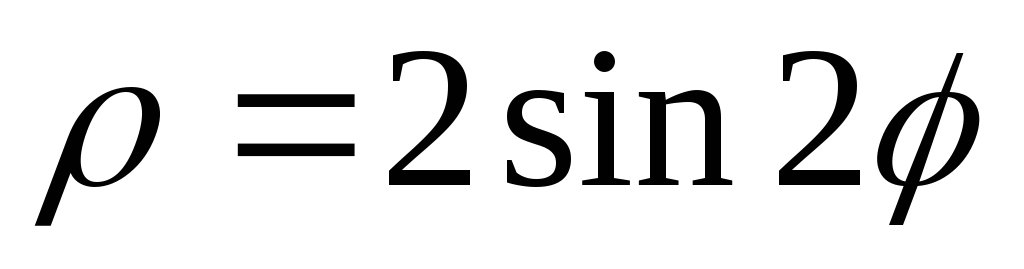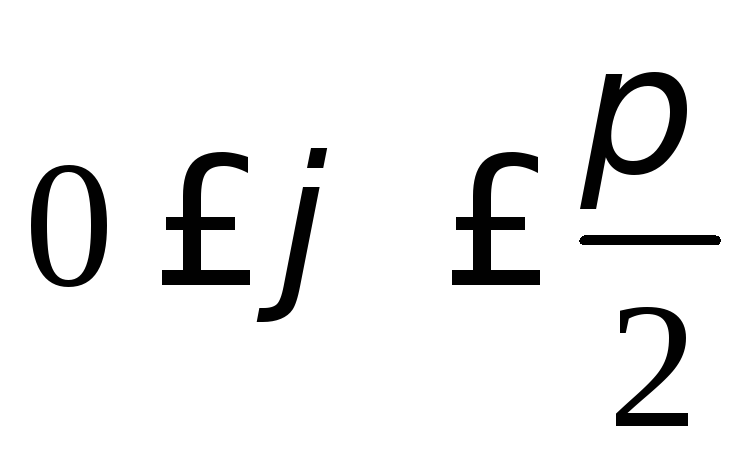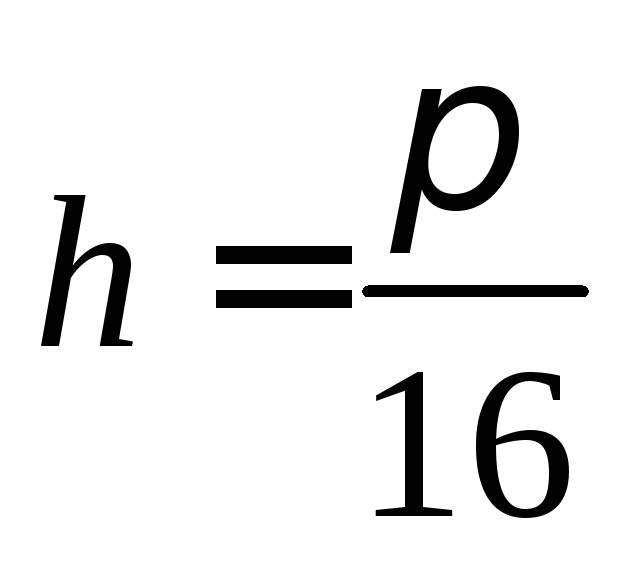
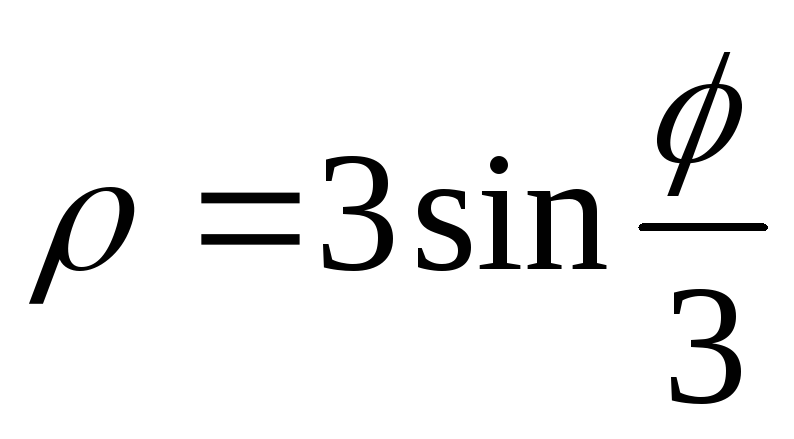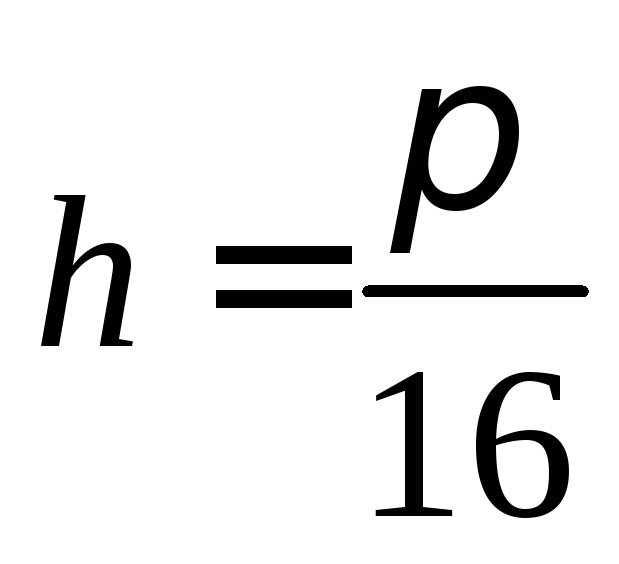
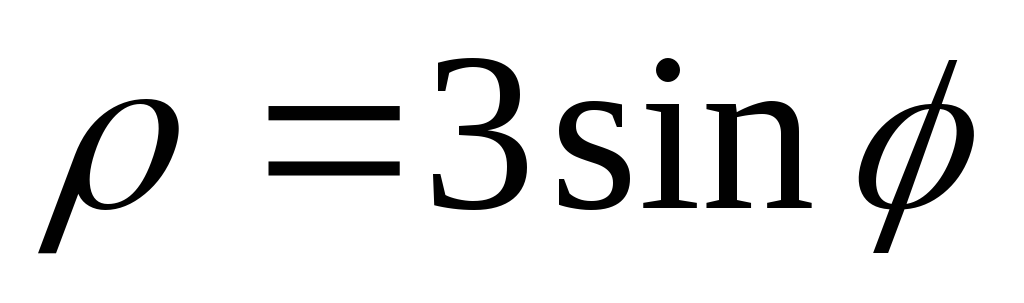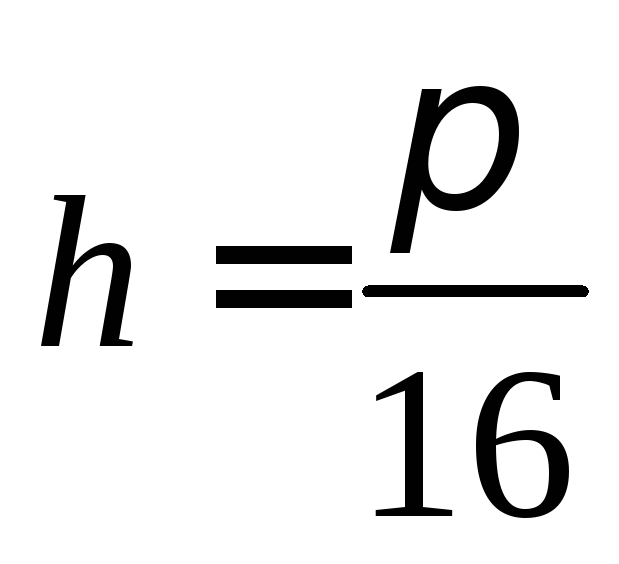
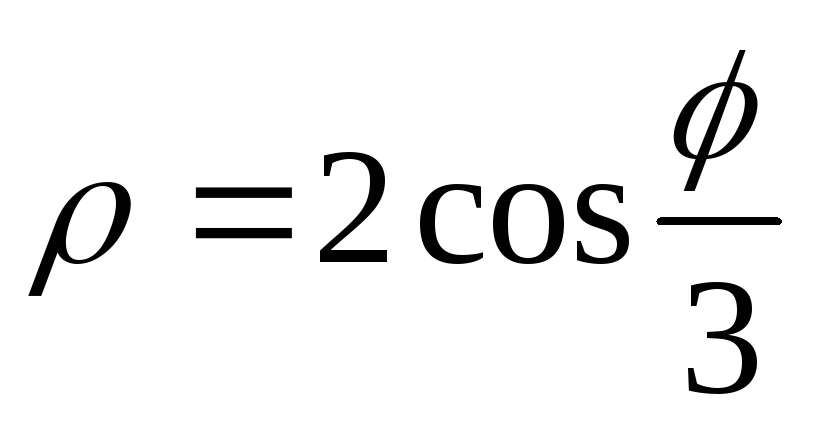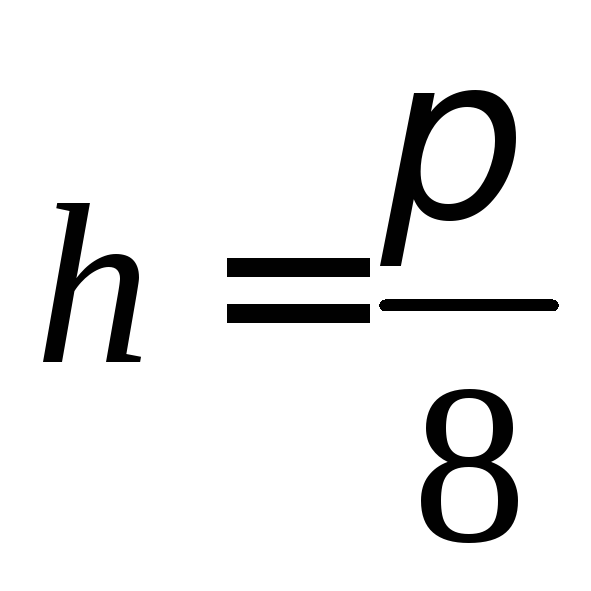
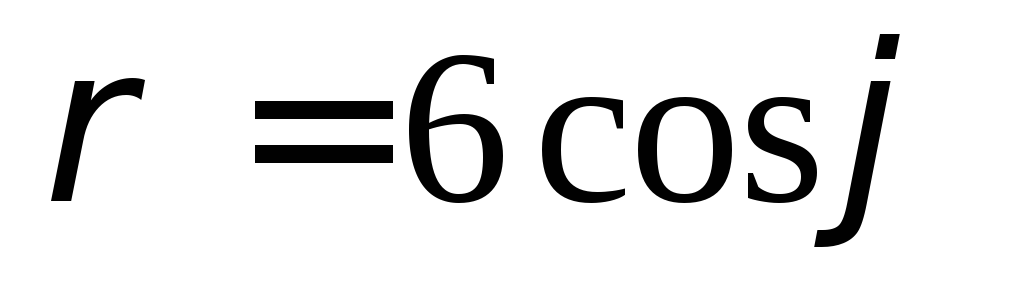
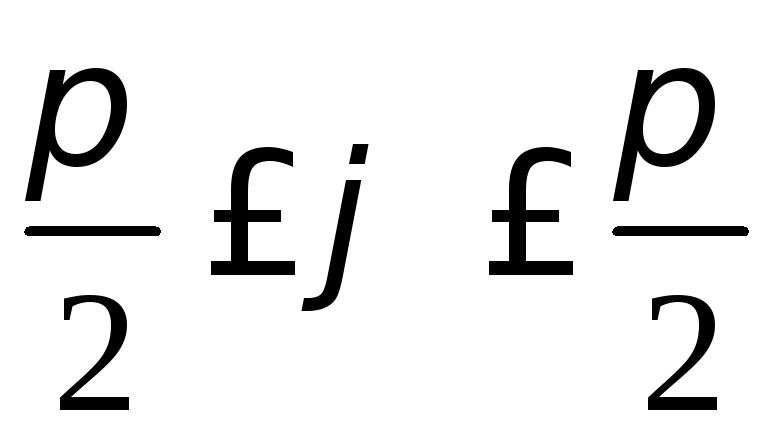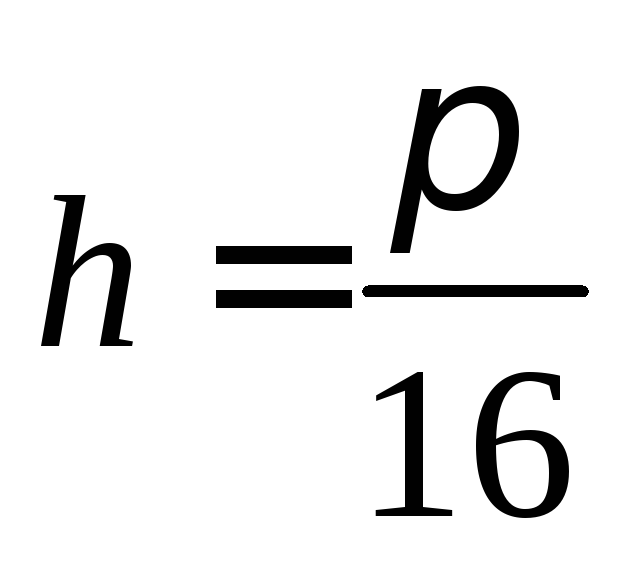
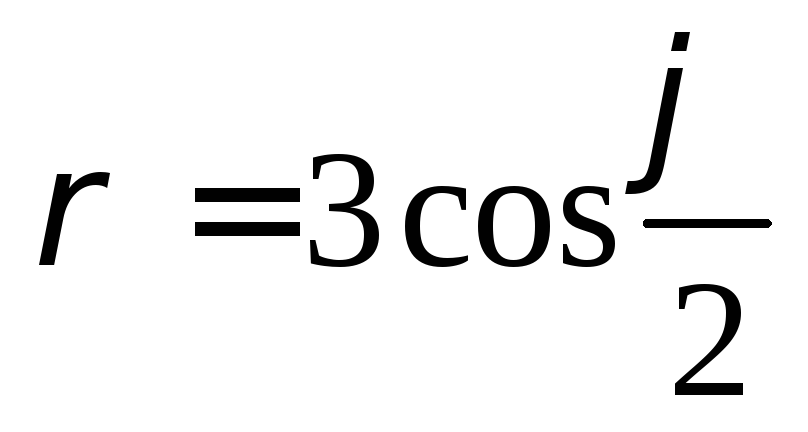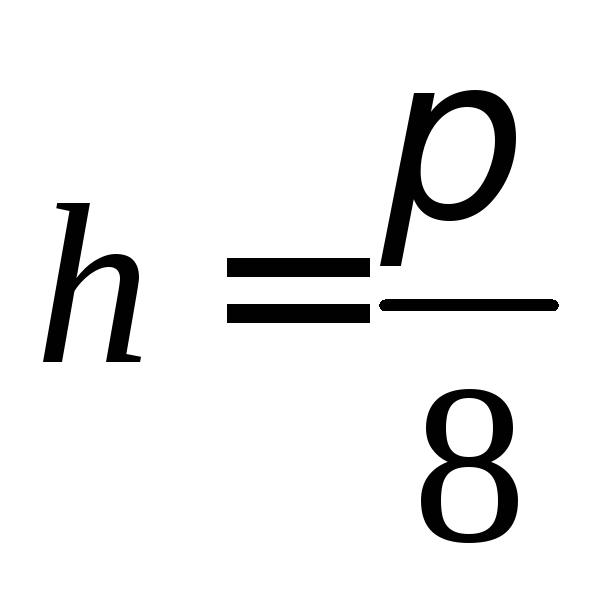
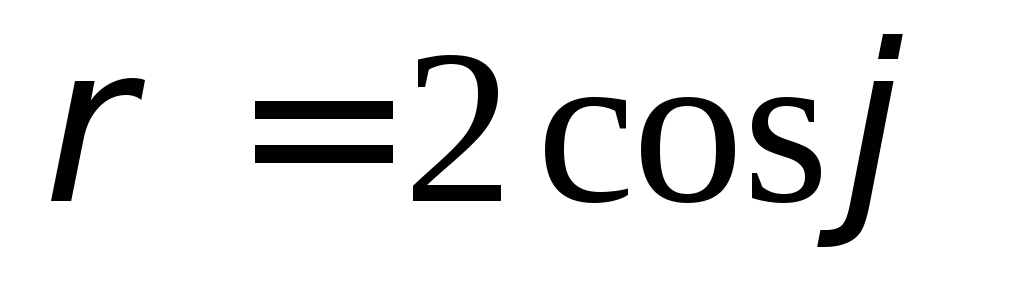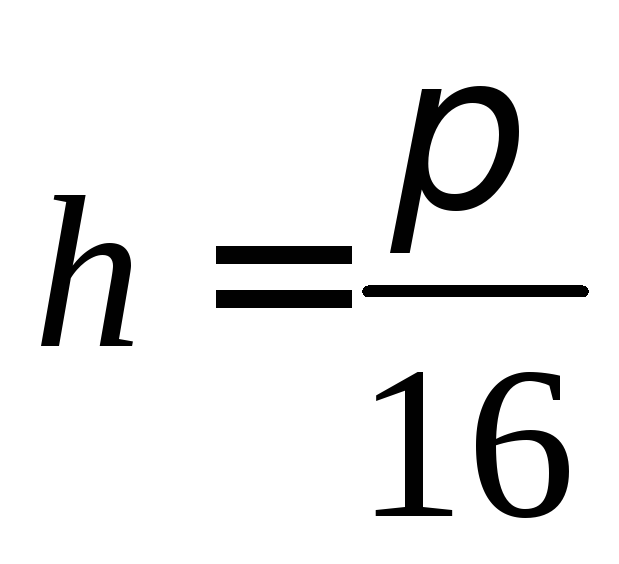
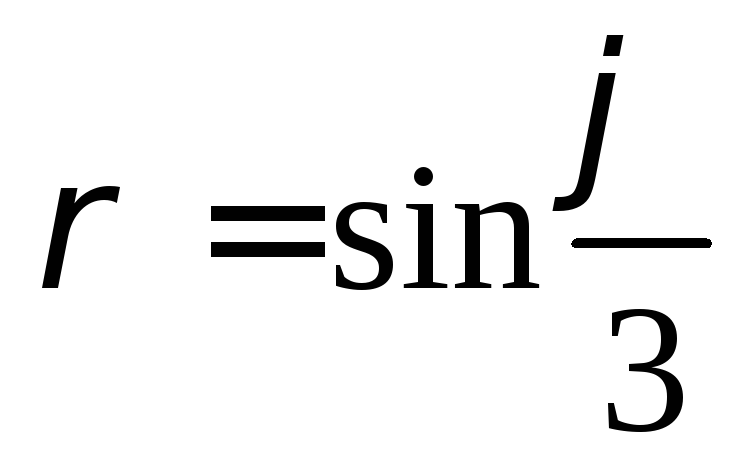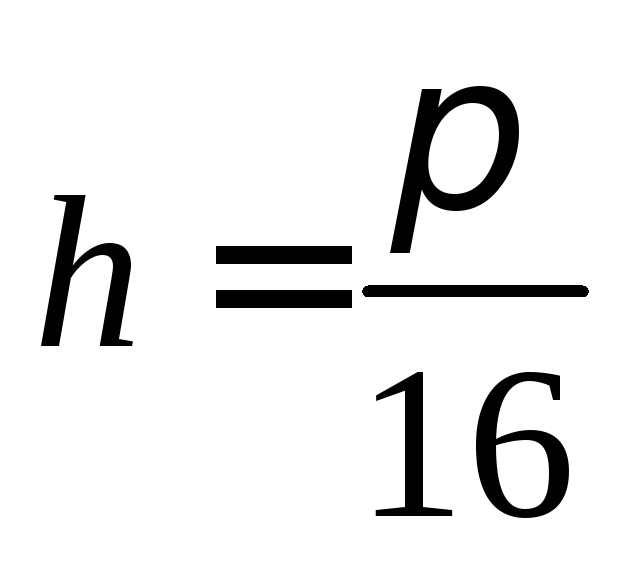
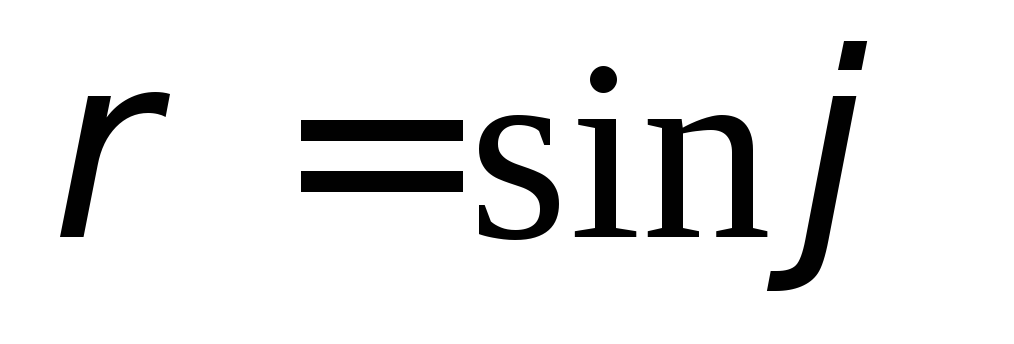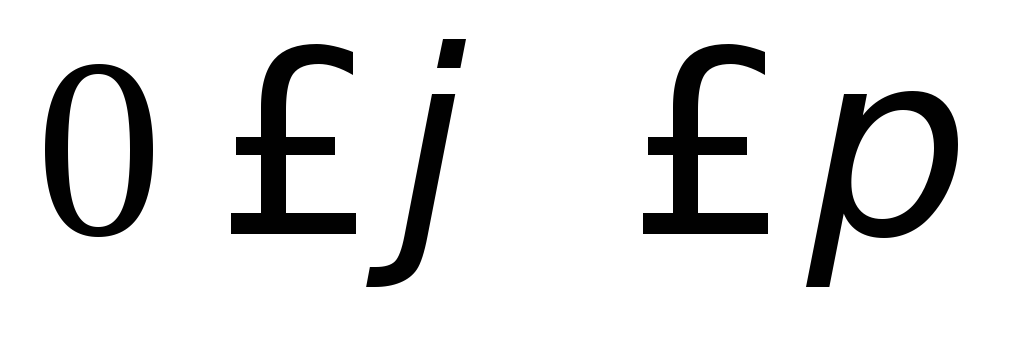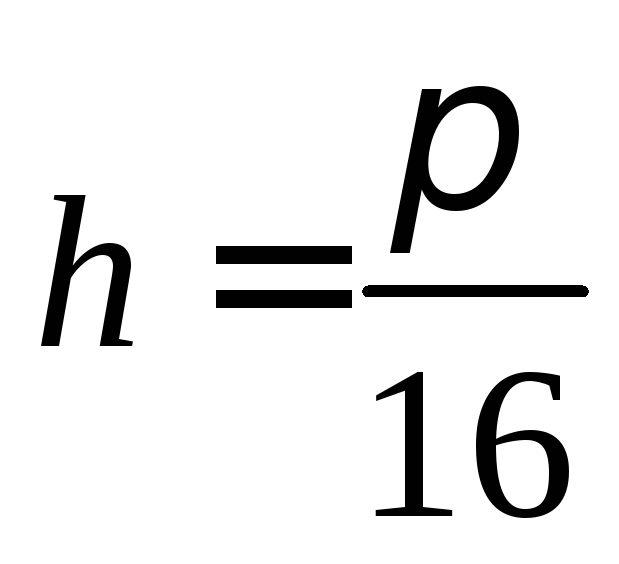
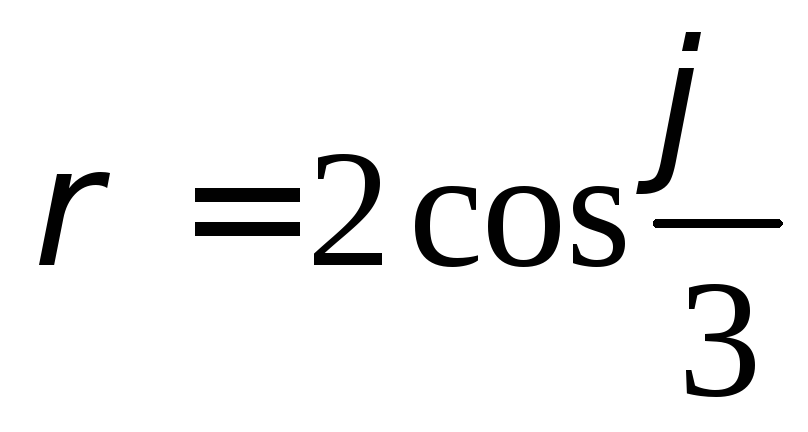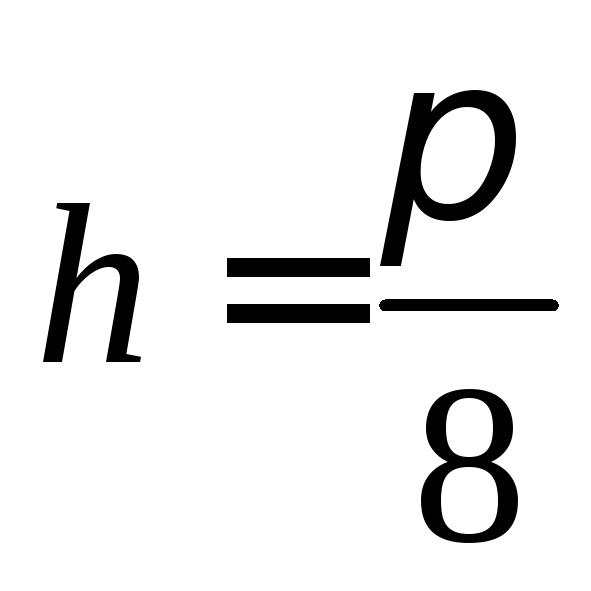
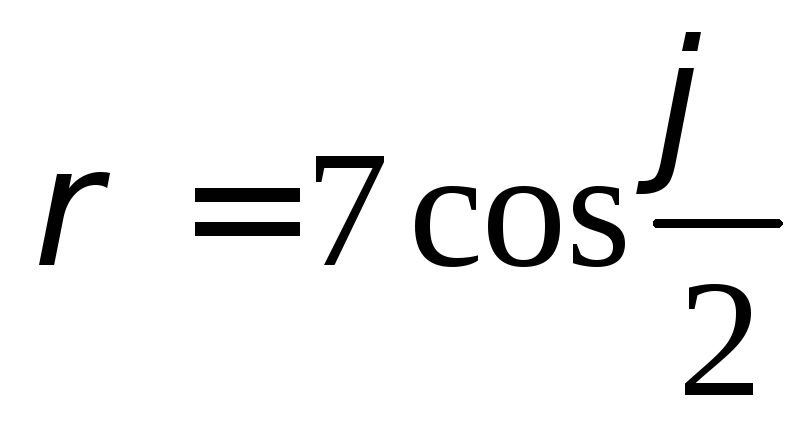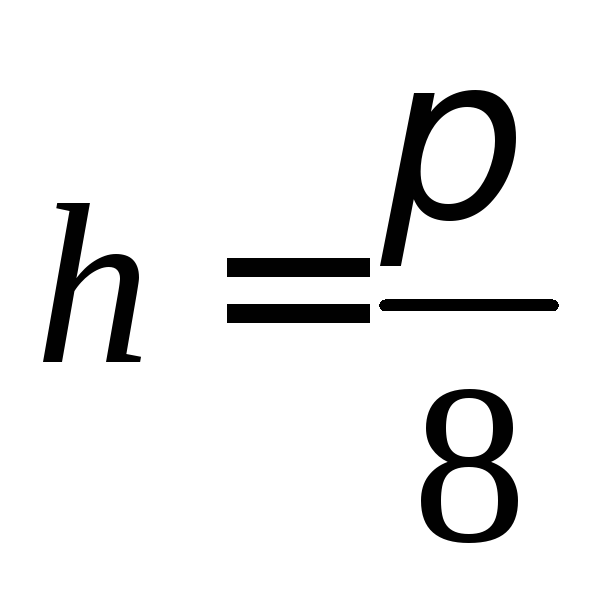
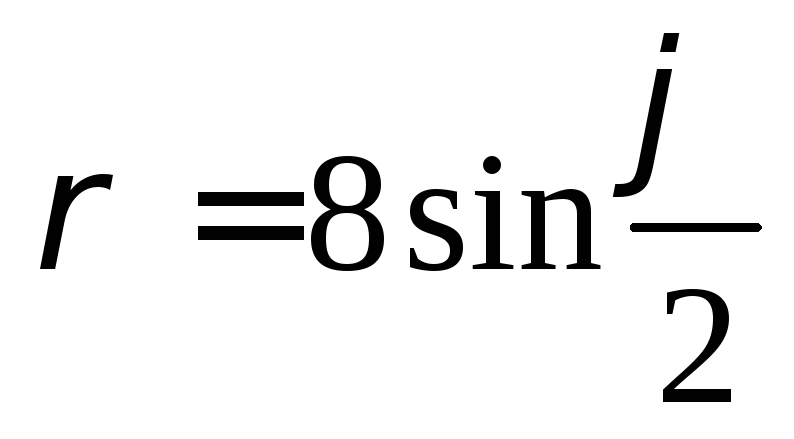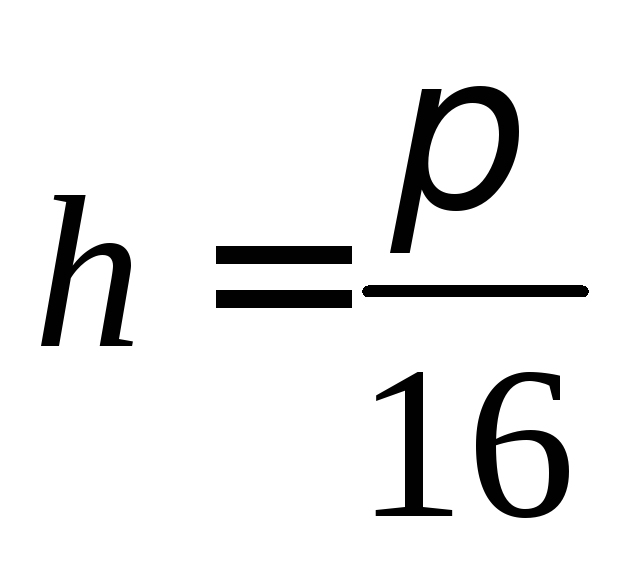