Понижение степени тригонометрия: Формулы понижения степени тригонометрических функций

как выполняется понижение для тригонометрических функций

Понижение степени в тригонометрии

Формулы понижения степени позволяют выразить тригонометрическую функцию n-ной степени через синус и косинус первой степени кратного значению n угла.

Применяемые формулы, доказательства

Формулы понижения степени выводятся из формул двойных, тройных и т.д. углов, которые в свою очередь являются следствием формул сложения и вычитания аргументов (метод заключается в представлении данных тождеств в виде суммы двух равных углов).

Формула понижения степени синуса и косинуса

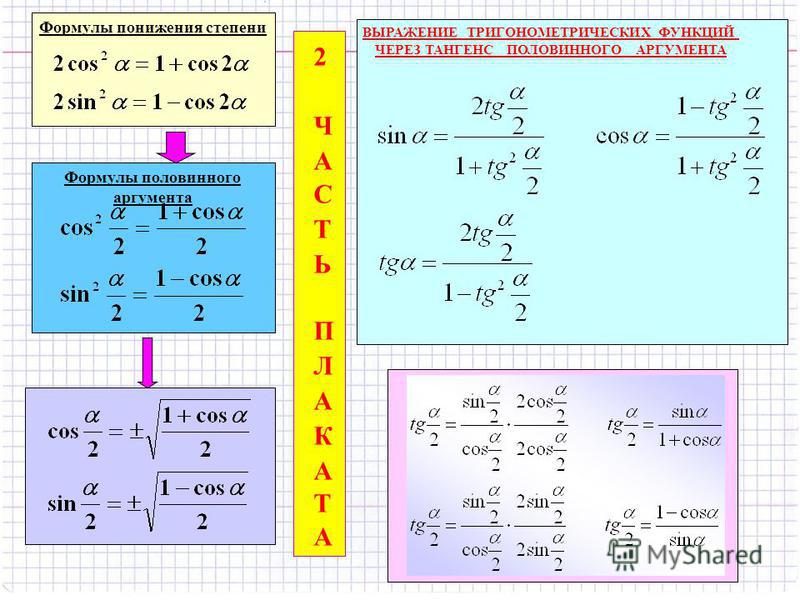
Общий вид формул понижения степени для синуса и косинуса отличается для четных и нечетных степеней. Для четных (n = 2, 4, 6, …) они выглядят следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(\sin^n\left(\alpha\right)=\frac{\mathrm C_\frac n2^n}{2^n}+\frac1{2^{n-1}}\cdot\sum_{k=0}^{{\textstyle\frac n2}-1}{(-1)}^{{\textstyle\frac n2}-k}\cdot\mathrm C_k^n\cdot\cos\left((n-2k)\alpha\right)\)

\(\cos^n\left(\alpha\right)=\frac{\mathrm C_\frac n2^n}{2^n}+\frac1{2^{n-1}}\cdot\sum_{k=0}^{{\textstyle\frac n2}-1}\mathrm C_k^n\cdot\cos\left((n-2k)\alpha\right)\)

Для нечетных степеней (n = 3, 5, 7, …) в общем виде формулы записываются так:

\(\sin^n\left(\alpha\right)=\frac1{2^{n-1}}\cdot\sum_{k=0}^{\textstyle\frac{n-1}2}{(-1)}^{{\textstyle\frac{n-1}2}-k}\cdot\mathrm C_k^n\cdot\sin\left((n-2k)\alpha\right)\)

\(\cos^n\left(\alpha\right)=\frac1{2^{n-1}}\cdot\sum_{k=0}^{\textstyle\frac{n-1}2}\mathrm C_k^n\cdot\cos\left((n-2k)\alpha\right)\)

На практике чаще всего используются формулы для второй степени, немного реже — для третьей и четвертой. 2\left(x\right)d2x=\int2\cdot\frac{1+\cos\left(2x\right)}2d2x=\int1+\cos\left(2x\right)d2x\)

Так как выражение под знаком интеграла является многочленом, проинтегрируем каждую его часть по очереди:

\(\int1+\cos\left(2x\right)d2x=\int1d2x+\int\cos\left(2x\right)d2x=x+\sin\left(2x\right)+\mathrm C\)

Урок 8. Тригонометрические формулы. Практика 11 класс онлайн-подготовка на Ростелеком Лицей

 

 

Подготовка к ЕГЭ по математике

 

Эксперимент

Урок 8. Тригонометрические формулы.

Практика

Конспект урока

Построим наше занятие следующим образом – рассмотрим примеры на преобразования тригонометрических выражений с использованием наиболее часто встречающихся формул из тех, которые мы ввели в лекции к уроку.

Такие преобразования важно уметь делать при решении некоторых типов тригонометрических уравнений.

 

Формулы тригонометрических функций суммы/разности аргументов

 

 

Начнем с формул тригонометрических функций суммы/разности аргументов.

 

Задача №1. Упростить выражение .

 

Формулы двойного и тройного аргументов

 

 

Теперь приведем пример задания с использованием формул двойного аргумента.

 

Задача №2. Упростить выражение .

Обратим внимание, что в числителе и знаменателе дроби записаны выражения, похожие на формулы косинуса двойного угла, только с обратным знаком. Умножим числитель и знаменатель дроби на  и подставим указанные формулы.

 

Формулы понижения степени

 

 

Задача, в которой будут использоваться формулы понижения степени.

 

Задача №3. Преобразовать в произведение .

Воспользуемся формулой понижения степени для косинуса, которая имеет вид . При использовании этой формулы следует понимать, что аргумент косинуса увеличивается в два раза, а не просто становится «».

 

Формулы суммы/разности тригонометрических функций

 

 

Переходим к примеру, в котором пригодятся формулы суммы/разности тригонометрических функций. 

 

Задача №4. Преобразовать в произведение .

Умение преобразовывать в произведение бывает полезным при решении уравнений, в которых по одну сторону равенства находится ноль. Тогда используется правило, что при умножении нескольких выражений одно из них точно равно нулю, если результат произведения равен нулю. Но пока решать уравнения не будем, а потренируемся в преобразованиях.

Сгруппируем слагаемые попарно, чтобы к ним можно было применить формулы сложения/вычитания тригонометрических функций:

В ходе преобразований воспользовались нечетностью функции синус.

 

Формулы произведения тригонометрических функций

 

 

Упростим выражение с использованием формул произведения тригонометрических функций.

 

Задача №5. Упростить выражение .

Подойти к решению можно двумя способами: преобразовать произведение тригонометрических функций в разность или расписать по формуле суммы разности аргументов. Первый подход в данном случае более оптимальный. Его и продемонстрируем, а вы можете самостоятельно решить вторым способом и сверить результаты.

В процессе преобразований важно не запутаться, т.к. в роли аргументов выступают  и , а такие же выражения присутствуют и в формуле произведения синусов.

Пример с использованием универсальной тригонометрической замены мы рассматривать на этом занятии не будем, т.к. этот прием тесно связан именно с решением определенных тригонометрических уравнений. Мы вспомним о нем на соответствующем уроке.

 

Сложение гармонических колебаний

 

 

Сейчас же рассмотрим задачу с применением формулы сложения гармонических колебаний.

 

Задача №6. Преобразовать выражение  к одной тригонометрической функции.

Воспользуемся формулой сложения гармонических колебаний или как ее еще иногда называют «метод введения вспомогательного угла»:

,

где вспомогательным углом является .

 

Воспользуемся нечетностью синуса и четностью косинуса и внесем минус к аргументу синуса и косинуса, чтобы выражение превратилось в сумму и стало похожим на общую формулу:

Более подробно:  и .

Теперь видно, что в роли параметра , аргумент . 

Вычислим вспомогательный угол . Мы пока не говорили об обратных тригофункциях, по плану они у нас на следующем уроке, т.к. их удобно рассматривать непосредственно перед тригонометрическими уравнениями. Пока объясним вычисление арктангенса очень просто — находим в таблице значений тригонометрических функций при каком угле тангенс равен , это угол , он и соответствует значению арктангенса.

Подставим выписанные величины в общую формулу.

Из-под корня вынесли полный квадрат.

 

Заключение

 

 

На этом практическом занятии мы привели примеры упрощения тригонометрических выражений с использованием основных формул преобразований тригонометрических функций, это в дальнейшем пригодится нам при решении некоторых уравнений.

 

Угол депрессии – определение, формула, примеры

Угол депрессии образуется, когда наблюдатель смотрит на объект сверху вниз. Это угол, образованный между горизонтальной линией, направленной прямо к глазу наблюдателя, и линией взгляда. Давайте узнаем больше об угле депрессии в этой статье.

1.	Что такое Угол депрессии?
2.	Угол депрессии Терминология
3.	Формула угла депрессии
4.	Угол наклона против угла возвышения
5.	Угол депрессии в треугольнике
6.	Часто задаваемые вопросы об угле депрессии

Что такое угол депрессии?

Угол наклона — это «угол, образованный между горизонтальной линией и линией обзора, когда наблюдатель смотрит вниз на объект, известен как угол депрессии».

Он измеряет изменение угла нашего зрения, когда мы смотрим вниз. Предположим, вы стоите на кухне и смотрите прямо, и вдруг вы замечаете ползущее по полу насекомое. Итак, это немедленное изменение угла вашего взгляда с прямого на нисходящий и есть угол депрессии.

Угол депрессии Терминология

Угол депрессии включает следующую терминологию:

• Наблюдатель (лицо, которое наблюдает)
• Объект (объект, за которым наблюдает наблюдатель)
• Горизонтальная линия (горизонтальный луч, начинающийся от наблюдателя)
• Линия видимости (линия, соединяющая наблюдателя и объект)

Угол наклона — это угол между горизонтальной линией и линией визирования. На следующем рисунке наблюдатель находится в точке «О», а объект — в точке «В». Пусть ОА — горизонтальная линия, а ОВ — линия прямой видимости. Таким образом, угол, образованный между этими двумя, то есть угол АОВ, является углом депрессии.

Формула угла депрессии

Формула угла наклона аналогична формулам основных тригонометрических соотношений. Если известны любые две стороны образовавшегося прямоугольного треугольника, то мы легко можем найти искомый угол, используя формулы угла наклона, которые приведены ниже.

Угол наклона против угла возвышения

Угол наклона и угол подъема противоположны друг другу. При угле наклона объект располагается ниже наблюдателя, а при угле возвышения — над наблюдателем. Если вы стоите на своей террасе и смотрите на солнце, то угол возвышения будет образовываться. С другой стороны, если вы будете смотреть на стоящую на дороге собаку со своей террасы, то образуется угол депрессии. В обоих случаях мы используем тригонометрические углы для нахождения высот и расстояний. Давайте поймем разницу между углом депрессии и возвышения на изображении, приведенном ниже.

На изображении выше θ — это угол подъема, а α — угол наклона.

Угол депрессии в треугольнике

В прямоугольном треугольнике угол впадины образован вершиной перпендикулярного отрезка. Первоначально он находится снаружи треугольника, но мы используем теорему о альтернативных внутренних углах, чтобы найти альтернативный угол внутри треугольника. Например, на приведенном ниже изображении, если наблюдатель стоит в точке А и смотрит вниз на точку С, то угол депрессии ‘а’ формируется относительно горизонтальной оси AD. Но ∠DAC = ∠ACB (используя теорему об альтернативных углах). Итак, теперь в треугольнике ABC угол наклона равен ∠ACB, который можно использовать для определения величины недостающей стороны треугольника.

☛ Похожие темы:

Ознакомьтесь с этими интересными статьями, чтобы узнать больше о концепции угла депрессии и связанных с ней темах.

• Тригонометрическая таблица
• Тригонометрический калькулятор

 

Угол наклона Примеры

1. Пример 1: Если человек, стоящий на вершине здания высотой 50 футов, смотрит на свою дочь, стоящую на расстоянии 30 футов от здания, под каким углом образуется депрессия?

   Решение: Дано, что высота здания 50 футов, а расстояние между зданием и девушкой 30 футов. Теперь на данном рисунке угол наклона обозначен x° (поскольку угол депрессии и угол x совпадают, если использовать теорему о чередующихся внутренних углах). Используя формулу для нахождения угла депрессии, получаем tan x = 50/30.

   ⇒ тангенс х = 5/3

   ⇒ х = тангенс ^-1 (5/3)

   Ответ: Следовательно, угол депрессии тангенс ^-1 (5/3).

2. Пример 2: Найдите значение x на данном рисунке.

   Решение: На приведенном выше рисунке есть два угла депрессии, образованные из точки A: ∠BAC=30° и ∠DAC=60°. Мы знаем, что ∠DAC=∠ADO (используя теорему об альтернативных внутренних углах). Итак, ∠ADO=60°. Применяя формулу угла наклона в △AOD, мы получаем tan 60° = AO/OD.

   ⇒ √3 = 10/x

   ⇒ x = 10/√3 единиц

   Ответ: Следовательно, значение x равно 10/√3 единиц.

3. Пример 3: С монгольфьера, летящего на высоте 100 футов, угол депрессии человека на землю составляет 30 градусов. Найдите длину веревки, которая связывает человека на земле с воздушным шаром.

   Решение:

   Пусть длина веревки равна x (в футах).

   Здесь мы написали, что угол у человека равен 30 градусам по теореме об альтернативном внутреннем угле.

   Теперь примените синус к треугольнику,

   sin 30 = 100/x

   x = 100/(sin 30) = 100/(1/2) = 200 футов

   Ответ: Длина веревки = 200 футов

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по углу депрессии

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле депрессии

Что такое определение угла депрессии в тригонометрии?

В тригонометрии угол наклона — это угол, образованный между горизонтальной линией и линией взгляда, когда мы смотрим на объект вниз. В этом ракурсе объект, на который мы смотрим, всегда располагается ниже горизонтальной оси или линии.

Что такое угол возвышения и угол падения?

Угол возвышения и наклона формируются по обе стороны от горизонтальной линии, которая представляет собой прямую линию, образующую угол 90 градусов с объектом. Когда мы смотрим вверх, образуется угол возвышения, а когда мы смотрим вниз на какой-либо предмет, образуется угол депрессии. Оба важны для определения высоты и расстояния больших структур.

Какова формула для угла депрессии?

Формула угла наклона аналогична формулам основных тригонометрических соотношений, которые приведены ниже:

• sin x = перпендикуляр/гипотенуза
• cos x = основание/гипотенуза
• tan x = перпендикуляр/основание

Эти три формулы можно использовать для нахождения угла депрессии, на основе которого даны две стороны прямоугольного треугольника.

Как рассчитать угол депрессии?

Угол наклона – это угол, образованный между горизонтальной линией и линией визирования, которая находится ниже горизонтальной линии. Он всегда образует прямоугольный треугольник между наблюдателем, линией и объектом. Для вычисления угла депрессии можно использовать любую из основных тригонометрических формул синуса, косинуса и тангенса, в зависимости от того, какие две стороны треугольника даны.

Как найти расстояние по углу падения?

Чтобы найти расстояние с углом наклона, мы можем использовать тригонометрические формулы для расчетов. Предположим, девушка стоит на вершине 10-метровой башни, образуя угол наклона 45 градусов с велосипедом, стоящим на дороге. Тогда расстояние между велосипедом и башней можно найти, используя формулу касательной, которая выглядит следующим образом: тангенс 45° = 10/расстояние. Теперь тангенс 45°=1, поэтому 1 = 10/расстояние, что означает, что расстояние равно 10 единицам.

Угол наклона и наклона совпадают?

Угол наклона – это угол, который образуется над горизонтальной осью. Это то же самое, что и угол подъема. Угол депрессии такой же, как и угол склонения, так как оба формируются ниже горизонтальной оси с наклоном вниз.

Как угол депрессии связан с реальной жизнью?

Угол наклона используется для измерения высот и расстояний, требующих больших вычислений. Он используется в архитектуре, технике, науке и т. д.

Как найти угол возвышения и впадины?

Угол возвышения — это угол между горизонтальной линией взгляда и объектом, когда человек смотрит на объект вверх. Тогда как угол депрессии — это угол между горизонтальной линией взгляда и объектом, когда человек смотрит на объект сверху вниз.

Какое значение имеют углы возвышения и депрессии?

Одним из основных аспектов использования угла возвышения и депрессии является то, что он используется в основном в текстовых задачах по тригонометрии, когда речь идет о прямой видимости. Эти углы используются при решении тригонометрических задач, таких как синус, косинус и тангенс, а также обратные тригонометрические функции.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по углу депрессии

Калькулятор угла депрессии

Создано Kenneth Alambra

Отредактировано Dominik Czernia, PhD и Jack Bowater

2 Последнее обновление: 02.

09.2013

Какой угол депрессии? Определение угла депрессии

Калькулятор угла депрессии. Как найти угол депрессии?

Пример расчета по нахождению угла депрессии

Хотите узнать больше?

Часто задаваемые вопросы

Этот калькулятор угла наклона определяет угол, на который наклонная линия отклоняется от горизонтали в направлении вниз. Как и в нашем калькуляторе высот, в этом калькуляторе используется понятие наклона линии под углом.

В этом калькуляторе вы узнаете:

• Что такое угол депрессии;
• Как найти угол депрессии; и
• Как использовать этот калькулятор угла депрессии.

Прочитав этот текст, вы повсюду найдете углы депрессии с формулой угла депрессии. Давайте начнем!

🙋 Если вы хотите глубже погрузиться в математическую концепцию уклона, наш калькулятор уклона для вас.

Какой угол депрессии? Определение угла депрессии

Простейшее определение угла депрессии состоит в том, что это угол между горизонталью и частью линии, которая находится ниже горизонтали. На изображении ниже, когда кошка смотрит вниз на точка А , она создает определенный угол депрессии от горизонтали.

Иногда мы также можем видеть угол наклона, используемый для обозначения наклона поверхности, такой как склон горы или проезжая часть. Однако для получения такой информации мы обычно используем аналог угла депрессии — уровень возвышения.

Калькулятор угла наклона. Как найти угол депрессии?

Поскольку теперь мы знаем, что такое угол депрессии, давайте научимся его находить! Мы можем определить угол депрессии, используя геодезическое оборудование, такое как инженерный переход или клинометр. Эти устройства представляют собой оптические инструменты, которые имеют функции измерения угла и могут мгновенно дать нам нужный угол. Однако мы также можем использовать математику, чтобы найти угол депрессии. Но сначала нам нужно знать два расстояния: горизонтальное расстояние между зрителем и объектом и их вертикальное расстояние , как показано на рисунке ниже:

Если у вас уже есть значения этих измерений, вы можете ввести их в наш калькулятор угла наклона. Чтобы сделать это вручную, подставьте эти значения в формулу угла депрессии, полученную из функции арктангенса в тригонометрии.

Мы используем функцию арктангенса, потому что, если мы внимательно посмотрим на соответствующие измерения, мы увидим, что мы фактически сформировали прямоугольный треугольник , и что мы имеем дело со сторонами, смежными и противоположными интересующему нас углу. С учетом сказанного ниже приведена формула угла депрессии: )

Пример расчета нахождения угла депрессии

Время для примера угла депрессии. Предположим, нам нужно найти угол наклона α линии взгляда мальчика от верхней части слайда к девочке в нижней части слайда, как показано на рисунке ниже. Мы видим, что горизонтальное расстояние между детьми равно 3,0 метра и вертикальное расстояние между их линиями взгляда 1,5 метра .

Используя формулу угла депрессии, мы вычисляем угол депрессии α следующим образом:

α = арктангенс (расстояние по вертикали / расстояние по горизонтали)

α = арктангенс (1,5 метра / 3,0 метра)

3 3

α = arctan(0,5)

α = 26,56505118° ≈ 26,565°

Теперь из приведенных выше расчетов мы можем сказать, что угол депрессии составляет около 9, α0049 26,565° от горизонтали.

Хотите узнать больше?

Если вам известен угол наклона и хотя бы одно из измерений расстояния (горизонтальное или вертикальное расстояние), мы также можем вычислить другие части прямоугольного треугольника, образованного с помощью функций синуса, косинуса и тангенса. Вы можете узнать больше об этом в нашем калькуляторе прямоугольного треугольника.

Часто задаваемые вопросы

Угол наклона равен углу подъема?

Да . Если бы два человека смотрели друг на друга с разной высоты, угол, под которым человек сверху должен был бы смотреть вниз, был бы равен углу, под которым человек снизу должен был бы смотреть вверх. На диаграмме это будет представлено в виде чередующихся углов на поперечной линии.

Каков максимальный угол наклона?

90° — максимальный угол наклона. Угол наклона должен быть меньше или равен 90°. Угол наклона 90° будет эквивалентен взгляду на объект прямо вниз.

Как найти расстояние по углу наклона?

Чтобы найти расстояние между двумя точками на разных высотах с использованием угла наклона, выполните следующие действия:

1. Измерьте расстояние по вертикали или разницу высот, a .

   No related posts.