Онлайн урок: Порядок выполнения действий по предмету Математика 5 класс
Изучая числовые и буквенные выражения, способы упрощения выражений, свойства арифметических операций, мы рассматривали в основном простые выражения, значение которых найти было несложно.
Сегодня на уроке мы будем рассматривать выражения, в которых содержатся сразу несколько арифметических операций и несколько пар скобок.
Выясним, в какой последовательности необходимо выполнять математические операции при нахождении значения выражения.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Узнаем, какие действия называют действиями первой и второй ступени, зачем нужны скобки.
Разберем множество различных примеров, которые позволят нам лучше усвоить данную тему.
Любой человек каждый день решает множество различных задач: простых и сложных.
Многие из них решаются по определенным правилам- алгоритмам.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
С алгоритмами мы уже не раз встречались на наших уроках, решая задачи и уравнения, рассматривая различные правила и свойства, совершая вычисления в столбик и др.
Выясним зависит ли значение выражения от порядка выполнения арифметических операций, обязательно ли выполнять действия в определенном порядке.
Рассмотрим следующий пример:
Катя и Федя решали пример, в котором необходимо было найти сумму числа 24 и произведения чисел 8 и 2.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Катя записала пример: 24 + 8 ∙ 2 и принялась выполнять арифметические действия по порядку.
Первым делом она нашла сумму чисел 24 и 8.
Сложив 24 и 8, у нее получилось число 32.
24 + 8 = 32.
Затем полученный результат (число 32) она умножила на 2.
В итоге у нее получилось:
32 ∙ 2 = 64.
Ответ: 64.
Федя записал пример: 24 + 8 ∙ 2 и стал решать его иным способом.
Сначала он нашел произведение чисел 8 и 2.
Умножив 8 на 2, у него получилось число 16.
8 ∙ 2 = 16.
Затем к 24 прибавил полученное произведение.
В итоге получил следующее равенство:
16 + 24 = 40.
Ответ: 40.
Исходные выражения, которые записали Катя и Федя, были одинаковые (содержали определенную последовательность чисел и знаков).
Дети меняли только порядок следования математических операций.
В итоге получили различные значения одного и того же выражения.
Получается, что порядок выполнения арифметических действий влияет на результат вычислений.
Чуть позже мы выясним, кто же решил пример правильно: Катя или Федя.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat.
Эта информация доступна зарегистрированным пользователям
Очень часто в математических выражения присутствует сразу несколько арифметических операций, таких как сложение, вычитание, умножение и деление.
Чтобы найти значение такого выражения, необходимо соблюдать порядок действий, который регламентируется определенными правилами.
Рассмотрим правила выполнения арифметических действий в выражениях без скобок.
1. Математическое выражение вычисляется по частям, математические операции выполняются по порядку слева направо (от начала к концу выражения).
2. Арифметические действия делят на действия первой ступени и действия второй ступени.
Сложение и вычитание- это действия первой ступени.
Умножение и деление- это действия второй ступени.
3. Если в выражении без скобок присутствуют действия только первой ступени (сложение и вычитание), то действия выполняются в порядке их следования (слева направо).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
4. Если в выражении без скобок присутствуют только действия второй ступени (умножение и деление), то данные действия выполняются в порядке их следования (слева направо).
Пример.
Дано выражение 15 ∙ 6 ÷ 3 ∙ 10.
Определим порядок действий в выражении и найдем его значение.
Данное выражение не содержит скобки, и в нем присутствуют только действия второй ступени (умножение и деление), следовательно, действия выполнять необходимо слева направо по порядку их следования.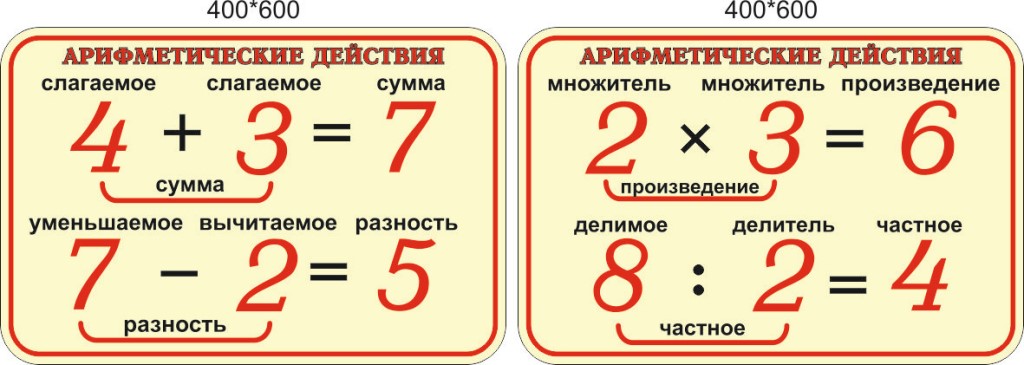
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
5. Если в выражении отсутствуют скобки, и оно содержит действия первой и второй ступени, то сначала выполняются действия второй ступени (умножение и деление) в порядке их следования слева направо, затем выполняются действия первой ступени (сложения и вычитания) так же в порядке их следования слева направо.
Пример.
Определите порядок действий в выражении 137 — 17 ∙ 2 + 81 ÷ 3 и найдите его значение.
Данное выражение не содержит скобки, в нем присутствуют действия первой и второй ступени.
Следовательно, действия будем выполнять по порядку слева направо: сначала умножение и деление, а затем вычитание и сложение.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Вспомним пример, рассмотренный нами в начале урока, где Катя и Федя решали пример.
Решим этот пример сами, соблюдая порядок следования арифметических операций, и выясним, кто из ребят нашел правильный ответ.
Было дано выражение 24 + 8 ∙ 2.
В данном выражении присутствуют действия первой и второй ступени, соответственно, сначала мы должны выполнить умножение, затем полученный результат стожить.
Обозначим порядок действий в выражении и найдем его значение.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В математике есть специальный символ, который указывает нужный порядок действий в выражении, этот символ называется скобки.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
1. Запомните правило!
Действия, записанные в скобках, выполняются в первую очередь.
На примере рассмотрим использование скобок для указания порядка действий или изменении этого порядка.
Пример.
Дано выражение 48 ÷ 8 — 4.
Найдем значение этого выражения, используя правило, которое определяет порядок выполнения действий в математических выражениях.
Так как скобок в данном примере нет, то первым действием выполняется деление, затем- вычитание.
В результате получим следующее равенство:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Ответ: 4.
Если выражение будет содержать все те же числа и математические операции, но будет записано в виде: 48 ÷(8 — 4), то в первую очередь выполняется действие в скобках, а затем- деление.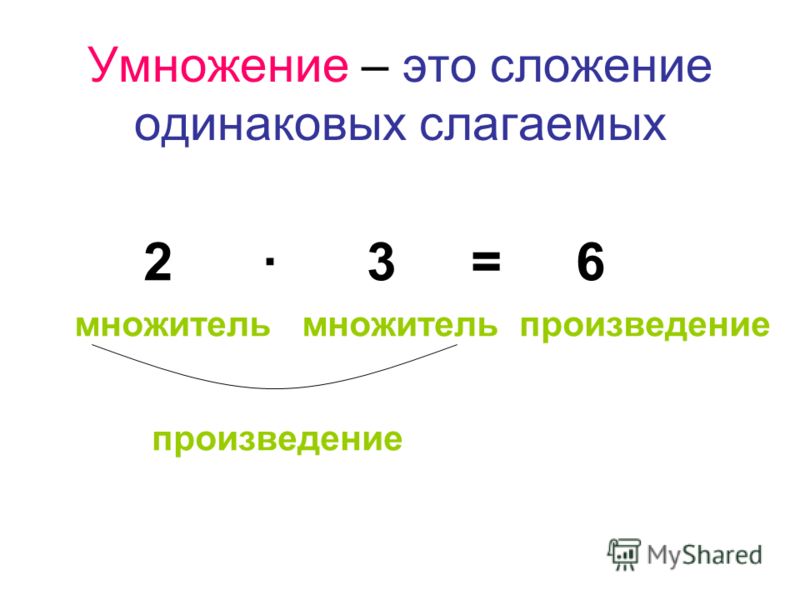
В итоге получим следующий результат:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Ответ: 12.
Мы можем заметить, что, изменив порядок действий с помощью скобок, изменилось значение выражения.
2. Если в скобках присутствуют действия первой и второй ступени, то в скобках сохраняется известный нам порядок действий: слева направо выполняются сначала действия деления и вычитания, затем по порядку слева направо сложение и вычитание.
Рассмотрим пример.
Определим порядок действий в выражении 100 — (26 ÷ 2 + 27) + 52 и найдем его значение.
Это выражение содержит скобки, поэтому выполним сначала действия в них.
Внутри скобок присутствуют действия первой и второй ступени.
Следовательно, выполним деление, затем сложение, находящееся в скобках.
Так как оставшиеся за скобками действия- это действия первой ступени, то они выполняются по порядку слева направо.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
3. Существуют выражения, которые содержат несколько пар скобок, указывающих порядок выполнения действий.
Существуют выражения, которые содержат несколько пар скобок, указывающих порядок выполнения действий.
В таком случае выполняются действия последовательно по порядку слева направо: сначала в первой паре скобок, затем во второй паре, далее в третьей и т.д. (пока есть скобки), и только потом выполняются все остальные действия, которые находятся за скобками, согласно правилам, определяющим порядок выполнения математических действий в выражениях.
Рассмотрим данное правило на примере.
Определим порядок действий в выражении (8 + 14 ∙ 3) — 2 ∙ (4 — 1) и найдем его значение.
Это выражение содержит скобки, поэтому выполним сначала действия в них.
Первым делом выполним все действия в первой скобке, причем сначала найдем произведение чисел, а затем сложение.
После этого выполняется действие во второй скобке.
Далее все остальные действия по уже известным нам правилам.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
4. Иногда возникает ситуация, когда в выражении встречаются сложное сочетание скобок- вложенные скобки (будто скобки с выражениями вложены друг в друга).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Последовательность действий для такого выражения определяется следующим правилом:
Если скобки содержат внутренние скобки, то сначала выполняются действия в них, затем математические операции проводят, продвигаясь последовательно ко внешним скобкам.
В качестве примера определим порядок действий в выражении
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
1) Первым делом выполним действие, которое находится в круглых скобках.
200 + 100 = 300
В исходное выражение вместо выражения, стоящего в круглых скобках, запишем найденное его значение.
{[300 ∙ 5 — 300] — 10 ∙ 20} ÷ 20 — 10
Далее выполняем действия, находящиеся в квадратных скобках, соблюдая очередность действий первой и второй ступеней.
2) Найдем произведение 300 и 5.
300 ∙ 5 = 1500
3) Из полученного произведения вычтем 300.
1500 — 300 = 1200
Вместо выражения, которое находилось в квадратных скобках, запишем его значение.
{1200 — 10 ∙ 20} ÷ 20 — 10
Далее выполняем действия, находящиеся в фигурных скобках, соблюдая очередность действий первой и второй ступеней.
4) Найдем произведение 10 и 20.
10 ∙ 20 = 200
5) Полученный результат вычтем из 1200.
1200 — 200 = 1000
Подставим вместо выражения, стоящего в фигурных скобках, его значение.
1000 ÷ 20 — 10
В оставшейся части исходного выражения больше скобок нет, в нем присутствуют действия первой и второй ступени.
Следовательно, действия будем выполнять по порядку слева направо.
6) Сначала выполним деление:
1000 ÷ 20 = 50
7) Затем из полученного частного вычтем 10.
50 — 10 = 40
В результате получили ответ: число 40.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Порядок действий в выражениях можно изменять с помощью основных свойств сложения, вычитания, умножения и деления.
Например, дано выражение 7 ∙ 2 ∙ 55.
В данном выражении удобнее использовать сочетательное свойство умножения, а не выполнять действия по порядку.
Сначала найдем произведение 2 и 55, и только потом полученное произведение умножим на 7.
7 ∙ 2 ∙ 55 = 2 ∙ 55 ∙ 7 = 110 ∙ 7 = 770.
Свойства арифметических операций часто используют для упрощения выражений.
Важно отметить, что установленный порядок действий в выражениях без скобок и со скобками справедлив как для числовых выражений, так и для буквенных.
Представим в общем виде порядок выполнения арифметических действий в виде схемы.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Эту же программу вычислений можно представить в виде схемы, выполняя действия в определенном порядке, заполняя при этом последовательно пустые ячейки.
В нижней ячейке записывается ответ.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Порядок выполнения действий в математике: правила, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Арифметика Порядок действий в математике
ru Математика Арифметика Порядок действий в математике
В данной публикации мы рассмотрим правила в математике касательно порядка выполнения арифметических действий (в том числе в выражениях со скобками, возведением в степень или извлечением корня), сопроводив их примерами для лучшего понимания материала.
- Порядок выполнения действий
- Общее правило
- Примеры со скобками
- Возведение в степень/извлечение корня
Отметим сразу, что действия рассматриваются от начала примера к его концу, т.е. слева направо.
Общее правило
сначала выполняются умножение и деление, а затем сложение и вычитание полученных промежуточных значений.
Давайте подробно рассмотрим пример: 2 ⋅ 4 + 12 : 3.
Над каждым действием мы написали число, которое соответствует порядку его выполнения, т.е. решение примера состоит из трех промежуточных действий:
- 2 ⋅ 4 = 8
- 12 : 3 = 4
- 8 + 4 = 12
Немного потренировавшись в дальнейшем можно все действия выполнять цепочкой (в одну/несколько строк), продолжая исходное выражение. В нашем случае получается:
В нашем случае получается:
2 ⋅ 4 + 12 : 3 = 8 + 4 = 12.
Если подряд идут несколько действий умножения и деления, то они также выполняются подряд, и их можно объединить при желании.
Решение:
- 5 ⋅ 6 : 3 = 10 (совместное выполнение действий 1 и 2)
- 18 : 9 = 2
- 7 + 10 = 17
- 17 – 2 = 15
Цепочка примера:
7 + 5 ⋅ 6 : 3 – 18 : 9 = 7 + 10 – 2 = 15.
Примеры со скобками
Действия в скобках (если они есть) выполняются в первую очередь. А внутри них действует все тот же принятый порядок, описанный выше.
Решение можно разбить на действия ниже:
- 7 ⋅ 4 = 28
- 28 – 16 = 12
- 15 : 3 = 5
- 9 : 3 = 3
- 5 + 12 = 17
- 17 – 3 = 14
При расстановке действий выражение в скобках можно условно воспринимать как одно целое/число. Для удобства мы выделили его в цепочке ниже зеленым цветом:
15 : 3 + (7 ⋅ 4 – 16) – 9 : 3 = 5 + (28 – 16) – 3 = 5 + 12 – 3 = 14.
Скобки в скобках
Иногда в скобках могут быть еще одни скобки (называются вложенными). В таких случаях сперва выполняются действия во внутренних скобках.
Раскладка примера в цепочку выглядит так:
11 ⋅ 4 + (10 : 5 + (16 : 2 – 12 : 4)) = 44 + (2 + (8 – 3)) = 44 + (2 + 5) = 51.
Возведение в степень/извлечение корня
Данные действия выполняется в самую первую очередь, т.е. даже до умножения и деления. При этом если они касаются выражения в скобках, то сначала производятся вычисления внутри них. Рассмотрим пример:
Порядок действий:
- 19 – 12 = 7
- 72 = 49
- 62 = 36
- 4 ⋅ 5 = 20
- 36 + 49 = 85
- 85 + 20 = 105
Цепочка примера:
62 + (19 – 12)2 + 4 ⋅ 5 = 36 + 49 + 20 = 105.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Экспоненты, умножение и сложение – MathFour
Рубрики: Алгебра; Будьте первым, кто поделится своими мыслями — оставьте комментарий ниже!
Это четвертая книга из серии Объяснение порядка действий.
Чтобы ознакомиться с другими статьями этой серии, нажмите здесь, чтобы перейти к введению.
Порядок операций можно свести к трем «настоящим» операциям.
Скобки — это просто способ сгруппировать элементы, а не настоящая операция. Поэтому они не считаются реальной операцией.
Поскольку деление — это просто умножение, перевернутое с ног на голову, нам не нужно включать его отдельно. Точно так же вычитание — это сложение на слуху. Так что его тоже выкидываем.
Теперь у нас есть только три: показатели степени, умножение и сложение.
Экспоненты — это ярлык для умножения.
В предыдущей статье о запоминании правил экспоненты я записал это видео о экспонентах:
Вы видите, что 3 x 3 x 3 x 3 равно 3 4 . Экспонента — это сокращение для умножения.
Умножение — это быстрый способ сложения.

Точно так же, когда мы перегружены сложением одних и тех же чисел снова и снова, как в видео, 4 + 4 + 4 + 4 + 4, мы можем использовать умножение, чтобы сократить это: 5 x 4.
Следуйте сокращению эволюция.
Эволюция быстрого доступа выглядит следующим образом:
- Сначала появилось дополнение.
- Затем мы создали умножение, чтобы упростить сложение.
- Затем мы создали показатели степени, чтобы упростить умножение.
Итак, когда вы занимаетесь арифметикой, мы должны сначала использовать «недавние» сокращения (возведение в степень), затем «старые» сокращения (умножение), а затем «обычные» арифметические действия (сложение). Помните, что вычитание — это сложение, а деление — это умножение.
И имейте в виду, что нам нужно следить за группировкой или чем-либо изолированным скобками, барами абсолютного значения или дробью. Инструменты группировки/изоляции всегда важнее других правил работы.
Изображение из ВикипедииЧто, если ваш ответ не совпадает с ответом на обратной стороне книги?
В некоторых учебниках умножение выполняется перед делением. Это означает, что задача 9 3 x 2 будет показывать другой ответ (3/2) на страницах решения этого учебника, чем тот, который вы получили бы после ОоО, которое я здесь описываю (6). Эти тексты редки, но я их видел. Так что держите глаза открытыми.
Это означает, что задача 9 3 x 2 будет показывать другой ответ (3/2) на страницах решения этого учебника, чем тот, который вы получили бы после ОоО, которое я здесь описываю (6). Эти тексты редки, но я их видел. Так что держите глаза открытыми.
Порядок операций — это набор правил, которые мы согласовали. Это означает, что пока учебник четко определяет их порядок, которому они будут следовать, они могут делать такие вещи.
Если вы не знаете, что делать первым, потребуйте скобки. (Да, вы можете это сделать.) Или поставьте круглые скобки в учебнике вашего ребенка, чтобы помочь ему.
Наборы задач должны быть там, чтобы обеспечивать, а не путать.
Что вы думаете? Это помогает или мешает тому, как вы всегда относились к порядку операций? Поделитесь своими мыслями в комментариях.
Статьи по теме
Этот пост может содержать партнерские ссылки. Когда вы используете их, вы поддерживаете нас, чтобы мы могли продолжать предоставлять бесплатный контент!
Порядок операций | Brilliant Math & Science Wiki
Бывший блестящий член, Матин Насери, Сатвик Голечха, а также
способствовал
Содержимое
- Общие мнемоники для порядка операций
- Сложение и умножение
- Экспоненты
- Скобки
- Смотрите также
Есть два распространенных мнемонических приема для запоминания правильного порядка операций. Однако при их использовании важно помнить, что истинный порядок операций определен выше, и, в частности, этот порядок операций не делает различий между умножением и делением (или сложением и вычитанием) при упорядочивании.
Однако при их использовании важно помнить, что истинный порядок операций определен выше, и, в частности, этот порядок операций не делает различий между умножением и делением (или сложением и вычитанием) при упорядочивании.
PEMDAS или «Пожалуйста, извините, моя дорогая тетя Салли»:
- P арентесы
- E Экспоненты
- М умножение
- Д ивижн
- A дополнение
- S вычитание
БОДМАС:
- B ракетки
- O ряды (показатели и радикалы)
- Д ивижн
- M умножение
- A дополнение
- S вычитание
Обратите внимание, что наивное обращение с любым из них может привести к ошибкам, поскольку как сложение/вычитание, так и умножение/деление должны группироваться и оцениваться слева направо. Более точной мнемоникой может быть PE(MD)(AS) и BO(DM)(AS).
Более точной мнемоникой может быть PE(MD)(AS) и BO(DM)(AS).
Одним из требований является выполнение умножения перед сложением. Например, в выражении 2+3×4 2 + 3 х 4 2+3 х 4 мы получим ответ 5 х 4 = 20 5 х 4 = 20 5 х 4 = 20, если мы начнем с добавления 2 и 3, но мы получим 2 + 12 = 14 2 + 12 = 14 2 + 12 = 14, если сначала умножим. Поскольку важно, чтобы все интерпретировали выражение 2+3×4 2 + 3 \times 4 2+3×4 одинаково, мы просто определить правильный порядок, в котором умножение выполняется первым. Таким образом, 2+3×4=2+(3×4)=2+12=14 2 + 3 х 4 = 2 + ( 3 х 4 ) = 2 + 12 = 14 2+3 х 4=2+ (3×4)=2+12=14.
Сколько будет 2×4+3×5 2 х 4 + 3 х 5 2×4+3×5?
Следуя правильному порядку операций, мы видим, что мы должны вычислить 2×4 2 \times 4 2×4 и 3×5 3 \times 5 3×5, прежде чем делать какое-либо сложение.
Таким образом, правильный ответ: 2×4+3×5=8+15=23 2 х 4 + 3 х 5 = 8 + 15 = 23 2 х 4 + 3 х 5 = 8 + 15 = 23. □_\квадрат□
Что такое 48÷2×12? 48 \дел 2 \умножить на 12 ? 48÷2×12?
Если бы мы небрежно следили за PEMDAS, ответом было бы сначала выполнить умножение, что дало бы нам 48÷24=2 48 \div 24 = 2 48÷24=2.

