Таблица логарифмов, формулы и примеры
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Определения и таблица логарифмов
Иногда при расчетах необходимо знать значения логарифмов некоторых величин, но их нельзя вычислить точно. Было составлено ряд таблиц для упрощения вычислений.
Таблица натуральных логарифмов
|
Единицы Десятки |
0 |
1 |
2 |
3 |
4 |
5 |
|
7 |
8 |
9 |
|
0 |
– |
0 |
0,6931 |
1,0986 |
1,3863 |
1,6094 |
1,7918 |
1,9459 |
2,0794 |
2,1972 |
|
1 |
2,3026 |
2,3979 |
2,4849 |
2,5649 |
2,6391 |
2,7081 |
2,7726 |
2,8332 |
2,8904 |
2,9444 |
|
2 |
2,9957 |
3,0445 |
3,091 |
3,1355 |
3,1781 |
3,2189 |
3,2581 |
3,2958 |
3,3322 |
3,3673 |
|
3 |
3,4012 |
3,434 |
3,4657 |
3,4965 |
3,5264 |
3,5553 |
3,5835 |
3,6109 |
3,6376 |
3,6636 |
|
4 |
3,6889 |
3,7136 |
3,7377 |
3,7612 |
3,7842 |
3,8067 |
3,8286 |
3,8501 |
3,8712 |
3,8918 |
|
5 |
3,912 |
3,9318 |
3,9512 |
3,9703 |
3,989 |
4,0073 |
4,0254 |
4,0431 |
4,0604 |
4,0775 |
|
6 |
4,0943 |
4,1109 |
4,1271 |
4,1431 |
4,1589 |
4,1744 |
4,1897 |
4,2047 |
4,2195 |
4,2341 |
|
7 |
4,2485 |
4,2627 |
4,2767 |
4,2905 |
4,3041 |
4,3175 |
4,3307 |
4,3438 |
4,3567 |
4,3694 |
|
8 |
4,382 |
|
4,4067 |
4,4188 |
4,4308 |
4,4427 |
4,4543 |
4,4659 |
4,4773 |
4,4886 |
|
9 |
4,4998 |
4,5109 |
4,5218 |
4,5326 |
4,5433 |
4,5539 |
4,5643 |
4,5747 |
4,5850 |
4,5951 |
|
10 |
4,6052 |
4,6151 |
4,625 |
4,6347 |
4,6444 |
4,654 |
4,6634 |
4,6728 |
4,6821 |
4,6913 |
Таблица и формула перехода от натуральных логарифмов к десятичным
Если известен натуральный логарифм некоторого числа , то десятичный логарифм этого числа, согласно свойствам логарифма, будет равен
где .
Итак, десятичный логарифм числа равен произведению натурального логарифма этого же числа и числа .
|
Десятки Единицы |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0,0000 |
4,3430 |
8,6859 |
13,0288 |
17,3718 |
21,7147 |
26,0577 |
30,4006 |
34,7436 |
39,0865 |
|
1 |
0,4343 |
4,7772 |
9,1202 |
13,4631 |
17,8061 |
22,1490 |
26,4920 |
30,8349 |
35,1779 |
39,5208 |
| 2 |
0,8686 |
5,2115 |
9,5545 |
13,8974 |
18,2404 |
22,5833 |
26,9263 |
31,2692 |
35,6122 |
39,9551 |
|
3 |
1,3029 |
5,6458 |
9,9888 |
14,3317 |
18,6747 |
23,0176 |
27,3606 |
31,7035 |
36,0464 |
40,3894 |
|
4 |
1,7372 |
6,0801 |
10,4231 |
14,7660 |
19,1090 |
23,4519 |
27,7948 |
32,1378 |
36,4807 |
40,8237 |
|
5 |
2,1715 |
6,5144 |
10,8574 |
15,2003 |
19,5433 |
23,8862 |
28,2291 |
32,5721 |
36,9150 |
41,2580 |
|
6 |
2,6058 |
6,9487 |
11,2917 |
15,6346 |
19,9775 |
24,3205 |
28,6634 |
33,0064 |
37,3493 |
41,6923 |
|
7 |
3,0401 |
7,3830 |
11,7260 |
16,0689 |
20,4118 |
24,7548 |
29,0977 |
33,4407 |
37,7836 |
42,1266 |
|
8 |
3,4744 |
7,8173 |
12,1602 |
16,5032 |
20,8461 |
25,1891 |
29,5320 |
33,8750 |
38,2179 |
42,5609 |
|
9 |
3,9086 |
8. |
12,5945 |
16,9375 |
21,2804 |
25,6234 |
29,9663 |
34,3093 |
38,6522 |
42,9952 |
Таблица и формула для перехода от десятичных логарифмов к натуральным.
Пусть известно значение десятичного логарифма некоторого положительного числа , тогда натуральный логарифм этого числа можно вычислить по формуле
то есть натуральный логарифм числа равен произведению десятичного логарифма этого числа и числа, обратного к числу :
|
Десятки Единицы |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0,0000 |
23,026 |
46,052 |
69,078 |
92,103 |
115,129 |
138,155 |
161,181 |
184,207 |
207,233 |
|
1 |
2,3026 |
25,328 |
48,354 |
71,380 |
94,406 |
117,431 |
140,458 |
163,484 |
186,509 |
209,535 |
|
2 |
4,6052 |
27,631 |
50,657 |
73,683 |
96,709 |
119,734 |
142,760 |
165,786 |
188,812 |
211,838 |
|
3 |
6,9078 |
29,934 |
52,959 |
75,985 |
99,011 |
122,037 |
145,062 |
166,089 |
191,115 |
214,140 |
|
4 |
9,2103 |
32,236 |
55,262 |
78,288 |
101,314 |
124,340 |
147,365 |
170,391 |
193,417 |
216,443 |
|
5 |
11,513 |
34,539 |
57,565 |
80,590 |
103,616 |
126,642 |
149,668 |
172,694 |
195,720 |
218,746 |
|
6 |
13,816 |
36,841 |
59,867 |
82,893 |
105,919 |
128,945 |
151,971 |
174,997 |
198,022 |
221,048 |
|
7 |
16,118 |
39,144 |
62,170 |
85,196 |
108,221 |
131,247 |
154,273 |
177,299 |
200,325 |
223,351 |
|
8 |
18,421 |
41,447 |
64,472 |
87,498 |
110,524 |
133,550 |
156,576 |
179,602 |
202,627 |
225,653 |
|
9 |
20,723 |
43,749 |
66,775 |
89,801 |
112,827 |
135,853 |
158,878 |
181,904 |
204,930 |
227,956 |
| Понравился сайт? Расскажи друзьям! | |||
Десятичный логарифм в математике — свойства, условия и примеры вычислений » Kupuk.
 net
netСтепенные уравнения считаются довольно сложными выражениями. Одним из видов их записи является десятичный логарифм. Он встречается в формулах настолько часто, что имеет собственное название и обозначение. Выражение характеризуется двумя переменными, которые на первых порах многие путают. Для того чтобы их вычислить, необходимо руководствоваться правилами и алгоритмом. При этом всё что относится к обычным логарифмам справедливо и для десятичного.
Понятия и термины
Впервые упоминание о логарифмах встречается в XIX веке в астрономических вычислениях. Сам же термин ввёл в обиход математик Спейдел. В 1893 году обозначать натуральный логарифм буквами ln предложил немецкий учёный Прингсхейм. Но лишь только в книге «Введение в анализ бесконечности» Эйлер дал определения логарифмам и описал их свойства, выделив при этом выражение с основанием равным десяти.
Существует несколько определений логарифмов. Для того чтобы разобраться в сущности термина нужно представить себе любое простое уравнение, содержащее степень. Например, 3x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.
Например, 3x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.
Теперь можно рассмотреть другое уравнение: 3x = 7. Если попробовать его решить, то можно обнаружить, что подобрать неизвестное значение будет довольно сложно. Интуитивно можно понять, что ответ будет располагаться между числом три в степени один и три в степени два. Искомое число и было решено назвать логарифмом. Записывается он как x = log3 7. Читается же формула как икс равный логарифму семи по основанию три.
Цифра, стоящая в нижнем регистре записи, называется основанием, а в верхней части аргументом. То есть любое выражение вида cx = k можно записать как x = logc k. Эта запись очень удобна для обозначения иррациональных чисел.
Логарифм можно записать только при выполнении условия: logp K = b, где pb = k, p > 0, k > 0, p ≠ 0. Существует три вида логарифма:
Существует три вида логарифма:
- Обыкновенный. Им называют выражение определённого числа по основанию.
- Десятичный. Определение логарифма связано с указаннім основанием равным десяти.
- Натуральный. Это логарифм, у которого в основании иррациональная постоянная составляет 2,72, то есть является экспонентной.
Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна, так как используя определение, запись можно переписать в виде: 102 = 100. Для того чтобы научиться решать задачи по нахождению логарифмов нужно знать их свойства, формулы сокращённого умножения и правила вычисления степеней.
Свойства и формулы
Формулы сокращённого умножения изучают в средней школе на уроках алгебры. Учащимся предлагается выучить семь основных выражений, собранных в таблицу. С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:
Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:
На этих формулах основаны свойства десятичных логарифмов. Большинство задач можно решить, зная только эти закономерности. Первое свойство вытекает из самого определения выражения: logp pv = v. Для доказательства этого свойства можно использовать рассуждение, что если logі p = v, то iv = p. Тогда отношение logk p / logk I будет равняться: logk iv / logk I = v * logk i / logk I = v = logі p. Что и требовалось доказать.
Второе и третье свойство помогает определить сумму логарифмов и посчитать их разницу. Согласно ему сумма выражений с одинаковым основанием равняется их произведению: logp i + logp c = logp (i * c). А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.
А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.
Четвёртое свойство позволяет при необходимости степень выносить за знак логарифма: logk iv = n * logk i. Пятое правило гласит, что если в основании логарифма стоит степень, то её можно переместить за знак функции: logkn i = 1/ n * logk i. В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.
Следующее свойство сообщает, что если основание и аргумент имеют степень, то эти показатели можно вынести за знак выражения как дробь: logkn * im = (m/n) * logki. При этом если степени совпадают по своему значению, это правило можно записать как log k n i n = log k i. Седьмое свойство помогает решать логарифмы с разным основанием. Так, любой логарифм можно записать в виде равенства: log k i = log c i / log c k.
Эти свойства применимы к любым видам логарифмов. При этом существует ещё одно позволяющее поменять местами основание и аргумент. Для этого нужно просто единицу разделить на логарифм: log k b = 1 / log k b.
Дифференцирование и функция
Производная десятичного логарифма определяется, как отношение в числителе которого стоит единица, а в знаменателе показатель. Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.
Её график определён при p больше нуля. Нужно найти производную по переменной p. По определению производной она ограничивается лимитом: t’ = lim t * ((p + Δ p) – t(p)) / (Δp) = = lim t ( log (p + Δ p) – log p / (Δp)). Используя свойства логарифмов это выражение можно преобразовать до вида: (1/p) * logc (1+ Δp / p)p/Δp.
Воспользовавшись свойством формулу можно упростить и записать: t’ = 1/t * logc p = (1/t) * (1/ln p) = 1 / t * ln p. То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.
То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.
Интеграл функции можно записать выражением: ∫ ln x dx = x * ln x – x + C. Находят его способом интегрирования по частям. Этим методом выражение сводится к более простому виду.
Функцию десятичного логарифма можно записать как y = lg x. График имеет вид плавной возрастающей кривой, которую ещё называют логарифмикой. К основным характеристикам функции относят:
- Неупорядоченность.
- Область определения, лежащую в интервале от нуля до плюс бесконечности.
- Множество значений, принадлежащих области от минус бесконечности до плюс.
- Пересечение графика с осью абсцисс в точке (1; 0).
- Возрастание кривой на всей области определения.
- Отсутствие минимума и максимума.
- Знакопостоянство промежутков для значений ординаты больше нуля, принадлежащих области от единицы до плюс бесконечности и для ординаты меньше нуля от нуля до единицы.

Функция монотонная, то есть всё время она не убывает и не возрастает. Иными словами, она всегда неотрицательная или неположительная, но при этом всюду дифференцируемая. Производная для выражения находится с помощью формулы: (d/dx) lg x = lg e / x. Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.
Примеры решения задач
При решении задач на сложение или вычитание логарифмов для быстрого вычисления нужно использовать знания, что десятичное выражение единицы всегда равняется нулю. А также то, что десятичный логарифм десятков, сотен, тысяч и подобных чисел будет иметь столько положительных единиц, сколько нулей содержит число. Например, lg 1000 = 3, lg 1 00000 = 5. В то же время логарифм дробных выражений наподобие 1/10, 1/100, то есть с нулями после единицы в делителе, в ответе будет иметь столько отрицательных цифр, сколько нулей содержится в знаменателе. Например, lg 0,001 = -3.
Например, lg 0,001 = -3.
При решении тождеств, содержащих тригонометрические функции, поможет и сборник таблиц Брадиса. Это пособие, в котором собраны ответы для чаще всего встречающихся типовых выражений.
Следующие типы примеров наиболее часто предлагаются в школе для самостоятельного решения:
 Левую часть уравнения можно представить в виде степенного многочлена: 3 * lg 0,09 – 2 * lg 27 = 3 * lg (9/102) – 2 * lg 27 = 3 * lg (3/10)2 – 2 * lg 33 = 3 * 2 * lg (3/10) – 2 * 3 * lg 3 = 6 * lg (3/10) – 6 * lg 3. Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно.
Левую часть уравнения можно представить в виде степенного многочлена: 3 * lg 0,09 – 2 * lg 27 = 3 * lg (9/102) – 2 * lg 27 = 3 * lg (3/10)2 – 2 * lg 33 = 3 * 2 * lg (3/10) – 2 * 3 * lg 3 = 6 * lg (3/10) – 6 * lg 3. Используя свойство частного логарифма полученное выражение можно представить как 6 * (lg 3 * lg 10) – 6 * lg 3. Теперь нужно открыть скобки и привести подобные слагаемые: 6 * lg 3 – 6 * lg10 – 6*lg 3 = — 6. Подставив полученное значение в исходное неравенство можно утверждать что оно неверно.Найти корень уравнения: lg (4×2 — 16x + 144) = lg 2 x + lg(2 x+ 6). Используя свойства знак логарифма можно вынести за скобки: lg (4×2 — 16x + 144) = lg (4×2 + 12x). В правой и левой части стоит одинаковое действие – логарифмирование. Поэтому на него можно сократить. В итоге получится: 4×2 — 16x + 144 = 4×2 + 12x. После объединения подобных членов уравнение примет вид двоичного: -4x +144 = 0 или x = 144 / 4 = 36.
Но бывает так, что самостоятельно решить задачу довольно сложно из-за громоздкости записи уравнения. При этом не так сложно провести вычисления, как правильно выбрать алгоритм решения. Поэтому в таких случаях используют так называемые онлайн-калькуляторы.
Использование онлайн-калькулятора
Использовать сервисы предлагающие услуги по вычислению десятичного логарифма, довольно удобно. Всё, что требуется от пользователя, — это интернет-канал и браузер с поддержкой флеш-технологии. Доступ к онлайн-калькуляторам предоставляется бесплатно, при этом даже нет необходимости в регистрации или указании каких-либо данных.
Онлайн-расчётчики позволяют не только получить быстрый и правильный ответ вычисления выражения любой сложности, но и предоставляют подробное решение с пояснениями. Кроме того, на страницах таких сервисов содержится краткая теория с примерами. Так что проблем с понятием, откуда взялся ответ возникнуть не должно.
Программы, используемые для расчётов, написаны на Java и включают в свой алгоритм все необходимые формулы. Пользователь, загрузив сервис должен ввести условие задачи в специально предложенную формулу и нажать кнопку «Решение» или «Вычислить». После чего буквально через две три секунды появится ответ с поэтапным решением.
Такие сервисы будут полезны не только учащимся для проверки своих знаний, но и даже инженерам, проводящим сложные вычисления. Ведь самостоятельный расчёт требует повышенного внимания и скрупулёзности. При этом любая незначительная ошибка приведёт к неправильному ответу. В то же время появление ошибки при вычислении на онлайн-калькуляторе практически невозможно.
По мнению пользователей, из нескольких десятков существующих сайтов можно выделить тройку лидеров:
- Kontrolnaya-rabota.
- Umath.
- Allcalc.

- Nauchniestati.
- Allworks.
Приведённые онлайн-калькуляторы для десятичного логарифма имеют интуитивно понятный интерфейс. Используемые программы написаны российскими программистами и не содержат рекламного и вредоносного кода. Решив несколько задач с помощью этих порталов, пользователь научится самостоятельно вычислять любые логарифмические уравнения. То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.
Log по основанию 10. Что такое логарифм
Нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными . При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg , а не log ; при этом число десять, определяющие основание, не указывают. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.
Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.
Целая часть десятичного логарифма числа а именуется характеристикой , а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а указывается как , а мантисса как {lg а }.
Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно = 0, {lg 2} ≈ 0,3010.
Подобно и для lg 543,1 ≈2,7349. Соответственно, = 2, {lg 543,1}≈ 0,7349.
Соответственно, = 2, {lg 543,1}≈ 0,7349.
Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.
Характерные признаки десятичных логарифмов.
Первый признак десятичного логарифма. целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.
Возьмем, lg 100 = 2, lg 1 00000 = 5.
Обобщенно, если
То а = 10 n , из чего получаем
lg a = lg 10 n = n lg 10 = п .
Второй признак. Десятичный логарифм положительной десятичной дроби , показанный единицей с предыдущими нулями, равен — п , где п — численность нулей в представлении этого числа, учитывая и нуль целых.
Рассмотрим, lg 0,001 = — 3, lg 0,000001 =-6.
Обобщенно, если
,
То a = 10 -n и получается
lga= lg 10 n =-n lg 10 =-п
Третий признак. {-5}=\)\(\frac{1}{32}\)
{-5}=\)\(\frac{1}{32}\)
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например , вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
\(\log_{4}{16}=2\)
\(\log_{3}\)\(\frac{1}{3}\) \(=-1\)
в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
\(\log_{\sqrt{5}}{1}=0\)
г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе. {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)
Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)
Перед нами . Перенесем \(4\) вправо.
И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)
Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
Ответ : \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).
 {\log_{6}{5}}\)
{\log_{6}{5}}\)Решение :
Ответ : \(25\)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}. {a}}\)
{a}}\)
Пример : Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение :
Ответ : \(1\)
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла.
 Нет такой степени!
Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b
будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.

Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т. к. множитель всего один;
к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459…
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1 ; ln e 2 = 2 ; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Определение логарифма
Логарифм с основанием a — это функция y(x) = log a x , обратная к показательной функции с основанием a: x(y) = a y .
Десятичный логарифм — это логарифм по основанию числа 10 : lg x ≡ log 10 x .
Натуральный логарифм — это логарифм по основанию числа e : ln x ≡ log e x .
2,718281828459045…
;
.
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x
.
Слева изображены графики функции y(x)
= log a x
для четырех значений основания логарифма : a = 2
,
a = 8
,
a = 1/2
и a = 1/8
.
На графике видно, что при a > 1
логарифм монотонно возрастает. С увеличением x
рост существенно замедляется. При 0
С увеличением x
рост существенно замедляется. При 0
Свойства логарифма
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 | 0 |
| Область значений | — ∞ | — ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | — ∞ | |
| — ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом :
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b
,
имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a .
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e .
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n
— целое,
то будет одним и тем же числом при различных n .
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
логарифмический калькулятор с основанием 4 | ICalc
Log Base 4 Calculator (Калькулятор логарифма 4) находит результат функции логарифмирования по основанию 4; Вычислить логарифмическое основание 4 числа.
Что такое номер
Список журналов 4 таблицы значений функций, журнал по основанию 4 чисел.
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 1 (log 4 (1)) = 0,0000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 2 (log 4 (2)) = 0,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 3 (log 4 (3)) = 0,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 4 (log 4 (4)) = 1,0000000000
Согласно калькулятору Log Base 4, значение log base 4 of 5 (log 4 (5)) = 1,1609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 6 (логарифм 4 (6)) = 1,2924812504
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 7 (логарифм 4 (7)) = 1,4036774610
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 8 (log 4 (8)) = 1,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 9 (log 4 (9)) = 1,5849625007
. логарифмической базы 4 из 11 (логарифм 4 (11)) = 1,7297158093
логарифмической базы 4 из 11 (логарифм 4 (11)) = 1,7297158093
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 12 (логарифм 4 (12)) = 1,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 13 (log 4 (13)) = 1,8502198591
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 14 (log 4 (14)) = 1,74610
. логарифмической базы 4 из 16 (логарифм 4 (16)) = 2,0000000000
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 17 (логарифм 4 (17)) = 2,0437314206
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 18 (log 4 (18)) = 2,0849625007
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 19 (log 4 (19)) = 2,1239637567
Согласно калькулятору Log Base 4, значение log base 4 из 20 (log 4 (20)) = 2,1609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 21 (логарифм 4 (21)) = 2,1961587114
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 22 (логарифм 4 (22)) = 2,2297158093
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 23 (log 4 (23)) = 2,2617809780
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 24 (log 4 (24)) = 2,2924812504
. логарифмической базы 4 из 26 (логарифм 4 (26)) = 2,3502198591
логарифмической базы 4 из 26 (логарифм 4 (26)) = 2,3502198591
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 27 (логарифм 4 (27)) = 2,3774437511
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 28 (log 4 (28)) = 2,4036774610
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 29 (log 4 (29)) = 2,4289
6
Согласно калькулятору Log Base 4, значение log base 4 из 30 (log 4 (30)) = 2,4534452978
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 31 (логарифм 4 (31)) = 2,4770981552
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 32 (логарифм 4 (32)) = 2,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 33 (log 4 (33)) = 2,5221970597
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 34 (log 4 (34)) = 2,5437314206
.логарифмической базы 4 из 36 (логарифм 4 (36)) = 2,5849625007
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 37 (логарифм 4 (37)) = 2,6047266828
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 38 (log 4 (38)) = 2,6239637567
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 39 (log 4 (39)) = 2,6427011094
Согласно калькулятору Log Base 4, значение log base 4 of 40 (log 4 (40)) = 2,6609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 41 (логарифм 4 (41)) = 2,6787760023
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 42 (логарифм 4 (42)) = 2,6961587114
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 43 (log 4 (43)) = 2,7131323774
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 44 (log 4 (44)) = 2,7297158093
.логарифмической базы 4 из 46 (логарифм 4 (46)) = 2,7617809780
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 47 (логарифм 4 (47)) = 2,7772944258
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 48 (log 4 (48)) = 2,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 49 (log 4 (49)) = 2,8073549221
Согласно калькулятору Log Base 4 значение log base 4 of 50 (log 4 (50)) = 2,8219280949
логарифмической базы 4 из 51 (логарифм 4 (51)) = 2,8362126710
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 52 (логарифм 4 (52)) = 2,8502198591
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 53 (log 4 (53)) = 2,8639602273
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 54 (log 4 (54)) = 2,8774437511
.логарифмической базы 4 из 56 (логарифм 4 (56)) = 2,74610
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 57 (логарифм 4 (57)) = 2,9164450071
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 58 (log 4 (58)) = 2,92896
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 59 (log 4 (59)) = 2,9413215247
. логарифмической базы 4 из 61 (логарифм 4 (61)) = 2,9653686688
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 62 (логарифм 4 (62)) = 2,9770981552
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 63 (log 4 (63)) = 2,9886399617
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 64 (log 4 (64)) = 3,0000000000
Согласно калькулятору Log Base 4, значение log base 4 of 65 (log 4 (65)) = 3,0111839065
логарифмической базы 4 из 66 (логарифм 4 (66)) = 3,0221970597
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 67 (логарифм 4 (67)) = 3,0330445952
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 68 (log 4 (68)) = 3,0437314206
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 69 (log 4 (69)) = 3,0542622284
Согласно калькулятору Log Base 4, значение log base 4 of 70 (log 4 (70)) = 3,0646415085
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 71 (логарифм 4 (71)) = 3,0748735598
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 72 (логарифм 4 (72)) = 3,0849625007
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 73 (log 4 (73)) = 3,0949122794
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 74 (log 4 (74)) = 3,1047266828
Согласно калькулятору Log Base 4, значение log base 4 of 75 (log 4 (75)) = 3,1144093452
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 76 (логарифм 4 (76)) = 3,1239637567
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 77 (логарифм 4 (77)) = 3,1333932703
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 78 (log 4 (78)) = 3,1427011094
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 79 (log 4 (79)) = 3,15181
Согласно калькулятору Log Base 4, значение log base 4 of 80 (log 4 (80)) = 3,1609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 81 (логарифм 4 (81)) = 3,1699250014
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 82 (логарифм 4 (82)) = 3,1787760023
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 83 (log 4 (83)) = 3,1875197157
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 84 (log 4 (84)) = 3,1961587114
Согласно калькулятору Log Base 4, значение log base 4 of 85 (log 4 (85)) = 3,2046954681
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 86 (логарифм 4 (86)) = 3,2131323774
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 87 (логарифм 4 (87)) = 3,2214717479
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 88 (log 4 (88)) = 3,2297158093
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 89 (log 4 (89)) = 3,2378667155
Согласно калькулятору Log Base 4, значение log base 4 of 90 (log 4 (90)) = 3,2459265482
Согласно калькулятору Log Base 4, значение логарифма по основанию 4 из 91 (логарифм 4 (91)) = 3,2538973201
Согласно калькулятору логарифма по основанию 4 значение логарифма по основанию 4 из 92 (log 4 (92)) = 3,2617809780
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 93 (log 4 (93)) = 3,2695794056
Согласно калькулятору Log Base 4 значение Лог основание 4 из 94 (log 4 (94)) = 3,2772944258
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 95 (log 4 (95)) = 3,2849278042
Согласно калькулятору Log Base 4 , значение логарифмической базы 4 из 96 (логарифм 4 (96)) = 3,2924812504
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 97 (log 4 (97)) = 3,2999564211
.Логарифм по основанию 4 из 99 (log 4 (99)) = 3,3146783100
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 100 (log 4 (100)) = 3,3219280949Онлайн калькулятор логарифмов в любое основание → LOG(x)
Вычисление логарифмов онлайн без использования калькуляторов и формул возможно благодаря нашему инструменту. Вам нужно только ввести базовое значение логарифма и число, к которому вы хотите применить операцию.
Помните, что теория говорит нам, что логарифм числа по данному основанию — это показатель степени, до которого мы должны возвести основание, чтобы получить то же число. Это теоретическое утверждение отражено в следующей математической формуле:
Познакомившись с теорией немного подробнее, вы можете перейти к расчету логарифма онлайн с помощью нашего инструмента:
При желании вы также можете рассчитать neperian логарифмы que son aquellos en los que la base соответствуют al valor del número ‘e’.
Por supuesto, también tenemos una sección dedicada a la operación del antilogarithm — операция, обратная логарифму числа.
Разделы статей
- Что нужно знать о логарифмах
- Свойства логарифмов
- Решаемые упражнения на логарифм
- Что такое основание логарифма?
- Как решить уравнение с логарифмами?
- Вычисление логарифмов в Excel
- Для чего нужны логарифмы?
- Как работает калькулятор логарифмов
- Как решать логарифмы с помощью инженерного калькулятора
Что нужно знать о логарифмах
Функция логарифма по своему определению влечет за собой ряд условий, которые мы должны знать, чтобы избежать ошибок в вычислениях:
- Невозможно вычислить логарифм в отрицательном основании числа.
- Не существует логарифма отрицательного числа или логарифма нуля.
- Логарифм числа 1 равен нулю: log x 1 = 0
- Логарифм по основанию x числа x равно 1: log x x = 1
- Логарифм по основанию x степени по основанию x равен показателю степени: log x x n = n
Свойства логарифмов
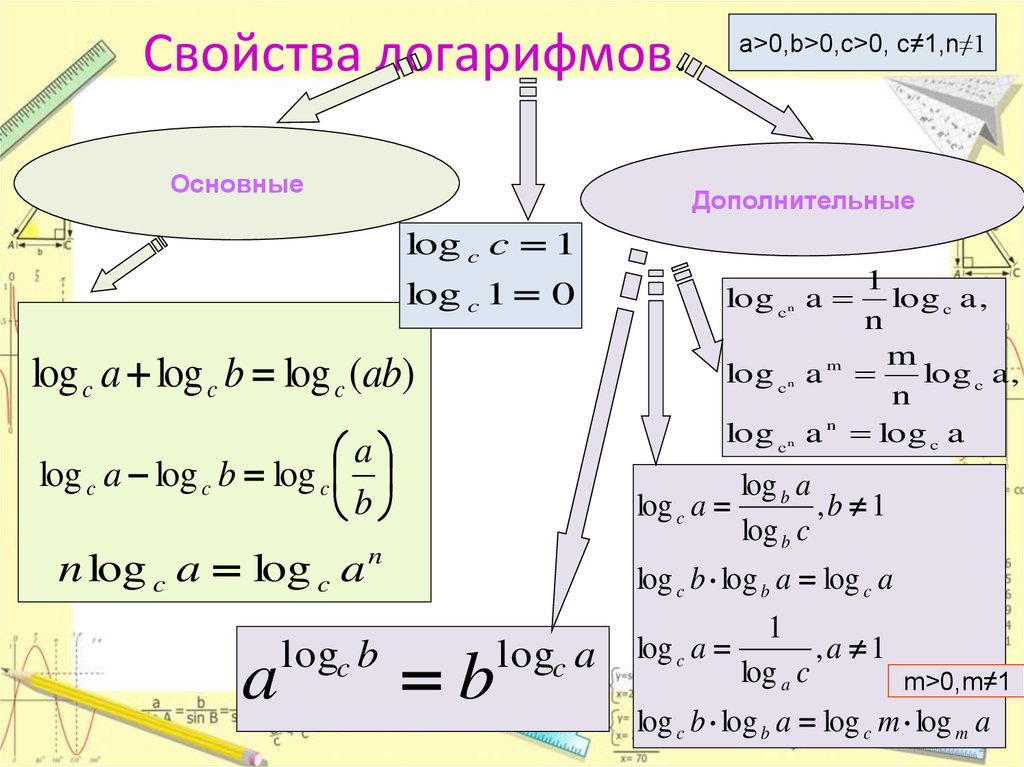
В дополнение к вышеизложенному, выполнение операций с логарифмами подчиняется ряду свойств, о которых мы упомянем ниже.
Когда вы сталкиваетесь с упражнениями на логарифмирование, очень важно помнить о них, так как они могут значительно облегчить вам поиск результата:
- Логарифм произведения равен сумме логарифмов множителей:
- Логарифм деления равен вычитанию логарифмов делимого минус логарифм делителя:
- Логарифм степени эквивалентен произведению показателя степени на логарифм основания степени:
- Логарифм корня можно выразить следующим образом:
Решаемые упражнения на логарифмы
- Чтобы выполнить изменение основания Если мы используем новое основание, мы должны разделить частное логарифма числа в новом основании на логарифм исходного основания:
Чтобы помочь вам понять, как решать логарифмы, давайте рассмотрим несколько распространенных примеров.
Каков логарифм числа 2
Когда основание логарифма не указано, мы возьмем основание 10 как типичное значение:
log(2) = x → 2 = 10 x
число мы должны поднять до 10, чтобы получить 2? Ответ 0,3.
Следовательно, log(2) = 0,3
Каков логарифм числа 50Если у нас все еще есть сомнения в том, как считать логарифмы, давайте рассмотрим другой пример, в котором нас просят вычислить журнал 50 . Опять же, поскольку основание не указано, мы возьмем 10 в качестве типичного значения:
log(50) = x → 50 = 10 x
На первый взгляд мы знаем, что x должно быть значением между 1 и 2 , так как 10 1 = 10 (мы недосчитались) и 10 2 = 100 (мы перебрали).
В этом случае ответ таков, что log(50) = 1,70
Если у вас есть сомнения или вы хотите решить конкретный журнал, напишите комментарий, и мы поможем вам с упражнением.
Какое основание логарифма?Если нас попросят вычислить основание логарифма Если мы не увидим его снова, нам придется вернуться к формуле, которую мы видели в начале. Давайте посмотрим на это еще раз:
log a (b) = x → b = a x
Базовое значение логарифма равно a, но как его получить, если нам дано как сколько стоит логарифм числа ? Чтобы лучше понять это, давайте посмотрим на практический пример:
log a (8) = 3 → 8 = a 3
Чтобы получить основание, мы должны найти число, которое возведение в куб дает нам 8. Это простая операция, поскольку мы знаем что для очистки мощности операция переходит на противоположную сторону в виде корня. То есть:
a = ∛8 = 2
Мы вычислили кубический корень из 8, и результат равен 2. Следовательно, основание нашего логарифма равно 2.
Если непонятно, мы собираемся увидеть другое упражнение, в котором нас просят выяснить, что является основанием логарифма:
log a (16) = 2 → 16 = a 2
В этом случае решение простое, так как нам нужно будет только вычислить квадратный корень из 16:
a = √16 = 4
Есть вопросы? Спросите нас!
Как решить уравнение с логарифмами?Чтобы решить уравнение с логарифмами , вы должны применить свойства и формулу определения логарифмов , которые мы видели выше. Выражение логарифма в виде степени поможет вам выполнить множество простых упражнений, но для более сложных вам также придется использовать свойства.
Например, давайте решим следующее уравнение с логарифмами:
log x + log 4 = log 32
Сумма двух логарифмов может быть выражена как произведение. Следовательно, приведенное выше уравнение выглядит так:
log4x = log32
Мы очищаем, и у нас остается следующее:
4x = 32
x = 8
По логике есть уравнения с логарифмами, которые решать гораздо сложнее и их решение будет не таким очевидным, как в предыдущем примере.
Вычисление логарифмов в Excel
Если вы хотите создать свой собственный калькулятор логарифмов с помощью Excel В функции LOG вы должны использовать функцию LOG, которая позволит вам вычислять логарифмы числа в любом основании.
Чтобы использовать эту формулу, выберите ячейку в электронной таблице и введите эту функцию:
=LOG(A1;B2)
Вы должны иметь в виду, что:
- A1 — это координата ячейки в какой номер для которого вы хотите вычислить его логарифм.
- B2 — основание логарифма.
После написания формулы для решения логарифмов в Excel Если у вас есть новый расчет, вы получите автоматический расчет, чтобы использовать его в любое время.
Для чего нужны логарифмы?
Логарифмы родились как инструмент, облегчающий решение арифметических и геометрических упражнений. Таким образом, мы избегаем сложных операций умножения и деления. Как мы видели ранее, логарифм способен преобразовывать умножение в сложение и деление в вычитание.
Но, какие логарифмы для ? На этот вопрос нет однозначного ответа, потому что логарифмы используются во многих областях и поэтому используются в экономике, банковском деле, статистике, рекламе, медицине, психологии, физике, технике, биологии, геологии, астрономии, химии, геодезии, авиации, музыке и т. длинный и тд.
Именно по этой причине вам очень важно знать , как решать логарифмы , и очень хорошо понимать его свойства.
Как работает калькулятор логарифмов
В этом видео мы записали, как пользоваться нашим калькулятором логарифмов , чтобы у вас не возникло сомнений, как решить эту операцию с помощью нашего инструмента.
Для решить логарифмы онлайн просто введите значение основания и введите число. Затем нажмите кнопку расчета, чтобы получить журнал (x).
Если у вас все еще есть сомнения при вычислении логарифмов, оставьте нам комментарий, и мы постараемся помочь вам как можно скорее. Мы надеемся, что наши 9Страница 0316 для решения логарифмов помогла вам.
Как решать логарифмы с помощью научного калькулятора
Если у вас есть научный калькулятор, вы можете решать логарифмы очень просто.
В качестве примера мы взяли научный калькулятор Casio, но правда в том, что у большинства брендов и простых калькуляторов есть клавиша, предназначенная для вычисления логарифмов .
Вы сможете легко идентифицировать его, потому что verás las letras «бревно» выгравировано на его поверхности, поэтому вам нужно только нажать на него, написать число, логарифм которого вы хотите получить, и нажать клавишу равенства (=), чтобы узнать результат.
Обратите внимание, что по умолчанию калькулятор логарифмов выполняет операцию с логарифмом по основанию 10, но если нам нужно его изменить, мы также можем это сделать без проблем.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Калькулятор логарифмического правдоподобия и размера эффекта
Чтобы использовать этот мастер, введите частоты для одного слова и размеры корпуса и нажмите кнопку расчета.
Корпус 1 Корпус 2 Частота слова Размер корпуса Примечания:
1.Введите простые числа без запятых. (или другие нечисловые символы), так как они будут путать калькулятор!
2. Мастер LL показывает знак плюс или минус перед значением логарифмической вероятности чтобы указать чрезмерное или недостаточное использование соответственно в корпусе 1 по сравнению с корпусом 2.
3. Само значение логарифмического правдоподобия всегда является положительным числом. Однако мой сценарий сравнивает относительные частоты между двумя корпусами, чтобы вставить индикатор для «+» чрезмерное использование и «-» недостаточное использование корпуса 1 по сравнению с корпусом 2.Как рассчитать логарифмическую вероятность
Логарифмическая вероятность рассчитывается путем построения таблицы непредвиденных обстоятельств следующим образом:
Corpus 1 Corpus 2 Total Frequency of word a b a+b Frequency of other words c-a d-b c+d-a-b Итого c d c+d Обратите внимание, что значение «c» соответствует количеству слов в корпусе.
один, а «d» соответствует количеству слов в корпусе два (N ценности). Значения «a» и «b» называются наблюдаемыми значениями (O), тогда как нам нужно рассчитать ожидаемые значения (E) в соответствии с следующая формула:
В нашем случае N1 = c, а N2 = d. Итак, для этого слова E1 = c*(a+b) / (c+d) и E2 = d*(a+b)/(c+d). Расчет ожидаемых значений занимает учитывая размер двух корпусов, поэтому нам не нужно нормализуйте цифры перед применением формулы. Мы можем тогда рассчитать значение логарифмического правдоподобия по этой формуле:
Это равносильно вычислению логарифмической вероятности G2 следующим образом: G2 = 2*((a*ln (a/E1)) + (b*ln (b/E2)))
Примечание 1: (спасибо Stefan Th. Gries) Форма логарифмического правдоподобия Расчет, который я использую, взят из исследования Рида и Кресси, процитированного в Rayson and Garside (2000), а не форму, полученную в Dunning (1993).
Примечание 2: (спасибо Крису Брю) Чтобы сформировать логарифмическое правдоподобие, мы вычисляем сумму по членам формы х*ln(х/Е).
Для строго положительного x легко вычислить эти члены, в то время как если x равно нулю, ln (x / E) будет отрицательной бесконечностью. Однако предел x * ln (x), когда x стремится к нулю, по-прежнему равно нулю, поэтому при суммировании мы можем просто игнорировать ячейки, где x = 0. Вычисление ln(0) возвращает ошибку, например, MSExcel и библиотека C-math.
Чем выше значение G2, тем значительнее разница между два показателя частоты. Для этих таблиц G2 равен 3,8 или выше. значимо на уровне p
95-й процентиль; 5% уровень; р 99-й процентиль; 1% уровень; р 99,9-й процентиль; уровень 0,1%; р 99,99-й процентиль; уровень 0,01%; п Расчет размера эффекта
Наряду с мерой логарифмического правдоподобия на этой странице реализованы следующие меры размера эффекта:
- %DIFF — см. Gabrielatos and Marchi (2012)
Костас также предоставил FAQ с более подробной информацией.- Фактор Байеса (BIC) — см. Wilson (2013)
Вы можете интерпретировать приблизительный коэффициент Байеса как степень доказательства против нулевой гипотезы следующим образом:
0-2: не стоит большего, чем простое упоминание
2-6 : положительное свидетельство против H0
6-10: сильное свидетельство против H0
> 10: очень сильное свидетельство против H0
Для отрицательных оценок шкала читается как «за», а не «против» (Уилсон, личное сообщение).- Размер эффекта для логарифмического правдоподобия (ELL) — см. Johnston et al (2006)
ELL варьируется от 0 до 1 (включительно). Джонстон и др. сказать, «интерпретация проста как пропорция максимального отклонения между наблюдаемые и ожидаемые пропорции».- Относительный риск — см. ссылки ниже
- Log Ratio — см. блог CASS Эндрю Харди, как интерпретировать это
Обратите внимание, что если какое-либо слово имеет нулевую частоту, то автоматически применяется небольшая корректировка (0,5 наблюдаемой частоты который затем нормализуется), чтобы избежать ошибок деления на ноль.- Соотношение шансов — см. ссылки ниже
Дополнительная литература
Для подробного сравнения логарифмической вероятности и статистики хи-квадрат см.
Rayson P., Berridge D. and Francis B. (2004). Расширение правила Кокрана для сравнения частоты слов между корпусами. В томе II Purnelle G., Fairon C., Dister A. (ред.) Le poids des mots: Материалы 7-й Международной конференции по Статистический анализ текстовых данных (JADT 2004), Лувен-ла-Нев, Бельгия, 10-12 марта 2004 г. , Presses universitaires de Louvain, стр. 926–936. ISBN 2-930344-50-4.
Логарифмический критерий правдоподобия можно использовать для сравнения корпусов. См.
Rayson, P. and Garside, R. (2000). Сравнение корпусов с использованием частотного профилирования. В материалах семинара по Сравнивая корпуса, проводится в связи с 38-м ежегодным собранием Ассоциации компьютерной лингвистики (ACL 2000) . 1–8 октября 2000 г., Гонконг, стр. 1–6.Более подробный обзор различных статистических данных см.:
Райсон, стр. (2003). Матрица: статистический метод и программный инструмент для лингвистического анализа посредством корпусное сравнение. кандидат наук диссертация , Ланкастерский университет.Чтобы узнать больше об использовании логарифмического правдоподобия при сравнении на уровне тегов, см.
:
Rayson, P. (2008). От ключевых слов к ключевым семантическим доменам. Международный журнал корпусной лингвистики . 13:4 стр. 519-549. DOI: 10.1075/ijcl.13.4.06rayКалькулятор распределения хи-квадрат (Stat Trek) позволяет легко вычислить кумулятивные вероятности, основанные на статистике хи-квадрат.
Аналогичный калькулятор есть в Институте фонетических наук в Амстердаме.
См. также Даннинг, Тед. (1993). Точные методы статистики неожиданностей и совпадений. Компьютерная лингвистика , том 19, номер 1, стр. 61-74. (pdf)
Эндрю Харди создал система проверки значимости который вычисляет хи-квадрат, логарифмическое правдоподобие и точный критерий Фишера для таблиц непредвиденных обстоятельств с использованием R.
Растет движение в корпусной лингвистике и других областях. (например, психология) отказаться от проверки нулевой гипотезы и p-значений, и для расчета мер размера эффекта, а также значений значимости.
Для обсуждения этих мер и зачем они нам нужны, см. следующие ресурсы, презентации и публикации:
Существует ряд других работ, связанных с использованием проверки значимости, статистика ключевости и сравнение корпусов, например. Килгаррифф (2005), Пако и Бестген (2009 г.)), Барон и др. (2009), Уилсон (2013) а также Лиффийт и др.
- Размер эффекта CEP932 в котором обсуждаются меры, включая d Коэна, коэффициент корреляции Пирсона r и отношение шансов.
- Вацлав Брезина (2014) Размеры эффектов в корпусной лингвистике: ключевые слова, словосочетания и диахроническое сравнение. Представлено на конференции ICAME 2014, Ноттингемский университет. [Вацлав использует D Коэна в качестве меры размера эффекта.]
- Величина эффекта для критерия хи-квадрат который описывает такие меры, как Phi, V Крамера, Отношение шансов и Относительный риск
- Статистика для объяснения психологии Тестирование нулевой гипотезы и размеры эффекта, которые, например, утверждают «Если небольшое различие между средними значениями двух групп не является значимым, когда я тестирую 100 человек, должен ли я внезапно прийти в восторг от точно такой же разницы, если после тестирования 1000 человек я обнаружу, что теперь она значительна?»
- Грис, Стефан Т.
(2014) Таблицы частот, размеры эффектов и исследования. В Дилане Глинне и Джастине Робинсон (ред.), Корпусные методы семантики: количественные исследования полисемии и синонимии, 365–389.. Амстердам и Филадельфия: Джон Бенджаминс. [В этой статье Стефан использует показатели размера эффекта Phi, отношение шансов для таблиц 2 x 2 и V Крамера для больших таблиц r-by-c.]
- Логарифмический коэффициент Эндрю Харди который на самом деле является двоичным журналом относительного риска и может применяться только к 2 x 2 стола вместе с коэффициентом шансов.
- Джонстон, Дж. Э., Берри, К. Дж. и Мильке, П.В. (2006) Меры размера эффекта для тестов согласия хи-квадрат и отношения правдоподобия. Перцептивные и моторные навыки: том 103, выпуск, стр. 412–414. DOI: 10.2466/pms.103.2.412-414 [Это представляет меру размера эффекта, применимую к логарифмической вероятности.]
- Кубергер А., Фриц А., Шерндль Т. (2014) Предвзятость публикации в психологии: диагноз, основанный на корреляции между размером эффекта и размером выборки.
PLoS ONE 9(9): e105825. doi:10.1371/journal.pone.0105825
- Джеффри Т. Лик и Роджер Д. Пэн (2015) Статистика: значения P — это только верхушка айсберга Nature 520, 612 (30 апреля 2015 г.) doi: 10.1038/520612a [Эта статья призывает нас не сосредотачиваться только на статистике: «Статистики и люди, которых они обучают и с которыми они сотрудничают, должны прекратить спорить о значениях P и не допустить, чтобы остальная часть айсберга пошла ко дну науки».]
- Дональд Шарп (2015) Ваш критерий хи-квадрат статистически значим: что теперь? Практическая оценка, исследования и оценка. Том 20, номер 8, апрель 2015 г.
- Блог Скотта Вайнгарта за 2013 г. Друзья не позволяют друзьям вычислять p-значения (без их полного понимания)
- Блог и статья Шона Уоллиса о Меры ассоциации для таблиц непредвиденных обстоятельств
- Камминг, Г. (2014) Новая статистика: почему и как. Психологическая наука. 25(1), стр. 7-29. DOI: 10.1177/0956797613504966 [Упоминает, что D Коэна широко используется, но имеет подводные камни.
]
- Габриэлятос, К. и Марчи, А. (2012) Keyness: Соответствующие показатели и практические вопросы. Международная конференция CADS 2012. Дискурсивные исследования с помощью корпуса: больше, чем сумма анализа дискурса и вычислений?, 13–14 сентября, Болонский университет, Италия. [Представляет меру размера эффекта %DIFF, которую, по мнению Костаса и Анны, следует применять к попарным сравнениям корпусов для расчета ключевости.]
- Грис, Стефан Т. (2005) Проверка значимости нулевой гипотезы частоты слов: продолжение Килгарриффа. Корпусная лингвистика и лингвистическая теория 1(2). 277-294. [Стефан сравнивает хи-квадрат, p-значения, V Крамера, d Коэна и d*, а также Поправки Бонферрони и Холма для апостериорного тестирования.]
Загружаемая электронная таблица
Я сделал электронную таблицу, включающую расчет логарифмического правдоподобия и набор мер размера эффекта: SigEff.

 2516
2516
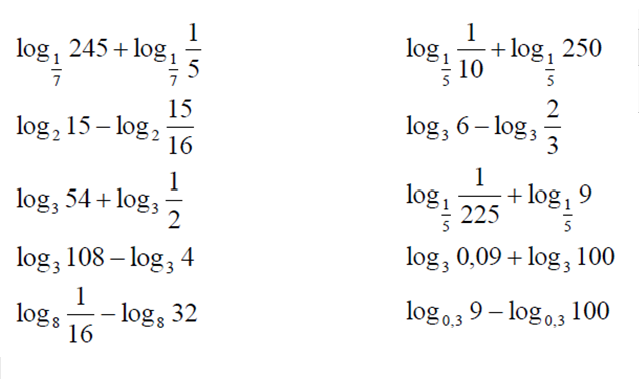
 Нет такой степени!
Нет такой степени!

 логарифмической базы 4 из 36 (логарифм 4 (36)) = 2,5849625007
логарифмической базы 4 из 36 (логарифм 4 (36)) = 2,5849625007  логарифмической базы 4 из 46 (логарифм 4 (46)) = 2,7617809780
логарифмической базы 4 из 46 (логарифм 4 (46)) = 2,7617809780  логарифмической базы 4 из 56 (логарифм 4 (56)) = 2,74610
логарифмической базы 4 из 56 (логарифм 4 (56)) = 2,74610  Логарифм по основанию 4 из 99 (log 4 (99)) = 3,3146783100
Логарифм по основанию 4 из 99 (log 4 (99)) = 3,3146783100  Por supuesto, también tenemos una sección dedicada a la operación del antilogarithm — операция, обратная логарифму числа.
Por supuesto, también tenemos una sección dedicada a la operación del antilogarithm — операция, обратная логарифму числа. Когда вы сталкиваетесь с упражнениями на логарифмирование, очень важно помнить о них, так как они могут значительно облегчить вам поиск результата:
Когда вы сталкиваетесь с упражнениями на логарифмирование, очень важно помнить о них, так как они могут значительно облегчить вам поиск результата:



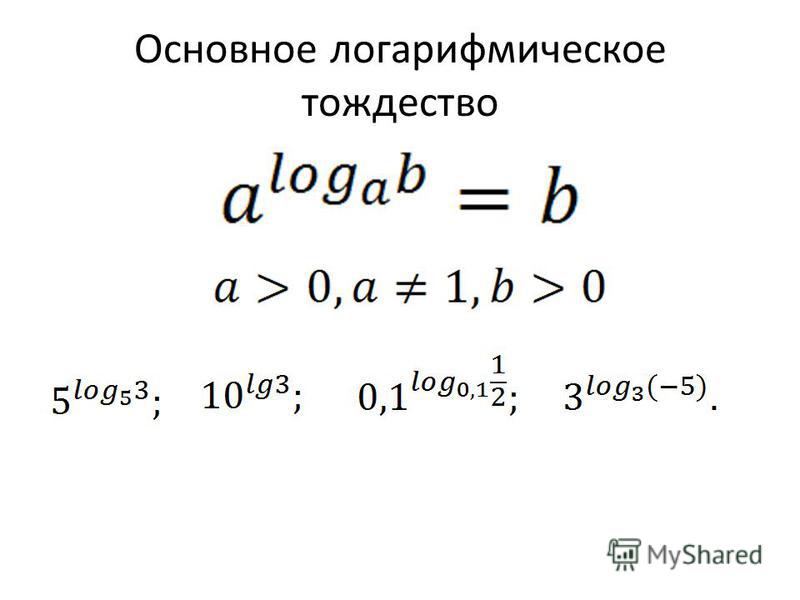

 Введите простые числа без запятых.
(или другие нечисловые символы), так как они будут путать
калькулятор!
Введите простые числа без запятых.
(или другие нечисловые символы), так как они будут путать
калькулятор!  один, а «d» соответствует количеству слов в корпусе два (N
ценности). Значения «a» и «b» называются наблюдаемыми значениями (O),
тогда как нам нужно рассчитать ожидаемые значения (E) в соответствии с
следующая формула:
один, а «d» соответствует количеству слов в корпусе два (N
ценности). Значения «a» и «b» называются наблюдаемыми значениями (O),
тогда как нам нужно рассчитать ожидаемые значения (E) в соответствии с
следующая формула:  Для строго положительного x легко вычислить эти члены,
в то время как если x равно нулю, ln (x / E) будет отрицательной бесконечностью.
Однако предел
x * ln (x), когда x стремится к нулю, по-прежнему равно нулю, поэтому при суммировании мы можем просто
игнорировать ячейки, где x = 0.
Вычисление ln(0) возвращает ошибку, например,
MSExcel и библиотека C-math.
Для строго положительного x легко вычислить эти члены,
в то время как если x равно нулю, ln (x / E) будет отрицательной бесконечностью.
Однако предел
x * ln (x), когда x стремится к нулю, по-прежнему равно нулю, поэтому при суммировании мы можем просто
игнорировать ячейки, где x = 0.
Вычисление ln(0) возвращает ошибку, например,
MSExcel и библиотека C-math.
 , Fairon C., Dister A. (ред.)
Le poids des mots: Материалы 7-й Международной конференции по
Статистический анализ текстовых данных
(JADT 2004), Лувен-ла-Нев, Бельгия, 10-12 марта 2004 г. ,
Presses universitaires de Louvain, стр. 926–936. ISBN 2-930344-50-4.
, Fairon C., Dister A. (ред.)
Le poids des mots: Материалы 7-й Международной конференции по
Статистический анализ текстовых данных
(JADT 2004), Лувен-ла-Нев, Бельгия, 10-12 марта 2004 г. ,
Presses universitaires de Louvain, стр. 926–936. ISBN 2-930344-50-4. :
:  Для обсуждения этих мер и зачем они нам нужны,
см. следующие ресурсы,
презентации и публикации:
Для обсуждения этих мер и зачем они нам нужны,
см. следующие ресурсы,
презентации и публикации: (2014)
Таблицы частот, размеры эффектов и исследования.
В Дилане Глинне и Джастине Робинсон (ред.), Корпусные методы семантики: количественные исследования полисемии и синонимии, 365–389.. Амстердам и Филадельфия: Джон Бенджаминс.
[В этой статье Стефан использует показатели размера эффекта Phi, отношение шансов для таблиц 2 x 2 и V Крамера для больших таблиц r-by-c.]
(2014)
Таблицы частот, размеры эффектов и исследования.
В Дилане Глинне и Джастине Робинсон (ред.), Корпусные методы семантики: количественные исследования полисемии и синонимии, 365–389.. Амстердам и Филадельфия: Джон Бенджаминс.
[В этой статье Стефан использует показатели размера эффекта Phi, отношение шансов для таблиц 2 x 2 и V Крамера для больших таблиц r-by-c.] PLoS ONE 9(9): e105825. doi:10.1371/journal.pone.0105825
PLoS ONE 9(9): e105825. doi:10.1371/journal.pone.0105825 ]
]