Последовательность решения примеров: Порядок действий в Математике

Действия какой ступени выполняются в первую очередь?

Ответьте на вопрос: —

Какой порядок действий при решении длинного выражения?

Порядок выполнения действий при решении выражения.

В математике последовательность выполнения действий разделена на две ступени:
к первой ступени относятся действия — сложение и вычитание, ко второй ступени — умножение и деление.
При нахождении значения выражения в первую очередь выполняются действия заключённые в скобки (если имеются), далее выполняются действия второй ступени и в последнюю очередь действия первой ступени.
Порядок действий обозначается слева направо.

Пример:

1. Слева направо обозначим действия в скобках.

2. Вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия второй ступени.
Действия второй ступени — умножение и деление.

3. Вновь вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия первой ступени.
Действия первой ступени — сложение и вычитание.

Всего 10 действий. Выполняем их по проставленному порядку.

Выполним действия в скобках:

18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8

1. 27 — 25 = 2
2. 6 + 4 = 10

   После выполнения действий в скобках выражение стало выглядеть так:

   18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8

   Теперь выполним все действия второй ступени — умножение и деление:

   18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8

3. 8 : 2 = 4
4. 2 · 8 = 16
5. 4 · 10 = 40
6. 16 : 8 = 2

   После выполнения действий второй ступени выражение стало выглядеть так:

   18 + 4 — 16 + 40 + 2

   Теперь выполним все действия первой ступени — сложение и вычитание:

   18 + 4 — 16 + 40 + 2

7. 18 + 4 = 22
8. 22 — 16 = 6
9. 6 + 40 = 46
10. 46 + 2 = 48

    18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8 = 48

Коротко:

Известные и великие математики

ученые средневековья и современности, и их вклад в мировую науку

Пафнутий Чебышёв

Русский математик и механик
Дата рождения: 16 мая 1821
Место рождения: Акатово, Боровский уезд, Калужская губерния, Российская империя
Дата смерти: 8 декабря 1894 (73 года)

Биография

Первоначальное воспитание и образование получил дома: грамоте его обучила мать Аграфена Ивановна. Арифметике, французскому языку и музыке обучала двоюродная сестра Авдотья Квинтилиановна Сухарёва. Одним из детских увлечений будущего учёного было изучение механизмов игрушек и автоматов, которые сам придумывал и изготовлял их.

В 1832 году семья переехала в Москву. В Москве с Пафнутием математикой и физикой занимался П. Н. Погорельский — один из лучших учителей Москвы, у которого в том числе учился, в пансионе Вейденгаммера, и И. С. Тургенев. Латынь Пафнутию Чебышёву преподавал в то время студент-медик, а в будущем главный врач Шереметевской больницы А. Т. Тарасенков.

Летом 1837 года Чебышёв поступил в Императорский Московский университет на вторе физико- математическе отделение философского факультета и начал изучение математики . Существенное влияние на формирование круга научных интересов молодого Чебышёва оказал его учитель — профессор прикладной математики и механики Московского университета Николай Дмитриевич Брашман.

В 1841 году Пафнутий Чебышёв его окончил.

В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел, геометрии, теории эллиптических функций и практической механике.

В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел, геометрии, теории эллиптических функций и практической механике.

В 1849 году Чебышёв защитил в Петербургском университете докторскую диссертацию «Теория сравнений», после чего в 1850 году он стал профессором Петербургского университета; данную должность он занимал до 1882 года. Работая в Петербургском университете, Чебышёв близко сошёлся с профессором прикладной математики О. И. Сомовым, который тоже был учеником Н. Д. Брашмана, и эти отношения переросли в глубокую дружбу. В семейном плане Чебышёв был одинок, и это обстоятельство также способствовало его сближению с большой семьёй Сомова.

Интерес к механизмам сохранялся у Чебышёва и в зрелые годы. В 1852 году Чебышёв совершил научную командировку в Великобританию, Францию и Бельгию, в ходе которой он ознакомился с практикой зарубежного машиностроения, с музейными коллекциями машин и механизмов, с работой заводов и фабрик, а также встречался с крупнейшими математиками и механиками: О. Коши, Ж. Лиувиллем, Ж.

-А. Серре, Л. Фуко, Ш. Эрмитом, Дж. Сильвестром, А. Кэли, Т. Грегори. После этого он некоторое время преподавал практическую механику в Петербургском университете и Александровском лицее.

В 1853 году академики П. Н. Фусс, В. Я. Струве, Б. С. Якоби, В. Я. Буняковский представили Чебышёва к избранию в адъюнкты Петербургской академии наук, особо отметив важность его работ в области практической механики. В том же году он был избран в адъюнкты, а в 1856 году стал экстраординарным академиком.

В 1858 году в связи с его работами по теории шарнирных параллелограммов и теории приближения функций академики В. Я. Буняковский, М. В. Остроградский, Э. Х. Ленц, Б. С. Якоби, А. Я. Купфер, О. В. Струве подписали представление к избранию Чебышёва ординарным академиком. И 1859 году Чебышёв избран ординарным академиком. Стал почётным членом Московского университета.

С 22 февраля 1860 года — ординарный профессор.

С 10 июля 1863 года — член Учёного комитета Министерства народного просвещения.

С 30 августа 1863 года — действительный статский советник.

Чем знаменит:

• В 1840/1841 учебном году, участвуя в студенческом конкурсе Императорского Московского университета, Пафнутий Чебышёв получил серебряную медаль за работу по нахождению корней уравнения n-й степени которую написал ещё в 1838 году и сделаную на основе алгоритма Ньютона
• Работы по теории вероятностей — изъяв из неё расплывчатые формулировки и неправомерные утверждения и превратив её в строгую математическую дисциплину
• Работы по теории чисел
• Работы по математическому анализу
• Работы по прикладной математике и механике
• Работы по «стопоходящей машины»
• Создатель автоматического арифмометра
• оздатель модели инвалидной коляски
• оздатель
• Работы по

Алгоритм.

Примеры задач

---

A. Время в зазеркалье

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	1 секунда
Ограничение памяти	512 Mb
Ввод	стандартный ввод или input.txt
Вывод	стандартный вывод или output.txt

В офисе, где работает Бомбослав, установлены стильные дизайнерские часы. Их циферблат имеет стандартную разметку: на окружности расположены 60 делений, соответствующих минутам, 12 из которых (начиная с расположенного вверх от центра окружности, далее равномерно с шагом в пять делений) сделаны крупнее остальных, то есть соответствуют часам. Стильными эти часы делает тот факт, что циферблат не содержит никаких цифр, так как предполагается, что всем хорошо известно, какое деление соответствует какому значению текущего времени.

Сегодня над рабочим местом Бомбослава повесили такие часы. Периодически поглядывая на них, он сначала заметил некоторую странность в направлении движения стрелок. Приглядевшись внимательнее, Бомбослав обнаружил, что на самом деле над его рабочим местом находится зеркало, а часы расположены на стене за его спиной. Это означает, что Бомбослав видит циферблат отражённым относительно вертикальной оси, проходящей через его центр. Теперь он хочет научиться быстро определять настоящее текущее время, зная время, которое показывается на отражённом циферблате.

Часы устроены таким образом, что обе стрелки движутся дискретно, то есть часовая стрелка всегда указывает на одно из 12 крупных делений, соответствующее текущему количеству часов, а минутная стрелка на одно из 60 делений, соответствующее текущему количеству минут.

Формат ввода

В единственной строке входных данных записаны два целых числа h и m(0≤h≤11, 0≤m≤59) — положение часовой стрелки и положение минутной стрелки в отражённом циферблате соответственно. h=0 означает, что часовая стрелка указывает вертикально вверх, h=3 соответствуют стрелке, направленной строго направо, h=6 — стрелка смотрит вертикально вниз, h=9 — строго налево. Аналогичные указания верны для минутной стрелки для значений m=0, m=15, m=30и m=45

Формат вывода

Выведите два целых числа x и y(0≤x≤11, 0≤y≤59) — реальное значение текущего времени на часах.

Пример 1

Пример 2

Примечания

На картинке изображён первый тестовый пример. Левый циферблат соответствует тому, что видит Бомбослав, а правый — реальному положению стрелок. Часовая стрелка изображена красным цветом, а минутная синим.

Решение

Решение

Рассмотрим движение «прямой» и «отражённой» стрелки. За то время, которое «прямая» стрелка повернётся на некоторый угол, «отражённая» повернётся на тот же угол, но в другую сторону, то есть суммарный угол поворота стрелок равен полному обороту. Для каждой стрелки независимо вычислим её позицию. Для часовой это 12 минус текущая позиция, а для минутной — 60 минус текущая позиция. В обоих случая надо не забыть заменить 12 или 60 на ноль.

B. Фактор палиндромности

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	1 секунда
Ограничение памяти	512Mb
Ввод	стандартный ввод или input.txt
Вывод	стандартный вывод или output.txt

Аркадий — большой фанат использования машинного обучения в любой задаче. Он верит в безграничную силу волшебства этой популярной молодой науки. Именно поэтому Аркадий постоянно придумывает всё новые и новые факторы, которые можно вычислить для различных объектов.

Напомним, палиндромом называется строка, которая одинаково читается от начала к концу и от конца к началу. Для каждой строки в своей базе данных Аркадий хочет найти самую короткую её подстроку, состоящую хотя бы из двух символов и являющуюся палиндромом. Если таких подстрок несколько, Аркадий хочет выбрать лексикографически минимальную.

Формат ввода

В единственной строке входных данных записана одна строка из базы Аркадия — непустая последовательность строчных букв английского алфавита. Длина строки составляет не менее 2 и не превосходит 200 000 символов.

Формат вывода

Выведите минимальную по длине подстроку строки из входных данных, состоящую хотя бы из двух символов и являющуюся палиндромом. Напомним, что среди всех таких строк Аркадий хочет найти лексикографически минимальную.

Пример 1

Пример 2

Примечания

Говорят, что строка a=a1a2 … an) лексикографически меньше строки b=b1b2 … bm) если верно одно из двух условий:

• либо nm и a1=b1, a2=b2,  …, an=bn,  то есть первая строка является префиксом второй;
• либо есть такая позиция 1≤i≤min(n,m), что a1=b1, a2=b2 . .., ai-1=bi-1 и ai=bi,  то есть, в первой позиции, в которой строки различаются, в первой строке стоит меньшая буква.

Решение

Решение

Пусть существует какая-то подстрока, являющаяся палиндромом. Если мы уберём первый и последний символ палиндрома, оставшаяся строка тоже будет палиндромом. Будем повторять процесс до тех пор, пока не останется строка из двух или трёх букв (в зависимости от чётности).

Подстрок длины два или три всегда линейное количество, и суммарная их длина также линейна, поэтому среди таких строк ответ можно выбрать наивным алгоритмом. Если же ни одна из подстрок такой длины не является палиндромом, то выведем -1.

C. Разделите их все

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	1 секунда
Ограничение памяти	512Mb
Ввод	стандартный ввод или inpu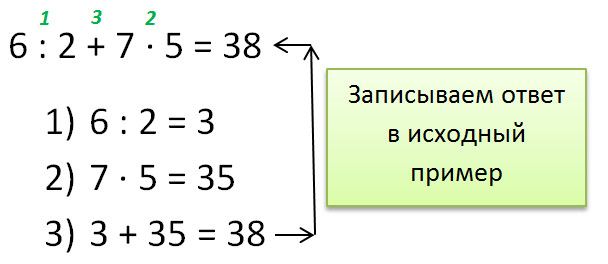t. txt
Вывод	стандартный вывод или output.txt

После работы Оля и Толя решили вместе сходить в тир. После прохождения вводного инструктажа и получения оружия они оказались на позициях для стрельбы, а напротив них находятся n мишеней. Все мишени можно считать фигурами, нанесёнными на бесконечную плоскость, при этом каждая мишень является кругом или прямоугольником, мишени могут накладываться и пересекаться произвольным образом.

Перед тем как начать стрельбу, Оля и Толя хотят убедиться, что они смогут однозначно идентифицировать результаты своих выстрелов.

Для этого они договорились провести прямую, которая поделит плоскость с мишенями на две части. Однако, чтобы никому не было обидно, они хотят провести прямую таким образом, чтобы каждая мишень была поделена ровно пополам, то есть для каждого круга и каждого прямоугольника должно быть верно, что прямая делит его на две фигуры равной площади. Когда Оля и Толя наконец закончили прорабатывать все условия разделения мишеней на две части, они начали сомневаться, что провести такую прямую вообще возможно, и просят вас ответить на этот вопрос.

Формат ввода

В первой строке входных данных записано целое число n(1≤n≤100 000) — количество мишеней. Каждая из последующих n строк содержит целое число ti(0≤ti≤1),  обозначающее тип мишени. Если ti=0,  то мишень является кругом и далее следуют три целых числа ri, xi и yi,  определяющие радиус и координаты центра круга соответственно (1≤ri≤1000, −10 000≤xi, yi≤10 000) Если же ti=1,  то мишень является прямоугольником, который затем определяют восемь целых чисел x1,i, y1,i, x2,i, y2,i, x3,i, y3,i, x4,i, y4,i — координаты всех четырёх вершин (−10 000≤xj,i, yj,i≤10 000),  перечисленных в порядке обхода по часовой стрелке или против часовой стрелки. Гарантируется, что данные четыре вершины образуют прямоугольник ненулевой площади.

Формат вывода

Если существует прямая, которая поделит каждый из имеющихся кругов и прямоугольников на две части одинаковой площади, выведите “Yes”. В противном случае выведите “No”.

Пример 1

Пример 2

Пример 3

Решение

Решение

Для решения этой задачи нам потребуется простой геометрический факт, что прямая делит окружность на две равные части, если и только если она проходит через её центр. Аналогично для прямоугольника, прямая делит его на две части равной площади, если и только если она проходит через точку пересечения диагоналей. В обоих случаях достаточность следует из симметрии относительно этой точки, а необходимость может быть установлена проведением через эту точку прямой, параллельной данной.

Теперь нам требуется лишь проверить, правда ли, что все центры заданных во входных данных фигур лежат на одной прямой. Для удобства будем рассматривать удвоенные координаты центров, тогда для получения центра прямоугольника достаточно сложить координаты двух противоположных вершин.

Если среди построенного множества точек не более двух различных, то ответ точно положительный. В противном случае рассмотрим любую пару различных точек и проверим, что все остальные точки лежат на определяемой этой парой прямой. Наиболее удобный способ проверить, что три точки a, b и c (a≠b) лежат на одной прямой ~— использовать векторное произведение векторов b-a и c-a.  Итоговая сложность решения: O(n). 

D. Задача для собеседования

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	3 секунды
Ограничение памяти	512Mb
Ввод	стандартный ввод или input.txt
Вывод	стандартный вывод или output.txt

Алексей регулярно проводит собеседования с кандидатами на позицию стажёра. И хотя он провёл уже не одну сотню собеседований, в последнее время этот процесс даётся ему нелегко — кандидаты стали без труда решать все годами протестированные и отработанные задачи Алексея!

Делать нечего, и в преддверии очередного собеседования Алексей придумал новую задачу. Имеется числовая последовательность, на первом шаге состоящая из двух чисел 1. На каждом следующем шаге между каждыми двумя соседними элементами добавляется новый элемент, равный их сумме. После первых нескольких шагов последовательность выглядит следующим образом:

• 1 1
• 1 2 1
• 1 3 2 3 1
• 1 4 3 5 2 5 3 4 1

На собеседовании Алексей хочет попросить кандидата написать программу, которая по заданному числу n будет определять, сколько раз число n будет встречаться в последовательности на n-м шаге? Алексей ещё не научился решать свою задачу, но слышал, что кандидат, с которым он сейчас будет проводить собеседование, добился высоких результатов в спортивном программировании, поэтому, скорее всего, легко справится с этим вопросом.

Формат ввода

Во входных данных записано единственное число n(1≤n≤1013). 

Формат вывода

Выведите одно целое число, равное количеству вхождений числа n в описанную в условиях последовательность на шаге n.

Пример 1

Пример 2

Решение

Решение

Докажем несколько лемм.

Лемма 1. Числа, оказавшиеся на каком-то шаге соседними, являются взаимно простыми.

Докажем по индукции. База очевидна (1 и 1 взаимно просты). Пусть доказано для n шагов. Все числа, выписанные на n+1 -м шаге, являются суммой двух соседних на n-м шаге чисел, то есть суммой двух взаимно простых чисел. Но НОД (a+b, b)=НОД (a, b)=1.  Лемма доказана.

Лемма 2. Никакая упорядоченная пара соседних чисел (a, b) не может возникнуть в последовательности более одного раза (ни на одном шаге, ни на разных).

Пусть это не так, тогда отметим номер k шага, на котором в первый раз возникло повторение (то есть повторилась пара, существующая на этом или на предыдущем шаге). Пусть пара (p, q) возникла на k-м и на i≤k -м шаге. Но тогда, если p>q , то p было построено как сумма соседей q и p-q (если pq , то q было построено как сумма p и q-p ), то есть на k-1 -м и на i-1-м шагах также существовало повторение, что противоречит нашему предположению. Лемма доказана.

Лемма 3. Любая упорядоченная пара взаимно простых чисел неизбежно будет соседней на некотором шаге.

Пусть мы имеем числа pq, стоящие рядом на некотором шаге и пусть p>q (без ограничения общности). Тогда p было получено как сумма p-q+q , то есть на предыдущем шаге рядом стояли p-q и q. Если p-qq , то два шага назад справа от q стояло число 2q-p , если p-q>q , то слева от p-q стояло число p-2q и так далее. Так как p и q взаимно просты, то на каком-то шаге этот процесс, по сути являющийся разновидностью алгоритма Евклида, приведёт к тому, что с одной стороны окажется 1, а с другой — некоторое натуральное число. Но пара (1, x) или (x, 1) для любого x будет соседней последовательности на x-м шаге. А так как действия восстанавливаются однозначно, то это значит, что и исходная пара (p, q) в какой-то момент встретится в качестве соседней.

Таким образом, каждая упорядоченная пара взаимно простых чисел ровно один раз встречается в качестве соседей в заданной последовательности. Поэтому задача сводится к подсчёту количества упорядоченных пар взаимно простых чисел, дающих в сумме n. Так как если p и n взаимно просты, то и p и (n-p взаимно просты, то количество таких пар можно поставить в однозначное соответствие количеству чисел, взаимно простых с n, или значению функции Эйлера от n.

Подсчёт же количества таких чисел является известной задачей и опирается на мультипликативность функции Эйлера: если n=p1k1·p2k2· … ·pnkn , то взаимно простых с n чисел будет (p1k1-p1k1-1)·(p2k2-p2k2-1)· … (pnkn-pnkn-1) Раскладываем n на простые множители за время O(n) .

E. Резервное копирование

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	5 секунд
Ограничение памяти	512Mb
Ввод	стандартный ввод или input.txt
Вывод	стандартный вывод или output.txt

Для обеспечения сохранности пользовательских данных Аркадий постоянно изобретает и тестирует новые схемы организации резервного копирования. В этот раз он пронумеровал все имеющиеся у него компьютеры с данными от 1 до n и для каждого компьютера с номером от 1 до n-1 назначил резервный компьютер pi При этом он строго соблюдал правило, что номер компьютера для резервного копирования всегда больше номера самого компьютера, то есть pi>i . По этой причине у компьютера с номером n компьютера для резервного копирования нет.

В ходе текущего эксперимента Аркадий выбрал некоторую конфигурацию значений pi и будет последовательно отключать компьютеры по одному каждую секунду. Эксперимент заканчивается, когда Аркадий отключает компьютер с номером n. Изначально на каждом компьютере находится некоторый блок данных размера 1. При отключении компьютера с номером x изначально расположенный на нём блок данных размера 1 передаётся на компьютер с номером px , при этом, если на компьютере номер x находились другие блоки данных (полученные от других компьютеров при их отключении), то они исчезают. Если же компьютер px уже отключен, то и блок данных с компьютера x никуда не передаётся и тоже исчезает.

Аркадий хочет, чтобы эксперимент продолжался как можно дольше, но он вынужден соблюдать ещё одно дополнительное ограничение: если на каком-либо компьютере собирается k блоков данных, то в целях сохранности железа этот компьютер необходимо тут же выключить в течение следующей

Формат ввода

В первой строке входных данных записано целое число t(1≤t≤20) — количество тестовых примеров.

Далее следует t описаний тестовых примеров, каждое описание начинается со строки содержащей два целых числа n и k(1≤n≤100 000, 2≤k≤10) — количество компьютеров, участвующих в эксперименте и предельное количество блоков данных на одном компьютере соответственно. Вторая строка содержит n-1 число p1, p2, … pn-1(i+1≤pi≤n) .

Формат вывода

Для каждого из t тестовых примеров выведите одно целое число — максимально возможную продолжительность эксперимента, то есть максимальный номер секунды, на которой Аркадий может отключить компьютер с номером n.

Пример

Решение

Решение

В задаче нам дано корневое дерево, на каждом шагу одна из вершин дерева удаляется. При этом, если корень вершины ещё не был удалён, его значение увеличивается на 1 (изначально все значения равны 1). Если значение какой-то вершины становится равным k, то именно она удаляется на следующем шаге. Требуется максимизировать номер шага на котором будет удалена корневая вершина.

Заметим, что если у корневой вершины менее k-1 потомка, то можно удалить все вершины дерева, перед тем как трогать вершину номер n. В противном случае все дети корня разделяются на три множества: те, чьи поддеревья будут удалены полностью, те, у которых корень останется нетронутым, и одно поддерево, после удаления корня которого мы удаляем и саму вершину n. Сделаем обход в глубину нашего дерева и будем поддерживать три значения динамического программирования:

a(v) равняется количеству вершин, которые можно удалить в данном поддереве, если можно удалить вершину v и не обязательно последней. Несложно заметить, что a(v) равняется размеру поддерева.

b(v) равняется количеству вершин, которые можно удалить в данном поддереве, если вершина v должна остаться нетронутой. Равняется a(v)-1 , если у вершины v менее k-1 сына. В противном случае нужно выбрать каких-то k-2 потомка, для которых будет использовано значение a(u) и для всех остальных использовать b(u) . В качестве таких k-2 потомков выгодно взять вершины с максимальной разницей a(u)-b(u) .

c(v) равняется количеству вершин, которые можно удалить в данном поддереве, если можно удалить вершину v, но она должна быть последней удалённой вершиной поддерева. Величина c(n) и будет являться ответом на задачу. Требуется выбрать какие-то k-2 потомка, для которых будет использовано значение a(u) , одного потомка, для которого мы используем c(u) и для всех остальных к ответу добавится b(u) . Переберём, для какого из потомков будет использовано c(u) (то есть кто будет последним удалённым потомком, после чего будет удалена и вершина v). Теперь среди оставшихся требуется взять сумму всех значений b(u) и k-2 максимальных a(u)-b(u) . Для этого достаточно иметь предподсчитанными сумму всех b(u) и список сыновей, упорядоченных по a(u)-b(u) . Если вершина x, для которой мы решили взять значение c(x) попадает в вершины с максимальной разностью, то использовать следующую k-1 вершину (такая обязательно есть, иначе мы просто уничтожаем всё поддерево).

Итоговая сложность решения O(n log n)

F. Процессоры-лжецы

Отправить решение задачи на платформе Яндекс.Контест

Условие задачи

Ограничение времени	3 секунды
Ограничение памяти	512Mb
Ввод	стандартный ввод или input. txt
Вывод	стандартный вывод или output.txt

Для испытания новых алгоритмов машинного обучения Евгений использует n·m процессоров, расположенных в единичных клетках платы размера n×m . Таким образом, процессоры занимают n рядов, по m процессоров в каждом. При этом два процессора считаются соседними, если они расположены в соседних клетках одного ряда, или на одной и той же позиции в соседних рядах.

В результате неудачного эксперимента с новым алгоритмом некоторые из процессоров научились врать Евгению. Однако, благодаря тому, что была использована только базовая версия алгоритма, если какой-то процессор начинает врать, то он будет делать это всегда, поэтому результаты его работы всё ещё несложно интерпретировать.

Теперь перед Евгением стоит задача определить, какие из процессоров постоянно выдают неверную информацию, но сначала он хочет оценить масштаб проблемы. Для этого он послал каждому из процессоров вопрос: верно ли, что среди соседних ему процессоров есть и исправные процессоры, и процессоры-лжецы? На удивление Евгения, все процессоры ответили на такой запрос утвердительно.

Теперь он хочет узнать, какое минимальное количество процессоров-лжецов может находится на плате?

Формат ввода

В единственной строке входных данных записаны два целых числа n и m(1≤n≤7, 1≤m≤100) — количество рядов в плате и количество процессоров в одном ряду соответственно.

Формат вывода

Выведите одно целое число — минимальное возможное количество процессоров-лжецов на плате, при котором каждый процессор мог сообщить Евгению, что среди его соседей есть и исправные процессоры и процессоры-лжецы.

Пример 1

Пример 2

Примечания

Одним из возможных решений в первом тесте является (испорченные процессоры отмечены как 1):
100
001

Решение

Решение

Воспользуемся тем фактом, что n≤7 и будем вычислять динамику по профилю. Пусть мы заполнили первых i столбцов таблицы, причём на первых i-1 столбце все процессоры вернули ожидаемый результат. Тогда, для того чтобы продолжить заполнять таблицу нам важно лишь знать, какие из процессоров врут среди последних двух столбцов.

Посчитаем dp(i, m1, m2) , где i меняется от 1 до m, а m1 и m2~— битовые маски от 0 до 2n-1 . Значением динамики будет минимальное количество процессоров-лжецов, которое потребуется, чтобы заполнить первые i столбцов так, чтобы среди первых i-1 столбца все процессоры вернули ожидаемый результат, а состояние процессоров в последнем и предпоследнем столбце были равны m1 и m2 соответственно. Всего различных состояний O(m·22n) . Наконец, для вычисления перехода будет перебирать новую маску m3 и пробовать перейти в состояние dp(i+1, m2, m3) .

Работая с масками с помощью предподсчёта и битовых операций получим результат O(m·23n) . Работу программы можно значительно ускорить, если предпосчитать все корректные переходы их каждой пары масок (m1, m2) (то есть запомнить все подходящие к ним маски m3 ).

Упражнение: придумайте, как получить решение за время O(nm22n) .

Практические задачи на арифметические последовательности — ChiliMath

Направление: Внимательно прочитайте каждый вопрос по арифметическим последовательностям, а затем ответьте на дополнительные вопросы.

---

1) Укажите, является ли последовательность арифметической или нет. Объясните, почему да или почему нет.

Последовательность A : — 1,{\rm{ }} — 3,{\rm{ }} — 5,{\rm{ }} — 7,{\rm{ }} \ldots

Последовательность B : — 3,{\rm{ }}0,{\rm{ }}4,{\rm{ }}7,{\rm{ }} \ldots

Ответ

Решение:

Последовательность A является арифметической последовательностью, поскольку каждая пара последовательных элементов имеет общую разность, равную -2, то есть d=-2.

С другой стороны, последовательность B , а не  – арифметическая последовательность. Между парами последовательных терминов в последовательности нет общего различия.

---

2) Найдите следующий член в приведенной ниже последовательности.

Ответ

Решение:

Последовательность имеет общую разность 5. Чтобы перейти к следующему члену, прибавьте предыдущий член на 5. Например, от 4 до 9, вы добавляете 5 к 4, чтобы получить 9. То есть 4 + 5 = 9.

---

3) Найдите следующие два члена в приведенной ниже последовательности.

Ответ

Решение:

Общая разница между соседними терминами равна \large- {1 \over 3} . Используйте это значение, чтобы получить два следующих друг за другом термина. Убедитесь, что вы правильно складываете или вычитаете дроби с разными знаменателями. Если вам нужен дополнительный урок по этому вопросу, посмотрите его.

---

4) Если последовательность имеет первый член {a_1} = 12 и общую разность d=-7. Напишите формулу, описывающую эту последовательность. Используйте формулу арифметической прогрессии.

Ответ

Решение:

Так как мы знаем значения первого члена, {a_1} = 12, и общую разность, d = -7, единственное, что нам нужно сделать, это подставить эти значения в формулу.

Или вы можете еще больше упростить свой ответ, избавившись от круглых скобок и комбинируя одинаковые термины. Оба решения должны быть приемлемы. Если вы не уверены, спросите своего учителя.

---

5) Запишите формулу, описывающую последовательность 6,{\rm{ }}14,{\rm{ }}22,{\rm{ }}30,{\rm{ }}…

Ответ

Решение:

Первый член равен 6, что означает {a_1} = 6. Общая разность d=8.

Подставьте эти значения, чтобы получить требуемую формулу:

или в более упрощенной форме;

---

6) Найти 45 ^-й член арифметической прогрессии — \,9,{\rm{ }} — 2,{\rm{ }}5,{\rm{ }}12,{\ rm{ }}… 

Ответ

Решение:

Найдите правило, определяющее последовательность, используя формулу арифметической последовательности. Первый член {a_1} = -9а общая разница d=7.

Подставляем эти значения в формулу, получаем

Теперь мы можем найти 45 ^-й член,

---

7) Напишите формулу последовательности с двумя заданными членами, {a_5} = -32, и {a_{18}} = 85.

Ответ

Решение:

Используйте информацию о каждом члене, чтобы построить уравнение с двумя неизвестными, используя формулу арифметической последовательности.

• Для {a_5} = -32

• Для {a_{18}} = 85

Решите систему уравнений, используя метод исключения. Умножьте уравнение № 1 на −1 и добавьте его к уравнению № 2, чтобы исключить {a_1}.

После нахождения значения общей разности теперь легко найти значение первого слагаемого. Обратно подставьте d=9 в любое из двух уравнений, чтобы найти {a_1}.

Мы будем использовать уравнение № 1 для этого,

Поскольку {a_1} = -68 и d = 9, формула, которую мы ищем,

---

Вас также могут заинтересовать:

Определение и основные примеры арифметической последовательности

Формула арифметической последовательности

Формула арифметической последовательности

последовательностей — словесные задачи | Шмуп

Предыдущий Следующий

Последовательности, особенно арифметические и геометрические, хороши для текстовых задач.

Задачи с последовательностями бывают двух основных видов. Если бы эти вкусы были мороженым, они были бы ванилью и каменистой дорогой. Возможно, нам придется найти

• значение определенного термина a _n . Это стандартная ванильная проблема.
    
• значение n , при котором термы делают что-то конкретное. Это более сложная проблема с каменистой дорогой.

В общем, хорошей стратегией является выписывание первых нескольких членов рассматриваемой последовательности, чтобы мы могли видеть структуру членов. Может быть, мы сможем сделать это с рожком мороженого в руке.

Пример задачи

Старая история гласит, что крестьянин получил награду от короля и попросил риса: одно зерно положить на первую клетку шахматной доски, две зерна на вторую клетку, четыре на третью клетку , и так далее. В каждом квадрате должно было быть вдвое больше зерен, чем в предыдущем квадрате.

1. Сколько зерен риса будет на 32-й клетке?
     
2. В каком квадрате ровно 512 зерен риса?

Ответ.

Если мы посмотрим на первые несколько членов, то увидим закономерность:

Квадрат n ^th содержит 2 ^{n – 1} зерен риса. У нас есть

a _n = 2 ^{n – 1}

, где n – квадрат, а a _n

– сколько квадратов риса на 9 зернах. Теперь мы готовы ответить на вопросы.

1. На вопрос «Сколько зерен риса будет на 32-й клетке?» просит нас найти значение 32-го члена. Нет проблем:

   a ₃₂ = 2 ³¹ = 2 147 483 648.
    

2. На вопрос «Какой квадрат будет содержать ровно 512 зерен риса?» спрашивает нас, какое значение N делает A _N = 512 2 ^{n – 1}
   бревно ₂ 512 = n – 1
   9 = n – 1
   n = 10

   Это означает, что 10-й квадрат будет содержать ровно 512 зерен риса.

Будьте осторожны: Один из типов задач на последовательность требует от нас найти значение a _n .