3. Построение графиков функций
В основном вы строили графики «по точкам», т. е. для заданной функции находили контрольные точки,,,и т. д., отмечали их на координатной плоскости и, полагаясь на интуицию, соединяли найденные точки плавной кривой. Как выбирали эти контрольные точки? Иногда обдуманно, например, строили вершину параболыу = ах2 + bх + с или специально искали точки пересечения графика функцииу=f(x)с осями координат. Но чаще выбор контрольных точек был случайным, «по наитию».
Графики любых функций строят по точкам.
Но в тех случаях, когда вид графика
заранее неизвестен, эти точки надо
выбирать со смыслом — уметь выделять
особо важные точки графика, которые
определяют его структуру. Об этом мы
уже говорили выше, когда строили
графики функций у = 2х3 +Зх2— 1 иу =Зx4— 16х3+ 24x2— 11.
— стационарные и критические точки;
— точки экстремума;
— точки пересечения графика с осями координат;
— точки разрыва функции.
В тех случаях, когда речь идет о построении графика незнакомой функции, когда заранее невозможно представить вид графика, полезно применять определенную схему исследования свойств функции, которая помогает составить представление о ее графике. Когда такое представление составится, можно приступить к построению графика по точкам.
В курсе математического анализа разработана универсальная схема исследования свойств функции и построения графика функции, позволяющая строить весьма сложные графики. Для наших нужд будут достаточны упрощенные варианты указанной схемы.
1)Если функцияу =f(x)непрерывна на всей числовой прямой,
то достаточно найти стационарные и
критические точки, точки экстремума,
промежутки монотонности, точки
пересечения графика с осями координат
и при необходимости выбрать еще несколько
контрольных точек.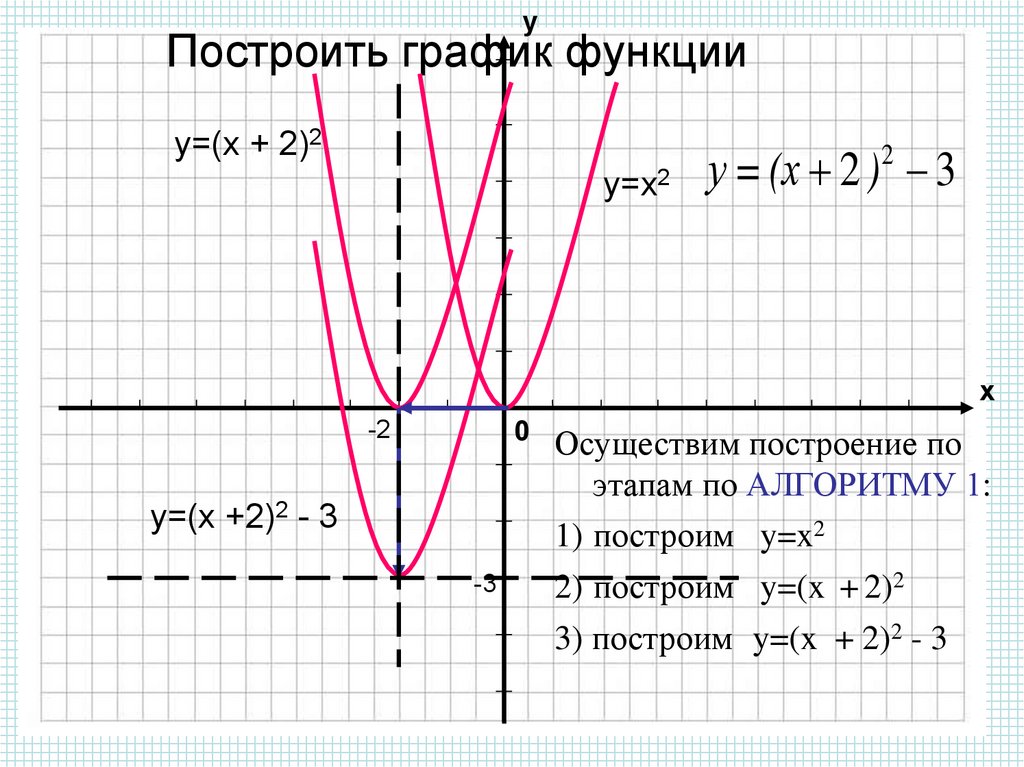
2)Если функцияу =f(x)определена не на всей числовой прямой, то начинать следует с отыскания области определения функции (если область не задана) и с указания ее точек разрыва.
3)Полезно исследовать функцию на четность, поскольку графики четной или нечетной функции обладают симметрией (соответственно относительно осиуили относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при , азатем достроить симметричную ветвь.
4)Если то, как известно, прямая
у = bявляетсягоризонтальной асимптотойграфика функцииу = f(х).Асимптоту следует строить на координатной плоскости, она дает своеобразный ориентир для графика.
5)Горизонтальная асимптота
характеризуется условием: если,
тоу.При условии: еслих—>а,тоу,
— прямаях=аявляетсявертикальной
асимптотойграфика функцииу = f(х).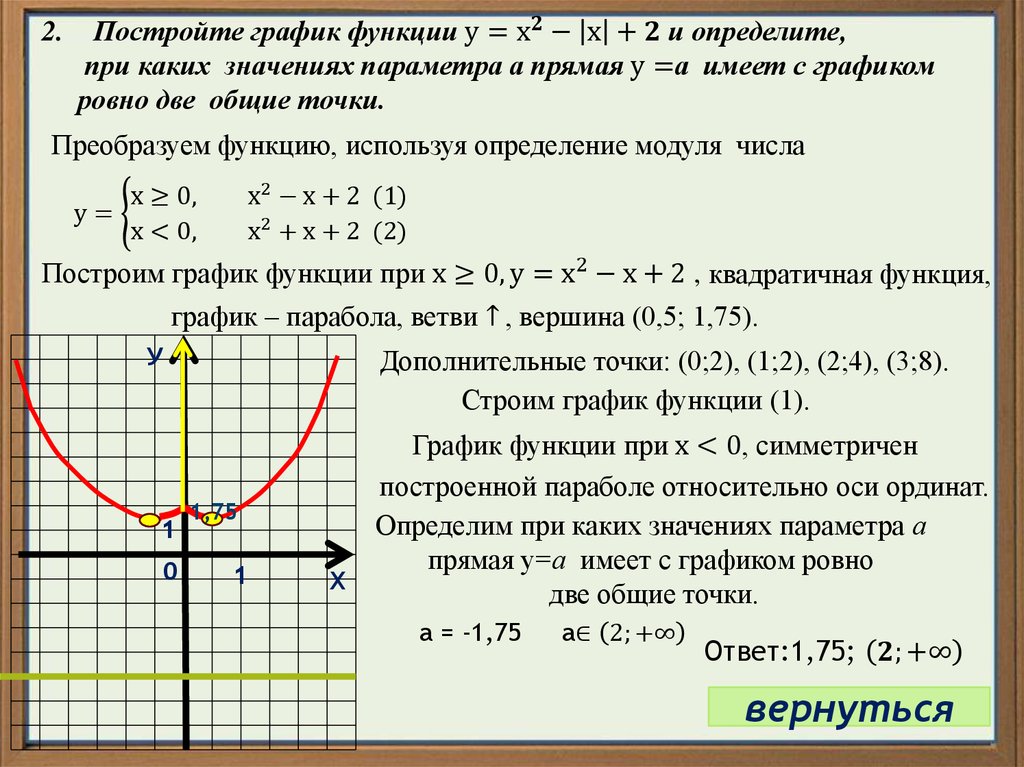
Самый распространенный признак существования вертикальной асимптоты заключается в следующем:
если приx=а знаменатель обращается в нуль, а числитель отличен от нуля, то х=а — вертикальная асимптота графика функцииу = f(х).
В следующих примерах учтем все вышеуказанные обстоятельства и построим графики функций, придерживаясь определенной схемы.
Применение производной для отыскания наибольших и наименьших значении величин
075. Способы построения графиков функций
Анализ графиков элементарных функций показывает, что если известен график функции , то при помощи геометрических преобразований можно построить график более сложной функции.
Рассмотрим некоторые способы построения графиков при помощи геометрических преобразований.
1. График функции получается из графика увеличением всех ординат этого графика в раз, если и уменьшение ординат графика в раз, если (рис. 5.47).
5.47).
Пример 3. Постройте график функции .
Решение. Сначала построим график функции .
Увеличим все ординаты этого графика в 2 раза и получим график функции (рис. 5.48).
Ответ. График функции показан на рис. 5.48 сплошной линией.
2. График функции получается из графика сжатием графика вдоль оси , если и растяжением графика вдоль оси , если .
Пример 4. Постройте графики функций и .
Решение. Составим таблицу некоторых значений функций и (табл. 5.3).
Таблица 5.3 – Значения функций , ,
Для функции основным периодом будет . Тогда основной период функции равен , а основной период функции равен .
По данным таблицы 5.3 построим графики всех трех функций (рис. 5.49).
Вывод. Из графика функции сжатием его вдоль оси получается график функции , а график функции получается растяжением графика функции вдоль оси
Ответ.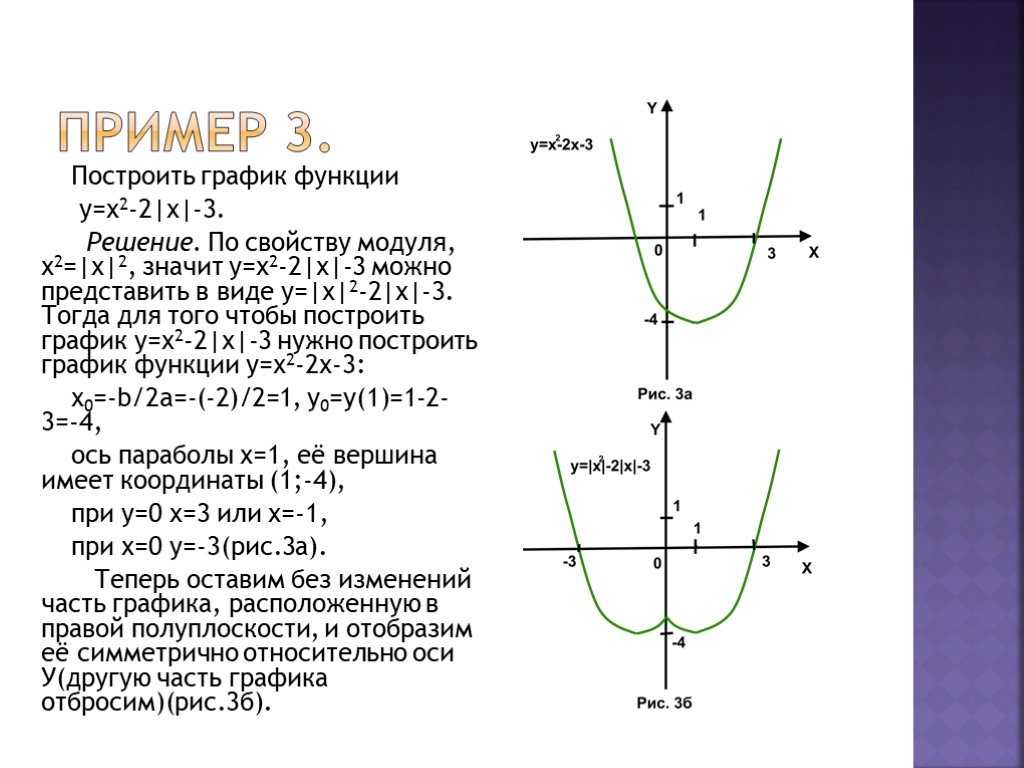 График функции показан на рис. 5.49 точечной линией. График функции показан на рис. 5.49 пунктирной линией.
График функции показан на рис. 5.49 точечной линией. График функции показан на рис. 5.49 пунктирной линией.
3. График функции Получается сдвигом графика вдоль оси на величину влево (в отрицательном направлении оси ), если и вправо (в положительном направлении оси ), если .
Пример 5. Постройте графики функций и .
Решение. Составим таблицу некоторых значений функций и (табл. 5.4).
Таблица 5.4 – Значения функций , ,
–4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 | 4 | |
36 | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | |
16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | |
4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
Построим графики этих функций по данным таблицы 5.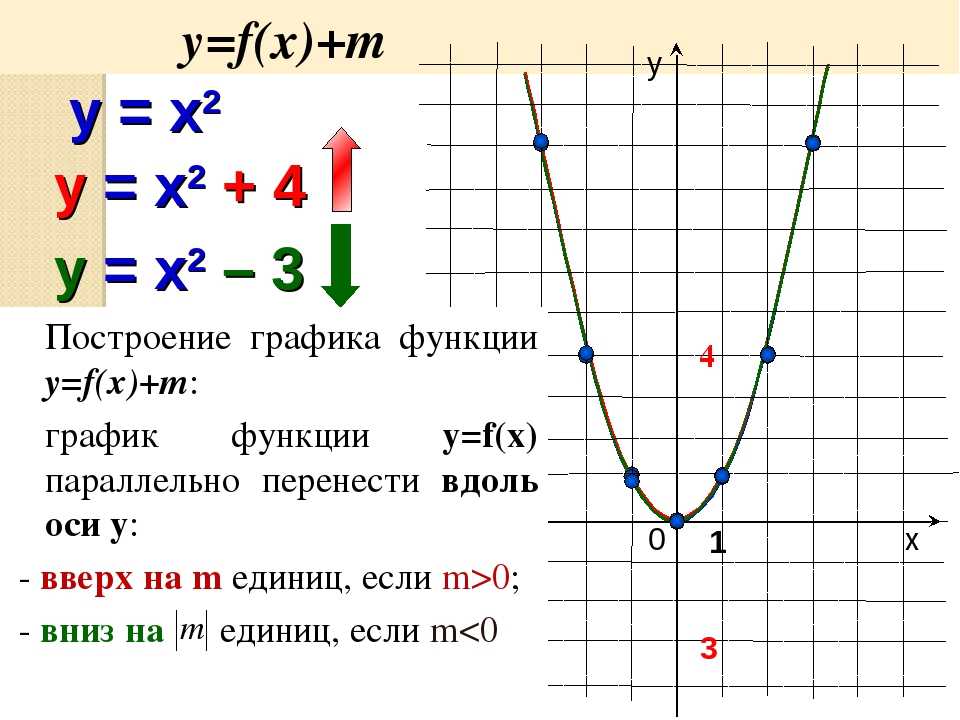 4 (рис. 5.50).
4 (рис. 5.50).
Вывод. График функции получается сдвигом графика на 2 единицы вдоль оси влево (в отрицательном направлении оси ), а график функции получается сдвигом графика на 2 единицы вдоль оси вправо (в положительном направлении оси ).
Ответ. График функции показан на рис. 5.50 точечной линией. График функции показан на рис. 5.50 пунктирной линией.
Пример 6. Постройте график функции .
Решение. Сначала построим график функции . Сдвинем его на 3 единицы влево (по правилу построения графика функции ). При этом вертикальная асимптота гиперболы тоже сдвинется на 3 единицы влево. Следовательно, график функции имеет две асимптоты: и . Найдем координаты точки пересечения графика с осью : ; .
Ответ. График функции показан на рис. 5.51 сплошной линией.
4. График функции Получается сдвигом графика на величину в положительном направлении оси (вверх), если и в отрицательном направлении оси (вниз), если .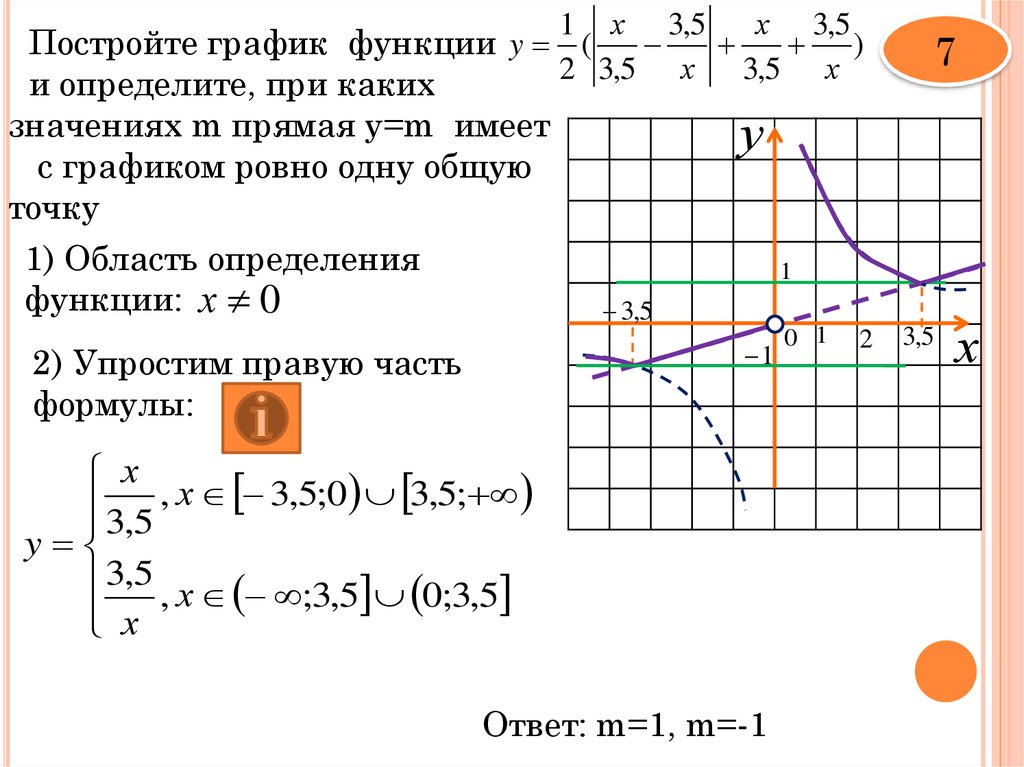
Пример 7. Постройте графики функций и .
Решение. Составим таблицу некоторых значений функций , и (табл. 5.5).
Таблица 5.5 – Значения функций , ,
–3 | –2 | –1 | 0 | 1 | 2 | 3 | |
7 | 2 | -1 | -2 | -1 | 2 | 7 | |
4 | 1 | 0 | 1 | 4 | 9 | ||
11 | 6 | 3 | 2 | 3 | 6 | 11 |
Построим графики этих функций по данным таблицы 5.5 (рис. 5.52).
Вывод.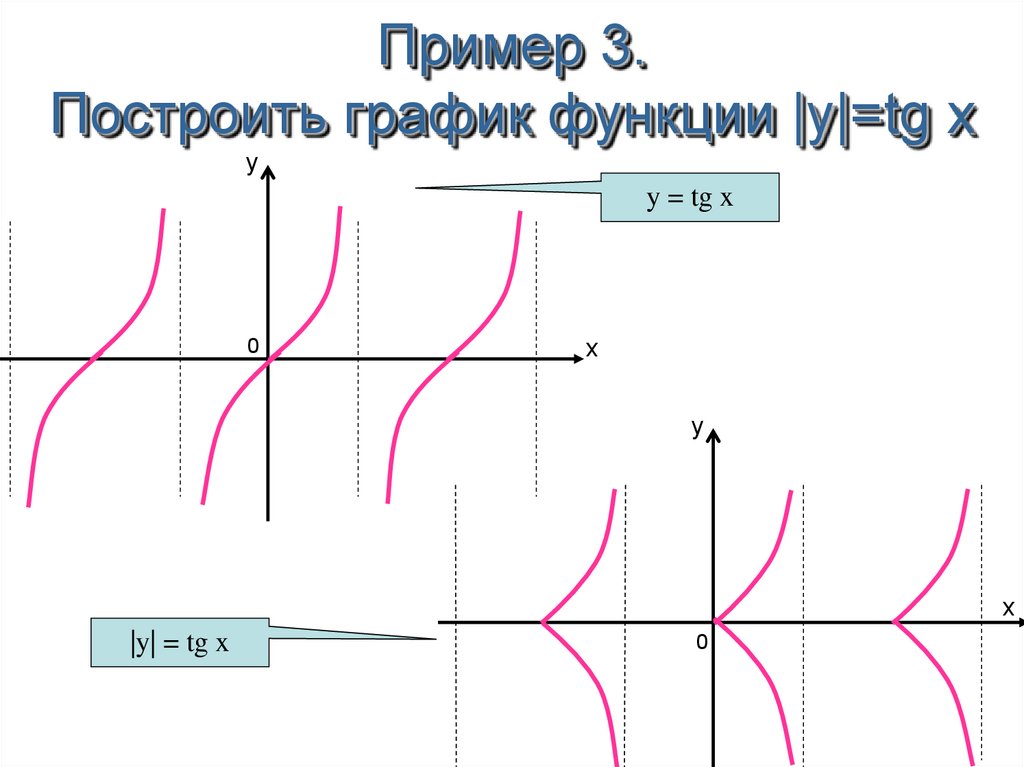 График функции получается сдвигом графика на 2 единицы вниз вдоль оси а график функции получается сдвигом графика на 2 единицы вверх вдоль оси .
График функции получается сдвигом графика на 2 единицы вниз вдоль оси а график функции получается сдвигом графика на 2 единицы вверх вдоль оси .
Ответ. График функции показан на рис. 5.52 пунктирной линией. График функции показан на рис. 5.52 точечной линией.
Пример 8. Постройте график функции .
Решение. Сначала построим график функции . Сдвинем его на 2 единицы вниз (по правилу построения графика функции ). При этом горизонтальная асимптота гиперболы тоже сдвинется на 2 единицы вниз. Следовательно, график функции имеет две асимптоты: и . График функции пересекает ось .
Ответ. График функции показан на рис. 5.53 сплошной линией.
5. График функции Получается симметричным отображением графика функции относительно оси .
Пример 9. Постройте графики функций и .
Решение. Составим таблицу некоторых значений этих функций (табл.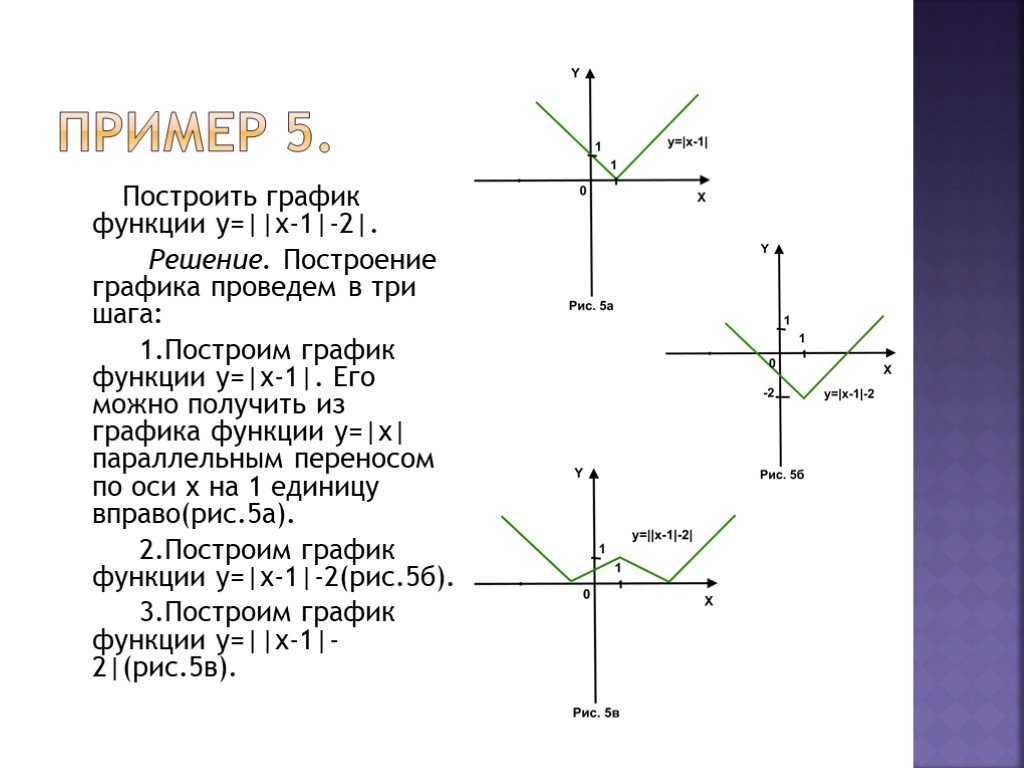 5.6).
5.6).
Таблица 5.6 – Значения функций та
1 | 2 | 3 | 4 | 5 | |
6 | 3 | 2 | 3 | 6 | |
-6 | -3 | -2 | -3 | -6 |
Построим графики этих функций по данным таблицы 5.6 (рис. 5.54).
Вывод. График функции получается симметричным отображение графика относительно оси .
Ответ. График функции показан на рис. 5.54 сплошной линией. График функции показан на рис. 5.54 пунктирной линией.
Пример 10. Постройте график функции .
Решение. Построим одну полуволну графика функции . Произведем ее сжатие вдоль оси с коэффициентом 3 и растяжение вдоль оси с коэффициентом 2, а затем симметричное преобразование относительно оси Получим график функции (рис. 5.55 а).
5.55 а).
На рисунке 5.55 а показана одна полуволна графика, а на рисунке 5.55 б – весь график.
Ответ. График функции показан на рис. 5.55 (б) сплошной линией.
6. График функции получается симметричным отображением графика функции относительно оси .
Пример 11. Постройте графики функций и .
Решение. Составим таблицу некоторых значений этих функций (табл. 5.7).
Таблица 5.7 – Значения функций та
–3 | –2 | –1 | 0 | 1 | 2 | 3 | |
1 | 2 | 4 | 9 | ||||
9 | 4 | 2 | 1 |
Построим графики этих функций по данным табл.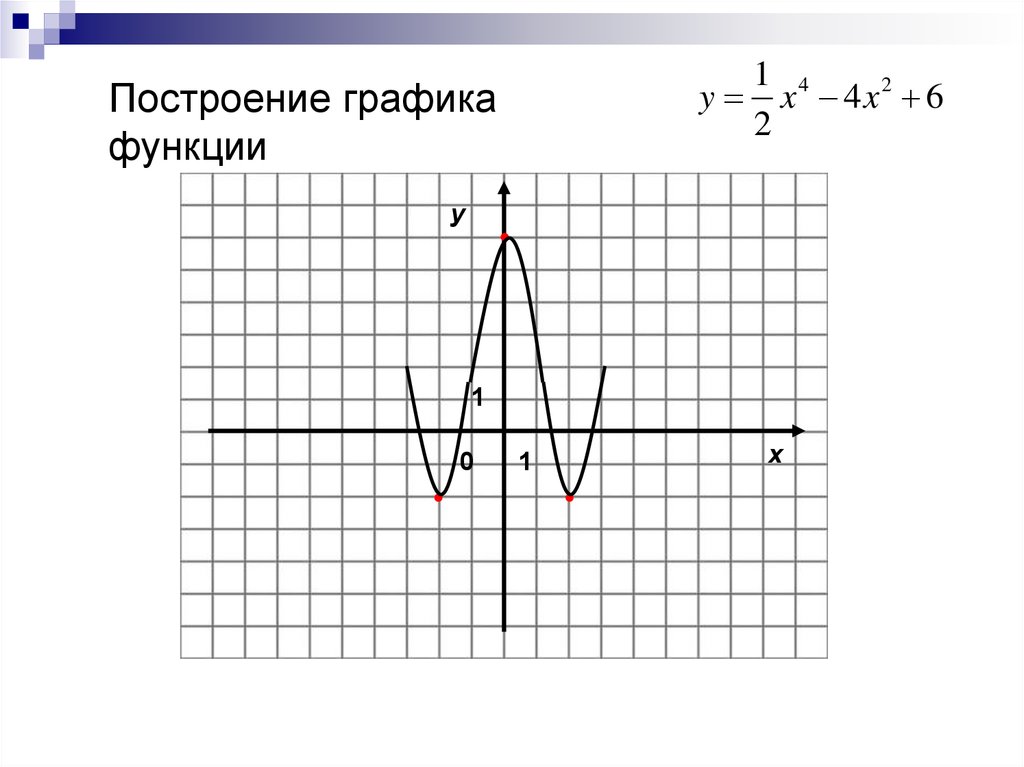 5.7 (рис. 5.56).
5.7 (рис. 5.56).
Вывод. График функции получается симметричным отображение графика относительно оси .
Ответ. График функции показан на рис. 5.56 сплошной линией. График функции показан на рис. 5.56 пунктирной линией.
Пример 12. Постройте график функции .
Решение. Строим график функции и симметрично отображаем его относительно оси .
Ответ. График функции показан на рис. 5.57 сплошной линией.
7. График функции получается из графика функции симметричным отображением относительно оси части графика, которая лежит под осью (). Часть графика над осью () остается без изменений.
Пример 13. Постройте график функции .
Решение. Составим таблицу некоторых значений функции (табл. 5.8).
Таблица 5.8 – Значения функции
0 | 1 | 2 | 3 | 4 | |
3 | 0 | -1 | 0 | 3 |
Из решения уравнения находим, что нулями функции будут два значения: и .
Найдем координаты вершины параболы:
; .
По полученным результатам построим график функции (рис. 5.58).
Интервалами положительности для этой функции будут интервалы . Интервалом отрицательности будет .
Из определения модуля функции запишем:
На интервале значения функций и совпадают и по величине и по знаку, а на интервале значения функций совпадают по величине, но противоположны по знаку.
Вывод. График функции получается из графика функции симметричным отображением относительно оси той части графика, которая лежит ниже оси .
Ответ. График функции показан на рис. 5.58 сплошной линией.
8. График функции получается из графика функции так: график функции сохраняется только при , и отображается симметрично относительно оси (рис. 5.59).
Пример 14. Постройте график функции .
Решение. Учитывая определение модуля, функцию можно записать так:
Составим таблицу значений функции по этим формулам на соответствующих интервалах (табл.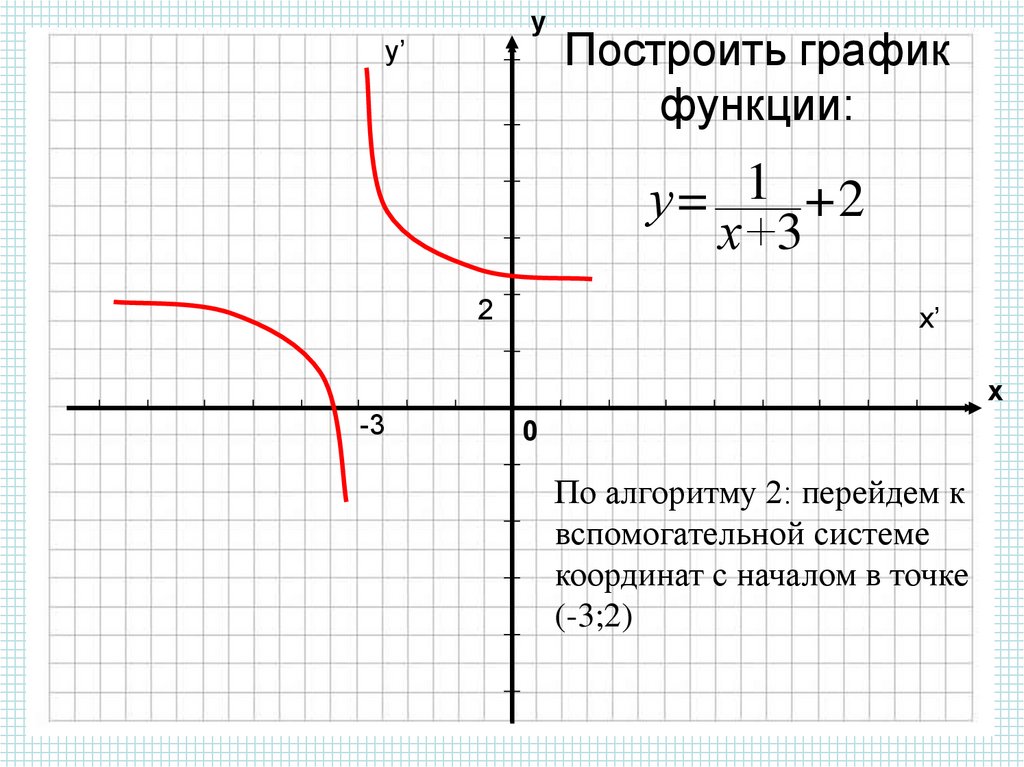 5.9).
5.9).
Таблица 5.9 – Значения функции
-3 | -2 | -1 | 0 | 1 | 2 | 3 | |
4 | 1 | 0 | 1 | 0 | 1 | 4 |
По данным этой таблицы построим график функции (рис. 5.60).
Вывод. Как видно из рис. 5.60 график функции получается из графика функции симметричным отображение части графика при относительно оси .
Ответ. График функции показан на рис. 5.60 сплошной линией.
Пример 15. Постройте график функции .
Решение. Заданная функция содержит как модуль аргумента, так и модуль функции.
Перепишем формулу заданной функции в виде: .
Построим параболу квадратичной функции без модуля аргумента. Это будет график функции , смещенный на 1 вправо вдоль оси и на 4 вниз вдоль оси . Осью симметрии графика будет прямая . Координатами вершины параболы будут и (рис. 5.61).
Это будет график функции , смещенный на 1 вправо вдоль оси и на 4 вниз вдоль оси . Осью симметрии графика будет прямая . Координатами вершины параболы будут и (рис. 5.61).
График функции будет получен из графика симметричным отображением части графика при относительно оси (рис. 5.62).
График модуля функции получается симметричным отображением относительно оси части графика функции , которая находится под осью (рис. 5.63).
Ответ. График функции показан на рис. 5.63 сплошной линией.
| < Предыдущая | Следующая > |
|---|
GraphPad Prism 9 Руководство по подгонке кривой
Prism предлагает анализ функции графика, но фактически не анализирует никаких данных. Вместо этого он генерирует кривые из уравнения, которое вы выбираете, и параметров, которые вы вводите.
Как: Построить график функции
1. Начните с любой таблицы данных или графика, нажмите «Анализ», откройте папку «Создать кривую» и выберите «Построить график функции».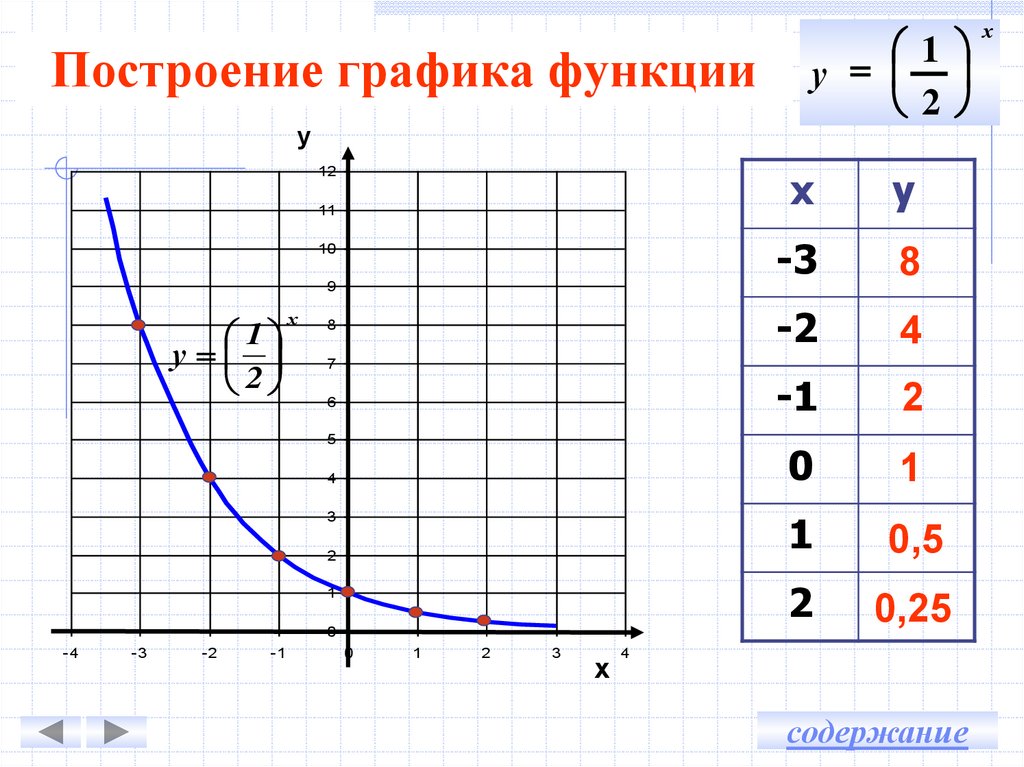
2. На первой вкладке (Функция) выберите уравнение, начальное и конечное значения X и количество кривых, которые вы хотите построить.
3. На второй вкладке (Опции) выберите, хотите ли вы построить первую производную, вторую производную или интеграл функции. «Кривая» на самом деле представляет собой набор координат X и Y, которые определяют серию точек, которые соединяются, образуя кривую. Вы можете выбрать количество сегментов линии, которые будут определять кривую. Нет особых причин менять значение по умолчанию (150), если только вы не хотите отображать только часть кривой на некоторых графиках, и в этом случае вам следует увеличить это значение.
4. На третьей вкладке (Значения параметров) введите значения параметров (или щелкните значок рыболовного крючка, чтобы просмотреть анализ крючка или информацию о константах).
Советы по построению графика функции
Построение семейства кривых
Если вы решите построить более одной кривой (выбор на первой вкладке), остальная часть диалогового окна работает немного иначе.
Вы хотите, чтобы один параметр в уравнении менялся от кривой к кривой. Не определяйте это в уравнении. Вместо этого определите значения на третьей вкладке.
Вы также захотите пометить столбцы вычисляемой таблицы. Есть два способа сделать это. В нижней части второй вкладки (Параметры) укажите, хотите ли вы маркировать каждую кривую вручную (введите метки в верхней части третьей вкладки) или хотите, чтобы каждый столбец был маркирован с использованием значения одного из параметров. Последнее обычно имеет больше смысла и проще.
Если вам нужно сделать что-то более сложное, помните, что вы можете написать уравнение, чтобы некоторые строки применялись только к определенным наборам данных. Поместите перед строкой, которая относится только к столбцу A и т. д.
В верхней части третьей вкладки перечислены все кривые, которые вы создадите. Выберите одну или несколько из этих кривых (или нажмите «выбрать все»), а затем введите значения параметров ниже. Часто вы захотите сначала нажать «выбрать все» и ввести большинство параметров. Затем щелкните по одной кривой за раз и введите значение параметра, которое варьируется между кривыми.
Затем щелкните по одной кривой за раз и введите значение параметра, которое варьируется между кривыми.
Построение каждой кривой на отдельном графике
По умолчанию Prism создает график, содержащий все кривые на одном графике. Если вы хотите, чтобы каждая кривая была на своем графике, перейдите в таблицу результатов, найдите раскрывающееся меню «Создать» на панели инструментов (выглядит как зеленый знак «плюс») и выберите «Новый график существующих данных…». В появившемся диалоговом окне выберите создание одного графика для каждого набора данных (в данном контексте набор данных — это кривая).
Если вы планируете увеличить и построить только часть кривой
Кривая определяется по умолчанию как 150 сегментов линии. Это создает гладкую кривую. Но если вы затем измените диапазон значений X, показанных на графике, будет видна только часть этих сегментов линии, и кривая может показаться грубой. Чтобы устранить эту проблему, вернитесь в диалоговое окно параметров на вкладку «Параметры» и увеличьте количество сегментов линии до гораздо большего значения.
Объединение двух кривых на одном графике
График ниже объединяет две построенные функции на одном графике. В первый раз, когда я построил график функции, я выбрал распределение Гаусса с X в диапазоне от -3 до 3. Я установил среднее значение на 0,0, стандартное отклонение на 1,0 и амплитуду на 100,0 (произвольно, так как я скрыл эту ось) . Затем я повторил этот анализ, но на этот раз установил диапазон X от 1,3 до 3,0. Я поместил обе кривые на один график (Изменить.. Добавить наборы данных — помните, что кривая, созданная в результате этого анализа, является «набором данных» для Prism). Для более короткой кривой я решил создать заливку области.
Часть 4
Часть 4МАТКАД ТУТОР
Часть 4: Графики Функции
Чтобы помочь в визуализации функции, вы можете использовать MathCad для создания графика.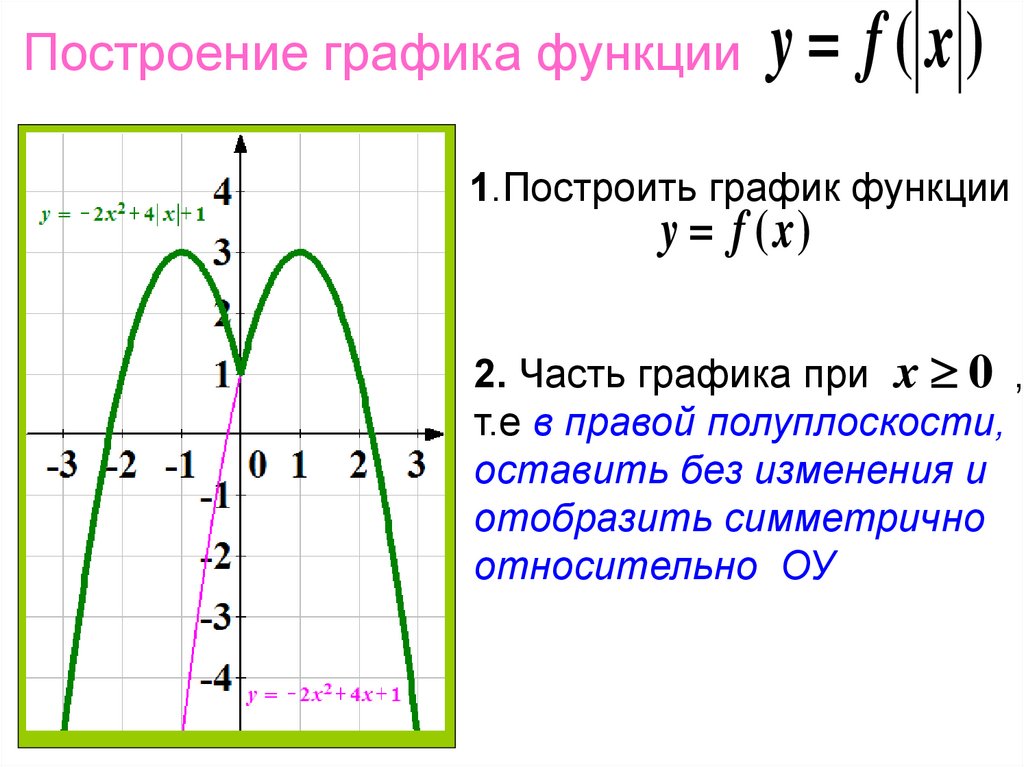 Первым шагом в создании такого вспомогательного средства является определение функции.
Первым шагом в создании такого вспомогательного средства является определение функции.- Например, давайте определим функцию f , определяемую как f(x) = 2x + 3 . Введите
- f(x) : 2x + 3
- f(x) := 2x + 3
Теперь создадим график f .
- Нажмите на графическую палитру на ваша панель инструментов. Затем нажмите X-Y Plot .
- : В окно вставляется пустой график. Перетащите график на желаемое местоположение, которое должно быть где-то ниже области, где вы определили ваша функция.
- Вставьте x в отведенное место под горизонтальной осью.
- Вставить f(x) в пустое место расположен слева от вертикальной оси.
- Чтобы настроить пределы графика, щелкните где-нибудь над графиком. Затем введите:
- x:0,1;10
 Синтаксис: [начальное значение для x , изменение x , конечное значение для x ]. Это будет отображаться как
Синтаксис: [начальное значение для x , изменение x , конечное значение для x ]. Это будет отображаться как- x:=0,1…10
- MathCad также позволяет отображать другие функции на том же графике. теперь посмотрите оба графика в окне графиков.
- Вы также можете изменить цвета графиков. Инструкции, данные здесь, изменят цвет графика ф .
- Дважды щелкните поле графика; окно появится несколько вкладок.
- Выберите СЛЕДЫ . Ты увидишь список из нескольких следов.
- Нажмите на трассировку 1 , которая быть f(x) .
- Нажмите на стрелку рядом с цветами в нижней части окна и выберите один из них.
- Теперь нажмите OK.
модули на math.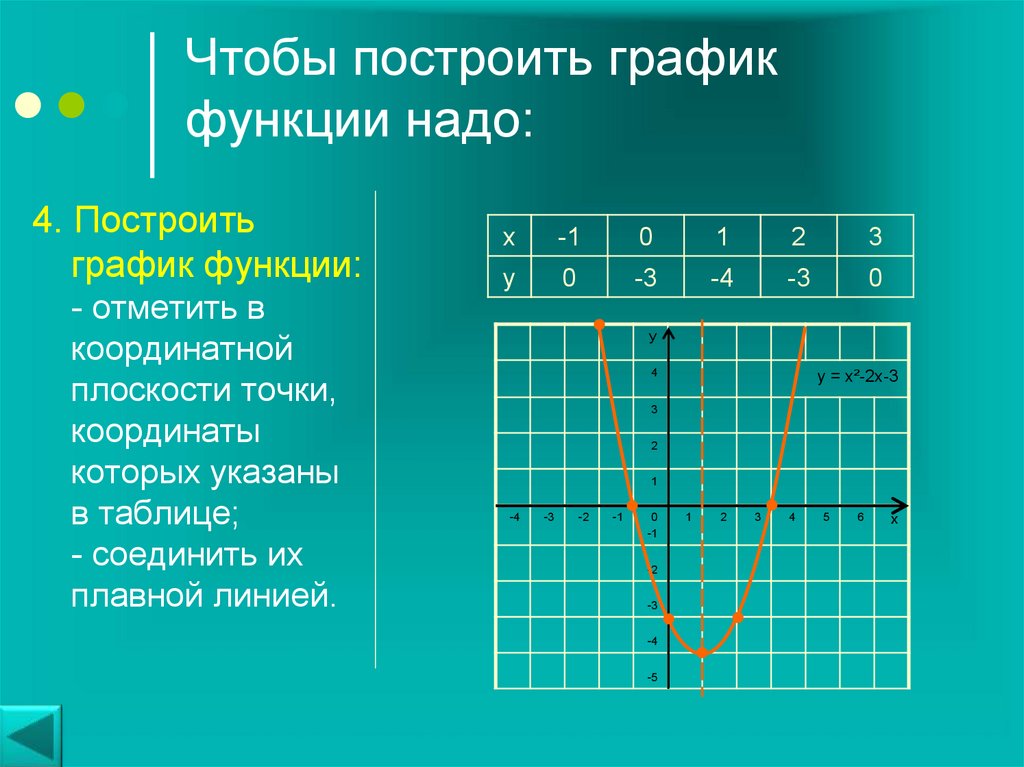 |

 Синтаксис: [начальное значение для x , изменение x , конечное значение для x ]. Это будет отображаться как
Синтаксис: [начальное значение для x , изменение x , конечное значение для x ]. Это будет отображаться как